Гидромеханика буровых жидкостей. Основные понятия и определения

1. Гидромеханика буровых жидкостей

Основные понятия и
определения.
ИПК. Кафедра Бурения
УГТУ.

2.

Жидкость в гидравлике рассматривается как совокупность
материальных точек (частиц) в ограниченном объеме. Принимается,
что материальные частицы жидкости заполняют пространство без
пустот и разрывов. В этом заключается суть тезиса о непрерывности и
сплошности жидкой среды. Сказанное полностью относится к буровым
промывочным жидкостям. Из сказанного следует, что реальная
жидкость заменяется на ее модель, причем модели могут изменяться
(усложняться или упрощаться), в зависимости от целей исследований.
Буровой раствор является, как правило, суспензией: твердые
частицы (глина, выбуренная порода, утяжелитель) взвешены в
жидкости и не осаждаются в ней под действием сил тяжести. Такие
суспензии называют седиментационно устойчивыми, несмотря на то,
что плотность твердых частиц, равномерно распределенных в жидкой
фазе, кратно превышает плотность жидкости. Устойчивость таких сред
и дает возможность заменить реальную жидкость с явно выраженным
дискретно меняющимся распределением массы, на модельную
жидкость, имеющей плотность, равную средней плотности бурового
раствора, подчиняющеюся тезису о непрерывности (сплошности)
среды. Это позволяет рассматривать все механические характеристики
жидкой среды (плотность, давление, скорость и т.д.) как функции
координат точки пространства и времени, причем в большинстве
случаев эти функции предполагаются непрерывными и
дифференцируемыми.

3.

На выделенный внутри жидкости некоторый объем, находящийся в
равновесии (в покое или в состоянии динамического равновесия)
действуют силы, которые бывают двоякого рода: поверхностные и
объемные.
Поверхностные силы, как следуют из названия, - это такие силы,
которые распределены по поверхности выделенного объема и по своей
величине пропорциональны этой поверхности. К ним относятся силы
упругости, поверхностного натяжения, вязкости, давления
окружающей среды и т.п.
Объемные (массовые) силы действуют на всю массу жидкости.
Пример: силы тяжести, силы инерции и т.п.
И те, и другие приводят к возникновению деформаций и,
следовательно, напряжений. В гидромеханике нормальные напряжения
(от сил, действующих нормально к элементарной площадке) принято
называть давлением. В покоящейся жидкости это давление называют
обычно гидростатическим, а в движущейся – гидродинамическим.

4.

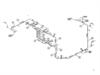
Реограммы жидкостей реологически стационарных систем:
а – вязкая жидкость (1), псевдопластичная жидкость (2), дилатантная
жидкость (3);
б – вязко-пластичная жидкость (модель Кэссона-Шульмана);
в – вязко-пластичная жидкость (модель Бингама);
г – вязко-пластичная жидкость (модель Шведова);
д – тиксотропно-вязко-пластичная жидкость.

5.

Реологической моделью жидкости называется зависимость касательdu
dy
ных напряжений о от градиента скорости сдвигаγ (или
). Реологи-
ческие модели заданы уравнениями с определеными реологическими
параметрами и отражают идеальное поведение реальных тел (табл.1).
Жидкости, в которых при постоянной скорости деформации напряжения сдвига уменьшаются во времени, называют тиксотропными.
К наиболее распространенным тиксотропным системам относятся глинистые суспензии, тампонажные цементные растворы, некоторые продукты питания краски и т.д.
Реологические модели и их константы.
Реологическая
модель
Ньютона
ШведоваБингама
Реологическое
уравнение
Реологические параметры
μ - динамическая вязкость, Па·с
τ μ γ
τ τ o η γ τ - динамическое напряжение сдвига, Па;
o
η - пластическая (структурная) вязкость,
Размерность
в ед. СИ
F·T/L2
F/L2
F·T/L2
Па·с
Оствальда-деВаале
ГершеляБалкли
Де-Хавена
K - мера консистентности, Па·сn;
τ K γ
n - показатель поведения (нелинейность)
n
τ τ o K γ τo - динамическое напряжение сдвига, Па;
K
n
n
τ
ηo
1 Cτ
n
γ
- мера консистентности, Па·с ;
n - показатель поведения (нелинейность)
ηo - кажущаяся вязкость при скорости
F·Tn/L2
безразм.
F/L2
F·Tn/L2
безразм.
F·T/L2
сдвига, близкой к нулю, Па·с;
C - эмпирическая константа;
n - показатель поведения (нелинейность)
безразм.
безразм.

6.

Участок С1С2 – это выдержка во времени системы на
верхней границе по градиенту скорости, при которой
происходило «разжижение» системы (в вискозиметре
поддерживается постоянная скорость вращения до того
момента, пока не стабилизируется показание по углу
поворота пружины φ). Ниспадающая кривая, таким образом,
является реограммой системы, тиксотропная структура
которой предварительно разрушена (на участке С1С2).

7.

Достоинства реометров типа Куэтта:
компактность и малый объем жидкости, необходимый для измерений;
возможность создания в зазоре постоянной скорости сдвига;
легкость контроля за температурой и ее регулирование;
хорошая воспроизводимость экспериментальных данных.
Недостатки:
непригодность их для исследования грубых суспензий, если зазоры
малы;
возникает погрешность в результатах из-за осаждении твердой фазы
в процессе измерений;
варьирование угла закручивания может происходить вследствие изменения концентрации в радиальном направлении под действием
центробежных сил.
Уменьшение угла закручивания во времени можно объяснить разрушением гелевой структуры жидкости и изменением концентрации
твердой фазы суспензии в осевом или радиальном направлении.

8.

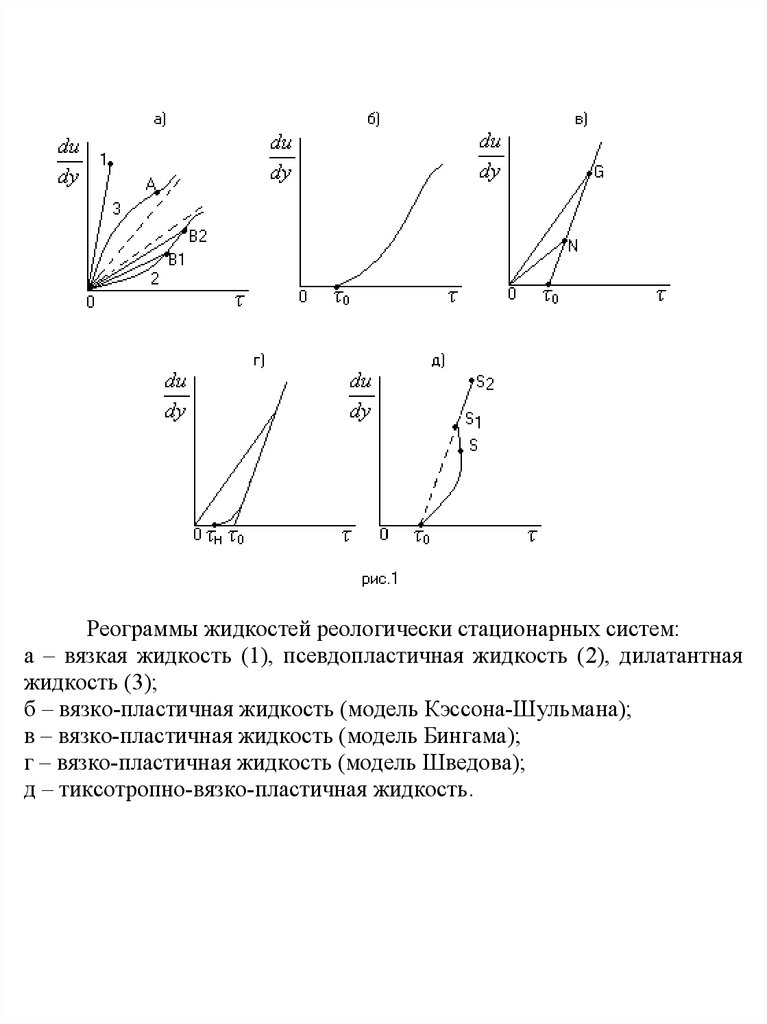
Технические данные ВСН-3
Диапазон измерения касательных напряжений и предельного
статического напряжения сдвига (СНС):
дин мг
Па
см 2
2
см
для пружины № 1
0-45
0-450
для пружины № 2
0-90
0-900
Диапазон измерения динамической вязкости ньютоновских
жидкос-тей при 200 об/мин:
Па•с
сП
для пружины № 1
0,001 - 0,2
1 - 200
для пружины № 2
0,001 - 0,4
1 - 400
Основная приведенная погрешность измерения касательных напряжений не должна превышать 3%, динамической вязкости 5%, отклонение частоты вращения от номинальной 2% при температуре окружающей среды и жидкости 20 5 С.
Внутренний диаметр гильзы, мм
Наружный диаметр измерительного элемента
Высота измерительного элемента
Максимальный угол поворота измерительного элемента
Константа А
Па с об
мин град
для пружины № 1
для пружины № 2
0,15 0,003
0,30 0,006
Константа В
c об
мин
1
+0,025
-0,010
Константа k
Па
град
для пружины № 1
для пружины № 1
0,1675 0,0045
0,335 0,009
44 + 0,039
39,62 – 0,039
60 – 0,19
0 270 + 5
сП об
мин град
150 3
300 6
сП см 2 об
мин дин
100
+2,5
-1,0
дин град
см 2
1,675 0,045
3,35 0,09

9.

Касательные напряжения и градиенты скорости сдвига определяют-ся по следующим формулам:
=А
(2)
= / B
(3)
где - скорости вращения гильзы (для ВСН-3 соответственно 200,
300, 400 и 600 об/мин).
Константу В можно определить и проверить по формуле:
В=
3000
D
ln
π
d
(4)
где d - диаметр измерительного элемента, мм;
D - внутренний диаметр гильзы, мм
Динамическая вязкость по модели Ньютона определяется по формуле:
= А В
(5)
где - динамическая вязкость, Па•с (сП);
-угол поворота шкалы, град;
-скорость вращения гильзы, об/мин.
ВНИМАНИЕ! Измерение динамической вязкости всех ньютоновских
жидкостей проводить при закрытых радиальных отверстиях в гильзе с
помощью тарировочных резиновых колец.

10.

Динамическая вязкость и предельное динамическое напряжение
сдвига по модели Шведова-Бингама определяются экспресс методом
по формулам:
(6)
(7)
= А В
о = А
где - структурная (пластическая) вязкость, Па•с (сП);
дин
;
2
см
о -динамическое напряжение сдвига, Па
и -углы поворота шкалы в град, измеренные соответственно при
скоростях вращения гильзы 1 и 2 об/мин.
При отсутствии вискозиметров можно использовать эмпирические уравнения, которые дают малую ошибку, когда раствор представляет собой глинистую либо шламовую суспензию. В случае химической обработки приведенные ниже формулы весьма условны:
= 0,033 – 0,022
о = 8,5 – 7
(8)
(9)
3
где - плотность бурового раствора [г/см ]; и о в единицах СИ
Мера консистенции К [Па с] и показатель нелинейности n по модели Оствальда-де Ваале приближенно можно найти из формул:
600
300
n = 3,32 lg
К = А
300
n
300
(10)
(11)
где 300 и 600 - углы поворота шкалы в град, измеренные соответственно при скоростях вращения гильзы 600 и 300 об/мин.

11.

Более точно выбор модели и ее параметры можно найти, используя метод наименьших квадратов.
При использовании программируемых микрокалькуляторов или
ПЭВМ конечные соотношения для определения реологических констант имеют вид:
4
Для модели Ньютона
i
i
1
4
(13)
1
m
1
m
Для моделей Гершеля-Балкли
и Оствальда-де Ваале
1
1
m
2
i
2
(14)
m
i i
1
(15)
1
m
m
n
m
m i
1
1
m
Для модели Шведова-Бингама
o
m
m i i i i
m
m
1
1
m xi yi xi yi
1
m x xi
1
1
m
2
i
m
К exp
y
i
1
m
2
(16)
m
n xi
1
m
КСР=(1-n) К 100(n-1)
где m - число обрабатываемых точек (для ВСН-3 m = 4);
КСР - iкритерий сдвигового разжижения, Па•сn;
x = ln i , y = ln i - для модели Оствальда- де Ваале
x = ln , y = ln( i- о) - для модели Гершеля-Балкли
(17)
(18)

12.

Сжимаемость жидкостей.
Капельные жидкости под воздействием
давления меняют свой объем. Это свойство
характеризуется коэффициентом объемного
сжатия
βV,
представляющим
собой
относительное изменение объема жидкости на
изменение давления на единицу:
V м 2
V
V p Н
Величина,
обратная
βV
называется
H
модулем объемного расширения kV 2 .
м
Температурное расширение оценивается
коэффициентом объемного расширения βt:
V
V
V t
Примечание:
Известно, что при изменении действия на 10 МПа
объем жидкости уменьшается на 0,5%.,

13.

Теплофизические свойства буровых растворов.
Теплофизические свойства любого вещества
связаны между собой следующим соотношением:
λТ=асρ,
где λТ – коэффициент теплопроводности; а –
коэффициент температуропроводности; с – удельная
теплоемкость; ρ – плотность.
Коэффициент λ выражает то количество тепла в
джоулях, которое проходит в течении одной секунды
через стенку толщиной в 1 м и площадью 1 м2 при
разностях температур на поверхностях стенки, равной
10С:
C
QT
m t
Теплофизические свойства буровых растворов
начали всерьез определять только после 1962 года.
Установлено, что величина удельной теплоемкости «С»
с увеличением плотности уменьшается и находится в
ккал
или, что то же самое, от
кг 0 С
Дж
. Объясняется это тем, что
кг 0 С
пределах от 0,86 до 0,40
3,68·103 до 1,67•103
глина
обладает
низкой
теплоемкостью (около 0,22
по
сравнению
с
водой
ккал
Дж
или 0,92•103 0 ) и
0
кг С
кг С
снижает первоначальную теплоемкость воды (4,19•103
Дж
).
кг 0 С
Предложена
эмпирическая
формула
для
определения удельной теплоемкости водных суспензий
глины:
С=[0,334+0,6745ρ-3,3]·4,19·103
где ρ – плотность суспензии в
г
.
см 3
Дж
кг 0 С

14.

p0
p
z
z0
g
g
или
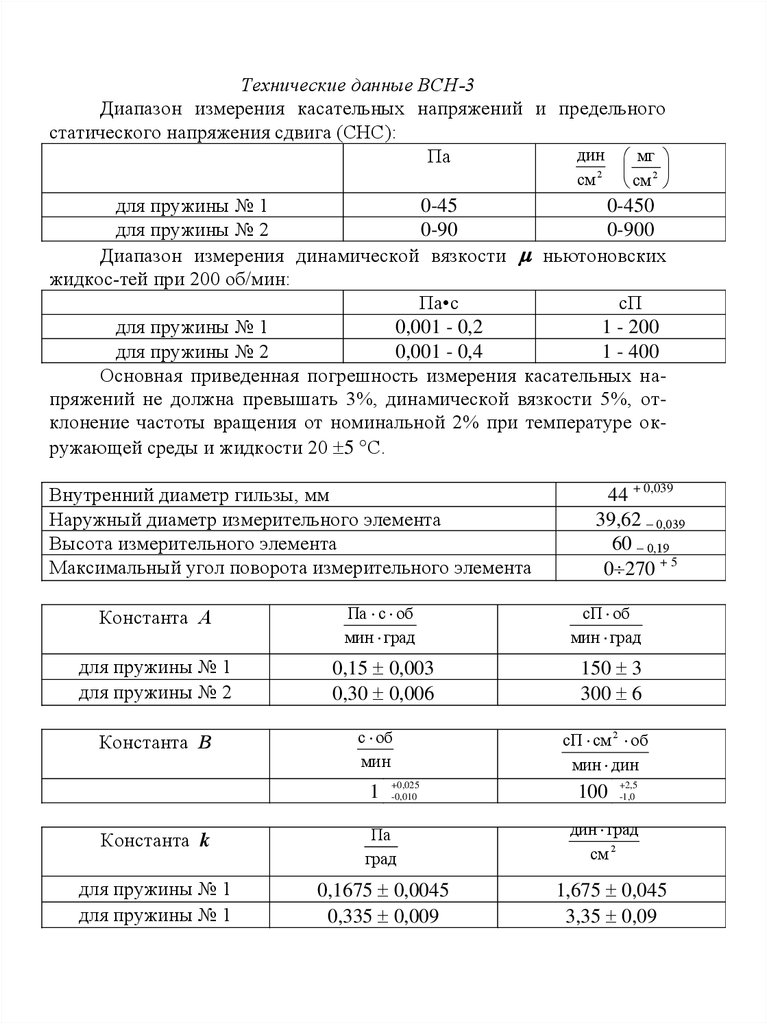
Основное уравнение гидростатики, обычно представляют в виде:
р=р0+ρg(z0-z )
р=р0+ρgh,
где h – глубина погружения под уровень жидкости, где давление
известно.

15.

li
li
p0 4
D di
diв
p0
li
li
4
D di
d iв
pост
li
li
4 0
D di
diв
0
pост
li
li
4
D di
d iв

16.

р рo e
gMh
mRyT
Эта формула известна под именем барометрической
Для природных газов чаще используется формула:
p po e
0 , 03415 z zo
mT
допустимо величину 0,03415 принять равной 10-4
mT
p po e
z zo 10 4

17.

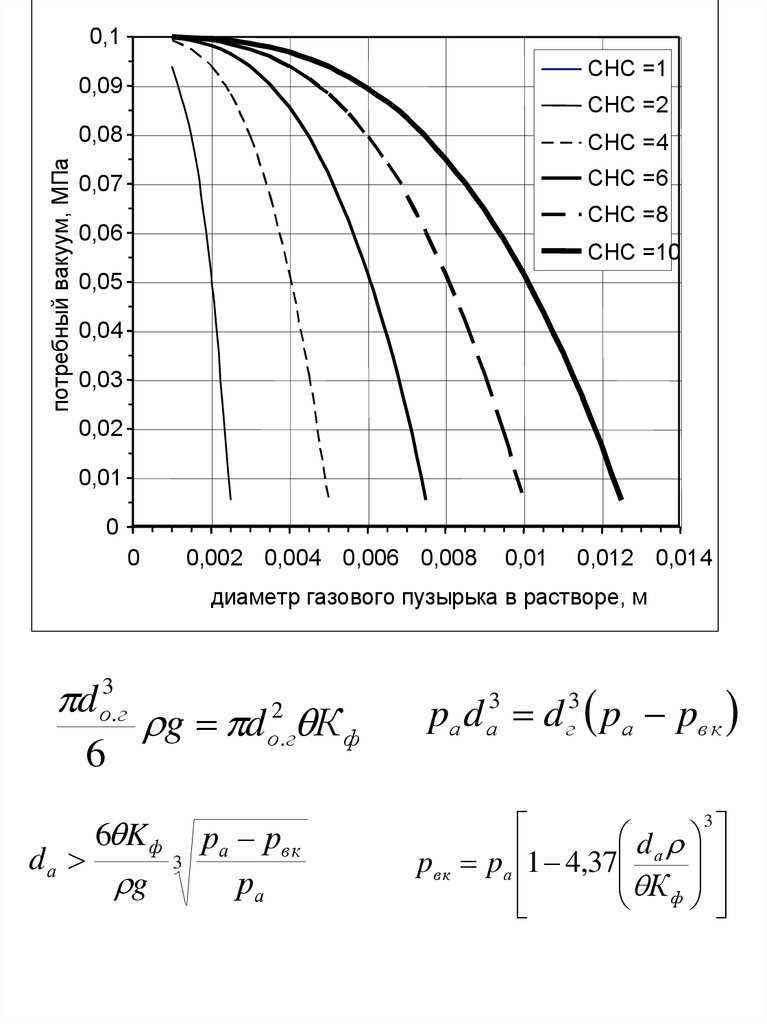
0,1
СНС =1
потребный вакуум, МПа
0,09
СНС =2
0,08
СНС =4
0,07
СНС =6
СНС =8
0,06
СНС =10
0,05
0,04
0,03
0,02
0,01
0
0
0,002 0,004 0,006 0,008
0,01
0,012 0,014
диаметр газового пузырька в растворе, м
d о3.г
6
dа
g d К ф
6 K ф
g
2
о. г
3
ра рв к
ра
pа d а3 d г3 pа pвк
3
dа
pвк pа 1 4,37
К
ф

18.

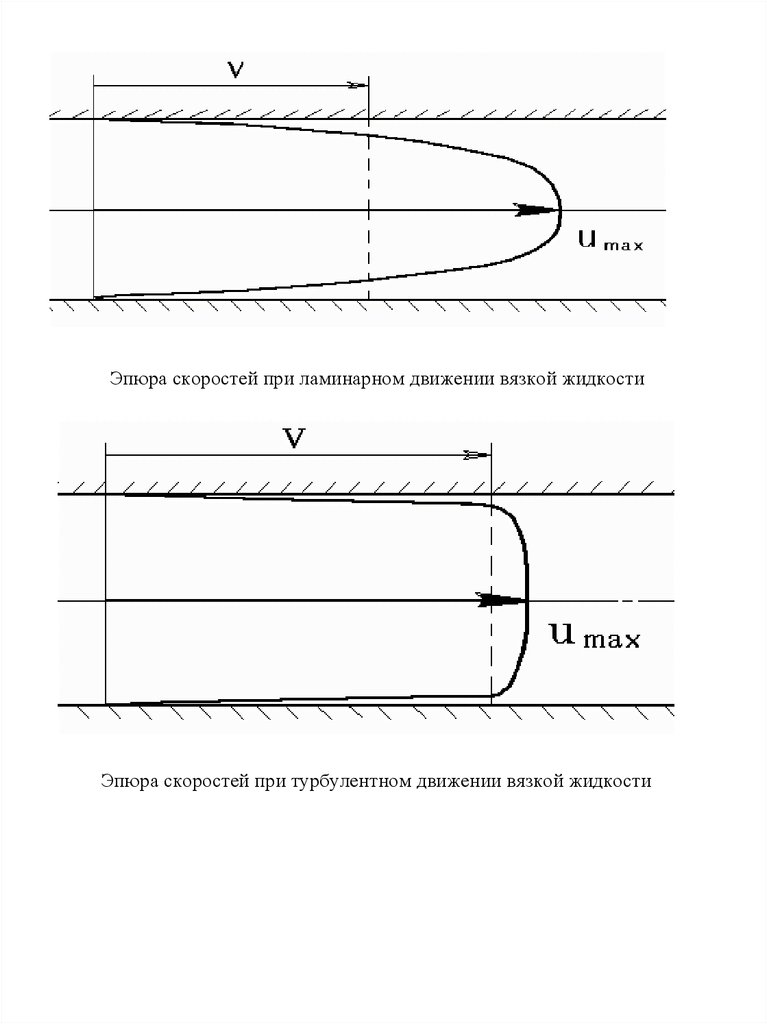
Эпюра скоростей при ламинарном движении вязкой жидкости
Эпюра скоростей при турбулентном движении вязкой жидкости

19.

0
u
1
2
3
5
4
uo
0
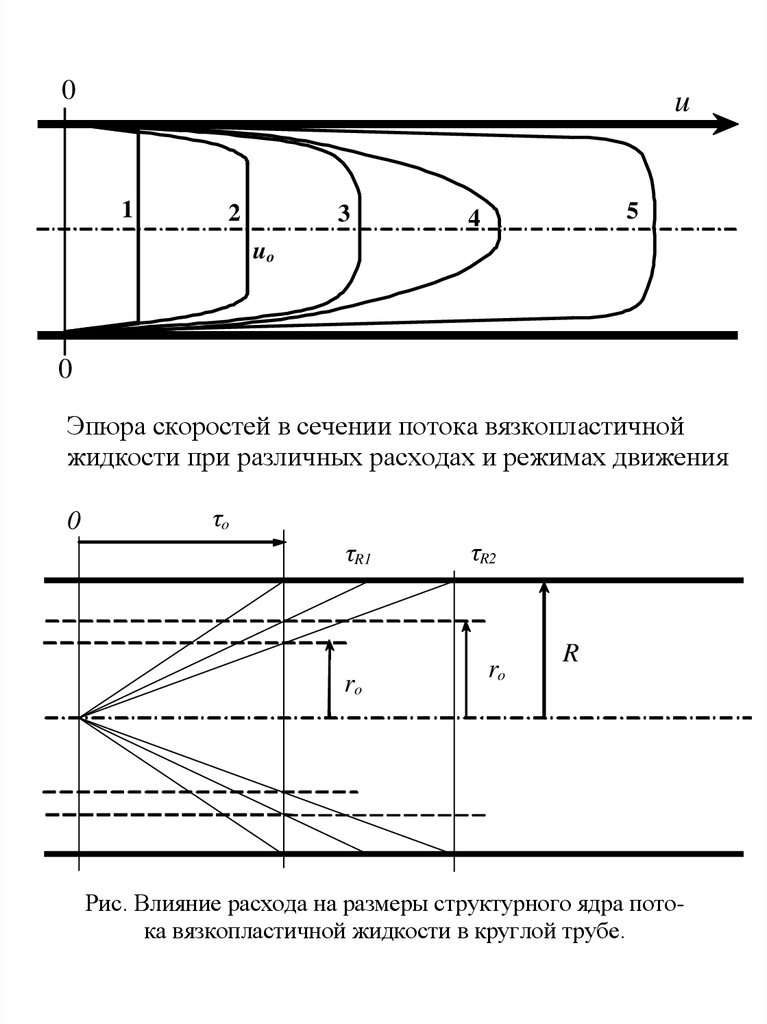
Эпюра скоростей в сечении потока вязкопластичной
жидкости при различных расходах и режимах движения
0
τo
τR1
ro
τR2
ro
R
Рис. Влияние расхода на размеры структурного ядра потока вязкопластичной жидкости в круглой трубе.

20.

l
τR
0
τ
y
p1
R
p2
2R
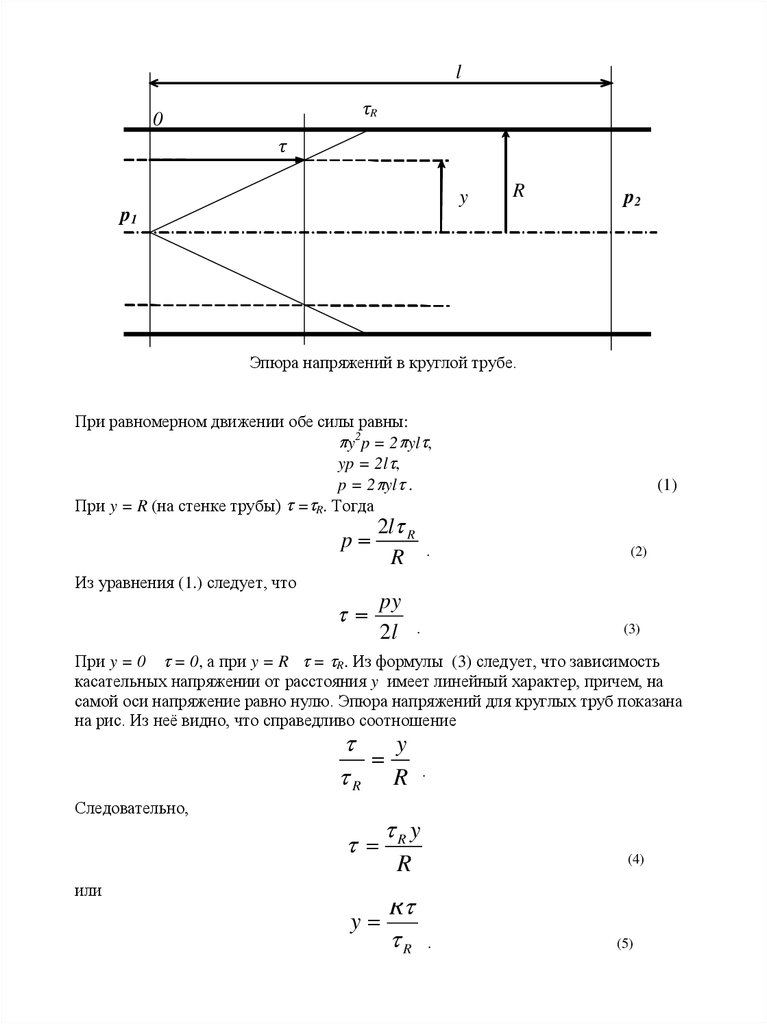
Эпюра напряжений в круглой трубе.
При равномерном движении обе силы равны:
y2p = 2 yl ,
yp = 2l ,
p = 2 yl .
При y = R (на стенке трубы) = R. Тогда
p
2l R
R
py
2l
.
(1)
(2)
Из уравнения (1.) следует, что
.
(3)
При y = 0 = 0, а при y = R = R. Из формулы (3) следует, что зависимость
касательных напряжении от расстояния y имеет линейный характер, причем, на
самой оси напряжение равно нулю. Эпюра напряжений для круглых труб показана
на рис. Из неё видно, что справедливо соотношение
y
R R
Следовательно,
или
y
.
R y
(4)
R
R
R
.
(5)

21.

Вывод уравнения, описывающего профиль (эпюру) скоростей
в круглой трубе при ламинарном или структурном режиме движения.
Отправных моментов два:
- доказанный ранее факт прямолинейности эпюры напряжении в круглой
трубе; это выражается формулами (1) и (3);
- существование строгой количественной зависимости между и градиентом
скорости du/dy, что конкретно выражается реологическими моделями.
Первый момент, как было показано, сводится, в частности, к соотношению (5):
R
y
.
R
Дифференцируя, имеем:
dy
R
R
d
.
(7)
Рис. К выводу уравнения расхода вязкопластичной жидкости.
Второй момент свидетельствует о существовании реологического уравнения
du
f ,
dy
а, следовательно, и обратной ей, так называемой реологической функции:
du
.
dy
(8)
Здесь знак (? ) должен быть потому, что скорость u с увеличением y уменьшается
(знаки приращений u и y не совпадают).
Например, для ВПЖ реологическое уравнение имеет вид:
du
dy
o

22.

Вывод уравнения профиля скоростей для случая движения
вязкопластичной жидкости в круглой трубе при структурном режиме
движения.
Подставим в уравнение (10) реологическую функцию (9):
R
R
R
R
0
R
R
u
d
d
d
0 d
R
R
R
R
R
R
R R2 2 R
R R 2 R 0
1 2
1 .
0 R 0
R 2 2 R
2 R R
Чтобы избавиться от R , вспомним уравнение (2), из которого следует:
R
pR
.
2l
(11)
Подставим (11) в последний результат и одновременно заменим / R на y/R в
соответствии с (4):
pR 2
y 2 R o
y
1 2
u
1 .
4 L R R
Окончательно:
u
p
R 2 y 2 o R y
.
4 l
(12)
Ранее было показано, что при y = ro u = uo , где uo скорость движения "твердого"
структурного ядра. Следовательно,
uo
p
R 2 ro2 o R ro
.
4 l
(13)
Выразим p в последнем уравнении через остальные:
p uo
o R ro 4 l
4 l
R 2 ro2
R 2 ro2
p uo
4 ol
4 l
R 2 ro2 R ro
.
,
(4.14)
Формула (14) не имеет практического значения. Дело в том, что измерить или каким-то
косвенным методом вычислить uo , ro практически невозможно. Имеют конкретное
значение уравнения (12) и (13). На их основе получена формула Букингэма.

23.

4
R p
4 po 1 po
Q
1
8 l 3 p 3 p
Это уравнение носит имя Букингэма, и было получено им в 1921 году
4
po
2l o
R
4
R p
4 2l o 1 2l o
Q
1
8 l 3 Rp 3 Rp
4
Обозначим po/p через
Sen
8
4
1 4
1
3
3
2 ol 4 ol
p
R
d
po

24.

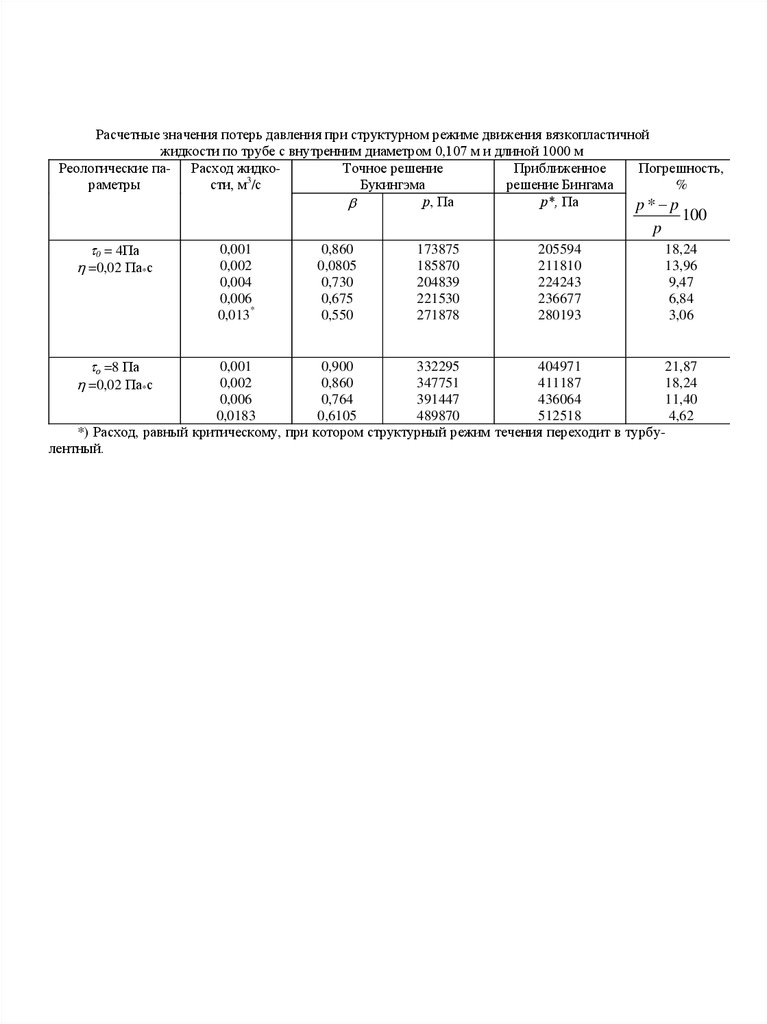
Расчетные значения потерь давления при структурном режиме движения вязкопластичной
жидкости по трубе с внутренним диаметром 0,107 м и длиной 1000 м
Реологические па- Расход жидкоТочное решение
Приближенное
Погрешность,
раметры
сти, м3/с
Букингэма
решение Бингама
%
р, Па
р*, Па
p* p
p
0 = 4Па
=0,02 Па*с
о =8 Па
=0,02 Па*с
0,001
0,002
0,004
0,006
0,013*
0,860
0,0805
0,730
0,675
0,550
173875
185870
204839
221530
271878
205594
211810
224243
236677
280193
100
18,24
13,96
9,47
6,84
3,06
0,001
0,900
332295
404971
21,87
0,002
0,860
347751
411187
18,24
0,006
0,764
391447
436064
11,40
0,0183
0,6105
489870
512518
4,62
*) Расход, равный критическому, при котором структурный режим течения переходит в турбулентный.

25.

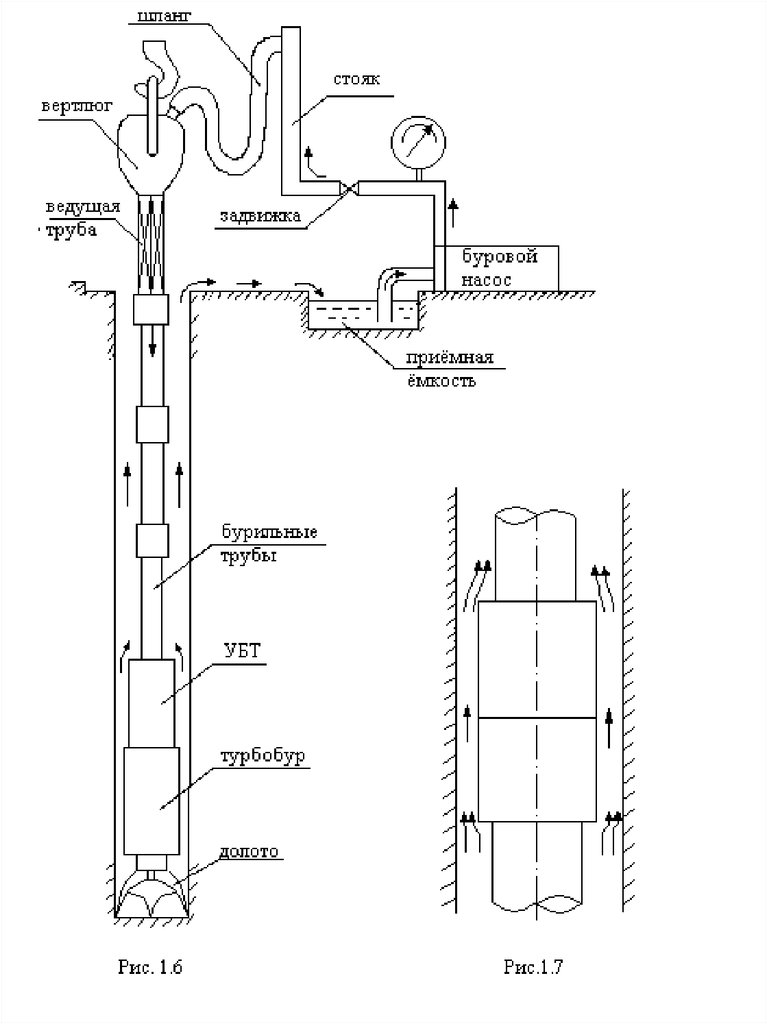
Рис.. Циркуляционная система скважины.

26.

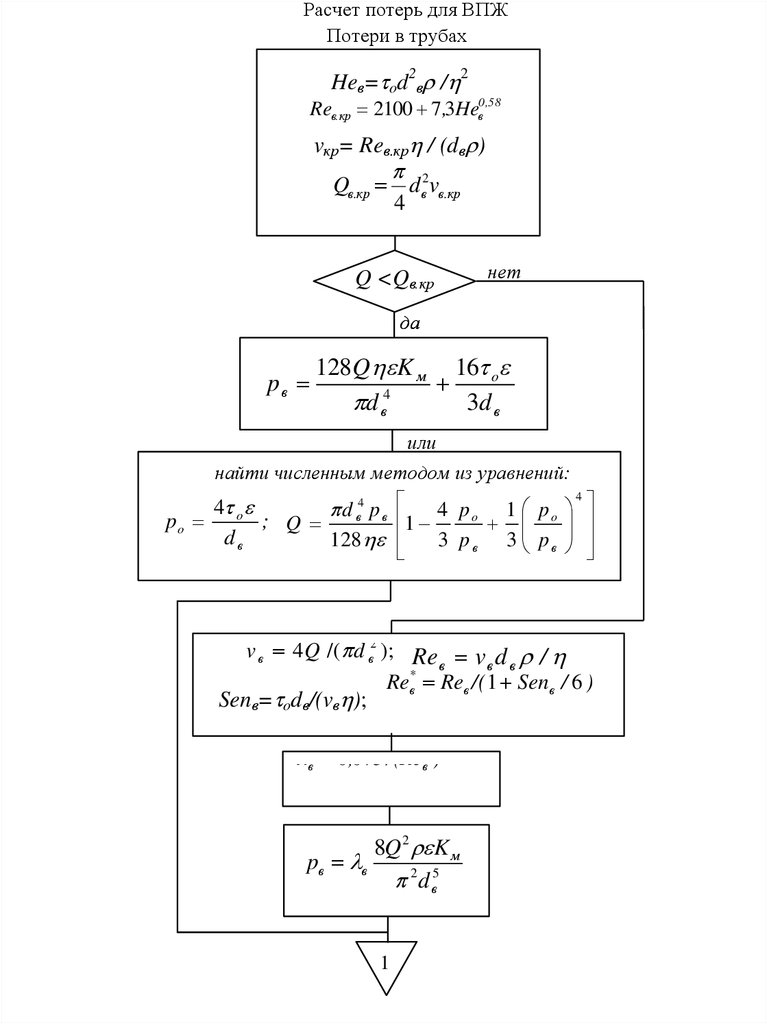
Расчет потерь для ВПЖ
Потери в трубах
Heв= od2в / 2
Reв.кр 2100 7,3Heв0,58
vкр= Reв.кр / (dв )
Qв.кр dв2vв.кр
4
Q <Qв.кр
нет
да
pв
128 Q K м 16 o
4
d в
3d в
или
найти численным методом из уравнений:
4
4 o
d в4 p в 4 p o 1 p o
po
; Q
1
dв
128
3 p в 3 p в
v в 4Q /( d в2 ); Re v d /
в
в в
Re*в Reв /( 1 Senв / 6 )
Senв= odв/(vв );
в 0 ,075 /(Re*в )0 ,125
8Q 2 K м
pв в
2 d в5
1

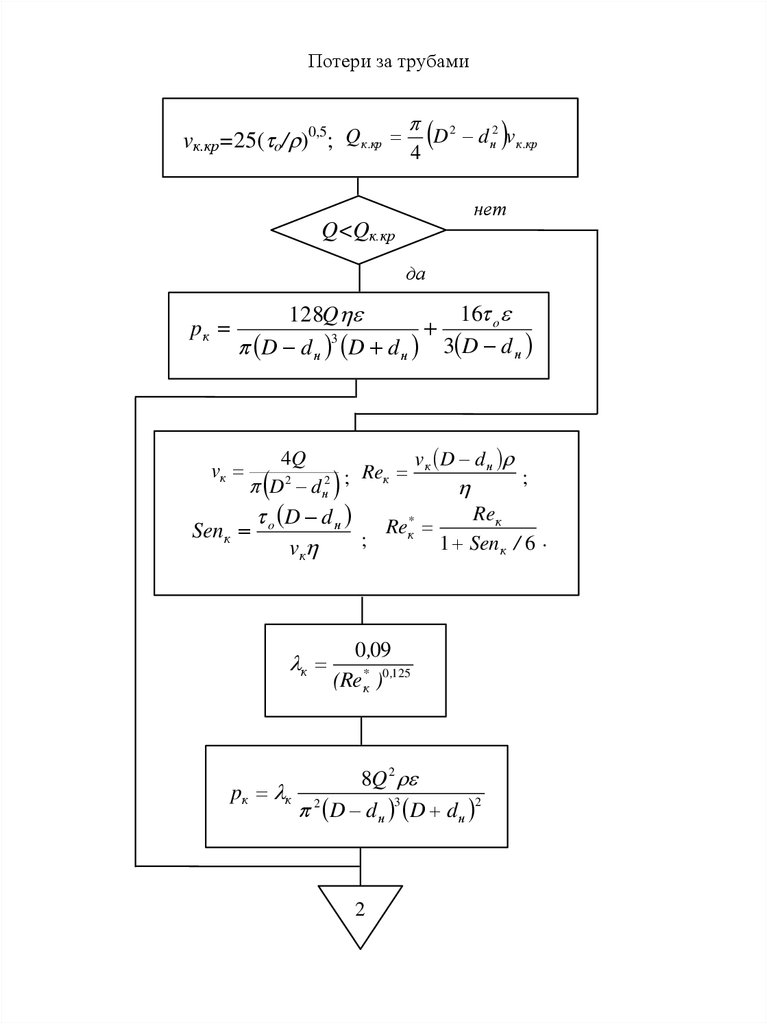
27.

Потери за трубами
vк.кр=25( o/ )0,5; Qк .кр
D
4
2
d н2 v к .кр
нет
Q<Qк.кр
да
pк
16 o
128Q
D d н 3 D d н 3 D d н
4Q
v к D d н
Re
к
;
D 2 d н2 ;
Reк
D d н Re*
Sen к o
к
;
1 Sen к / 6 .
v
vк
к
к
0,09
(Re *к )0 ,125
8Q 2
pк к 2
D d н 3 D d н 2
2

28.

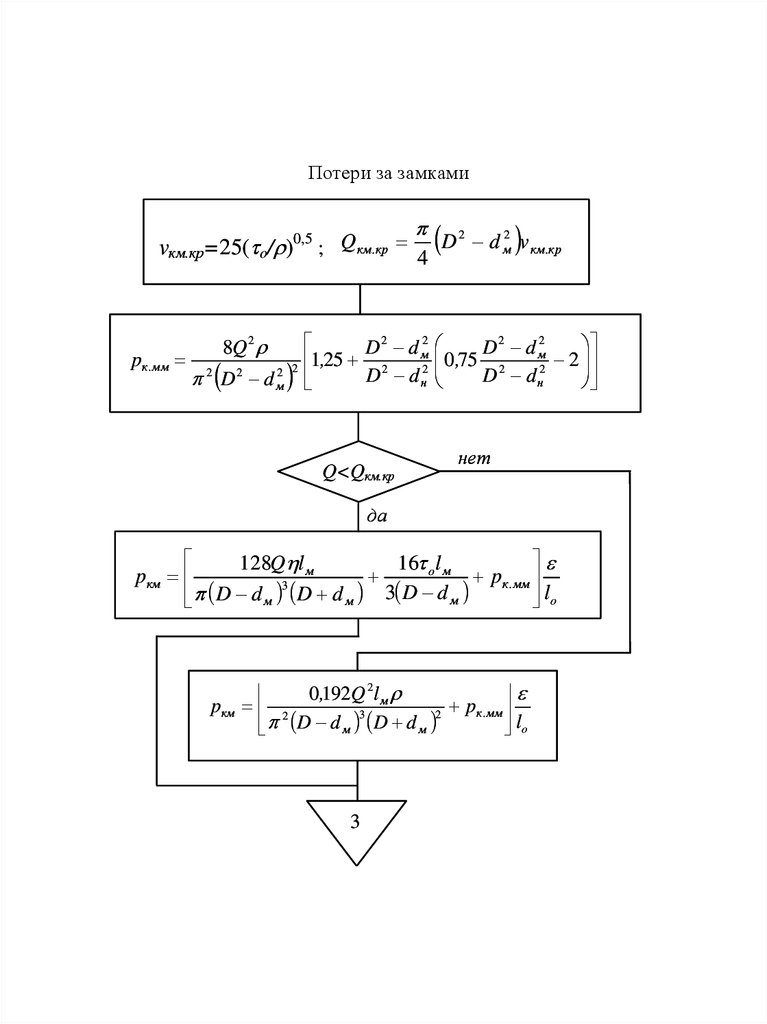
Потери за замками
2
2
vкм.кр=25( o/ )0,5 ; Q км .кр 4 D d м v км .кр
pк .мм
8Q 2
2 D 2 d м2
2
D 2 d м2
D 2 d м2
1
,
25
0
,
75
2
2
2
2
2
D
d
D
d
н
н
Q<Qкм.кр
нет
да
128Q l м
16 o l м
pкм
p
к . мм
3
D d м D d м 3 D d м
lo
pкм
0,192Q 2 l м
2
p
к
.
мм
3
2
D d м D d м
lo
3

29.

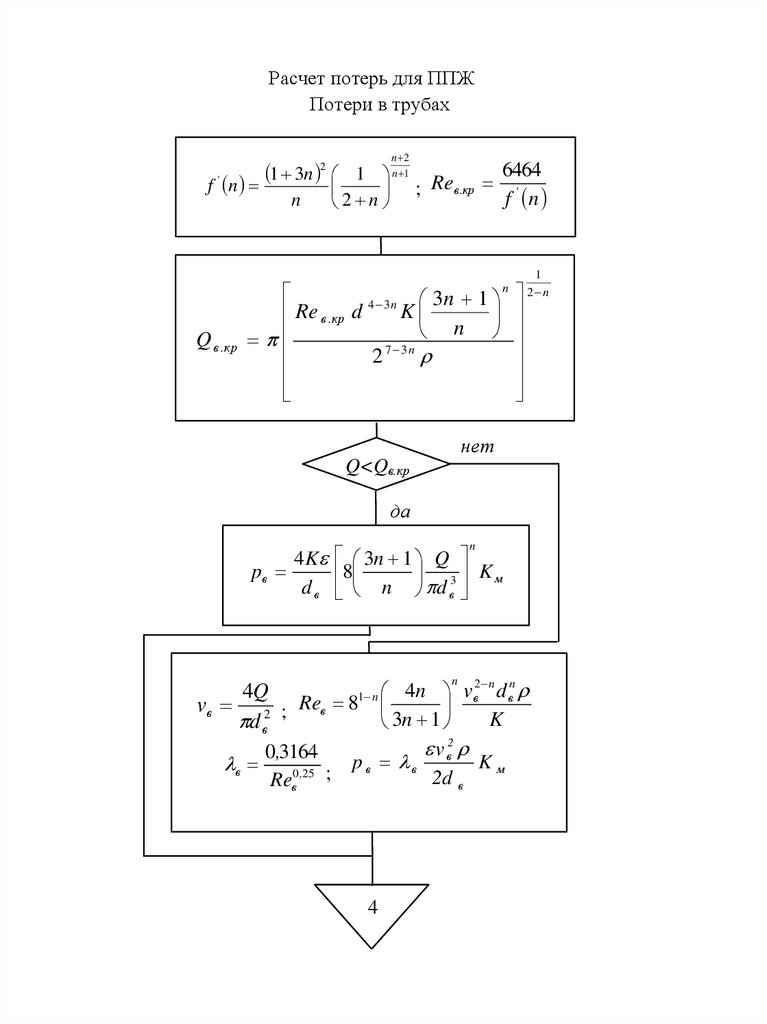
Расчет потерь для ППЖ
Потери в трубах
n 2
1 3n 2
f ' n
n
Q в .кр
6464
1 n 1 Re
;
в .кр
f ' n
2 n
3n 1
4 3n
K
Re в .кр d
n
7 3n
2
n
1
2 n
нет
Q<Qв.кр
да
4 K
pв
dв
n
3n 1 Q
8 n d 3 K м
в
2 n n
4Q
1 n 4 n vв d в
vв 2 ; Reв 8
K
d в
3n 1
2
v в
0,3164
p
Kм
в
в
в
0 ,25 ;
n
2d в
Reв
4

30.

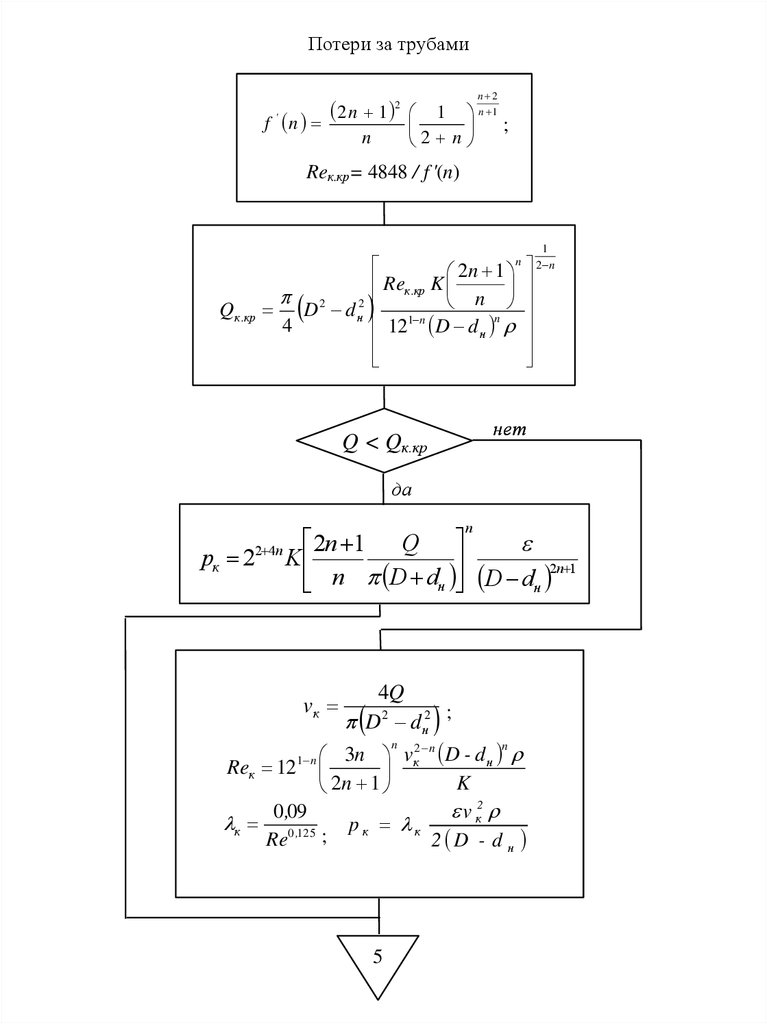
Потери за трубами
2 n 1 2
f ' n
n
n 2
1 n 1
;
2 n
Reк.кр= 4848 / f '(n)
Qк .кр
2n 1
Reк .кр K
2
n
2
D d н
4
121 n D d н n
n
1
2 n
нет
Q < Qк.кр
да
n
2n 1
Q
pк 22 4n K
2n 1
n D dн D dн
4Q
D 2 d н2 ;
n 2 n
n
v к D - d н
1 n 3n
Reк 12
K
2n 1
0,09
v к2
к 0 ,125
pк к
vк
Re
2 D - d н
;
5

31.

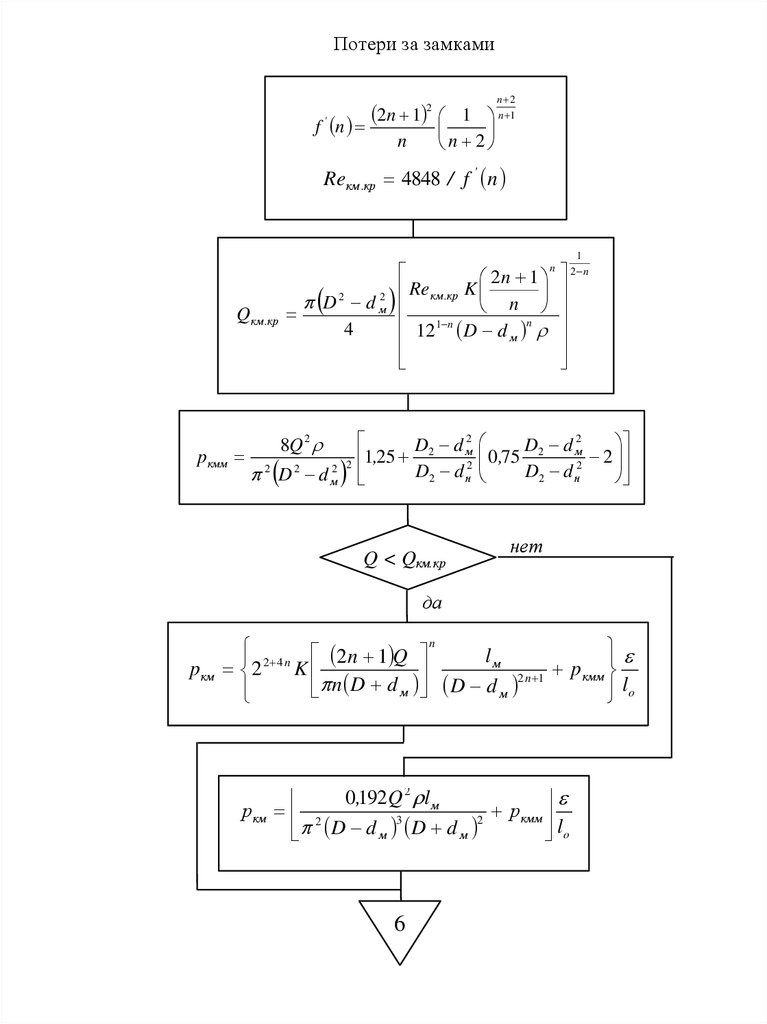
Потери за замками
2
2n 1
'
f n
n
n 2
1 n 1
n 2
Reкм .кр 4848 / f ' n
2n 1
Re км .кр K
D d
n
12 1 n D d м n
4
2
Q км .кр
pкмм
2
м
8Q 2
2 D 2 d м2
2
D2 d м2
1,25
D2 d н2
Q < Qкм.кр
n
1
2 n
D2 d м2
0 ,75
2
D2 d н2
нет
да
p км
n
2 n 1 Q
lм
2 4 n
2
K
p
кмм
2 n 1
lo
n D d м D d м
р км
0 ,192 Q 2 l м
2
р
кмм
3
2
D d м D d м
lo
6

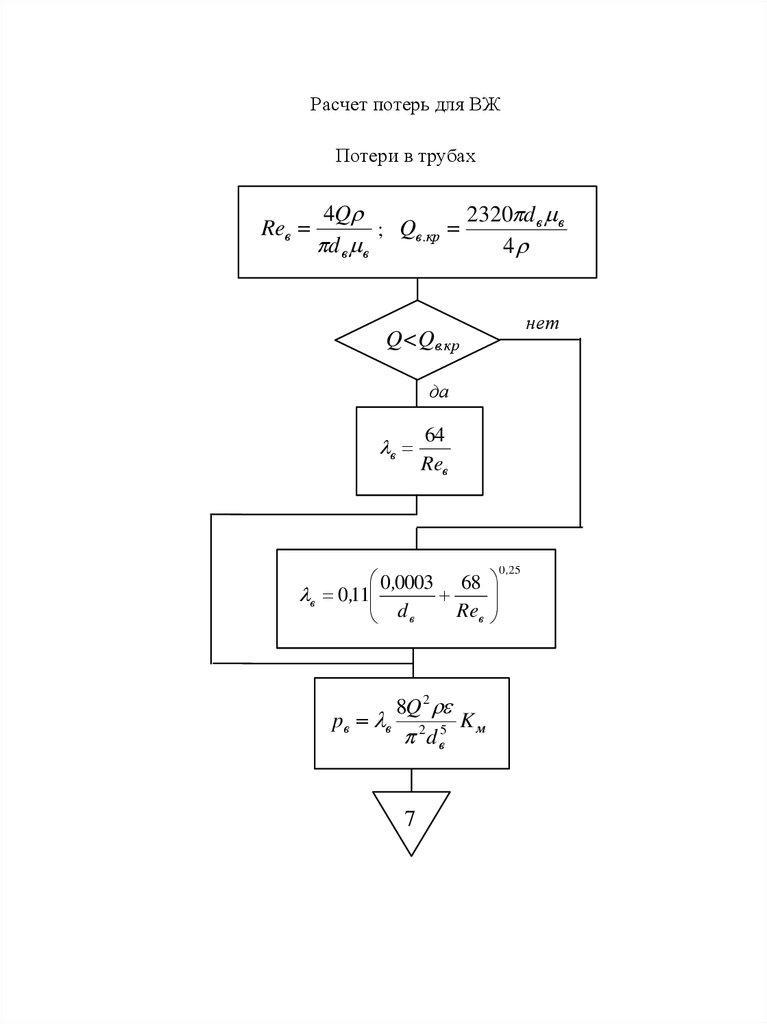
32.

Расчет потерь для ВЖ
Потери в трубах
Reв
4Q
2320 d в в
; Qв .кр
d в в
4
нет
Q<Qв.кр
да
в
64
Reв
0,0003 68
в 0,11
d
Re
в
в
8Q 2
pв в 2 5 K м
dв
7
0 ,25

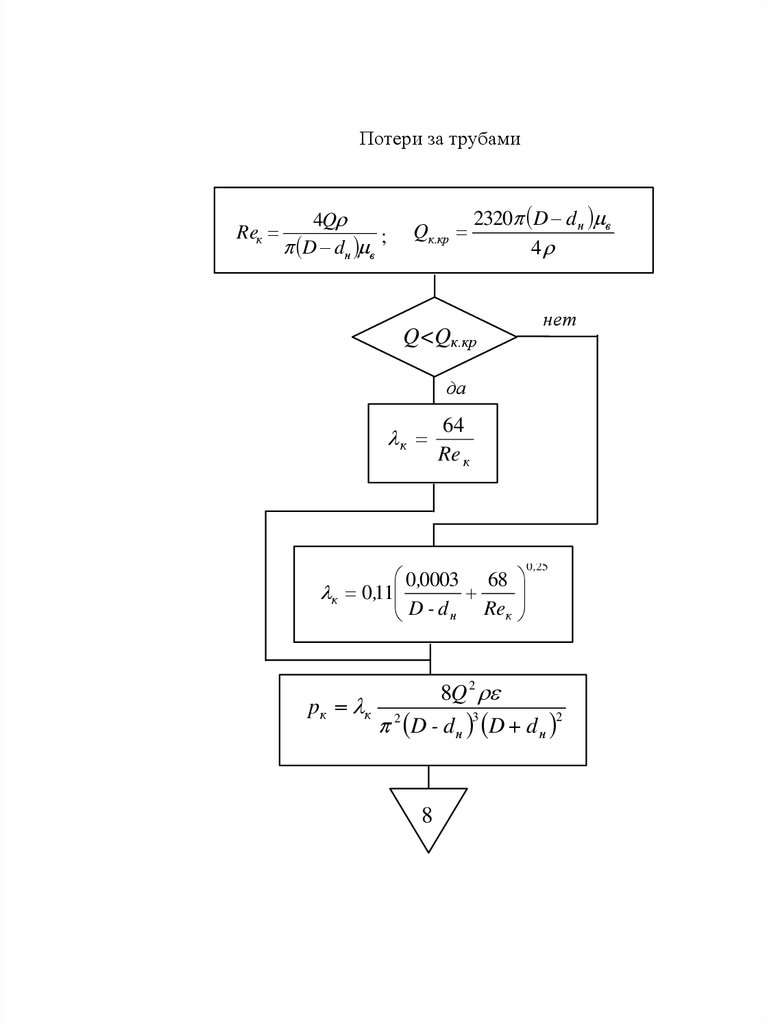
33.

Потери за трубами
Reк
4Q
;
D dн в
Qк .кр
2320 D d н в
4
Q<Qк.кр
нет
да
к
64
Re к
0 ,0003 68
к 0 ,11
D - d н Reк
0 ,25
8Q 2
pк к 2
D - d н 3 D d н 2
8

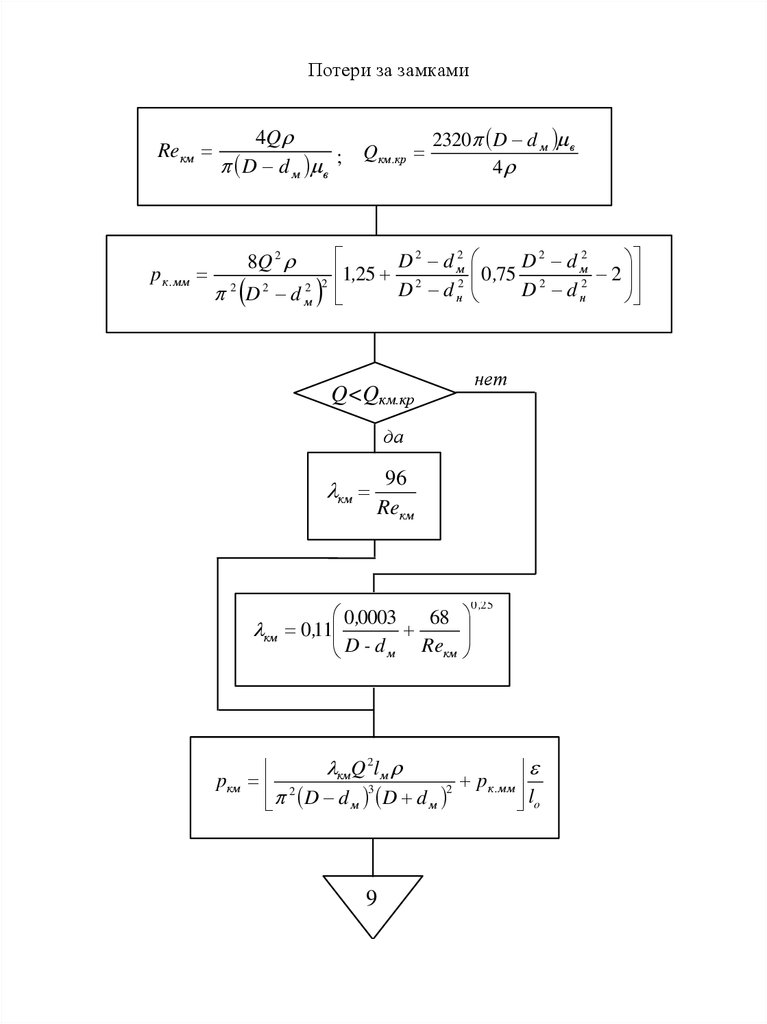
34.

Потери за замками
Re км
p к . мм
4Q
D d м в ;
8Q 2
2 D 2 d м2
2
Qкм .кр
2320 D d м в
4
D 2 d м2
1,25 2
D d н2
Q<Qкм.кр
D 2 d м2
0 ,75 2
2
2
D
d
н
нет
да
км
км
pкм
96
Reкм
0,0003
68
0,11
D
d
Re
м
км
0 ,25
кмQ 2 l м
2
p
к . мм
3
2
D d м D d м
lo
9

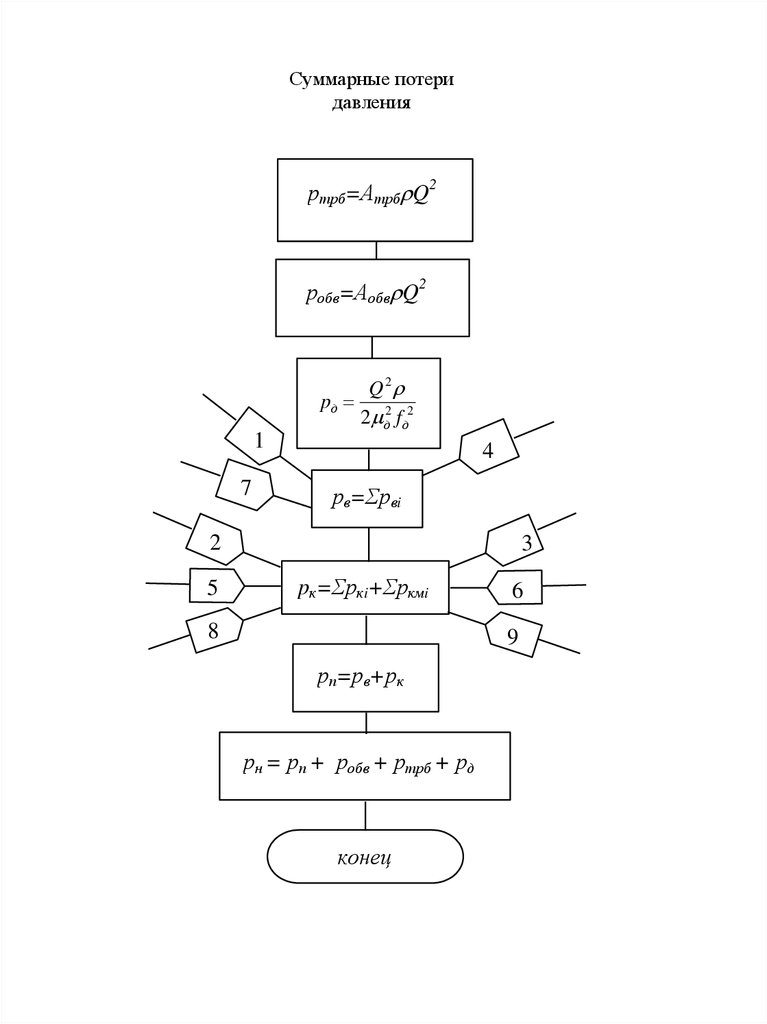
35.

Суммарные потери
давления
ртрб=Атрб Q2
робв=Аобв Q2
Q2
pд 2 2
2 д f д
1
7
4
рв=Σрвi
2
5
3
pк=Σpкi+Σpкмi
8
6
9
рп=рв+рк
рн = рп + робв + ртрб + рд
конец

36.

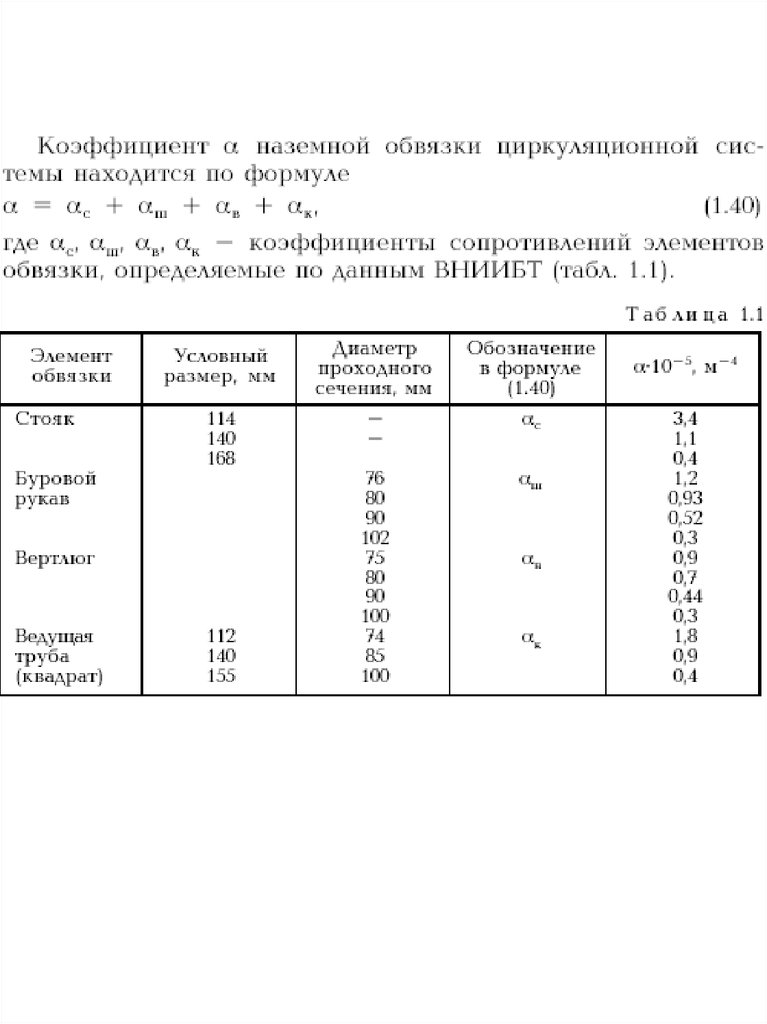
37. Потери на долоте

Q
pд
2 2
2 д f д
2
8Q
pд 2 2 2 2
dо z д
2
н п
д
2
2
2
2
п н п
п = 0,82, н=0,985

38.

Рис. Насадка гидромониторного долота.
Рис. Схема промывочного узла гидромониторного долота.

39.

do
lo
lc
d
pос
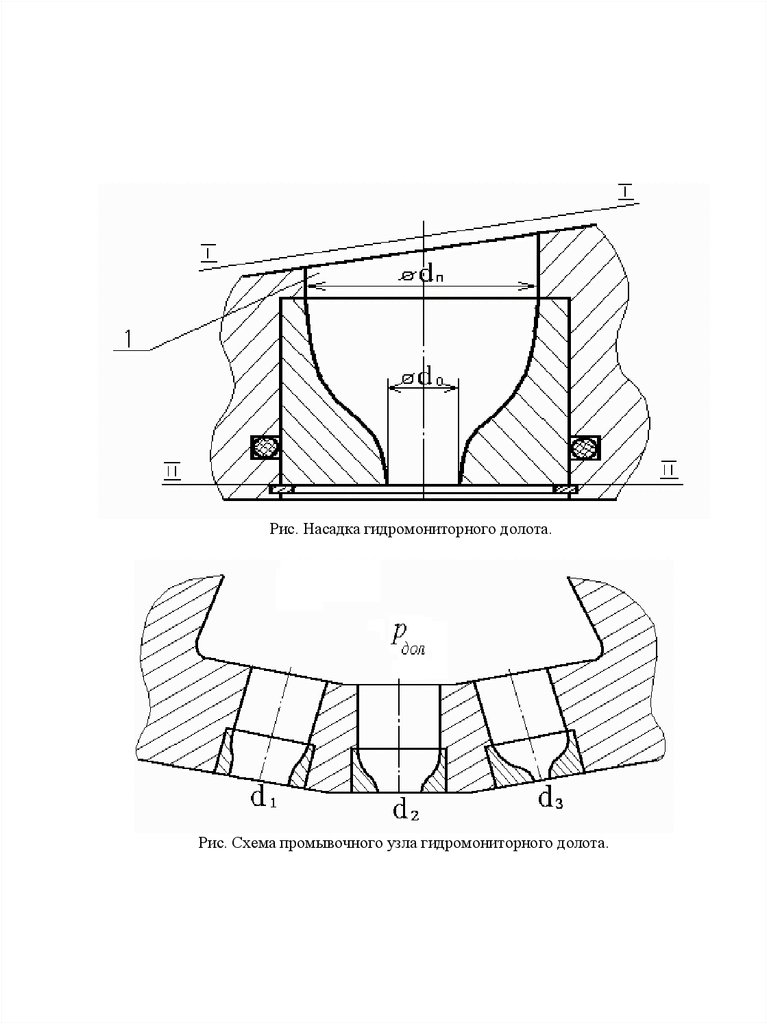
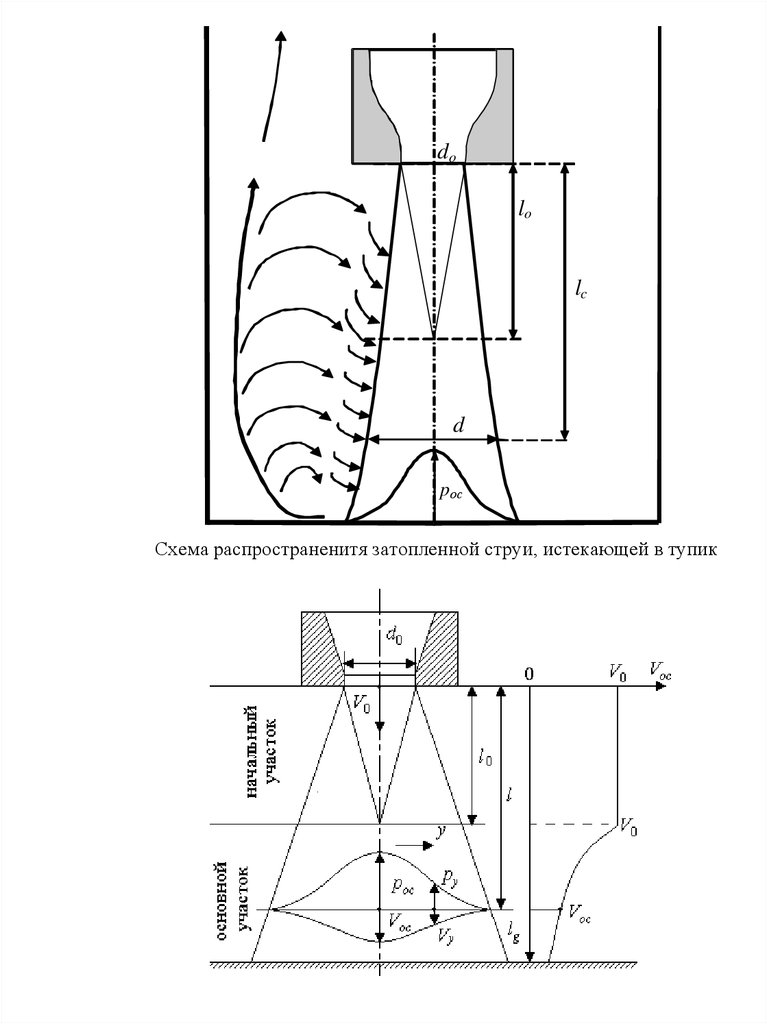
Схема распространенитя затопленной струи, истекающей в тупик

40.

А.К. Козодой предложил упрощенную модель распространения
затопленной струи, которая сводится к тому, что граница струи
представляет собой коническую поверхность, в том числе и в
пределах начального участка. Совместив эту схему с известным
положением о постоянстве количества движения по сечениям
струи, он получил широко используемые формулы для
определения диаметра струи d и гидродинамического давления
по ее оси pос (рис. выше):
d d o ( 1 am ) ,
m = lс / do ,
pо = po ,
po vo / 2 ,
2
1 am0
1
am
mo = lo / dн ,
2
,
где d - текущий диаметр струи;
- относительная величина осевого гидродинамического
давления струи (сокращенно в дальнейшем изложении:
“относительное осевое давление струи”);
vo - средняя начальная скорость струи на выходе из
насадки;
lo, lс - соответственно расстояния до начального и
текущего (на основном участке) сечений струи;
a - коэффициент расширения струи;
mo - относительная длина ядра струи;
m - безразмерное (относительное) расстояние от насадки;
- плотность жидкости.

41.

д
1
1,052 0,435 2
f o d o2
2
fп dп
д
1
d о4
1,052 0,435 4
dп
vo2
d o4
1,052 0,435 4
pд
2
dп
8Q 2
d o4
pд 2 2 2 1,052 0,435 4
do z
dп
2
8
,
42
Q
do
2
Q
2 2
pд z 3,5 4
dп
0 , 25

42.

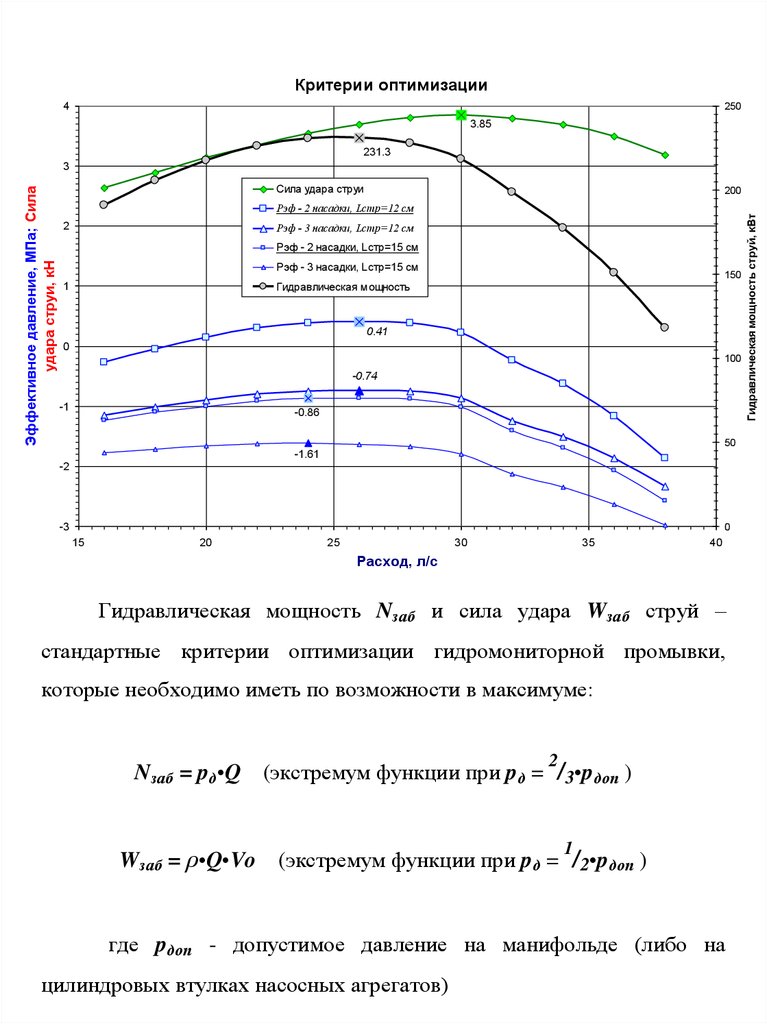
Критерии оптимизации
4
250
3.85
231.3
Сила удара струи
200
Рэф - 2 насадки, Lстр=12 см
2
Рэф - 3 насадки, Lстр=12 см
Рэф - 2 насадки, Lстр=15 см
Рэф - 3 насадки, Lстр=15 см
1
150
Гидравлическая мощность
0.41
0
100
-0.74
-1
-0.86
50
-1.61
-2
-3
0
15
20
25
30
35
40
Расход, л/с
Гидравлическая мощность Nзаб и сила удара Wзаб струй –
стандартные критерии оптимизации гидромониторной промывки,
которые необходимо иметь по возможности в максимуме:
2
Nзаб = pд•Q (экстремум функции при pд = /3•pдoп )
1
Wзаб = ρ•Q•Vo (экстремум функции при pд = /2•pдоп )
где pдоп - допустимое давление на манифольде (либо на
цилиндровых втулках насосных агрегатов)
Гидравлическая мощность струй, кВт
Эффективное давление, МПа; Сила
удара струи, кН
3

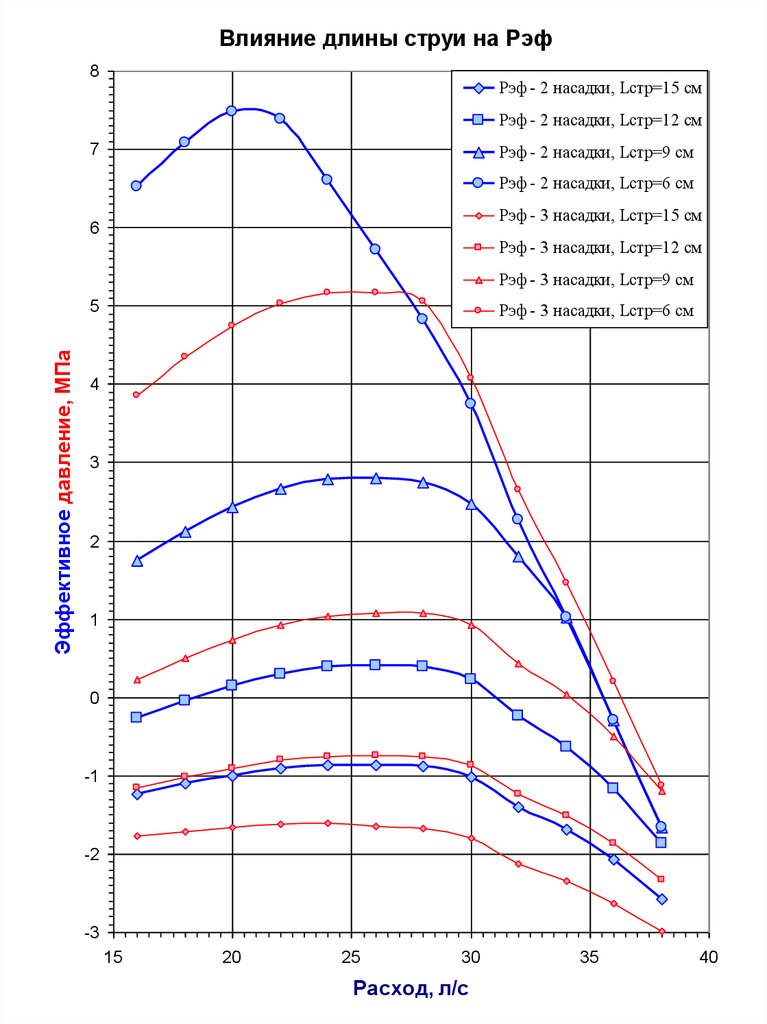
43.

Влияние длины струи на Рэф
8
Рэф - 2 насадки, Lстр=15 см
Рэф - 2 насадки, Lстр=12 см
7
Рэф - 2 насадки, Lстр=9 см
Рэф - 2 насадки, Lстр=6 см
Рэф - 3 насадки, Lстр=15 см
6
Рэф - 3 насадки, Lстр=12 см
Рэф - 3 насадки, Lстр=9 см
Эффективное давление, МПа
5
Рэф - 3 насадки, Lстр=6 см
4
3
2
1
0
-1
-2
-3
15
20
25
30
Расход, л/с
35
40

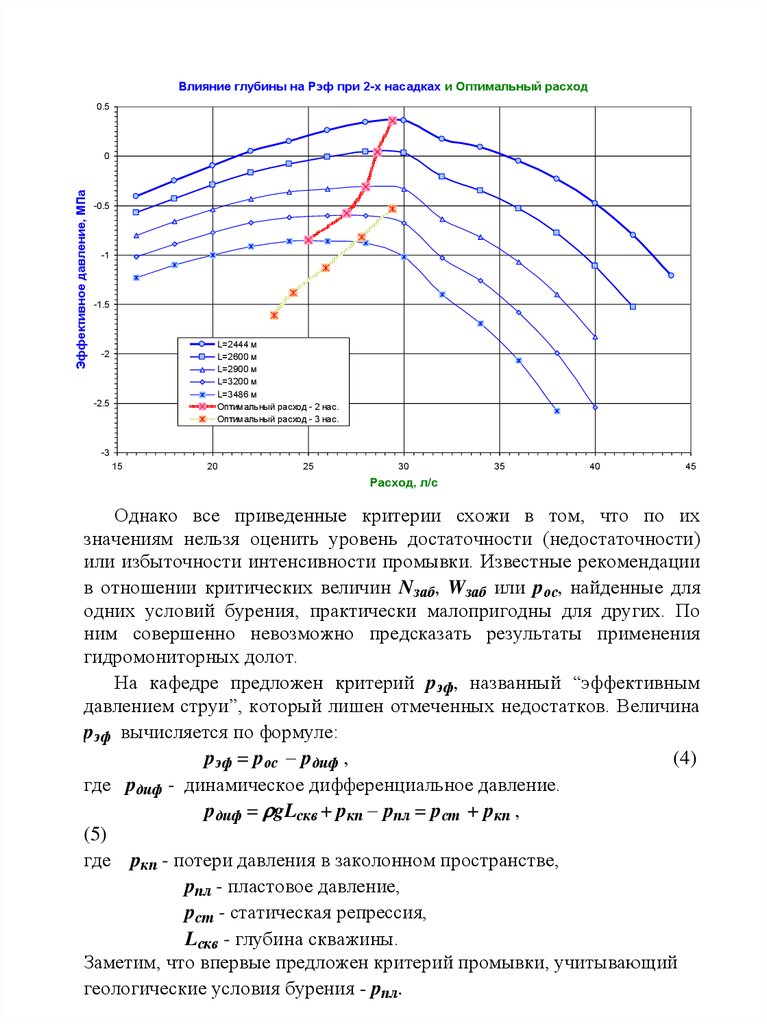
44.

Влияние глубины на Рэф при 2-х насадках и Оптимальный расход
0.5
Эффективное давление, МПа
0
-0.5
-1
-1.5
L=2444 м
L=2600 м
L=2900 м
L=3200 м
L=3486 м
Оптимальный расход - 2 нас.
Оптимальный расход - 3 нас.
-2
-2.5
-3
15
20
25
30
35
40
45
Расход, л/с
Однако все приведенные критерии схожи в том, что по их
значениям нельзя оценить уровень достаточности (недостаточности)
или избыточности интенсивности промывки. Известные рекомендации
в отношении критических величин Nзаб, Wзаб или pос, найденные для
одних условий бурения, практически малопригодны для других. По
ним совершенно невозможно предсказать результаты применения
гидромониторных долот.
На кафедре предложен критерий pэф, названный “эффективным
давлением струи”, который лишен отмеченных недостатков. Величина
pэф вычисляется по формуле:
pэф = pос pдиф ,
(4)
где pдиф - динамическое дифференциальное давление.
pдиф = gLскв + pкп pпл = pст + pкп ,
(5)
где pкп - потери давления в заколонном пространстве,
pпл - пластовое давление,
pст - статическая репрессия,
Lскв - глубина скважины.
Заметим, что впервые предложен критерий промывки, учитывающий
геологические условия бурения - pпл.

45.

1 ,2
220
1
200
2
3
0 ,4
140
0 ,2
120
0
100
1
-0 ,2
80
-0 ,4
60
-0 ,6
40
16
20
24
28
Эффективное давление струи, МПа
160
2,5
2
1,5
1
0,5
0
-0,5
-1
-1,5
1000
32
Р а с х о д ж и д к о с ти , д м 3 /с
5
1
1'
4
2
2'
3
3
Эффективноедавлениеструи, МПа
3'
3'
2
3
1'
2'
1
2
-1
-2
2500
3000
2000
2500
3000
3500
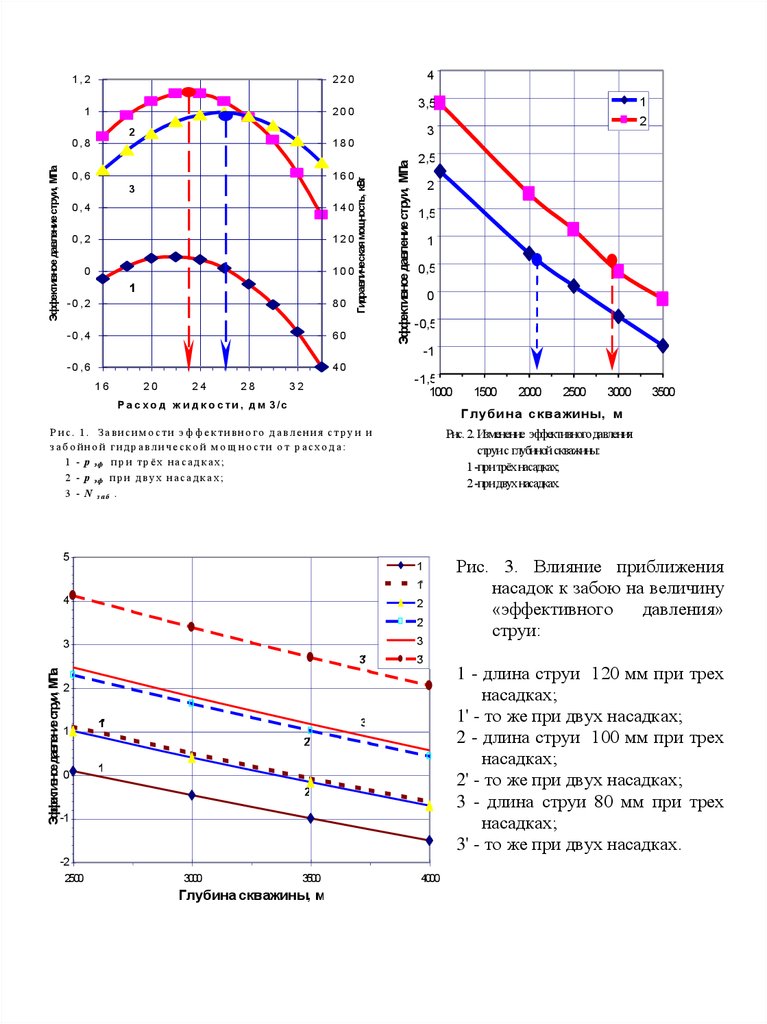
Рис. 2. Изменение эффективного давления
струи с глубиной скважины:
1 -при трёх насадках;
2 -при двух насадках.
2 - p эф п р и д в у х н а с а д к а х ;
3 - N за б .
0
1500
Г л у б и н а с к в а ж и н ы, м
Р и с. 1 . З ави си м о сти э ф ф екти вн о го д авлен и я стр уи и
заб о й н о й ги д р авли ч еско й м о щ н о сти о т р асхо д а:
1 - p эф п р и т р ё х н а с а д к а х ;
1
2
3
180
0 ,6
1
3,5
Гидравлическая мощность, кВт
Эффективное давление струи, МПа
0 ,8
4
3500
Глубина скважины, м
4000
Рис. 3. Влияние приближения
насадок к забою на величину
«эффективного
давления»
струи:
1 - длина струи 120 мм при трех
насадках;
1' - то же при двух насадках;
2 - длина струи 100 мм при трех
насадках;
2' - то же при двух насадках;
3 - длина струи 80 мм при трех
насадках;
3' - то же при двух насадках.

46. Гидравлическая характеристика скважины (ГХС). Гидравлическая характеристика насосов (ГХН). Их совмешение с учетом технологических и техни

Гидравлическая
характеристика скважины
(ГХС).
Гидравлическая
характеристика насосов
(ГХН).
Их совмешение с учетом
технологических и
технических ограничений

47.

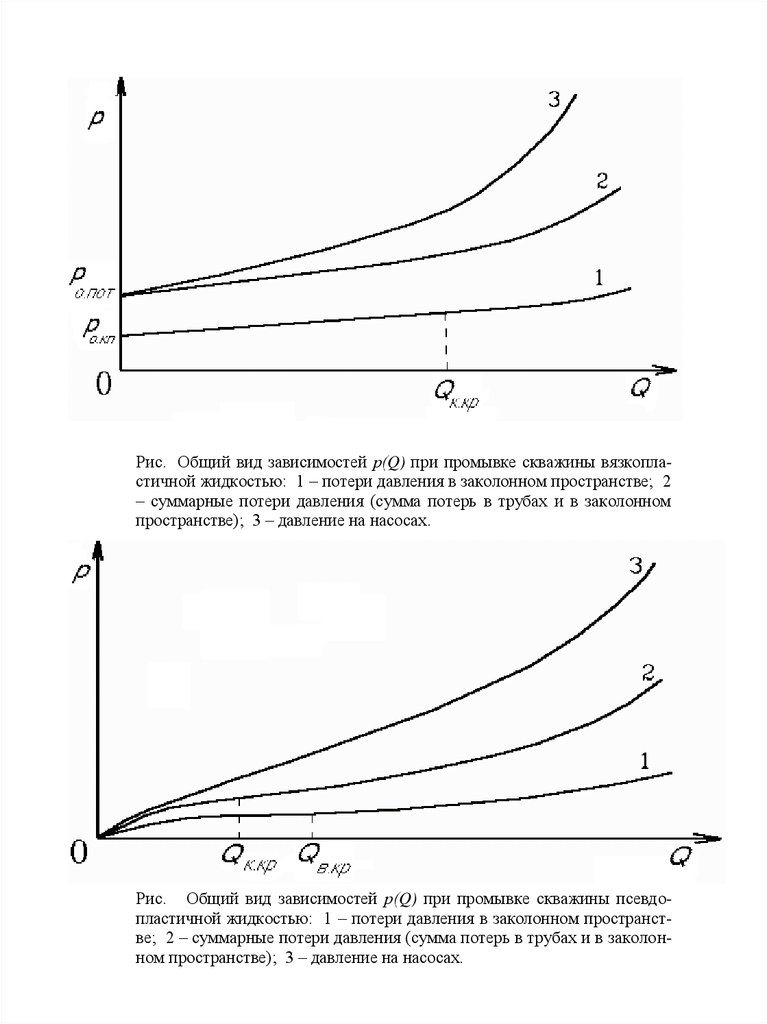
Рис. Общий вид зависимостей р(Q) при промывке скважины вязкопластичной жидкостью: 1 – потери давления в заколонном пространстве; 2
– суммарные потери давления (сумма потерь в трубах и в заколонном
пространстве); 3 – давление на насосах.
Рис. Общий вид зависимостей р(Q) при промывке скважины псевдопластичной жидкостью: 1 – потери давления в заколонном пространстве; 2 – суммарные потери давления (сумма потерь в трубах и в заколонном пространстве); 3 – давление на насосах.

48.

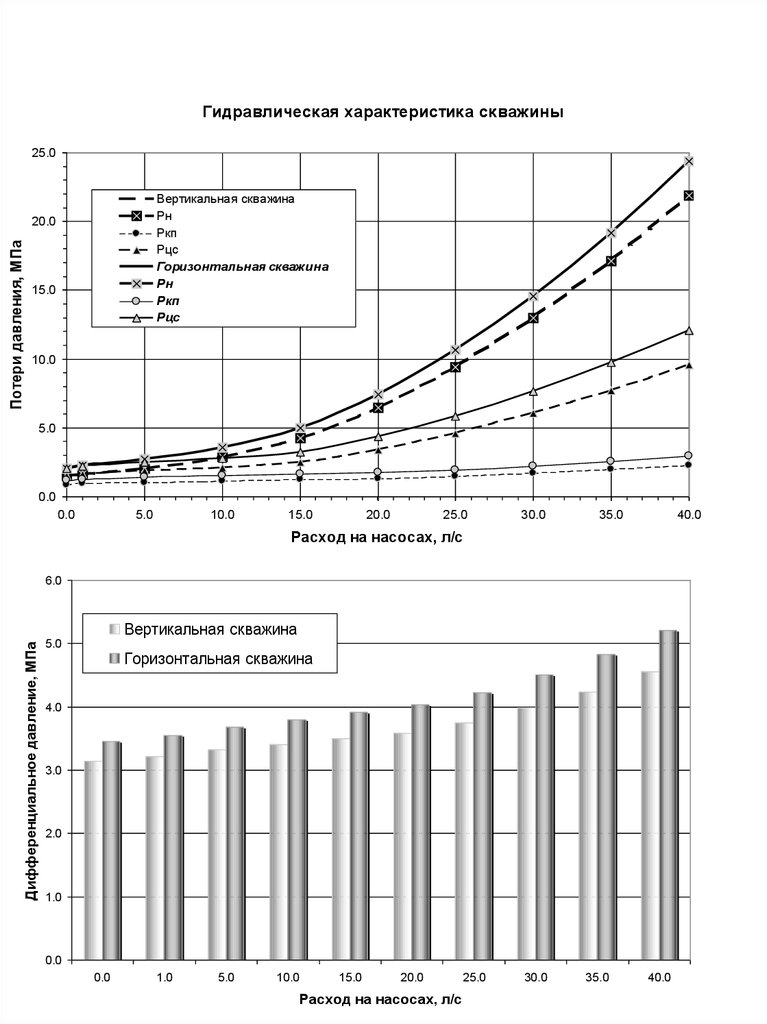
Гидравлическая характеристика скважины
25.0
Вертикальная скважина
Pн
Pкп
Рцс
Горизонтальная скважина
Pн
Pкп
Рцс
Потери давления, МПа
20.0
15.0
10.0
5.0
0.0
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
40.0
Расход на насосах, л/с
Дифференциальное давление, МПа
6.0
Вертикальная скважина
5.0
Горизонтальная скважина
4.0
3.0
2.0
1.0
0.0
0.0
1.0
5.0
10.0
15.0
20.0
Расход на насосах, л/с
25.0
30.0
35.0
40.0

49.

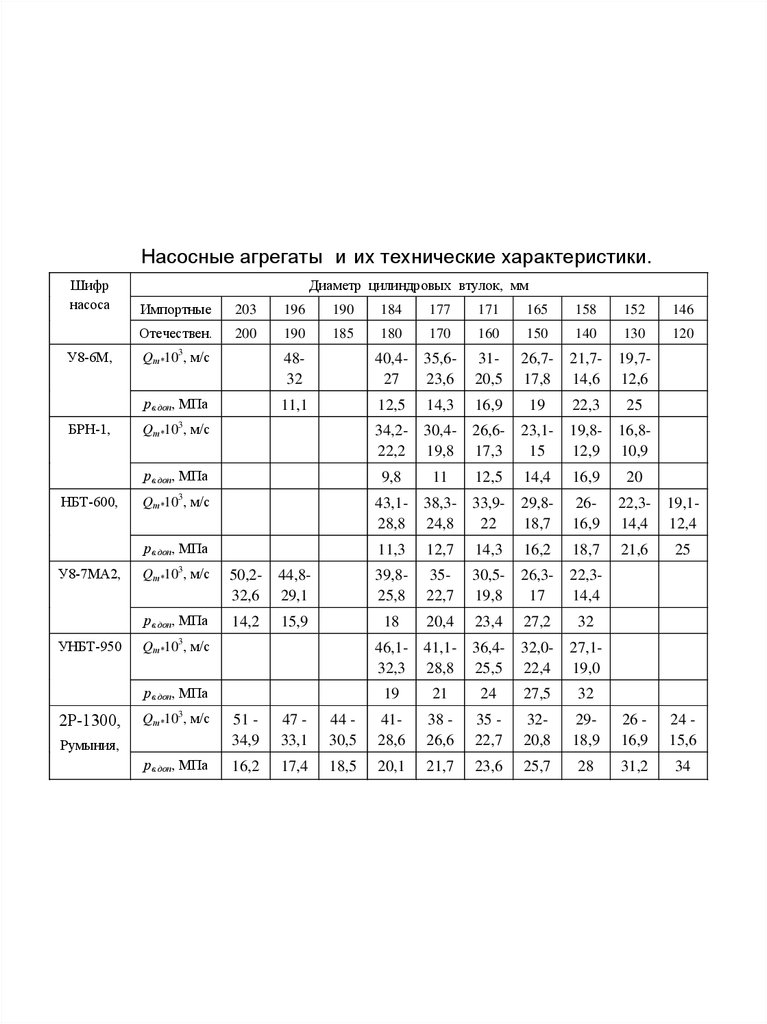
Насосные агрегаты и их технические характеристики.
Шифр
насоса
У8-6М,
БРН-1,
НБТ-600,
У8-7МА2,
УНБТ-950
2Р-1300,
Диаметр цилиндровых втулок, мм
Импортные
203
196
190
184
177
171
165
158
152
146
Отечествен.
200
190
185
180
170
160
150
140
130
120
3
Qт*10 , м/с
4832
40,427
35,623,6
3120,5
26,717,8
рв.доп, МПа
11,1
12,5
14,3
16,9
19
Qт*10 , м/с
34,222,2
30,4- 26,6- 23,119,8 17,3
15
рв.доп, МПа
9,8
3
3
11
12,5
21,7- 19,714,6 12,6
22,3
25
19,8- 16,812,9 10,9
14,4
16,9
20
Qт*10 , м/с
43,128,8
38,3- 33,9- 29,824,8
22
18,7
2616,9
22,3- 19,114,4 12,4
рв.доп, МПа
11,3
12,7
14,3
16,2
18,7
21,6
25
22,314,4
3
Qт*10 , м/с
50,232,6
44,829,1
39,825,8
3522,7
30,5- 26,319,8
17
рв.доп, МПа
14,2
15,9
18
20,4
23,4
3
27,2
32
Qт*10 , м/с
46,132,3
рв.доп, МПа
19
21
24
27,5
32
3
41,1- 36,4- 32,028,8 25,5 22,4
27,119,0
Qт*10 , м/с
51 34,9
47 33,1
44 30,5
4128,6
38 26,6
35 22,7
3220,8
2918,9
26 16,9
24 15,6
рв.доп, МПа
16,2
17,4
18,5
20,1
21,7
23,6
25,7
28
31,2
34
Румыния,

50.

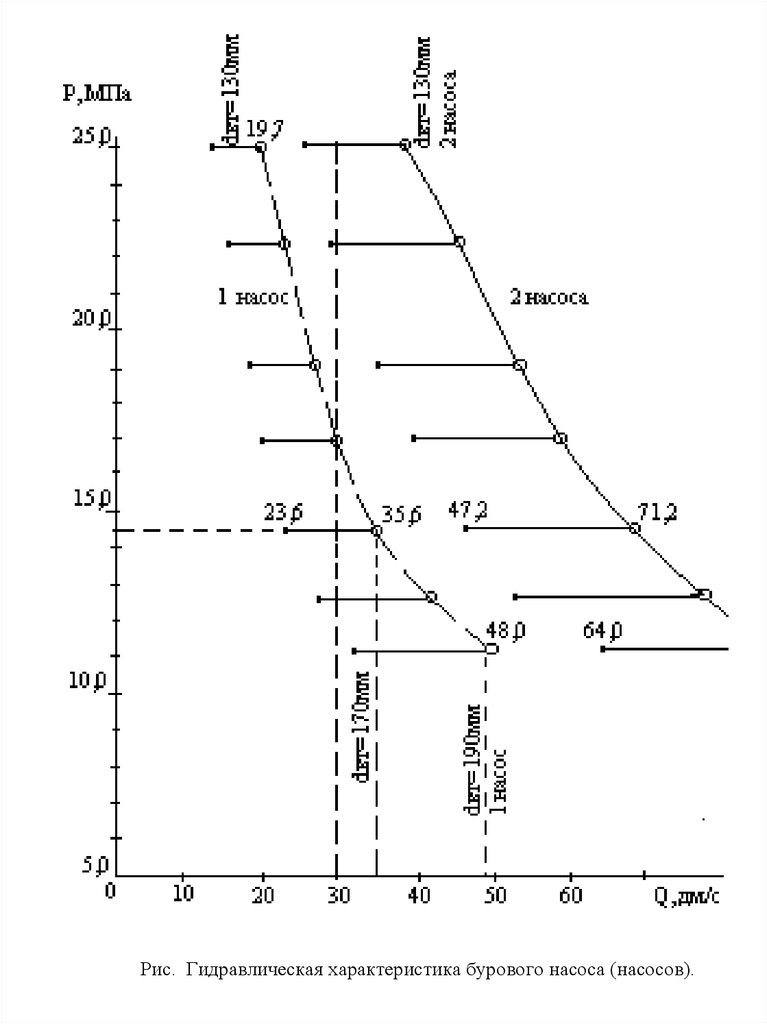
Рис. Гидравлическая характеристика бурового насоса (насосов).

51.

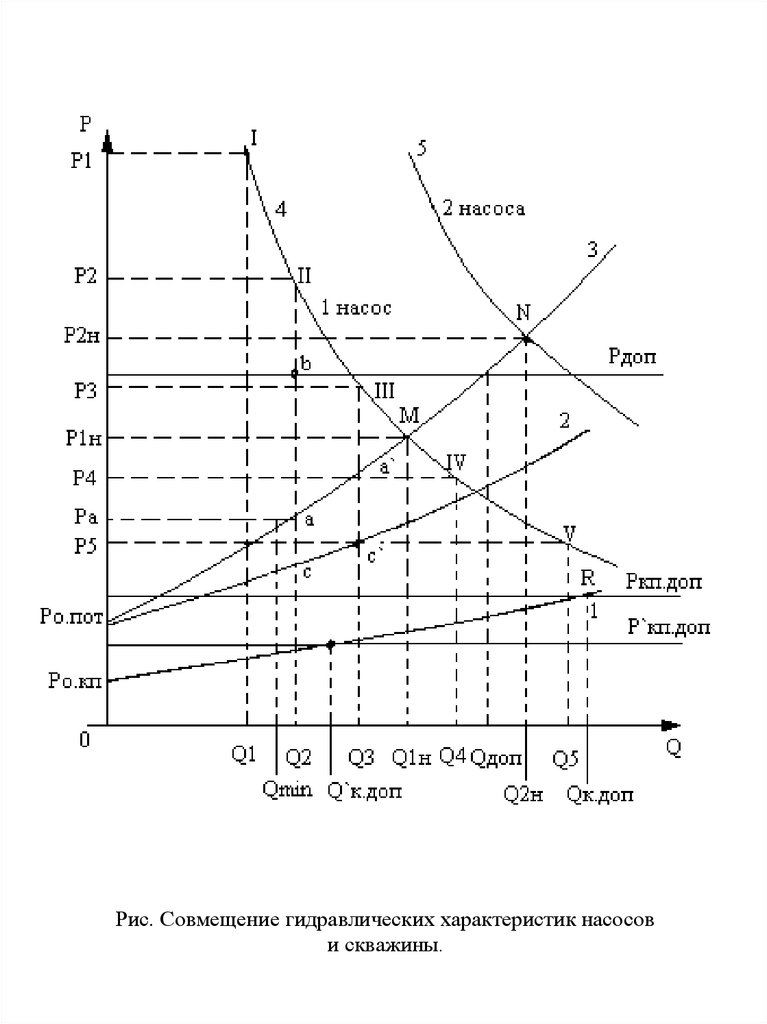
Рис. Совмещение гидравлических характеристик насосов
и скважины.

52.

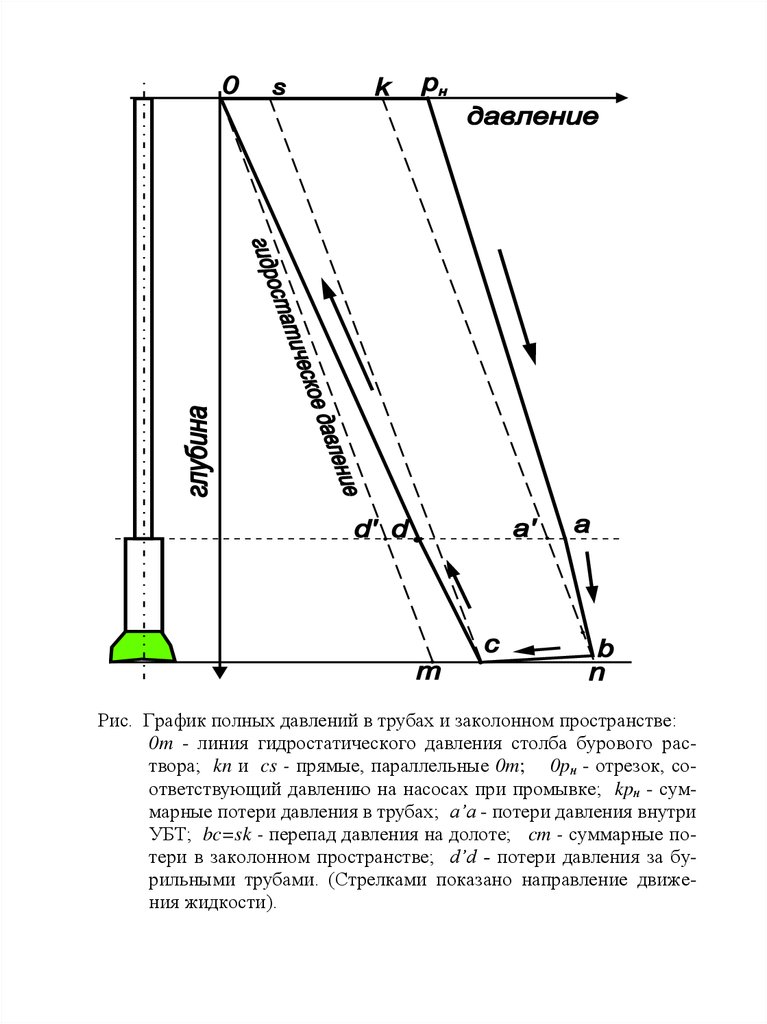
Рис. График полных давлений в трубах и заколонном пространстве:
0m - линия гидростатического давления столба бурового раствора; kn и cs - прямые, параллельные 0m; 0pн - отрезок, соответствующий давлению на насосах при промывке; kpн - суммарные потери давления в трубах; a’a - потери давления внутри
УБТ; bc=sk - перепад давления на долоте; cm - суммарные потери в заколонном пространстве; d’d - потери давления за бурильными трубами. (Стрелками показано направление движения жидкости).

53.

Методика определения гидродинамических
давлений
при равномерном движении труб.
Постановка задачи. Вывод уравнения скорости спутного
потока.
Попытки строго теоретического решения задачи выглядят не
очень убедительными, прежде всего, по причине неустойчивости во
времени эпюры скоростей, о чем говорилось выше. С другой стороны,
не вызывает у практиков вдохновения громоздкость решений,
требующих применения вспомогательных таблиц и т.п. и потому трудно
реализуемые даже на ЭВМ.
В практике расчетов гидродинамического давления pгд или
допустимых скоростей uдоп спуска (подъема) колонн предпочтение (и
вполне заслуженное) отдается методике, предложенной впервые Ормсби
и базирующейся на использовании принципа суперпозиции и понятия
эквивалентной скорости. Принимается, что суммарный эффект влияния
Qск и Qвт “эквивалентен” потерям давления при промывке скважины с
эквивалентной скоростью vэкв , определяемой по формуле:
vэкв = uт Kск + uт dн2/(D2 – dн2).
Перейдем к эквивалентному расходу:
Qэкв = vэкв (D2 - dн2)/ 4;
Qэкв = uт Kск (D2 - dн2)/ 4 + uт dн2/4.
Первое слагаемое в уравнении - это отражение влияния Qск на
pгд, а второе – численно равно Qвт.
Чтобы найти pгд для заданной скорости движения uт в случае
движения одноразмерной колонны, достаточно расход Qэкв считать
расходом промывки Q через заданную колонну в той же скважине и,
пользуясь известными методиками и формулами для промывки, найти
потери давления в затрубном пространстве. Эти потери и будут
численно равны искомому гидродинамическому давлению при спуске
колонны (с положительным знаком) или при ее подъеме (с обратным
знаком).
Kск=0,5 0,38 , где = r/R=dн/D.