Похожие презентации:
Произвольная система сил. Условие и уравнения равновесия для произвольной системы сил. Теоремы Пуансо
1. Произвольная система сил. Условие и уравнения равновесия для произвольной системы сил. Теоремы Пуансо и о моменте равнодействующей
2.
• Произвольная система сил• Теорема Пуансо (Основная теорема
статики)
• Условие равновесия произвольной системы
сил
• Теорема Вариньона
3. Произвольная система сил
• Произвольная система сил – система сил,линии действия которых могут не
пересекаются в одной точке.
! сходящаяся система сил - частный случай
произвольной.
4.
Теорема ПуансоГлавным моментом M A системы сил {F1 , F2 ,..., Fn }
относительно точки А называется сумма моментов
всех сил системы относительно этой точки:
M A M A (F )
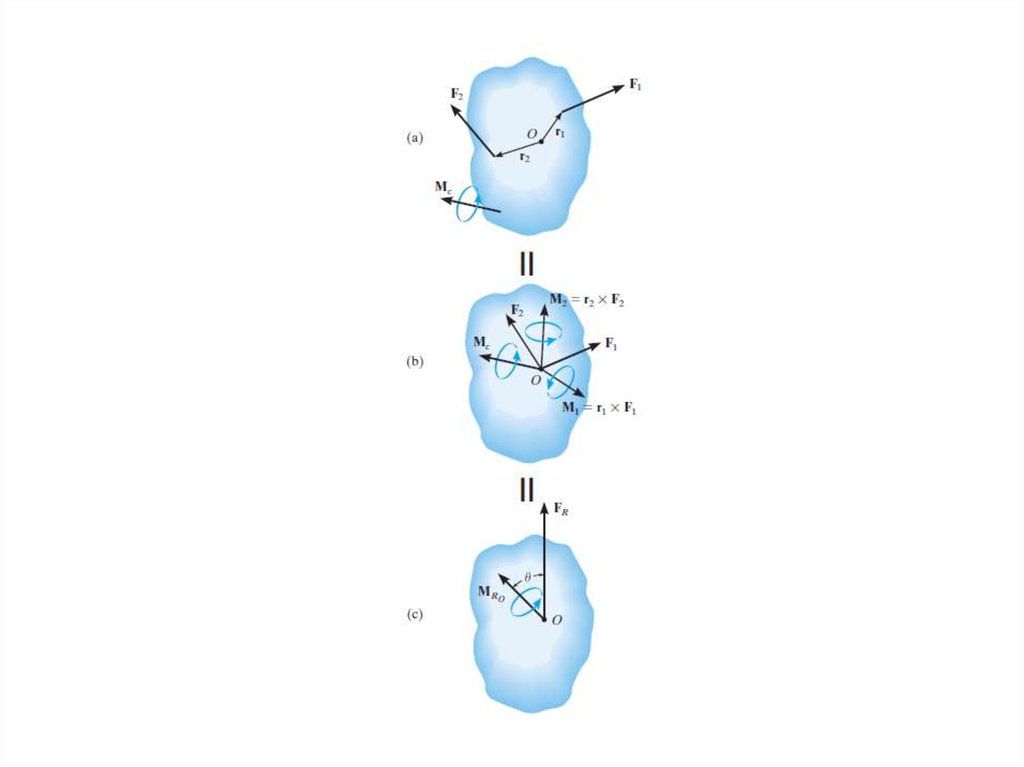
Теорема. Произвольная система сил {F1 , F2 ,..., Fn } ,
действующая на твердое тело, эквивалентна
системе, состоящей из силы R и пары сил {P1 , P2 } .
Сила равна главному вектору системы сил и
приложена в произвольно выбранной точке А
(центре приведения), момент пары равен главному
моменту системы сил относительно этой точки:
{F1 , F2 ,..., Fn }экв.{R , {P1 , P2 }} и M ({P1 , P2 }) M A
5.
6.
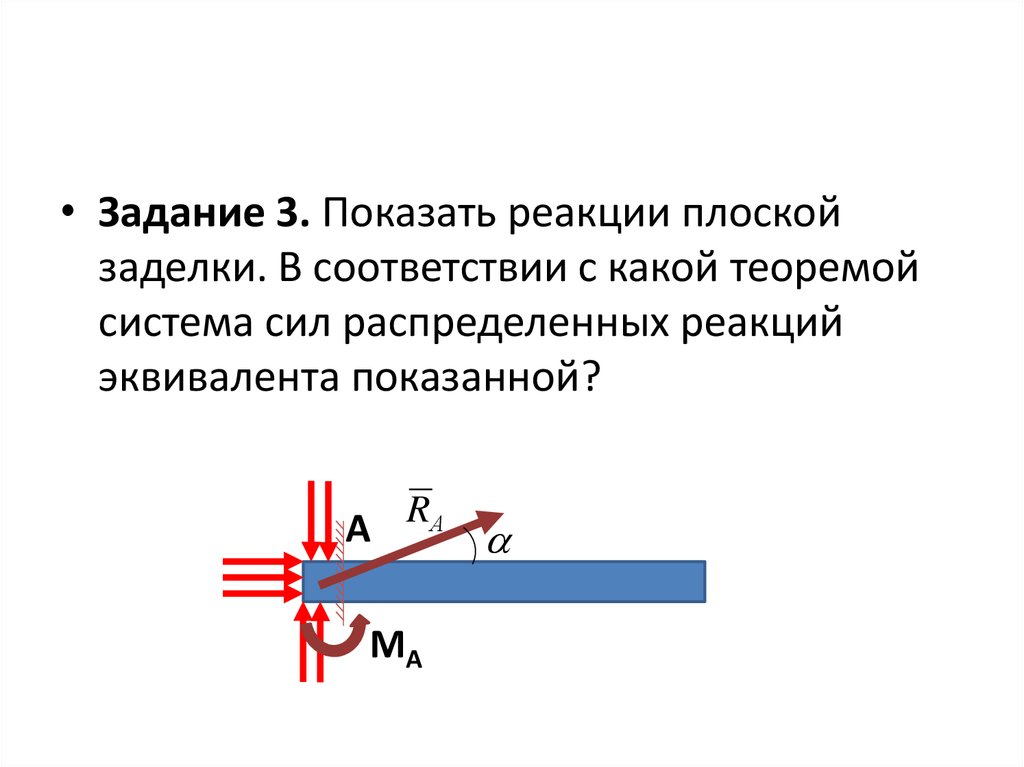
• Задание 3. Показать реакции плоскойзаделки. В соответствии с какой теоремой
система сил распределенных реакций
эквивалента показанной?
А
RА
MА
7. Условие равновесия произвольной системы сил
R 0, M A 0• Плоская система сил
X 0, Y 0, M
A
0
• Пространственная система сил
X 0, Y 0, Z 0,
M 0, M 0, M
x
y
z
0
8.
• Плоская система сил1) X 0,
2) X 0,
Y 0, M 0
M 0, M 0,
A
B
A
причем ось x не перпендикулярна АВ
3) M С 0,
M
B
0,
А, В, С одной прямой
M
A
0,
9. Теорема Вариньона
Если система имеетравнодействующую, то ее
момент относительно любого
центра (или оси) равен сумме
моментов всех сил системы
относительно того же центра
(или оси)
M A ( F ) M A ( Fx ) M A ( Fy )
10.
M O ( F ) M O ( Fx ) M O ( Fy )11.
• Задание 3. Определить момент силы Fотносительно точки K по теореме
Вариньона, если длины сторон
прямоугольника 2 и 7.
M K ( F ) M K ( Fx ) M K ( Fy ) 2F cos 7 F sin
F
Fx
K
Fy







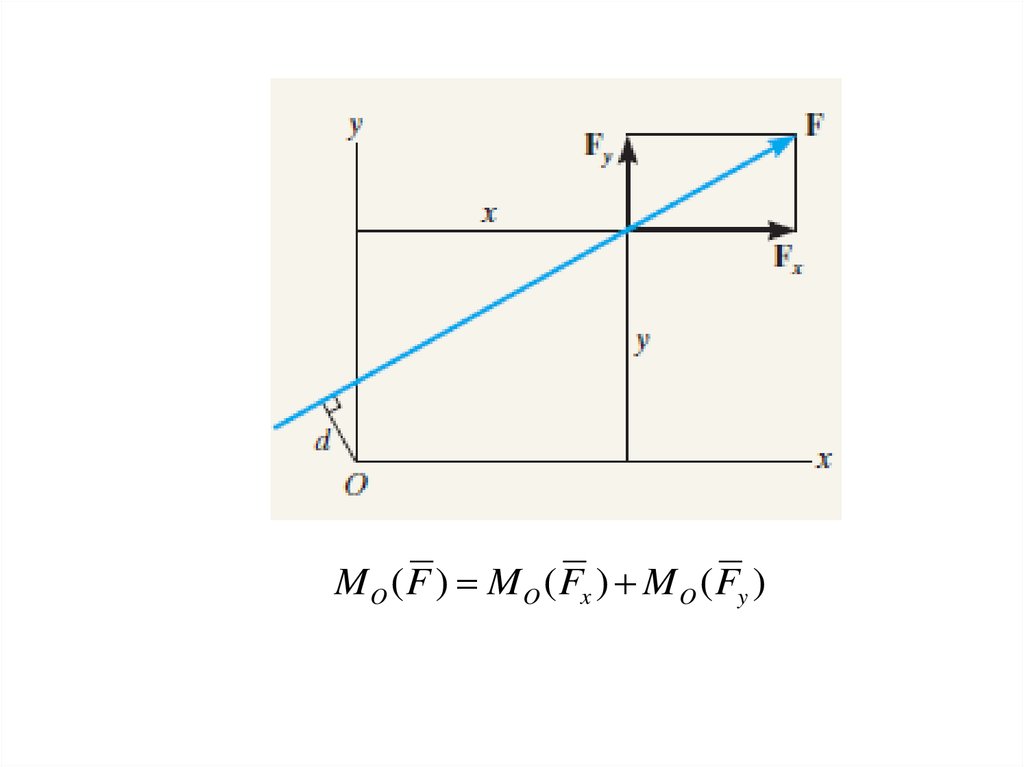

 Физика
Физика








