Методы поиска решений в пространстве состояний

1.

Методы поиска решений в
пространстве состояний
1

2.

Поиск решений в пространстве состояний задачи
нахождение пути на графе от вершины,
представляющей
начальное
состояние,
к
вершине (вершинам), представляющей целевое
состояние.
Методы поиска решений подразделяются
на:
• методы слепого перебора
(неинформированные)
• методы направленного перебора
(эвристические).
2

3.

Методы слепого перебора
• метод поиска в ширину,
• метод поиска в глубину,
• метод равных цен.
Рассмотрим деревья, а не произвольные
графы. Для перебора деревья проще
графов прежде всего потому, что путь от
корня до данной вершины единственен.
3

4.

Глядя на граф, человек сразу видит решение,
т.к. граф обозрим. Но для графов больших
размеров все выглядит гораздо сложнее.
Компьютер находится в положении человека с
микроскопом, который способен видеть лишь
1 см2.
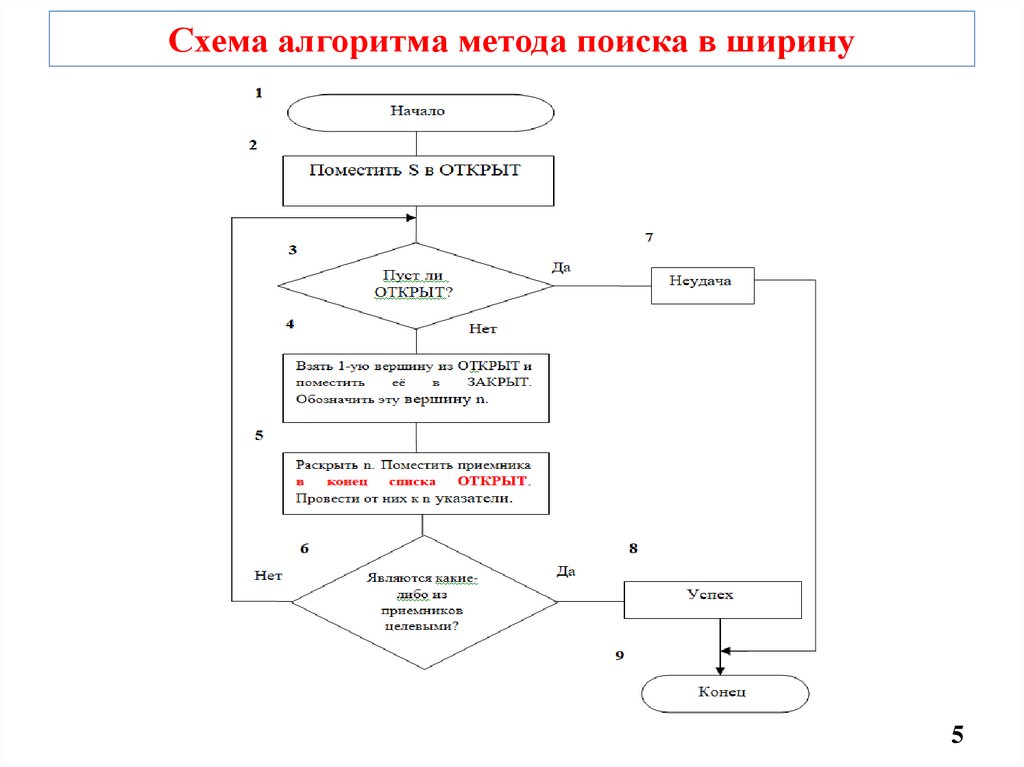
• Список ЗАКРЫТ – вершины были
исследованы и в настоящий момент не
представляют интереса.
• Список ОТКРЫТ – вершины, которые
предлагаются для исследования на
следующих шагах.
4

5.

Схема алгоритма метода поиска в ширину
5

6.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
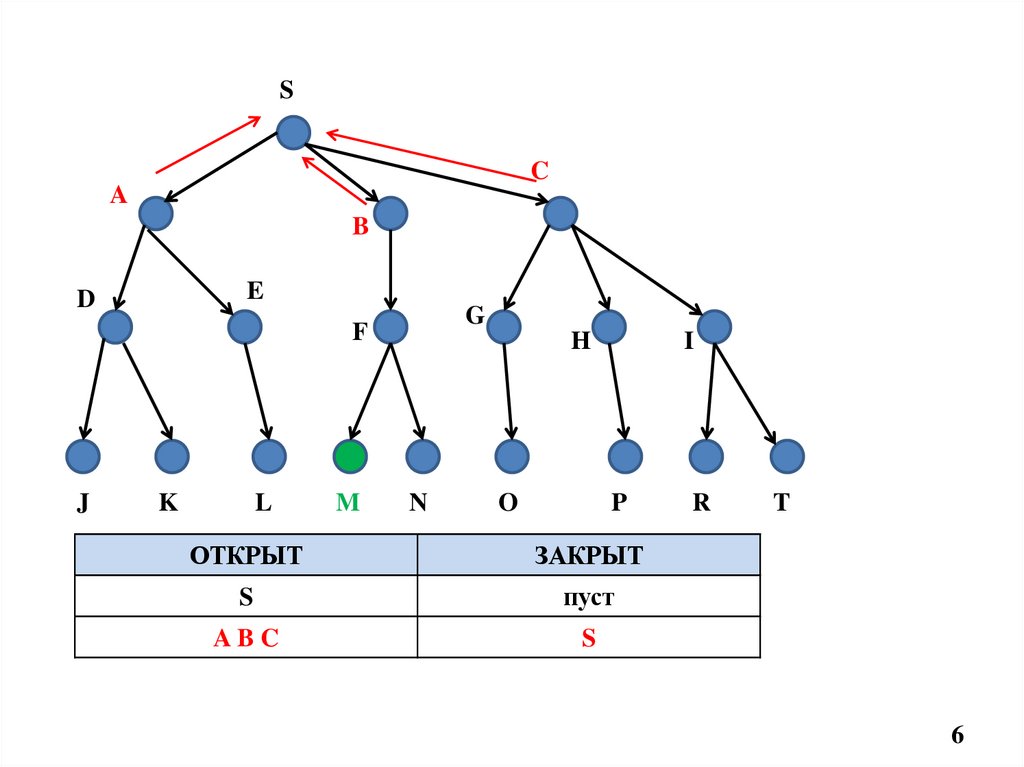
ОТКРЫТ
ЗАКРЫТ
S
пуст
ABC
S
R
T
6

7.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
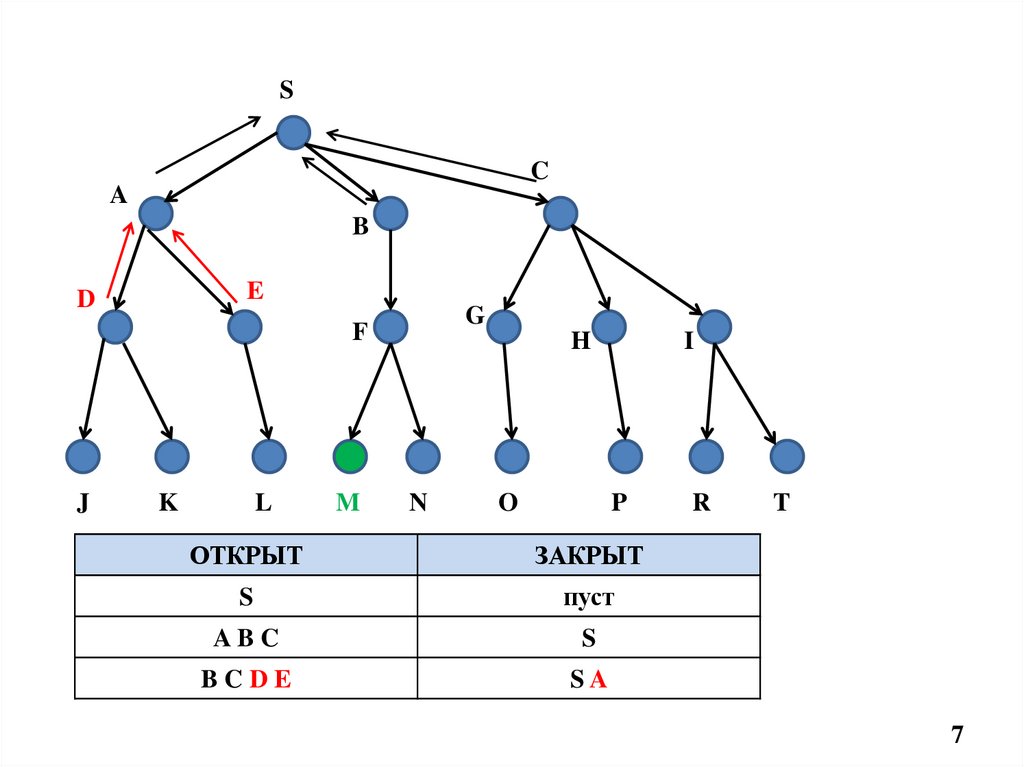
ОТКРЫТ
ЗАКРЫТ
S
пуст
ABC
S
BCDE
SA
R
T
7

8.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
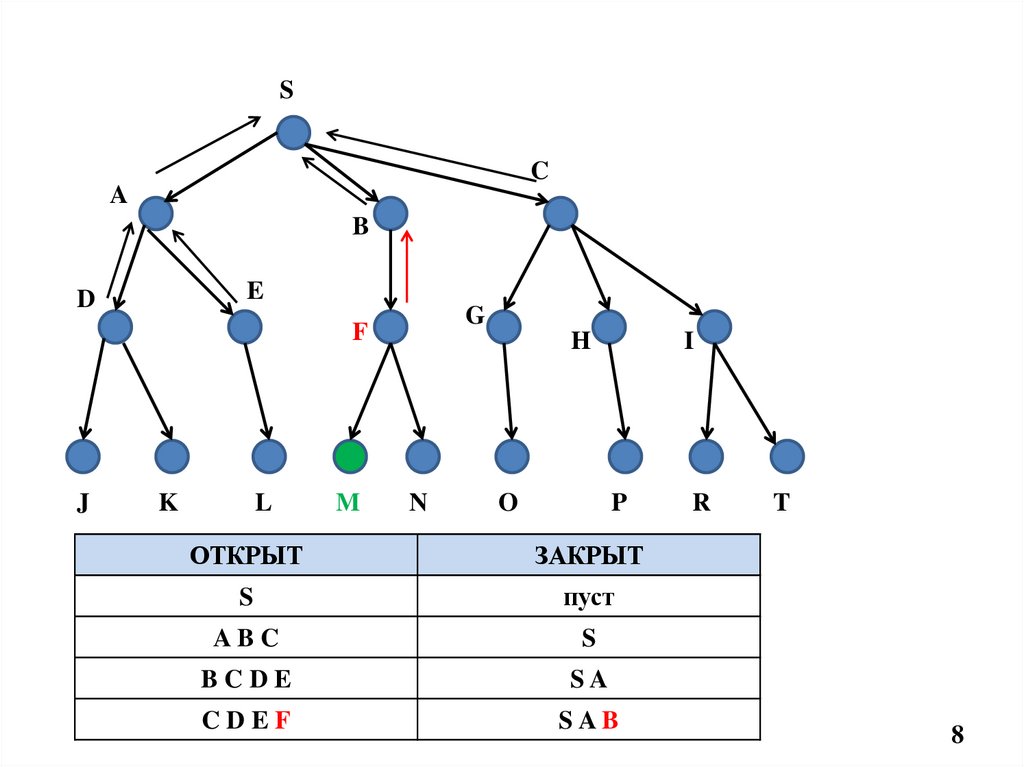
ОТКРЫТ
ЗАКРЫТ
S
пуст
ABC
S
BCDE
SA
CDEF
SAB
R
T
8

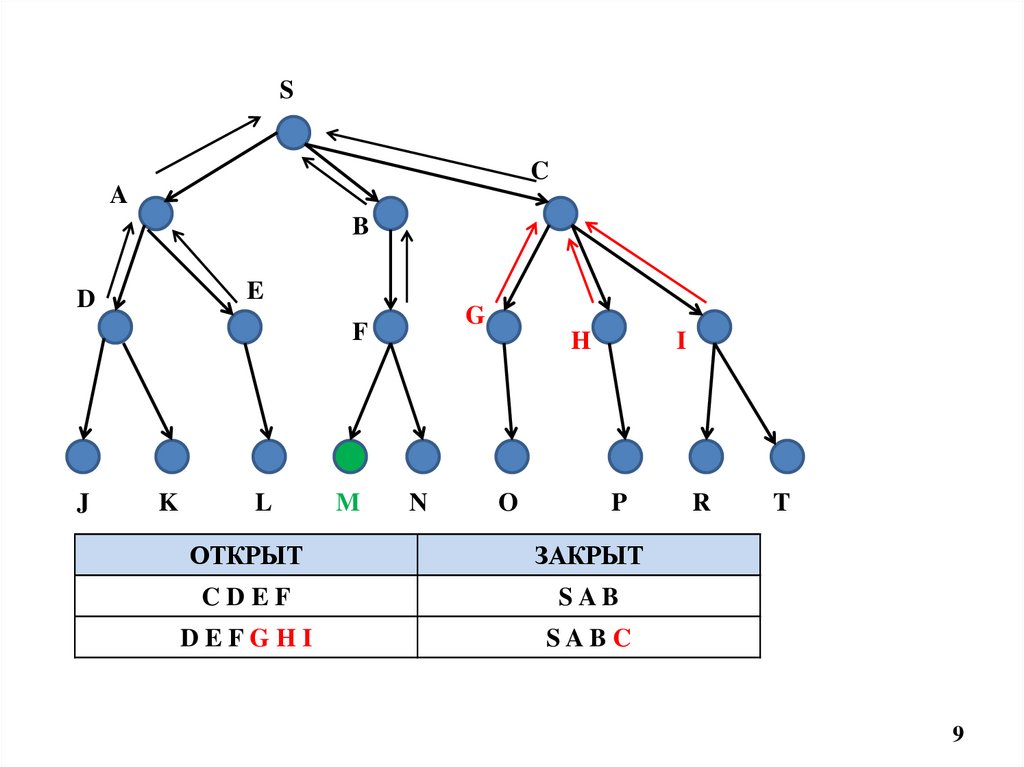
9.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
CDEF
SAB
DEFGHI
SAB C
R
T
9

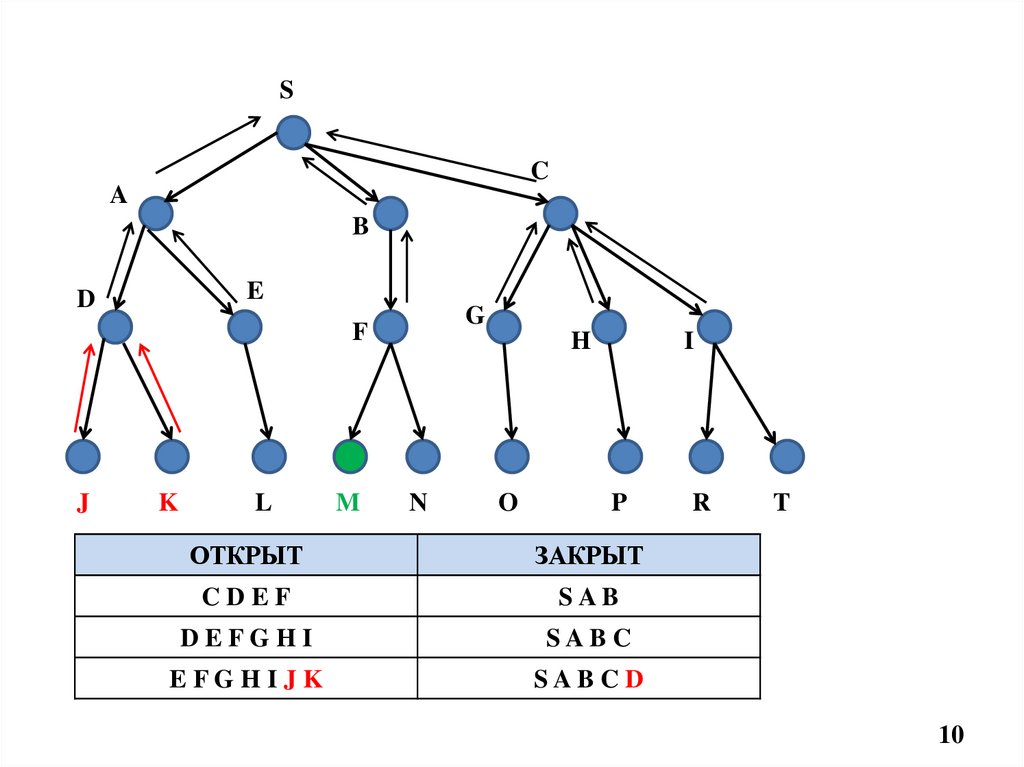
10.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
CDEF
SAB
DEFGHI
SAB C
EFGHIJK
SAB CD
R
T
10

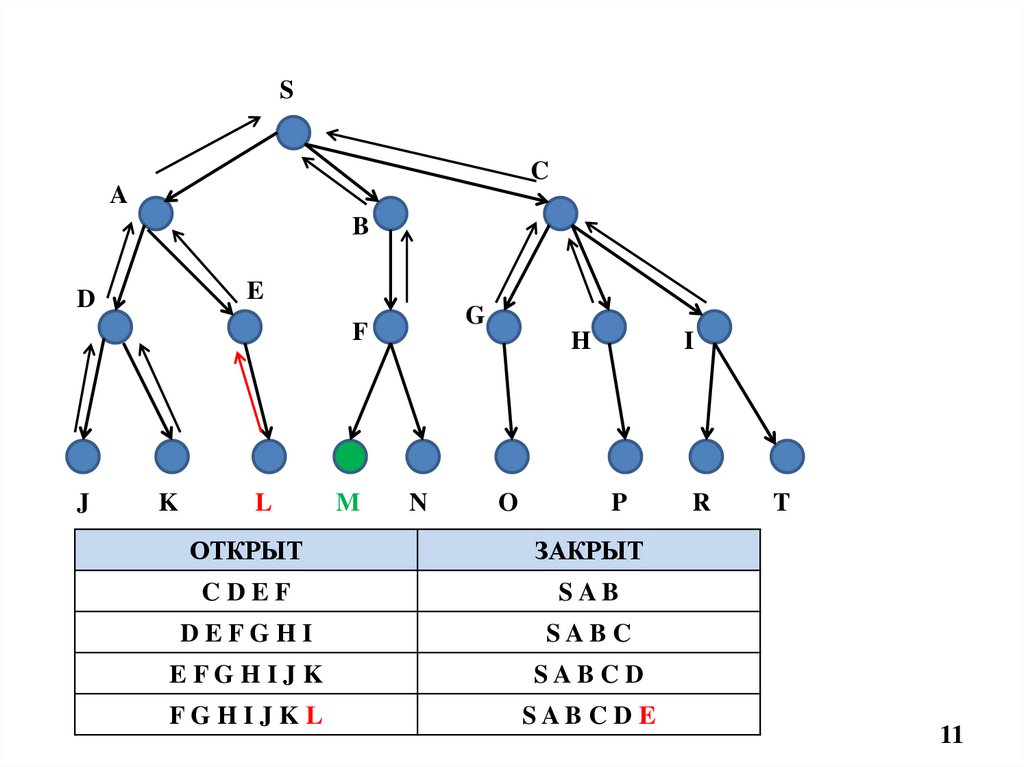
11.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
CDEF
SAB
DEFGHI
SAB C
EFGHIJK
SAB CD
FGHIJKL
SAB CD E
R
T
11

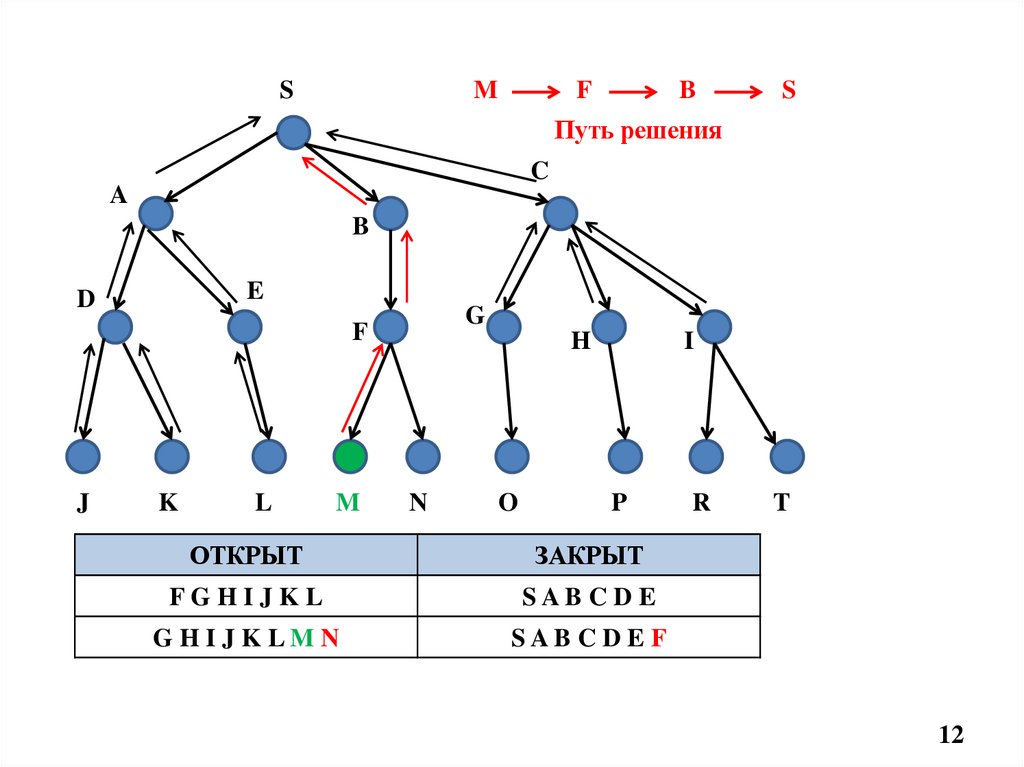
12.

S
M
F
B
S
Путь решения
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
FGHIJKL
SAB CD E
GHIJKLMN
SAB CD E F
R
T
12

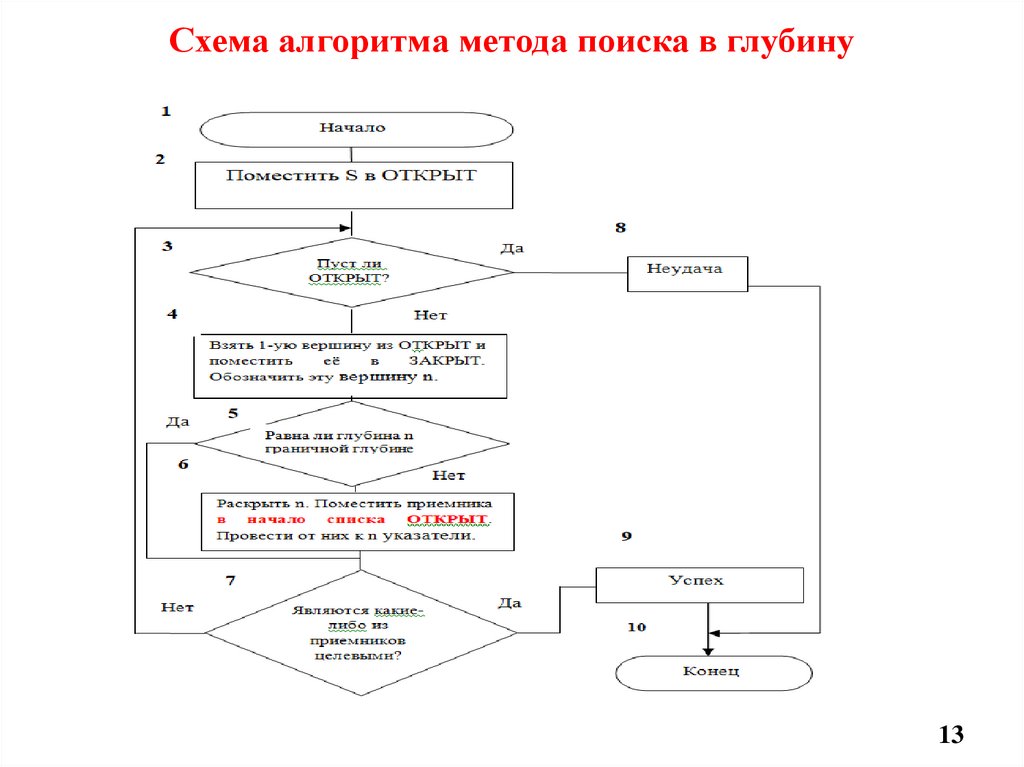
13.

Схема алгоритма метода поиска в глубину
13

14.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
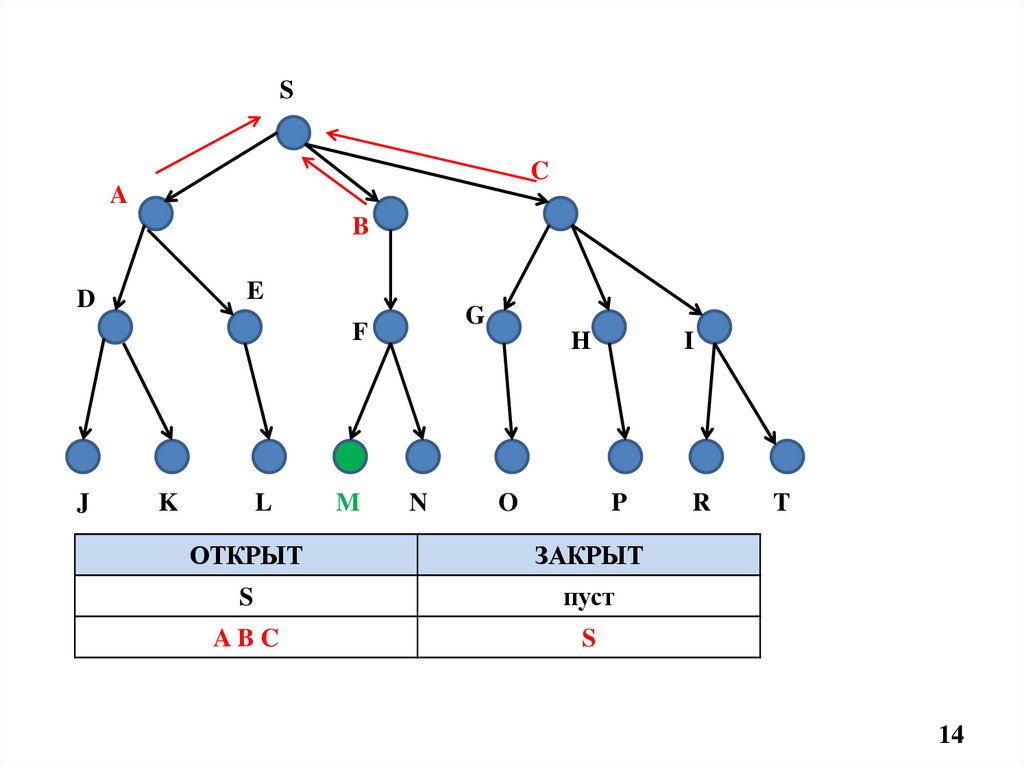
ОТКРЫТ
ЗАКРЫТ
S
пуст
ABC
S
R
T
14

15.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
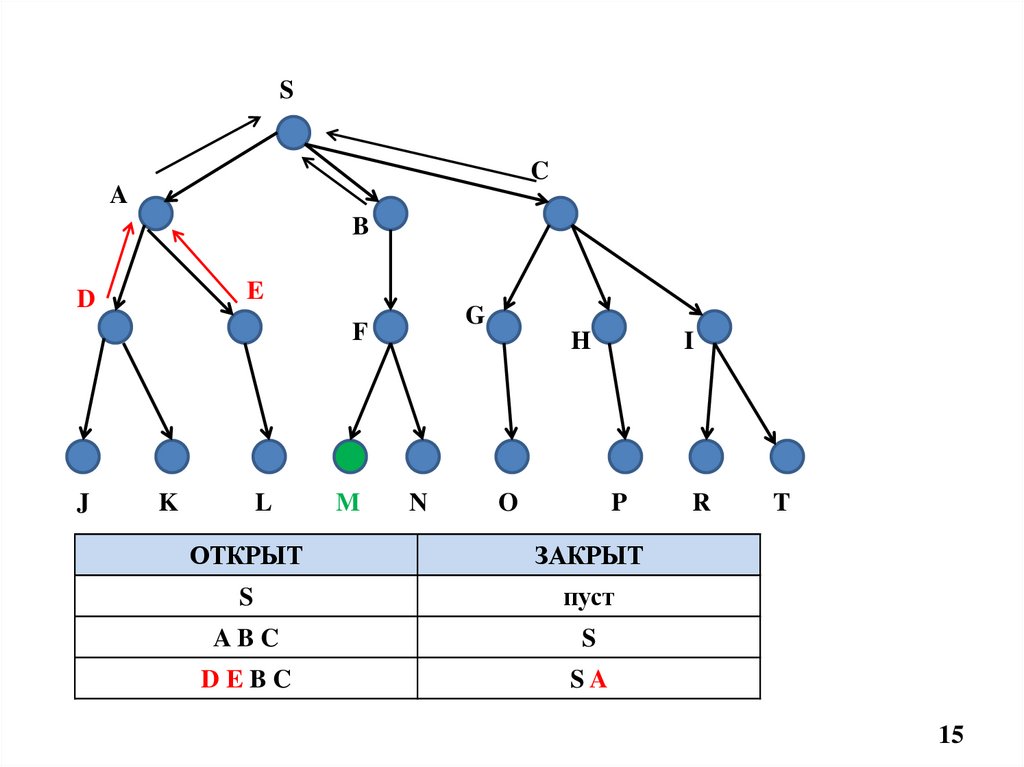
ОТКРЫТ
ЗАКРЫТ
S
пуст
ABC
S
DEBC
SA
R
T
15

16.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
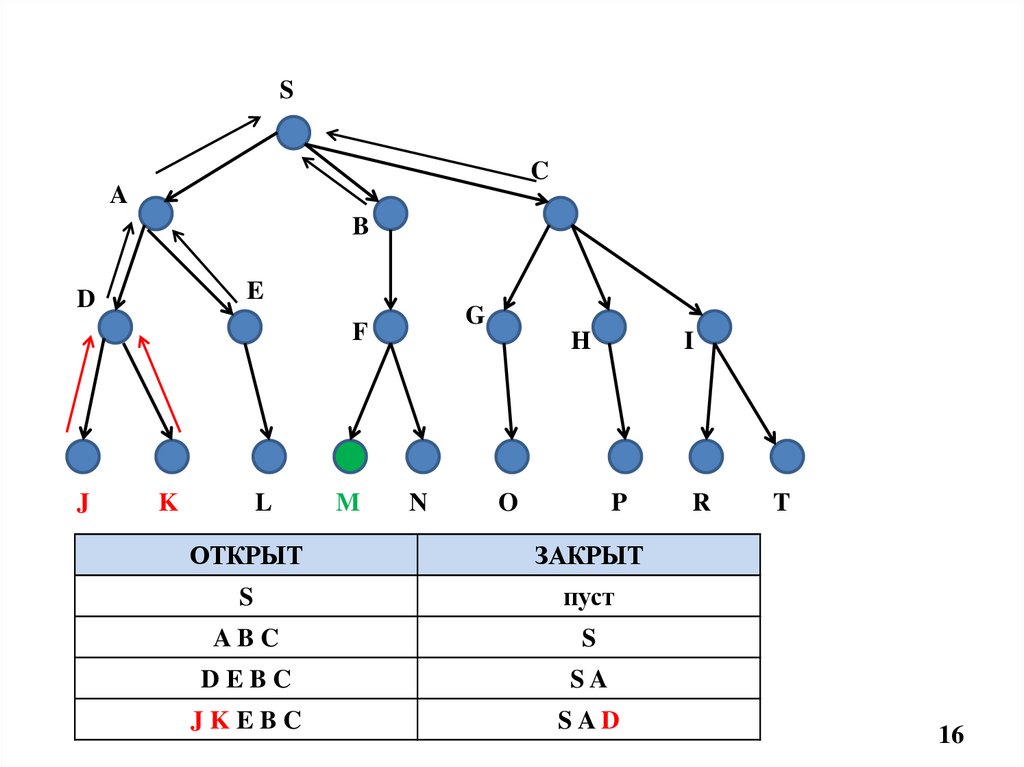
ОТКРЫТ
ЗАКРЫТ
S
пуст
ABC
S
DEBC
SA
JKEBC
SAD
R
T
16

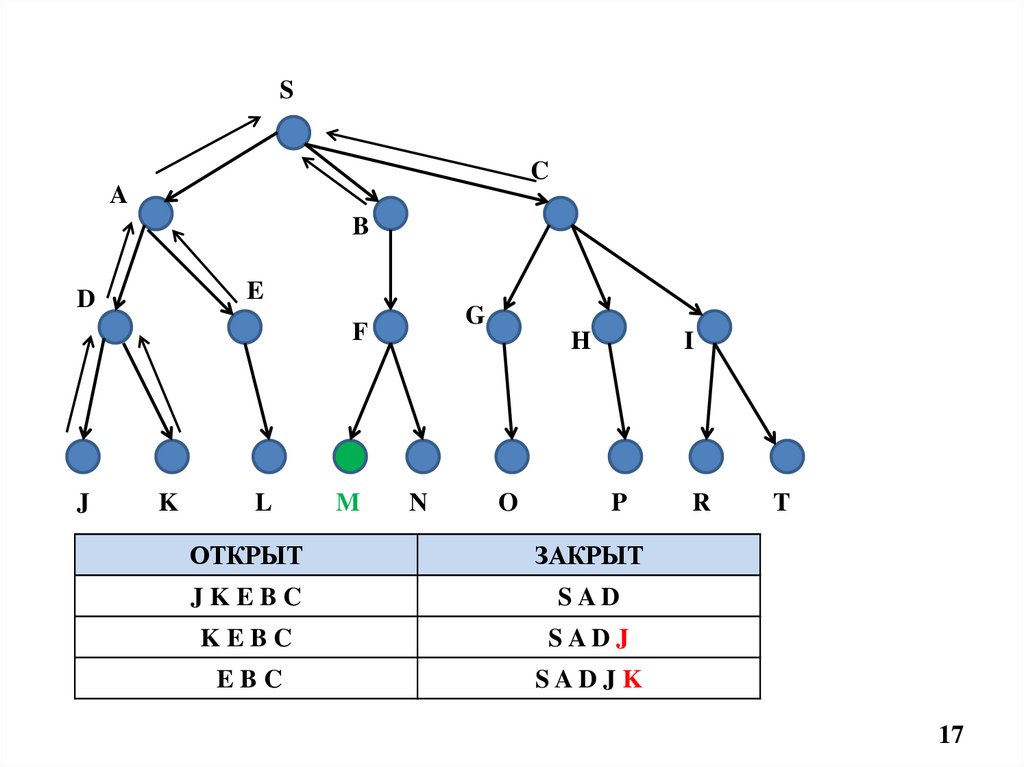
17.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
JKEBC
SAD
KEBC
SAD J
EBC
SAD JK
R
T
17

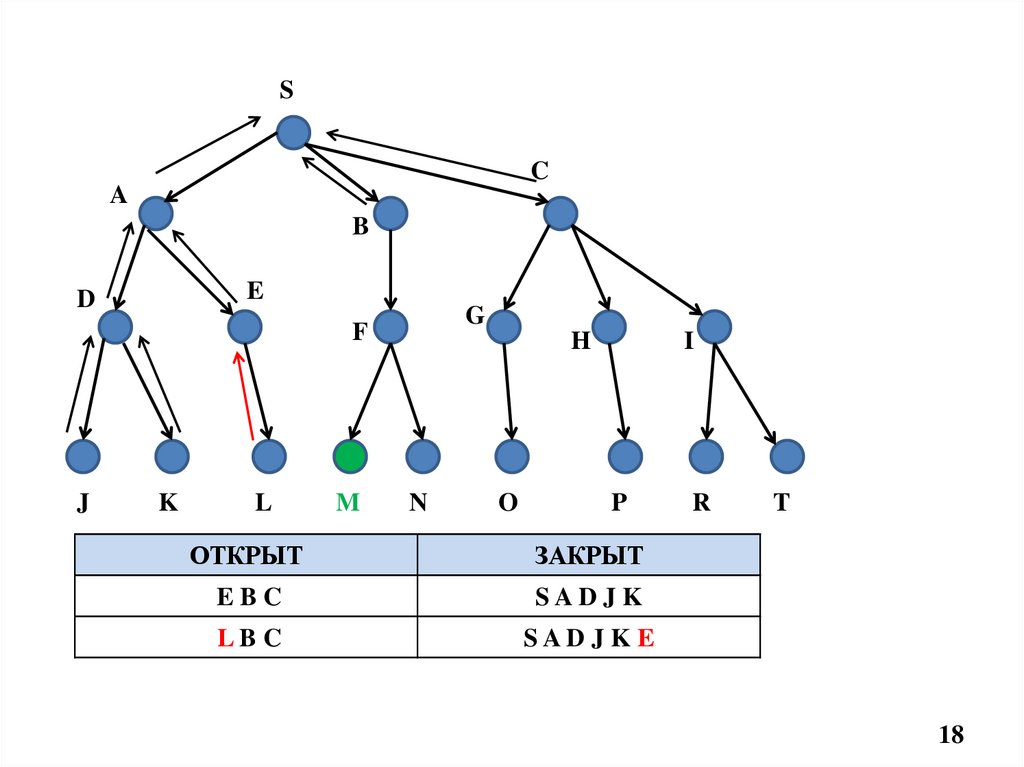
18.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
EBC
SAD J K
LBC
SAD J K E
R
T
18

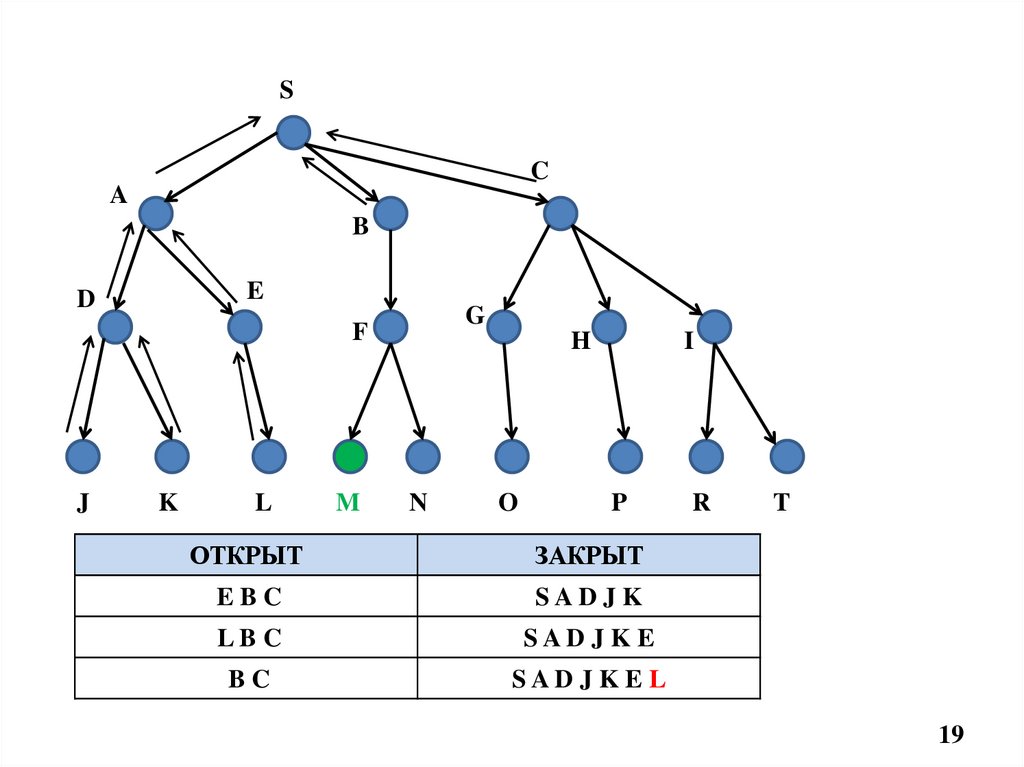
19.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
EBC
SAD J K
LBC
SAD J K E
BC
SAD JK EL
R
T
19

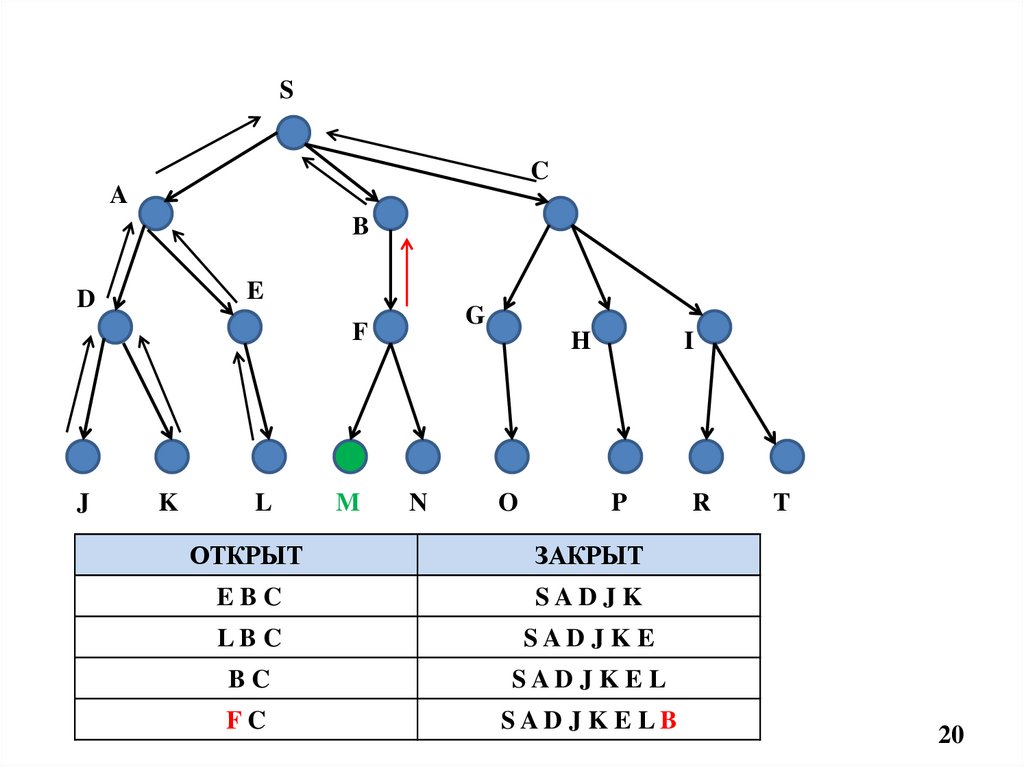
20.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
EBC
SAD J K
LBC
SAD J K E
BC
SAD JK EL
FC
SAD J K ELB
R
T
20

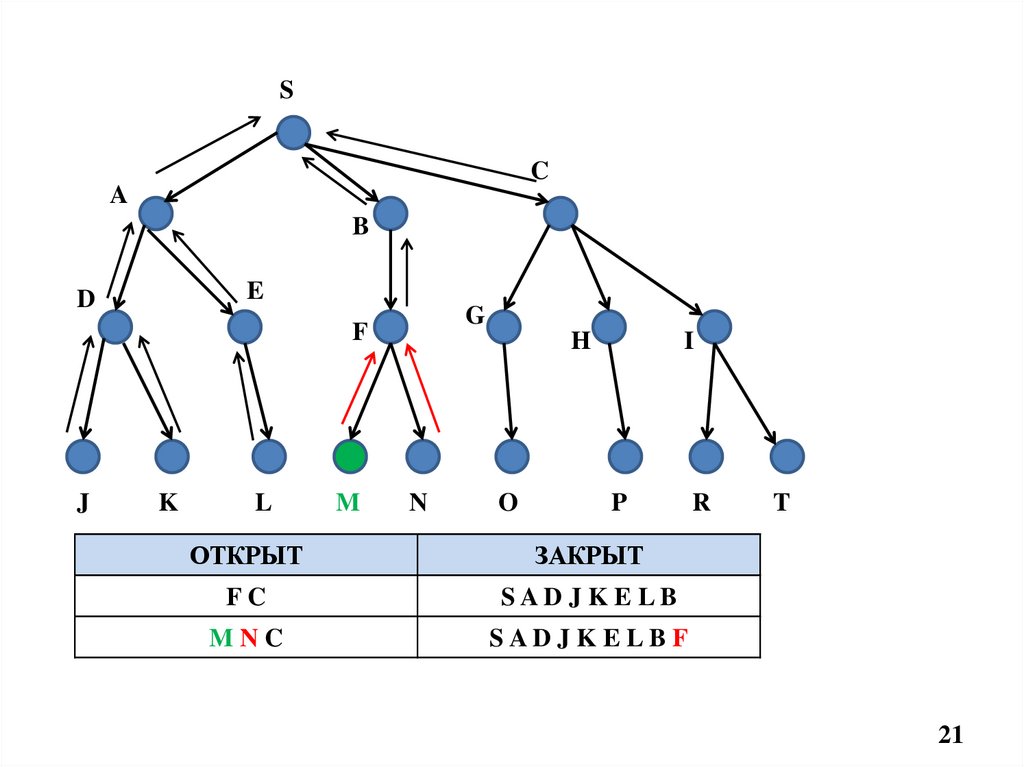
21.

S
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
ОТКРЫТ
ЗАКРЫТ
FC
SAD J K ELB
MNC
SAD J K ELB F
R
T
21

22.

S
M
F
B
S
Путь решения
C
A
B
E
D
G
F
J
K
L
M
H
N
O
I
P
R
T
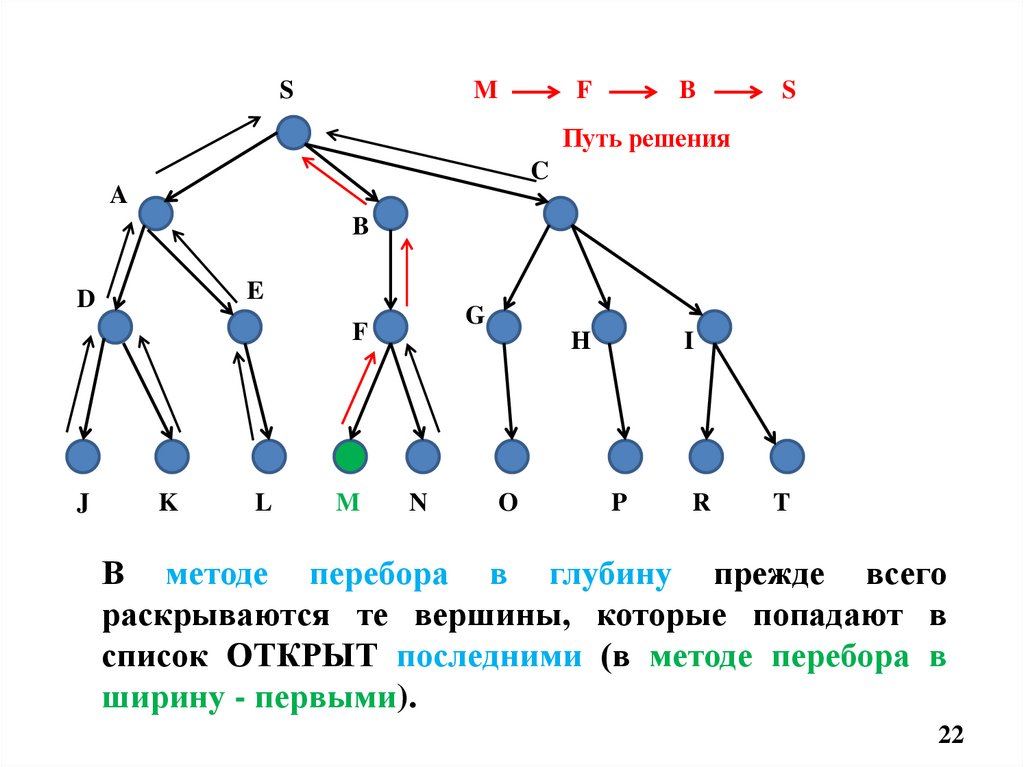
В методе перебора в глубину прежде всего
раскрываются те вершины, которые попадают в
список ОТКРЫТ последними (в методе перебора в
ширину - первыми).
22

23.

Метод равных цен
• является более общим вариантом метода поиска в ширину и
позволяет найти некоторый путь от начальной вершины к
целевой, стоимость которого минимальна. При этом
предполагается, что задана функция стоимости c(ni, nj), дающая
стоимость перехода от вершины ni к вершине nj (трудоемкость
использования
некоторого
правила
продукций).
При
реализации метода равных цен запоминается стоимость пути,
построенного от начальной вершины S к вершине n. Обозначим
ее g(n):
g(s)=0
g(nj)= g(ni)+ с(ni,nj),
где ni – родитель nj.
• Алгоритм поиска решения методом равных цен отличается от
алгоритма поиска в ширину, что для очередного раскрытия
выбирается та вершина из списка ОТКРЫТ, которая имеет
минимальную стоимость, т.е. в методе равных цен вершины
23
раскрываются в порядке возрастания стоимости .

24.

S
2
C
A
1
1
B
2
D
2
E
3
F
1
2
1
3
J
I
H
G
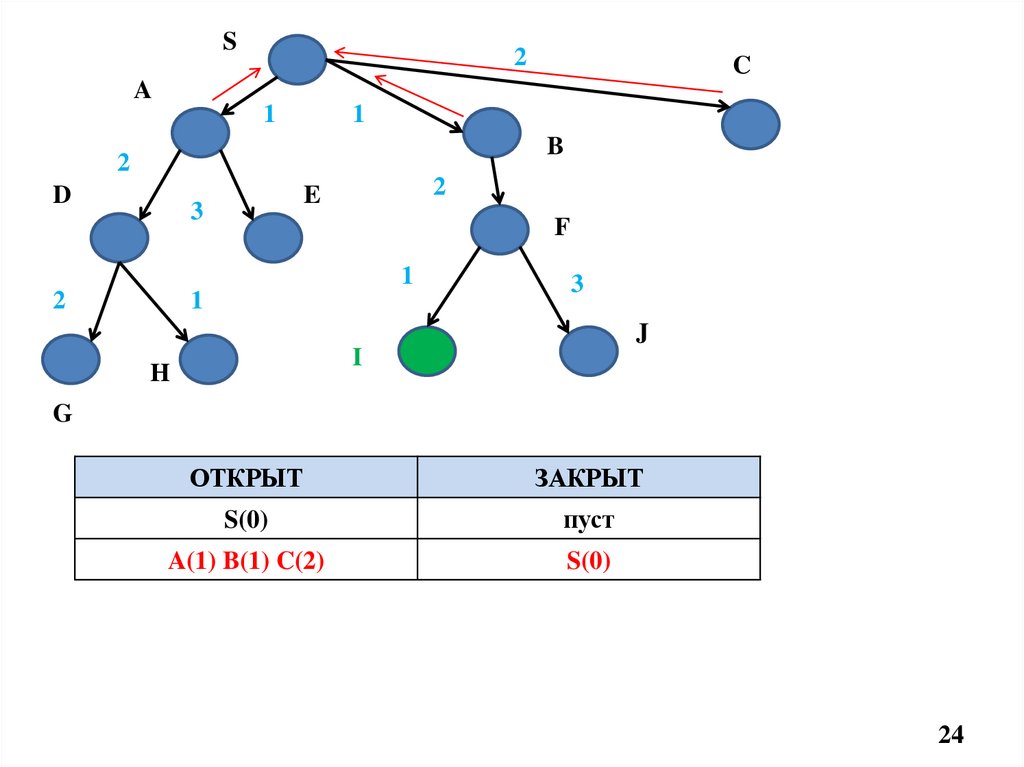
ОТКРЫТ
ЗАКРЫТ
S(0)
пуст
A(1) B(1) C(2)
S(0)
24

25.

S
2
C
A
1
1
B
2
D
2
E
3
F
1
2
1
3
J
I
H
G
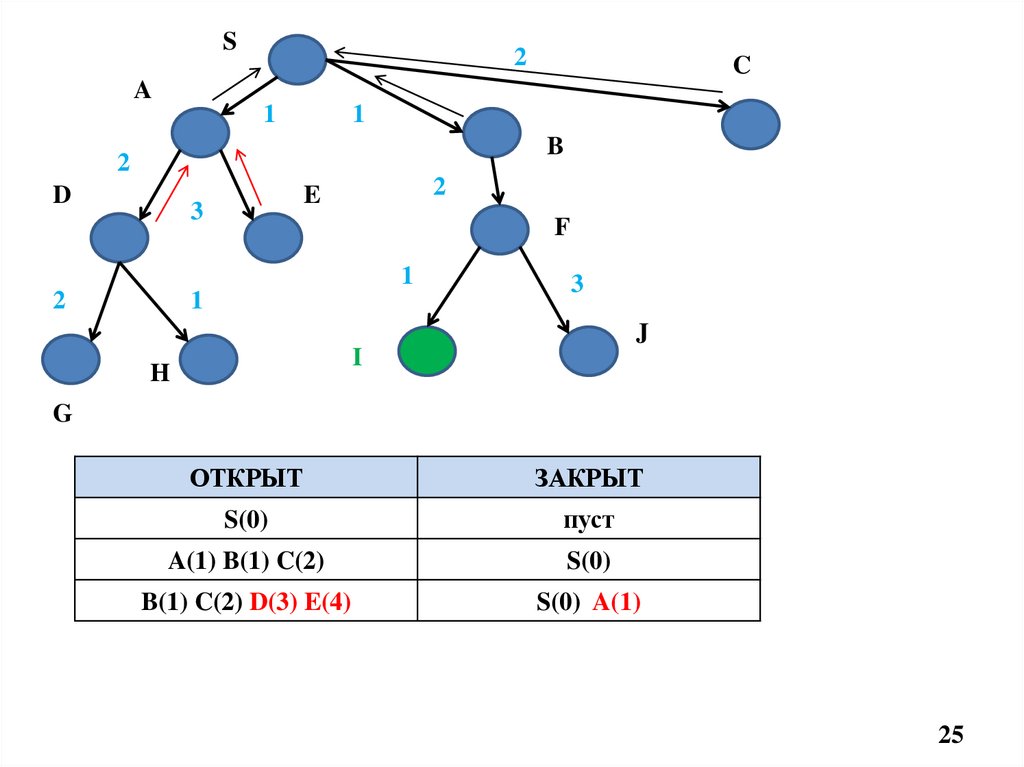
ОТКРЫТ
ЗАКРЫТ
S(0)
пуст
A(1) B(1) C(2)
S(0)
B(1) C(2) D(3) E(4)
S(0) A(1)
25

26.

S
2
C
A
1
1
B
2
D
2
E
3
F
1
2
1
3
J
I
H
G
ОТКРЫТ
ЗАКРЫТ
S(0)
пуст
A(1) B(1) C(2)
S(0)
B(1) C(2) D(3) E(4)
S(0) A(1)
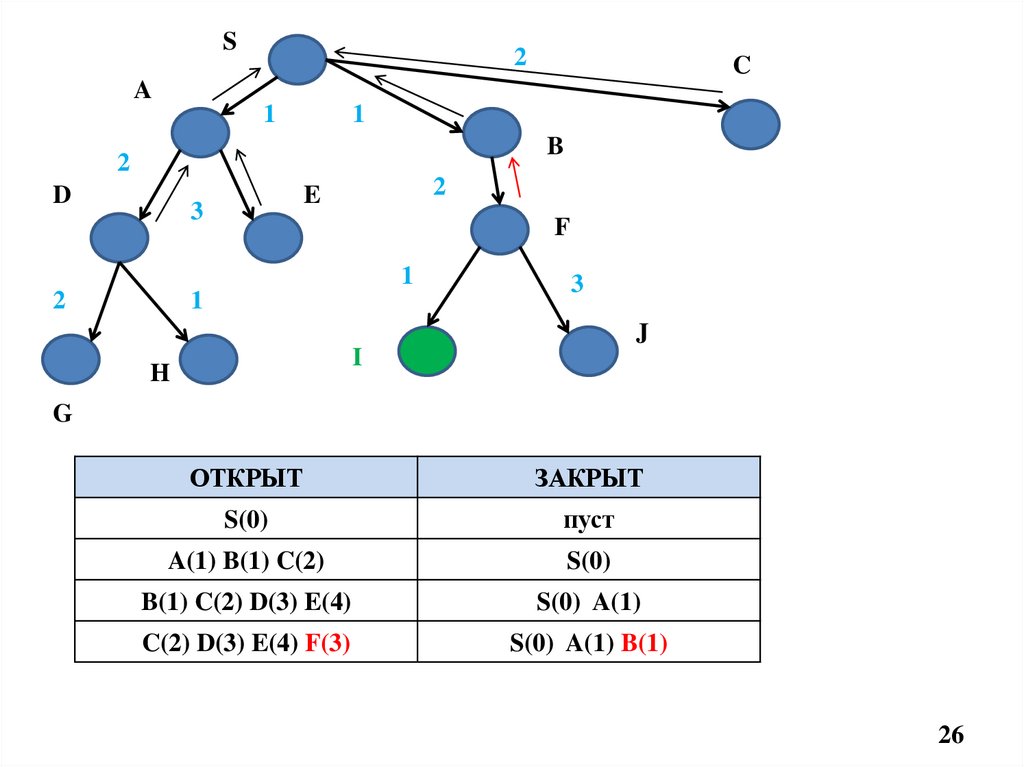
C(2) D(3) E(4) F(3)
S(0) A(1) B(1)
26

27.

S
2
C
A
1
1
B
2
D
3
2
E
F
1
2
1
3
J
I
H
G
ОТКРЫТ
ЗАКРЫТ
C(2) D(3) E(4) F(3)
S(0) A(1) B(1)
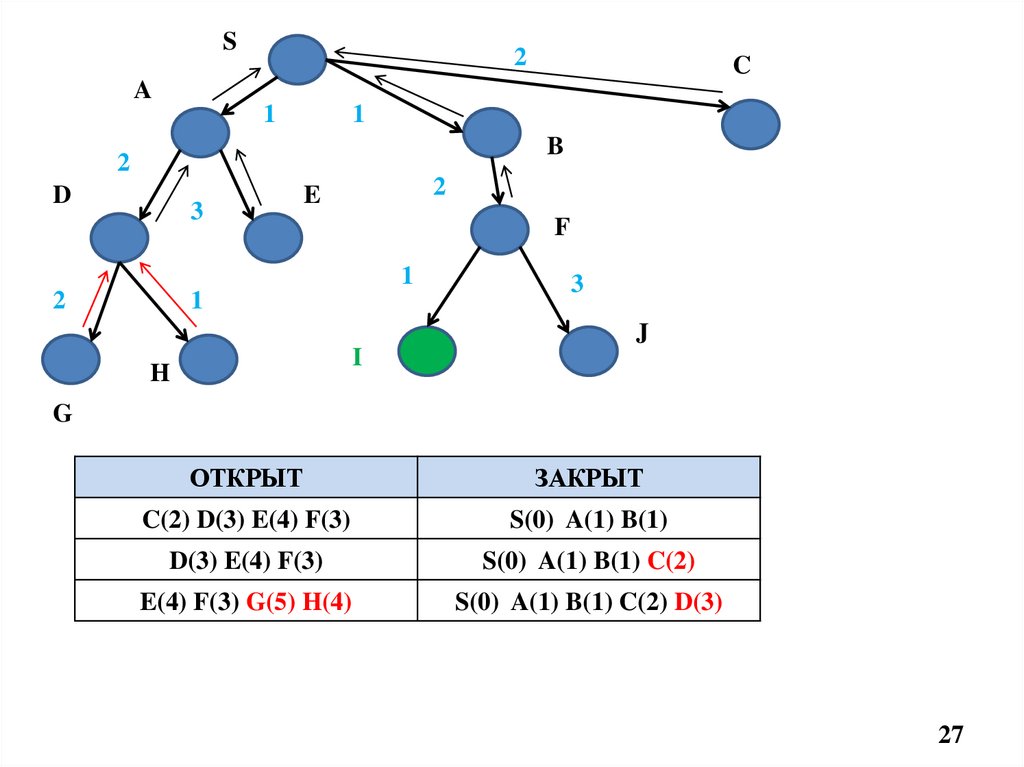
D(3) E(4) F(3)
S(0) A(1) B(1) C(2)
E(4) F(3) G(5) H(4)
S(0) A(1) B(1) C(2) D(3)
27

28.

S
2
C
A
1
1
B
2
D
3
2
E
F
1
2
1
3
J
I
H
G
ОТКРЫТ
ЗАКРЫТ
C(2) D(3) E(4) F(3)
S(0) A(1) B(1)
D(3) E(4) F(3)
S(0) A(1) B(1) C(2)
E(4) F(3) G(5) H(4)
S(0) A(1) B(1) C(2) D(3)
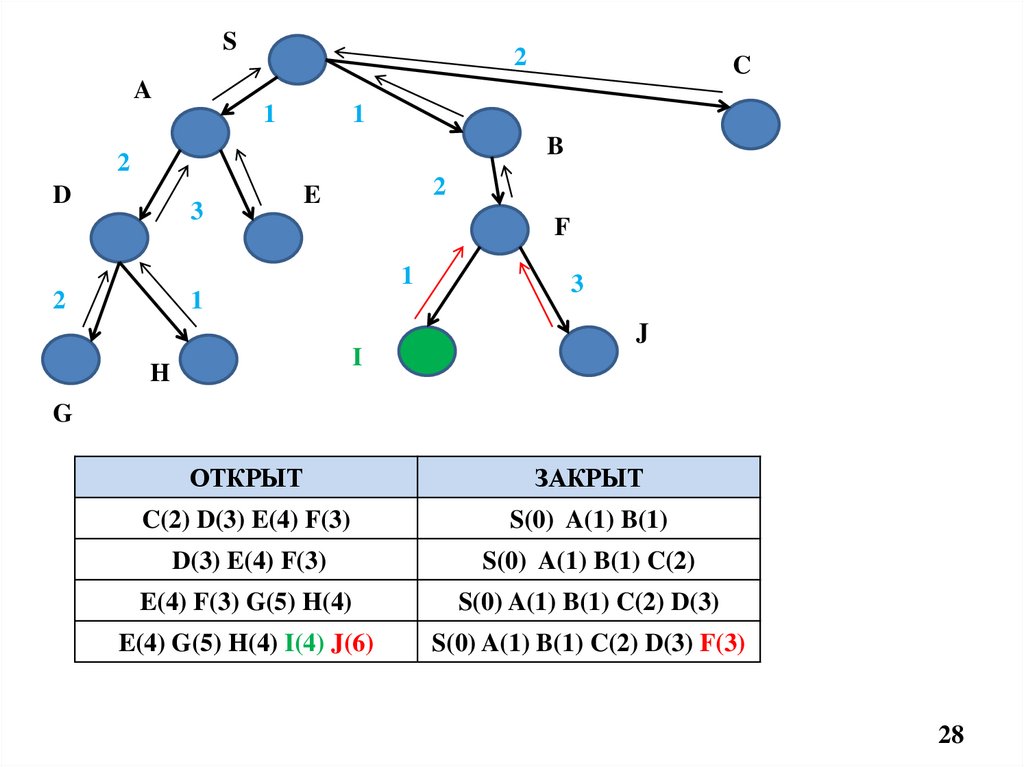
E(4) G(5) H(4) I(4) J(6)
S(0) A(1) B(1) C(2) D(3) F(3)
28

29.

S
2
C
A
1
1
B
2
D
3
2
E
F
1
2
1
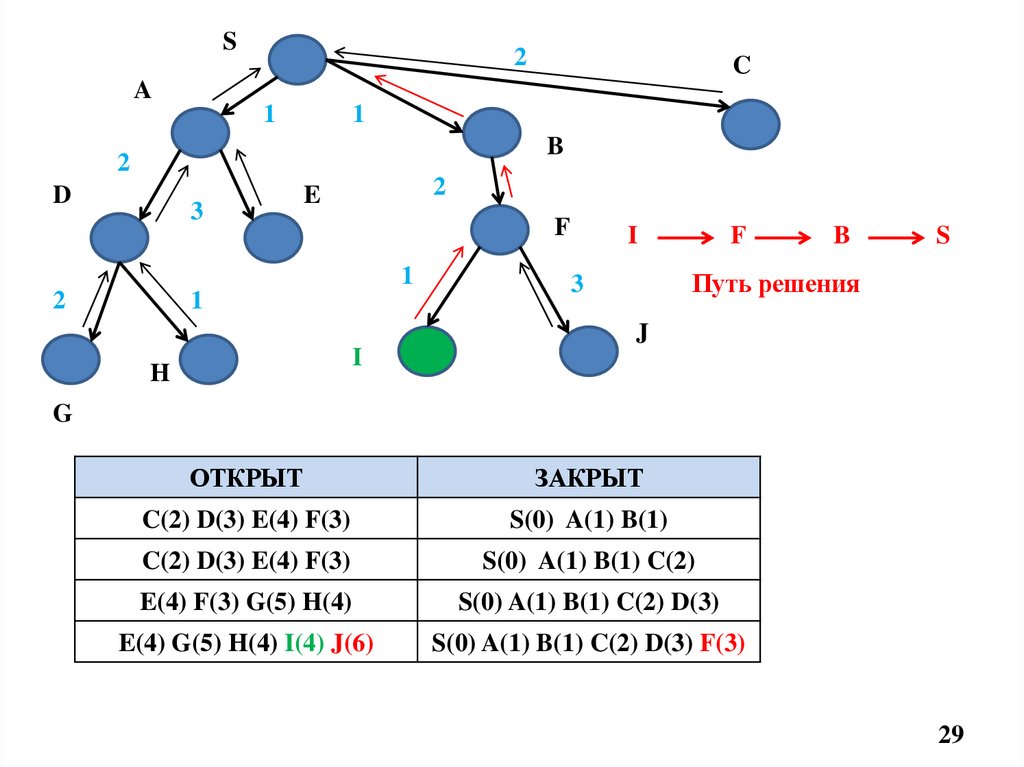
I
F
B
S
Путь решения
3
J
I
H
G
ОТКРЫТ
ЗАКРЫТ
C(2) D(3) E(4) F(3)
S(0) A(1) B(1)
C(2) D(3) E(4) F(3)
S(0) A(1) B(1) C(2)
E(4) F(3) G(5) H(4)
S(0) A(1) B(1) C(2) D(3)
E(4) G(5) H(4) I(4) J(6)
S(0) A(1) B(1) C(2) D(3) F(3)
29

30.

Если известно, что в графе есть
несколько терминальных (целевых)
вершин,
то
процесс
решения
продолжается, так как нет гарантии, что
не будет найдена ещё одна терминальная
вершина с меньшей оценкой стоимости
пути.
30

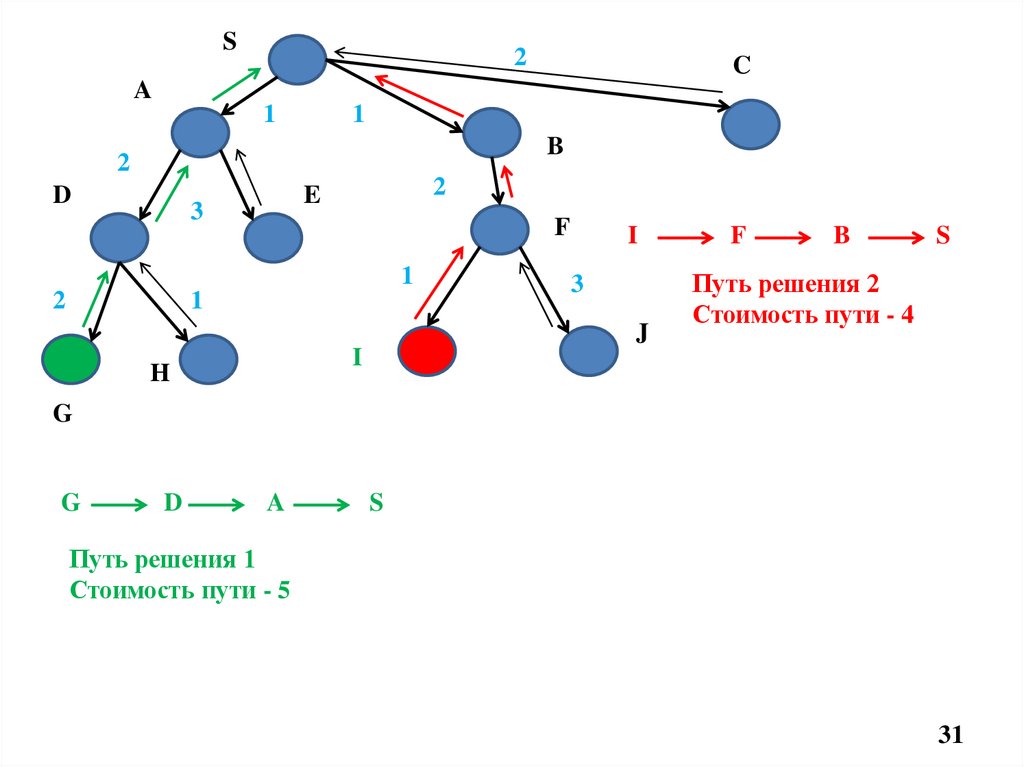
31.

S
2
C
A
1
1
B
2
D
2
E
3
F
1
2
1
I
3
J
F
B
S
Путь решения 2
Стоимость пути - 4
I
H
G
G
D
A
S
Путь решения 1
Стоимость пути - 5
31

32.

Общая процедура поиска на графе
Если перебор осуществляется не на
деревьях, а на произвольных графах
приведенные алгоритмы усложняются.
Такое усложнение связано с тем, что при
поиске на произвольных графах в список
ОТКРЫТ
может
быть
добавлена
вершина, которая уже есть в списке
ОТКРЫТ или ЗАКРЫТ. При этом
необходимо проводить дополнительную
коррекцию указателей.
32

33.

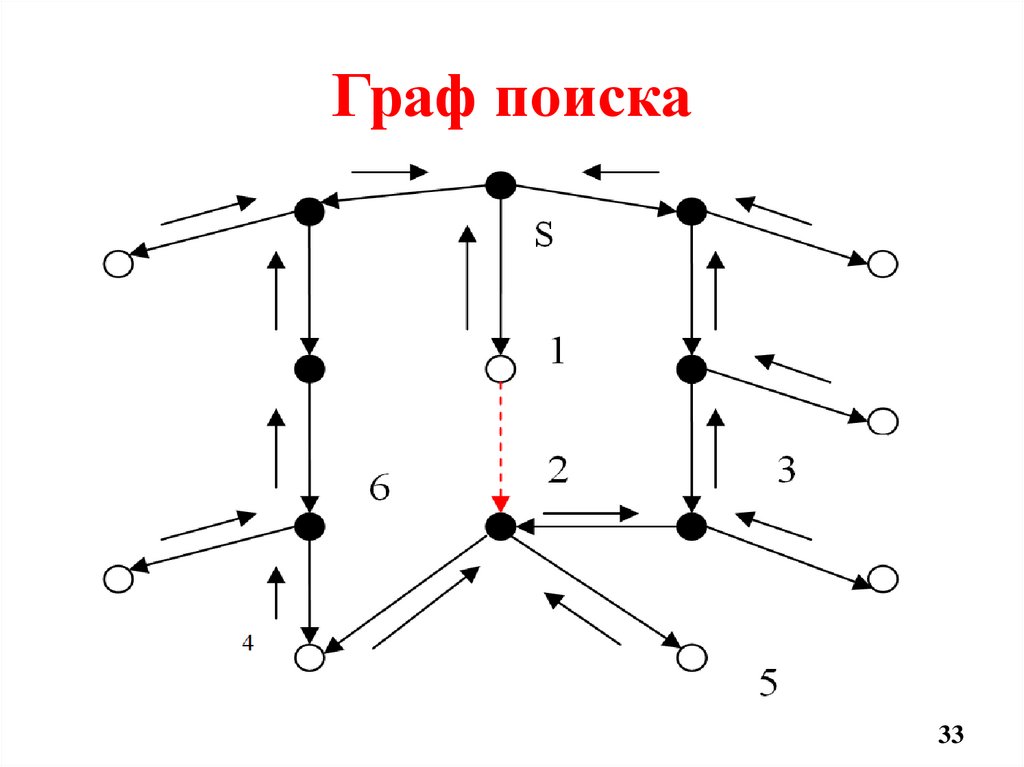
Граф поиска
33

34.

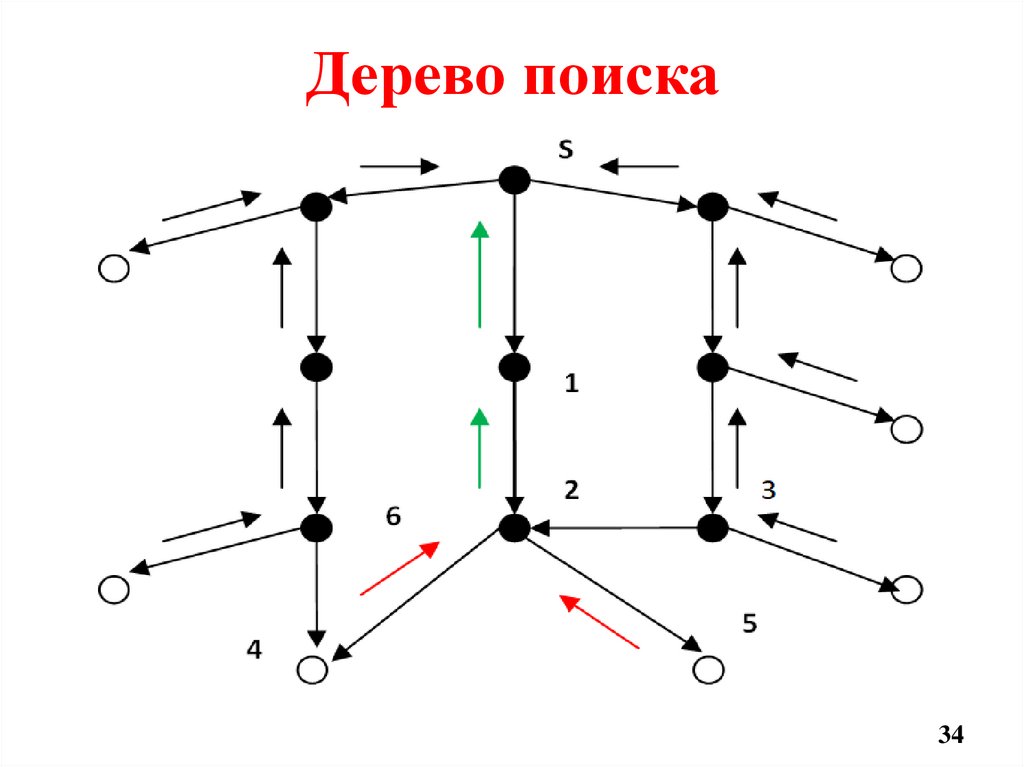
Дерево поиска
34

35.

Пусть процесс поиска породил граф
поиска и дерево поиска, показанные на
слайдах 33-34.
Стрелки
около
дуг
являются
указателями, определяющими родителей
вершины.
Зачерченные вершины находятся в
списке ЗАКРЫТ, а остальные – в списке
ОТКРЫТ в момент, когда алгоритм
выбирает вершину 1 для раскрытия.
Пусть стоимости дуг равны 1.
35

36.

Процедура коррекции указателей
Пусть на каком –то этапе алгоритма уже построен некоторый граф G,
являющейся частью неявно заданного графа задачи. Этот граф называется
графом поиска.
Тогда при раскрытии вершины n порождается множество М преемников. Эти
преемники или
не входят в граф G. Для тех вершин из М, которые не входят в G к n
проводятся указатели (данный случай и только он имел место при поиске на
деревьях. При поиске на деревьях граф поиска совпадает с деревом поиска.);
2)
уже входят в граф G поиска (т.е. были построены ранее и вошли в списки
ОТКРЫТ или ЗАКРЫТ) . В этом случае выполняется процедура коррекции
указателей:
1. Для каждого элемента из М, который уже был в списках ОТКРЫТ и ЗАКРЫТ,
рассчитывается стоимость пути через n и если она меньше осуществляется
переориентировка указателя на n.
2. Для каждого элемента из М, уже находящегося в списке ЗАКРЫТ
рассчитывается стоимость пути до каждого его потомка и если она меньше
ранее вычисленной осуществляется переориентировка его указателя. В
результате такой корректировки указателей дерево поиска на каждом
этапе алгоритма сохраняет лишь тот путь к вершине n, стоимость которого
минимальна.
1)
36

37.

Стратегия
управления
(поиска)
определяет порядок раскрытия вершин
из
списка
ОТКРЫТ.
Чтобы
унифицировать запись алгоритма поиска
при различных стратегиях, положим, что
из списка ОТКРЫТ будет выбираться
всегда 1-ый элемент, а стратегия
управления
будет
выражаться
в
соответствующем
упорядочении
элементов в списке ОТКРЫТ.
37

38.

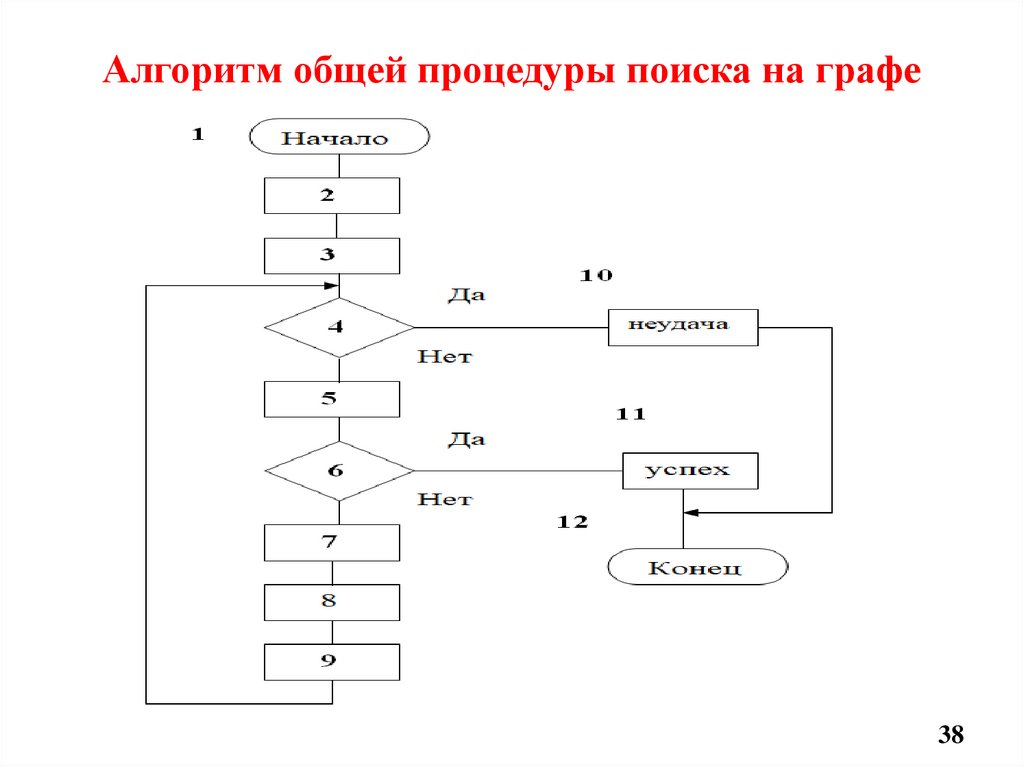
Алгоритм общей процедуры поиска на графе
38

39.

1. Начало.
2. Создать граф поиска G, состоящий лишь из начальной
вершины S. Занести S в список ОТКРЫТ.
3. Создать список ЗАКРЫТ, который в начале пуст.
4. Пуст ли ОТКРЫТ? Если ОТКРЫТ пуст, то неудача
(блок 10).
5. Выбрать первую вершину в ОТКРЫТ, убрать ее из
ОТКРЫТ и поместить в ЗАКРЫТ. Обозначить эту
вершину через n.
6. Если n – целевая вершина – успех (блок 11), окончание
работы с решением, полученным в результате
прослеживания пути в G вдоль указателей от n к S.
7. Раскрыть вершину n, порождая множество М ее
преемников, не являющихся предками n. Поместить в G
эти элементы множества М как преемники n.
39

40.

8. Вести указатель к n от тех элементов из М, которые еще не
были в G (т.е. ни в ОТКРЫТ, ни в ЗАКРЫТ). Добавить эти элементы
в ОТКРЫТ. Для каждого элемента из М, который уже был в
ОТКРЫТ или ЗАКРЫТ, решить, нужно ли переориентировать
указатели на n (см. процедуру коррекции). Для каждого элемента из
М, уже находящегося в ЗАКРЫТ, принять решение относительно
каждого его потомка в G – нужно ли переориентировать его
указатель (см. процедуру коррекции).
9. Переупорядочить список ОТКРЫТ в соответствии с некоторой
произвольной схемой, либо с эвристической значимостью. Перейти к
этапу 4.
При поиске на деревьях этап 8 общего алгоритма упрощается,
т.к. никакие элементы из множества М преемников не были ранее в
ОТКРЫТ и ЗАКРЫТ и переориентация указателей не требуется.
40