Похожие презентации:
Методы сортировки и поиска
1. Методы сортировки и поиска
Краткий обзор2. Двоичный (бинарный) поиск в упорядоченном массиве
330
1
2
3
4
5
6
7
1
3
4
8 10 14 16 21 24 27 31 33 36 38 42 44 50 51 53 59
L
8
9
M
10
11
12
13
14
15
16
17
18
19
H
const int
NMAX = 100;
int a[NMAX];
int binSearch(int data[], int rzm_data, int search_key)
{
int L,H,M;
L=0;
H=rzm_data-1;
while (L < H)
{
M = (L + H) / 2;
if (data[M] < search_key) L = M + 1; else H = M;
}
if (data[L] == search_key)
return L; else return -1;
}
3. Сортировки массива
Сортировка простыми обменами (метод «пузырька»)void bubbleSort(int data[], int rzm_data)
{ int
i, j, tmp;
for (i=1; i<rzm_data; i++)
for (j=0; j<rzm_data-i; j++)
if (data[j] > data [j+1])
{
tmp = data[j];
data[j] = data[j+1];
data[j+1] = tmp;
}
}
4 27 51 14 31 42 1
4 27 14 31 42 1
4 14 27 31 1
4 14 27 1
4 14 1
4
1
8 24 3 59 33 44 53 16 10 38 50 21 36
8 24 3 51 33 44 53 16 10 38 50 21 36 59
8 24 3 42 33 44 51 16 10 38 50 21 36 53 59
8 24 3 31 33 42 44 16 10 38 50 21 36 51 53 59
8 24 3 27 31 33 42 16 10 38 44 21 36 50 51 53 59
8 14 3 24 27 31 33 16 10 38 42 21 36 44 50 51 53 59
4. Шейкер-сортировка
Это модификация «пузырьковой» сортировки, котораяучитывает два дополнительных требования:
• 1) устранение «лишних» просмотров массива, т.е.
если массив уже отсортирован за первые проходы,
последующие проходы не делаем. Пример:
12,3,5,7,9,10.
• 2) смена направлений прохода массива: сначала
проходим от начала к концу, по том – от конца к
началу, потом снова от начала к концу и т.д. Это
позволяет уменьшить число проходов по массиву.
Пример: 5,7,9,10,12,3.
5. Сортировка простым выбором
void Sort_vybor(int data[], int rzm_data)
{ int i,j,k,x;
for (i=rzm_data-1; i>0;i--)
{
k = i;
for (j=0; j<i; j++)
if (data[j]>data[k]) k=j;
if (k!=i)
{ x = data[k];
data[k] = data[i];
data[i] = x;
}
}
}
6.
Сортировка простыми вставками (простыми включениями)4 27 51 14 31 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 14 27 51 31 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 14 27 31 51 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 14 27 31 42 51 1
8 24 3 59 33 44 53 16 10 38 50 21 36
void simpleInsertionSort(int data[], int rzm_data)
{
int i,j,c;
for (i=1; i<rzm_data; i++)
{ c = data[i];
j = i-1;
while (j>=0 && data[j]>c)
{
data[j+1] = data[j];
j--;
}
data[j+1] = c;
}
}
7.
Сортировка двоичными (бинарными) вставкамиvoid BinaryInsertionSort(int data[], int rzm_data)
{
int i,j,left,right,sred,x;
for (i=1; i<rzm_data; i++)
if (data[i-1]>data[i])
{
x=data[i];
left=0;
right=i-1;
do
{
sred=(left+right)/2;
if (data[sred]<x)
left= sred+1;
else right= sred-1;
}
while (left<=right);
for (j=i-1; j>=left; j--) data[j+1]= data[j];
data[left]=x;
}
}
8. Сортировка Шелла (сортировка с убывающим шагом)
Идея метода: делим массив на k1 групп, каждую группусортируем, далее делим массив на k2 групп (k2<k1),
снова сортируем полученные группы, далее на k3
групп (k3<k2<k1), и т.д. в конце делим на kn групп,
причем kn = 1, т.е. в конце сортируем весь массив.
Значения k1, k2, k3, …, kn называются приращениями.
Метод предложен Д.Л.Шеллом в 1959 году.
Д.Кнут дает оценку метода при грамотном выборе
значений приращений – O(n1,2).
Лучшим считается выбор в качестве значений
приращений взаимно простых чисел.
9.
Сортировка Шелла1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
4 27 51 14 31 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 10 3 14 21 36 1
8 24 38 50 31 42 53 16 27 51 59 33 44
step=7
step=3
1
8
3
4 10 36 14 21 24 27 44 31 33 50 16 38 51 59 42 53
1
4
3
8 10 21 14 27 16 31 24 36 33 38 42 50 44 53 51 59
1
3
4
8 10 14 16 21 24 27 31 33 36 38 42 44 50 51 53 59
step=2
step=1
10.
Сортировка Шеллаvoid ShellSort(int data[], int rzm_data)
{ int step,i,j,c;
step = rzm_data;
// Шаг поисков и вставки
do
{ // Вычисляем новый шаг
step = step / 3 + 1;
// Производим сортировку простыми вставками с заданным шагом
for (i=step; i<rzm_data; i++)
{
c = data[i];
j = i-step;
while (j >= 0 && data[j] > c)
{ data[j+step] = data[j];
j = j-step;
}
data[j+step] = c;
}
}
while (step !=1);
}
Количество перестановок элементов
(по результатам экспериментов со случайным массивом)
n = 25
n = 1000
n = 100000
Сортировка Шелла
50
7700
2 100 000
Сортировка простыми вставками
150
240 000
2.5 млрд.
11.
Алгоритм слияния упорядоченных массивов4
14
27
51
1
3
8
24
31
42
59
void merge(int a[], int b[], int na, int nb,
int c[], int &nc)
{ int ia,ib,ic;
ia = ib = ic = 0;
while (ia < na && ib < nb)
{
if (a[ia]<b[ib])
{ c[ic] = a[ia];
ia++;
}
else
{ c[ic] = b[ib];
ib++;
}
ic++;
}
while (ia < na)
{ c[ic] = a[ia];
ia++; ic++;
}
while (ib < nb)
{ c[ic] = b[ib];
ib++; ic++;
}
nc = ic;
}
12. Сортировка фон Неймана (слиянием)
Метод основан на идее слияния двух отсортированныхчастей массива, поэтому первоначально массив
разбивается на две части, которые независимо
сортируются, а затем результаты сливаются в
единое целое. С каждой из частей выполняются
аналогичные действия, до тех пор, пока количество
элементов в сортируемой части массива не станет
равно двум. В этом случае выполняется простое
сравнение элементов и их перестановка, если она
необходима.
Метод слияний – один из первых в теории алгоритмов
сортировки. Он предложен Дж. Фон Нейманом в 1945
году.
В алгоритме метода реализован один из
фундаментальных принципов информатики –
«разделяй и влавствуй».
13.
Сортировка фон Неймана (слиянием)1
2
3
4
5
6
7
4 27 51 14 31 42 1
И так далее…
8
9
10
11
12
13
14
15
16
17
18
19
20
8 24 3 59 33 44 53 16 10 38 50 21 36
14.
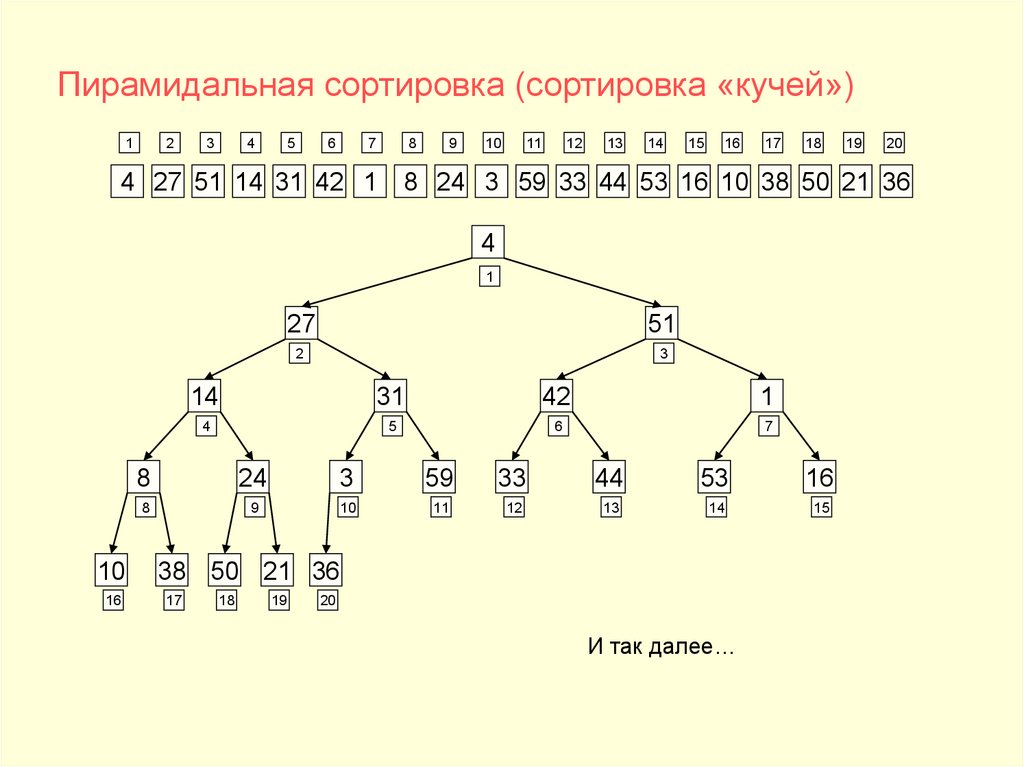
Пирамидальная сортировка (сортировка «кучей»)1
2
3
4
5
6
7
8
4 27 51 14 31 42 1
9
10
11
12
13
14
15
16
17
18
1
16
27
51
2
3
14
31
42
1
4
5
6
7
8
24
3
59
33
44
53
16
8
9
10
11
12
13
14
15
38 50 21 36
17
18
19
20
8 24 3 59 33 44 53 16 10 38 50 21 36
4
10
19
20
И так далее…
15.
Пирамидальная сортировка (продолжение)59
1
51
53
2
3
50
36
42
44
4
5
6
7
24
38
31
8
9
10
4
10
8
21
3
16
17
18
19
20
14
11
27
33
1
16
12
13
14
15
И так далее…
16. Быстрая сортировка (сортировка Хоара)
В алгоритме быстрой сортировки сочетаются три идеи:• 1) разделение сортируемого массива на две части, левую и правую;
• 2) взаимное упорядочение двух подмассивов так, чтобы все элементы
левого подмассива не превосходили элементов правого подмассива;
• 3) рекурсия, при которой подмассив упорядочивается точно таким же
способом, как и весь массив.
Разделение массива на два взаимно упорядоченных подмассива:
• Обозначим за Х элемент, находящийся посередине массива М
• Осуществляем два встречных просмотра массива: двигаемся слева
направо, пока не найдем элемент M[i]>X и справа налево, пока не
найдем элемент M[j]<X. Эти элементы «нарушают порядок»!
• Меняем местами элементы «нарушающие порядок»
• Продолжаем процесс "встречных просмотров с обменами", пока два
идущих навстречу друг другу просмотра не встретятся.
17.
Быстрая сортировка (сортировка Хоара)1
2
3
4
5
6
7
4 27 51 14 31 42 1
8
9
10
11
12
13
14
15
16
17
18
19
20
8 24 3 59 33 44 53 16 10 38 50 21 36
h
l
1
3
4 10 8 14 51 42 24 27 59 33 44 53 16 31 38 50 21 36
1
3
4
8 10 14 36 42 24 27 21 33 44 50 16 31 38 51 53 59
1
3
4
8 10 14 31 16 24 27 21 33 36 50 44 42 38 51 53 59
1
3
4
8 10 14 21 16 24 27 31 33 36 38 44 42 50 51 53 59
1
3
4
8 10 14 16 21 24 27 31 33 36 38 44 42 50 51 53 59
1
3
4
8 10 14 16 21 24 27 31 33 36 38 42 44 50 51 53 59
18. Быстрая сортировка (сортировка Хоара)
void quicksort(int A[], int L, int R){
int i,j,bar,tmp;
i=L;
j=R;
bar=A[(L+R)/2];
do
{ while (A[i]<bar) i++;
while (bar<A[j]) j--;
if (i<=j)
{ if (i<j) { tmp=A[i]; A[i]=A[j]; A[j]=tmp; }
i++; j--;
}
}
while (i<=j);
if (L<j) quicksort(A,L,j);
if (i<R) quicksort(A,i,R);
}
Вызов в основной программе:
quicksort(a,0,n-1);
19.
Сортировка подсчетом0
1
2
3
4
5
6
7
8
9
2
1
0
6
5
4
3
2
1
7
6
10
3
9
8
7
14
13
12
10
11
4
14
0
16
15
14
2
17
16
1
19
18
17
2
20
19
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
4
7
1
4
1
2
1
8
4
3
9
3
4
3
6
0
8
0
1
6
for (i=0; i< k; i++)
C[i]=0;
for (i=0; i<n; i++)
C[A[i]]=C[A[i]] + 1;
for (j=1; j<k; j++)
C[j]=C[j] + C[j - 1];
for (i=n-1; i>=0; i--)
{ C[A[i]] = C[A[i]] - 1;
B[C[A[i]]] = A[i];
}
20.
Цифровая сортировка4 27 51 14 31 42 1
8 24 3 59 33 44 53 16 10 39 50 21 36
После сортировки по последней цифре:
10 50 51 31 1 21 42 3 33 53 4 14 24 44 16 36 27 8 59 39
После устойчивой сортировки по первой цифре:
1
3
4
8 10 14 16 21 24 27 31 33 36 39 42 44 50 51 53 59



















 Информатика
Информатика








