Похожие презентации:
О некоторых задачах ЕГЭ по атомной и ядерной физике
1.
О некоторых задачах ЕГЭ по атомнойи ядерной физике
Кодификатор по физике атома и атомного ядра
•Планетарная модель атома
•Постулаты Бора. Излучение и поглощение фотонов при переходе
атома с одного уровня на другой
•Линейчатые спектры. Спектр уровней атома водорода
n = 1, 2, 3, …
13,6 эВ
En
, где
•Лазер
n2
•Нуклонная модель ядра Гейзенберга – Иваненко. Заряд ядра.
Массовое число ядра. Изотопы.
•Энергия связи нуклонов в ядре. Ядерные силы
Дефект массы
2.
Кодификатор по атомной и ядерной физике• Импульс частицы:
p mv
m0 c
2
1
• Радиоактивность: альфа-распад, электронный распад,
позитронный распад, гамма-излучение.
t
T
Закон радиоактивного распада: N N 0e t N 0 2
Дополнительно ( Еще что не вошло в кодификатор)
•Энергия свободной частицы Ek
m0c 2
m0c 2
1 2
•Энергия покоя свободной частицы: E0 = m0c2,
m c
E mc 2 0
• Связь массы и энергии свободной частицы:
• Активность радиоактивного распада: А = ∆N/∆t
Релятивистский закон сохранения энергии
2
2
m
c
E
m
c
01 кин.1 02 Eкин.2
2
1
2
3.
Задачи по теме:Планетарная модель атома. Постулаты Бора. Излучение и поглощение
фотонов при переходе атома с одного уровня на другой. Линейчатые
спектры. Спектр уровней атома водорода
Атом позитрония состоит из электрона и позитрона, обращающихся вокруг их
общего неподвижного центра масс. Позитрон имеет массу, равную массе
электрона и заряд, противоположный заряду электрона. Для орбиты
движения частицы с минимальным радиусом выполняется условие
квантования rp h , где р – импульс электрона или позитрона. Найдите
импульс позитрона на этой орбите.
Решение:
1. Использовать понятие приведенной массы электрона: me = m/2,
2. Использовать 2 закон Ньютона для одной частицы,
2
2
2
2
(1) m ke ; m 2 ke ; p 2 k me ;
2r
( 2r ) 2
2r
2r
3. Использовать условие квантования импульса электрона для
h
h
определения радиуса,
m r
;r
( 2)
2
p
4. Решить систему уравнений, получить искомую величину импульса.
p k
e 2 m
2h
0,5 10 24
кгм
.
с
4.
Задачи по теме:Планетарная модель атома. Постулаты Бора. Излучение и поглощение
фотонов при переходе атома с одного уровня на другой. Линейчатые
спектры. Спектр уровней атома водорода
На рисунке представлены энергетические уровни электронной оболочки
атома и указаны частоты фотонов, излучаемых и поглощаемых при
некоторых переходах между ними. Какова максимальная длина волны
фотонов, излучаемых атомом при любых возможных переходах между
уровнями Е1, Е2, Е3 и Е4, если ν13 = 7·1014 Гц, ν24 = 5·1014 Гц, ν32 = 3·1014 Гц?
Решение
1. Запишем 2 постулат Бора для заданных
переходов с учетом поглощения и излучения
h 43 E4 E3 ; (1)
энергии:
h 13 E1 E3 ; (2)
h 24 E2 E4 ; (3)
2.
h 32 E3 E2 (4)
Решаем систему уравнений и определяем
наименьшую частоту и наибольшую длину
волны: 2 1014 Гц,
1,5 10 6 м
43
м акс
5.
Задачи по теме:Планетарная модель атома. Постулаты Бора. Излучение и поглощение
фотонов при переходе атома с одного уровня на другой. Линейчатые
спектры. Спектр уровней атома водорода
Электрон, имеющий импульс p = 2·10–24 кг·м/с, сталкивается с
покоящимся протоном, образуя атом водорода в состоянии с энергией
En (n = 2). В процессе образования атома излучается фотон. Найдите
частоту ν этого фотона, пренебрегая кинетической энергией атома.
Уровни энергии электрона в атоме водорода задаются формулой.
E n = − 13,6 /n 2 эВ, где n = 1, 2, 3, … .
Решение: 1. В начальный момент энергия взаимодействия протона
и электрона равна нулю. В процессе захвата электрона протоном
энергия уменьшается, происходит излучение. При покоящимся
19
электроне: Е2 3,4 10 0,53 1015 Гц.
h
6,4 10 34
2. Запишем закон сохранения энергии при наличии импульса у
Ee E2 ;
электрона:
E
p2
21 h ;
2me
n
3. Определим частоту фотона, равную 4,16 1015 Гц.
6.
Задачи по теме:Планетарная модель атома. Постулаты Бора. Излучение и поглощение
фотонов при переходе атома с одного уровня на другой. Линейчатые
спектры. Спектр уровней атома водорода
Е,эВ
Предположим, что схема энергетических уровней
атомов некоего вещества имеет вид, показанный на
0
рисунке и атомы находятся в состоянии с энергией Е1.
Е2
Электрон, столкнувшись с одним из таких атомов,
-2
отскочил, приобретя некоторую дополнительную
-5
Е1
энергию. Импульс электрона после столкновения с
покоящимся атомом оказался равным 1,2 10-24 кг м/с.
определите кинетическую энергию электрона до
-8,5
Е0
столкновения. Возможностью испускания света
атомом при столкновении с электроном пренебречь.
Решение. 1. Записать закон сохранения энергии для системы атом –
электрон: ∆ ЕА = - ∆ Еэл.
2. Записать значение энергии электрона
через импульс после
p2
столкновения: Ee 2 Ee1 Ee 2m ;
3. Рассчитать кинетическую энергию электрона до столкновения:
р2
(1,2 10 24 ) 2
Е1
Е
3,5 4,96 3,5 1,46эВ
2м
1,6 10 19 2 9,1 10 31
7.
Задачи на расчет энергетического выхода реакции2
2
m
c
E
m
c
01 кин.1 02 Eкин.2
1 тип задач – расчет энергии реакции по разности энергий покоя при
условии, что Ек << E0
1. Определите энергетический выход ядерной реакции:
7
2
8
1
3 Li + 1H = 4Be +0n . Относительные атомные массы Li – 7,01601
а.е.м., H - 2,0141, Be – 8,00531, n – 1,009. (c2 = 931 МэВ/а.е.м.)
Решение: 931 [(8,00531 + 1,009) – (7,01601 + 2,0141)] = - 14,71
МэВ<0. Энергия выделяется при ядерной реакции.
2 тип задач – расчет энергии выхода по разности кинетических
энергий на основе закона сохранения импульса и энергии.
2. При реакции синтеза образуется ядро трития и протон и
выделяется 4,03 МэВ энергии. Какую кинетическую энергию уносит
протон, если суммарный импульс исходных частиц равен нулю, а
их кинетическая энергия пренебрежимо мала по сравнению с
выделившейся?
H 21 H 21 H 13 p11
mD
3
Ер
m p mD
Q
3 1
4,03 3,02МэВ
8.
Задачи на расчет энергетического выхода реакцииОпределите энергию ядерной реакции Li3 He2 B5 n0
Энергию считать положительной, если в процессе реакции она
выделяется и отрицательной, если она поглощается.
1. - 2,9 МэВ
2. 2,9 МэВ 3. 0 МэВ
4. 20530 МэВ
7
4
10
Решение.
m1 = 7,0143 + 4,0015 = 11,0158 а.е.м, m2 = 10,0102 + 1,00867 =
11,01887 а.е.м.
∆ m = m2 – m1 = 0, 00307 а.е.м >0 . Энергия поглощается: Е = 931*
0,00307 = 2,9 МэВ. (По указанию авторов следует приписать -.
Ответ: -2,9 МэВ)
1
9.
Задачи на движение свободной частицыСвободные частицы бывают легкими (позитрон, электрон) с энергией
покоя примерно 0,5 Мэв. В этом случае кинетическая энергия больше, чем
энергия покоя, поэтому они считаются релятивистками. У тяжелых частиц
Ек << E0 (~ 10 MэВ), . Таковыми являются протоны, нейтроны и мезоны. В
задачах должно быть указание, какой является частица. В зависимости от
этого следует решение с разной степенью приближенности.
Свободный пион (π0-мезон) с энергией покоя 135 МэВ движется со скоростью
V, которая значительно меньше скорости света. В результате его распада
образовались два γ-кванта, причём один из них распространяется в
направлении движения пиона, а другой – в противоположном направлении.
Энергия одного кванта на 10% больше, чем другого. Чему равна скорость
пиона до распада?
V
1
2
1 способ решения. Частица п – мезон
классическая:
v<<c, Eк <<E0п
10.
Задачи на движение свободной частицы1.
Записать закон сохранения импульса с учетом связи между
энергиями фотонов Е1 = 1,1 Е2, и импульса фотона
Еф
рф
m p1 p2
E1 E2 0,1E2
; (1)
c
c
с
.
2. Записать закон сохранения энергии , допустив, что Екп << E0
m c 2 E 0 E k E1 E2 2,1E2 (2);
3. Поделив (1) на (2) , получим v/c = 1/21 и v =c/21 = 14,6 106 м/с.
11.
Задачи на движение свободной частицы2 способ решения с учетом релятивистских эффектов
1.
2.
3.
Запишем закон сохранения импульса, считая что
пи-мезон релятивистская частица. m0
0,1E 2
(1 );
2
c
1 2
c
2
Определим полную энергию пи-мезона:
E mc 2
1
2
2
;
c2
Запишем релятивистский закон сохранения m0 c 2,1E (2 );
2
2
энергии:
1
c2
4.
m 0 c
Поделив (1) на (2) получаем тот же результат, v =
c/21 = 14,6 106 м/с. Значит, приближение в случае
1 допустимо.
12.
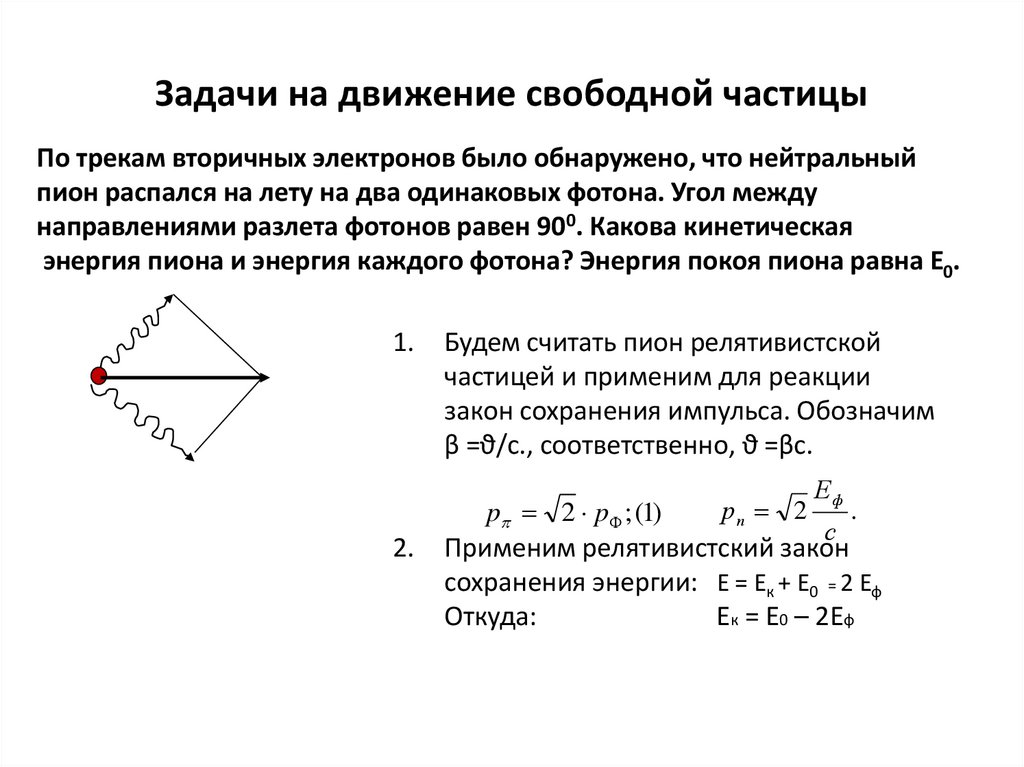
Задачи на движение свободной частицыПо трекам вторичных электронов было обнаружено, что нейтральный
пион распался на лету на два одинаковых фотона. Угол между
направлениями разлета фотонов равен 900. Какова кинетическая
энергия пиона и энергия каждого фотона? Энергия покоя пиона равна Е0.
1.
Будем считать пион релятивистской
частицей и применим для реакции
закон сохранения импульса. Обозначим
β =ϑ/с., соответственно, ϑ =βс.
Еф
2.
рп 2
.
p 2 p ; (1)
с
Применим релятивистский закон
сохранения энергии: Е = Ек + Е0 = 2 Еф
Откуда:
Ек = Е0 – 2Еф
13.
Задачи на движение свободной частицы3. Определим кинетическую энергию пи-мезона:
m0 c 2
1
2
2
Е к mc m0 c
m0 c 2 E 0 (
1)
2
2
1
1
4. Выразим релятивистский импульс пи-мезона , который подставим в
закон сохранения импульса. Отсюда определим энергию фотона:
E0
E0
E
m0
m c c
E0
2 ; E
;
p
0
2
2
2
2
2
c
1
c 1
c 1
c 1
2(1 )
5. Как видно, надо определить β . Решая систему уравнений найдем ее.
1
E0
1
1 2
2 E0
2(1 )
2
E0 ;
2 2 1
; ;
2
2
6. Определим энергию фотона и кинетическую энергию пиона
Е 0 ( 2 1) 2 Е Е 0 ;
Е
Е0 2 Е0
;
2
2
Ек Е0 ( 2 1).
14.
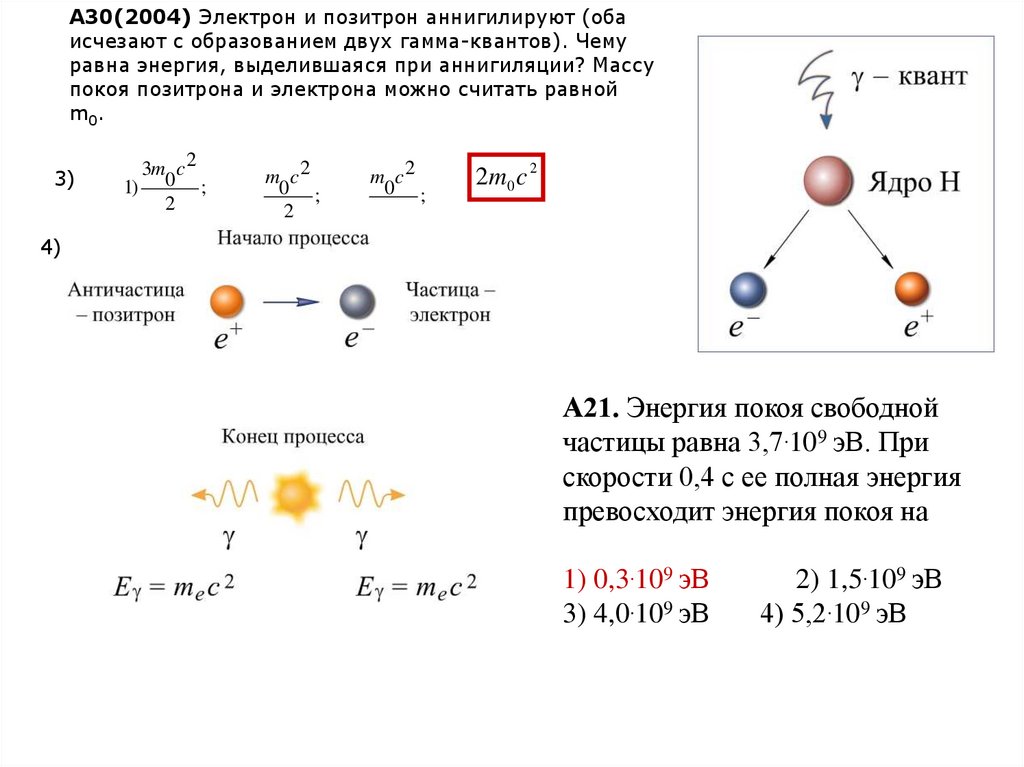
А30(2004) Электрон и позитрон аннигилируют (обаисчезают с образованием двух гамма-квантов). Чему
равна энергия, выделившаяся при аннигиляции? Массу
покоя позитрона и электрона можно считать равной
m0 .
3)
3m c 2
1) 0 ;
2
m c2
0 ;
2
m c2
0 ;
2m0 c 2
4)
А21. Энергия покоя свободной
частицы равна 3,7.109 эВ. При
скорости 0,4 с ее полная энергия
превосходит энергия покоя на
1) 0,3.109 эВ
3) 4,0.109 эВ
2) 1,5.109 эВ
4) 5,2.109 эВ
15.
Задачи на движение свободной частицыПи-мезон 2,4 10-28
кг распадается на два гамма кванта. Найдите модуль импульса
одного из образовавшихся гамма квантов в системе отсчета, где
первичный пион покоится.
Решение.
1. Записать закон сохранения импульса с учетом направления
движения фотонов: р1 = р2,
2. Записать закон сохранения энергии с учетом взаимосвязи энергии
фотонов с импульсом: mc 2 2 E 2 pc
Отсюда p = mc/2 = 3,6 10-20
кг м/с
16.
Задачи на радиоактивный распад(А) Радиоактивный изотоп имеет период полураспада 2 минуты. Из 100
ядер этого изотопа сколько ядер испытывает радиоактивный распад за 2
минуты?
1. Точно 50 ядер
2. 50 или немного меньше
3. 50 или немного больше
4. Около 50 ядер, может быть немного больше или немного меньше.
В. Большое число N радиоактивных ядер 161 Tb 65 распадается, образуя
стабильные дочерние ядра 66 Dy161. Период полураспада равен τ = 6,9
суток. Какое количество исходных ядер останется через 20,7 суток, а
дочерних – появится за 27,6 суток после начала наблюдений?
Установите соответствие между физическими величинами и их
значениями. ФИЗИЧЕСКАЯ ВЕЛИЧИНА (А, Б),
А) количество ядер 161 Tb65 через 20,7 суток
Б) количество дочерних ядер 161Dy66 через 27,6 суток
ЕЁ ЗНАЧЕНИЕ (ответы):
N/16 2) N/8 3) 7/8N
4) 15/16N
А – 2,
Б- 4
17.
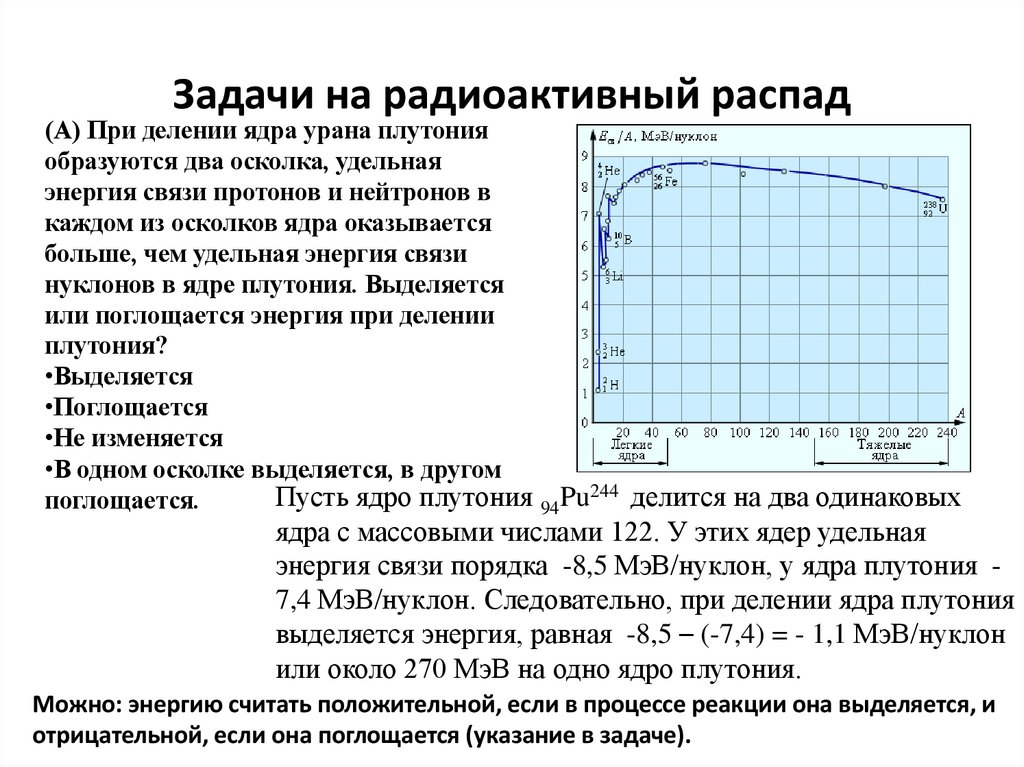
Задачи на радиоактивный распад(А) При делении ядра урана плутония
образуются два осколка, удельная
энергия связи протонов и нейтронов в
каждом из осколков ядра оказывается
больше, чем удельная энергия связи
нуклонов в ядре плутония. Выделяется
или поглощается энергия при делении
плутония?
•Выделяется
•Поглощается
•Не изменяется
•В одном осколке выделяется, в другом
Пусть ядро плутония 94Pu244 делится на два одинаковых
поглощается.
ядра с массовыми числами 122. У этих ядер удельная
энергия связи порядка -8,5 МэВ/нуклон, у ядра плутония 7,4 МэВ/нуклон. Следовательно, при делении ядра плутония
выделяется энергия, равная -8,5 – (-7,4) = - 1,1 МэВ/нуклон
или около 270 МэВ на одно ядро плутония.
Можно: энергию считать положительной, если в процессе реакции она выделяется, и
отрицательной, если она поглощается (указание в задаче).
18.
Задачи на радиоактивный распадВ урановой среде в начальный момент
времени под действием нейтрона
разделилось одно ядро урана 235. Пусть
каждые два нейтрона из числа возникающих
при делении вызывают новую реакцию в
среднем через 10-8 с. Сколько ядер
разделится через 10-7 с?
1) 210 2) 10 3) 108
107
В реакции радиоактивного превращения ядра К в Са вылетает одна
частица с массой покоя не равной нулю.
1. Нейтрон
2. Позитрон
3. Протон
4. Электрон
19.
Задачи на радиоактивный распадОбразец, содержащий радий, за 1 испускает 3,7 1010 альфа-частиц.
За 1 ч выделяется энергия 100 Дж. Каков средний импульс альфачастиц? Масса альфа - частицы равна 6,7 10-27 кг. Энергией отдачи
ядер, гамма-излучением и релятивистскими эффектами пренебречь
1. Определить энергию одной альфа-частицы: E = ∆E/Nt .
2. Определить импульс через энергию: p = √2Em.
Активность радиоактивного элемента уменьшилась в 4 раза за 32 дня.
Определить период полураспада этого элемента.
1. 2 суток
2. 4 суток
3. 8 суток
4. 16 суток
Решение.
1. Активность – число распавшихся ядер за секунду – пропорционально
t
числу оставшихся ядер. Отсюда –
T
А1 N 1
2
t 2 4 2 2 ;
А2 N 2
T
2 T
2. Период полураспада 16 суток.
















 Физика
Физика








