Пропускная способность непрерывного канала с аддитивным гауссовым шумом. Лекция 15

1.

Лекция 15.
Пропускная способность
непрерывного канала с аддитивным
гауссовым шумом.

2.

Под гауссовым каналом связи понимают
математическую модель реального канала,
удовлетворяющего следующим требованиям:
1) физические параметры канала известны и
детерминированы;
2) полоса пропускания канала ограничена полосой
Fk герц;
3) в канале действует аддитивный гауссов белый
шум (с равномерным частотным спектром и
нормальным распределением амплитуд);
4) статистическая связь между сигналом и шумом
отсутствует, а ширина спектра сигнала и помехи
ограничена полосой пропускания канала.

3.

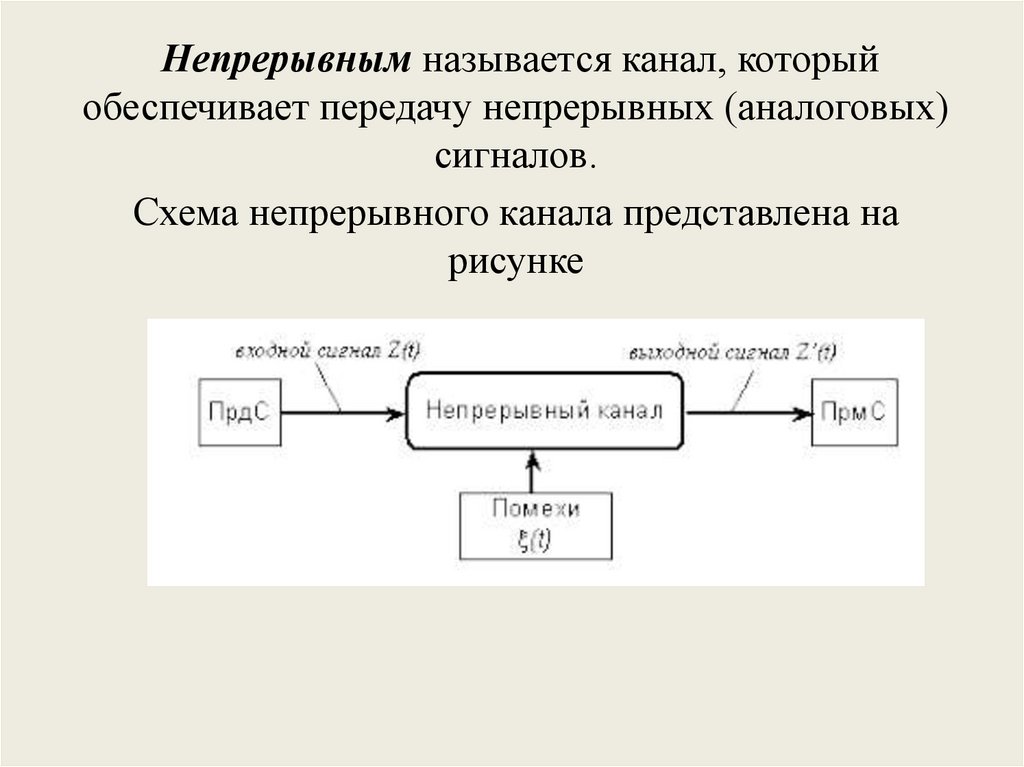
Непрерывным называется канал, который
обеспечивает передачу непрерывных (аналоговых)
сигналов.
Схема непрерывного канала представлена на
рисунке

4.

Непрерывные сигналы, поступающие в канал связи
из передатчика (ПрдС) описываются некоторой
непрерывной функцией времени Z(t). Ограничения
на значения этой функции задаются величиной
средней мощности передаваемых сигналов PZ.
Другой характеристикой непрерывного канала
является полоса пропускания – интервал частот
сигналов, которые могут распространяться в данном
канале νmin – νmax. Если по своему физическому
смыслу Z является напряжением или силой
электрического тока, то при неизменном
электросопротивлении канала связи мощность
сигнала определяет его амплитуду и средний квадрат
значения параметра сигнала.

5.

Сигналы на выходе канала Z'(t), поступающие в
приемник (ПрмС), также являются аналоговыми и
формируются они в результате сложения сигналов на
входе канала и помех - их можно описать некоторой
непрерывной функцией времени ξ(t), в результате:
Z'(t) = Z(t) + ξ(t).
Явный вид функции помех заранее неизвестен.
Поэтому для количественного описания
прохождения сигналов по непрерывному каналу
приходится принимать ту или иную модель помех и
модель канала.

6.

Наиболее распространенной является модель
гауссовского канала: принимается, что помехи,
будучи непрерывными случайными величинами,
подчиняются нормальному (гауссовскому)
статистическому распределению с математическим
ожиданием (средним значением) равным нулю. Эта
функция имеет единственный параметр, квадрат
которого называется дисперсией и имеет смысл
средней мощности помех в канале с единичным
электросопротивлением.
Если в пределах полосы пропускания средняя
мощность помех оказывается одинаковой на всех
частотах, а вне этой полосы она равна нулю, то
такие помехи называются белым шумом.

7.

Предположим по указанному гауссовскому каналу
передается непрерывный сигнал ZТ(t) со средней
мощностью
На выходе канала фиксируется
сигнал VТ(t), который искажен аддитивным
гауссовским шумом ξ(t) со средней мощностью

8.

Будем считать, что длительность Т передаваемого
сигнала достаточно велика, так что в соответствии с
теоремой Котельникова можно заменить
непрерывные реализации ZТ(t) и VТ(t)
последовательностями из
отсчётов, взятых
через интервалы
, где Fk – полоса
пропускания. Тогда среднее количество информации,
передаваемой по каналу
где H(V) и HZ(V) – априорная и апостериорная
энтропии N-мерного случайного вектора V.

9.

По определению гауссова канала помеха аддитивна
и статистически независима с входным сигналом,
поэтому
где
- энтропия N-мерного случайного вектора
помехи, компонентами которого являются
случайные величины в соответствующих сечениях
непрерывного аддитивного гауссова белого шума
ξ(t).

10.

Среднее количество информации, передаваемое по
каналу:
где h(v) – дифференциальная энтропия одного
отсчёта выходного сигнала.
Скорость передачи информации по непрерывному
гауссову каналу связи:
Пропускная способность непрерывного канала:

11.

По предположению в гауссовом канале связи
средняя мощность сигнала и помехи ограничены.
При ограничении на величину дисперсии
наибольшее значение h(v) достигается в случае
нормального распределения. Шум ξ(t) по
предположению имеет нормальное распределение,
следовательно, для того, чтобы выходной сигнал
имел нормальное распределение необходимо, чтобы
входной сигнал также был нормальным и
центрированным (т к центрированность сигнала
при заданной средней мощности соответствует
максимальному значению дисперсии).

12.

Кроме того, входной сигнал, в пределах заданной
полосы частот должен иметь равномерный
энергетический спектр. Только в этом случае можно
говорить о независимости отсчётов.
Пропускная способность непрерывного гауссова
канала тогда равна:

13.

Если выполнено необходимое условие
неискаженной передачи, то достаточные условия
всегда могут быть выполнены путем
соответствующих преобразований сигнала.
Объём сигнала определяется как
,а
необходимое условие его неискаженной
передачи . Достаточные условия
неискаженной передачи:
Предельное количество информации, которое
может быть передано по гауссовому каналу связи за
время

14.

1. При фиксированной Fk пропускная способность
определяется только отношением мощностей
сигнала и помех. Ограничение пропускной
способности непрерывного канала связано с
тем, что любые используемые для связи сигналы
имеют конечную мощность.
2. C = 0 только при PZ = 0. Т.е. непрерывный канал
обеспечивает передачу информации даже в том
случае, если уровень шумов превышают уровень
сигнала.
3. Повысить пропускную способность
непрерывного канала можно за счет расширения
полосы пропускания.