Приведение системы сил к заданному центру

1.

Лекция 3С
1
Приведение системы сил к заданному центру
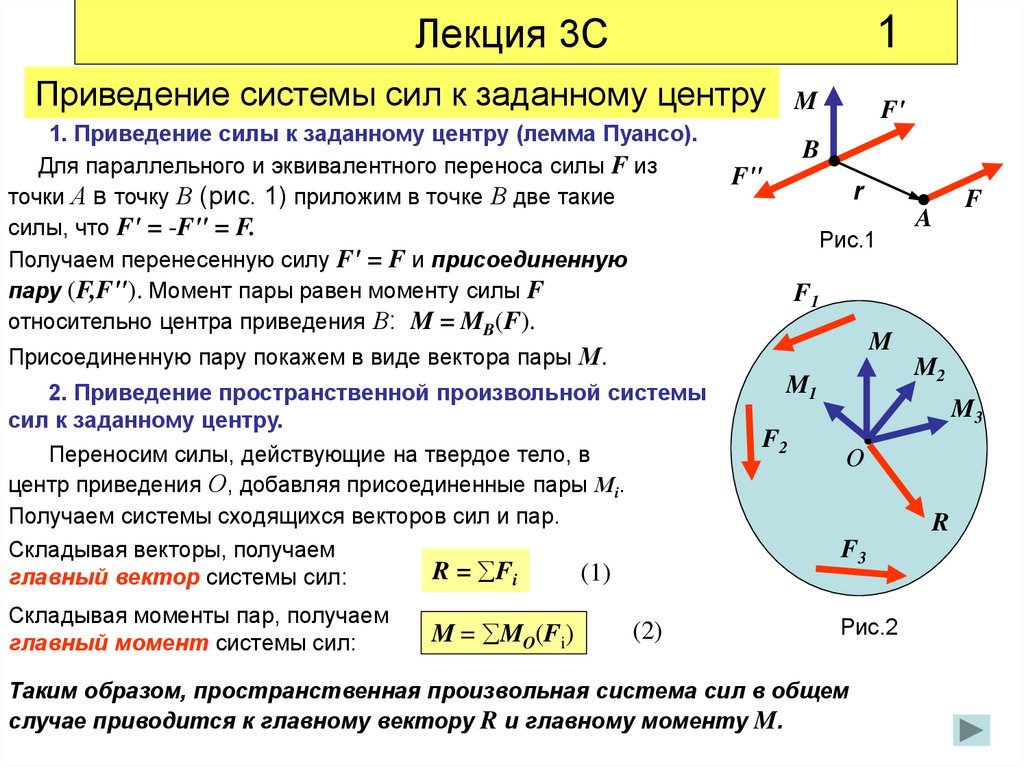
1. Приведение силы к заданному центру (лемма Пуансо).
Для параллельного и эквивалентного переноса силы F из
точки А в точку В (рис. 1) приложим в точке В две такие
силы, что F' = -F" = F.
Получаем перенесенную силу F' = F и присоединенную
пару (F,F"). Момент пары равен моменту силы F
относительно центра приведения В: M = MB(F).
M
F'
B
F"
r
Рис.1
Переносим силы, действующие на твердое тело, в
центр приведения О, добавляя присоединенные пары Мi.
Получаем системы сходящихся векторов сил и пар.
Складывая векторы, получаем
R = Fi
(1)
главный вектор системы сил:
Складывая моменты пар, получаем
главный момент системы сил:
M = MO(Fi)
M
M2
M1
F2
M3
O
R
F3
(2)
F
F1
Присоединенную пару покажем в виде вектора пары М.
2. Приведение пространственной произвольной системы
сил к заданному центру.
A
Рис.2
Таким образом, пространственная произвольная система сил в общем
случае приводится к главному вектору R и главному моменту M.

2.

Лекция 3С
2
3. Изменение главного момента при перемене центра приведения.
Главный вектор R не зависит от центра приведения.
R
Перенесем его из прежнего центра приведения А в новый B,
и для сохранения эквивалентности преобразования добавим
присоединенную пару, момент которой равен моменту силы MA
R относительно нового центра приведения:
MB
MB(R)
B
A
M B R BA R
Рис.3
Главный момент MA, как вектор свободный, переносим в точку В.
Главный момент MВ получим как сумму моментов MB(R) и MA:
M B M A BA R
(3)
4. Вычисление главного вектора и главного момента.
Проецируя (1) на оси координат, получим
Rx = Fix , Ry = Fiy , Rz = Fiz .
Модуль главного вектора R
Rx2 Ry2 Rz2 .
Ry
Rx
R
, cos R
, cos R z .
Направляющие косинусы cos R
R
R
R
Проецируя (2) на оси координат, получим
MOx= Mx= Mix = (yiFiz-ziFiy), MOy= My= Miy = (ziFix-xiFiz), MOz= Mz= Miz= (xiFiy-yiFix).
Модуль главного момента M O
Направляющие косинусы
M x2 M y2 M z2 .
cos M
My
Mx
M
, cos M
, cos M z .
M
M
M

3.

Лекция 3С
3
z
5. Приведение плоской произвольной системы сил.
Главный вектор плоской произвольной системы сил расположен в
плоскости сил, а главный момент перпендикулярен к ней, MO R, рис.4.
Расчет главного вектора и главного момента ведется по формулам:
Rx = Fix , Ry = Fiy .
R R R .
2
x
2
y
MO = MiO = (xiFiy – yiFix).
Ry
Rx
cos R
, cos R
.
R
R
MO
O
y
R
x
Рис.4
6. Условия равновесия пространственной произвольной системы сил.
В векторной форме: R = 0,
MO = 0.
В скалярной форме: R = F = 0, M = M = (y F – z F ) = 0,
x
ix
x
ix
i iz
i iy
F2
Ry = Fiy = 0, My = Miy = (ziFix – xiFiz) = 0, (4а)
Rz = Fiz = 0,
z
(4)
F1
Mz = Miz = (xiFiy – yiFix) = 0.
F3
x
7. Условия равновесия плоской произвольной системы сил.
Rx = Fix = 0, Ry = Fiy = 0.
MO = MiO = (xiFiy – yiFix) = 0.
Рис.5
(5)
y
F1
8. Условия равновесия системы параллельных сил.
Пространственной, рис.5,
Rz = Fiz = 0, Mx = Mix = (yiFiz – ziFiy) = 0, My = Miy = (ziFix – xiFiz) = 0.
(6)
Плоской, рис.6,
Ry = Fiy = 0, MO = MiO = (yiFix – xiFiy) = 0.
(7)
F4
y
O
F3
F2
Рис.6
x

4.

Лекция 3С
4
z
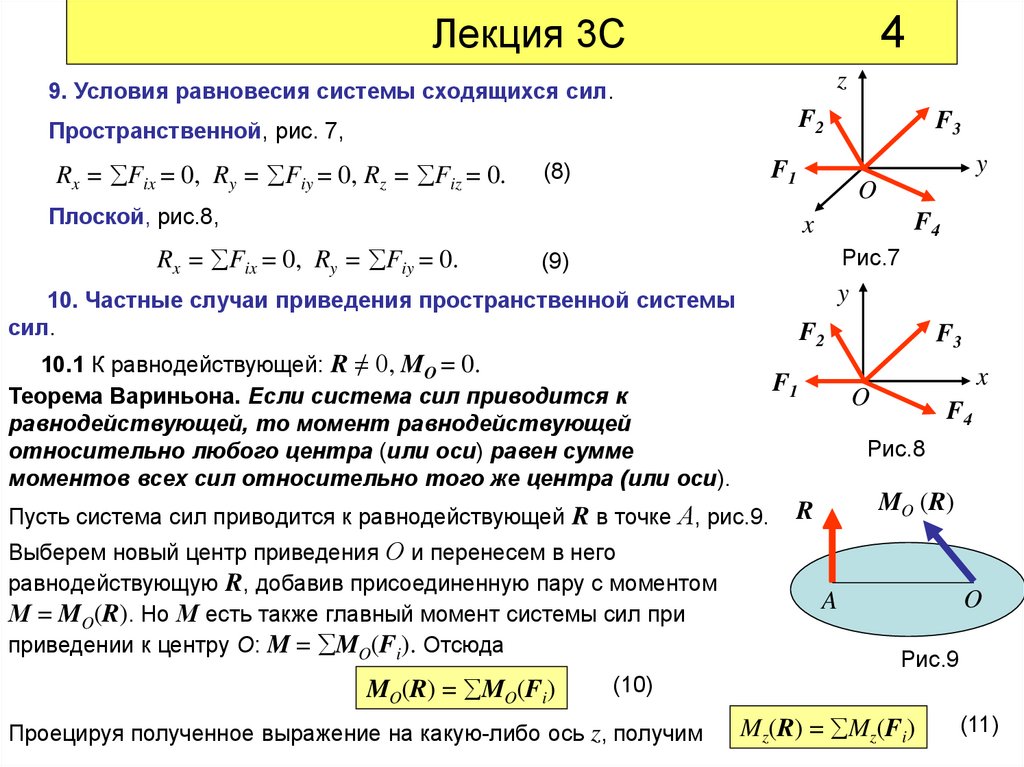
9. Условия равновесия системы сходящихся сил.
F2
Пространственной, рис. 7,
Rx = Fix = 0, Ry = Fiy = 0, Rz = Fiz = 0.
F3
y
F1
(8)
Плоской, рис.8,
O
F4
x
Rx = Fix = 0, Ry = Fiy = 0.
Рис.7
(9)
y
10. Частные случаи приведения пространственной системы
сил.
F2
10.1 К равнодействующей: R ≠ 0, MO = 0.
Теорема Вариньона. Если система сил приводится к
равнодействующей, то момент равнодействующей
относительно любого центра (или оси) равен сумме
моментов всех сил относительно того же центра (или оси).
F1
MO(R) = MO(Fi)
x
O
F4
Рис.8
Пусть система сил приводится к равнодействующей R в точке А, рис.9.
Выберем новый центр приведения О и перенесем в него
равнодействующую R, добавив присоединенную пару с моментом
М = MO(R). Но М есть также главный момент системы сил при
приведении к центру О: M = MO(Fi). Отсюда
F3
MO (R)
R
O
A
Рис.9
(10)
Проецируя полученное выражение на какую-либо ось z, получим
Mz(R) = Mz(Fi)
(11)

5.

Лекция 3С
5
10.2 К главному моменту: R = 0, M ≠ 0. При этом величина главного момента не зависит
от центра приведения.
Из формулы M B M A BA R
(см. ф. 3 ) следует, что при R = 0 MB = MA.
10.3 К главному вектору и главному моменту, причем R MO, рис.10.
Эту систему можно упростить еще более, сведя к равнодействующей.
Представим главный момент MO в виде пары сил (R', R")
такой, что силы R" = -R и расположены на одной прямой.
MO
Силы R и R", как взаимно уравновешенные, можно удалить.
Остается равнодействующая R' = R, приложенная в точке
О1. Плечо d определяется по формуле: d = MO / R.
R"
R'
R
O
d
O1
Рис.10
10.4 К главному вектору и главному моменту, причем = R, MO ≠ 900.
10.4а Приведение системы сил к динаме (динамическому винту).
Динама – совокупность главного вектора и главного момента,
имеющих общую линию действия, рис.11. При совпадении
направлений главного вектора и вектора главного момента
динамический винт – правый. В противном случае – левый.
F1
Общая линия действия называется центральной винтовой
осью системы сил.
Пусть система сил приведена к главному вектору и главному
моменту в центре приведения О, причем ≠ 900, рис.12.
MO
R
F2
Центральная
винтовая ось
Рис.11

6.

Лекция 3С
6
Разложим момент MO на MO1 || R и MO2 R, причем MO1 = MOcos , MO2 = MOsin .
Момент MO2 представим в виде пары сил (R', R") согласно п. 3:
R = R' = -R". MO2 = R' d = R'' d, где d – плечо пары.
Силы (R, R") устраним, как уравновешенные. Получим силу R
= R', приложенную в точке O1 на расстоянии d = MOsin /R.
Момент MO1, как вектор свободный, перенесем в точку О1.
Тем самым получен динамический винт.
R
MO
M O1 M O cos
R R R
2
x
2
y
2
z
M O2 M M .
;
2
O
2
O1
MO1
d
O1
O
Расчет величин MO1 и MO2 по проекциям Mx, My, Mz и Rx, Ry, Rz M
O2
получим из формулы MO R = MO R cos = Mx Rx + My Ry + Mz Rz:
M x Rx M y Ry M z Rz
R'
R"
Центральная
винтовая ось
Рис.12.
Уравнение центральной винтовой оси получим, исходя из формулы M O OO1 R R ,
или
i
M xi M y j M z k x
Rx
M x yRz zR y
Rx
j
y
Ry
k
z Rx i R y j Rz k ,
Rz
M y zRx xRz
Ry
M z xRy yRx
Rz
.
откуда

7.

Лекция 3С
7
10.4б Приведение к двум скрещивающимся силам, рис.13.
MO
R
Покажем пару MO в виде пары из двух сил (R1,R2).
Сложив силы R1+ R = Q, получим две
скрещивающиеся силы - Q и R2.
d
Q
R2
O
R1
O1
Рис. 13
10.5 Главный вектор и главный момент равны нулю, R = 0, MO = 0, то есть система
сил уравновешена.
11. Инварианты системы сил.
Инвариантами системы сил называют векторные или скалярные величины, не
изменяющиеся при перемене центра приведения.
1-ый инвариант – главный вектор системы сил : R = Fi, (I1 = Rx2 + Ry2 + Rz2).
2-ой инвариант – скалярное произведение главного вектора и главного момента:
I2 = R MO = RxMOx + RyMOy + RzMOz. Умножим формулу MO1 = MO + O1O R скалярно
на R : MO1 R = MO R + (O1O R) R . Так как (O1O R) R = 0 (R (O1O R)), то
MO1 R = MO R .
Равенство MO1 R = MO R можно записать так: MO1 R cos(MO1 R) = MO R cos(MO R). Или,
сократив на R, получим MO1 cos(MO1 R) = MO cos(MO R). Отсюда следует, что MO = min
когда главный вектор и главный момент совпадают по направлению.

8.

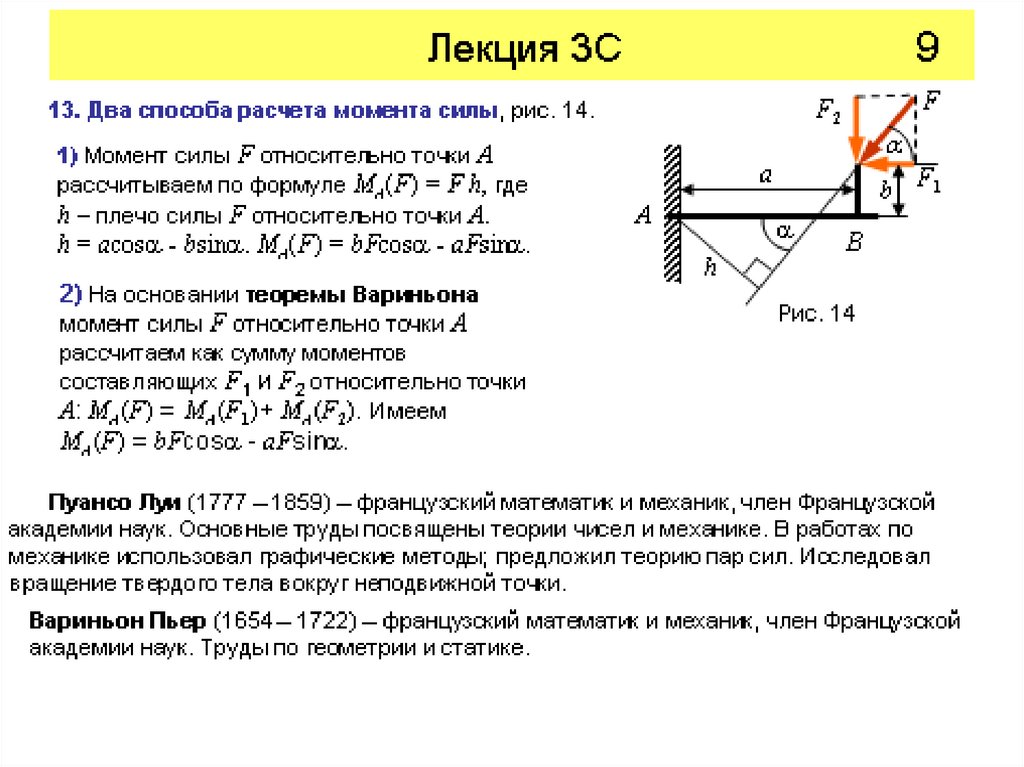
Лекция 3С
12. Порядок решения задач статики
1) Выделяем объект, равновесие которого рассматривается.
2) Показываем все известные (активные) силы.
3) Освобождаемся от связей и показываем реакции связей.
4) Определяем (классифицируем) систему сил и записываем
условия равновесия.
5) Составляем соответствующие уравнения равновесия.
6) Решаем полученную систему уравнений и находим искомые
величины.
8