Геометрические задачи

1.

Геометрические задачи
Научить
решать
учащихся
геометрические задачи - это значит не
только подготовить их к хорошей сдаче
экзамена, но и научить их логически
мыслить, доказательно отстаивать
свою точку зрения, уметь творчески
подходить к любому делу.

2.

Трудности решения
геометрических задач
• Не
существует
единых
алгоритмов
решения.
• Необходимость выбора метода решения
задачи и теоремы для решения конкретной
задачи (нескольких теорем) из большого
набора известных фактов.
• Нужно решить довольно много задач, чтобы
научиться их решать.

3.

Причины ошибок в решении
геометрических задач
• Незнание и/или непонимание аксиом,
определений,
теорем.
Неумение
их
применять.
• Невнимательное чтение условия и вопроса
задания. Вычислительные ошибки.
• Нарушения логики в рассуждениях.
Принятие ошибочных гипотез.
• Недостатки в работе с рисунком.

4.

Необходимые условия успеха при решении
задач по геометрии
• Уверенное владение основными понятиями
и их свойствами (определения, аксиомы,
теоремы, базовые задачи).
• Знание основных методов и приёмов
решения задач.
• Умение комбинировать методы и приёмы
решения задач.
• Наличие опыта решения задач.

5.

Специфические особенности методов
решения геометрических задач
• Большое разнообразие.
• Взаимозаменяемость.
• Трудность формального описания.
• Отсутствие чётких границ применения
(в отличие от алгебры).
• Использование комбинаций методов и
приёмов.

6.

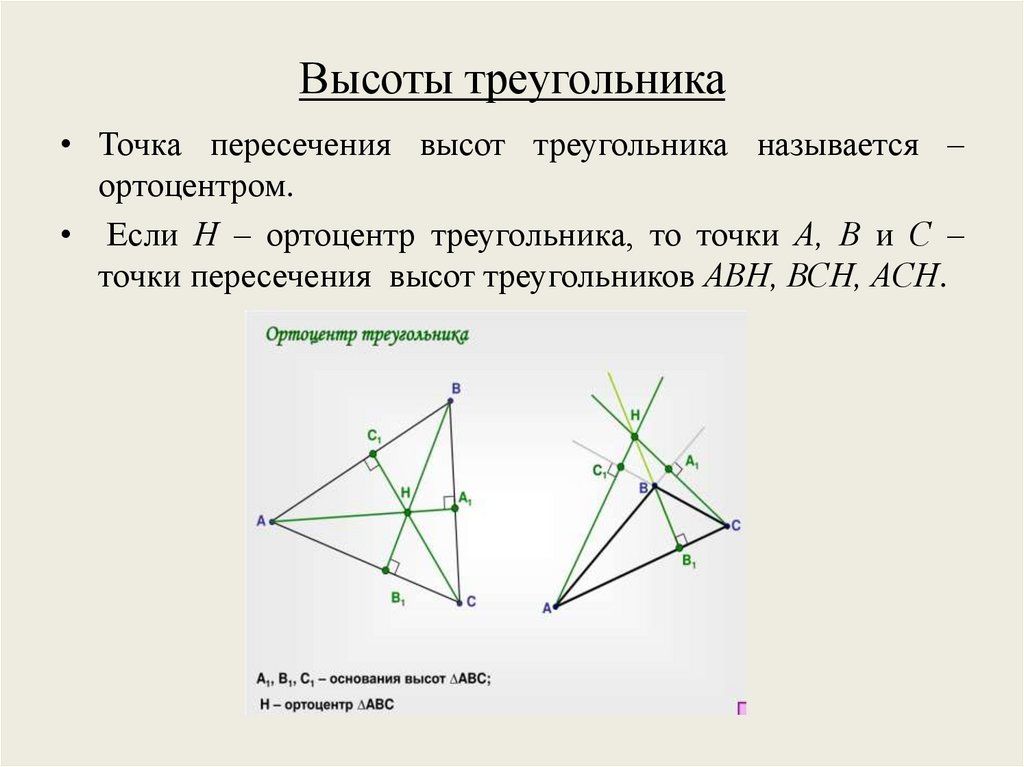
Высоты треугольника
• Точка пересечения высот треугольника называется –
ортоцентром.
• Если Н – ортоцентр треугольника, то точки А, В и С –
точки пересечения высот треугольников АВН, ВСН, АСН.

7.

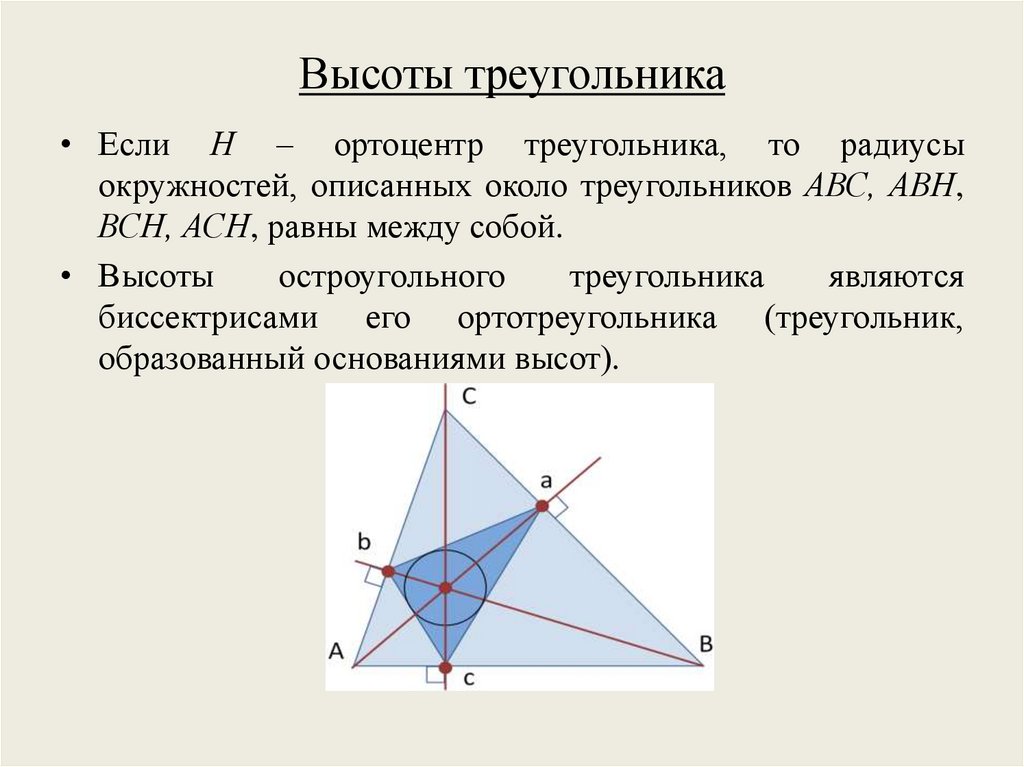
Высоты треугольника
• Если Н – ортоцентр треугольника, то радиусы
окружностей, описанных около треугольников АВС, АВН,
ВСН, АСН, равны между собой.
• Высоты
остроугольного
треугольника
являются
биссектрисами его ортотреугольника (треугольник,
образованный основаниями высот).

8.

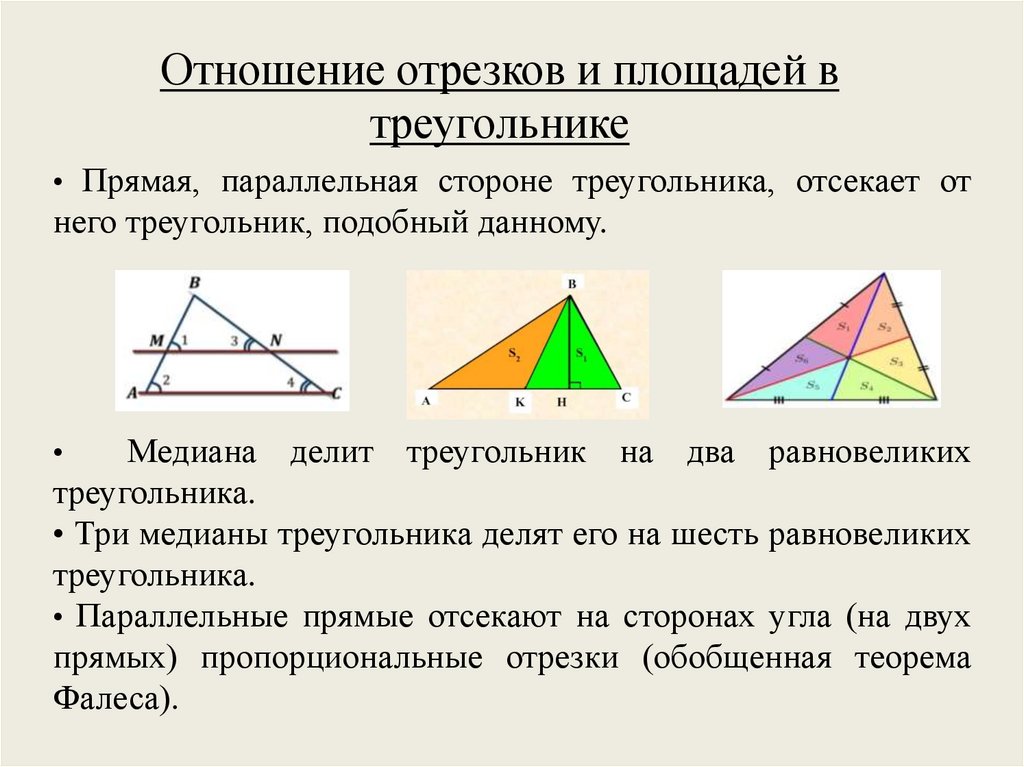
Отношение отрезков и площадей в
треугольнике
• Прямая, параллельная стороне треугольника, отсекает от
него треугольник, подобный данному.
Медиана делит треугольник на два равновеликих
треугольника.
• Три медианы треугольника делят его на шесть равновеликих
треугольника.
• Параллельные прямые отсекают на сторонах угла (на двух
прямых) пропорциональные отрезки (обобщенная теорема
Фалеса).

9.

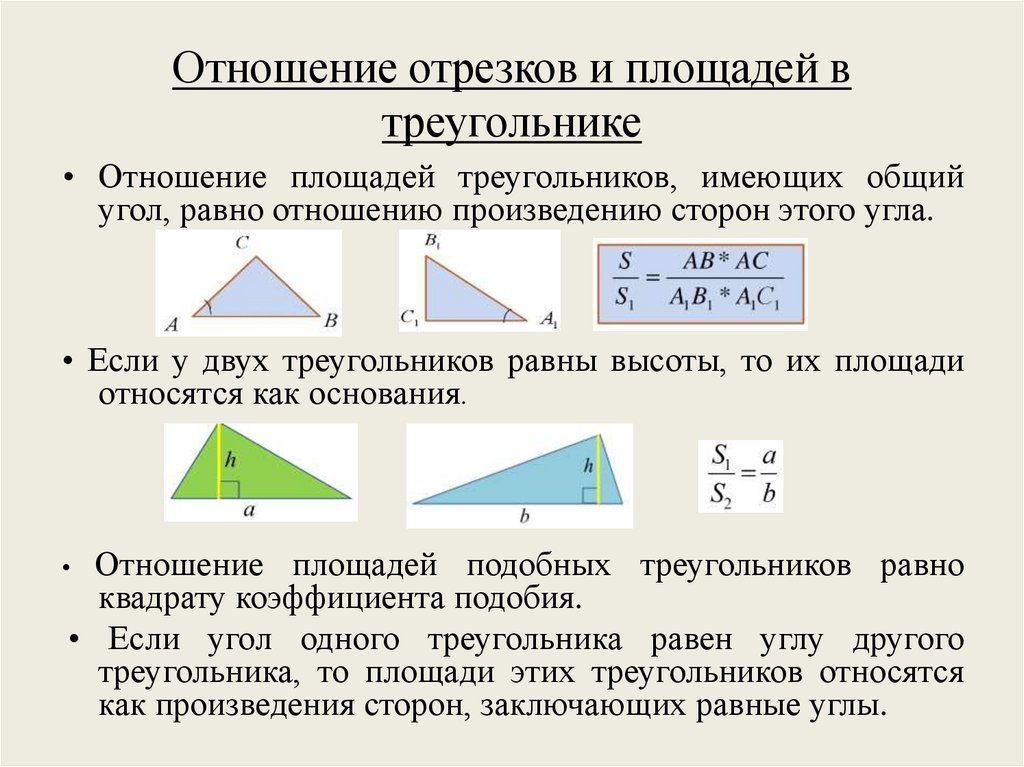
Отношение отрезков и площадей в
треугольнике
• Отношение площадей треугольников, имеющих общий
угол, равно отношению произведению сторон этого угла.
• Если у двух треугольников равны высоты, то их площади
относятся как основания.
Отношение площадей подобных треугольников равно
квадрату коэффициента подобия.
• Если угол одного треугольника равен углу другого
треугольника, то площади этих треугольников относятся
как произведения сторон, заключающих равные углы.

10.

Опорные задачи
Катет прямоугольного треугольника есть среднее
пропорциональное между гипотенузой и проекцией этого
катета на гипотенузу.
• Высота прямоугольного треугольника, проведённая из
вершины прямого угла на гипотенузу, есть среднее
пропорциональное между отрезками, на которые делится
гипотенуза этой высотой.
• Площади треугольников, имеющих равные основания и
равные высоты, равны.
• Отношение площадей треугольников, имеющих равные
высоты, равно отношению их оснований.

11.

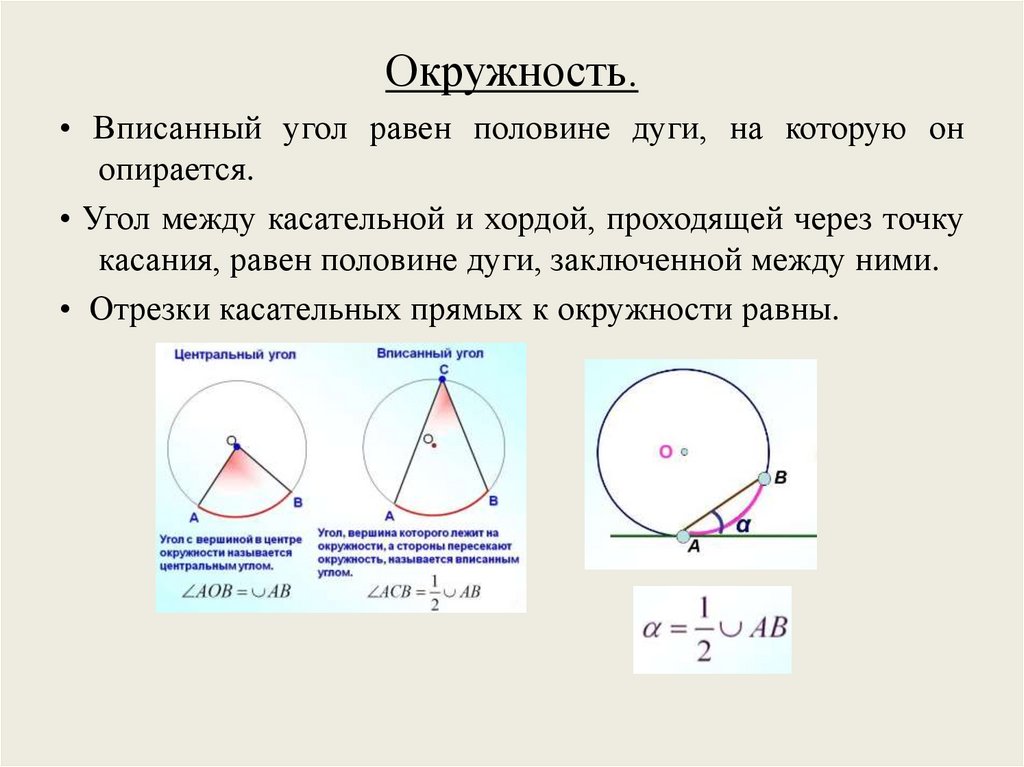
Окружность.
• Вписанный угол равен половине дуги, на которую он
опирается.
• Угол между касательной и хордой, проходящей через точку
касания, равен половине дуги, заключенной между ними.
• Отрезки касательных прямых к окружности равны.

12.

Взаимное расположение окружностей
• При любом способе касания точка касания и центры
окружностей лежат на одной прямой.
• При внешнем касании центры окружностей расположены
на линии центров по разные стороны от точки касания,
при внутреннем – по одну сторону.
• Расстояние между центрами касающихся окружностей
радиусов R и r ( R ≥ r ) равно (R + r) при внешнем касании
и (R – r) при внутреннем.

13.

Окружность, касательные, секущие и хорды
• Радиус ( диаметр), перпендикулярный хорде, делит хорду
пополам.
• Пересекающиеся окружности в точках А и A₁ имеют
общую хорду АА₁.
• Общая хорда двух пересекающихся окружностей,
перпендикулярна линии центров и делится ею пополам.

14.

Окружность, касательные, секущие и хорды
• Если две хорды пересекаются, то произведение отрезков
одной хорды равно произведению отрезков другой хорды.
•Пусть через точку А проведена касательная АВ к
окружности(В–точка касания) и секущая, пересекающая
окружность в двух точках D и C. Тогда АВ² = АC ⋅ AD.
• Пусть через точку А проведены секущие к окружности,
пересекающие её в точках первая В и С , а другая – D и E. Тогда
АВ ⋅ АС = АD⋅ АE.

15.

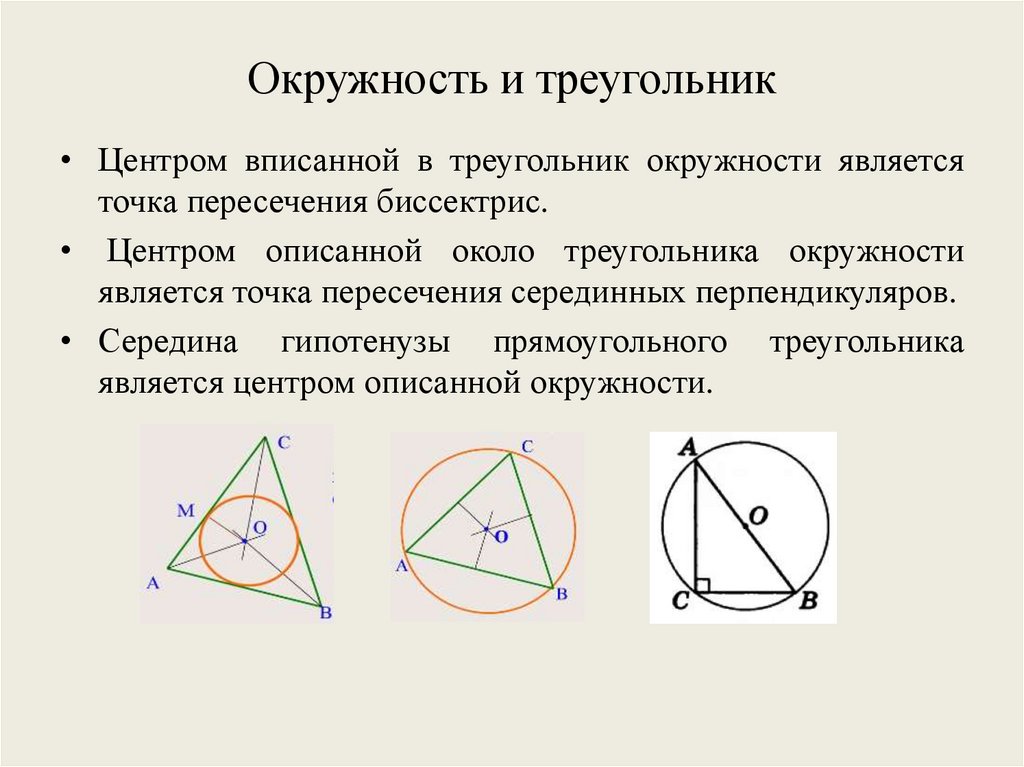
Окружность и треугольник
• Центром вписанной в треугольник окружности является
точка пересечения биссектрис.
• Центром описанной около треугольника окружности
является точка пересечения серединных перпендикуляров.
• Середина гипотенузы прямоугольного треугольника
является центром описанной окружности.

16.

Взаимное расположение окружности и
четырехугольника
• Трапеция вписана в некую окружность тогда и только
тогда, когда она является равнобедренной.
• Сумма
противоположных
углов
вписанного
четырехугольника равна 180°.
• Центр окружности, описанной около трапеции, лежит на
пересечении серединных перпендикуляров к сторонам
трапеции.
• Суммы
противоположных
сторон
описанного
четырехугольника равны

17.

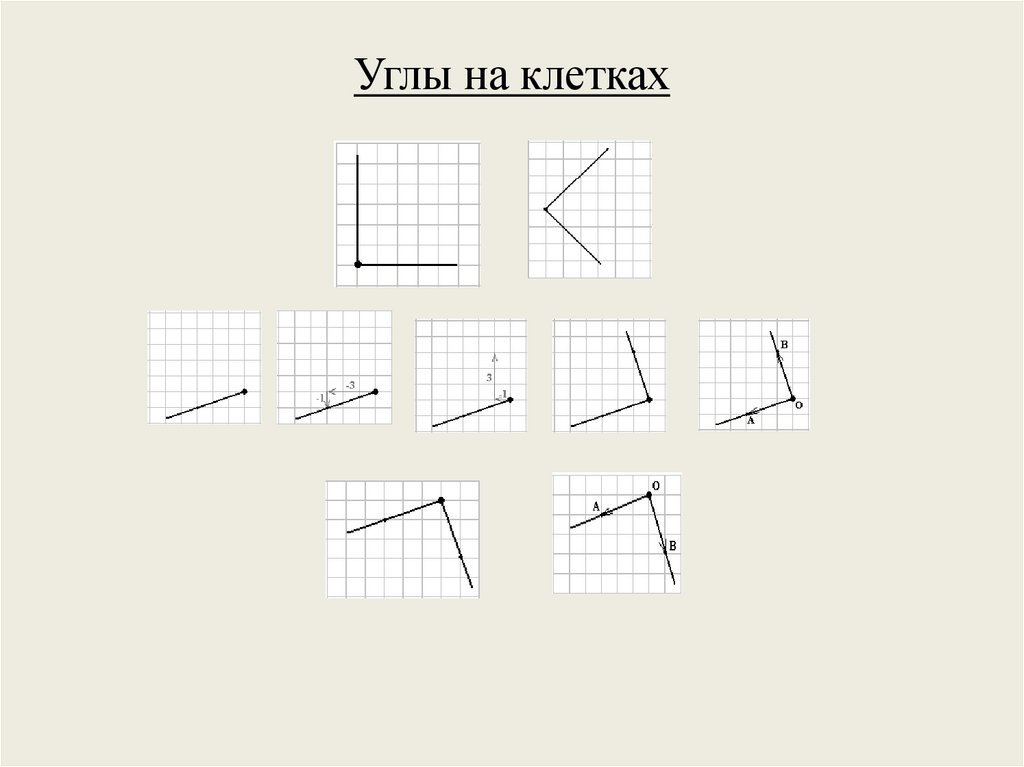
Углы на клетках

18.

Найти тангенс угла, изображенного на
рисунке.
Решение. Выделим на этом рисунке узлы сетки – точки А и
С. Рассмотрим треугольник АВС. Заметим, что он является
прямоугольным, к тому же катет ВС в 2 раза больше катета
АС. Отсюда следует, что тангенс угла В равен 1:2 = 0,5.

19.

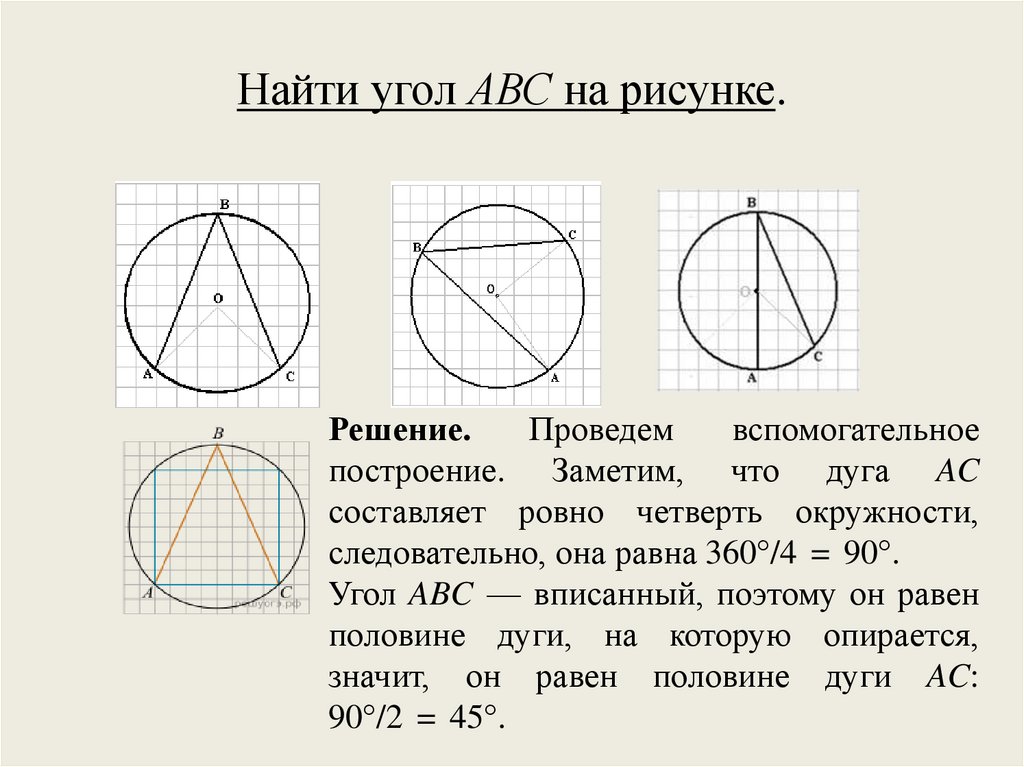
Найти угол АВС на рисунке.
Решение.
Проведем
вспомогательное
построение. Заметим, что дуга AC
составляет ровно четверть окружности,
следовательно, она равна 360°/4 = 90°.
Угол ABC — вписанный, поэтому он равен
половине дуги, на которую опирается,
значит, он равен половине дуги AC:
90°/2 = 45°.

20.

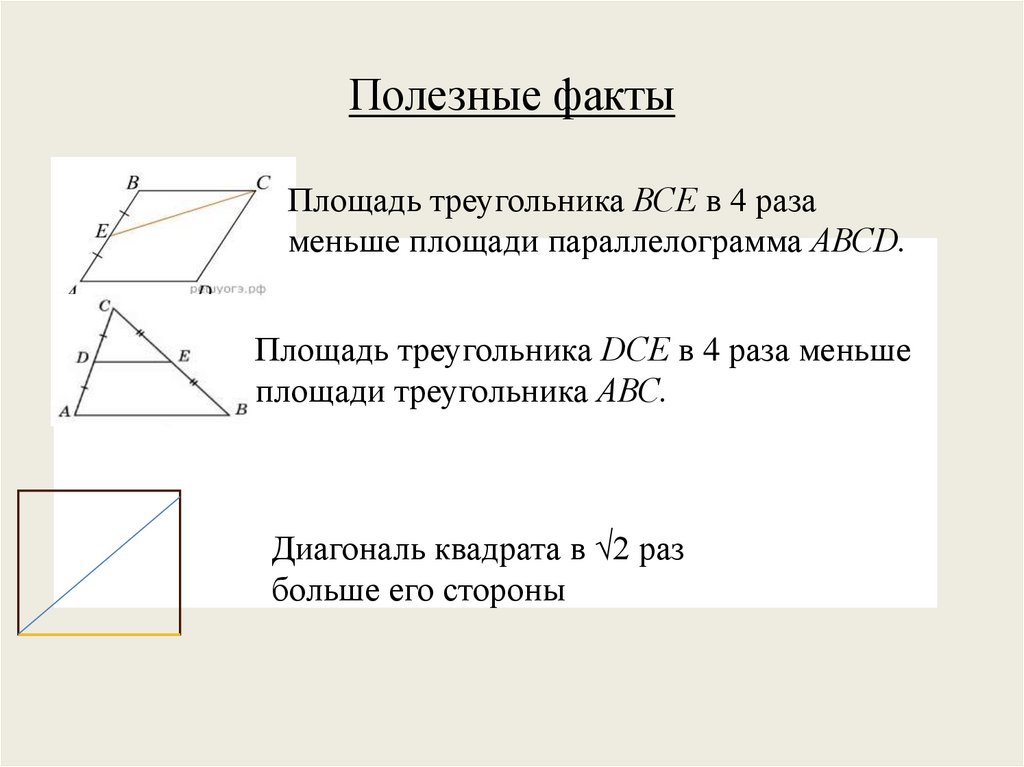
Полезные факты
Площадь треугольника ВСЕ в 4 раза
меньше площади параллелограмма АВСD.
Площадь
треугольника DСЕ
в 4 раза
• Площадь
треугольника
DСЕ
в 4 меньше
раза
треугольника
АВС.
меньшеплощади
площади
треугольника
АВС
• Диагональ
квадрата
раз больше
Диагональ
квадратавв√2
√2 раз
больше его стороны
его

21.

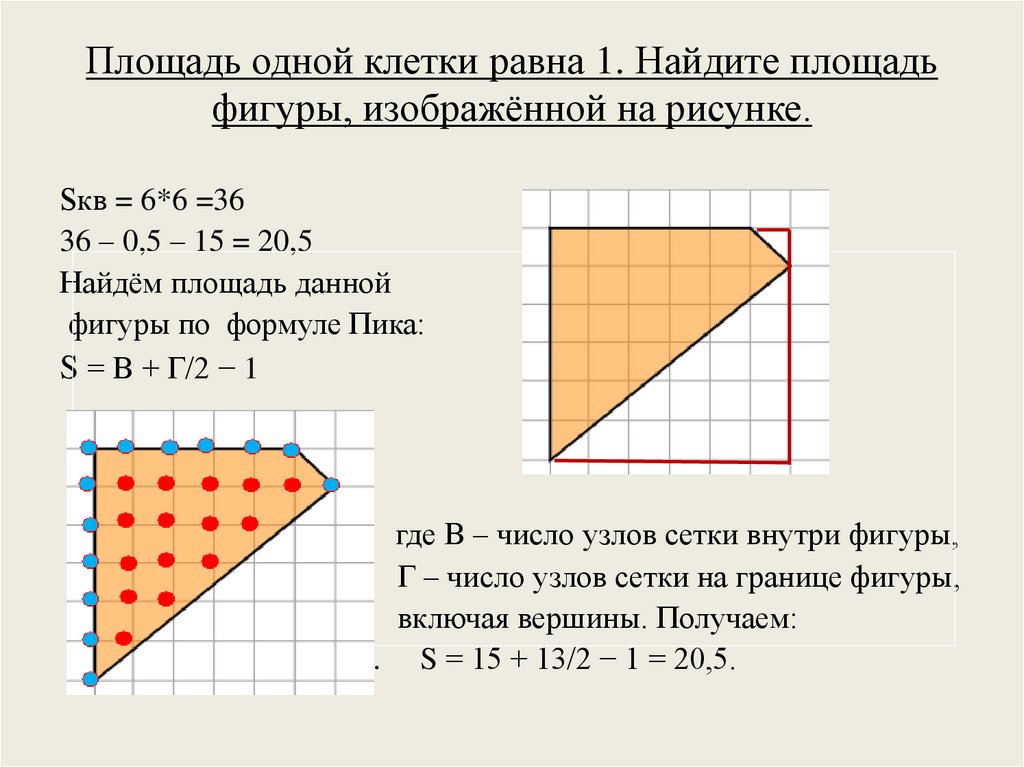
Площадь одной клетки равна 1. Найдите площадь
фигуры, изображённой на рисунке.
Sкв = 6*6 =36
36 – 0,5 – 15 = 20,5
Найдём площадь данной
фигуры по формуле Пика:
S = В + Г/2 − 1
где В – число узлов сетки внутри фигуры,
Г – число узлов сетки на границе фигуры,
включая вершины. Получаем:
S = 15 + 13/2 − 1 = 20,5. S = 15 + 13/2 − 1 = 20,5.

22.

«Геометрия полна приключений, потому что
за каждой задачей скрывается приключение
мысли. Решить задачу – это значит
пережить приключение»
Вячеслав Викторович Произволов.