Похожие презентации:
Правила вычисления производных. Из истории…
1. Правила вычисления производных
2. Из истории…
Честь открытияосновных законов
математического
анализа принадлежит
немецкому математику
Готфриду Вильгельму
Лейбницу
3. Из истории…
Дифференциальное исчисление - раздел математики, в котором изучаются
производные и дифференциалы функций и их применения к исследованию
функций, связан с именами И. Ньютона и Г. Лейбница (вторая половина
17 в.). Они сформулировали основные положения дифференциального и
интегрального исчисления, которые составляют основную часть
математического
анализа
(или
анализа
бесконечно
малых).
Дифференциальное исчисление даёт аппарат для исследования функций в
достаточно малой окрестности каждой точки. Центральные понятия
дифференциального исчисления: производная и дифференциал. Понятие
производной возникло из большого числа задач естествознания и
математики. Важнейшие из них — определение скорости прямолинейного
движения точки и построение касательной к кривой. Создание
дифференциального исчисления открыло новую эпоху в развитии
математики. Оно повлекло за собой появление ряда математических
дисциплин: теории рядов, дифференциальной геометрии, теории
дифференциальных уравнений. Методы математического анализа нашли
применение во всех разделах математики. Неизмеримо расширилась
область приложений математики к вопросам естествознания и техники.
"Лишь дифференциальное исчисление дает естествознанию возможность
изображать математически не только состояния, но и процессы: движение"
(Ф. Энгельс)
4. Повторим…
1. Определение производной функции.2. Формулы дифференцирования, полученные на
предыдущем занятии:
x 2x
x 3x
2
3
2
(kx b) k
C 0
далее
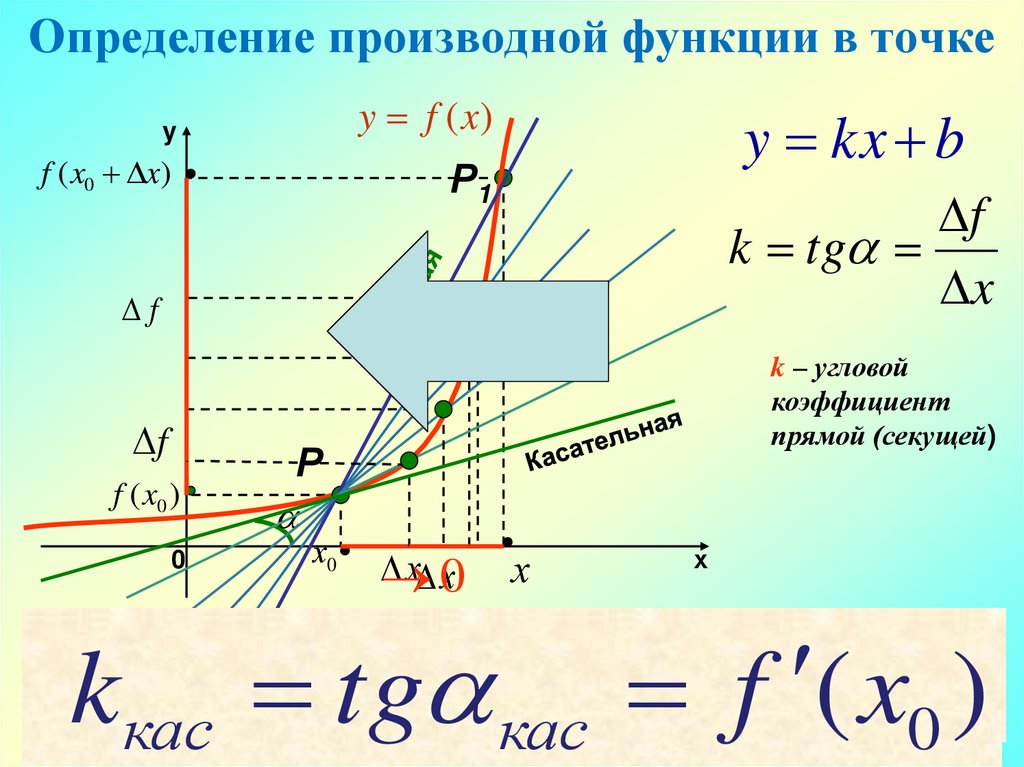
5. Определение производной функции в точке
y f (x)y
f ( x0 x)
y kx b
Р1
f
f
k tg
x
f
k – угловой
коэффициент
прямой (секущей)
f ( x0 )
0
Р
х0
х х0
х
х
kкас tg кас f ( x0 )
Производно
й функции
f ( x) вположение
точке х0 называется
Секущая стремится
занять
касательной.
То есть, касательная есть предельное положение
f
секущей.
число
, к которому стремится отношение
f ( x0 )
x x 0
6.
Правиладифференцирования
7. 1. Производная степенной функции
Для любого числа n илюбого х (х 0)
справедливо равенство:
( x ) n x
n
n 1
№ 1. Найдите производные
функций:
4
а) f ( x) x ;
100
f
(
x
)
x
;
б)
в) f ( x) x 5 ;
г) f ( x ) x;
1
д) y ( x ) ;
x
е) y ( x) x .
4
Дополнительно: y x 3
8. 2. Производная суммы функций
Если функции u и vдифференцируемы в
точке х0, то их сумма
дифференцируема в этой
точке и
(u v) u v
№ 2. Найдите производные
функций:
2
3
f
(
x
)
x
x
;
а)
б) f ( x) x x 2;
в) вычислите производную
функции при данном значении
аргумента:
f ( x) 1 x x x x5 , при x 2.
2
Коротко говорят:
производная суммы
(разности) равна сумме
(разности) производных.
3
Дополнительно:
f ( x) 5 x 4
4
9. 3. Производная произведения постоянной на функцию
Если функции uдифференцируема в точке х0,
а C – постоянная, то функция
Cu дифференцируема в этой
точке и
Cu Сu
Коротко говорят:
постоянный множитель
можно выносить за знак
производной
№ 3. Найти производные
функций:
4
а) y 3x ;
5
б) y 2 x ;
1 7
5
в) y x 4 x 2 x 1;
7
г) Решите уравнение f (x)=0,
2
если f ( x) 2 x 4 x.
Дополнительно: Решите
неравенство f (x) 0, если
1 3
f ( x) 4 x x .
3
10. 4. Производная произведения двух функций
Если функции u и vдифференцируемы в точке
х0, то их произведение
дифференцируемо в этой
точке и
(u v) u v u v
№ 4. Найдите производные
функций:
2
3
f
(
x
)
x
3
x
x
;
а)
3
;
f
(
x
)
2
x
3
1
x
б)
Дополнительно:
f ( x) 2 x 1 x 2 3x 1
11. 5. Производная частного
Если функции u и vдифференцируемы в точке
х0 и функция v не равна
нулю в этой точке то
частное дифференцируемо
в этой точке и
u u v u v
2
v
v
№ 5.
а) Найдите производную
функции
3x 2
;
5x 8
б) Вычислите значение
производной функции f в
данной точке:
y
f ( x)
3 x
, x 3.
2 x
Доп. № 215 (а)
12. Основные правила дифференцирования
nn
1
1.
( x ) n x
2.
(u v) u v
3.
Cu Сu
4.
(u v) u v u v
5. u u v u v
2
v
v
13. Ответы к проверочной работе
№1 вариант
№
1
1
2
y 21x 20
f ( x) 35x 6
3
f ( x) 6 x 3
4
5
Доп.
17
3
2
2
3
4
5
Доп.
2 вариант
y 38x 37
f ( x) 35x 4
f ( x) 12 x 4
-4
21
4
14. Домашнее задание
• Систематизировать полученные производные элементарныхфункций в таблицу.
• Из учебника А.Н. Колмогорова «Алгебра и начала
математического анализа 10-11»:
№ 212(в): Вычислите значения производной функции f данной
точке:
.
№ 213(в): Решите уравнение
.
№ 214(б): Решите неравенство
, если
, если
.














 Математика
Математика








