Похожие презентации:
Определение производной. Правила вычисления производных. Таблица производных
1.
2.
Урок 54.Тема: Определение производной.
Правила вычисления
производных. Таблица
производных
3.
Цели обучения:• 10.3.1.9 - знать определение производной функции и
находить производную функции по определению;
• 10.3.1.10 - находить производные постоянной функции и
степенной функции;
• 10.3.1.11 - знать и применять правила дифференцирования
4.
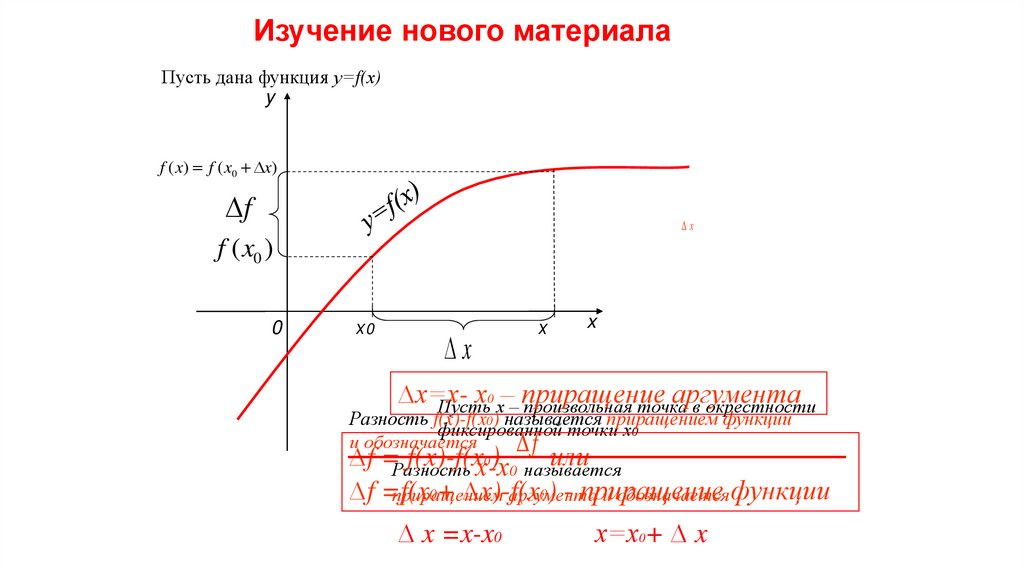
Изучение нового материалаПусть дана функция у=f(х)
y
f ( x) f ( x0 x)
f
x
f ( x0 )
0
х0
x
х
x
∆х=хх0 – приращение аргумента
Пусть х – произвольная точка в окрестности
Разность f(x)-f(x0) называется приращением функции
фиксированной точки х0
и обозначается
f
∆f =Разность
f(x)-f(xх-х
0)
или
0 называется
∆f =f(x
0+ ∆x)-f(x
0) - приращение
приращением
аргумента
и обозначается функции
∆ x =x-x0
х=х0+ ∆ x
5.
Определение производнойу
Если разностное отношение х имеет предел при х 0
то его называют производной функции в т. х0
lim
х 0
f ( x0 x ) f ( x0 )
y
lim
f ( x 0 )
x x 0
x
Вообще данную операцию называют
дифференцированием функции, а
производная – это результат
дифференцирования
6.
Пример:f ( x ) ( x ) и найти f ( x 0 ),
если x 0 3
2
1) y ( x0 x) x0 x0 2 x0 x x x0
2
2
2 x0 x x
2
2
2
2
x(2 x0 x)
y 2 x0 x x
2)
2 x0 x
x
x
x
3) lim (2 x0 x) 2 x0
2
x0
х 0
f ( x ) ( x ) 2 х - производная функции
- производная функции в т. х0
f ( 3 ) 2 ( 3 ) 6
т.е.
2
7.
Схема вычисления производной функции:1. Найти приращение функции на отрезке [ x; x+Δx]:
y y ( x x) y ( x)
2. Разделить приращение функции на приращение
аргумента: y
y ( x x) y ( x)
x
x
3. Найти предел отношения приращения функции к
приращению аргумента, когда приращение аргумента
стремится к нулю.
y
y ( x x) y ( x)
y lim
lim
x 0 x
x 0
x
8.
Задание: Найти производную функции:1.
y x
2.
y C , где С число
3.
4.
5.
3
y kx b, где k и b числа
1
y
x
y x
9.
Решение 1: Вычислить производную функции y x 31.
f f ( x x) f ( x) ( x x) x
3
3
x 3 3x 2 x 3x x 2 x 3 x 3
3x 2 x 3x x 2 x 3
2.
3.
y 3x 2 x 3x x 2 x 3
3x 2 3x x x 2
x
x
y
2
2
y lim
lim 3x 3 x x x
x 0 x
x 0
2
2
lim 3x lim 3x x lim x
x 0
2
x 0
3x 0 0 3x
x 0
2
10.
Таблица простейших производныхФУНКЦИЯ
ПРОИЗВОДНАЯ
(С )
0
( х )
1
( х )
n
1
х
( х )
nх
n 1
1
2
х
1
2 х
11.
Правила дифференцирования(вычисления производных)
(u v) u v
• (1)
• (2)
• (3)
• Следствия:
(uv) u v uv
u u v uv
2
v
v
Сv
С
1) (Сv) Сv 2) 2
v
v
12.
Примеры.1)
2)
3)
4)
х
f ( x)
9 1
f ( x) (2 x 3 х 2 4 х 12)
2
4
х
2
f ( x) 10
8 х
f ( x) (14 х )
3
13.
Примеры.х
6) f ( x)
4
3
2
2
7/1) f ( x) ( х (5 2 х))
7/2) f ( x) ( х (5 2 х)) (5 х 2 х )
2
2
3










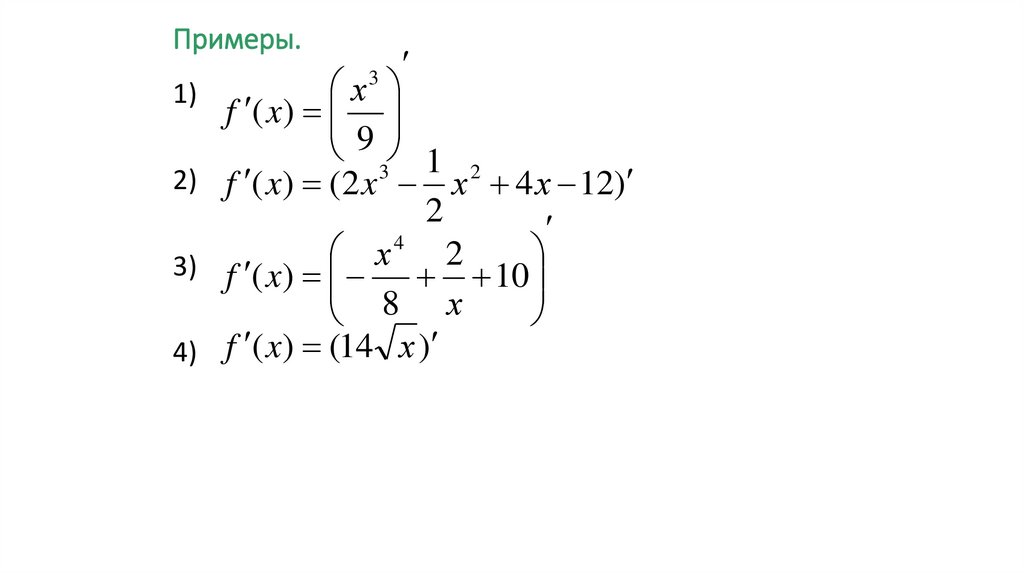

 Математика
Математика








