Похожие презентации:
Трехкомпонентные сплавы (лекция 8)
1.
Лекция 82.
Трехкомпонентные системыТрехкомпонентные сплавы – такие сплавы формируются
при сплавлении трех элементов или компонентов.
Трехкомпонентная фазовая диаграмма – фазовая
диаграмма для трех компонентов показывающая
имеющиеся фазы и их состав при различных
температурах. Для этих диаграмм требуется рисовать
трехмерное изображение и получать двухмерные
изотермические сечения. Для упрощения построения
сечений используются концентрационные треугольники.
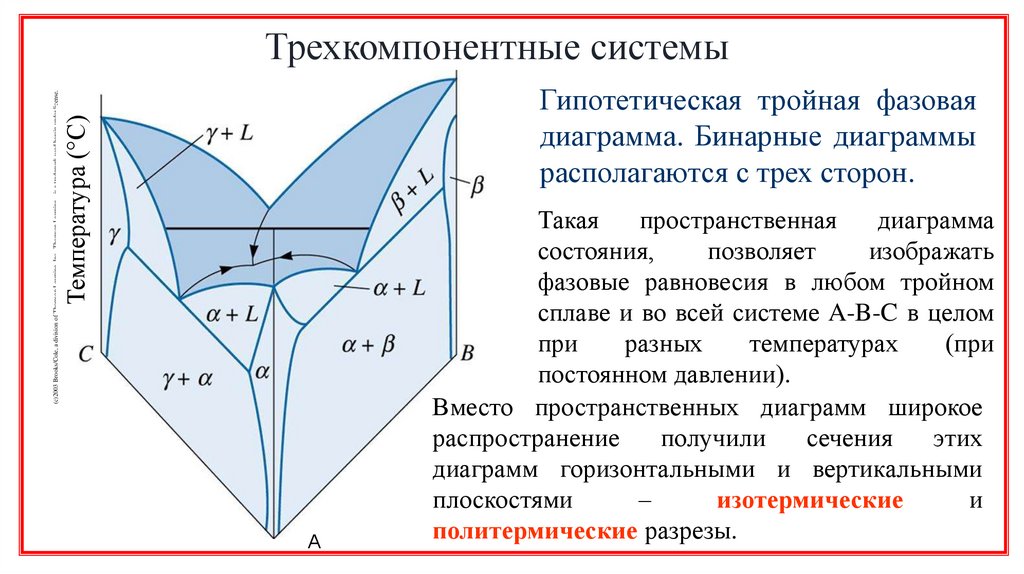
3.
Гипотетическая тройная фазоваядиаграмма. Бинарные диаграммы
располагаются с трех сторон.
Температура (°С)
(c)2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning ™ is a trademark used herein under license.
Трехкомпонентные системы
А
Такая
пространственная
диаграмма
состояния,
позволяет
изображать
фазовые равновесия в любом тройном
сплаве и во всей системе A-B-C в целом
при
разных
температурах
(при
постоянном давлении).
Вместо пространственных диаграмм широкое
распространение
получили
сечения
этих
диаграмм горизонтальными и вертикальными
плоскостями
–
изотермические
и
политермические разрезы.
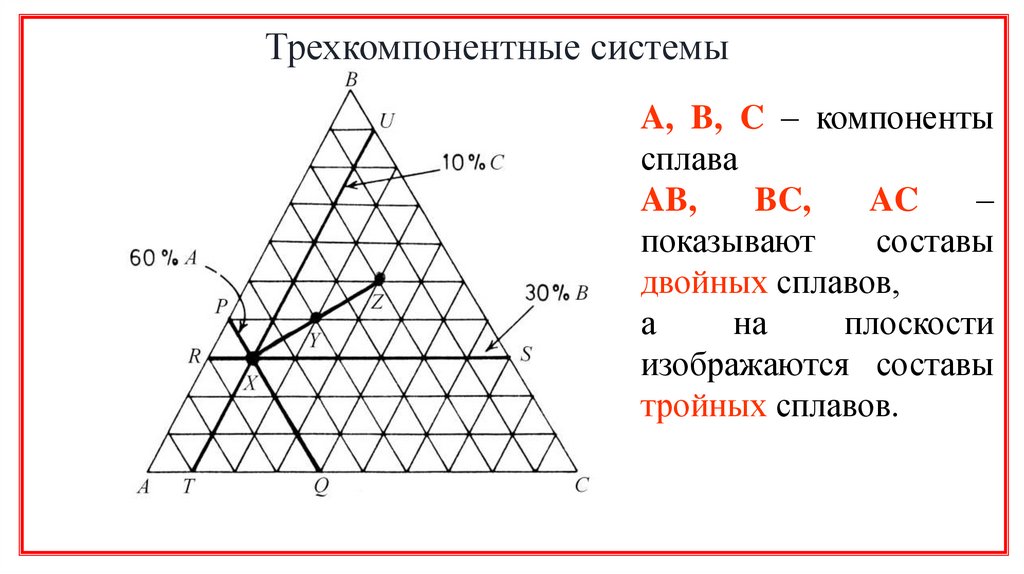
4.
Трехкомпонентные системыA, B, C – компоненты
сплава
AB,
BC,
AC
–
показывают
составы
двойных сплавов,
а
на
плоскости
изображаются составы
тройных сплавов.
5.
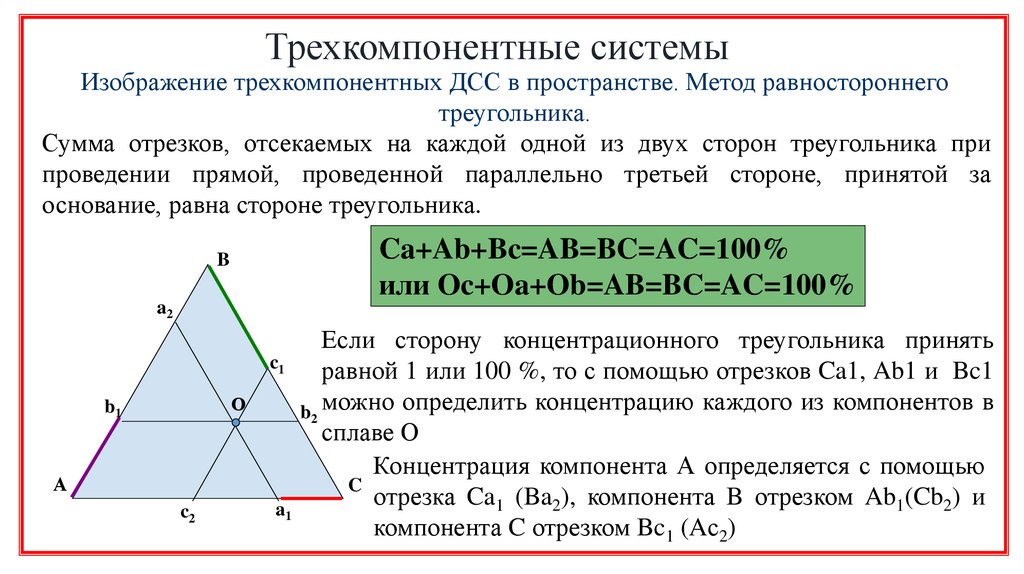
Трехкомпонентные системыИзображение трехкомпонентных ДСС в пространстве. Метод равностороннего
треугольника.
Сумма отрезков, отсекаемых на каждой одной из двух сторон треугольника при
проведении прямой, проведенной параллельно третьей стороне, принятой за
основание, равна стороне треугольника.
Ca+Ab+Bc=AB=BC=AC=100%
или Oc+Oa+Ob=AB=BC=AC=100%
B
a2
О
b1
А
c2
Если сторону концентрационного треугольника принять
c1
равной 1 или 100 %, то с помощью отрезков Ca1, Ab1 и Bc1
b2 можно определить концентрацию каждого из компонентов в
сплаве О
Концентрация компонента А определяется с помощью
C
отрезка Ca1 (Ba2), компонента B отрезком Ab1(Cb2) и
a1
компонента C отрезком Bc1 (Aс2)
6.
1. Все сплавы прямой, параллельной одной из сторон концентрационноготреугольника, содержат постоянное количество того компонента, который находится в
вершине треугольника, против этой прямой.
B
x1
y2
x2
M1
y2
M2
b1
b2
А
d
m
Сплавы
b1b2 содержат
постоянное
количество
компонента B, поскольку отрезки Ab1 и Cb2 для всех
сплавов имеют одну и ту же длину. Прямые такого типа
называют изоконцентратами. Для всех сплавов такой
прямой характерно постоянное суммарное содержание
двух других компонентов A и C, так как
100% – %B = %(A+C). Соотношение же между
C
концентрациями компонентов A и C может изменяться в
зависимости от того, где на прямой b1b2 находится
фигуративная точка заданного состава.
7.
2. Все сплавы прямой, проходящей через одну из вершин концентрационноготреугольника. Содержат в постоянном отношении те компоненты, которые
располагаются по обе стороны от этой прямой.
B
x1
y1
x2
M1
y2
M2
b1
b2
А
C
d
m
Сплавы прямой Bm характеризуются постоянным
отношением концентраций компонентов C/A. Если в
сплаве М1 содержание компонентов невелико
(фигуративная точка сплава близка к вершине
компонента B), то в сплаве М2 оно значительно, однако
отношение C/A в обоих сплавах остается одним и тем
же (M1x1/M1х2=M2y1/M2y2 или Bx1/By1=Bx2/By2) и
равным отношению C/A для двойного сплава m
(Cm/Am).
Добавление к сплаву m из системы A-C третьего компонента B не
изменяет отношение концентраций компонентов A и C, а только
уменьшает их суммарное количество.
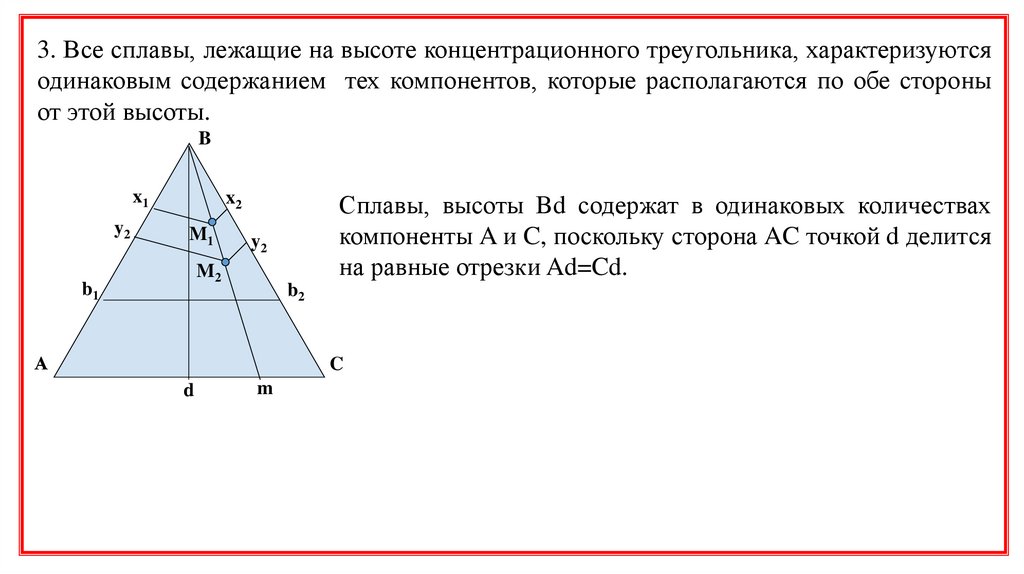
8.
3. Все сплавы, лежащие на высоте концентрационного треугольника, характеризуютсяодинаковым содержанием тех компонентов, которые располагаются по обе стороны
от этой высоты.
B
x1
y2
Сплавы, высоты Bd содержат в одинаковых количествах
компоненты A и C, поскольку сторона AC точкой d делится
на равные отрезки Ad=Cd.
x2
M1
y2
M2
b1
b2
А
C
d
m
9.
Трехкомпонентные системы(c)2003 Brooks/Cole, a division of Thomson
Learning, Inc. Thomson Learning™ is a trademark
used herein under license.
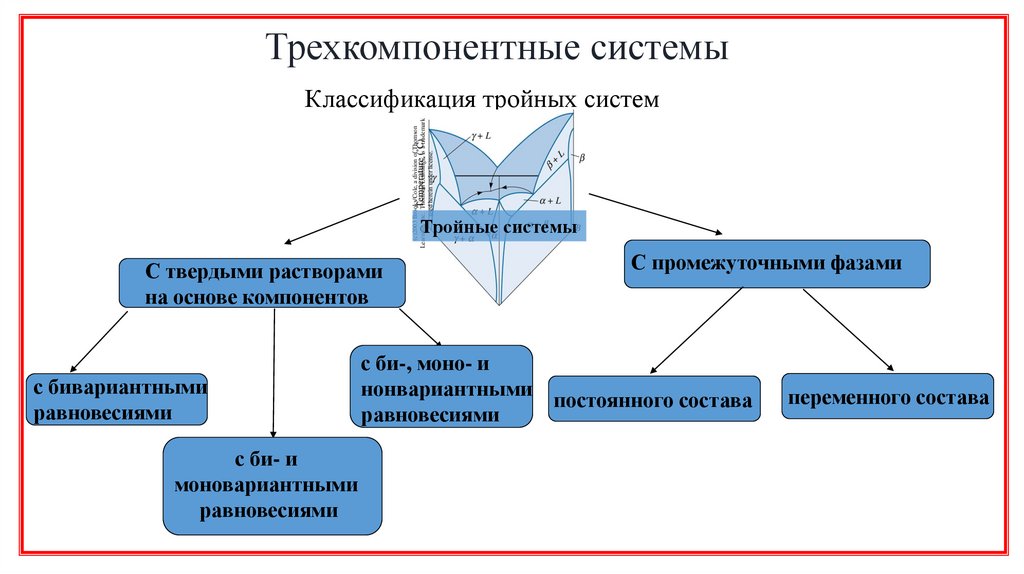
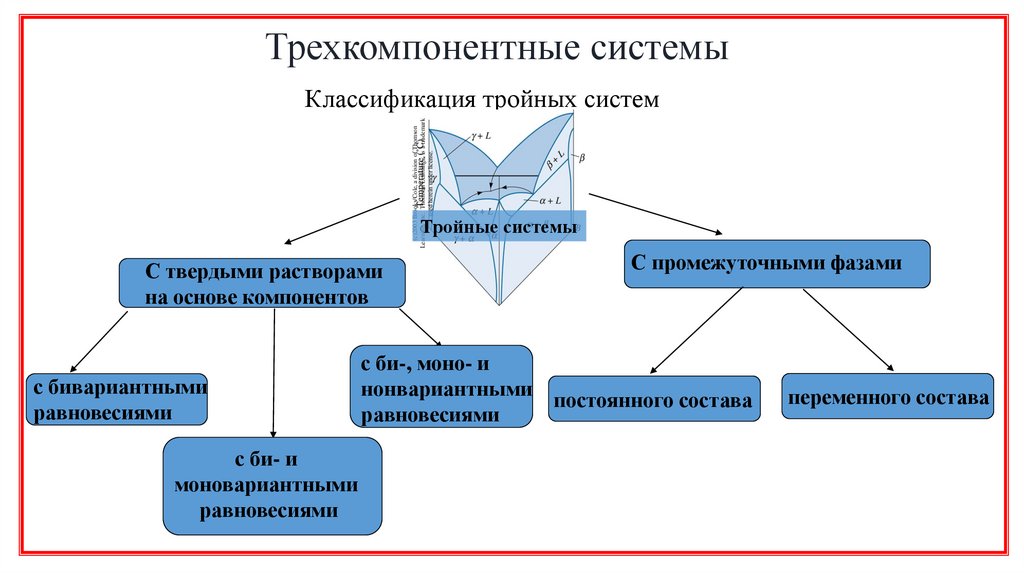
Классификация тройных систем
Тройные системы
С твердыми растворами
на основе компонентов
с бивариантными
равновесиями
с би- и
моновариантными
равновесиями
С промежуточными фазами
с би-, моно- и
нонвариантными
постоянного состава
равновесиями
переменного состава
10.
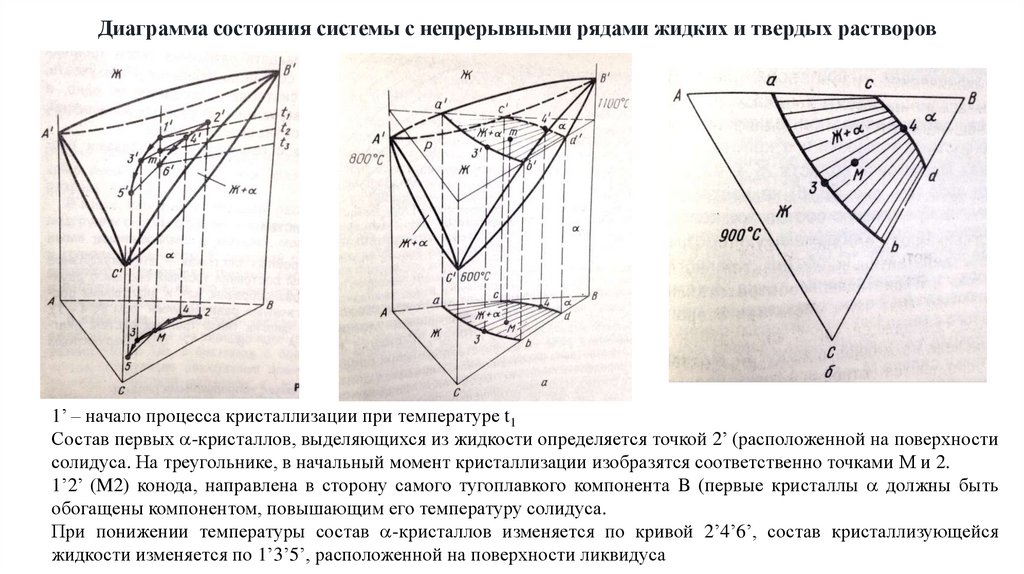
Диаграмма состояния системы с непрерывными рядами жидких и твердых растворов1’ – начало процесса кристаллизации при температуре t1
Состав первых -кристаллов, выделяющихся из жидкости определяется точкой 2’ (расположенной на поверхности
солидуса. На треугольнике, в начальный момент кристаллизации изобразятся соответственно точками М и 2.
1’2’ (M2) конода, направлена в сторону самого тугоплавкого компонента B (первые кристаллы должны быть
обогащены компонентом, повышающим его температуру солидуса.
При понижении температуры состав -кристаллов изменяется по кривой 2’4’6’, состав кристаллизующейся
жидкости изменяется по 1’3’5’, расположенной на поверхности ликвидуса
11.
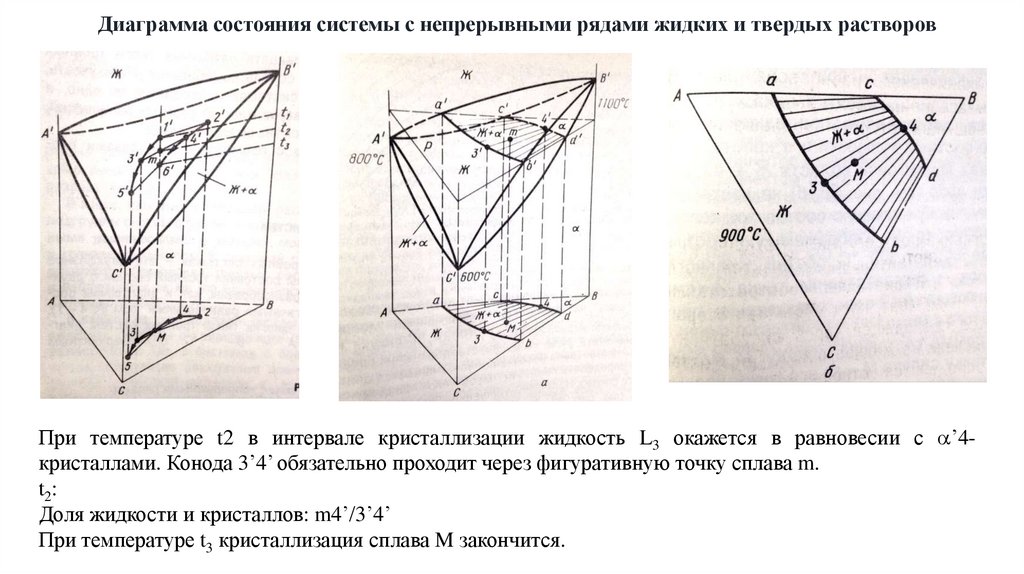
Диаграмма состояния системы с непрерывными рядами жидких и твердых растворовПри температуре t2 в интервале кристаллизации жидкость L3 окажется в равновесии с ’4кристаллами. Конода 3’4’ обязательно проходит через фигуративную точку сплава m.
t2:
Доля жидкости и кристаллов: m4’/3’4’
При температуре t3 кристаллизация сплава M закончится.
12.
13.
14.
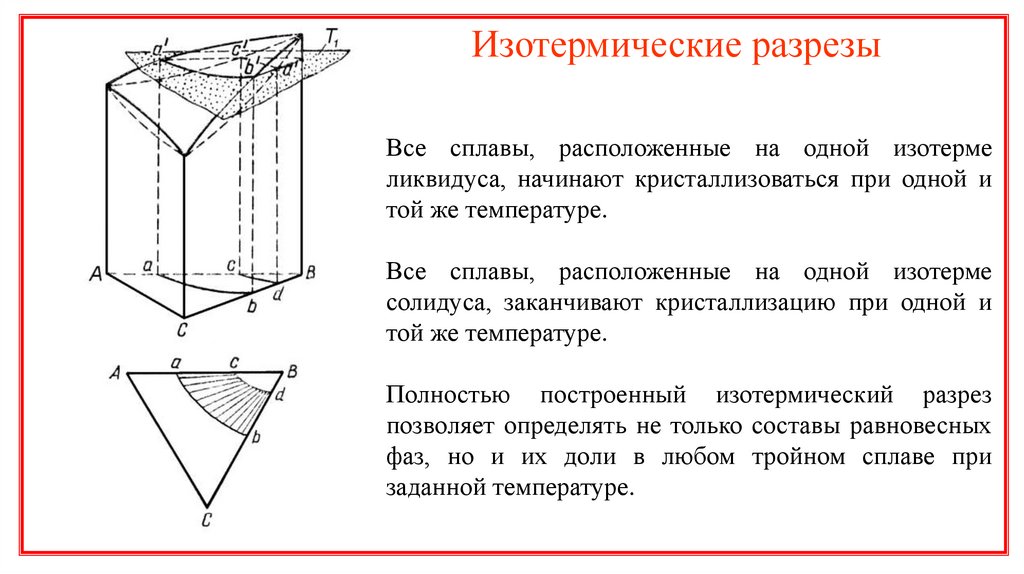
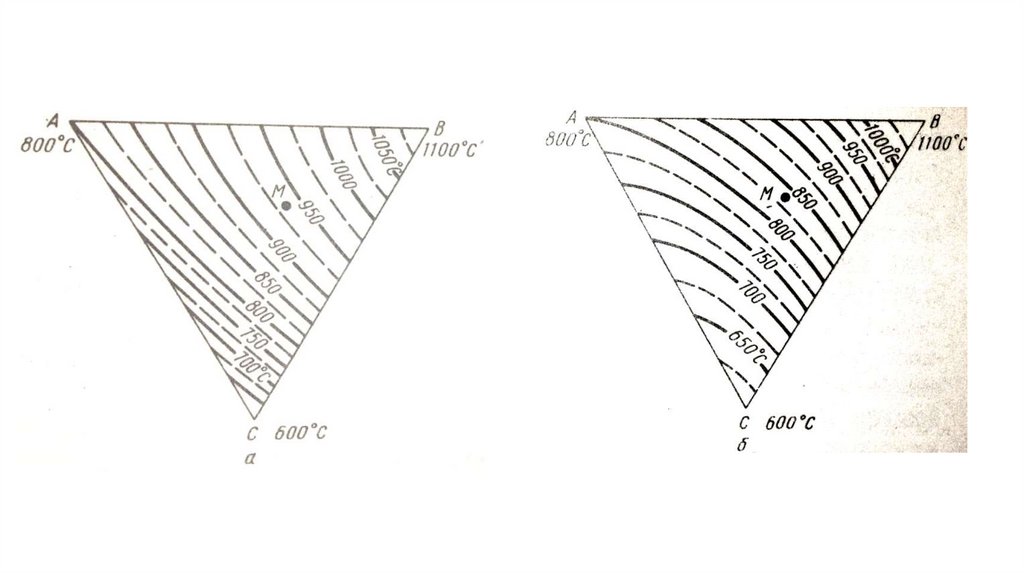
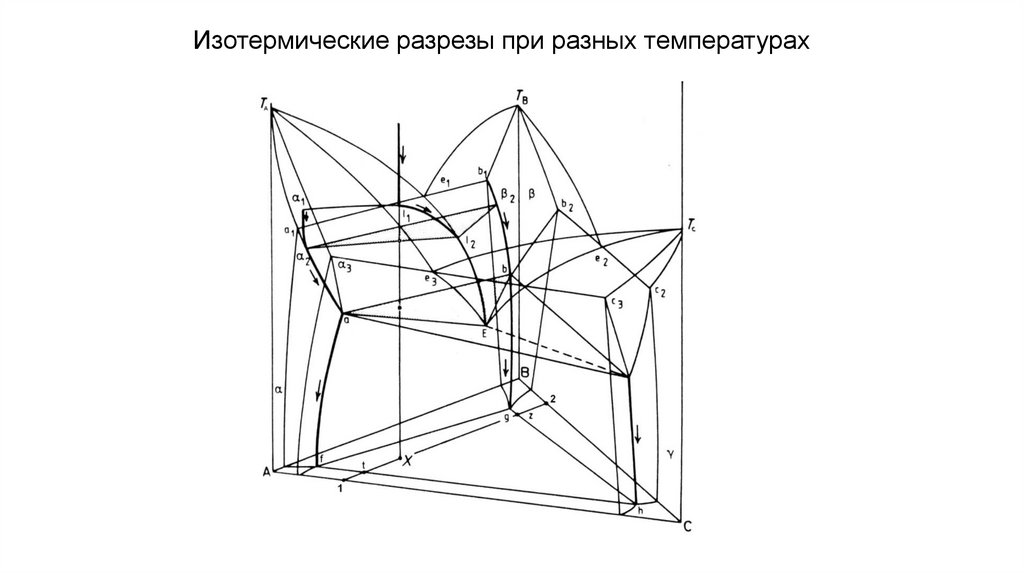
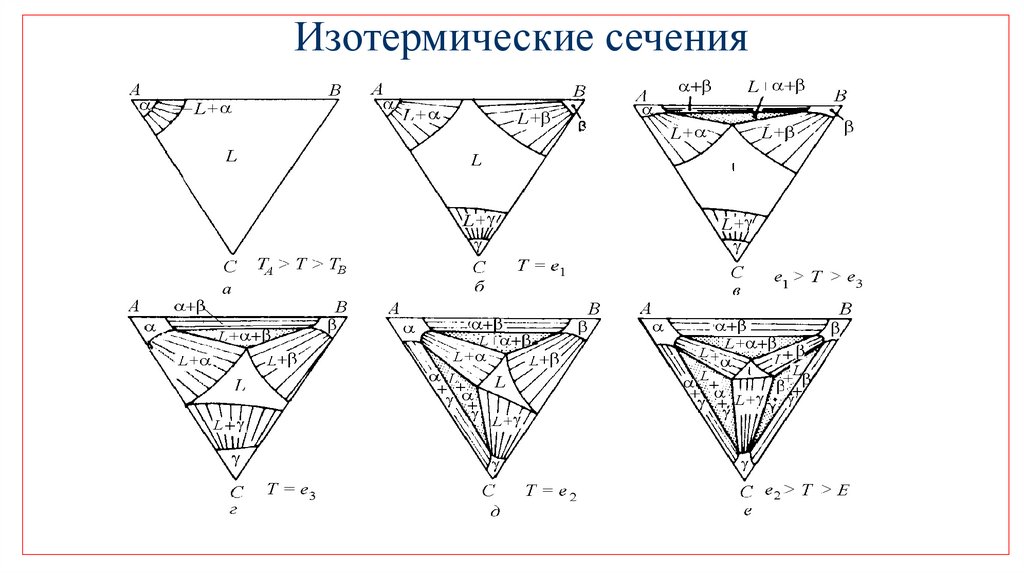
Изотермические разрезыВсе сплавы, расположенные на одной изотерме
ликвидуса, начинают кристаллизоваться при одной и
той же температуре.
Все сплавы, расположенные на одной изотерме
солидуса, заканчивают кристаллизацию при одной и
той же температуре.
Полностью построенный изотермический разрез
позволяет определять не только составы равновесных
фаз, но и их доли в любом тройном сплаве при
заданной температуре.
15.
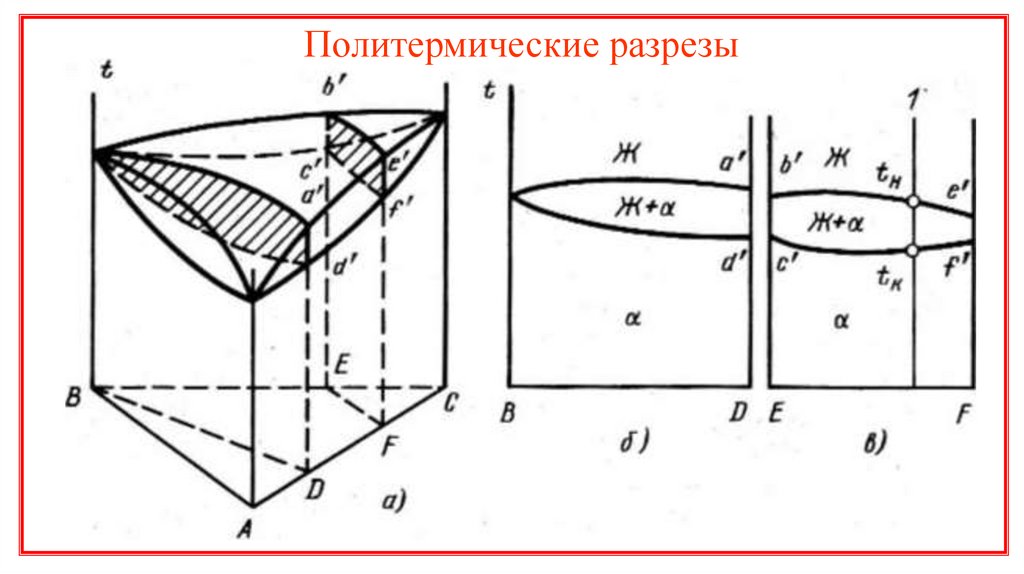
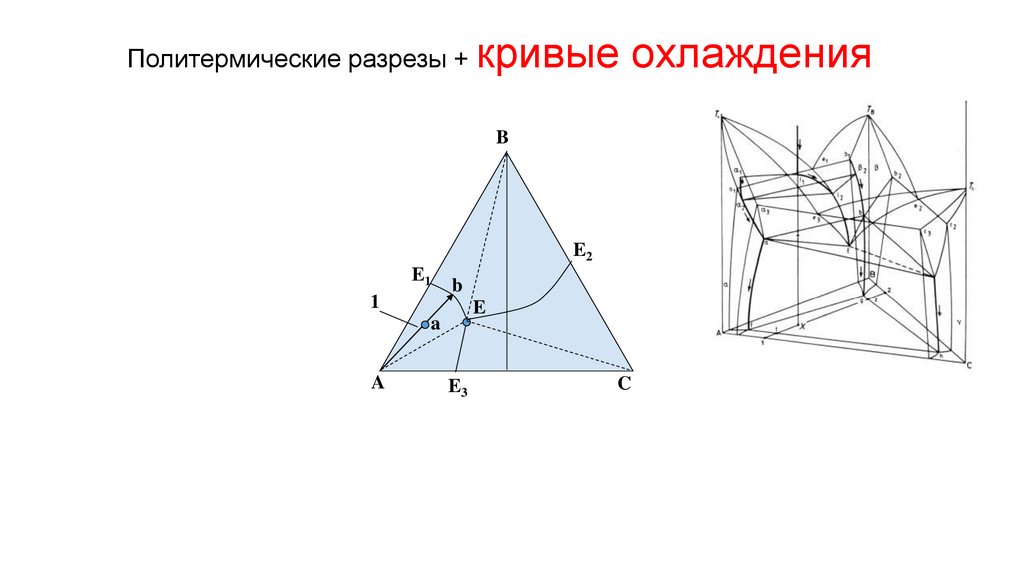
Политермические разрезы16.
17.
18.
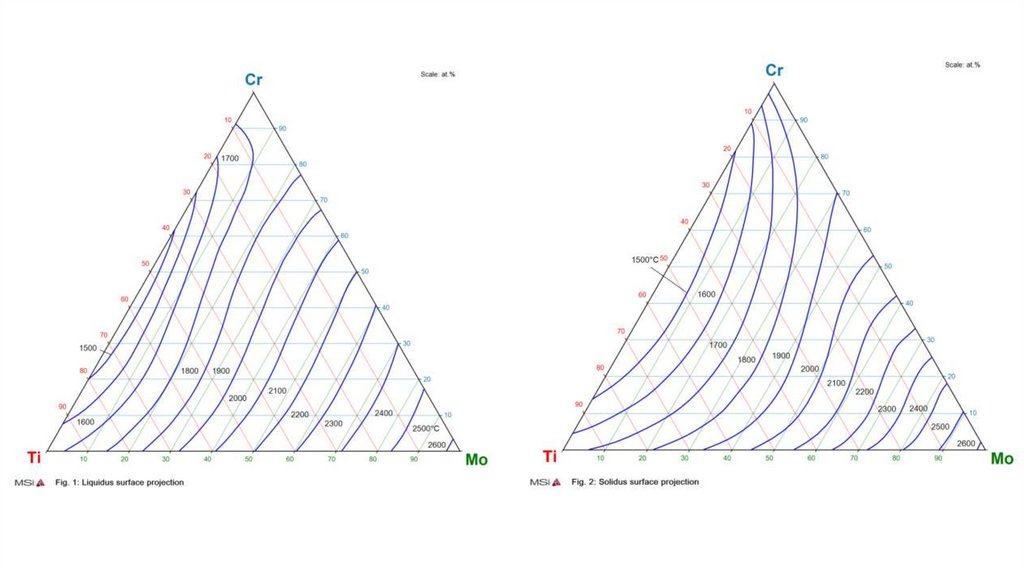
1. По заданному составу определить положение сплава наконцентрационном треугольнике.
2. Для этого сплава построить кривую охлаждения
3. На каждом характерном участке кривой охлаждения указать
число степеней свободы
4. Нарисовать структуру сплава при комнатной температуре
1 вариант 10%Мо-60%Ti-30%Cr
2 вариант 70%Mo-10%Cr-20%Ti
3 вариант 30%Cr-20%Ti-50%Mo
4 вариант 40%Сr-30%Mo-30%Ti
19.
Трехкомпонентные системы(c)2003 Brooks/Cole, a division of Thomson
Learning, Inc. Thomson Learning™ is a trademark
used herein under license.
Классификация тройных систем
Тройные системы
С твердыми растворами
на основе компонентов
с бивариантными
равновесиями
с би- и
моновариантными
равновесиями
С промежуточными фазами
с би-, моно- и
нонвариантными
постоянного состава
равновесиями
переменного состава
20.
Диаграмма состояния системы с нонвариантнымэвтектическим равновесием
Кристаллизация всех тройных сплавов
(при отсутствии растворимости в
твердом состоянии) заканчивается при
постоянной
температуре,
равной
температуре кристаллизации тройной
эвтектики. Поскольку жидкая фаза при
этой температуре в любом тройном
сплаве отвечает эвтектическому составу
(т. Е) и затвердевает с образованием
эвтектики, то горизонтальная плоскость,
проходящая
через
Е
является
плоскостью солидуса и проекция этой
плоскости совпадает с плоскостью
концентрационного треугольника.
21.
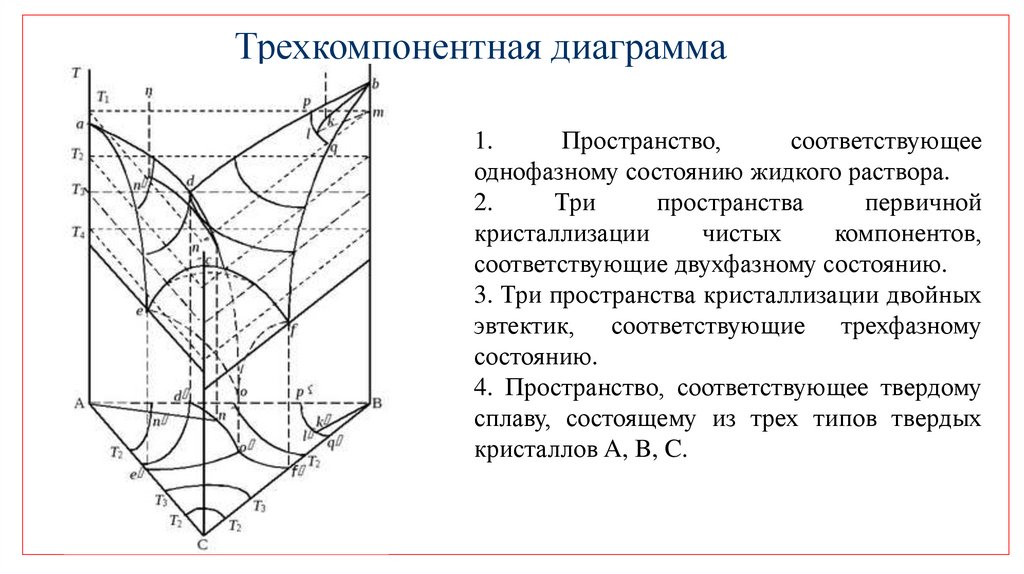
Трехкомпонентная диаграмма1.
Пространство,
соответствующее
однофазному состоянию жидкого раствора.
2.
Три
пространства
первичной
кристаллизации
чистых
компонентов,
соответствующие двухфазному состоянию.
3. Три пространства кристаллизации двойных
эвтектик, соответствующие трехфазному
состоянию.
4. Пространство, соответствующее твердому
сплаву, состоящему из трех типов твердых
кристаллов A, B, C.
22.
23.
24.
Видео25.
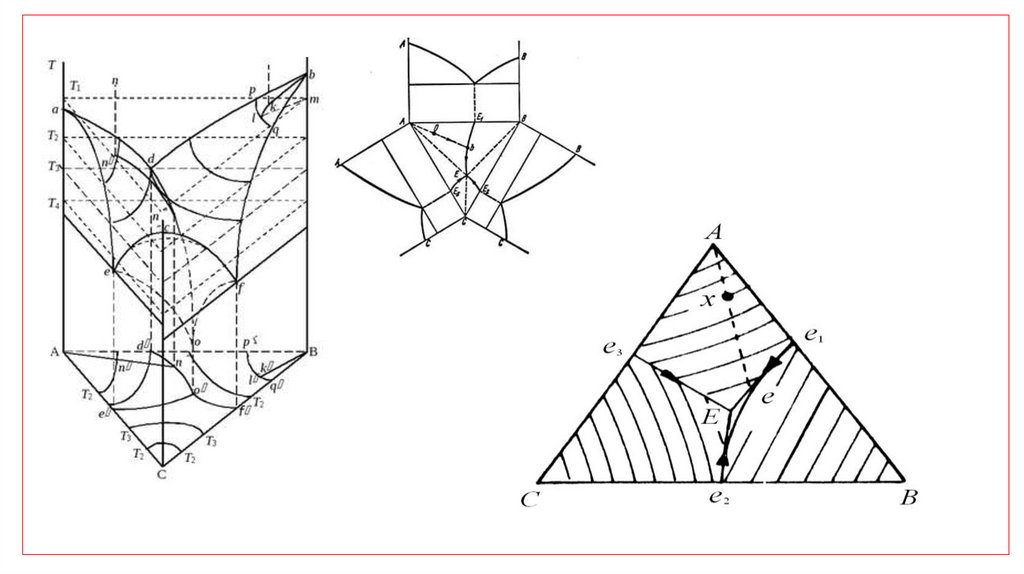
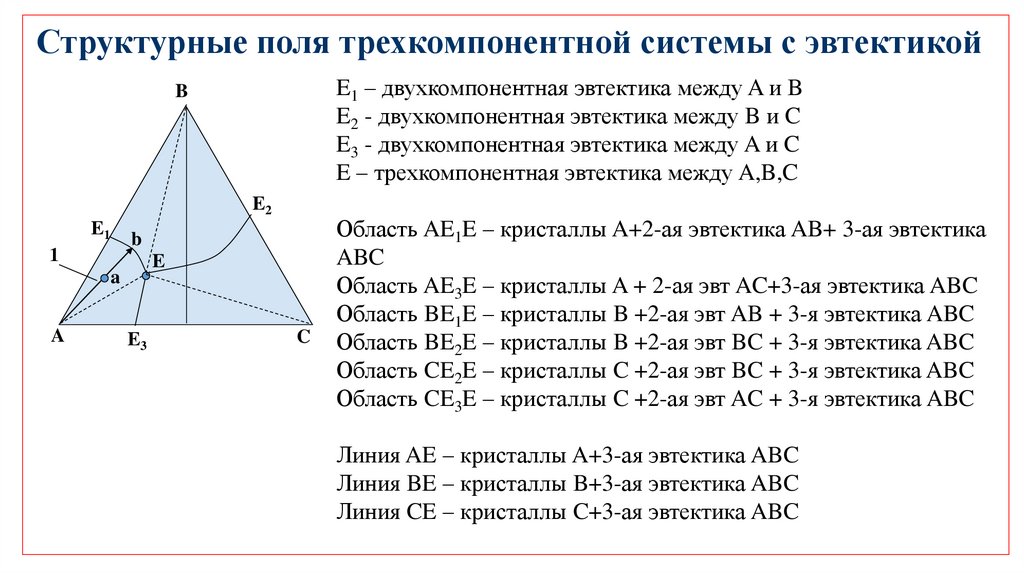
Структурные поля трехкомпонентной системы с эвтектикойE1 – двухкомпонентная эвтектика между A и B
E2 - двухкомпонентная эвтектика между B и C
E3 - двухкомпонентная эвтектика между A и C
E – трехкомпонентная эвтектика между A,B,C
B
E2
E1
b
1
E
a
A
E3
C
Область AE1E – кристаллы A+2-ая эвтектика AB+ 3-ая эвтектика
ABC
Область AE3E – кристаллы A + 2-ая эвт AC+3-ая эвтектика ABC
Область BE1E – кристаллы B +2-ая эвт AB + 3-я эвтектика ABC
Область BE2E – кристаллы B +2-ая эвт BC + 3-я эвтектика ABC
Область CE2E – кристаллы C +2-ая эвт BC + 3-я эвтектика ABC
Область CE3E – кристаллы C +2-ая эвт AC + 3-я эвтектика ABC
Линия AE – кристаллы A+3-ая эвтектика ABC
Линия BE – кристаллы B+3-ая эвтектика ABC
Линия CE – кристаллы C+3-ая эвтектика ABC
26.
Изотермические разрезы при разных температурах27.
Изотермические сечения28.
Политермические разрезы +кривые охлаждения
B
E2
E1
b
1
E
a
A
E3
C
29.
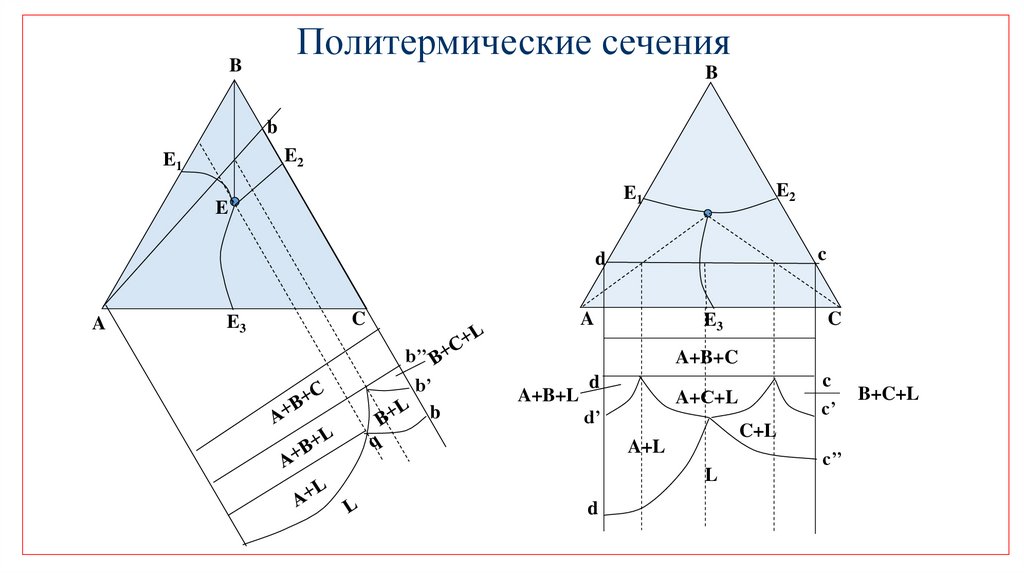
Политермические сеченияB
B
b
E2
E1
E2
E1
E
c
d
A
E3
C
A
b’’
b’
b
C
E3
A+B+C
A+B+L
d
A+С+L
d’
C+L
A+L
L
d
c
c’
c’’
B+C+L
30.
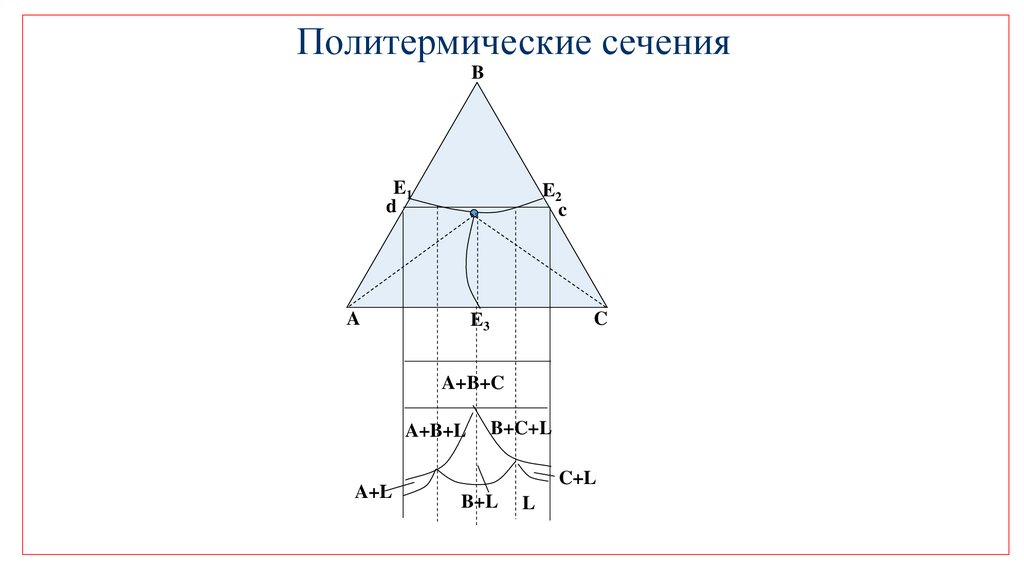
Политермические сеченияB
E1
d
E2
c
A
C
E3
A+B+C
A+B+L
A+L
B+C+L
C+L
B+L
L
31.
Кристаллизация сплавов в трехкомпонентной системеB
В точке a – начало выделения кристаллов A
От a до b – выделение кристаллов A
В точке b – начало кристаллизации двойной
эвтектики AB
От b до E – кристаллизация двойной эвтектики
В точке E – начало и конец кристаллизации тройной
эвтектики ABC
E2
E1
b
1
E
a
A
E3
C
32.
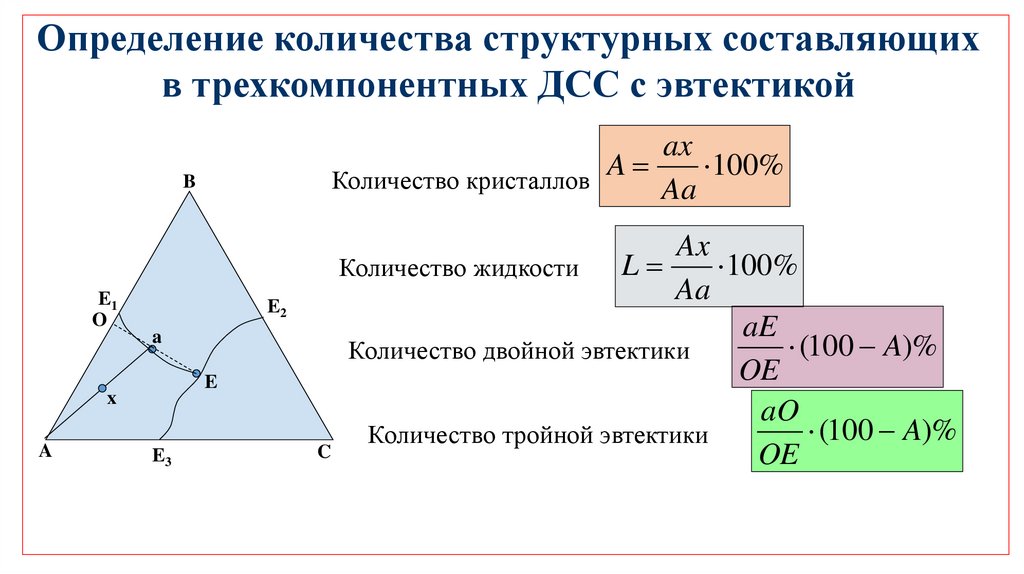
Определение количества структурных составляющихв трехкомпонентных ДСС с эвтектикой
ax
A
100%
Количество кристаллов
Aa
B
E1
O
E2
a
E
x
A
E3
Ax
L
100%
Количество жидкости
Aa
aE
(100 A)%
Количество двойной эвтектики
OE
aO
(100 A)%
Количество тройной эвтектики
C
OE
33.
https://materials.springer.com/periodictable#Видео индуса
https://yandex.ru/video/preview/?filmId=1739820062101597
847&from=tabbar&reqid=15876102636096031159212584732562408300124-vla1-1937V&text=lecture+25prof+R.N.+Ghosh+Kharagpur
34.
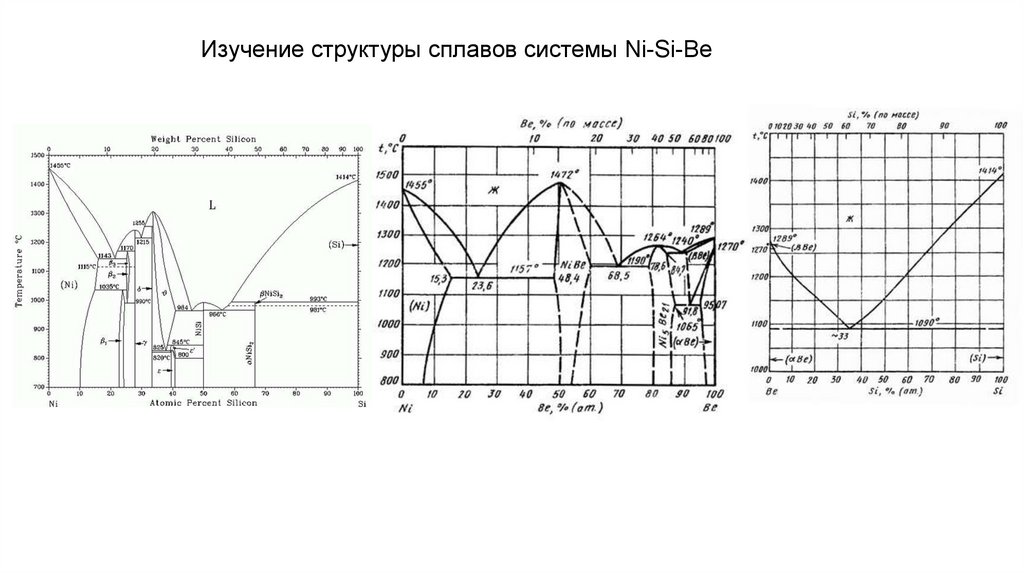
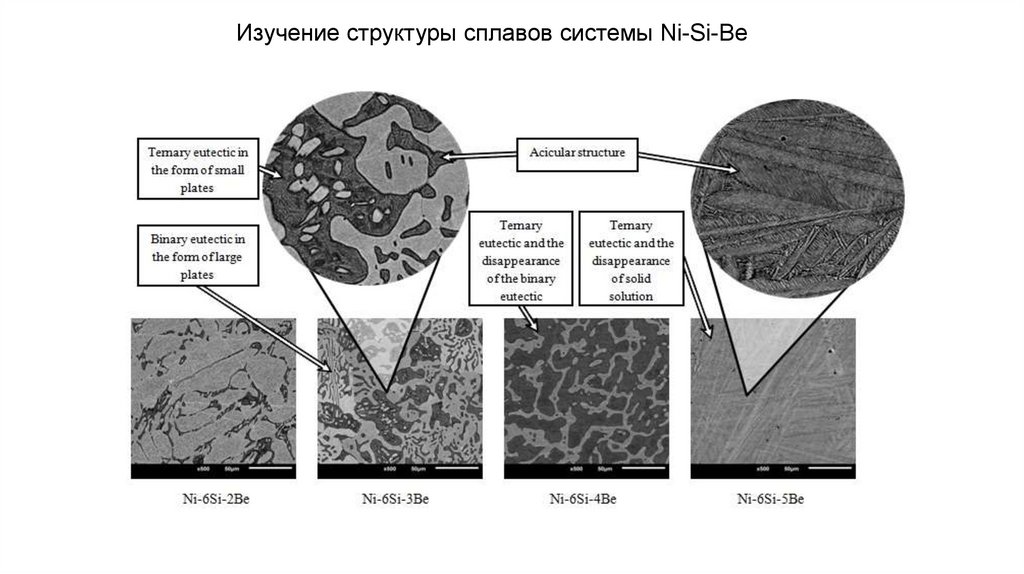
Изучение структуры сплавов системы Ni-Si-Be35.
Ni-4Si-2BeNi-4Si-3Be
Ni-4Si4Be
Ni-5Si-2Be
Ni-5Si-3Be
Ni-5Si-4Be
Изучение структуры сплавов системы Ni-Si-Be
36.
Ni-4Si-4Be37.
Ni-6Si-2BeNi-6Si-3Be
Ni-6Si-4Be
Ni-6Si-5Be
Ni-7Si-4Be
Ni-8Si-4Be
Изучение структуры сплавов системы Ni-Si-Be
38.
Изучение структуры сплавов системы Ni-Si-Be30 сплавов
39.
Изучение структуры сплавов системы Ni-Si-Be40.
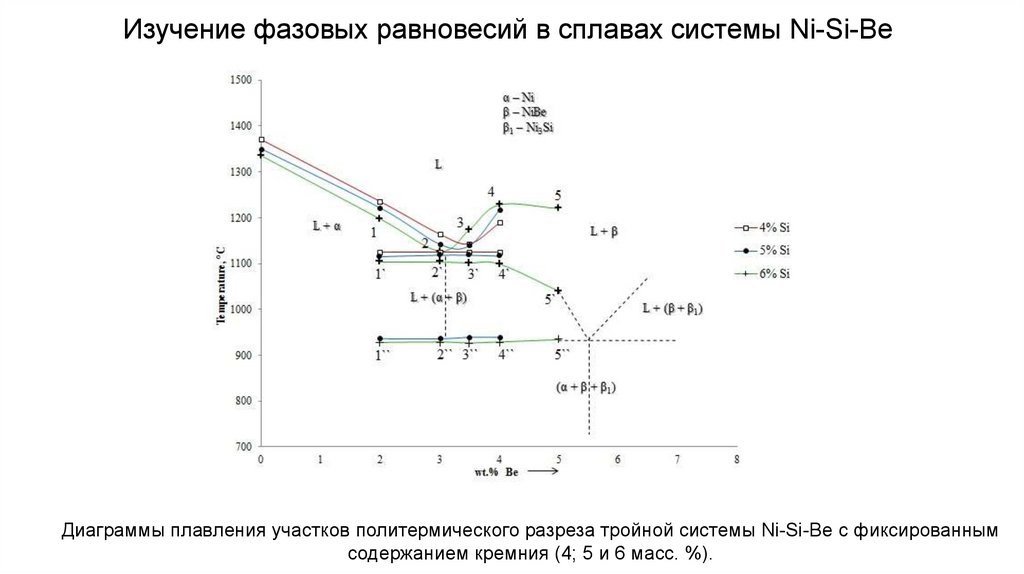
Изучение фазовых равновесий в сплавах системы Ni-Si-BeДиаграммы плавления участков политермического разреза тройной системы Ni-Si-Be с фиксированным
содержанием кремния (4; 5 и 6 масс. %).















 Химия
Химия








