Похожие презентации:
Построение таблиц истинности для логических выражений
1.
Выпишите пары соответствий впервом и втором столбцах:
1. Логика
1. ИСТИНА и ЛОЖЬ
2. Высказывание
2. Наука о формах и способах мышления
3. Алгебра логики
3. Наука об операциях над высказываниями
4. Значение логической
переменной
4. А
5. Логическая
переменная
5. Повествовательное предложение, содержание
которого однозначно может быть истинным или
ложным
2.
Проверьте ответы• 1 - 2;
• 2 - 5;
• 3 - 3;
• 4 - 1;
•5-4
3.
Вопросы :• Что такое высказывание?
• Какие бывают высказывания?
• Приведите пример простого
высказывания. Сложного
высказывания.
• Как обозначаются высказывания в
Алгебре логики?
• Чему могут быть равны логические
переменные?
4.
5.
6.
Построение таблиц истинностидля логических выражений
7.
8.
Построение таблиц истинности для логическихвыражений
• Таблица истинности – это
таблица, показывающая
истинность сложного
высказывания при всех
возможных значениях входящих
переменных.
9.
Построение таблиц истинности для логическихвыражений
• Конъюнкция –
логическая операция,
ставящая в
соответствие двум
высказываниям новое
высказывание,
которое является
истинным тогда и
только тогда, когда
оба исходных
высказывания
истинны.
• Для записи
конъюнкции
используются
следующие знаки:
И, ^, *, &.
• Конъюнкцию ещё
называют логическим
умножением.
10.
Построение таблиц истинности для логическихвыражений
• Дизъюнкция –
логическая операция,
которая двум
высказываниям
ставит в соответствие
новое высказывание,
являющееся ложным
тогда и только тогда,
когда оба исходных
высказывания ложны.
• Для записи
дизъюнкции
используются
следующие знаки:
ИЛИ, ˅, |, +.
• Дизъюнкцию ещё
называют логическим
сложением.
11.
Построение таблиц истинности для логическихвыражений
• Инверсия –
логическая
операция, которая
высказыванию
ставит в
соответствие новое
высказывание,
значение которого
противоположно
исходному.
• Для записи
инверсии
используются
следующие знаки:
НЕ, - , ¬.
• Инверсию ещё
называют
логическим
отрицанием.
12.
Построение таблиц истинности для логическихвыражений
• 1. Определить количество строк в таблице:
количество строк = 2n+1, где n – количество
логических переменных.
• 2. Определить количество столбцов в таблице:
количество столбцов = количеству логических
переменных + количество логических операций.
• 3. Построить таблицу истинности с указанным
количеством строк и столбцов, ввести названия
столбцов таблицы в соответствии с
последовательностью выполнения логических
операций с учетом скобок и приоритетов (¬, &,
V);
приоритеты: ( ), ¬, &, V.
• 4. Заполнить столбцы входных переменных
наборами значений.
• 5. Заполнить таблицу истинности, выполняя
логические операции в соответствии с
приоритетами действий.
• ¬(A&B)
Логических
переменных: 2,
операций: 2.
Количество строк:
22+1=5,
количество
столбцов:
2+2=4.
13.
Построение таблиц истинности для логическихвыражений
• Учебник: стр. 51 №8 (а, в)
Постройте таблицы истинности для
следующих логических выражений:
• а) В&(АVВ)
• в) А&(A˅B˅C)
14.
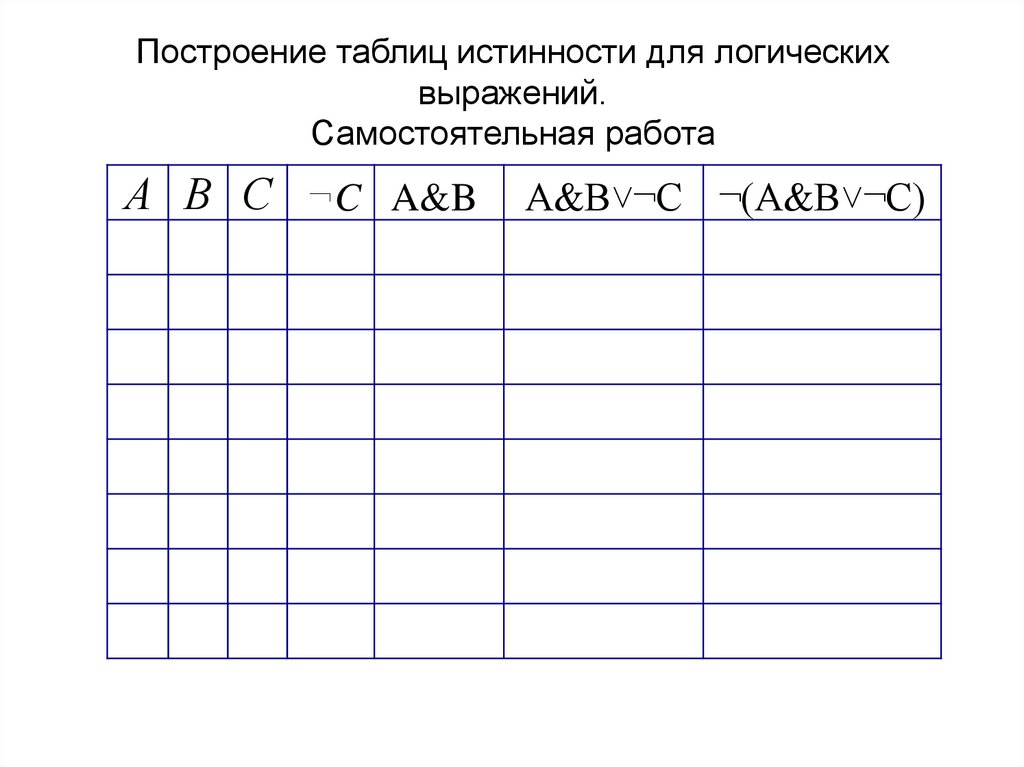
Построение таблиц истинности для логическихвыражений.
Самостоятельная работа
А В С ¬C A&B
A&B˅¬C ¬(A&B˅¬C)
15.
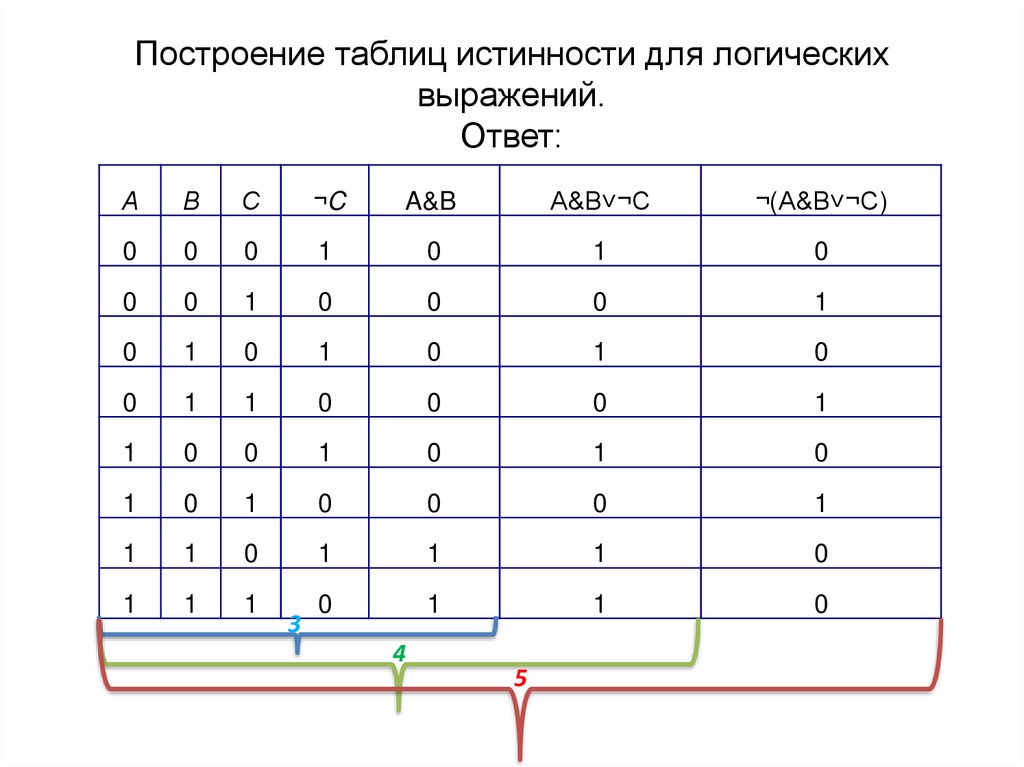
Построение таблиц истинности для логическихвыражений.
Ответ:
А
В
С
¬C
A&B
A&B˅¬C
¬(A&B˅¬C)
0
0
0
1
0
1
0
0
0
1
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
0
3
4
5
16.
ЗаключениеНа этом уроке мы:
изучили понятие «таблицы истинности»,
познакомились с алгоритмом построения
таблиц истинности,
а также научились строить их для составных
высказываний, не вникая в смысл самого
высказывания.
Д/З: учебник п.1.4.3, стр. 41-42, №8(б, г), 9 стр.
51.












 Информатика
Информатика