Функція. Область визначення і множина значень

3A n A M •51TA
" IMC n OBI Cl>YHKU.II. o s n A CTb IB M3HA "IEHHJI
I MHO>KMHA 3HAl lEHb G>YHKU.11.
c n o c o s M J A.QAIH HSI G>YHKL.11'1
1. l l 0 1£Jl.m m J £ tJIYK"tC i .
TE !
I
06 acmi6ua"a e""B
I
'
.
.
ipy KX Jli elO
(a6o • ipyKX l.J iOH411,b1£010
aaAe'1lKicm10)
•e H
•Z
- HM H , I l p H
B 8 3 H B RIO T L T & K y 3 8.JleaE H ICT l t M l
n a o M a am
•
• u
•
•.
,a;e J IK O l M B O 3 B 8 11e H BJO H e 3 8 . J l eZ B Ol 3 M l B B Ol
H K lH K O Z B OM.Y
.
Z HBH
Bl,ZJ;
0
l
Bl,ll;&
£• a a n e B B H M n p a B H J IOM £ ,ll;H B e 3'.118.'leH H J[ ,a a
J l e a t B O I 3 M I B H OI .
qUCJ&OBONJ
.
f

3.

3 A n A M •s:ir A lllTE !
'
Qdn. m10 BU3Ha..,,eHHJI, IJIYHX lf U 'II = f(z) H83RB8JOTL
BY BC X 3H&leHL,BKlX
Moxee B&fi)'B&TH apryMeBT
MBOZH
%.
K 3 H a H T H 0 6J I9 CT L B H n a - i e H H H
2
·
Y
x
,_
D (,y ) = (=oo; 0 ) LJ(O; + oo)
D (y) == {x E IR x :;t: O}
aoo D (y:) == IR\ {O}
...
.
YHKU:IJ:
.N"!!
8 111.1,ci>YHKlll.ili
0 6:-.ie.-MellllR
tt>op' ' .11-0na1111"
1
Y
= f' (x)
lf £.ill UC
.6y.i:.1io,.a1Kti q11cna
f (x)
2 y =
g1(x)
!> y=,f (x)
1
._
g(x) f. 10
I
H a M CH
1
H
K:
po6y m e,Ll;op B H I O f
l ll}Jl lO
Ui;IJ 3 11S KOM K B3J([p,a T H Olro
ft..;r)1;:: 0
,_
1
K«tptmB l\ Oi1<1e 311aJ:l)Jl t 1'iHCB
T i.IJL K l l B e BiJl.'t MH C IJlllCJl.O

4.

n p 111KJl All I 1 I3 Ha i i,n;iTh o 6 J ia CTb BH 3H al:IeH H 5I cpy H KII; I
y =
2
x ( x - 1) .
.QOBl.QHHK
:

5.

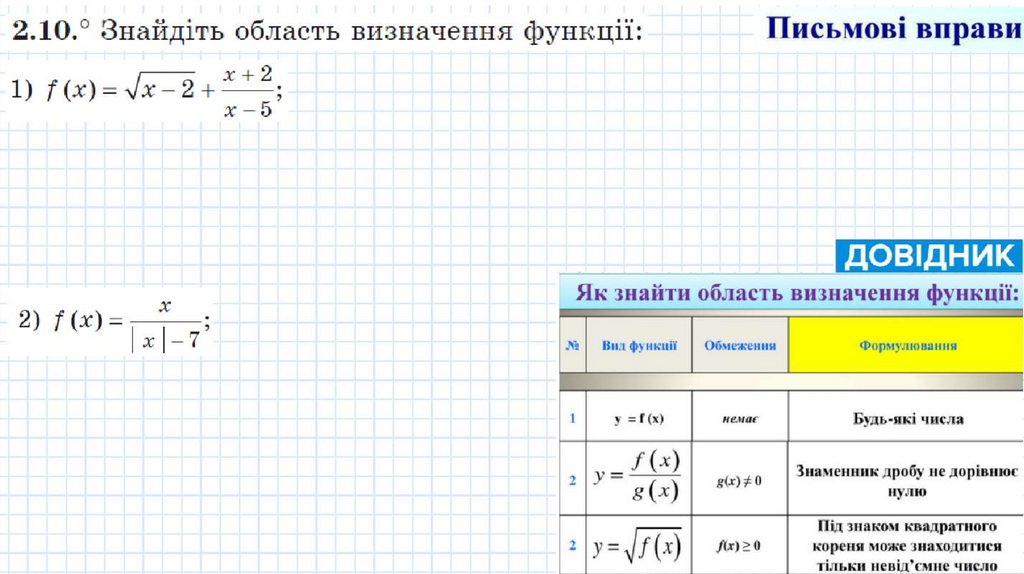
Iluch MOBi BnpaBH
2 .1 0.. 3 a alip;iTb o 6 J i a C T b B l i3H .a T. e H H J I cpyap;; i :
1
0
1) f (x ) =
2
.Jx- 2 + x + ;
x -5
.QOBl.QHHK
2 ) f (x ) = _ x_ .
x
7'
HK J H a i iT H o6JiaCTL B H 3H a ' l eH H H cl>YHKQil:
.N"!
1-
Bua Cl>Y HKUii
y = f (x)
lf t!.110£
f (x)
y =
g (x)
g(x) "I 0
= "' f
ftir) > 10
I
2
Oli.\1e-JKe1111
n
i
...,. y
.
ct>op'1) lIDB:1111111
6y.lllb HKi'IlllCA
'
3H311\'f elHEl K ,Apo6y He
a
op BHIOC
1-l• /llO
Iii.a; Jlia ECOl\t K83iJJ;paTHOro
i.copeue MO·>Ke 3113X(),Ll,
TllCH
'T.iJl bKH HCBi.Jl:'cl'ltlt:e ...llCJIO

6.

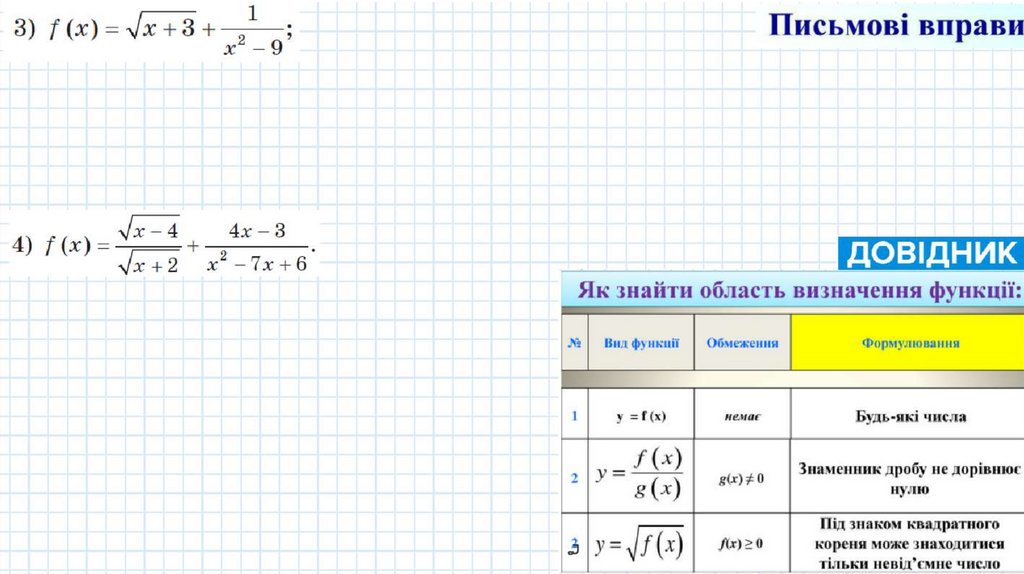
.3) f (x ) = ,Jx + 3 +
4 ) f (x) =
1
x2 - 9
IluchMOBi BnpaBH
;
4x - .3
.Jx- 4 + 2
.Jx + 2 x - 7x + 6
.QOBl.QHHK
:
HK JHaiiTH o6JiaCTL BH3Ha'leHHH cl>YHKQil
.N"!
Bua Cl>Y HKUii
I
2
y = f (x)
lf t!.110£
f (x)
y =
g (x)
g(x) "I 0
:3 y = ,f
...,.
.
Oli.\1e-JKe1111
n
ct>op'1) lIDB:1111111
6y.lllb HKi'IlllCA
'
3H311\'f elHEl K ,Apo6y He
a
op BHIOC
1-l• /llO
ftir) > 10
Iii.a; Jlia ECOl\t K83iJJ;paTHOro
i.copeue MO·>Ke 3113X(),Ll,
TllCH
·T.iJl bKH H CBi.Jl:' cl'lt lt:e ...llCJIO

7.

3 A n A M •s:ir A lllTE !
'
=
I
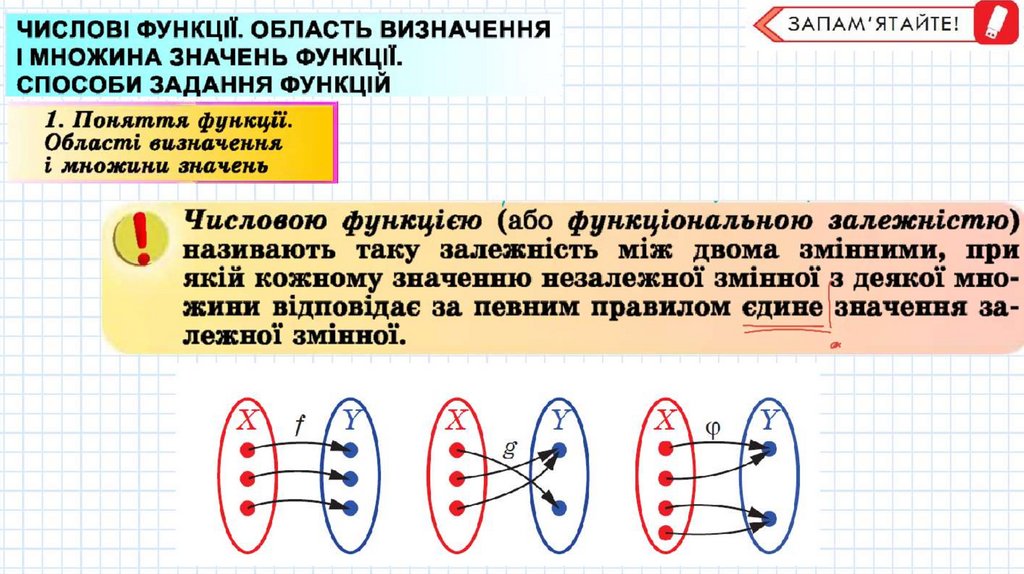
M 1W31CUKOKJ (a6o 0 6 1£acm10) a 1£a.1'e H "& tjlyHX'fli y
f(x ) &aaaaaIO'l'lt MBOat11Hy,
o cKJI aen.ca a ycix ' l l lceJI f(x), ;a;e x e D(f).
I loaHa"tlaIOTh n;10 M H Om H H Y q e p e 3 E( f) a6o E( y ).
3 Haii:TH MHO:>RHH.y 3 H a 'tle H :& cl>YHKD;ii:
,-
1) y = 3 - v x;
<l>yHKII,iR
D (y)
y = kx + b
(-oo; +oo)
E (y)
I'pacpiK
Jr, =I= 0, TO
E (y ) = (-oo ; +oo);
Ilp.s:rMa
.ff K ID;O
= 0, TO
E (y) = {b}
.5f K ID;O }
2) y = x 2 - 2x + 3.
(-oo; 0) U (O; +oo)
(-oo; 0) U (O; + oo)
rirrep6oJia
y = x2
(-oo; +oo)
O ; +oo)
[
IIapa6oJia
.Jx
[
O; +oo)
O ; +oo)
[
BiTKa
rrapa60JI11:
lj = <
li
k =I=
0
x
'
y =

8.

np IllKi i AJl I 2 I3 H a i i,!(iT b 0 6 .JiaCTb 3H a ' ! e H b <PY H K I J ; i l y =
2x . IlH CbMOBi onpaou
1 + x2

9.

2. Cnoco6u aa iJaHHsi
3A n AM •51TAlllTE!
<PY"" iu
I
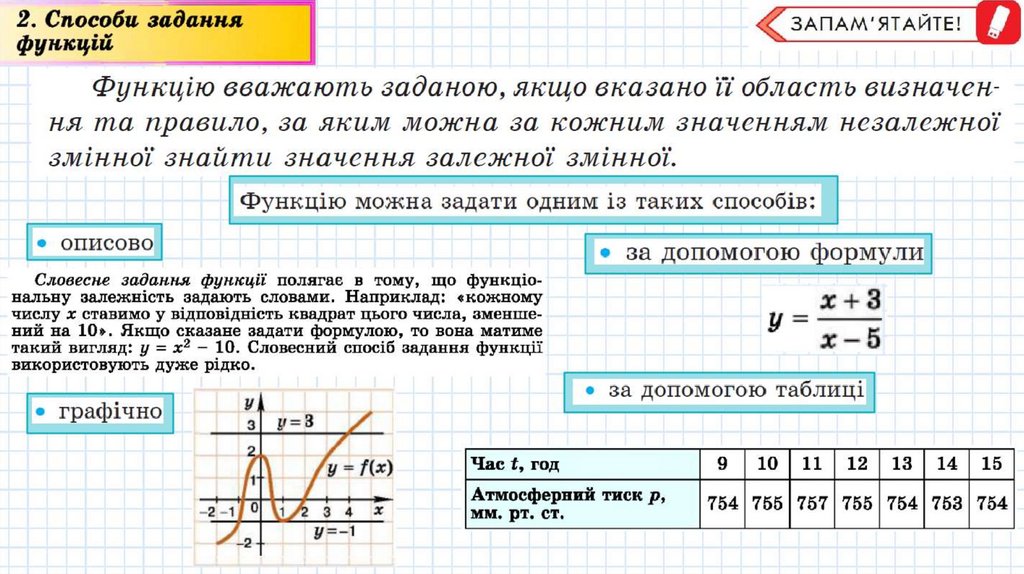
<Py n t e 4 i -,o 6 6 a :J1CaHJ m b 3 a i J a n o-,o , R-K U40 6te a a a n o ii 0 6 . n a c m b 6 U 3 H a t t e HH R m a n p a e u .no , 3 a R K UJVl JVlO:JICH a 3 a K O:JICH UJVl 3 H al.l eH HRJVl H e 3 a .ne:JICHO
•
•
v
•
•
i
3.lVl i H HOi 3 H a u m u 3 H a t t e H H R 3 a .ne:J1CHOi 3.lVl i H HOi .
<PyHK D;i:EO M OJI<Ha 3 a.zi;aT H o .zi;HH Mi3
I·
OIIHCOBOI
I
Ta K H X c n o c o o iB :
( • 3a .n;orroM or o ro q op MyJIH
I
C.noaec ne saiJan1t.1t tPYHKU;fi n o J I.ar a e e TO MY, m ;o <l>YHK
o
H a JI :bH Y 38.Jie:mH c T & aa,zi;aioT:D CJ IOBa.MH. H a n p u K J ia,zi;: • K O :litH OMY
&OI 'O q :e:c J ia , 3 M e H m e 'ClHCJ IY x CTSBB M O y B ,ll;IIOB ,ll;H CT& KBa,n;p a T
H H H H a 10 • . H K m ;o CK aa a a e aa,n;aT H «i><>P M YJ IOlO , TO BOH a M a T B M e
TBK B H BH r J I.a,n;: y = x 2 - 10. C n o :eec H B H c n o c 6 aa,n;a H H .H <l>YH KIi"
BB K OPH CTOBYlOT b ,zi;ym e p ,D;KO.
11
3
( • r p a cpitI HO ]
I • 3a ,n;onoMor o ro Ta6JIH i I
!f =
8
y = f (x )
1
-2 -1 0
-2
1:1ac t, I'OJJ;
ATMocct>epnn:ii THCK p,
1
3 4
y =- 1
x
MM. pT. CT,
12 13 14 15
754 755 757 755 754 753 754
9
10
11

10.

I lucLMOBi errpaeu
2 .1 .° K o m HoMy HaTy p aJihHOMY q HcJiy , 6 Jihl l IOMY 3a 10 , aJie MeHl l IO
MY B ,[( 20, I IOCTaBHJII I y B ,[(I IOB ,n;H CTh OCTat.r y rrp I I ,n;iJieHHi :o;ho r o
q n cJia Ha 5.
1) .HK HM crroc ooo M 3a,n;aHo :o;10 c}JyHK:o; 10?
2) .HKa oGJiaCTh 3Haq eHb u; e1 cpyHKIJ; 1?
3) 3 a,n;a:H:Te IJ;IO c}>YHK IJ; IO Ta6JII Iq Ho .

11.

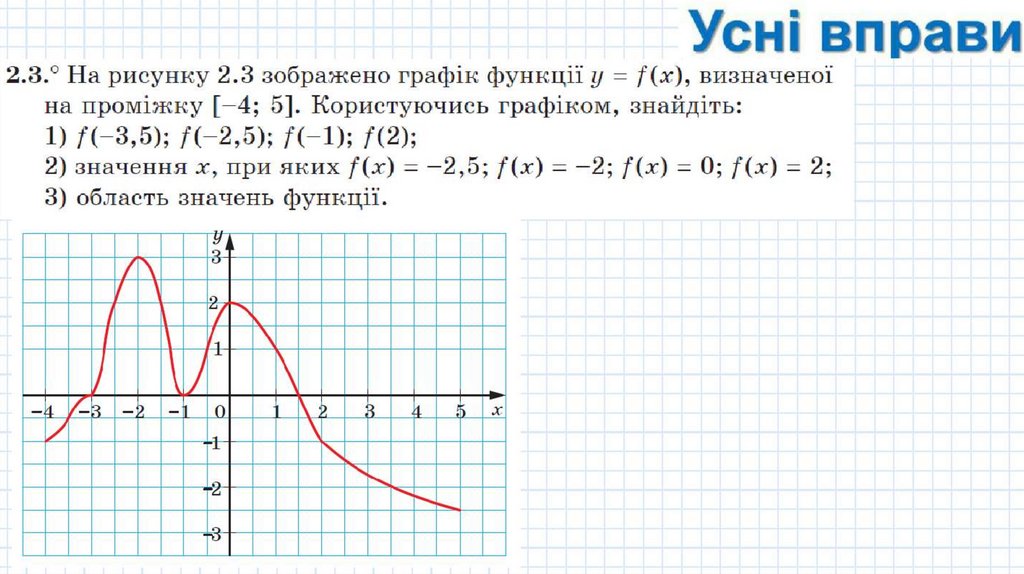
Y cH ien pae M
2 .3 .0 Ha p 11cyHRY 2.3 306pame Ho rpacpiR qlyHRIJ.il y = f (x ) , BM3Ha-creHo1
Ha rrp oMi:mRy [- 4; 5]. Kop HcTy10q11ch r p acpiRoM, 3HaiI.n;iTh :
1) f (- 3 , 5) ; f (- 2 ,5 ) ; f (- 1); f (2);
2) 3HaqeHH51 x , rr p H .HK H X f (x ) = - 2 ,5; f (x ) = - 2; f (x ) = O; f (x ) = 2;
3 ) 06 .rraCTb 3Ha-creHb q y HKII, .
:1
.
....
I
I
v
'
0
j
I
.,
/ _'
If
- L.1 - )
)
-
0
.L
-'c"',
"\}
"'I
..
\
\\
)
1
\
"
.......
r--.....
...........
x

12.

3 A n A M •s:ir A lllTE !
Ic Hy IOTb <PYHRI.I, 1, RRi Ha p 3HHX r r ip;MHOm HHa x o6JiacTi BH3Ha'l eHHR
3 p;aIOThCJI p 3HHMH <Pop MyJiaMn . H arrpHRJia,n;,
2
X ,
y = 2x - I,
R K IIJ;O X
1,
$IK IIJ;O x
>I.
I
TaR i cpyHR:o;i 1 Ha311BaIOTh
Crroci6 3 a,n;aHe
s1 <l_}yH:KII,ii: o,n;Hie10 a6o Ri.JibROMa Q_)op My J ia M H Ha3l!
Ba IOTh a H a J I T H q H H M .
I
3x - l , S K I U ; O X
2 .6 . ,I(aHO cpy HRrt; IO f (X) =
0
X
2
-
11,
·- 1 ,
5' .HR TTT
0 - 1<X < 4
.........._
'
H K IIJ;O X
>4 .
3 HaH,D;iT b: 1) f (- 3 ) ; 2) f (- 1) ; 3) f ( 2 ).; ·4 ) f (6,4).
IIH ChM OBi enpaeu

13.

,l(oMamne Ja6danna
1) f (x ) = J x + 4 +
1) f (x ) = .x 2 + 3 ;
2
x +I
;
2) f ( x ) = 6 - # ;
2.15.0 q H e «l.J Y H K IJ; J I B 3a e M H O O.ll;H 0 3 H a q H
D (y) H1a M H O I B I IH Y E (y ) :
1) y = .;
2) y = x 2 + 1;
M Bi
o 6 p a m e H H J IM M H O I B I IH I I
1
3) y = 2?
-x2 + 4, B K O X < l,
2.21. )];RHO tPYHKD;iIO f( x) =
X - 3, H K IIJ;O X
1.
/ ( - 2); f(O); f( l ) ; f(-3).

English Русский Правила