Похожие презентации:
Equations of math physics
1.
EQUATIONS OF MATH PHYSICS* Instructor: Dr. A. A.Kavokin
kavokin_alex@yahoo.com
2.
Purpose of this course is to provide the students, the futurescientist, and engineers with
methods of math modeling of
some physical phenomena and a seamless approach to
solution of a typical equations of mathematical physics.
3.
STRUCTURE, VOLUME AND CONTENT of THE DISCIPLINESubject: “EQUATIONS OF MATH PHYSICS” -2
- credits
Hou Task for SelfTitle of topic
Week
rs.
preparing
Lect.1.Introduction to PDE. Definitions, Simple 4 Common
1-2 Examples of PDE . Classification and Canonical forms
terminology.
(Sem.).
+2
PDE of Parabolic type: Applications: Heat equation,
Analysis of
Convective diffusion equation.
some
Lab.. Canonical forms of PDE.
Examples of
3-5 Lect.2. Hydraulic equations (Ground water with open 6 parabolic
surface. Oil strata). Correctness of task statements, +3 PDE
initial and boundary conditions.
Preparing to
Elliptical equations. Laplace and Poisson’s equations.
MidTerm
Principle of maximum.
Uniqueness of solution.
exam
Examples (Sem).
6
7
8
Lecture.3 Vibrating string equations. D’Alambert’s
2 Midterm ex.
solution. Some properties and uniqueness of solution/
+1
Examples (Sem )
Boundaries problems. Separation of variables. Method. 4
of Fourier series. Examples (Lect .and Sem.) .
+2
4.
STRUCTURE, VOLUME AND CONTENT of THE DISCIPLINENote!
A)The syllabus is given as a guideline and the rate as well as order of
priorities of coverage may be varied as instructor may feel necessary.
However, it is expected that the material required for the common exams will
have been covered by the date of exam.
B)
Grade assignments:
Quizzes + Assignments : 60% , Final Exam: 40%
5.
Introductions:What are subjects of mathematical physics?
Mathematical models of natural phenomena, which are described using :
- Algebraic equations (AE)
- Ordinal Differential Equations
- Partial Differential Equations
- Integral Equations
Solution of those equations as rule are continuous and even differentiable
functions, which not always can be found explicitly. So different methods
and approaches which is used for solution of above problems are subject
of this course.
6.
We will be studying functions u=u(x1;x2;;xn) and theirpartial derivatives. Here x1;x2;;xn are standard Cartesian
coordinates on Rn: We some times use the alternate
notation u(x;y);u(x;y;z);etc. We also write e.g. u(r;Θ;φ) for
spherical coordinates on R3; etc. We some times also have
a time "coordinate” t in which caset x1;;xn denotes
standard Cartesian coordinates on R1+n: We also use the
alternate notation x0=t: We use lots of different notation for
partial derivatives:
7.
CLASSIFICATION OF SECOND ORDER PDEGeneral form of PDE of 2nd order is:
8.
Classification of PDE similar to geometrical quadraticequation of the form:
Ax 2 Bxy Cy 2 Dx Ey F 0
2
IF discriminant B 4 AC is positive then it’s hyperbolic,
IF zero then parabolic,
If negative then elliptic.
Thus, we have the following PDE of 2nd order:
AU xx BU xy CU yy DU x EU y F 0
where coefficients A,…,F can be functions of X,Y .
This equation is hyperbolic , parabolic or elliptic at the
point (Xo, Yo) as the discriminant
2
B Xo, Yo 4 A( Xo, Yo )C ( Xo , Yo )
Is positive, zero or negative
9.
To transform equationAU xx BU xy CU yy DU x EU y F 0
to s.c. canonical form we input new variables:
v v( x, y ); s s ( x, y );
Now, the partial derivatives become:
U x U v v x U s s x ; U y U v v y U s s y ;
U xx U vv v x2 2U vs vx s x U ss s x2 U v vxx U s sxx ;
U xy U vv v x v y U vs ( v x s y v y sx ) U ss sx s y U v vxy U s sxy ;
vxs y
vx s y
U yy U vv v 2y 2U vs v y s y U ss s 2y U v v yy U s s yy ;
Substitute those PD in original equation we obtain:
10.
AU xx BU xy CU yy DU x EU y F 0U x =U v v x +U ss x ; U y =U v v y +U ss y ;
U xx =U vv v 2x +2U vs v x s x + U sss 2x +U v v xx +U ss xx ;
U xy =U vv v x v y +U vs (v xs y +v ys x )+ U sss xs v +U v v xy +U ss xy ;
U yy =U vv v 2y +2U vs v ys y + U sss 2y +U v v yy +U ss yy ;
Substitute those PD in the original equation we obtain:
A1U vv B1U vs C1U ss D1U v E1U s F1 0
where:
A1 Av x2 Bv y vx Cv 2y ; C1 As x2 Bs x s y Cs 2y ;
B1 2 Av x s x B (vx s y s x v y ) 2Cv y s y ;
D1 Av xx Bv x y Cv yy Dv x Ev y ;
E1 As xx Bs x y Cs yy Ds x Es y ; etc.
(*)
11.
So, transformed equation is of the same form as original, and we canverify , using (*) that it is of the same type :
B12 4 A1C1 ( v x s y v y s x )( B 2 4 AC )
CANONICAL FORM FOR PARABOLIC EQUATION. (Δ=0)
For parabolic PDE, Δ=0 , which can be true if B1=0 and C1 or A1 = 0.
Let, for example, A1 = 0:
A1 Av x2 Bv x v y Cv 2y 0;
vx
B
B
vx 2
vx
(
)
; (**)
A( ) B ( ) C 0 '
vy
2A
2A
vy
vy
It’s proved that in this case also B1=0;
Sionce we have some optional choice for v(x,y) , take it in form:
v(x,y)=C.
dv vx dx v y dy 0;
Now we vcan transform
(**)
dy
B in ODE;
dy
x
, i.e. we get ODE :
f ( x, y );
vy
dx 2 A
dx
General solution can be written in form ( x, y ) C ,
so we can take v( x, y ) ( x, y ), and an optional s( x, y )
12.
Consider the following examplex 2U xx 2 xyU xy y 2U yy 1 :
2
2
2 2
B1 4 A1C1 ( 2 xy ) 4( x y ) 0,
so, it's parabolic PDE .
vx
B 2 xy
y
2 v( x, y ) c x y c
vy
2A 2x
x
Line x y c
is called characteristic
A1 0, B1 0 , C1 y 2 , D1 2 xy;
y 2U ss 2 xyU v 1;
Let s y; then:
2v
2
U
U
1/
s
;
v
ss
2
s
So, in domain v > 0 it’s canonical form of parabolic PDE (not homogeneous)
13.
So, transformed equation is of the same form as original, and we canverify that
2
B1 4 A1C1 (vx s y v y s x )( B 2 4 AC )
Canonical form for Hyperbolic equation (discriminant is positive) ,
so choose A1=0; C1=0; and we obtain equations
vx 2
) B( v x ) C 0;
vy
vy
s
s
A( x )2 B( x ) C 0;
sy
sy
A(
from which , we can find:
vx
vy
sx
;
sy
;
From this we obtain formulas for V=V(x,y) and
S=S(x,y), which are called characteristics, and
finally get PDE in the following form:
2
U
(U ( x, t )) F (U ,
,U , x, y );
x y
x , y
14.
For general linear PDE of 2nd order , we can determine type usingcoefficients of correspondent quadratic form. ( Just definition).
Let, PDE:
n
2U
U
ai, j ( x1 ,.., xn ) x x F ( x ,...,U , x1 ,.., xn ) 0;
i , j 1
i
i j
Let’s consider correspondent quadratic form:
n
Q ai , j ( x1 ,.., xn ) ti t j
i , j 1
After converting it to canonical form :
n
QC bi ( s1 ,.., sn ) ti2 ,
i 1
we can classify (*) at given point
( x1 ,.., xn ) :
Elliptic if all bi of the same sign (not 0);
Parabolic if some of bi =0 and all other of the same sign;
Hyperbolic if one of bi has sign opposite to all other bj
(*)
15.
The development of models for dynamic systems is often basedupon the conservation laws of physics and other special
properties of a correspondent discipline. (it’s true for a s.c.
material systems, e.g. financial, banking, etc. What about IS?)
Conservation Laws of Engineering systems
In all of physics there are only six conservation laws.
Each describes a quantity that is conserved, that is, the total
amount is the same before and after something occurs.
These laws have the restriction that the system is closed ( isolated ),
that is, the system is not affected by anything outside it.
Conservation of charge
Conservation of momentum
Conservation of mass/energy
Conservation of angular momentum
Conservation of baryons
Conservation of leptons
Differential form of laws, what does derivative mean?
16.
- Conservation of charge ( analog of Kirhhov’s law)- Conservation of Linear momentum
Linear momentum (analog of 2nd law of motion established by
Isaac Newton 1642-1727): The sum of all forces (F) acting on
mass (m) particle causes a rate of change in the momentum of the
particle with respect to time (V-velocity):
d
F i dt [mV ]
i
- Conservation Law of Mass:
mass of in isolated (fluid,dynamic) system is constant (ρ – density):
d
d
(
m
)
[ V ]
i
dt
i dt
- Conservation of Energy:
The Energy in isolated system is constant.
The System can be mechanical, electrical, thermal, fluid or of
combined types. (it’s analog of the first law of thermodynamics “
sum of all power in and out is equal to the rate at which energy is
being stored in a control volume of the system”).
Example kinetic and potential energy.
2
Example kinetic and potential energy. (mgh, mv /2 )
Bernoully (1700-82) equation : P/d +v2/2+zg= const. (along a streamline).
17.
Simple, 1D Heat and Diffusion equations:Glossary:
Heat - тепло, нагревать,
Temperature - температура
Specific heat – теплоемкость
Thermal conductivity - теплопроводность
Thermal diffusivity - температуропроводность
Source – источник,
Joule’s heat (i*V*t) - Джоулево тепло
Gradient - градиент,
Density - плотность
Solution – раствор,
Dissolution - растворение
Concentration – концентрация
Diffusion – диффузия.
- Fourier’s Law says that heat flows from hot to cold regions at
a rate · > 0 proportional to the temperature gradient.
dT
J h ( s t )
dx
- Fick’s Law says that rate of diffusion (dissolved substance
flux) in a given direction is directly proportional to the
concentration gradient ( the grater the concentrations
difference, the faster the rate of diffusion)
dC
J C D ( s t )
dx
18.
Modeling: (derivation)Amount of heat Q(x,T*) = C d V T* ;
Where C – specific heat; d – density; V= S*Δx – volume.
Using
CLE and
Fourier’s law of thermal conductivity:
dT
J h ( s t )
dx
,
we obtain heat (heat transfer) equation: (e.g. for 1D rod ):
LoC:
Q(x*,t2) = Q(x*, t1) + (Jh1 – Jh2) S* Δt
C d V T(x*,t2)- C dV T(x*,t1) = (- λ ∂T(x1,t*) / ∂x + λ ∂T(x2,t*) / ∂x) S Δt
C d S Δx (T(x*,t2)- T(x*,t1)) = λ(∂T(x2,t*) / ∂x - ∂T(x1,t*) / ∂x) S Δt
Divide both parts of equation by ( S Δx Δt 0):
Or:
2
T ( x, t )
2
a
(T ( x, t )); { x ( x , x ); t 0}
t
x 2
where : a 2 /(C ) thermal diffusivity
1
1
19.
Using CLE and Fourier’s law of thermal conductivity:dT
J h ( s t )
dx
,
we obtain heat (heat transfer) equation: (e.g. for 1D rod ):
20.
Using Fick’s law , we can develop diffusion equation or convectivediffusion equation for concentration C(x,t) [g/m^3]:
C ( x, t )
2
C ( x, t )
D 2 (C ( x, t )) v (
);
t
x
x
where : D diffusion coeff ., [ m2 / s]
{ x ( x0 , x1 ); t 0}
v velosity of fluid flow, [ m / s]
Using Darcy’s law,
q K f
H
,
x
we can develop hydraulic head equation or sometimes called Bussinesc’s
equation: :
H ( x , t )
t
x
( K f H ( x , t )
H ( x , t )
x
) q( x, t );
( x ( x , x1 ); t 0)
where : H hydraulic head , [ m] { H P / dg z}
K f coeff. of filtration of fluid [ m / s],
0
21.
Boundary conditions:For domain Xo<x <X1 we have to define 2 boundary conditions:
1)At x=Xo
2) At x=X1
The most often used b.c. are:
U
A
BU F ( xk , t ) ,
x
at x xk , k {0,1}
Classification:
A=0, B≠ 0 - 1st type b.c. ( Derichlet’s)
A ≠ 0, B=0 - 2nd type b.c. ( Neuman’s)
A ≠ 0, B≠ 0 - 3rd type b.c. ( Newton’s, Robin’s)
Examples. Explanations.
Example of nonlinear condition:
U (0, t )
4
(U 4 (0, t ) TEnv
(t ) ),
x
at ( x 0 , t 0)
Stefan-Boltzman radiation law: U –temperature of object, T- temperature of
media/.
Equation with discontinuous coefficients ; Stefan’s and Verigin’s free
boundary problems and conditions at the moving boundary.
22.
If some function U(x,t) satisfies the following parabolic type PDE:U ( x, t )
2
U ( x, t )
a 2 (U ( x, t )) b (
) c(t )U ( x, t ); { x ( x0 , x1 ); t 0}(*)
t
x
x
where : a 0;
then we can reduce it to canonical form , using the substitution:
U ( x, t ) exp( x (t )) V ( x, t ),
Where unknown , (t ) have to be choosen to obtain canonical
parabolic PDE for V(x,t), i.e. :
V ( x, t )
2
a 2 (V ( x, t )); { x ( x0 , x1 ); t 0} (**)
t
x
So, ve can transfer main properties of (**) from (*) (examples for
steady state equations. )
23.
Well-posed and Ill-posed boundary problemsDef.: A Boundary problem for PDE is called well-posed (in
the sense of Hadamard), if
(1)a solution exists
(2) the solution is unique
(3) the solution depends continuously on the data
(initial conditions, boundary conditions, right hand side)
An ill posed problem is one which doesn’t meet the above
mentioned three criteria for being well posed.
(soln does not exist OR soln is not unique OR small change in
related data resulted huge change in soln)
Example:
U’’ =q ; 1st boundary problem is well-posed, but 2nd is not (Ill-posed)
24.
Maximum principle:Let given parabolic type equation:
U ( x, t )
2
a 2 (U ( x, t )); { x ( x0 , x1 ); 0 t T ; a 0} (*)
t
x
with initial and boundaries conditions:
U(x,0) = f(x); U(xo,t ) = f0(t); U(x1,t ) = f1(t) ;
(**)
( f ) M ;
fi - limited functions i.e. max
i 1,2,3
Then the maximum (minimum) values of U are attained either at t=0
or at X=Xo or at X=X1, i.e. at the boundaries point.
i
Corollary 1: Solution of equation (*) is unique (uniqueness
feature)
(idea of proof: if two functions are satisfying (*) and (**) then their difference
satisfying (**) with fi =0, hence It has to be 0 everywhere in domain (in accordance with
Max. principle)).
Corollary 2: Solution of equation (*) continuously depends on
initial and boundary conditions (**) (idea of proof: if two functions are satisfying
(*) and their difference satisfying (**) with |fi| ≤ε<<1, hence It has to satisfies the same
inequality everywhere in domain (in accordance with Max. principle). )
25.
Separation of variables method (parabolic type of PDE)Consider the equation:
2
U ( x, t )
a 2 2 (U ( x, t )); { x (0, ); t 0}
t
x
With initial condition : U ( x,0) f ( x) ,
and boundary conditions :U (0, t ) 0;
(1)
(2)
U ( , t ) 0; (3)
Idea of SVM is to represent U(x,t) as product of two functions, so that
each depends on one variable:
U ( x, t ) X ( x)* T (t );
(4)
After substitution (4) in (1) we obtain separate differential equations with
respect to X() and T():
X '' T '
2 c const.
X aT
26.
X ''T'
2 c const .
X
a T
There are possible 3 cases:
1) c 0; say, c 2 ,
X ( x ) c1e
x
c2e
x
; T (t ) c3e
a 2 2t
2) c 0;
X ( x ) c1x c2 ;
3) c 0;
let
T (t ) c3
с 2 .
i
x
i x
a 2 2t
X ( x ) c1e c2e
; T (t ) c3e
;
i 1
U(x,t) should remain finite as t -> ∞: (Maxim,principle) So, this + initial
condition can be satisfied only with soln 3) (or 2, under some constraints)
27.
Def Fourier series:f ( x)
k
ak eikwx .;
T
ak T e ikwx f ( x) dx; T 2
1
0
Note : Properties of orthogonality of eigen-function :
X '' X 0;
X '' X 0;
k
k
k
(1)
*X
m
m
m
m
(2)
*X
k
( m k )!
( ) X X
m
k
m
k
( X X ' X X ' )'
m
k
k
m
( ) X X dx ( X m X 'k X k X 'm )l0 0
l
m
k
0
m
k
hold for general eq.:
( p( x) X ')' ( x) X 0;
k
k
k
()
1
( p 0, 0) C[0,
l]
Next: Satisfying boundary conditions:
Convergence of series:
28.
2U ( x, t )
2
a 2 (U ( x, t )); { x (0, T ); t 0}
t
x
U ( x,0) f ( x); (2)
U (0, t ) 0;
(1)
U (T , t ) 0; (3)
U ( x, t ) X (t ) * T (t );
2 2t
i
x
i
x
a
X ( x ) c1e c2e
; T (t ) c3e
; i 1.
k 2
kw
T
Satisfying boundary conditions (3) we get:
If we choose C1 and C2 to satisfy BC, then U(x,t) will also satysfies BC
Any linear combinations of connected X(x)*T(t) satisfies (1) , hence, we can
represent soln in the following form:
k a2t
U ( x,t ) e
k
i x );
e
2k
(c ei x c
1k
k kw
k 2
T
To convert exp(iz) in sin() cos() form. we can use well-known Euler’s formula.
29.
Examples: Fourier series of stepwise functionA
,
0
x
T
/
2
f ( x)
0, T / 2 x T
f ( x) ak eikwx .;
k
1
T
e ikwx f ( x) dx A
ak T
0
T
T /2
ikwx dx
e
(*)
0
A ikwT /2
A e ik 1
T
2
1
ik T e
ik 2
0, k 2l i.e. even
We obtain using properties of (*) that ak A
, k 2l 1, i.e.odd
ik
1 sin 2 (2k 1) x
A
2
A
f
(
x
)
And finally:
T
2k 1
2
k 0
(
Convergence of series: is investigated for each of type of initial condition,
i.e. depends on f(x)
)
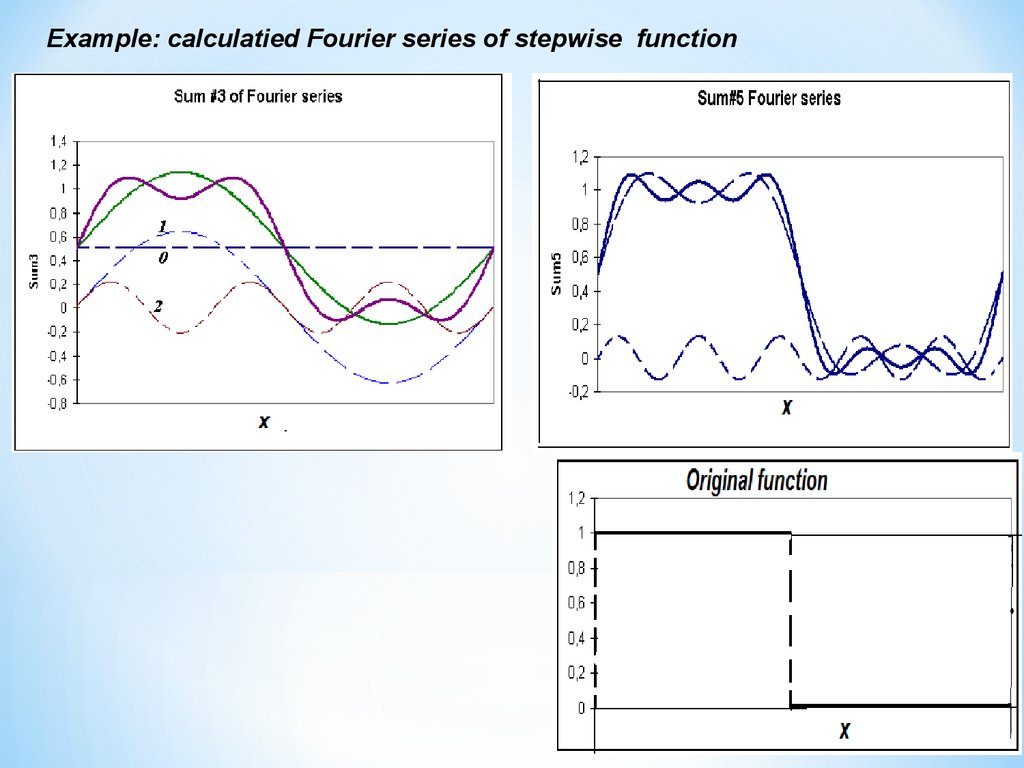
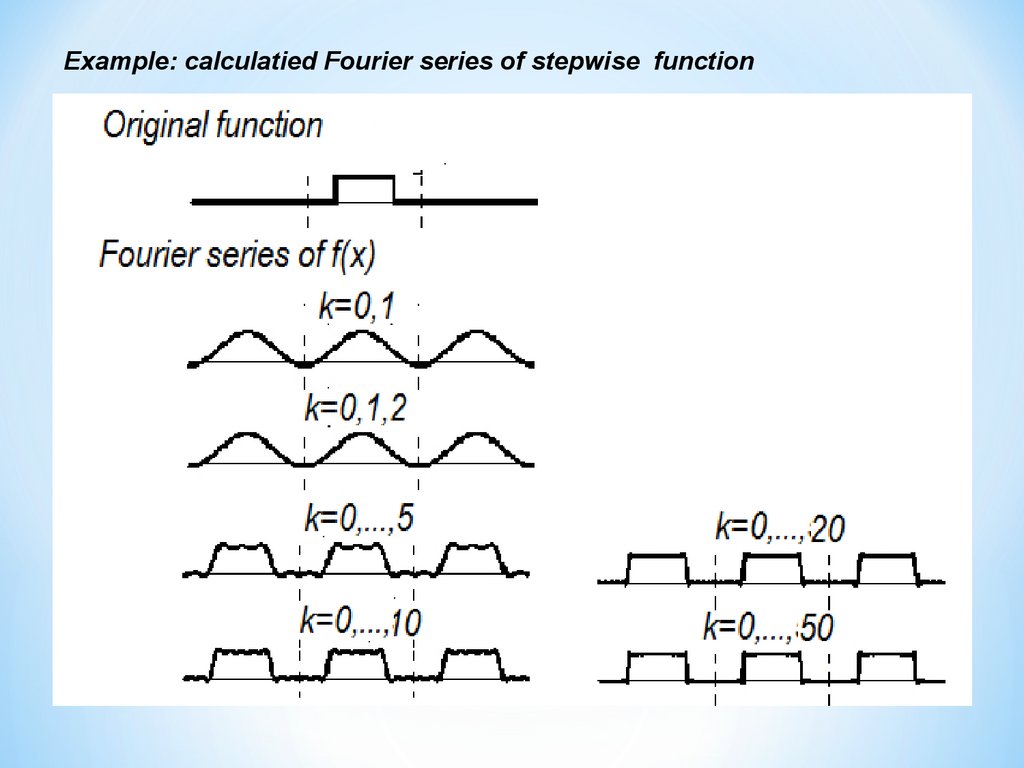
30.
Example: calculatied Fourier series of stepwise function31.
Example: calculatied Fourier series of stepwise function32.
Example.I C:
2
U ( x, t )
a 2 2 (U ( x, t )); { x (0, l ); t 0}
t
x
U ( x,0) f 0 ( x); (2)
BC:
U (0, t ) 0;
(1)
U (l , t ) 0; (3)
X '' T '
2 2 const.
X aT
Separation of
Variables method : U ( x, t ) X (t ) * T (t );
We have to choose - λ ^2
2 2t
a
X ( x ) c1 cos x c2 sin x ; T (t ) c3e
;.
Substitute in BC :
C1=0; λ = nπ / l
Substitute in initial
conditions: (IC)
n 0
U ( x, 0) an sin( n l x )
k 1
:Using property of orthogonality
Hence solution!
2 2
U ( x,t ) ane (n /l ) a t sin( n l x )
we obtain:
l
an 2l f 0 ( x) sin( n l x )dx
0
33.
Nonhomogeneous heat equation2
U ( x, t )
a 2 2 (U ( x, t )) f ( x, t ); { x (0, l ); t 0} (1)
t
x
U (T , t ) 0; (3)
I C: U ( x,0) f 0 ( x ); (2)
B C: U (0, t ) 0;
Suppose that f
( x,t ) f n (t ) sin( n l x )
k
1
f n (t ) 2 0 f ( x, t )sin( n x )dx
l
l
l
where :
We represent soluition of (1) in form: U ( x,t ) U 0 ( x, t ) U f ( x, t ); (4)
Where Uo -solution of homogeneous equation (see previous slide) and Uf soln of nonhomogeneous eq. (1),(3) which satisfies zero initial conditions (2).
Substitute f(x,t) in (1) we obtain differential equation for T(t) of Uf
dTn (t )
a 2 2 Tn (t ) f n (t ); { t 0}; Tn (0) 0;
dt
Eventually. from (4) we’ll find solution of problem (1)
Note: we can easily convert general (3) with f1(t), f2(t) into homogeneous (3)
E.g. Using substitution: U=U1+F(x,t) , where F(x,t) = f1(t) *(l-x)/l + f2(t) *x/l
34.
(We can apply Fourier Series only for case of finite domain).Infinite domain. Fundamental solution. (F.s.)
f ( x,t ,0,0)
1
2 t
f ( x,t , , )
2
x2 )
exp(
1
(t )
Now:
4a 2t
2
(
x
)
exp(
)
2
4a
(t )
Properties of Fundamental solution.
1 F.s. satisfies parabolic equation at any ( , )
( )
2
(
x
)
2 Function U ( x, t )
exp(
) d * f ( x,t, ,0)
2
4a t
2 t
2
U ( x, t )
U ( x, t )
satisfies parabolic eq. :
a 2
; { x ( , ); t 0}
2
t
x
with initial conditions :
U ( x,0) ( x ); ( x ) C *R
(Cauchy ' s problem)
C* - class of and uniformly continuous bounded functions. Proof: after substitution
(
x
)
1
z
U ( x,t ) ( x z 2a t ) exp( z 2 ) dz
( x)
,
transform
U(x,t)
into:
t 0
2a ( t )
35.
3) Duhamel’s principle:Function:
t
( x )2
q( , )
U ( x, t )
exp( 2
) d d ,
4a (t )
0 2 (t )
satisfies parabolic eq. :
U ( x, t ) 2 2U ( x, t )
a
q ( x, t ) ;
2
t
x
with initial condition:
U ( x,0) 0;
{ x ( , ); t 0} ,
q C *R
Examples simple-layer potential (1); double- layer potential (2);
t
( x x0 )
a2
1
exp( 2
)q( ) d
2
2 0 a (t )
4 a (t )
U1( x, t )
2
t
( x x0 )
( x x0 )2
1
exp( 2
) q( ) d
3/
2
2a 0 (t )
4 a (t )
U 2 ( x, t )
(1)
(2)
36.
Properties of potentials:Both U1(x,t) and U2(x,t ) satisfy heat equation:
U i ( x, t )
t
2
U i ( x, t )
2
a
;
2
x
{ x x0 ; t 0}, i 1, 2.
U2(x,t ) satisfy boundary condition:
lim U ( X , t ) q(t );
x x0 2
{ t 0};
To prove this, we make the substitution in (2):
then: t
U 2 ( x, t )
( x x0 )
;
2 2
4a z
z
( x x0 )
4a 2 (t )
2
( x x0 )
2
z2
z2
e q( t
) dz
e dz
x
x0 q(t )
2 2
( x x0 )
0
4a z
4 a 2t
Proof steps are very similar to those for property 2 of F.s. (see previous slide)
Examples in semi- infinite domain. (semi-bounded)
(*)
37.
Delta –function ([Paul Dirac 1902-1984 ])δ(t) is often defined as
Unit Impulse function
0, | t |
1
,
x
(
t
)
lim
where
x
(
t
)
0 2
1/
,
|
t
|
Some properties of δ(t) : (not unique)
a
f(τ)*δ(τ) dτ = f(0) ;
(a,b)?
b
a
f(τ)*δ(τ-t) dτ? ; (a,b)?
b
a
f(τ)*δ’(τ) dτ?
δ(at)= δ(t)/a;
b
δ(-t)= δ(t)? ;
(a><0)
38.
Delta- function and Fundamental solution of Parabolic PDEUsing Duhamel formula and properties of δ(t) we can find that F.s. is soln
of the nonhomogeneous heat equation with: f(x,t)= δ(t) δ(x)
2
U ( x, t )
2 U ( x, t )
a
( x ) (t ); { x ( , ); t 0}
2
t
x
: Duhamel’s formula
t ( ) ( )
U ( x, t )
0 2
(t )
exp(
( x )2
4a 2 (t )
( x 0)2
1
exp( 2
),
2 (t 0)
4a (t 0)
hence definition.
) d d
39.
Elliptical equations:General form of linear PDE of 2nd order with two variables X,Y:
AU xx BU xy CU yy DU x EU y F 0
This equation is elliptic at the point (Xo, Yo) if the discriminant is
negative, i.e.
2
B Xo, Yo 4 A( Xo , Yo )C ( Xo , Yo ) 0
2U ( x, y ) 2U ( x, y )
f ( x, t ); { x, y D( x, y )}
2
2
x
y
(1)
Or , Laplace’s equation :
2U ( x, y ) 2U ( x, y )
0; { x, y D( x, y )}
2
2
x
y
(2)
Elliptic type of PDE can describe, for example, steady state of
temperature (heat equation) or Continuity equation of incompressible
fluids ( law of mass conservation):
40.
We start study features of EPDE using Laplace’s equation :2U ( x, y ) 2U ( x, y )
0; { x, y D( x, y )}
(2)
2
2
x
y
If we denote boundary of domain D(x,y) as S(x,y) and nis
normal vector to S,
then it is possible to write different types of
boundary conditions for Laplace’s equation (2):
U F ( x, y ) ;
x, y S .
U
F ( x, y ) ;
x, y S
n
U
BU F ( x, y ); x, y S
n
Classification:
: 1st type ( Derichlet’s)
: 2nd type
( Neuman’s)
: 3rd type ( Newton’s, Robin’s)
41.
Solution of Laplace equation are close connected with s.c. Harmonicfunction in theory of complexes function;
Let w(x,y) = u(x,y)+ i v(x,y) ; If w(x,y) satisfies Riemann conditions:
u v
;
dx dy
u
v
;
dy
dx
in domain D( x, y )
then it is called HARMONIC functions. It’s easy to proof that both
u(x,y) and v(x,y) in H.f. satisfy Laplace equations in domain D(x,y)
H.f. have got some special properties.:
-- Theorem on Mean Value for H.f. :
Let U(x,y) be harmonic in circle D(x,y) of radius R with boundary
S(x,y) and center C(x0, y0). Then:
1
u (C )
u ( R, ) d
2
D
_
S
2 R
(*)
Similarly for 3D sphere with center C(x0, y0):
u (C )
1
4 R
2
3D _ S
d u ( R, , )d
Maximal./minimal principle and Corollaries:
(**)
42.
Maximal./minimal principle and Corollaries:If function U(x,y, ) is continuous in closed D and satisfies Laplace
equation ΔU=0 in the interior of D, then Max and Min of U can occur
only on the boundary of D or U = constant in the interior of D.
Stability Theorem: The solutions of the Dirichlet problem depend cotinuosly
on the boundary data
Uniqueness Theorem: The solutions of the Dirichlet problem is unique.
43.
Solution of boundary problem for Laplace equation , using Fourierseries method. (separation of variables method - SVM)
2U ( x, y ) 2U ( x, y )
0; D :{0 x x1 , 0 y y1}
2
2
x
y
U (0, y ) 0; U ( x1, y ) 0 ;
B.C.:
(*)
U ( x, 0) f 0 ( x); U ( x, y1 ) 0 ;
Separation of variables gives:
U ( x, y ) X ( x )Y ( y ) ; (*)
We have 3 options for C:
X ''( x )
Y ''( y )
X ( x)
Y ( y)
C ;
1) C 2 ( 0) : X C1e x C2e x ; Y C3 cos y C4 sin y ;
2) C 0 : X C1 x C2 ; Y C3 y C4 ;
y
3) C 2 ( 0) : X C1 cos x C2 sin x ; Y C3e
Which option is correct for problem (*) with above B.C. ?
C4e
y
;
Let’s check
44.
So, eventually we can find out that It’s possible only form of solution:y
3) C 2 ( 0) : X C1 cos x C2 sin x ; Y C3e
C4e
y
Two other options give trivial solution (U=0) ( ! ).
So, soln U λ(x,y) (depending on λ ) is as follows:
U ( x, y ) (C1 cos x C2 sin x) (C3e
From BC :
at x 0 : C1 0;
y
C4 e
y
);
n
at x x1 : ;
x1
n y
n
n y
U ( x, u ) C2 n sin( x x) (C3ne x1 C4 ne x1 ) ;
1
n 1
Hence:
We apply known Fourier’s technique, and finally obtain :
n
n
U ( x, u ) An sin( x x ) sinh( x ( y y1 )) ;
where:
1
1
e z e z
sinh( z )
( hyperbolic sin)
2
;
An
1
2
x1
n x
f
(
x
)
sin(
x ) dx
n y1
x1 sinh ( x ) 0
1
1
;
45.
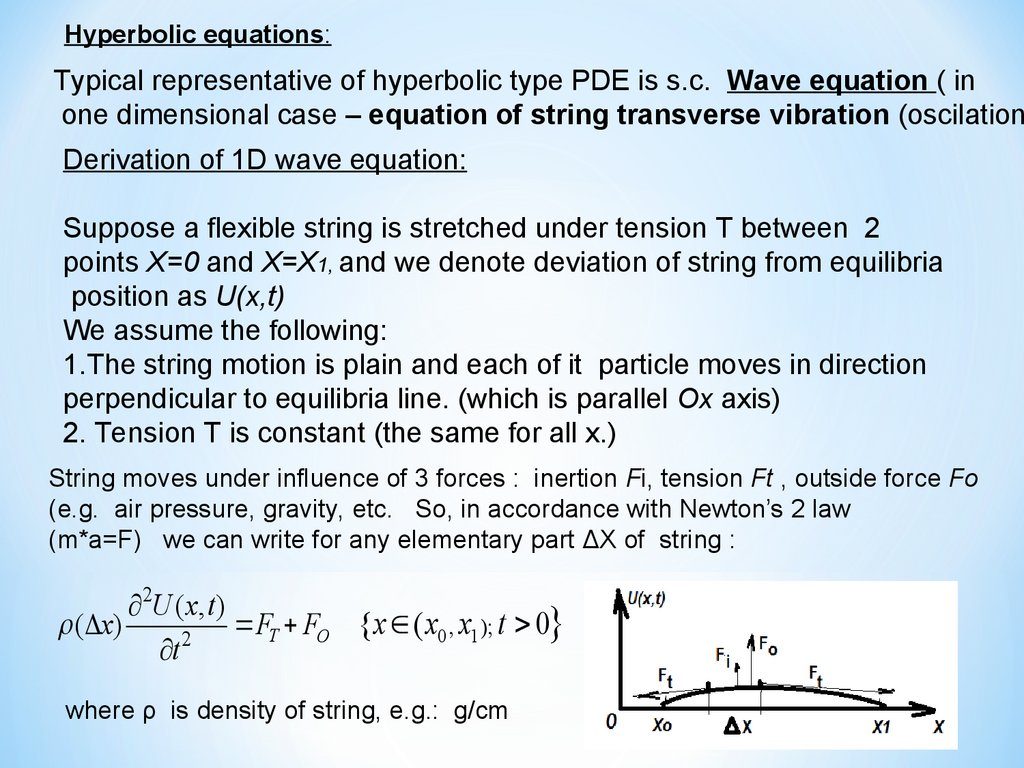
Hyperbolic equations:Typical representative of hyperbolic type PDE is s.c. Wave equation ( in
one dimensional case – equation of string transverse vibration (oscilation
Derivation of 1D wave equation:
Suppose a flexible string is stretched under tension T between 2
points X=0 and X=X1, and we denote deviation of string from equilibria
position as U(x,t)
We assume the following:
1.The string motion is plain and each of it particle moves in direction
perpendicular to equilibria line. (which is parallel Ox axis)
2. Tension T is constant (the same for all x.)
String moves under influence of 3 forces : inertion Fi, tension Ft , outside force Fo
(e.g. air pressure, gravity, etc. So, in accordance with Newton’s 2 law
(m*a=F) we can write for any elementary part ΔX of string :
2U ( x, t )
( x)
FT FO { x ( x0 , x1 ); t 0}
2
t
where ρ is density of string, e.g.: g/cm
46.
So, finally we obtain:or:
2U ( x, t )
2U ( x, t )
T
FO
2
2
t
x
{ x ( x0 , x1 ); t 0}
2U ( x, t ) 2 2U ( x, t )
c
F ( x, t ) { x ( x0 , x1 ); t 0};
2
2
t
x
c 2 T / ; F ( x, t ) F0 / .
Initial and boundary conditions:
U ( x, 0)
U ( x, 0) f 0 ( x);
f1 ( x); U ( x0 , t ) f 3 (t ); U ( x1, 0) f 4 (t );
t
(Example : 2D membrane transverse vibration.)
47.
D’Alambert solution:(infinite domain)
2
2U ( x, t )
2 U ( x, t )
c
2
t
x 2
{ x ( , ); t 0};
(*)
U ( x,0)
f1( x);
With initial conditions : U ( x,0) f 0 ( x);
t
Where fo and f1 are continuous and bounded functions:
1) We substitute new variable to obtain solution:
s x ct;
v x ct ;
and determine all necessary order derivatives;
s v
s
v
1;
c;
x x
t
t
2 s 2 s 2 v 2v
2 2 2 0;
2
x t x t
U
U s U v
U
U
c
c;
t
s t v t
s
v
48.
Then determine all necessary second order derivatives;2U
t
2
2U
s 2
2U
s 2
2U s v
2U v 2
( )
( )
2
2
t
v s t t
t
s
v
2U
2U
2
2
(c )
(c )
(c )2
v s
v 2
The same with second order derivative by x;
2
2 2
2
2
U
x
2
U
s
2
U
U
v s
v 2
;
So, finally we obtain other canonical form of HPDE:
2U
0 ;
v s
(**)
Integrating (**), we get:
U ( s, v ) ( s ) (v ) U ( x, t ) ( x ct ) ( x ct ) ; (***)
From (***) and initial conditions (*). we get D’Alambert’s formula:
1
1 x ct
U ( x, t ) f0 ( x ct ) f0 ( x ct ) x ct f1( z )dz ; (!!!)
2
2c
Example: fo = exp(x^2)
49.
Uniqueness of the solution for Wave equation:2
2U ( x, t )
U ( x, t )
2
c
F ( x, t ) { x ( x0 , x1 ); t 0};
2
2
t
x
(*)
We going to prove that for homogeneous eq. (*) with zero
initial and BC::
2
2U ( x, t )
U ( x, t )
2
c
{ x ( x0 , x1 ); t 0};
2
2
t
x
(**)
U |x x0 U |x x U |t 0 U t' |t 0 0 ;
1
We can prove that the following formula holds:
1 x1 2
E (t ) (c (U x ) 2 (U t ) 2 ) dx const. 0; (***)
2 x0
Difference of two solution of (*) satisfies (**), so, with using (***) we
can easily prove that the difference equals to 0, everywhere, hence
uniqueness.
50.
prove the formula:1 x1 2
E (t ) (c (U x ) 2 (U t ) 2 ) dx const. 0; (***)
2 x0
x1 2
E
( c (U xU xt ) (U tU tt )) dx (1st item integr-g by part)=
x0
dt
x1
U xU t | ( c 2 (U tU xx ) (U tU tt ))dx 0;
x1
x0
x0
{U ( x0 , t ) 0 U ( x1 , t ) U t ( x0 , t ) U t ( x1 , t ) 0
E
0; E (t ) const. 0; hence the theorem
dt
51.
Duhamel’s principle and fundamental solutionLet’s consider the non-homogeneous wave equation:
2
2U ( x, t )
2 U ( x, t )
c
F ( x, t ) { x ( x0 , x1 ); t 0};
2
2
t
x
(*)
Duhamel’s principle for such equation, using the D’Alambert formula with
correspondent initial conditions is
1
1 x ct
U ( x, t ) f0 ( x ct ) f0 ( x ct ) x ct f1( z )dz
2
2c
1 t x c (t )
0 x c(t ) F ( z , )dzd ;
2c
Using definition of fundamental solution (I,e. F(x,t)=δ(x)δ(t) and Duhamel’s
principle for equation with homogeneous initial conditions we obtain formula for
fundamental solution:
1 (ct | x |) 1/(2c ), if | x | ct ,
U .F .( x , t )
2c
{ 0,
if | x | ct
{0,1, ifif xx | 00 -x ( z ) dz,
where ( x )
and also known as the Heaviside "unit step function." The term can represent
either a piecewise constant function or a generalized function.
52.
Separation of variables method for Wave equation:2
2U ( x, t )
2 U ( x, t )
c
F ( x, t ) { x ( x0 , x1 ); t 0};
2
2
t
x
Initial and boundary conditions:
U ( x, 0)
U ( x, 0) f 0 ( x);
f1 ( x); U ( x0 , t ) 0; U ( x1, 0) 0;
t
Separation of variables gives:
U ( x, y ) X ( x)T (t ) ; (*)
We have 3 options for C:
2
x
1) C ( 0) : X C1e
X ''( x) T ''(t )
C ;
X ( x)
T (t )
C2e x ; T C3e t C4e t ;
2) C 0 : X C1x C2 ; T C3t C4 ;
3) C 2 ( 0) : X C1 cos x C2 sin x ; T C3 cos t C4 sin t;
53.
Eventually we have one options:3) C 2 ( 0) :
X C1 cos x C2 sin x ; T C3 cos t C4 sin t;
Therfore:
U (C1 cos x C2 sin x)(C3 cos t C4 sin t );
So, now we can repeat a typical process of separation of variables
using initial and boundary conditions:
54.
Glossary:Current - ток
Voltage – напряжение
Voltmeter - вольтметр
Power - мощность
[Capacity] Capacitor- конденсатор
[Inductance] coil – катушка индуктивности
Wire- провод.
[Resistance] Resistor- сопротивление
55.
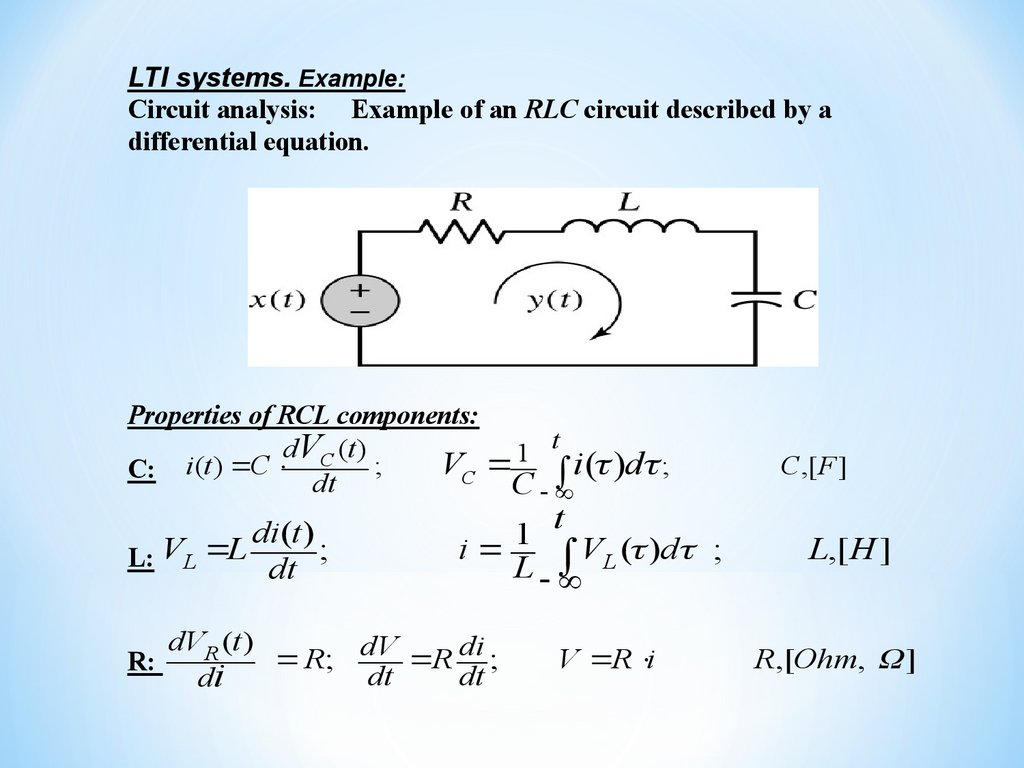
LTI systems. Example:Circuit analysis: Example of an RLC circuit described by a
differential equation.
Properties of RCL components:
t
dVC (t )
1
;
VC i ( )d ;
C: i(t ) C
dt
C
di(t )
V
L
;
L: L
dt
R:
t
i 1 VL ( )d ;
L
dVR (t )
R; dV R di ;
dt
dt
di
V R i
С ,[ F ]
L,[ H ]
R,[Ohm, ]
56.
2 laws of conservations:i(t ) 0;
For any node:
[1st Kirhhof ' s low]
For loop:
V (t ) 0; or VRCL (t ) VS ;
so, voltage around above loop:
VL+VR +Vc = x(t) or:
[2nd Kirhhof ' s low]
57.
td
i
(
t
)
1
L
R i(t )
i( )d x(t ); =>
C
dt
2
d
i(t ) R di(t ) 1 i(t ) dx(t ) ;
=> L
dt
C
dt
(dt )2
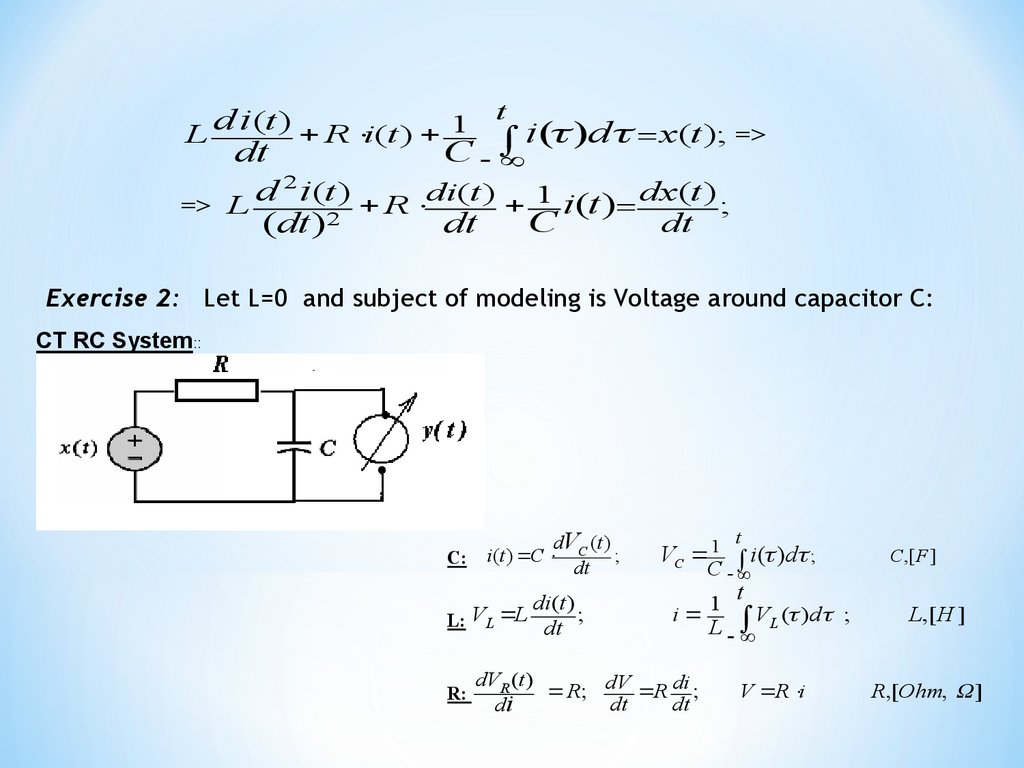
Exercise 2: Let L=0 and subject of modeling is Voltage around capacitor C:
CT RC System::
C:
dV (t )
i(t ) C C ;
dt
di(t )
L: VL L dt ;
R:
t
VC 1 i ( )d ;
C
t
i 1 VL ( )d ;
L
dVR (t )
R; dV R di ;
dt
dt
di
V R i
С ,[ F ]
L,[H ]
R,[Ohm, ]
58.
VR(t) + y(t) = x(t)t
R i(t ) 1
i( )d x(t );
C
R C dy y(t ) x(t );
dt
y(t) = yg + yp =
A exp(
1 t) 1
RC
t
exp[
RC
(*)
1 (t )] x( ) d ;
RC
59.
60.
HP/Compaq AlphaserverIBM BG/L
Grid Supercomputing
The computational grid is a new distributed computing paradigm, similar in spirit to the
electric power grid. It provides scalable high-performance mechanisms for discovering
and negotiating access to geographically remote resources. Performance of a wide
area network (WAN) increases by two orders (100)!! of magnitude every five years!
61.
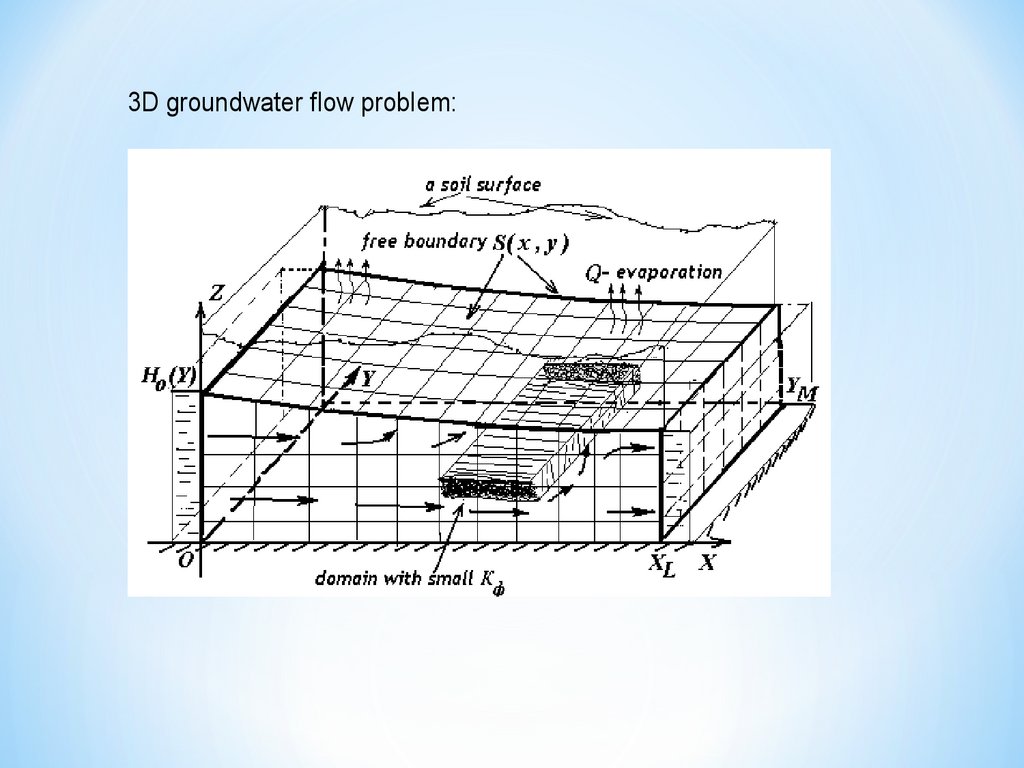
3D groundwater flow problem:62.
2D –middle section.Math model (hydrodynamic steady-state equation, Laplace’s equation ):
- Conservation Law of Mass:
mass of in isolated (fluid,dynamic) system is constant (ρ – density):
d
d
(
m
)
[ V ]
i
dt
dt
i
If an incompressible fluid, then dm/dt = 0 , so:
d
[ V ] 0;
ds
s.c.
s s ( x , y , z )
Continuity equation.
63.
Hydraulic head (synonym of potential energy)P ( x, y , z )
H ( x, y , z )
z;
g
Darcy’s law: Q= -K dH/dx; where Q – water flux in x direction;
K – coefficient of filtration. (this law means that fluid moves from point with greater
H to point with less H, and the faster the difference dH is greater)
Using mass conservation law and Darcy’s law one can derive continuity
equation ( Laplace equation, PDE of elliptical type)
(0 < X <L ; 0 < Y < S(X); 0< t < To )
64.
Hydraulic head (synonym of potential energy)P ( x, y , z )
H ( x, y , z )
z;
g
Darcy’s law: Q= -K dH/dx; where Q – water flux in x direction;
K – coefficient of filtration. (this law means that fluid moves from point with greater
H to point with less H, and the faster the difference dH is greater)
Using mass conservation law and Darcy’s law one can derive continuity
equation ( Laplace equation, PDE of elliptical type)
(0 < X <L ; 0 < Y < S(X); 0< t < To )
65.
Hydraulic head (synonym of potential energy)H ( x, y , z )
P ( x, y , z )
z;
g
Darcy’s law: Q= -K dH/dx; where Q – water flux in x direction;
K – coefficient of filtration. (this law means that fluid moves from point with greater
H to point with less H, and the faster the difference dH is greater)
Using mass conservation law and Darcy’s law one can derive continuity
equation ( Laplace equation, PDE of elliptical type)
(0 < X <L ; 0 < Y < S(X); 0< t < To )
66.
Problem: S(x) is unknown.(Free boundary problem)
Conditions for S(X):
1)
H(x, S(x)) = S(x)
2)
Iterative solution
67.
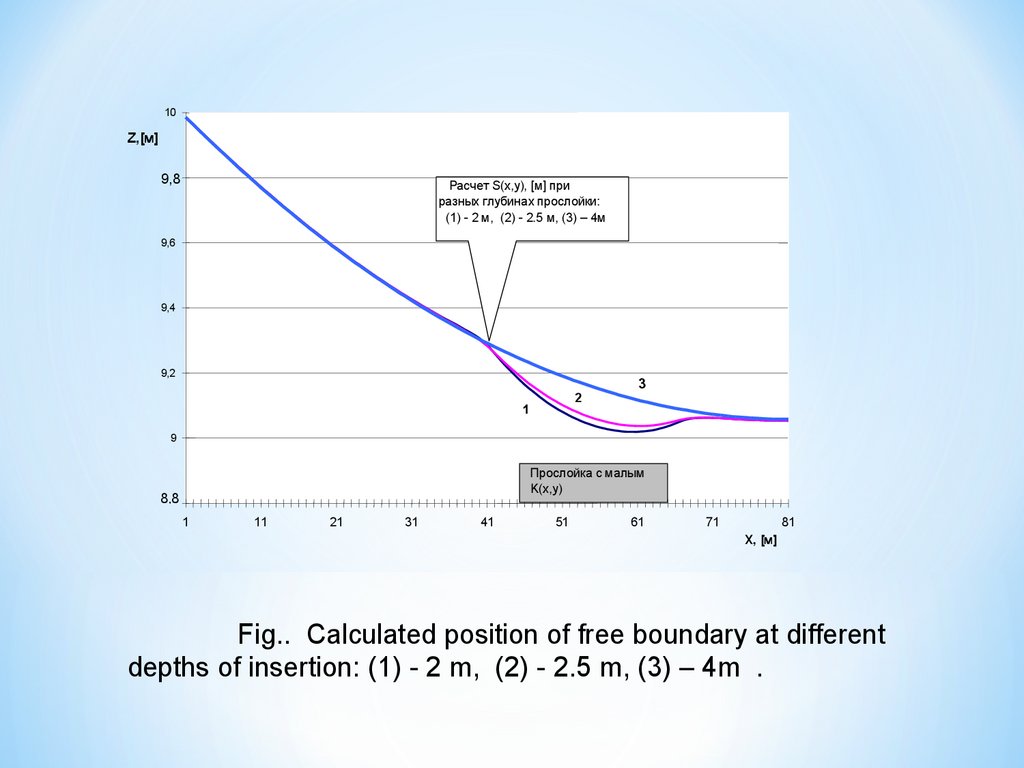
10Z,[м]
9,8
Расчет S(x,у), [м] при
разных глубинах прослойки:
(1) - 2 м, (2) - 2.5 м, (3) – 4м
9,6
9,4
9,2
2
1
3
9
Прослойка с малым
K(x,y)
8,8
1
11
21
31
41
51
61
71
81
X, [м]
Fig.. Calculated position of free boundary at different
depths of insertion: (1) - 2 m, (2) - 2.5 m, (3) – 4m .




















































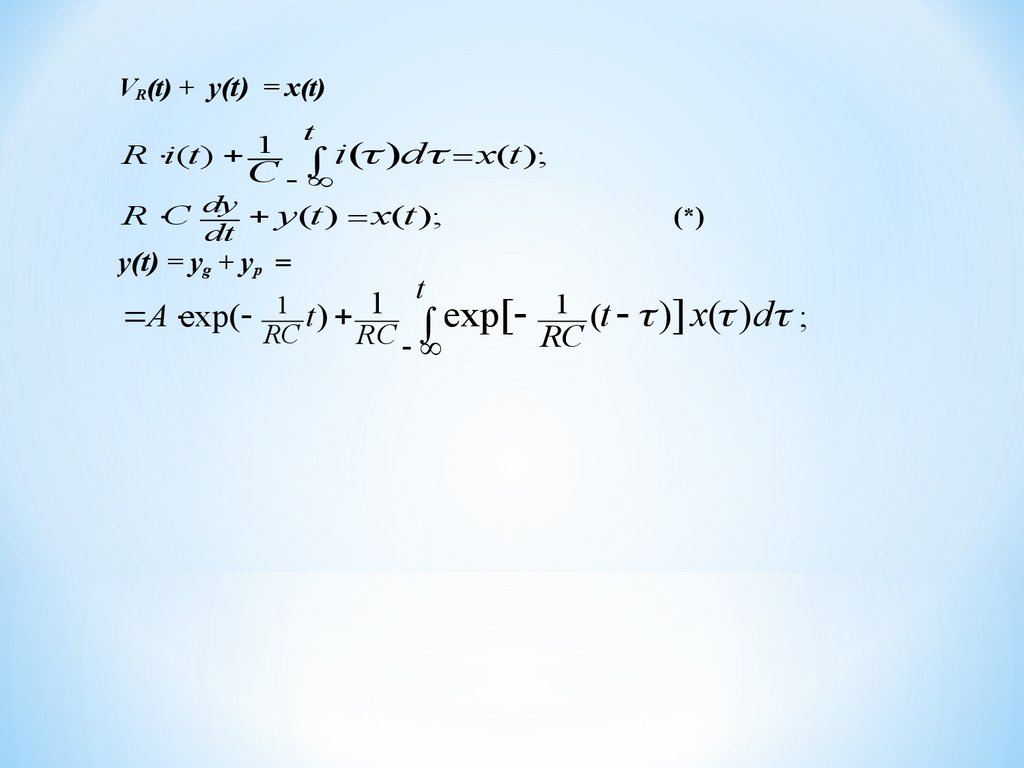







 Математика
Математика








