7кл _Рациональные числа

1.

Пусть каждый день и каждый час
Вам новое добудет.
Пусть добрым будет ум у вас,
А сердце умным будет.
С. Маршак

2.

09.09.2024
Алгебра, 7 класс

3. Зарождение алгебры

789-ок.850г.
Слово «алгебра» возникло после
появления трактата хорезмского
математика и астронома Мухаммеда
бен Муса аль-Хорезми.

4.

Наследие Аль-Хорезми и
сегодня остается
актуальным
Математик, астроном,
географ, историк
Мухаммад аль-Хорезми
жил и творил в конце
VIII-первой половине IX
веков.
Среди ученых того периода, ясно
сознававших прикладное значение науки,
Мухаммад аль-Хорезми занимал ведущее
место. Он был признан и современниками, и
потомками как выдающийся ученый.

5.

Его трактат по арифметике, основанный на
индийских числах, стал фундаментом системы
десятичных числовых позиций, которыми мы
пользуемся сегодня и которые нашли
применение в Европе. А имя ученого «АльХорезми» вошло в науку и увековечено в
термине "Алгоритм".
К сожалению, о жизни великого ученого, чьи
труды легли в основу многих
фундаментальных наук, о жизни "самого
выдающегося математика своего времени, а
если учесть атмосферу и обстоятельства того
периода, быть может, самого выдающегося
математика всех эпох" (Ж.Сартон), не
сохранилось почти никаких материалов.

6.

До XVIвека изложение алгебры велось
словесно.
Знаки « + » и « − » впервые встречаются
у немецких алгебраистов XVI века.
Знак « :+ » введен в XVII веке.
Франсуа Виет (1540-1603) –
французский математик –
ввел систему алгебраических
символов, стал числа
обозначать буквами,
разработал основы
элементарной алгебры.

7.

Различие между арифметикой
и алгеброй состоит в том, что
первая наука исследует свойства
данных, определенных величин,
между тем как алгебра
занимается изучением общих
величин, значение которых
может быть произвольное.

8.

09.09.2024
Алгебра, 7 класс

9.

Для счета предметов используются числа,
которые называются натуральными. Для
обозначения
множества
натуральных
чисел употребляется буква N - первая
буква латинского слова Naturalis
«естественный», «натуральный»
N - натуральные
1, 2, 3, 4, 5, …

10.

Натуральные
числа,
числа
им
противоположные и число нуль, образуют
множество
целых
чисел,
которое
обозначается Z - первой буквой немецкого
слова Zahl - «число».
…, -3, -2, -1, 0,
Z - целые
1, 2, 3, …

11.

Множество
чисел,
которое
можно
m
представить в виде
, называется
n
множеством рациональных чисел
и
обозначается буквой Q - первой буквой
французского
слова
Quotient
«отношение». Есть также версия, что
название рациональных чисел
латинским словом ratio – разум.
связано
с
…, -3, -2, -1, 0, 1, 2, 3, …
Q - рациональные
+ дроби

12.

Отношения между множествами
натуральных, целых и рациональных чисел
наглядно демонстрирует геометрическая
иллюстрация – круги Эйлера.
N Z Q

13.

Новые обозначения:
Математический символ ⊂ называют
знаком включения (одно множество
содержится в другом).
N - часть множества Z
можно писать N ⊂ Z,
Z - часть множества Q
можно писать Z ⊂ Q

14.

Новые обозначения:
Множества обозначают большими буквами,
элементы множества - маленькими буквами.
x не принадлежит множеству X
можно писать x ∉ X
A не является частью (подмножеством) B
можно писать A B.

15.

N Z Q
Число 5 ─ ?
N, Z, Q
Число ─ 7 ─ ?
Z, Q
Число ─ 6,7 ─ ?
Q
7
Число
─?
12
Q

16.

Перевести обыкновенную дробь в
десятичную:
Если в знаменателе стоят 2, 5, их
произведение или произведение
комбинаций этих чисел – всегда
КОНЕЧНАЯ ДЕСЯТИЧНАЯ ДРОБЬ!
3 3 25
75
4 4 25 100
= 0,75 – конечная десятичная дробь

17.

Существуют рациональные числа,
которые нельзя записать в виде
конечной десятичной дроби,
Например:
1
3 5
, , и т.д.
7 11 19

18.

Перевести обыкновенную дробь в
десятичную:
3
= 0,272727272727272727… 11
бесконечная
периодическая
десятичная дробь
Для краткости написания –
ПЕРИОД (круглые скобки)
0,272727272727272727…= 0,(27)

19.

Прочитайте дроби:
1) 0,(2)
4) -3,0(3)
2) 2,(21)
5) -0,1(6)
3) 1,(1)
6) 12,45(7)
чисто периодические
смешанные периодические

20.

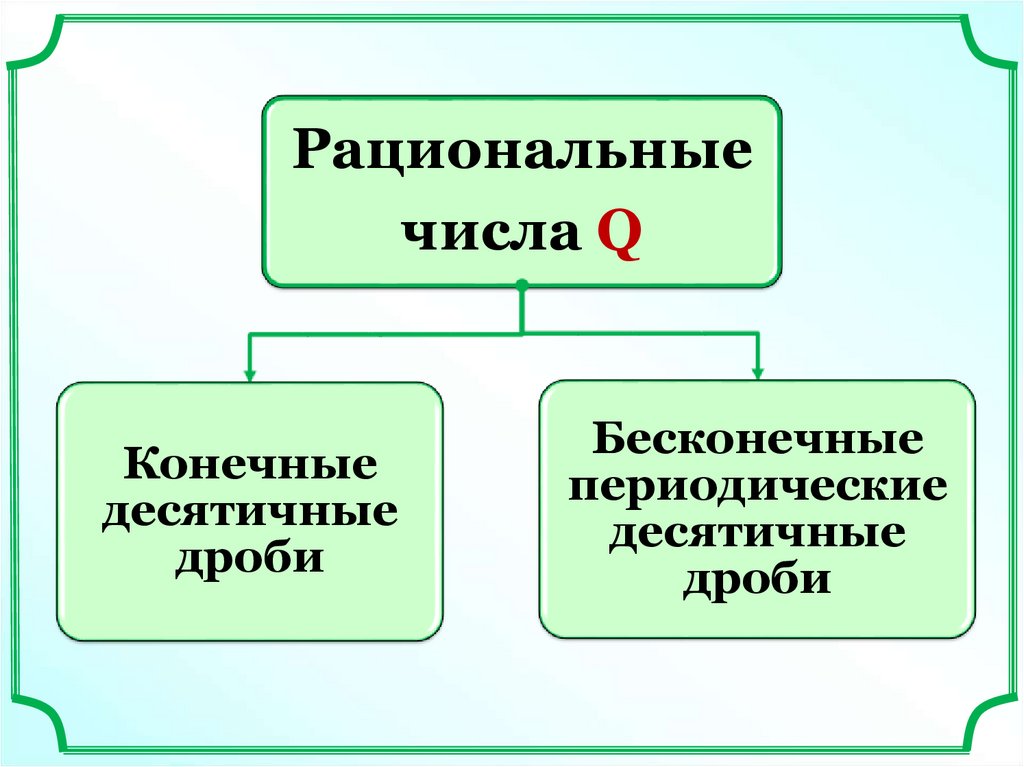
Рациональные
числа Q
Конечные
десятичные
дроби
Бесконечные
периодические
десятичные
дроби

21.

Любое рациональное число
можно записать в виде
бесконечной десятичной
периодической дроби?
5 = 5,000… = 5,(0)
-8,37 = −8,37000… = −8,37(0)
Дроби - ?

22.

Алгоритмы перевода рациональных
чисел в бесконечную десятичную
периодическую дробь
3
= 0,375 = 0,375(0)
8
3
= 0,272727… = 0,(27)
11
Делим числитель на
знаменатель

23.

Бесконечные десятичные
непериодические дроби представляют
иррациональные числа.
0,120120012000120000…
-3,272277222777…
3,1415926...

24.

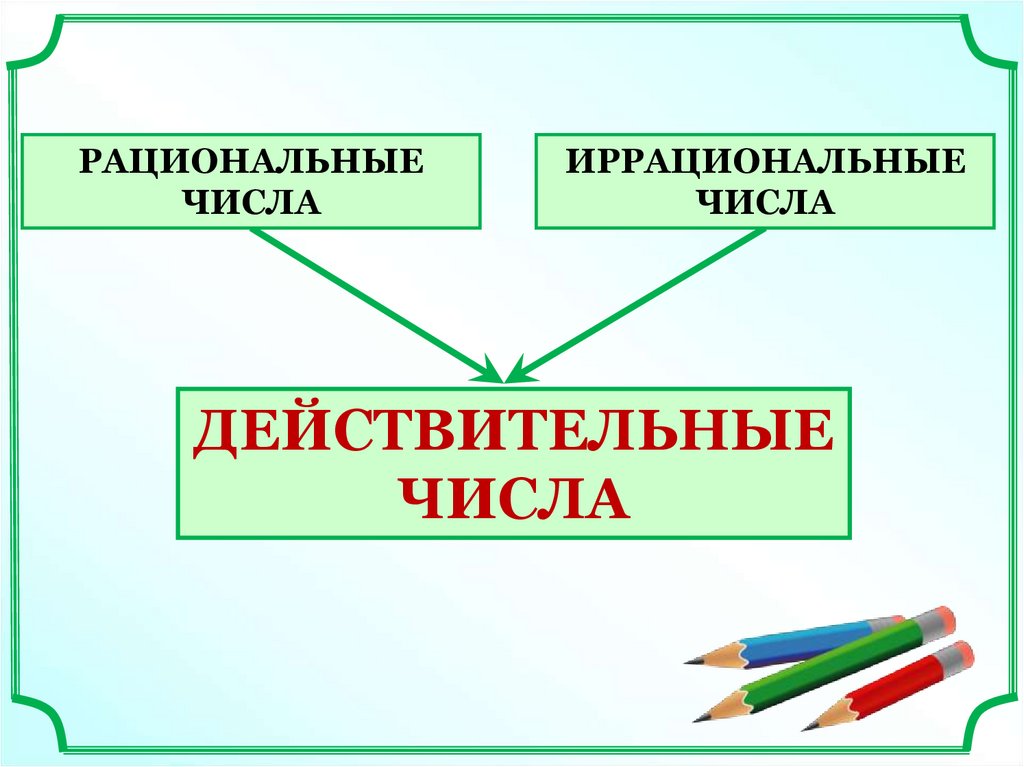
РАЦИОНАЛЬНЫЕ
ЧИСЛА
ИРРАЦИОНАЛЬНЫЕ
ЧИСЛА
ДЕЙСТВИТЕЛЬНЫЕ
ЧИСЛА

25.

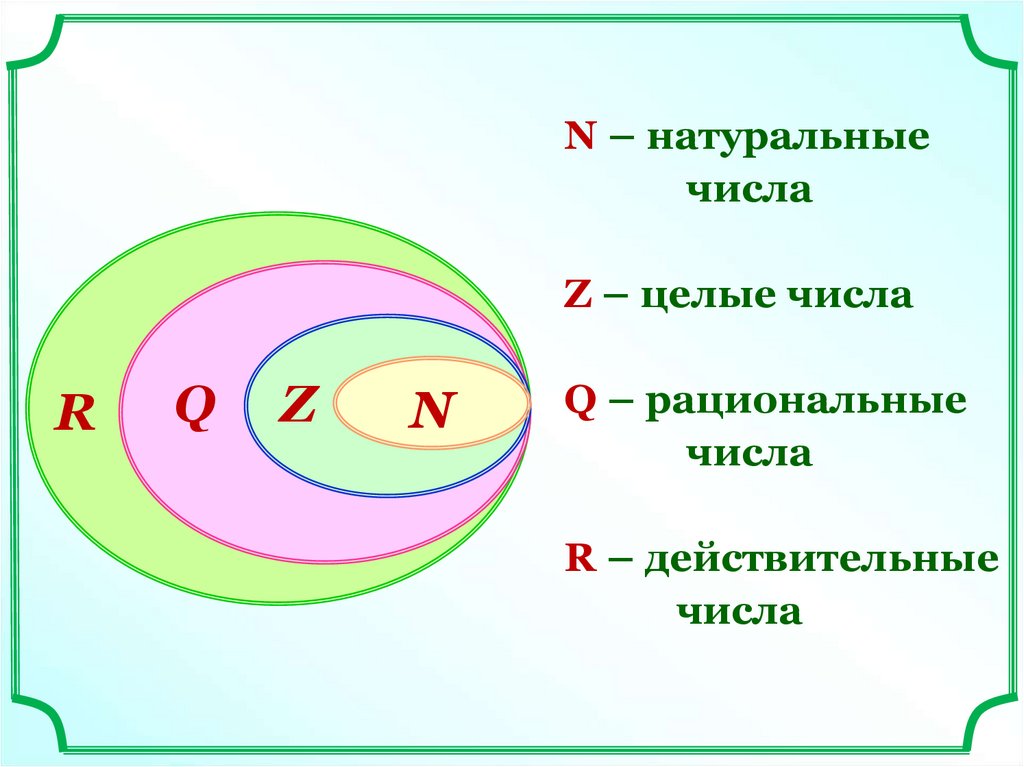
N – натуральные
числа
Z – целые числа
R
R
Q
Q
Z
N
Q – рациональные
числа
R – действительные
числа