Целые и рациональные числа. Действительные числа. Приближение действительных чисел конечными десятичными дробями

1.

Математика
Тема «Целые и рациональные числа.
Действительные числа.
Приближение действительных чисел конечными
десятичными дробями.»
Автор презентации:Дегтярева Мария Владиславовна
Дата создания презентации:02.10.2018

2.

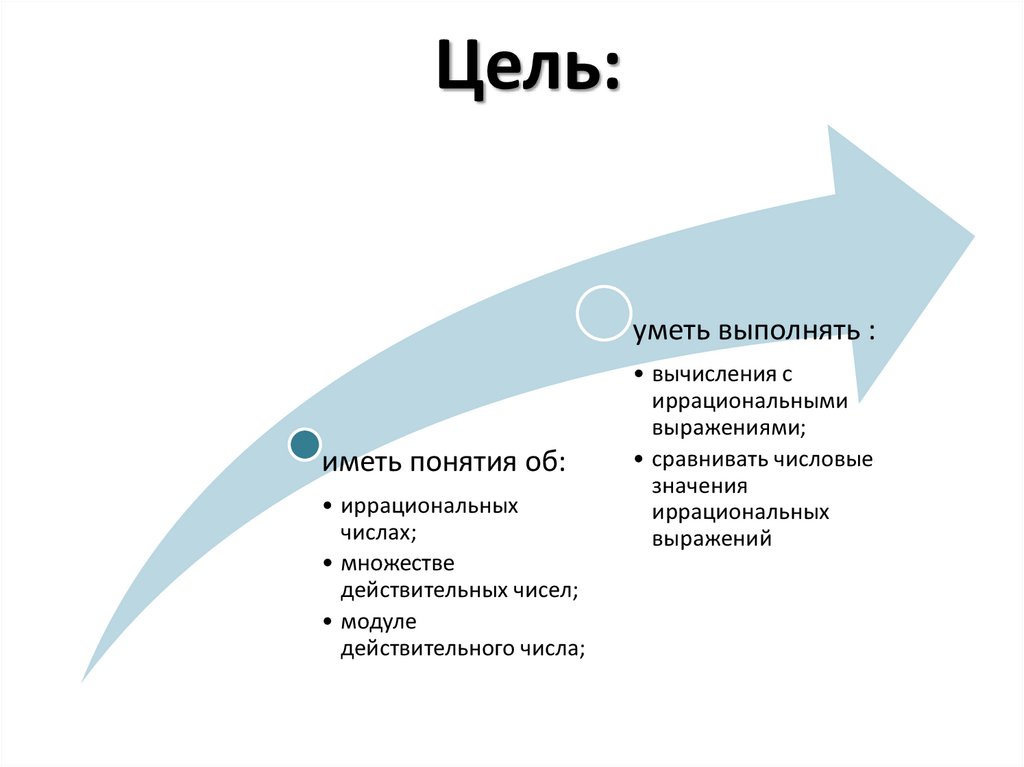
Цель:
уметь выполнять :
иметь понятия об:
• иррациональных
числах;
• множестве
действительных чисел;
• модуле
действительного числа;
• вычисления с
иррациональными
выражениями;
• сравнивать числовые
значения
иррациональных
выражений

3.

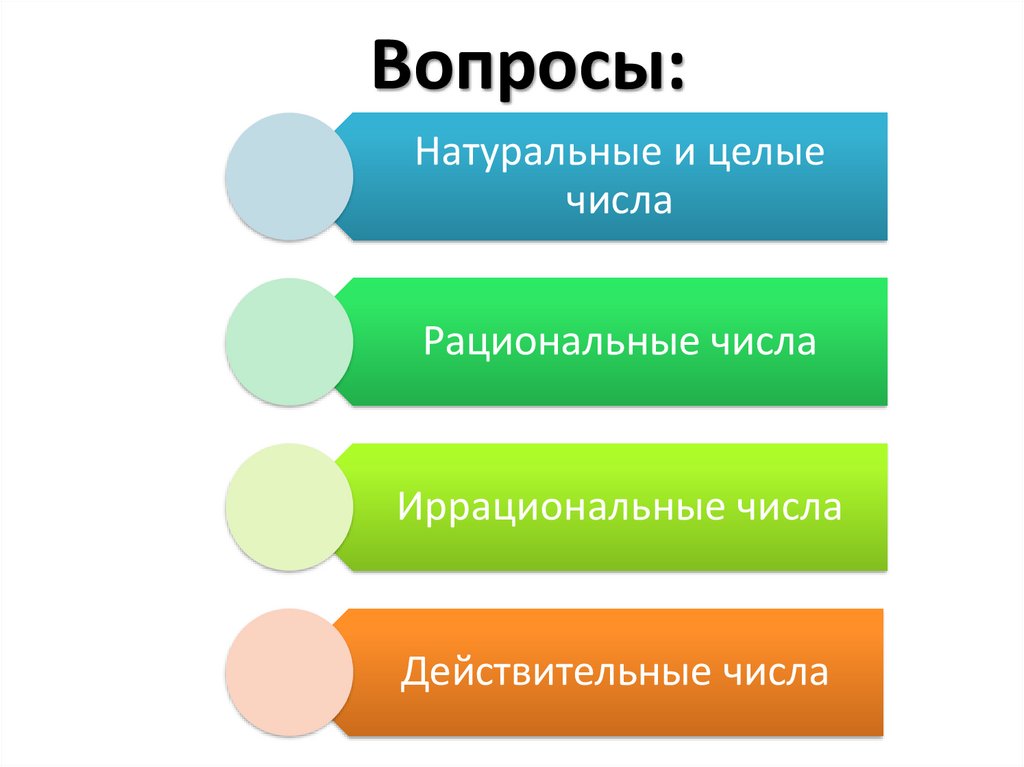
Вопросы:
Натуральные и целые
числа
Рациональные числа
Иррациональные числа
Действительные числа

4.

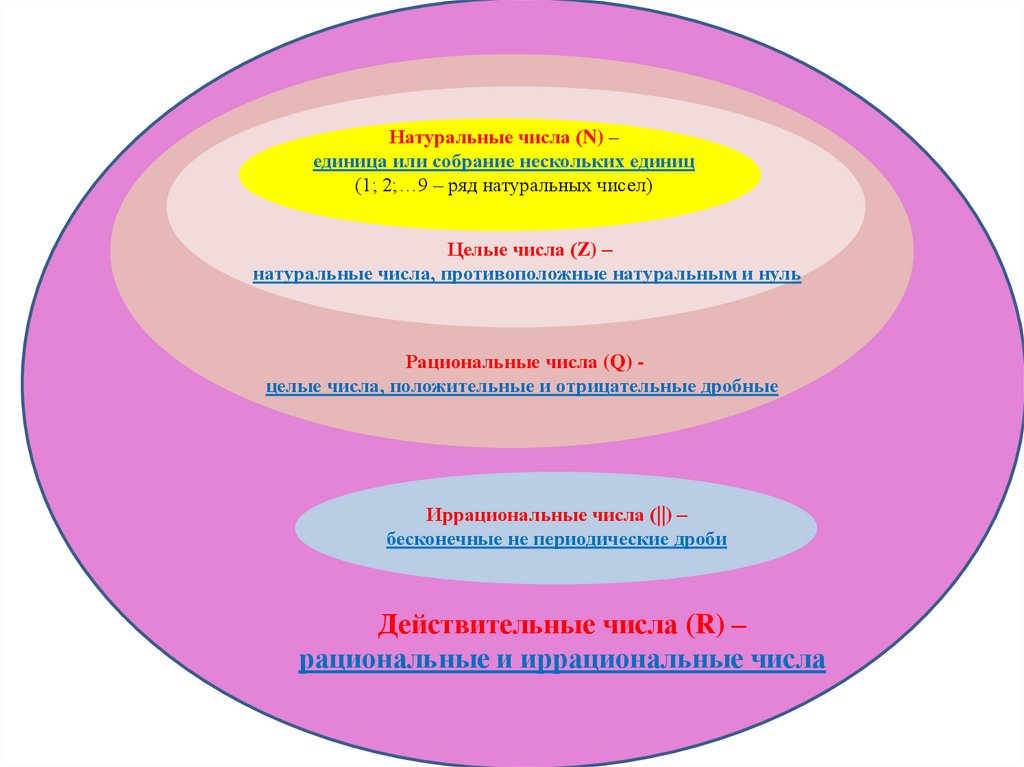
Натуральные числа (N) –
единица или собрание нескольких единиц
(1; 2;…9 – ряд натуральных чисел)
Целые числа (Z) –
натуральные числа, противоположные натуральным и нуль
Рациональные числа (Q) целые числа, положительные и отрицательные дробные
Иррациональные числа (||) –
бесконечные не периодические дроби
Действительные числа (R) –
рациональные и иррациональные числа

5.

Натуральные числа (N)
Простые -
делятся на себя и на единицу
Составные – остальные.
Четные делящиеся на 2 и число 0. (2п)
Нечетные – остальные (2п+1; 2п-1).
Любое составное число можно разложить на простые множители

6.

Простые числа
Если натуральное число имеет только два делителя –
само себя и 1, то его называют простым числом.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,
61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191,
193, 197, 199, 211, 223, 227, 229, … – простые числа.
Теорема 1. Любое, натуральное число а > 1 имеет хотя бы один
простой делитель.
Теорема 2. Множество простых чисел бесконечно.
Теорема 3. Расстояние между двумя соседними простыми числами
может быть больше любого наперед заданного натурального
числа.

7.

Cоставные числа
Если натуральное число имеет более двух делителей,
то его называют составным числом.
4, 6, 8, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28,
30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50,
51, 52, 54, 55, 56, 57, 58, 60, 62, 63, … – составные числа
1 не является ни простым, ни составным числом.
Основная теорема арифметики. Любое натуральное число (кроме 1)
либо является простым, либо его можно разложить на простые
множители.
Примеры: 210 = 2 ∙ 3 ∙ 5 ∙ 7;
56 = 2 ∙ 2 ∙ 2 ∙ 7.

8.

Делимость натуральных чисел
Для двух натуральных чисел a и b если
существует натуральное число q такое, что
выполняется равенство a = bq, то говорят, что
число a делится на число b.
a:b=q
…
a – делимое
b – делитель
q – частное
a b – а делится на b без остатка

9.

Свойства делимости
1о Если a ⋮ с и с ⋮ b, то a ⋮ b.
Пример: 144 ⋮ 12 и 12 ⋮ 3, то 144 ⋮ 3.
2о Если a ⋮ b и с ⋮ b, то (a + c) ⋮ b.
Пример: 84 ⋮ 3 и 63 ⋮ 3, то (84 + 63) ⋮ 3.
3о Если a ⋮ b и с не делится на b, то (a + c) не
делится на b.
Пример: 48 ⋮ 3 и 52 не делится на 3,
то (48 + 52) не делится на 3.

10.

Свойства делимости
4о Если a ⋮ b и (a + c) ⋮ b, то c ⋮ b.
Пример: 48 ⋮ 3 и (48 + 57) ⋮ 3, то 57 ⋮ 3.
5о Если a ⋮ b и с ⋮ d, то ac ⋮ bd.
Пример: 81 ⋮ 3 и 56 ⋮ 4, то (81∙56) ⋮ (3∙4).
6о Если a ⋮ b и с N, то ac ⋮ bc, и наоборот.
Пример: 48 ⋮ 12 и 11 N, то
(48∙11) ⋮ (12∙11), и обратно.

11.

Свойства делимости
7о Если a ⋮ b и с N, то ac ⋮ b.
Пример: 48 ⋮ 3 и 13 N, то (48∙13) ⋮ 3.
8о Если a ⋮ b и с ⋮ b, то для любых n, k N
следует (an + ck) ⋮ b.
Пример: 81 ⋮ 9 и 54 ⋮ 9, то (81∙17 + 54∙28) ⋮ 9.
9о Среди n последовательных натуральных
чисел одно и только одно делится на n.
Пример: среди трех последовательных
натур. чисел 111, 112, 113 только одно
делится на 3. (111 ⋮ 3)

12.

Признаки делимости
Для того, чтобы натуральное число делилось
На 2: необходимо и достаточно, чтобы последняя
цифра числа делилась на 2.
Пример: 56738 ⋮ 2 т.к. 8 ⋮ 2.
На 5: необходимо и достаточно, чтобы последняя
цифра числа делилась на 5 (0 или 5).
Пример: 56735 ⋮ 5 т.к. 5 ⋮ 5.
На 10: необходимо и достаточно, чтобы цифра
единиц была 0.
Пример: 56730 ⋮ 10.

13.

Признаки делимости
Для того, чтобы натуральное число делилось
На 4: необходимо и достаточно, чтобы делилось на
4 число, образованное двумя последними цифрами.
Пример: 56736 ⋮ 4, т.к. 36 ⋮ 4.
На 25: необходимо и достаточно, чтобы делилось на
25 число, образованное двумя последними цифрами.
Пример: 56775 ⋮ 25, т.к. 75 ⋮ 25.
На 8: необходимо и достаточно, чтобы делилось на 8
число, образованное тремя последними цифрами.
Пример: 56552 ⋮ 8, т.к. 552 ⋮ 8.

14.

Признаки делимости
Для того, чтобы натуральное число делилось
На 125: необходимо и достаточно, чтобы делилось
на 125 число, образованное тремя последними
цифрами.
Пример: 56375 ⋮ 125, т.к. 375 ⋮ 125.
На 3: необходимо и достаточно, чтобы сумма его
цифр делилась на 3.
Пример: 56742 ⋮ 3, т.к. (5+6+7+4+2) ⋮ 3.
На 9: необходимо и достаточно, чтобы сумма его
цифр делилась на 9.
Пример: 56545 ⋮ 9, т.к. (5+6+7+4+5) ⋮ 9.

15.

Признаки делимости
Для того чтобы натуральное число делилось
На 11: необходимо и достаточно, чтобы сумма его
цифр, взятых со знаком «+», стоящих на нечетных
местах, и сумма цифр, взятых со знаком «–»,
стоящих на четных местах, делилась на 11.
Пример: 8637519 ⋮ 11, т.к. (9-1+5-7+3-6+8) ⋮ 11.
На 7 (на 13): необходимо и достаточно, чтобы сумма
чисел, образующих грани, взятых со знаком «+» для
нечетных граней и со знаком «–» для четных граней,
делилась на 7 (на 13).
Пример: 254 390 815 ⋮ 7, т.к. (815-390+254) ⋮ 7.

16.

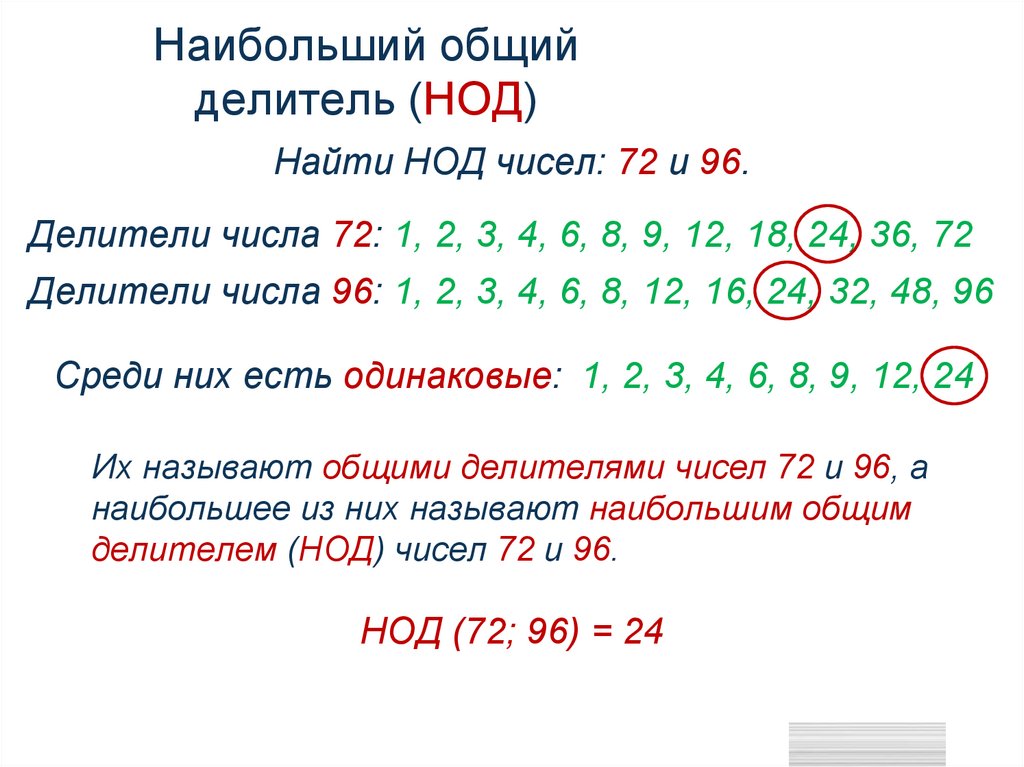
Наибольший общий
делитель (НОД)
Найти НОД чисел: 72 и 96.
Делители числа 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Делители числа 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Среди них есть одинаковые: 1, 2, 3, 4, 6, 8, 9, 12, 24
Их называют общими делителями чисел 72 и 96, а
наибольшее из них называют наибольшим общим
делителем (НОД) чисел 72 и 96.
НОД (72; 96) = 24

17.

Наибольший общий
делитель (НОД)
Два натуральных числа a и b называют взаимно
простыми числами, если у них нет общих делителей,
отличных от 1, т.е. НОД(a, b) = 1.
Пример: 35 и 36 взаимно простые числа,
т.к. НОД (35; 36) = 1.

18.

Наименьшее общее
кратное (НОК)
Найти НОК чисел: 12 и 18.
Кратные числа 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, …
Кратные числа 18: 18, 36, 54, 72, 90, 108, 126, 144, …
Среди них есть одинаковые: 36, 72, 108, 144, …
Их называют общими кратными чисел 12 и 18, а
наименьшее из них называют наименьшим общим
кратным (НОК) чисел 12 и 18.
НОК (12; 18) = 36
Автор: Семёнова Елена Юрьевна

19.

Разложение на
простые множители
7056 2 НОД (3780; 7056)=
= 22 ∙ 32 ∙ 7 = 252
3528 2
1764 2
882 2 НОК (3780; 7056)=
4 ∙ 33 ∙ 5 ∙ 72 =
=
2
441 3
= 105840
147 3
49 7
7 7
1
3780 = 22 ∙ 33 ∙ 5 ∙ 7
7056 = 24 ∙ 32 ∙ 72
3780 2
1890 2
945 3
315 3
105 3
35 5
7 7
1

20.

• Задание: разложить на простые множители числа; 1260; 248; 4725
• Найти НОК и НОД чисел (54; 72; ) ;(96; 124)(125; 325); (34; 68)

21.

Натуральные
и целые числа
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … –
ряд натуральных чисел N или (Z+)
-1, -2, -3, -4, -5, -6, -7, -8, -9, -10, -11, … –
ряд противоположных натуральным чисел Z–
…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … –
ряд целых чисел Z (Z+ и Z– и 0)

22.

Рациональные
числа
m
Рациональные числа – это числа вида
,
n
где m – целое число, а n – натуральное.
Q - множество рациональных чисел.
Любое рациональное число можно записать в виде
конечной десятичной дроби или в виде бесконечной
десятичной периодической дроби.
5
Примеры:
= 0,17(857142);
28
2
= 0,(285714);
7
6 = 6,000… = 6,(0); 7,432 = 7,432000… = 7,432(0).

23.

Рациональные
числа
Верно и обратное утверждение:
Любую бесконечную десятичную периодическую дробь
можно представить в виде обыкновенной дроби.
1
Примеры: 0,3333… = 0,(3) =
;
3
7
0,3181818… = 0,3(18) =
.
22

24.

Рациональные
числа
Записать в виде обыкновенной дроби бесконечную
десятичную периодическую дробь :
Пример (1 способ):
Пусть х = 1,(23) = 1,23232323…
Умножим х на 100, чтобы запятая переместилась
вправо на один период:
– 100х = 123,232323…
х = 1,232323…
100х – х = 122,000000…
Т.е. 99х = 122, откуда х =
122
99

25.

Рациональные
числа
Записать в виде обыкновенной дроби бесконечную
десятичную периодическую дробь :
Пример (2 способ):
Пусть 1,(23) = 1,232323… = 1 + 0,23 + 0,0023 + 0,000023 + …
Рассмотрим эту сумму 1 и суммы бесконечно убывающей
геометрической прогрессии: S = 1 + S1, где S1 = b1 / (1 – q) –
формула суммы бесконечно убывающей прогрессии со
знаменателем q = 0,01, и первым членом b1 = 0,23:
23
0,23
S1 =
=
99
1 – 0,01
23 122
S=1+
=
99
99

26.

Правило перевода смешанной периодической
дроби в обыкновенную
Чтобы обратить чистую периодическую дробь в обыкновенную,
нужно ее период сделать числителем, а в знаменателе записать
цифру 9 столько раз, сколько цифр в периоде.
23
1, 23 1
99
Чтобы обратить смешанную периодическую дробь в
обыкновенную, нужно из числа, стоящего после запятой до
второго периода, вычесть число, стоящее после запятой до
первого периода, и эту разность сделать числителем, а в
знаменатель записать цифру 9 столько раз, сколько цифр в
периоде, со столькими нулями справа, сколько цифр между
запятой и первым периодом.
437 4
433
1,4 37 1
990
1
990

27.

1. Необходимость дальнейшего расширения множества
чисел связана в основном с двумя причинами:
1)Рациональных чисел недостаточно для выражения
результатов измерений (длина диагонали квадрата со стороной 1
2) Такие числовые выражения не являются рациональными числами
3; 7;0,123456...;3 7; ; 5,24680...
иррациональным числом называется бесконечная
десятичная непериодическая дробь

28.

Иррациональные
числа
Иррациональным числом называют бесконечную
десятичную непериодическую дробь.
Термины «рациональное число», «иррациональное число»
происходят от латинского слова ratio – разум
(буквальный перевод: «рациональное число – разумное
число», «иррациональное число – неразумное число»).
Примеры:
0,1234567891011121314…
π ≈ 3,1415926535897932…
е ≈ 2,7182818284590452…
√11 ≈ 3,31662479035539…

29.

Объединение множества рациональных чисел и
множества иррациональных чисел
(бесконечных десятичных непериодических дробей)
даёт множество R действительных чисел
Действительным числом называется
бесконечная десятичная дробь, т.е. дробь вида
+ а0,а1а2а3… или - а0,а1а2а3… ,
Например:
где а0 - целое неотрицательное число,
а каждая из букв а1,а2,а3,… - одна из десяти цифр:
0,1,2,3,4,5,6,7,8,9
1) π = 3,1415… а0 = 3 а1=1 а2= 4 а3=1 а4=5 …
2)- √234 = - 15,297058… а0 = 15 а1=2 а2= 9 а3=7 а4=0 …
3)37,19 а0 = 37 а1=1 а2= 9 аn=0 при n≥3
Действительное число может быть
положительным, отрицательным или равным нулю.

30.

2. Арифметические операции над действительными числами
обычно заменяются операциями над их приближениями.
Вычислим сумму
2 3
с точностью до единицы:
2 3 1,4 1,7 3,1 3
с точностью до десятой:
2 1,4142135...
3 1,7320508...
2 3 1,41 1,73 3,14 3,1
с точностью до сотой:
2 3 1,414 1,732 3,146 3,15
Числа 3; 3,1; 3,15 и т.д. являются последовательными
приближениями значения суммы 2 3

31.

Множества чисел
N
Z
R
Q

32.

3. Все основные действия над рациональными числами
сохраняются и для действительных чисел
Переместительный, сочетательный и распределительный
законы, правила сравнения, правила раскрытия скобок и т.д.
4. Модуль действительного числа х обозначается |х| и
определяется так же, как и модуль рационального числа:
х, если _ х 0,
х
х, если_ х 0.

33.

Выводы:
. Все основные
действия над
рациональными
числами
сохраняются и для
действительных
чисел

34.

Источники информации:
1)Презентация Учителя математики Пивоваренок Н.Н.
ГОУ Школа №247
2)
Учебник для 10 класс
Ш.А.Алимов, ю.м.колягин и др.
15 изд. М.: Просвещение, 2007