Похожие презентации:
Интегрирование по частям
1.
2.
Тема:«Интегрирование по
… »
частям
3.
Вычислите интегралln
xdx
4.
Интеграл в общем видеf
(
x
)
dx
dV
U U ( x); V V ( X )
U
функции, имеющие непрерывные производные
dx обязательно входит в dV
Постоянная интегрирования С присутствует VdU
5.
f(
x
)
dx
U dV
UV V dU
Формула интегрирования по частям
6.
U dV UV V dUf
(
x
)
dx
dV
V
dU
7.
8.
Таблица интегралов берущихсяпо частям
I тип
II тип
P x sin xdx
P x cos xdx
P x e dx
P x a dx
x
x
x ln x dx, 1
P x ln x dx
arcsin x
arccos
x
P
x
dx
arctgx
arcctgx
За u принимаются подчеркнутые функции, за dV вся
остальная часть подынтегрального выражения.
P(x) – многочлен.
9.
10.
U dV UV V dUВычислить интеграл
ln
xdx
11.
U dV UV V dUU ln x
dV dx
12.
U dV UV V dU1
dU dx
x
V x
13.
U dV UV V dU1
x ln x x dx
x
14.
U dV UV V dUx ln x dx
т1
15. Ответ :
x ln x x C16.
Вычислить интеграл(
3
x
4
)
sin
2
xdx
17.
UdV
UV
VdU
U 3x 4
dV sin 2xdx
18.
UdV
UV
VdU
dU 3dx
1
V cos 2 x
2
19.
UdV
UV
VdU
1
1
(3x 4) cos 2 x cos 2 x 3dx
2
2
20.
UdV
UV
VdU
1
3
(3x 4) cos 2 x cos 2 xdx
2
2
т2
21. Ответ :
13
3 x 4 cos 2 x sin 2 x C
2
4
22.
23.
24.
25.
Домашнее задание1. Выполнить № 4.7
2. Вычислите ниже приведенные интегралы
x
arctgxdx
(
x
3
)
3
dx
x
( x 7) sin xdx


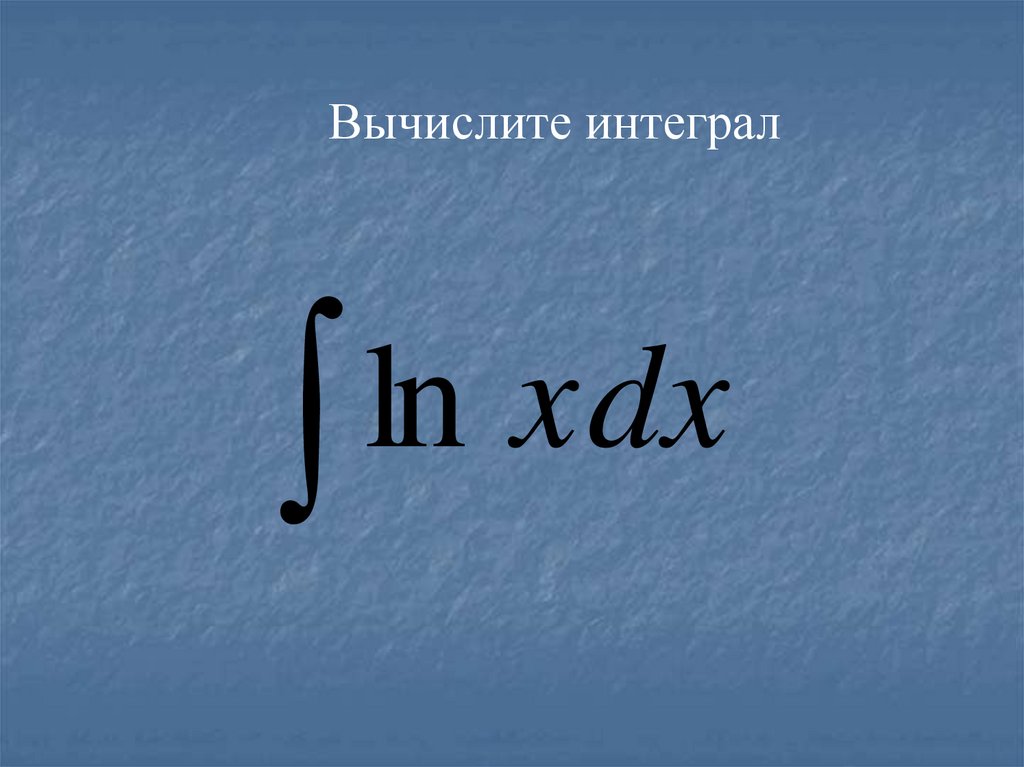

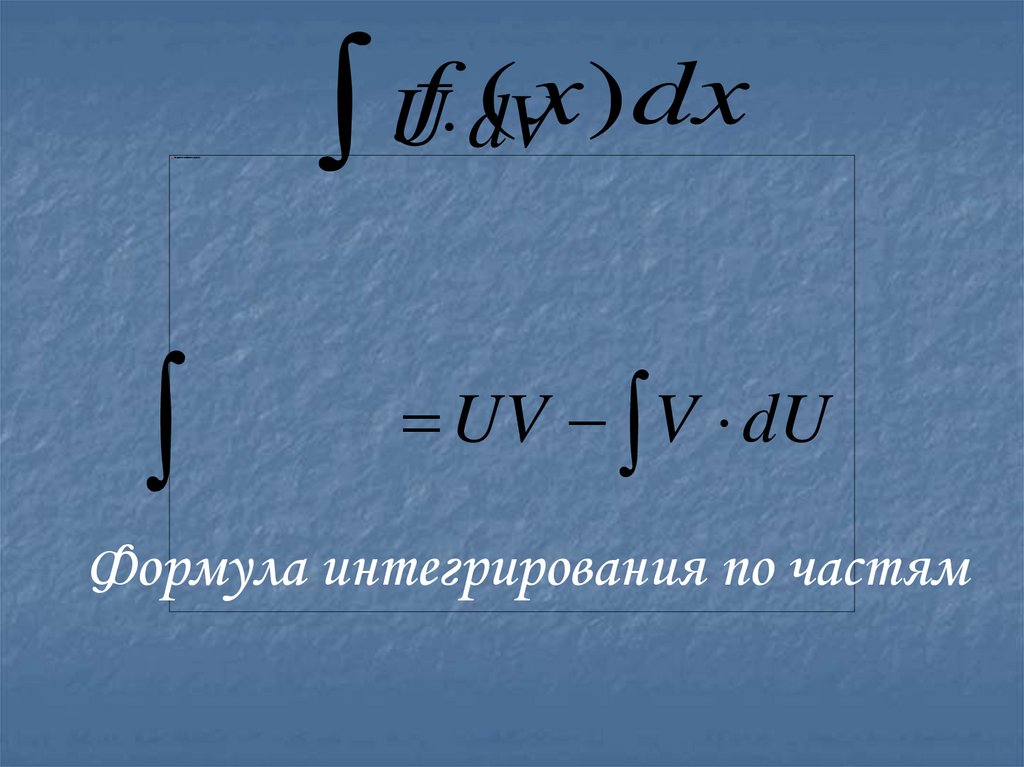
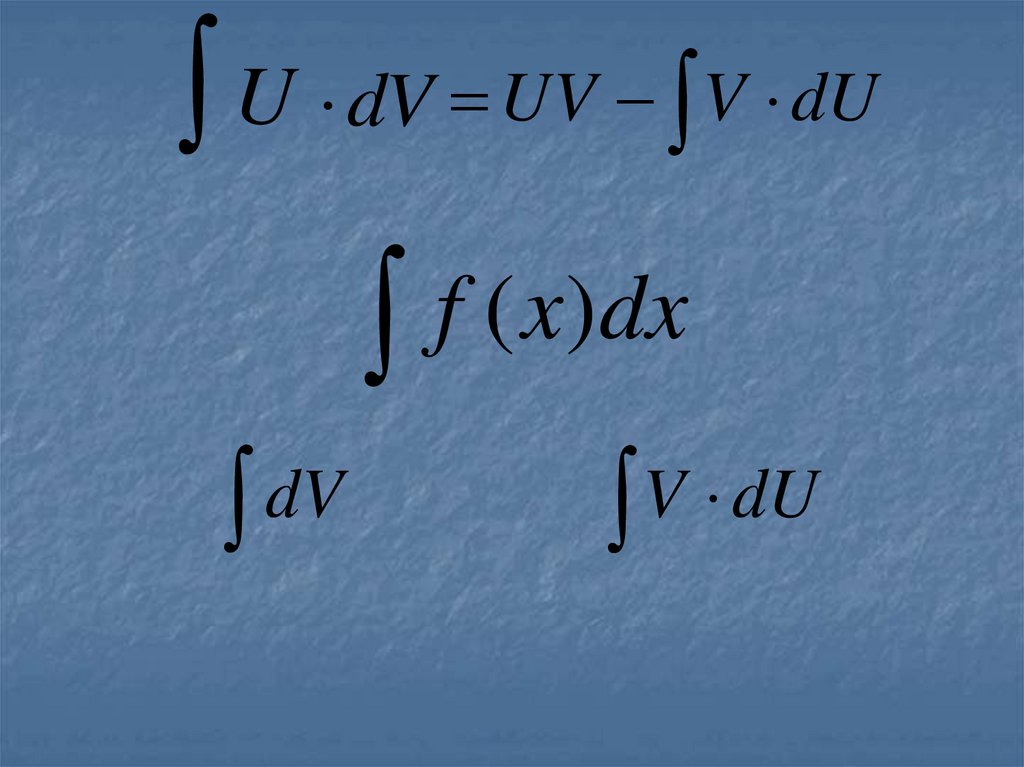




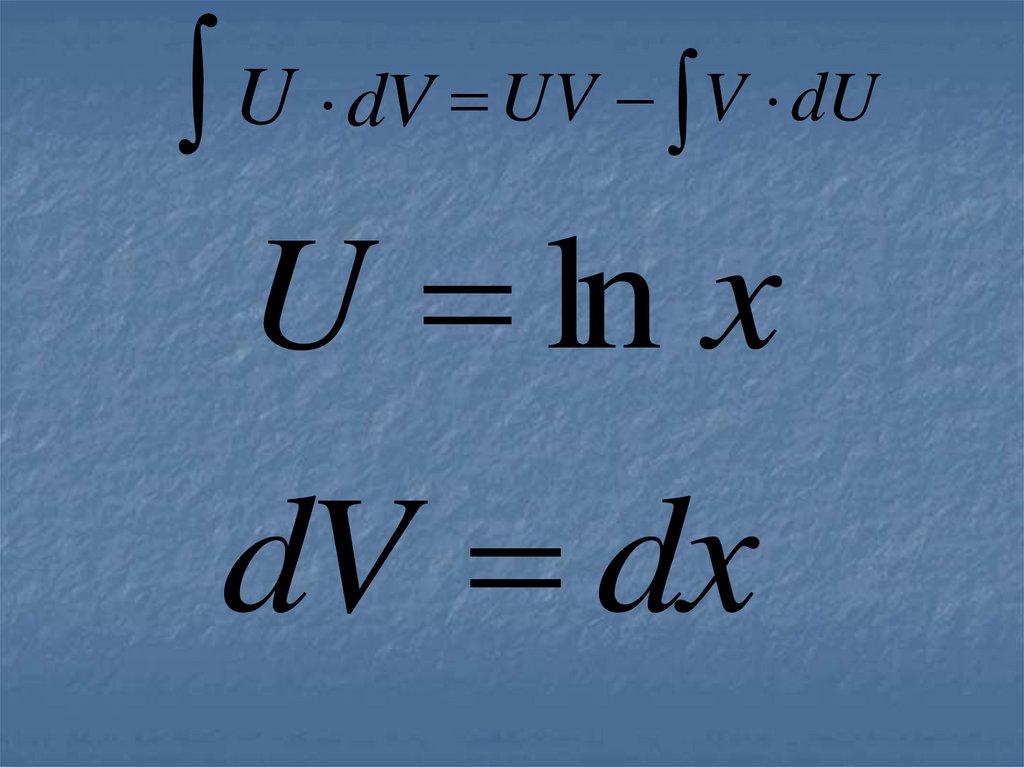
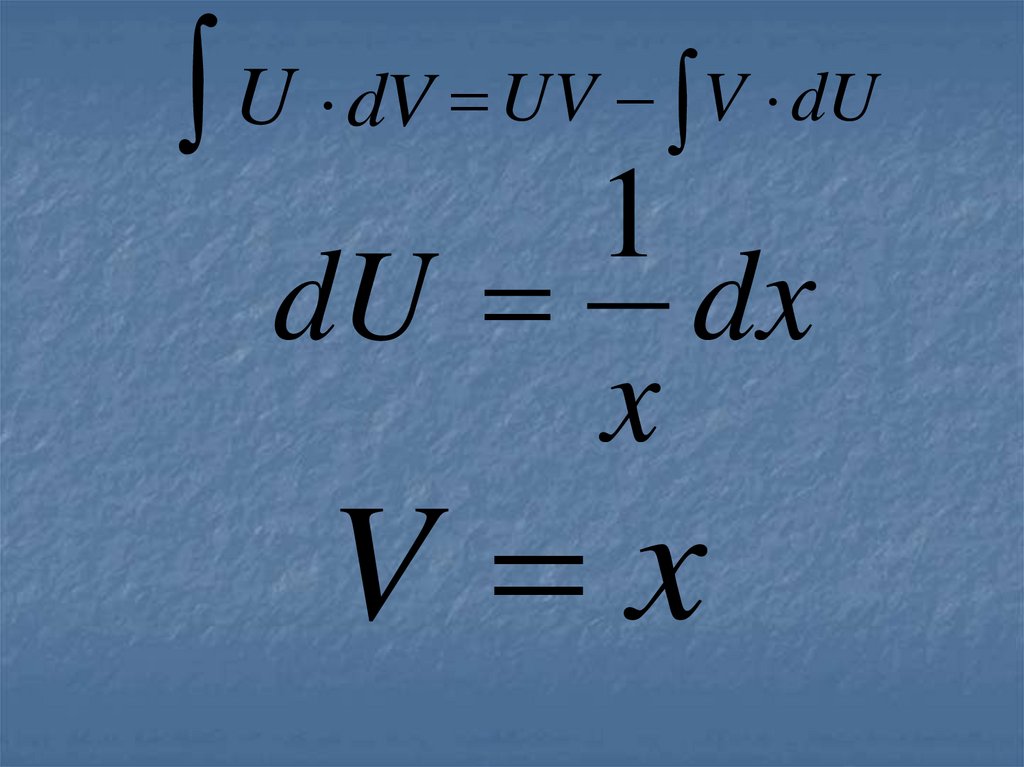
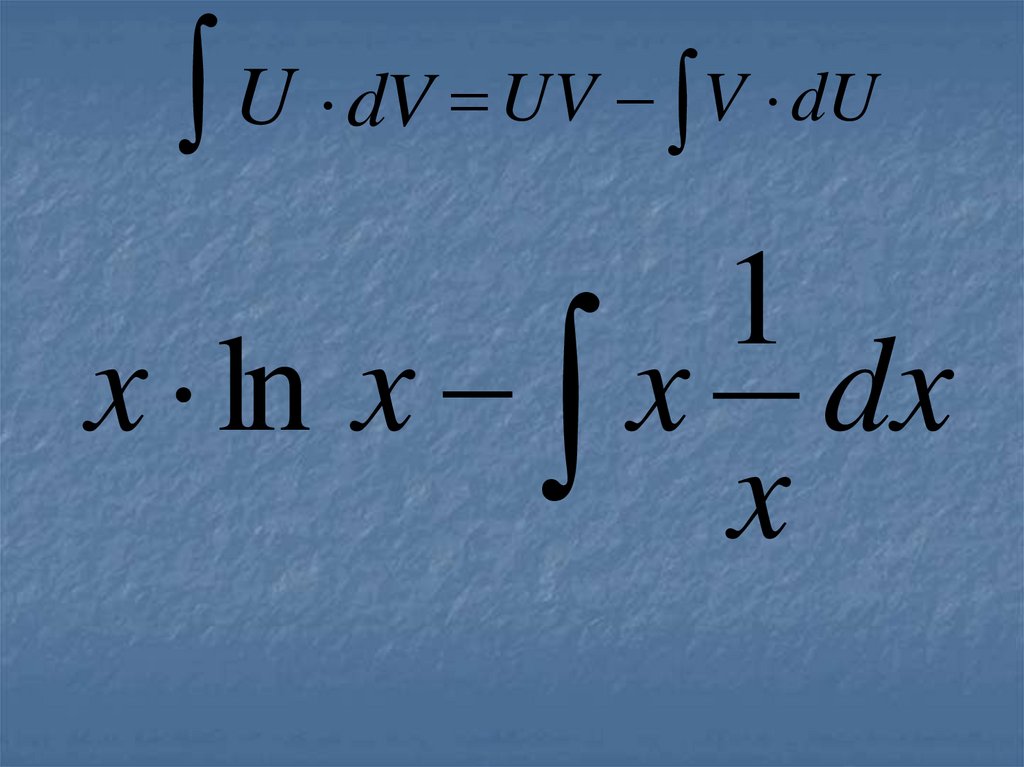
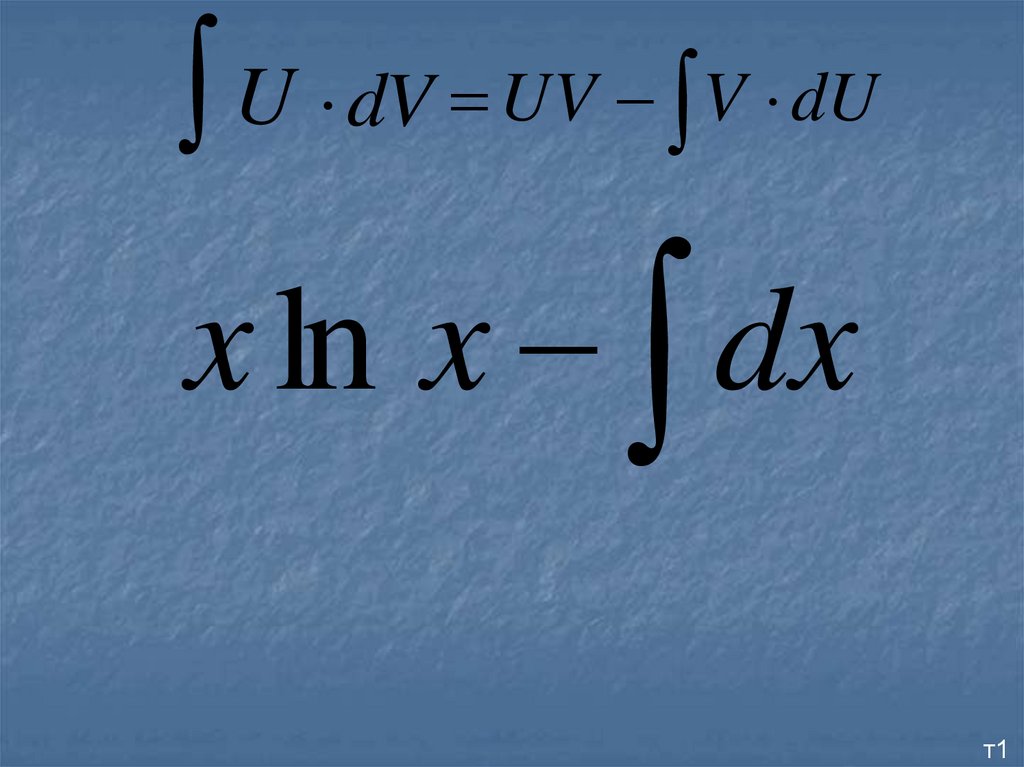
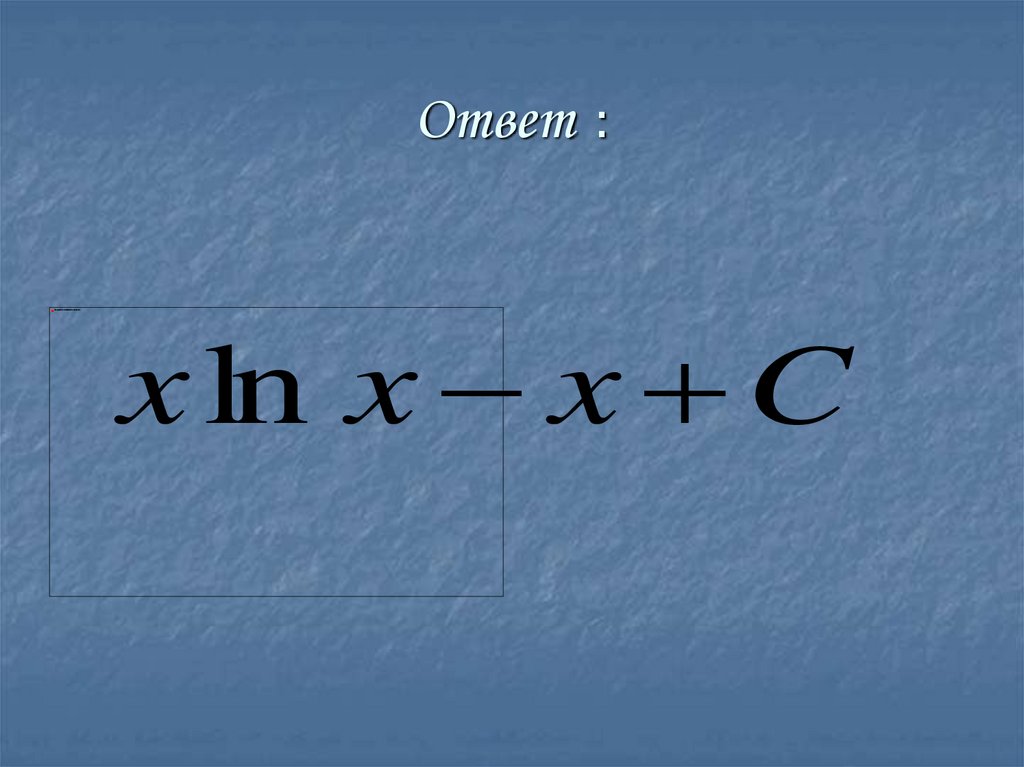

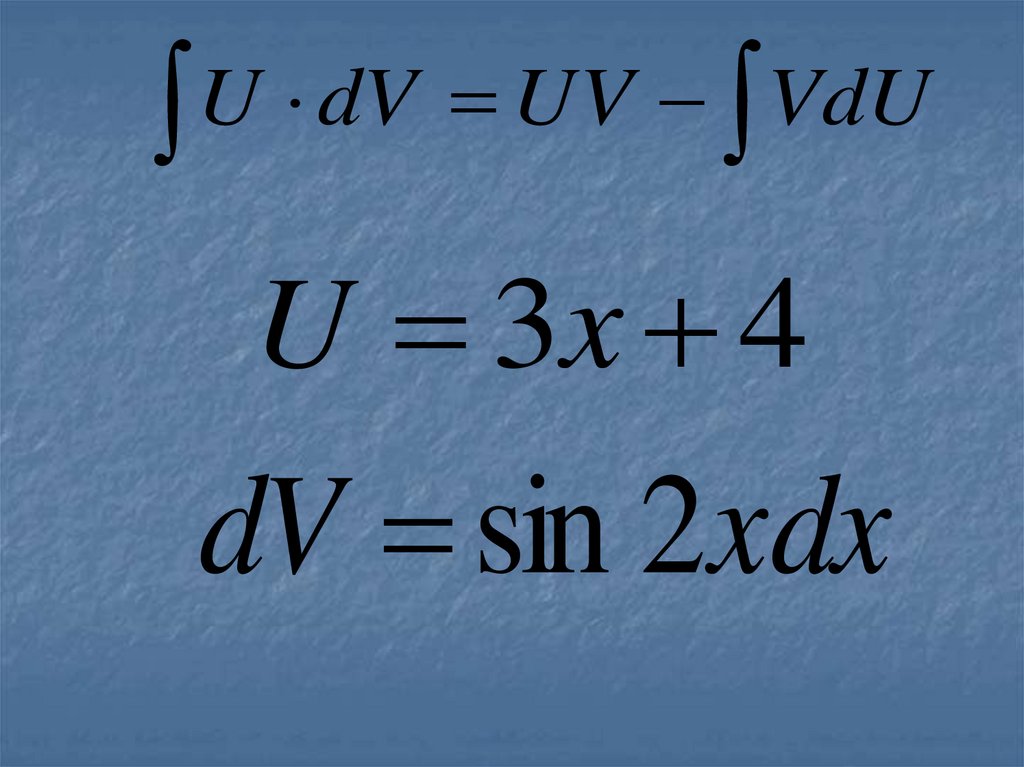
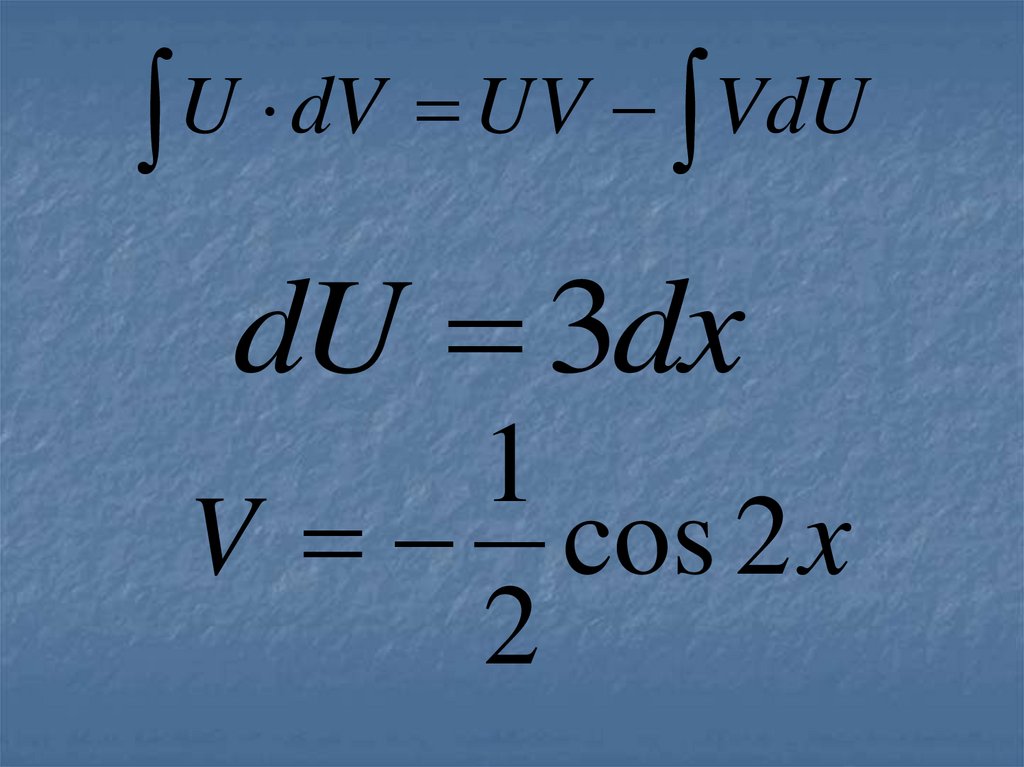
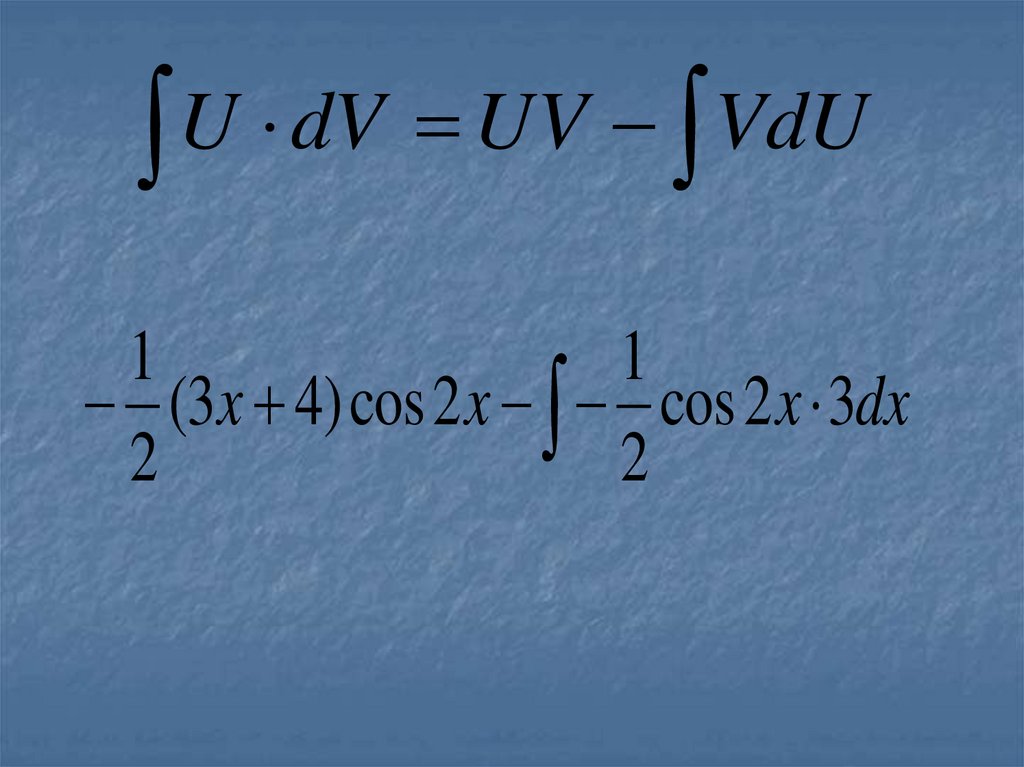
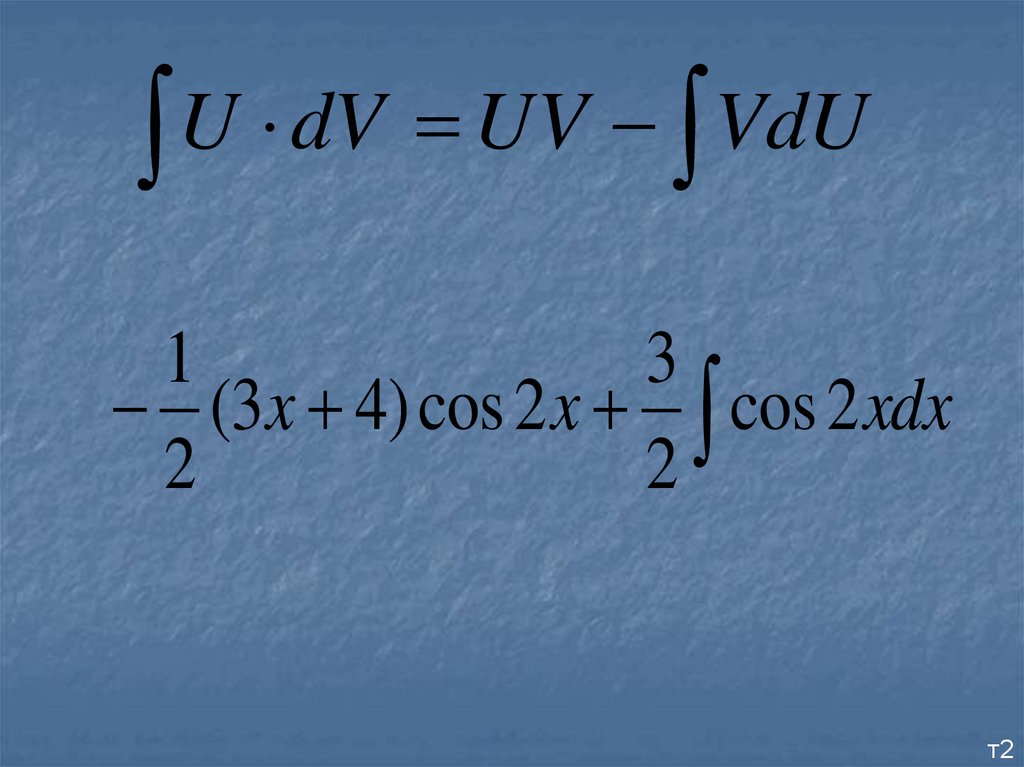


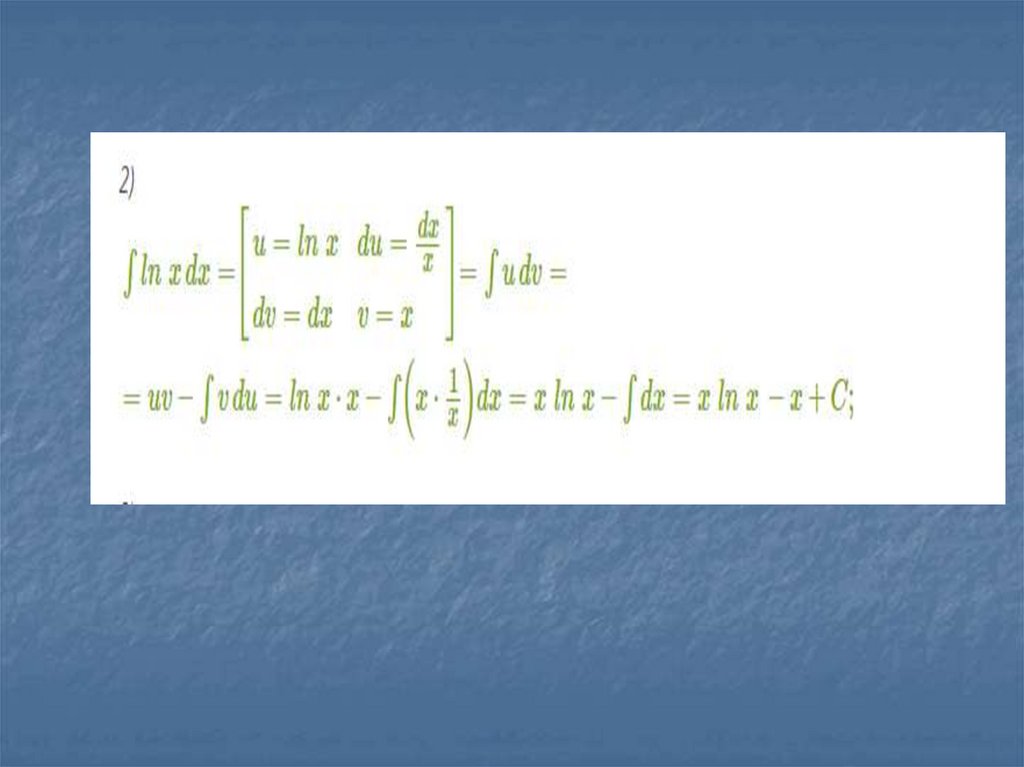
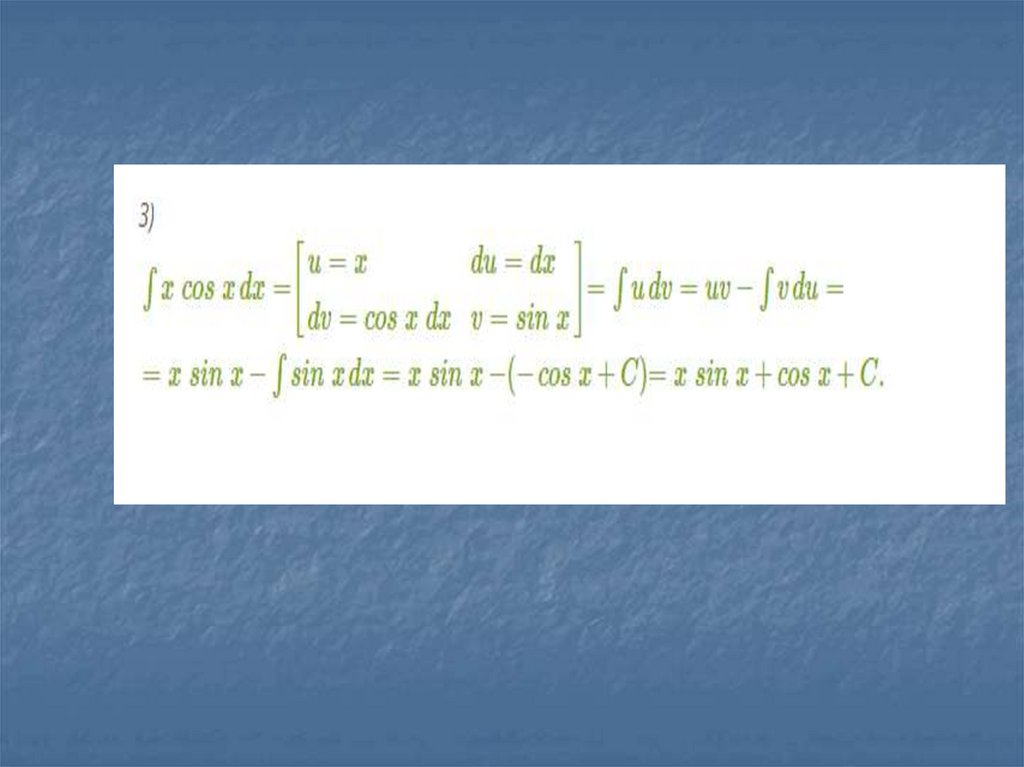

 Математика
Математика








