Похожие презентации:
Комплексные числа
1.
Вычислите:64
256
144
6,25
900
900igr.net
2.
Мнимаяединица
i – начальная буква французского слова
imaginaire – «мнимый»
3. Например,
3636
36 36
363636
( (( 111))) 36
36
1
6
i
36( (11 )36
1
6
i
1)
36
1
6
i
6i
Вычислите:
900
1
4
12,25
4.
2 ;3 3 2iiii4342431
2
i
i
(
(
1
1
)
)
i
i
i
;
i
;
2
1
1
;
;
2
1
4
3
3
3
2
2
2
2
2
3
2
i
i
i
i
i
(
i
i
i
(
1
)
i
i
;
4
3
2
i
1
;
4
3
2
i
1
;
iiii332 4
i
i
i
i
i
i
i
i
i
i
(
(
1
1
i
(
(
1
1
)
)
i
i
;
;
i
2
2
3
2
i
i
i
i
i
(
1
i
i
i
i
i
(
ii2ii53i4344i 4 i iiii2i(2ii4i3i3 i 3 i1 ( (() ( i 1 11 1) i))ii)i iii i i i ; i i ;i;i; ;i3 2ii222 2 ( (1( ) 1
iiii5545545i4i iii3444(3443iii
1
)
i
;
3
2
i
i
i
i
(
1
2
2
2
i
1
i
i
;
i
i
i
(
1
)
i
i
i
(
1
i
i
1
1
i
i
i
i
;
;
i
i
i
i
i
(
(
1
1
4
4
3
3
2
2
5
4
2
iiii345i545i 5
i
i
1
i
i
;
i
i
1
i
i
;
i
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
i
1
i
i
;
3
3
2
2
4
4
4
i
i
i
(
1
)
1
;
3
2
66565i
54i54i
24
i
i
i
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
i
i
i
i
1
1
i
i
;
i
;
4
3
i
1
i
i
;
3
6
5
5
2
2
2
5
4
iiii5566i6 4i4ii 5
i
i
i
(
1
i
i
i
i
1
;
i
i
i
i
i
2
i
i
i
i
55 ii
22
i
1
1
;
;
1
1
i
i
i
i
;
;
ii45i6656
i4i4 i5 5ii5 iii11 iiii i ii;i; 2iii222 11;;
i
i
6
i4i7i677676i i i i i5665665 i1 i i i i ii
11 i ii i ; i i ii
;; i i2i225 5 41 4;11;;
i6 1ii iii(
ii 1
iii7 i ii
i ;)ii ii i i 1 1i i;i; 11 i
iiii666767
(
(
1
1
i
i
;
;
5i5i 66 ii
22)) ii
i
i
(
1
i
i
;
7
i
(
1
i
i
;
5i5 i6 6ii6
2)
2)
i
i
i
i
i
i
i
1
1
;
;
i
i
(
1
)
i
7
7
7
1 1;;i
;55ii;;
ii5ii875877i i i i i76767 6i iii i i ii
i i (i(ii (
2 1 1i
)i1)2 )i
ii i16 6
;
i
i
i
i
i
i
i
i
i
i
(
(
1
1
)
)
i
i
i
;
;
i
i
i
i
i
i
1
.
8
7
i
i
1
.
.
8
7
i 77 8 i 66 7 i i i 1;
5.
Значения степеней числа iповторяются с периодом,
равным 4.
Найдем:
28
33
135
i ;i ;i .
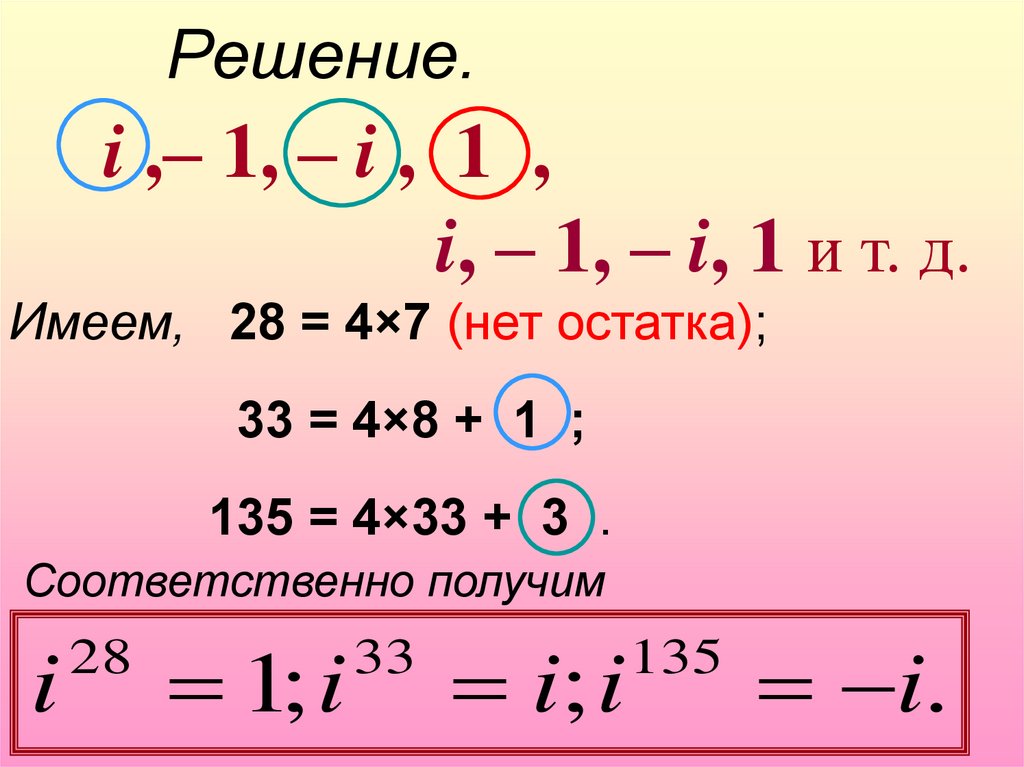
6.
Решение.i ,– 1, – i , 1 ,
i, – 1, – i, 1 и т. д.
Имеем, 28 = 4×7 (нет остатка);
33 = 4×8 + 1 ;
135 = 4×33 + 3 .
Соответственно получим
i
28
1; i
33
i; i
135
i.
7.
Вычислите:i1
i-i
i-1
i
216
143
66
43
2-i
i i
48
44
(i i -1 i ) i
13
14
15
32
8. Комплексные числа
Определение 1. Числа вида a + bi,где a и b – действительные числа,
i – мнимая единица,
называются комплексными.
a - действительная часть комплексного числа,
bi – мнимая часть комплексного числа,
b – коэффициентом при мнимой части.
9.
VII в.н.э.-квадратный корень из
положительного числа
имеет два значения –
положительное и
отрицательное,
а из отрицательных чисел
квадратные корни извлечь
нельзя:
нет такого числа х, чтобы
х2 = -9.
10. В XVI веке
в связи с изучениемкубических уравнений
оказалось необходимым
извлекать квадратные корни
из отрицательных чисел.
Первым учёным,
предложившим ввести
числа новой природы,
был Джорж Кордано.
11.
Он предложила а а
Кордано назвал такие величины
“чисто отрицательными” или даже
“софистически отрицательными”,
считая их бесполезными и
стремился не применять их.
12.
в 1572году
итальянский учёный
Бомбелли
выпустил книгу, в которой были
установлены первые правила
арифметических операций над
комплексными числами,
вплоть до извлечения из них
кубических корней.
13. Название “мнимые числа” ввёл французский математик и философ Р. Декарт
в 1637году
Название
“мнимые числа”
ввёл французский
математик и философ
Р. Декарт
14. один из крупнейших математиков XVIII века – Л. Эйлер предложил использовать первую букву французского слова imaginare (мнимый)
в 1777году
один из крупнейших
математиков
XVIII века –
Л. Эйлер
предложил использовать
первую букву
французского слова
imaginare (мнимый)
для обозначения
15.
В настоящее времякомплексные числа
используются
в математике
гораздо шире, чем
действительные
16.
Комплексныечисла имеют
прикладное значение
во многих областях
науки, являются
основным аппаратом
для расчетов
в электротехнике и
связи.
17. Применяются при конструировании ракет и самолетов
18. При вычерчивании географических карт
19. В исследовании течения воды, а также во многих других науках.
20. a + bi = c + di, если a = c и b = d.
Определение 2.a + bi = c + di, если
a = c и b = d.
21. Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x = – 7. Отсюда
Пример .Найти x и y из равенства:
3y + 5xi = 15 – 7i;
Решение.
Согласно условию равенства
комплексных чисел имеем
3y = 15, 5x = – 7.
7
Отсюда x , y 5.
5
22. (а+bi)
Сложение(а+bi)+(c+di)=(a+c) + (b+d)i
Вычитание
(а+bi)- (c+di) =(a-c) + (b-d)i
23. Выполните действия:
z1 = 2 + 3i, z2 = 5 – 7i.Найти: а) z1 + z2; б) z1 – z2;
Решение.
а) z1 + z2 =(2 + 3i) + (5 – 7i) =
=(2 + 5) + (3i – 7i) = 7 – 4i;
б) z1 – z2 =(2 + 3i) – (5 – 7i) =
=(2 – 5) + (3i + 7i) = – 3 + 10i;
24. Умножение
(а+bi)(c+di) == ac + аd i + bс i +
2
bd i
= (ac-bd) + (аd+bc)i
=
25. Выполните действия:
(2 + 3i)(5 – 7i) == (10+21) + (-14+15)i = 31+i
(5 + 3i)(5 – 3i) = 25-9i2 = 34
2
(2 – 7i)
2
= 4 - 28i + 49i
=-45-28i
2
2
2
25m +16 = 25m -16i =
= (5m-4i)(5m+4i)
26. Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой
частью.z1= a+bi и z2=a-bi
27. Деление
2 3i 2 3i 5 7i=
5 7i 5 7i 5 7i
11 29i
11 29
=
=
i
74
74 74
28.
Выполните действия:(2 3i ) (4 i )
27
4i
1 i
6 2i 1 i
4
8
i
4i =
4
i
=
1 i 1 i
2
=2
29. Домашняя работа
6317
13
82
72
34
1) (i +i +i +i )(i –i );
2) Найти x и y из равенства:
(2x + 3y) + (x – y)i = 7 + 6i.
6
2
i
2
3
i
3
123
3)
(1 i ) i
3 7i 2 5i



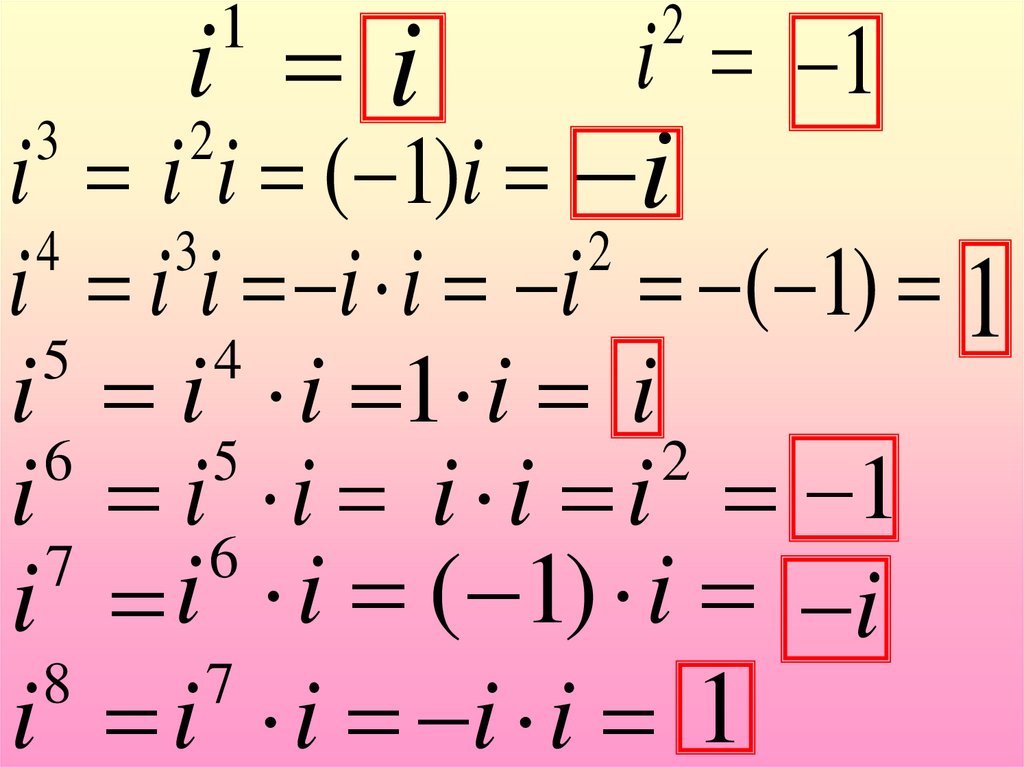















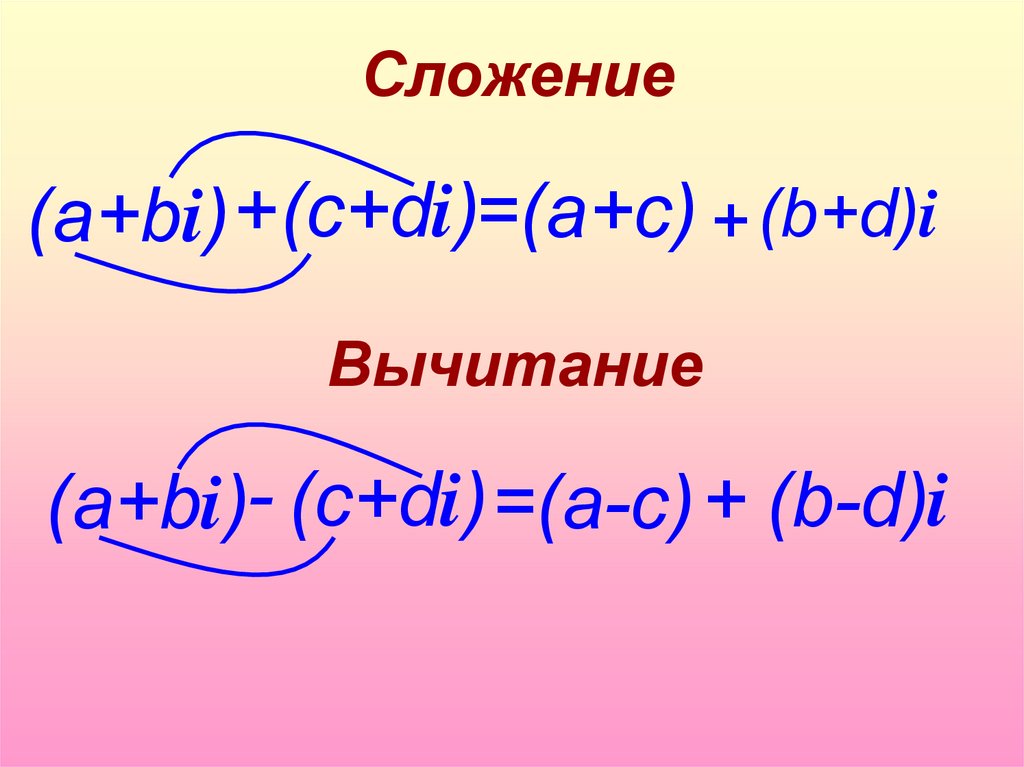







 Математика
Математика








