Похожие презентации:
Комплексные числа
1. Комплексные числа
2. Какие числовые множества Вам знакомы?
NZ
Q
R
• N – натуральные числа
• Z – целые числа
• Q – рациональные числа
• R – действительные
числа
3. Определение 1.
Числа видаa + bi,
где a и b – действительные числа,
i – мнимая единица,
называются комплексными.
a - действительная часть комплексного числа,
bi – мнимая часть комплексного числа,
b – коэффициентом при мнимой части.
4. Минимальные условия комплексного числа
• 1) Существует число, квадрат которого= -1.
• 2) Множество комплексных чисел
содержит все действительные числа.
• 3) Операции сложения, вычитания,
умножения и деления комплексных
чисел удовлетворяет обычным законом
арифметических действий.
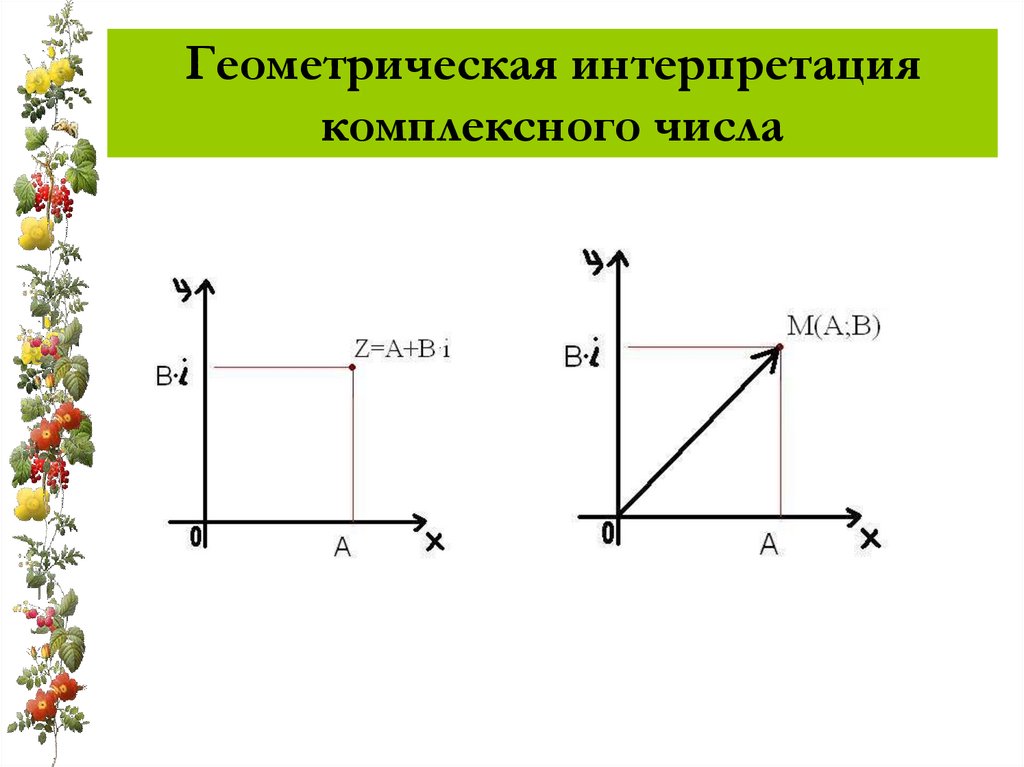
5. Геометрическая интерпретация комплексного числа
6. a + bi = c + di, если a = c и b = d.
Определение 2. Комплексные числаназываются равными
a + bi = c + di, если
a = c и b = d.
7. Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой
частью.z1= a+bi и z2=a-bi
8. (а+bi)
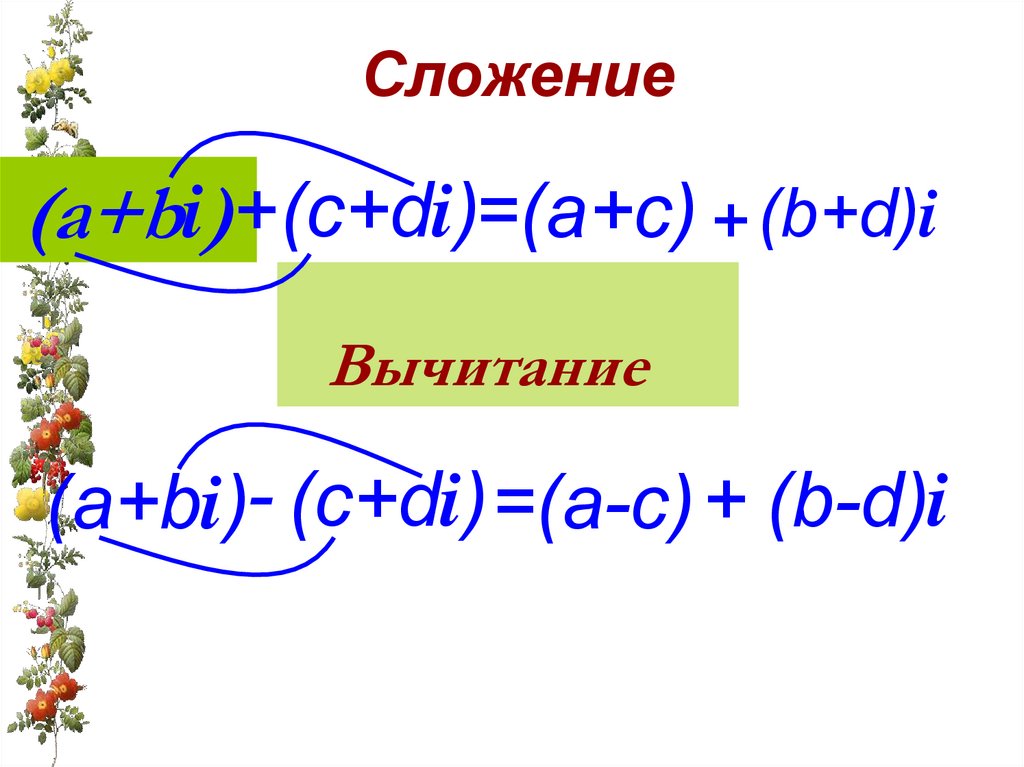
Сложение(а+bi)+(c+di)=(a+c) + (b+d)i
Вычитание
(а+bi)- (c+di) =(a-c) + (b-d)i
9. Умножение
(а+bi)(c+di) == ac + аd i + bс i +
2
bd i
= (ac-bd) + (аd+bc)i
=
10. Арифметические действия с комплексными числами в алгебраической форме
(а + bi) + (c + di) = (а + с) + (b + d)i(а + bi) - (c + di) = (а - с) + (b - d)i
(а + bi)·(с + di) = (ac - bd) + (ad + bc)i
a bi (a bi)(c di) ac bd bc ad
2
2
i
2
2
c di (c di)(c di) c d
c d
11. ПРИМЕР 1 :Выполните действия:
z1 = 2 + 3i, z2 = 5 – 7i.Найти: а) z1 + z2; б) z1 – z2;
Решение.
а) z1 + z2 =(2 + 3i) + (5 – 7i) =
=(2 + 5) + (3i – 7i) = 7 – 4i;
б) z1 – z2 =(2 + 3i) – (5 – 7i) =
=(2 – 5) + (3i + 7i) = – 3 + 10i;
12. ПРИМЕР 2:Выполните действия:
(2 + 3i)(5 – 7i) == (10+21) + (-14+15)i = 31+i
(5 + 3i)(5 – 3i) = 25-9i2 = 34
2
(2 – 7i)
2
= 4 - 28i + 49i
=-45-28i
2
2
2
25m +16 = 25m -16i =
= (5m-4i)(5m+4i)
13.
Пример 1: Даны комплексные числа z1, z2 :Найти 1) z1+ z2
2). z1- z2
3) z1 · z 2
Решение:
1 1 i
1 1i 1 1i
0,5 0,5i .
1 i 1 iРешение:
1 i2 2
Решение:
4)
1 1 i
11 11z i 1i 10 ,51 i1 0 ,51i - 1алгебраическая
форма.
1
i
z1 4 1(1 i i)1 z1i 4 1 1 4ii 21 4 i 24 i 1 i02,5 0,25i . 0,5 0,5i .
z2 1 i 1 i 1 i 2 z12 0, 5 2 0 ,52ii - алгебраическая
форма. форма.
0,5 0,5i - алгебраическая
z1
z
z
z
1
2
1
4(1 i)
44( 1 4 izi)2 4 2 44i2 i 4-iалгебраическая
форма.
4i 4i
2
2
2
2
i
z2
2
2
i2
2 i 2i2) 1=(0,5+2)+(-0,5+2)i=2,5+1,5
1). z1+ z12 =i (01,z 52i 0 ,151i ) i+ i (1РЕШЕНИЕ
i
2 2i - алгебраическая
форма.
2 2i - алгебраическая
форма.
2). z - z = (0,5 0,5i) - (2 2zi2) =(0,5-2)+(-0,5-2)i=-1,5-2,5
i
1
z
2
2
20i),5=(0,5+2)+(-0,5+2)i=2,5+1,5
i
5(0 ,5z01, 5+i0)z,·52(i=)2+ (0(2,5i) =(0,5·2-(-0,5)·2)+(0,5·2+(-0,5)·2)i=1-0
3).1).z1z·1z+2 =z2(=0,1).
i=1 i
i ) + (2 2i) =(0,5+2)+(-0,5+2)i=2,5+1,5
2). z1-0z,52= 2).
i
)2- (( 02,(5 02,i50), 5=(0,5-2)+(-0,5-2)i=-1,5-2,5
2i )) - (2( 02,5i)) =(0,5-2)+(-0,5-2)i=-1,5-2,5
2 0,5 2
0(0,5,5i z 1-00z,,552i=
1i 1
z
1
i
0
i
i
4).3). = · = (0,5 0,5i) · (22 22i) =(0,5·2-(-0,5)·2)+(0,5·2+(-0,5)·2)i=1-0
2
i=1
i=1
2i z1 · z 2 = (0 ,5 0,5i ) · (2 2i) 2=(0,5·2-(-0,5)·2)+(0,5·2+(-0,5)·2)i=1-0
4
4
z 2 z1 z22 3).
2 2
2 2
0,5 0,5i 0,5 2 ( 0,5 2) ( 0,5) 2 0,5 2
4). z1 = 4). z1 = 0,5 02,5i 20,5 2 2 ( 02,5 2 2) 2( 0,5i) 2 20 02 ,5i 2 i 0i 1 i 1 i
4 4
4
z 2 2 2i 2 22i 2
2 2
4
z
2
2 2
2 2
1
1
14.
Задание 1: Даны комплексные числа z1, z2 :Найти 1) z1+ z2
2). z1- z2
3) z1 · z 2
4) z1
z
2
Задание 1. z1 = -1 – i, z2 = 2 + 4i
Задание 2. z1 = 4 – 7i ,z2 = 3 - 4i
Задание 3. z1 = 2 + 2i , z2 = 5+6i
Задание 4. z1 = -3 + i ,z2 = -2+ 3i






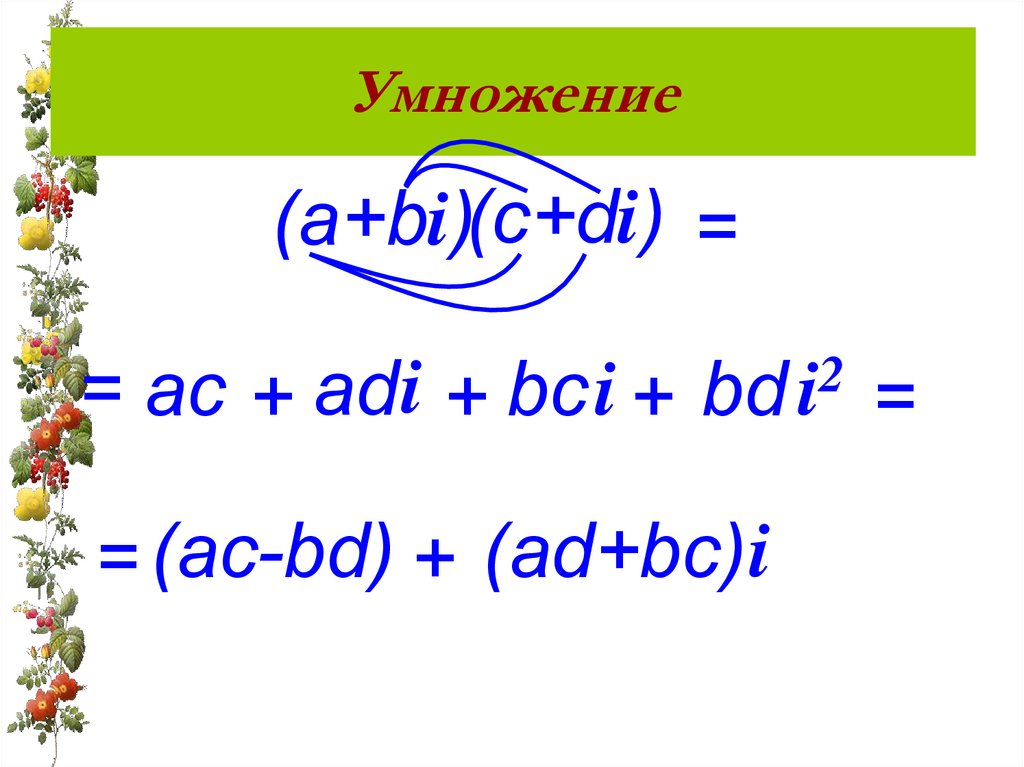





 Математика
Математика








