Сопротивление материалов. Модуль 1

1.

М
Е
Х
А
Н
И
К
А
Модуль 1.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Раздел 1. Введение. Основные понятия
Раздел 2. Геометрические характеристики плоских сечений
Раздел 3. Теория внутренних силовых факторов
Раздел 4. Понятие о напряжениях и деформациях в
точке твердого тела.
Раздел 5.
Лекционный курс - 8 час
Лабораторные занятия – 8 час
Самостоятельная работа : - Выполнение и защита РГР

2. План:

МЕХАНИКА
1
Раздел 1
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ОСНОВНЫЕ ПОНЯТИЯ
СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Основные понятия и определения
План:
1.1 Основные определения
1.2 Допущения (гипотезы) в сопротивлении материалов

3. Сопротивление материалов - наука о методах расчетов на прочность, жесткость и устойчивость элементов машин и сооружений

2
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Сопротивление материалов - наука
о методах расчетов на прочность, жесткость и
устойчивость элементов машин и сооружений
Прочность – это способность элемента
конструкции сопротивляться разрушению под
нагрузкой.
Жесткость – это способность элемента
конструкции сопротивляться деформациям.
Устойчивость – это способность элемента
конструкции сопротивляться воздействию
больших отклонений от равновесия при малых
изменениях нагрузки.

4. Гипотезы (допущения) сопротивления материалов

3
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Гипотезы (допущения)
сопротивления материалов
Материал считается однородным и
непрерывным, т. е. физико-механические
свойства во всех его точках одинаковы и
материал заполняет весь объем тела без
пустот.
Все рассматриваемые материалы
изотропны, т. е. обладают одинаковыми
упругими свойствами по всем
направлениям.

5. Гипотезы (допущения) сопротивления материалов

4
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Гипотезы (допущения)
сопротивления материалов
Деформации упругих тел, возникающие
под действием внешних сил, весьма малы
по сравнению с размерами самого тела.
Результат действия системы внешних
сил на тело равен сумме результатов
действия каждой силы в отдельности. Это
допущение – принцип независимости
действия сил.

6. План:

МЕХАНИКА
5
Раздел 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
Геометрические характеристики плоских
сечений
План:
2.1. Статический момент сечения
2.2. Моменты инерции
2.3. Моменты инерции при параллельном переносе и повороте осей
2.4. Главные оси и главные моменты инерции

7. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

6
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Влияние площади поперечного сечения,
формы сечения и расположения сечения
относительно приложенных нагрузок
на прочность и жесткость конструкции определяется
«геометрическими характеристиками плоских
сечений»
2А
А
А
А
А – площадь поперечного сечения (простейшая геометрическая
характеристика). Она входит в расчетные формулы, определяющие
прочность и жесткость при простом растяжении и сжатии.
В случаях кручения, изгиба и сложного сопротивления используются
более сложные геометрические характеристики: статический момент
(S), моменты инерции (I), моменты сопротивления(W).

8. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

7
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Статический момент площади
поперечного сечения
S y x dA = x · A,
A
S x y dA = y · A,
A
Обозначив через xc и y–c координаты центра тяжести
сечения, применяя теорему: сумма моментов
составляющих равна моменту равнодействующей,
можно записать: S y xc A, S x yc A.
Статический момент площади поперечного
сечения относительно оси – есть произведение
площади сечения на расстояние от оси до центра
тяжести сечения.

9.

8
ус
с
Формулы для определения положения центра
тяжести:
S
yc x ,
A
хс
хc
Sу
A
.
Центральные оси - оси, проходящие
через центр тяжести сечения
Sxc= 0, Syc = 0
Размерность ед. длины
Статический момент сечения может быть величиной
положительной, отрицательной, может быть равен 0. Для
вычисления статического момента сложного сечения
разбиваем его на простые элементы, для которых известными
являются площадь и положение центра тяжести.
Статический момент площади всего сечения относительно оси
определяется как алгебраическая сумма статических моментов
относительно заданной оси простых элементов, на которые
разбито сложное сечение.
3

10. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

9
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
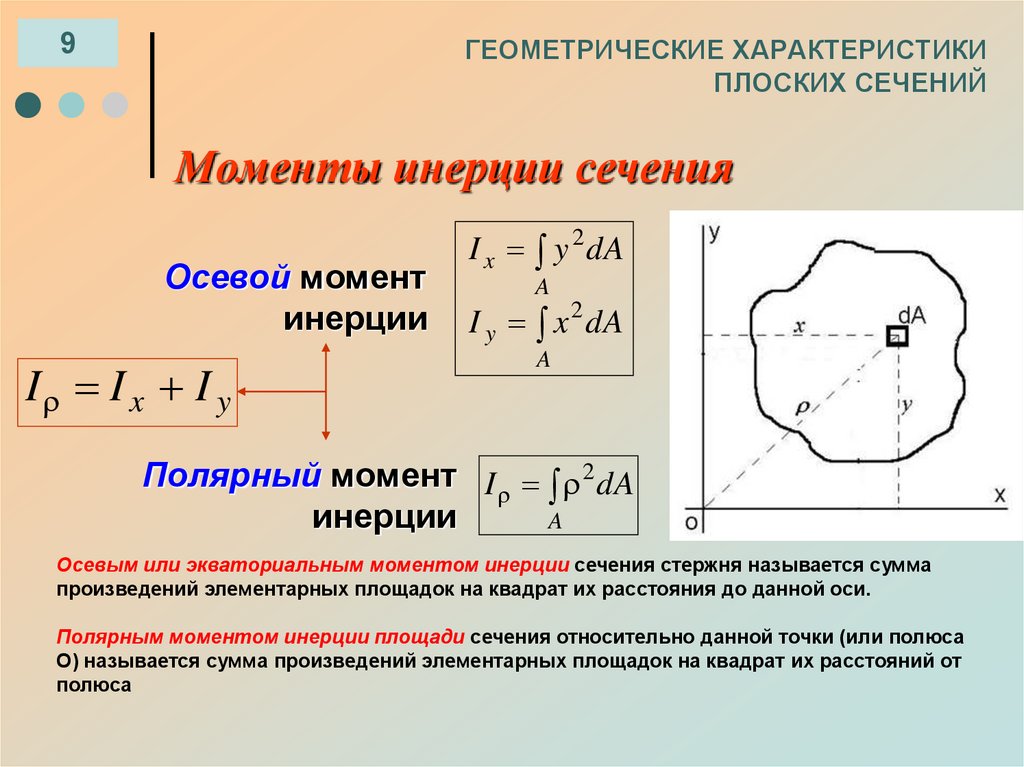
Моменты инерции сечения
Осевой момент
инерции
I I x I y
I x y 2 dA
A
I y x 2 dA
A
Полярный момент I 2 dA
инерции
A
Осевым или экваториальным моментом инерции сечения стержня называется сумма
произведений элементарных площадок на квадрат их расстояния до данной оси.
Полярным моментом инерции площади сечения относительно данной точки (или полюса
O) называется сумма произведений элементарных площадок на квадрат их расстояний от
полюса

11. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

10
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Моменты инерции сечения
Центробежный момент инерции – это сумма произведений
элементарных площадок на их расстояния от координатных
осей.
Центробежный момент инерции
I xy y x dA
A
По знаку центробежный момент инерции может быть больше,
меньше или равен нулю.
Оси, относительно которых центробежный момент
инерции равен нулю, называются главными осями инерции.
Если главные оси проходят через центр тяжести
сечения, то они называются главными центральными осями
инерции.
Единица измерения моментов инерции сечения – м4

12. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

11
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
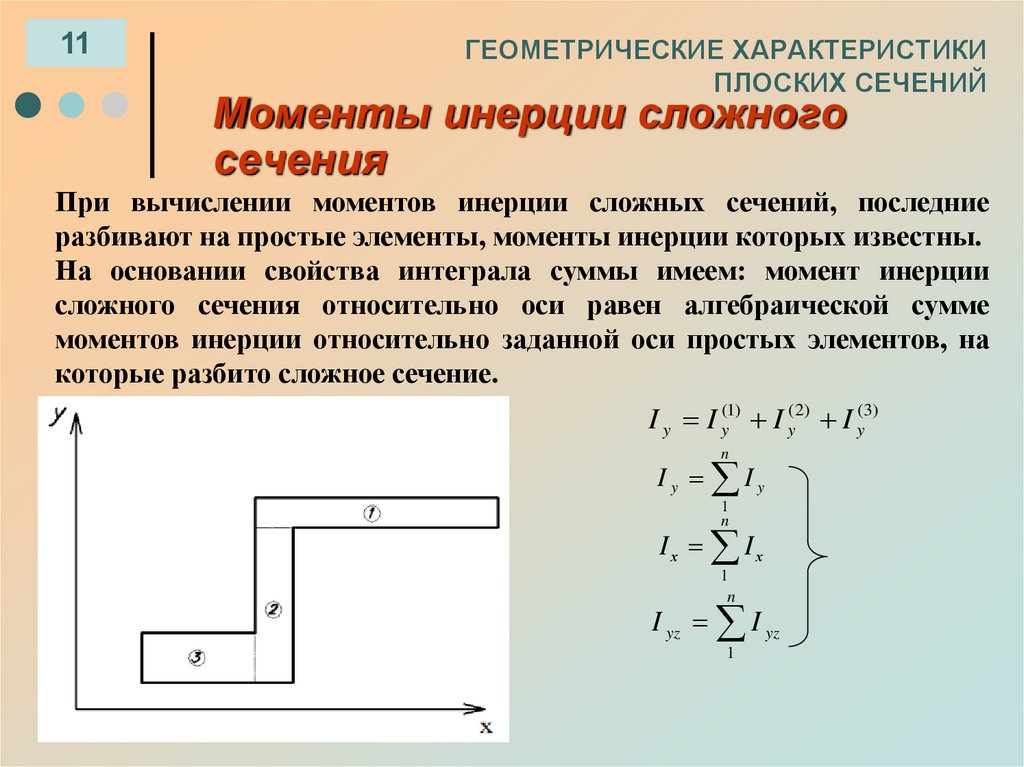
Моменты инерции сложного
сечения
При вычислении моментов инерции сложных сечений, последние
разбивают на простые элементы, моменты инерции которых известны.
На основании свойства интеграла суммы имеем: момент инерции
сложного сечения относительно оси равен алгебраической сумме
моментов инерции относительно заданной оси простых элементов, на
которые разбито сложное сечение.
I y I y(1) I y( 2) I y(3)
n
Iy Iy
1
n
Iх Iх
1
n
I yz I yz
1

13. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

12
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Моменты инерции при
параллельном переносе и
повороте осей
Ix = Ixс + a2 A,
Iy = Iyс + b2 A,
I xy I xс yс А а b
Момент инерции относительно любой оси равен моменту
инерции относительно центральной оси, параллельной
данной (или собственному моменту инерции) плюс
произведение площади сечения на квадрат расстояния между
осями.

14. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

13
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Моменты инерции при повороте
осей
Іu = Ix cos2α + Iy sin2α - Ixy sin2α ,
Iν = Ix sin2α + Iy cos2α + Ixy sin2α ,
Iuν =
Ix Iy
2
sin 2α + Ixy cos 2α.
Іu + Iν = Ix + Iy.
При повороте осей сумма моментов инерции
относительно двух взаимно
перпендикулярных осей, проходящих через
одну точку – есть величина постоянная

15. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

14
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Главные оси и главные моменты инерции
Главные оси сечения - это оси u и v, относительно которых
центробежный момент инерции Іuν = 0, а осевые моменты инерции Іu и
Iν имеют экстремальные значения max или min
tg 2 0
2 I xy
Ix Iy
Главные центральные оси - это
главные оси проходящие через центр тяжести
сечения
Главные моменты инерции
I max
min
Ix Iy
2
1
2
( I x I y )2 4 I xy
2
.

16. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

15
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Моменты сопротивления
Осевым моментом сопротивления называется
отношение момента инерции относительно данной
оси к расстоянию до наиболее удаленной точки
сечения, по отношению к этой оси.
Wy
Iy
хmax
Wх
Iх
ymax
Размерность момента сопротивления (ед. длины)3.
.
Относительно оси симметрии можно вычислить один
момент сопротивления. Если сечение не имеет оси
симметрии, то относительно каждой оси надо
вычислять по два момента сопротивления.

17. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

16
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Радиус инерции
Радиус инерции относительно некоторой оси можно получить
из равенства I A i 2
Относительно осей y и z:
iy
Iy
A
Iх
iх
A
По радиусам инерции строится эллипс инерции, с помощью
.
которого графически можно определить момент
инерции
относительно любой центральной оси.

18. План:

МЕХАНИКА
17
Раздел 3.
Теория внутренних силовых
факторов
План:
3.1 Классификация нагрузок. Анализ расчетной схемы.
3.2 Внешние силы.
3.3 Внутренние силы. Метод сечений.
3.4 Продольная сила.
3.5 Крутящий момент.

19. ВНЕШНИЕ СИЛЫ (нагрузки)

18
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
ВНЕШНИЕ СИЛЫ
(нагрузки)
Поверхностные
– результат непосредственного
контактного взаимодействия тела с
другими телами.
Объемные
приложены к каждой точке объема.
Это – собственный вес,
центробежные силы, силы
магнитного или электрического
взаимодействия.

20.

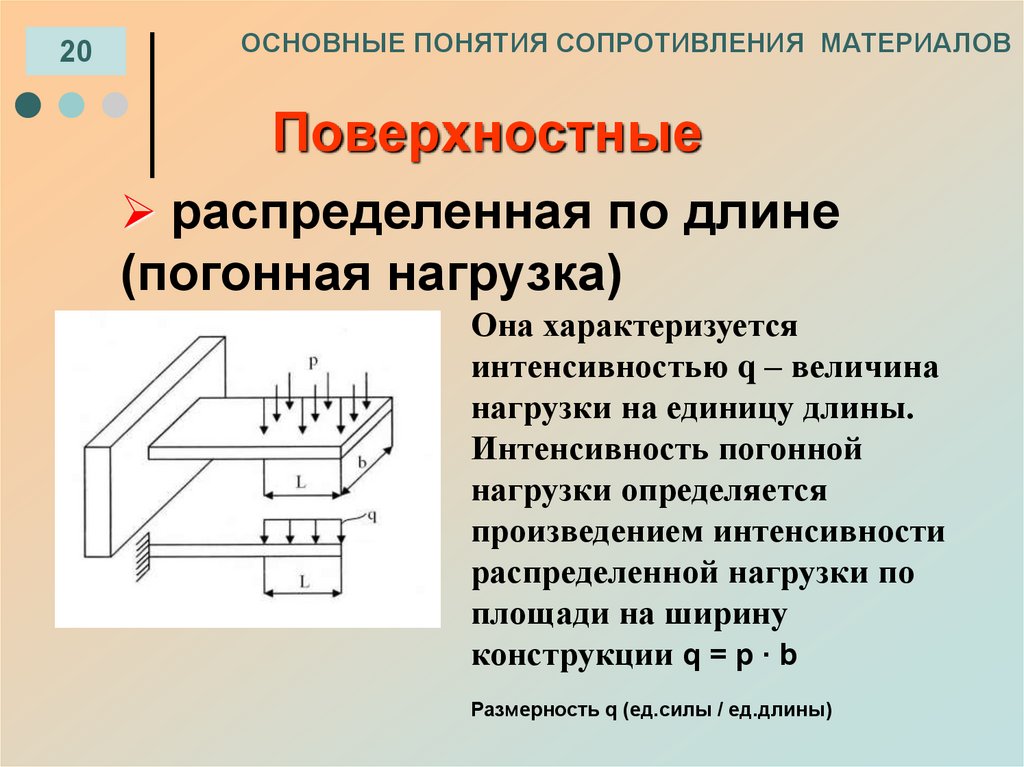
19
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Поверхностные
распределенные по площади
р
Давление снега на кровлю, давление
зерна на дно и стенки силосов, давление
воды на плотину и т.д.
Величина нагрузки приходящейся на единицу
площади, называется интенсивностью
нагрузки р.
Размерность р (ед.силы / ед.площади)

21.

20
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Поверхностные
распределенная по длине
(погонная нагрузка)
Она характеризуется
интенсивностью q – величина
нагрузки на единицу длины.
Интенсивность погонной
нагрузки определяется
произведением интенсивности
распределенной нагрузки по
площади на ширину
конструкции q = p ∙ b
Размерность q (ед.силы / ед.длины)

22.

21
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Поверхностные
сосредоточенные силы
передаются на конструкцию через небольшую
площадку и условно считают, что они приложены в
точке. Аоп – величина очень маленькая.
Распределенную нагрузку
можно собрать с площади, с
длины и заменить ее действие
сосредоточенной силой,
приложенной по центру
тяжести эпюры q.

23.

22
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Объемные нагрузки
приложены к каждой точке объема. Это –
собственный вес, центробежные силы, силы
магнитного или электрического
взаимодействия.
В зависимости от характера приложения
сил во времени различают нагрузки
статические и динамические.
Статическая нагрузка прикладывается сравнительно медленно
и плавно возрастает от нуля до своего конечного значения.
Возникающими при ее действии ускорениями и силами инерции
можно пренебречь.
Динамическая нагрузка меняет свою величину или направление
настолько быстро, что возникающее при этом ускорение создает
значительные инерционные силы, которые необходимо
учитывать в расчетах.

24.

23
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
СХЕМАТИЗАЦИЯ
КОНСТРУКЦИЙ
Типы используемых в
сопротивлении материалов
элементов конструкции

25.

24
СТЕРЖЕНЬ – элемент, у которого
b
один из размеров значительно
больше двух других (l >> a, b).
Наиболее широко используемый
элемент (вал, брус, балка, стойка)
l
a

26.

25
ПЛАСТИНА – элемент, у
которого один из размеров
значительно меньше двух
других (δ << a, b).
b
a

27.

26
Если пластина искривлена в
недеформированном
состоянии, то такой элемент –
ОБОЛОЧКА.
b
a

28.

27
МАССИВНОЕ ТЕЛО – все
размера примерно одинаковы
(a≈b≈c).
c
b
a

29.

28

30.

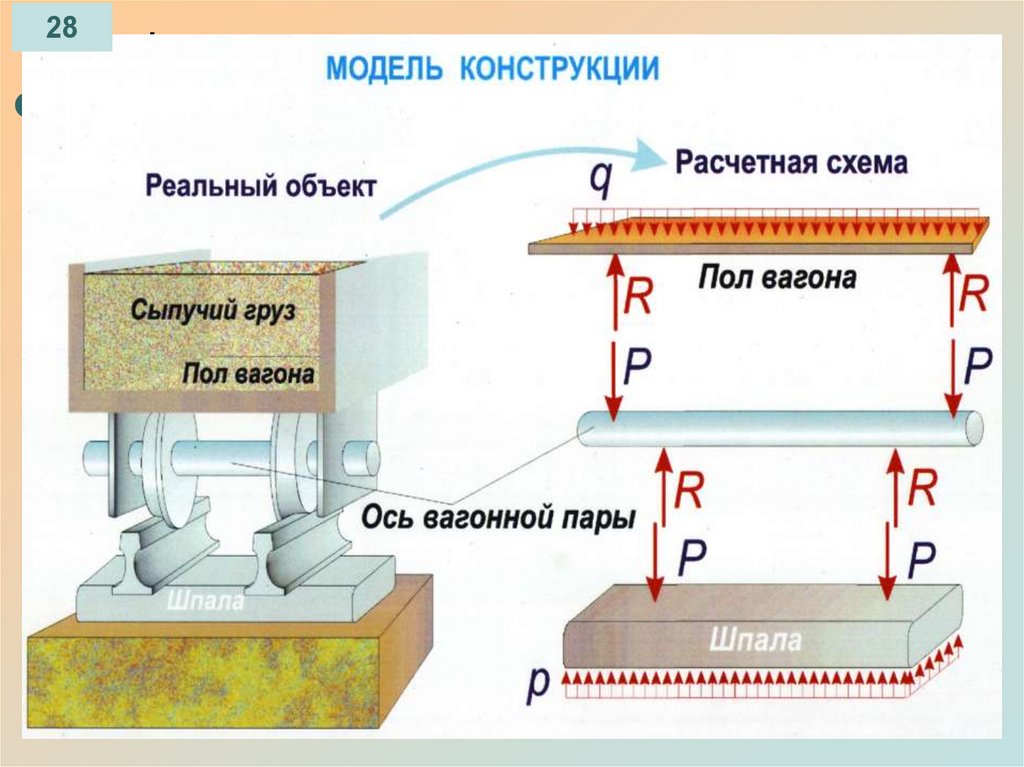
29
Метод сечений.
Внутренние усилия.
Под нагрузкой происходит взаимное перемещение
частиц тела, в результате чего появляются
внутренние усилия. Они стремятся восстановить
первоначальную форму и размеры тела.
Непосредственной причиной деформации и
разрушения является не нагрузка, а внутренние
усилия. Для вычисления внутренних усилий в
сечении применяется метод сечений.

31.

30
Метод сечений.
Стержень под действием внешних сил находится в
равновесии. Проводим в нем (мысленно) любое поперечное
сечение mn.Это сечение разделит стержень на две части А и
В, причем само сечение будет иметь две стороны – левую и
правую.
Отбросим одну из частей (в данном случае А, т.к. к ней
приложено большее количество сил).

32.

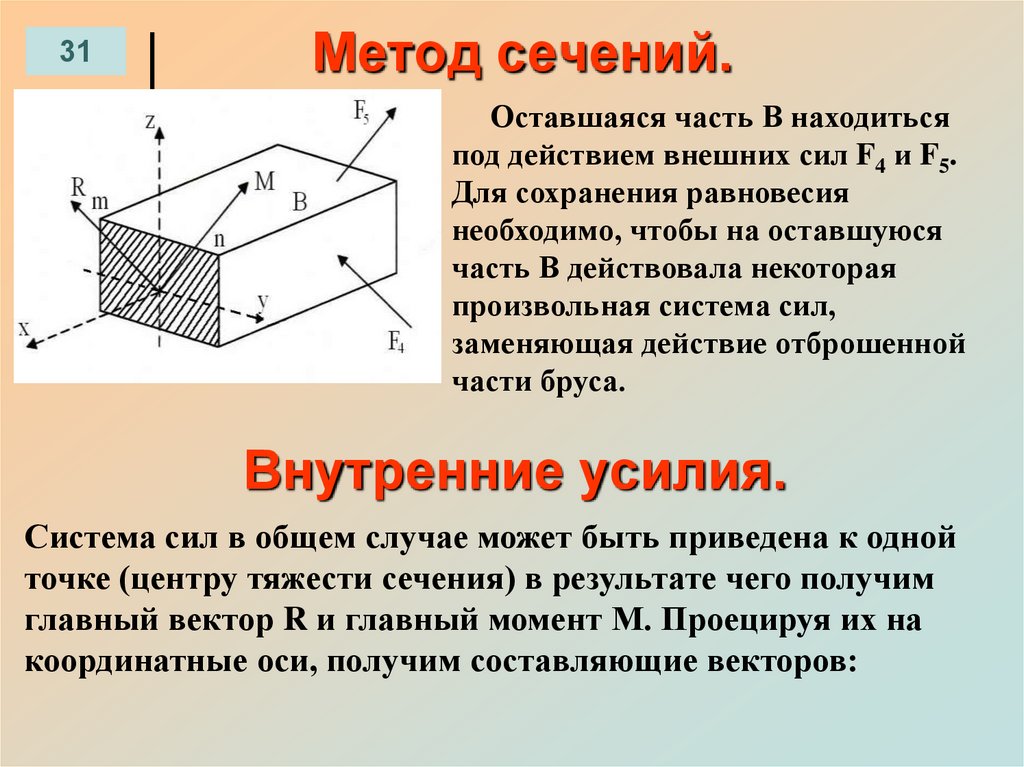
31
Метод сечений.
Оставшаяся часть В находиться
под действием внешних сил F4 и F5.
Для сохранения равновесия
необходимо, чтобы на оставшуюся
часть В действовала некоторая
произвольная система сил,
заменяющая действие отброшенной
части бруса.
Внутренние усилия.
Система сил в общем случае может быть приведена к одной
точке (центру тяжести сечения) в результате чего получим
главный вектор R и главный момент М. Проецируя их на
координатные оси, получим составляющие векторов:

33.

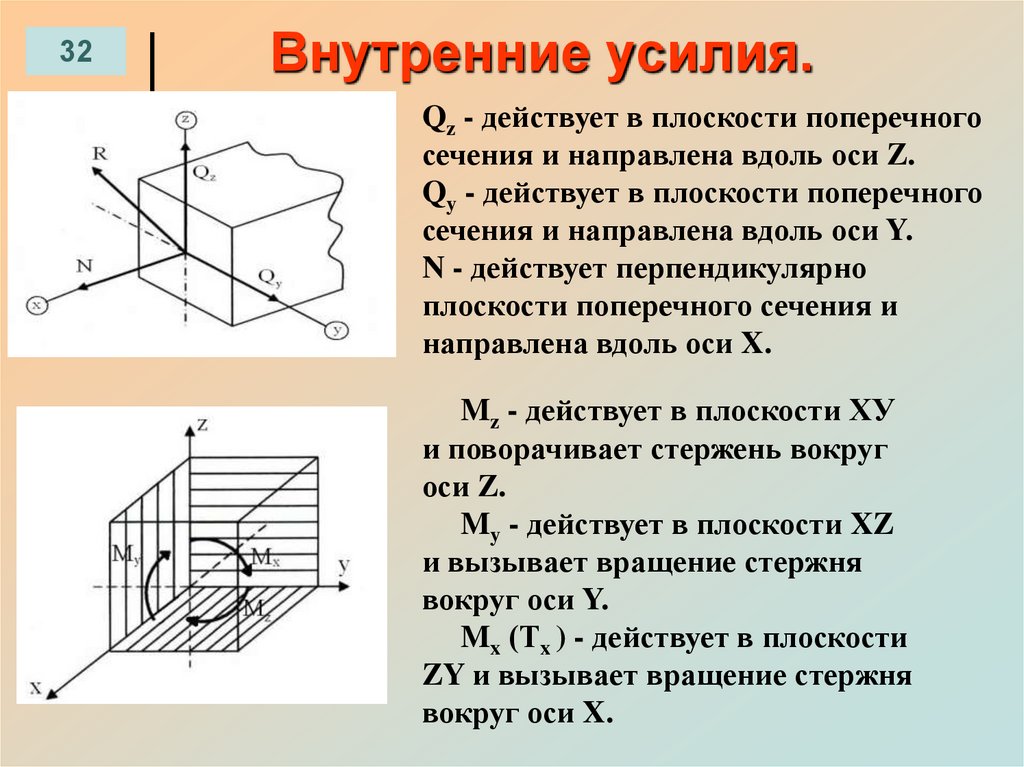
32
Внутренние усилия.
Qz - действует в плоскости поперечного
сечения и направлена вдоль оси Z.
Qy - действует в плоскости поперечного
сечения и направлена вдоль оси Y.
N - действует перпендикулярно
плоскости поперечного сечения и
направлена вдоль оси X.
Mz - действует в плоскости ХУ
и поворачивает стержень вокруг
оси Z.
My - действует в плоскости XZ
и вызывает вращение стержня
вокруг оси Y.
Mx (Тx ) - действует в плоскости
ZY и вызывает вращение стержня
вокруг оси X.

34.

33
Внутренние усилия.
Внутренние усилия определяются из шести
уравнений равновесия:
1. ∑ F(x) = 0 → N
4. ∑ mx(F) = 0 → T
2. ∑ F(у) = 0 → Qy
5. ∑ my(F) = 0 → My
3. ∑ F(z) = 0 → Qz
6. ∑ mz(F) = 0 → Mz

35. ЛЕКЦИЯ 3 План:

МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Растяжение и сжатие
ЛЕКЦИЯ 3
План:
3.1. Внутренние усилия при растяжении-сжатии
3.2. Внутренние усилия при кручении
3.3. Внутренние усилия при изгибе
3.4.

36. РАСТЯЖЕНИЕ И СЖАТИЕ

3.2
РАСТЯЖЕНИЕ И СЖАТИЕ
Правило знаков
продольных сил
N:

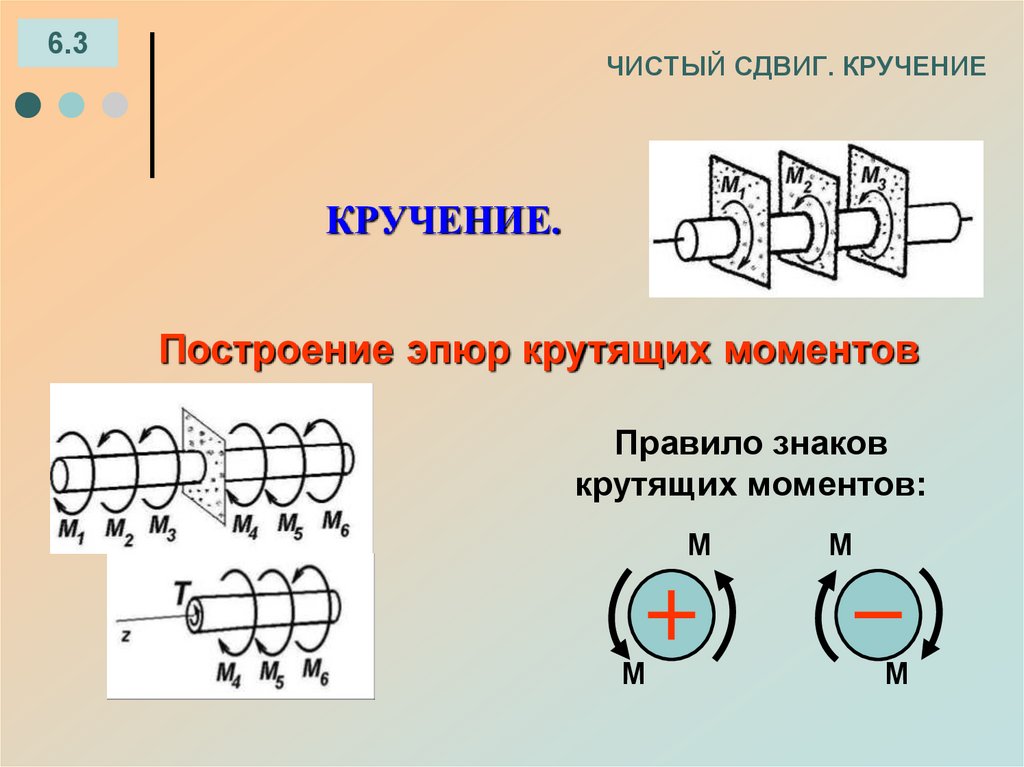
37. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ

6.3
ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
КРУЧЕНИЕ.
Построение эпюр крутящих моментов
Правило знаков
крутящих моментов:
М
М
М
М

38. ЛЕКЦИЯ 6 План:

6.1
МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Чистый сдвиг. Кручение
ЛЕКЦИЯ 6
План:
6.1. Чистый сдвиг
6.2. Кручение. Эпюры крутящих моментов
6.3. Напряжения при кручении
6.4. Деформации при кручении
6.5. Расчёт вала на прочность и на жёсткость

39. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ

6.2
ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
ЧИСТЫЙ СДВИГ - напряженное состояние, при
котором на гранях элемента конструкции возникают только
касательные напряжения
= G· ,
где
- угол сдвига;
G - модуль сдвига,
для стали G = 8 ·104 МПа
Для изотропных материалов :
G = E / [2(1 + )]

40. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ

6.3
ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
КРУЧЕНИЕ.
Построение эпюр крутящих моментов
Правило знаков
крутящих моментов:
М
М
М
М

41. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ

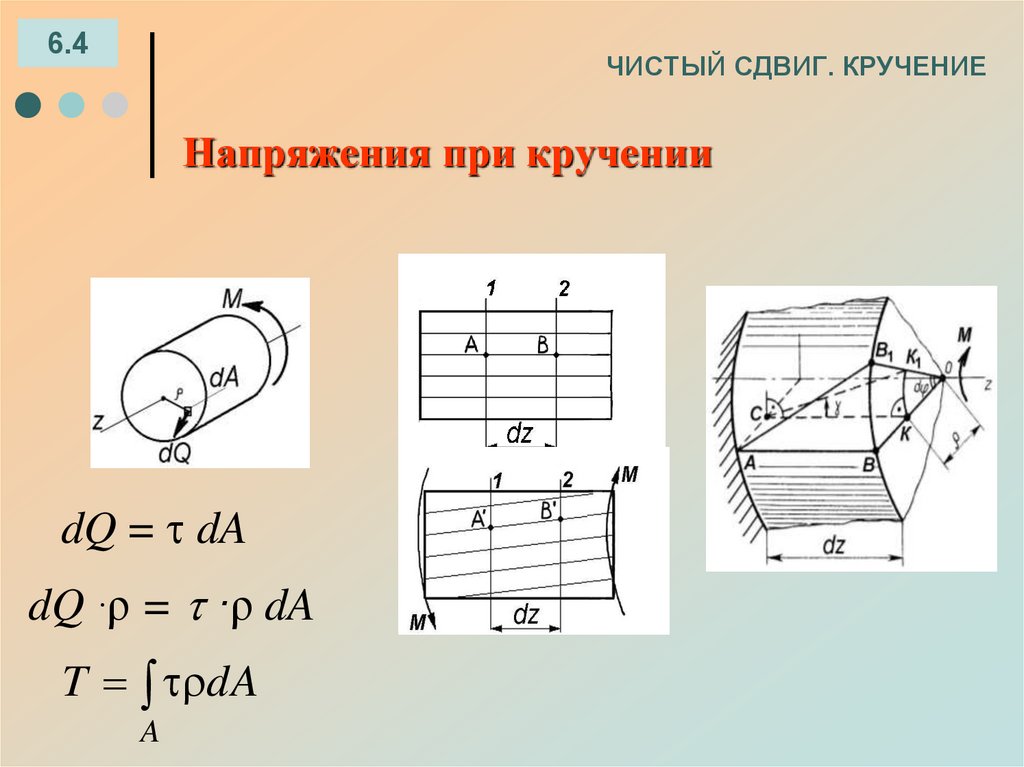
6.4
ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Напряжения при кручении
dQ = dA
dQ ·ρ = ·ρ dA
T dA
A

42. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ

6.5
ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Напряжения при кручении
КК dz d
d
dz
по закону Гука: = G·
d
G
dz
d
d T
- относительный
dz угол закручивания,
dz GI
d 2
d
G
dA G
I
dz A
dz
T
I

43. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ

6.6
ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Напряжения при кручении
T
T
max max
I
W
W I / max I / R 2 I / d
Для круглого сечения W = π d3/16 ≈ 0,2 d3
Для сечения в виде кольца
d
d
W = 0,2 D3(1- с4)
D

44. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ

6.7
ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Деформации при кручении
d
T
dz
GI
l GI
T
l GI
T
dz
dz
T
l
GI
GI - жесткость сечения вала при кручении

45. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ

6.8
ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Расчёт вала на прочность и жёсткость
Условие прочности вала
d 3
Tmax
0,2[ ]
max [ ]
Условие жесткости вала
Tmax
max
[ ]
W
[T ] [ ]W
T
max
[ ]
GI

46. ЛЕКЦИЯ 7 План:

7.1
МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Изгиб
ЛЕКЦИЯ 7
План:
7.1. Общие сведения
7.2. Внутренние силовые факторы при изгибе балки
7.3. Дифференциальные зависимости Журавского
7.4. Внутренние силовые факторы в сечениях рам

47. ИЗГИБ

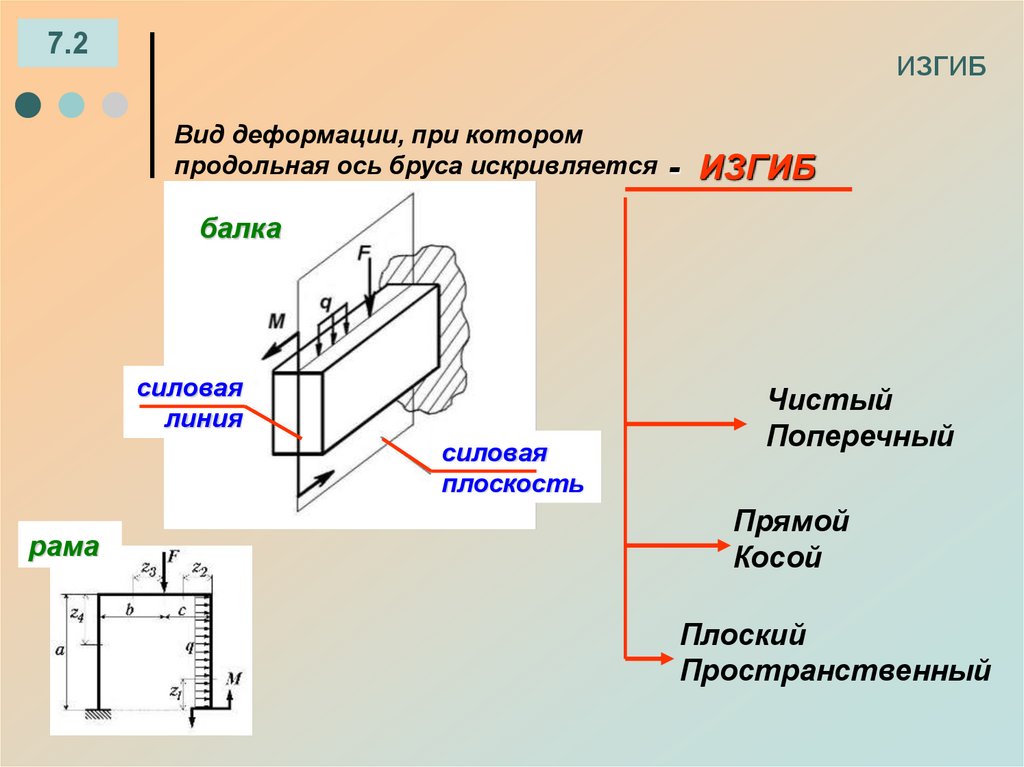
7.2
ИЗГИБ
Вид деформации, при котором
продольная ось бруса искривляется -
ИЗГИБ
балка
силовая
линия
силовая
плоскость
рама
Чистый
Поперечный
Прямой
Косой
Плоский
Пространственный

48. ИЗГИБ

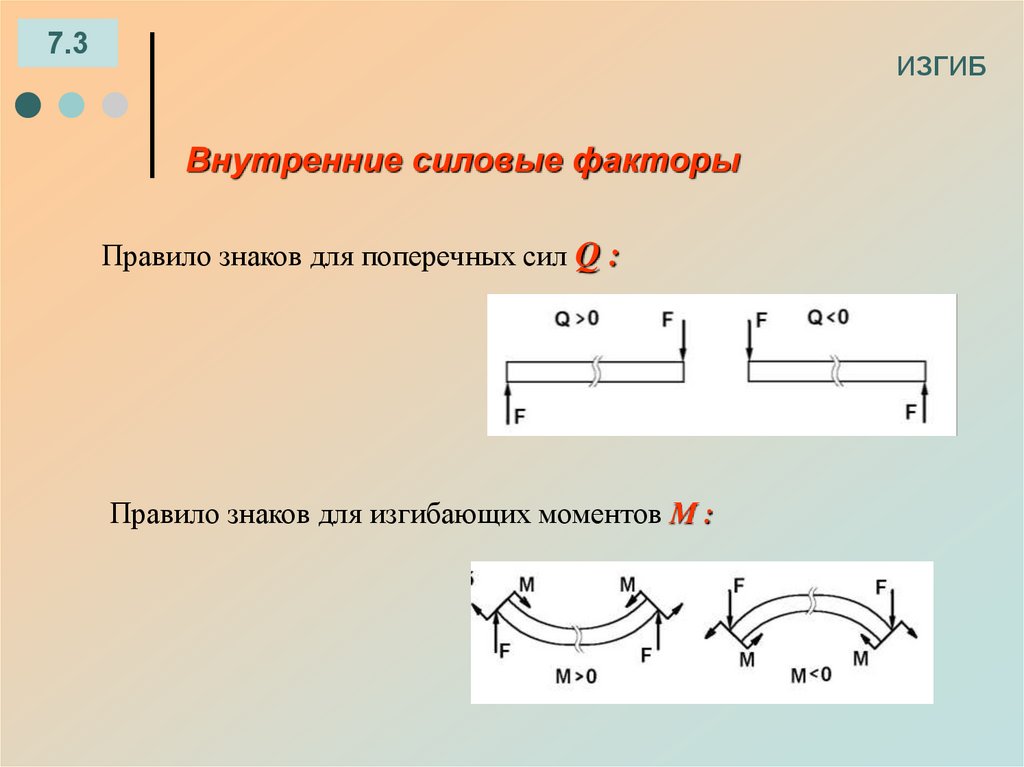
7.3
ИЗГИБ
Внутренние силовые факторы
Правило знаков для поперечных сил Q :
Правило знаков для изгибающих моментов М :

49. ИЗГИБ

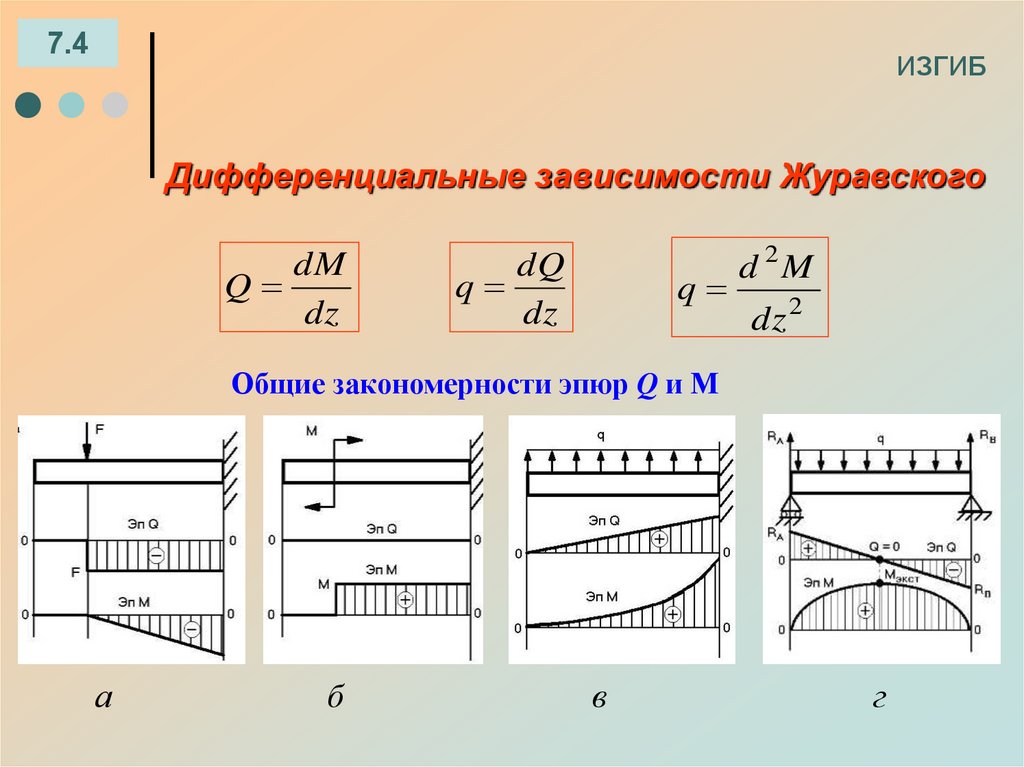
7.4
ИЗГИБ
Дифференциальные зависимости Журавского
dM
Q
dz
dQ
q
dz
q
d 2M
dz 2
Общие закономерности эпюр Q и М
а
б
в
г

50. ИЗГИБ

7.5
ИЗГИБ
ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ
В СЕЧЕНИЯХ РАМ
В сечениях стержней рамы кроме изгибающих
моментов M и поперечных сил Q, обычно действуют
еще и продольные силы N.
Границами характерных участков для рамы
- являются также места изменения направления оси
рамы.
При определении знаков внутренних силовых
факторов наблюдателю удобно располагать взгляд как
бы изнутри контура рамы.
При построении этих эпюр положительные
ординаты M, Q и N откладывают с внешней стороны,
а отрицательные – внутрь контура рамы.

51. ЛЕКЦИЯ 8 План:

8.1
МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Изгиб
ЛЕКЦИЯ 8
План:
8.1. Напряжения при чистом изгибе
8.2. Напряжения при плоском поперечном изгибе

52. ИЗГИБ

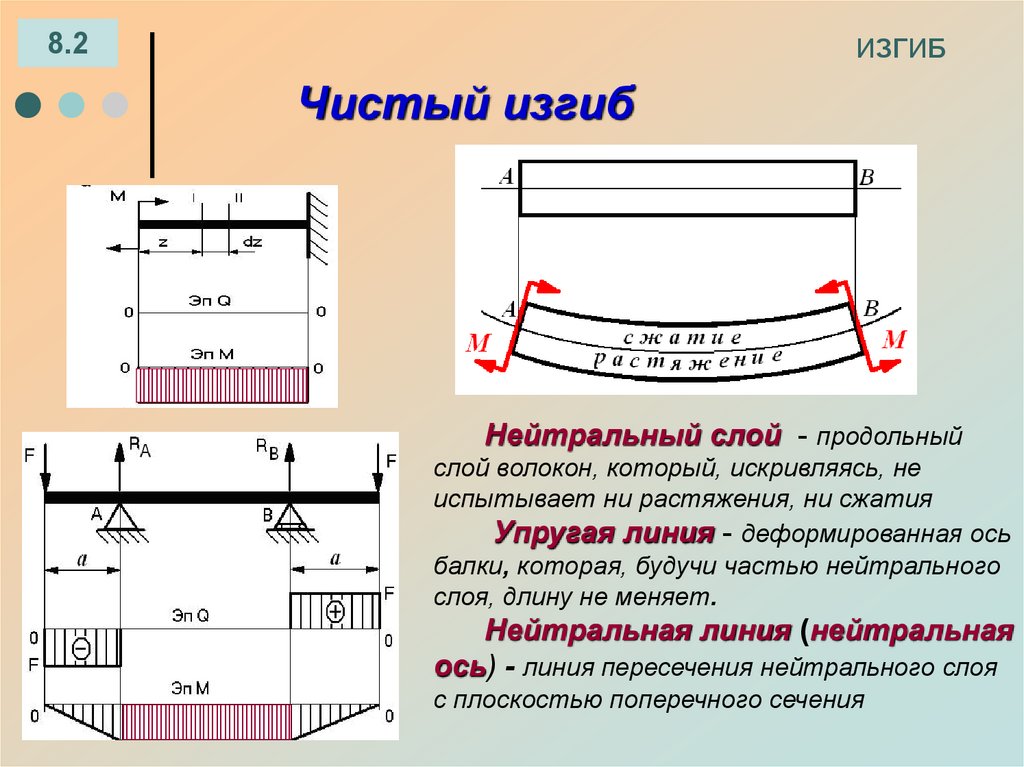
8.2
ИЗГИБ
Чистый изгиб
Нейтральный слой - продольный
слой волокон, который, искривляясь, не
испытывает ни растяжения, ни сжатия
Упругая линия - деформированная ось
балки, которая, будучи частью нейтрального
слоя, длину не меняет.
Нейтральная линия (нейтральная
ось) - линия пересечения нейтрального слоя
с плоскостью поперечного сечения

53. ИЗГИБ

8.3
ИЗГИБ
Напряжения при чистом изгибе
dz = ρ d .
M x y dA
A
ε = y/ρ.
σ =E·y /ρ.

54. ИЗГИБ

8.4
ИЗГИБ
Напряжения при чистом изгибе
Уравнения равновесия:
n
Fkz dA 0,
k 1
n
m x ( Fk ) dA y M 0,
k 1
n
A
k 1
A
m y ( Fk ) dA x 0.
Из первого уравнения равновесия:
dA
A
а так как
E
0, то
y dA S y 0
A
E
y dA 0,
A
Нейтральная ось проходит
через центр тяжести
сечения

55. ИЗГИБ

8.5
ИЗГИБ
Напряжения при чистом изгибе
Уравнения равновесия:
n
Fkz dA 0,
k 1
n
Третье из уравнений равновесия
E
dA
x
y x dA 0.
A
A
Так как
E
0,
y x dA I xy 0.
A
m x ( Fk ) dA y M 0,
k 1
n
A
k 1
A
m y ( Fk ) dA x 0.
то
Нейтральная линия совпадает с главной
центральной осью поперечного сечения
балки.

56. ИЗГИБ

8.6
ИЗГИБ
Напряжения при чистом изгибе
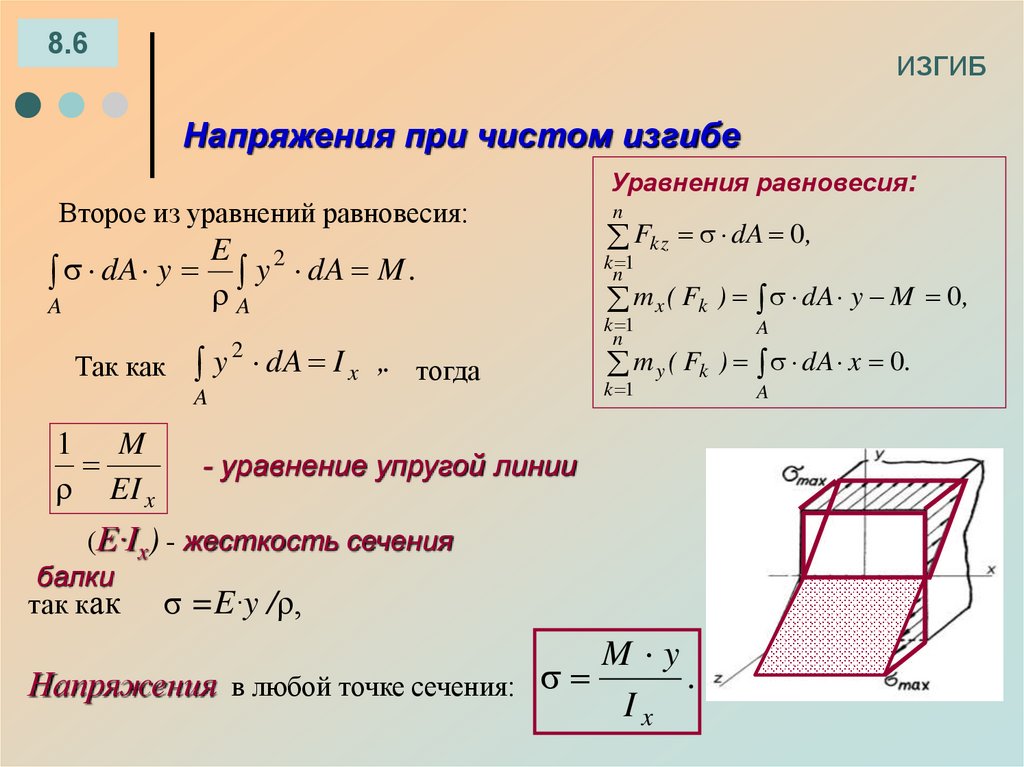
Второе из уравнений равновесия:
E 2
dA y y dA M .
A
A
2
y
dA I x ,. тогда
Так как
A
1 M
EI x
Уравнения равновесия:
n
Fkz dA 0,
k 1
n
m x ( Fk ) dA y M 0,
k 1
n
A
k 1
A
m y ( Fk ) dA x 0.
- уравнение упругой линии
(E·Ix) - жесткость сечения
балки
так как σ =E·y /ρ,
M y
.
Напряжения в любой точке сечения:
Ix

57. ИЗГИБ

8.7
ИЗГИБ
Напряжения при чистом изгибе
M y
.
Ix
Максимальное напряжение возникают в верхних
и нижних волокнах балки:
max
M y max
Ix
M
max
Wx
где:
Ix
Wx =
y max
- осевой момент сопротивления сечения
при изгибе

58. ИЗГИБ

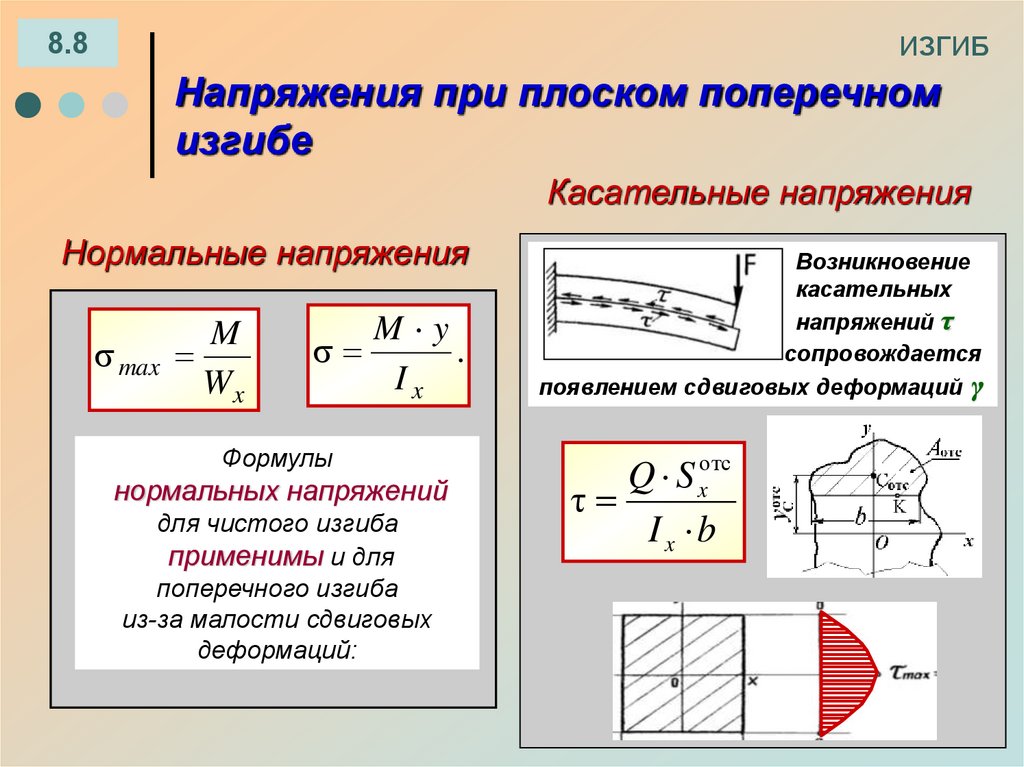
8.8
Напряжения при плоском поперечном
изгибе
Касательные напряжения
Нормальные напряжения
M
max
Wx
M y
.
Ix
Формулы
нормальных напряжений
для чистого изгиба
применимы и для
поперечного изгиба
из-за малости сдвиговых
деформаций:
Возникновение
касательных
напряжений τ
сопровождается
появлением сдвиговых деформаций γ
Q S xотс
τ
Ix b

59. ЛЕКЦИЯ 9 План:

9.1
МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Изгиб
ЛЕКЦИЯ 9
План:
9.1. Условие прочности при изгибе
9.2. Перемещения при изгибе

60. ИЗГИБ

9.2
ИЗГИБ
УСЛОВИЯ ПРОЧНОСТИ ПРИ ИЗГИБЕ
max [ ]
max
σ >> τ.
Момент сопротивления сечения
b
Wx= bh2/6
σmax , сравнивают с [σ] и делают
вывод о прочности балки.
Mx
max
Wx
h
Проверочный расчет: значение
d
Wx = πd 3/32
≈ 0,1d 3
Проектный расчёт:
M max
Wx
при известных значениях М и
допускаемого напряжения [σ]:
Расчёт допускаемой
нагрузки:
[ М ] [ ] Wx
при известных [σ] и Wx

61. ИЗГИБ

9.3
ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Прогиб балки у перемещение центра тяжести
поперечного сечения балки в
направлении, перпендикулярном
к ее оси.
у>0 если перемещение
происходит вверх.
Угол поворота сечения - угол, на который поворачивается
сечение по отношению к своему первоначальному положению.
>0 при повороте против хода часовой стрелки.

62. ИЗГИБ

9.4
ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Прогибы у и углы поворота
dy
связаны между собой: tgθ
y' θ
dz
1
y
.
3
2
1 y 2
y
M
2 32
EI x
1 y
Так как
y
1
, то
2
M
y
EI x
1 М
ЕI x
дифференциальное
уравнение упругой
линии
приближенное
дифференциальное
уравнение упругой линии

63. ИЗГИБ

9.5
ИЗГИБ
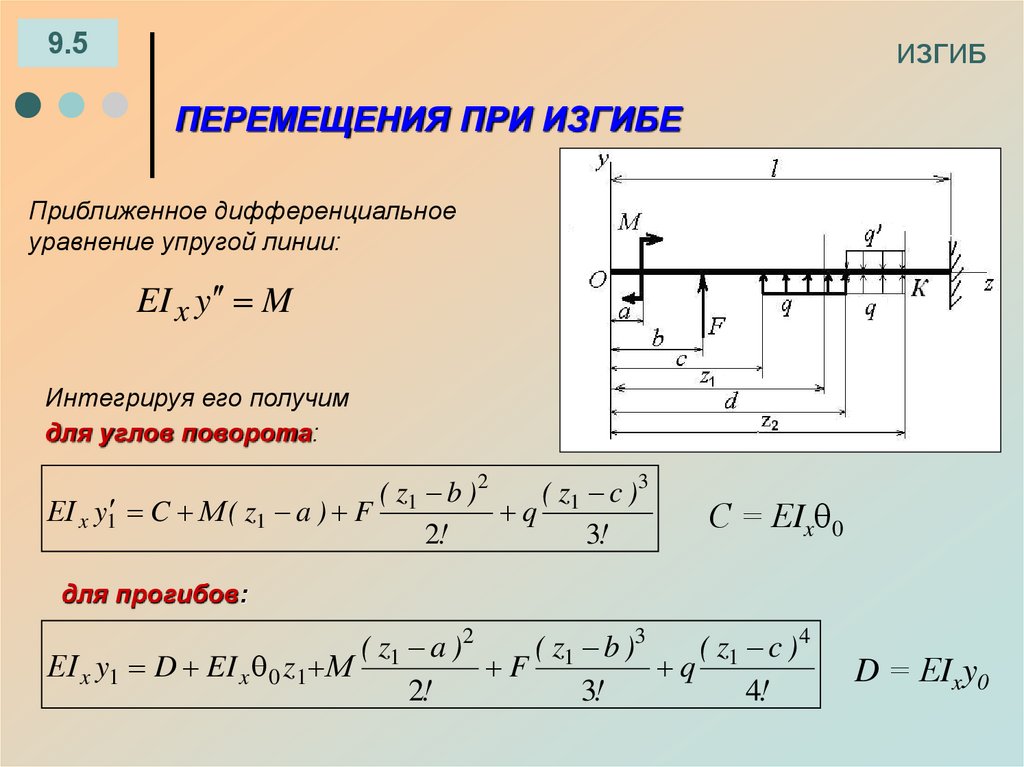
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Приближенное дифференциальное
уравнение упругой линии:
EI x y M
Интегрируя его получим
для углов поворота:
( z1 b )2
( z1 c )3
ЕI x y1 C М ( z1 a ) F
q
2!
3!
С = ЕIx 0
для прогибов:
( z1 a )2
( z1 b )3
( z1 c )4
ЕI x y1 D EI x 0 z1 М
F
q
2!
3!
4!
D = ЕIxy0

64. В общем виде УНИВЕРСАЛЬНЫЕ УРАВНЕНИЯ

9.6
ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
В общем виде УНИВЕРСАЛЬНЫЕ УРАВНЕНИЯ
для прогибов:
( z lq )
( z lM )2
( z lF )3
EI x у EI x y0 EJ x 0 z M
F
q
2!
3!
4!
4
для углов поворота :
( z lq )
( z lM )
( z l F )2
EI x EI x 0 M
F
q
1!
2!
3!
3
Начальные параметры находят из условий закрепления балки.
для консольной балки в заделке : y0 = 0, 0 = 0,
для балки на шарнирных опорах в опорных точках: yA = 0, yB = 0.

65. ИЗГИБ

9.7
ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Метод Мора:
В точке с искомым перемещением конструкцию
нагружают единичной силой, которая совершает
работу на возможном (искомом) перемещении.
Порядок определения перемещений :
1.
Строят «вспомогательную систему» и нагружают ее единичной
нагрузкой в точке с искомым перемещением .
2. Для каждого участка
системы записывают выражения изгибающих
.
моментов от приложенной нагрузки Мf и от единичной нагрузки - М1.
3. По всем участкам системы вычисляют и суммируют интегралы Мора,
получая в результате искомое перемещение :
M f M1
EI x
dz

66. ИЗГИБ

9.8
ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Правило Верещагина (графоаналитический способ)
Af – площадь эпюры изгибающего
момента Мf от заданной
нагрузки;
A f yc
yc – ордината эпюры от
единичной
EI x
нагрузки под центром
тяжести
эпюры Мf ;
EIx – жесткость сечения участка
балки.
Вычисления производятся по участкам,
на каждом из которых
прямолинейная эпюра должна быть без переломов.
Сложная эпюра Мf разбивается на простые фигуры.
Площадь каждой фигуры умножается на ординату под ее
центром тяжести

67. Раздел - 8. СЛОЖНОЕ СОПРОТИВЛЕНИЕ

МЕХАНИКА
Сопротивление материалов
Раздел - 8. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Напряжено-деформированное
состояние в точке
Сложное сопротивление бруса
ЛЕКЦИЯ 10
ЛЕКЦИЯ 11
ЛЕКЦИЯ 12

68. ЛЕКЦИЯ 10 План:

10.1
МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Теория напряженно-деформированного
состояния
ЛЕКЦИЯ 10
План:
10.1. Напряженное состояние в точке
10.2. Обобщенный закон Гука
10.3. Теории прочности

69. СЛОЖНОЕ СОПРОТИВЛЕНИЕ

10.2
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ - это
совокупность напряжений на множестве площадок,
которые можно провести через какую-либо точку тела
Закон парности
касательных напряжений :
τxy = τyx , τxz = τzx, τzy = τyz.
Главные площадки
1, 2, 3, - Главные напряжения
1 2 3
1 3
max
2
(с учетом знаков)

70. СЛОЖНОЕ СОПРОТИВЛЕНИЕ

10.3
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ
Различают
напряженные состояния :
- одноосное (линейное);
- двухосное (плоское);
- трехосное (объемное).
Линейное
напряженное состояние:
1≠ 0, 2 = 0, 3 = 0,
max= 1
max = 1/2 при = 45

71. СЛОЖНОЕ СОПРОТИВЛЕНИЕ

10.4
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ
Плоское
напряженное состояние:
1≠ 0, 2 ≠ 0, 3 = 0,
1 = x ;
2 = y ;
3 = 0
1
max ( x y ) ( x y )2 4 xy 2
2
min
Положение главных площадок
определяют по углу поворота осей ψ0:
2
tg 2 0
x y