Похожие презентации:
Основы логики
1. ОСНОВЫ ЛОГИКИ
…изсловесного царства, полного неопределённостей, в царство
математики, где отношения между объектами или высказываниями
определяется совершенно точно»
Г.В. Лейбниц
ОСНОВЫ
ЛОГИКИ
2. План занятия
Историческая справка
Алгебра логики
Понятие
Высказывание
Умозаключение
Алгебра (логики) высказываний
Понятия алгебры логики
Базовые логические операции
Таблица истинности
Таблица истинности для
конъюнкции
истинности
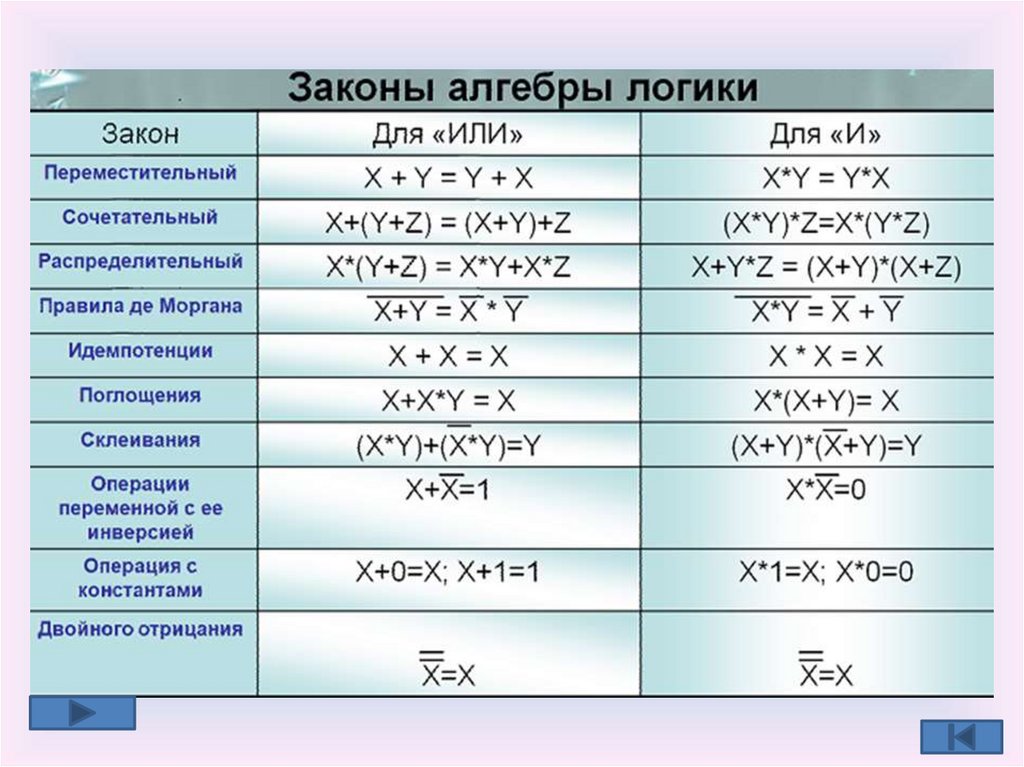
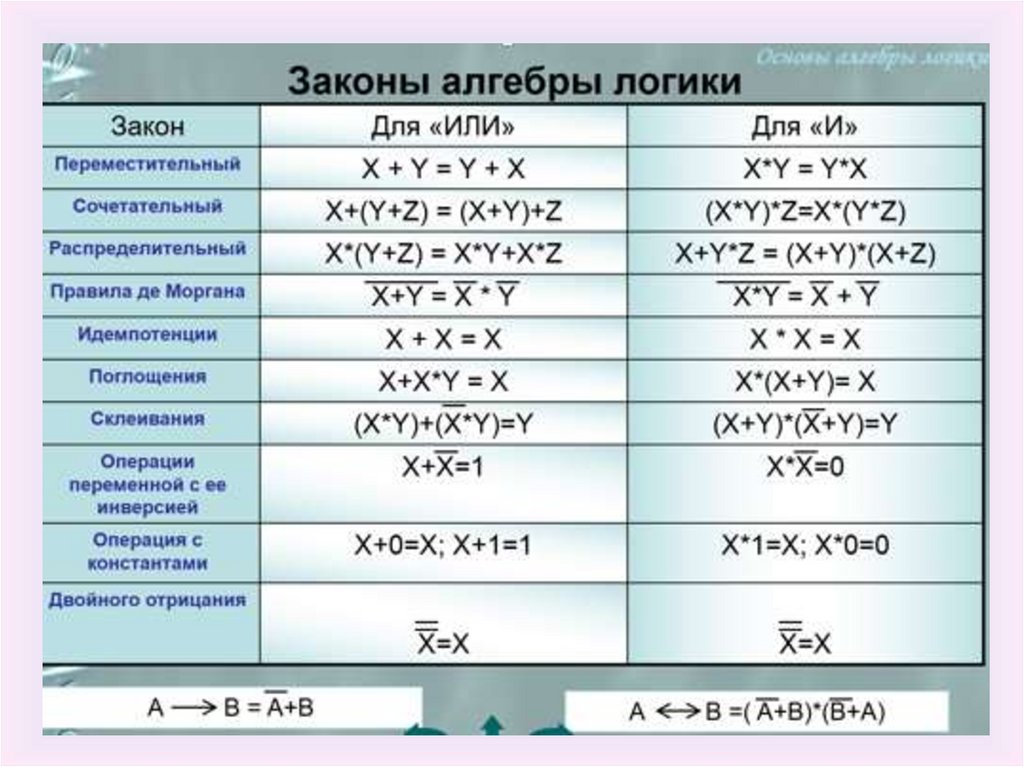
Законы алгебры логики
Таблица истинности для
дизъюнкции
Таблицы истинности для инверсии
Порядок выполнения логических
операций
Пример
Упражнения
Пример составления таблицы
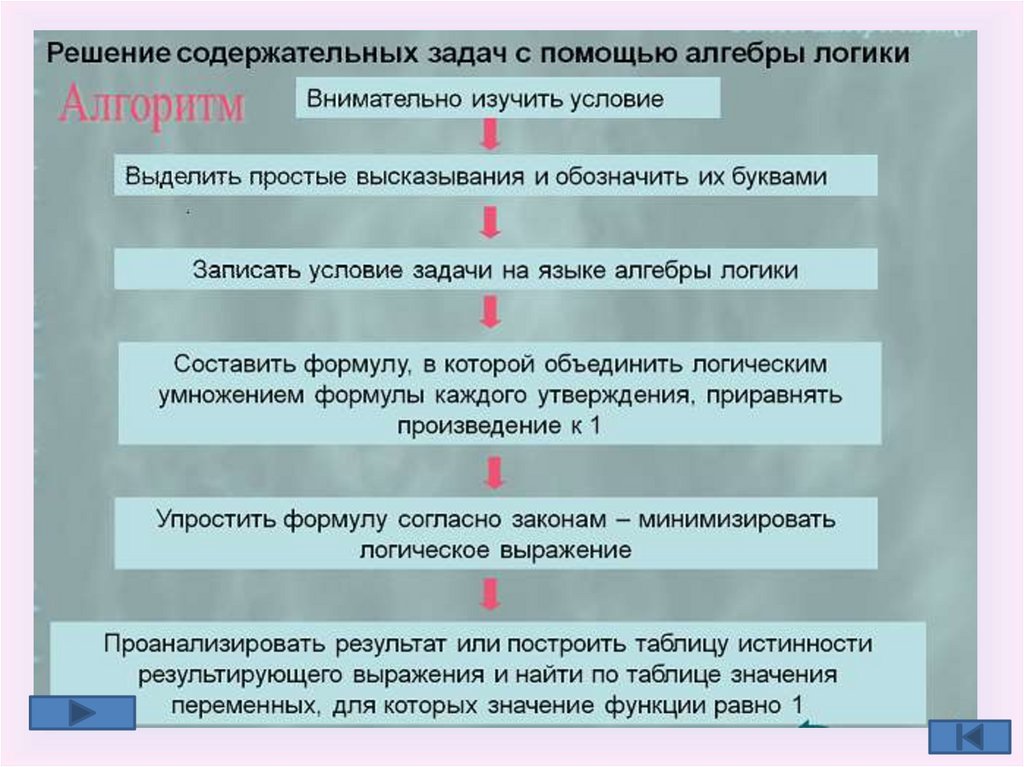
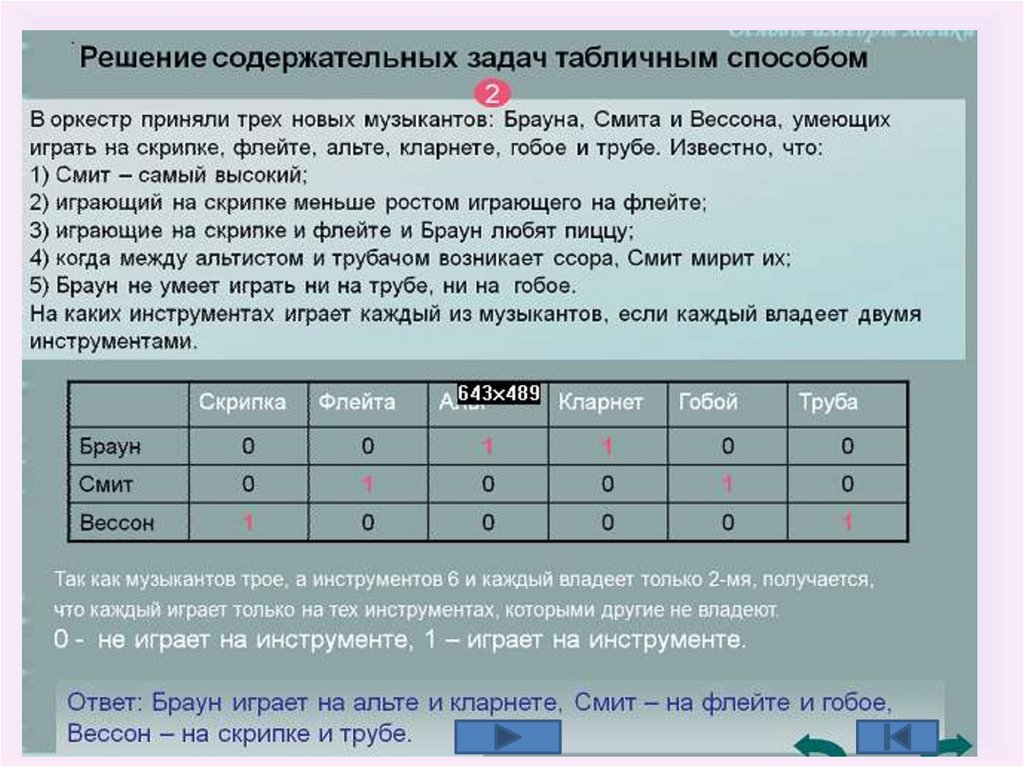
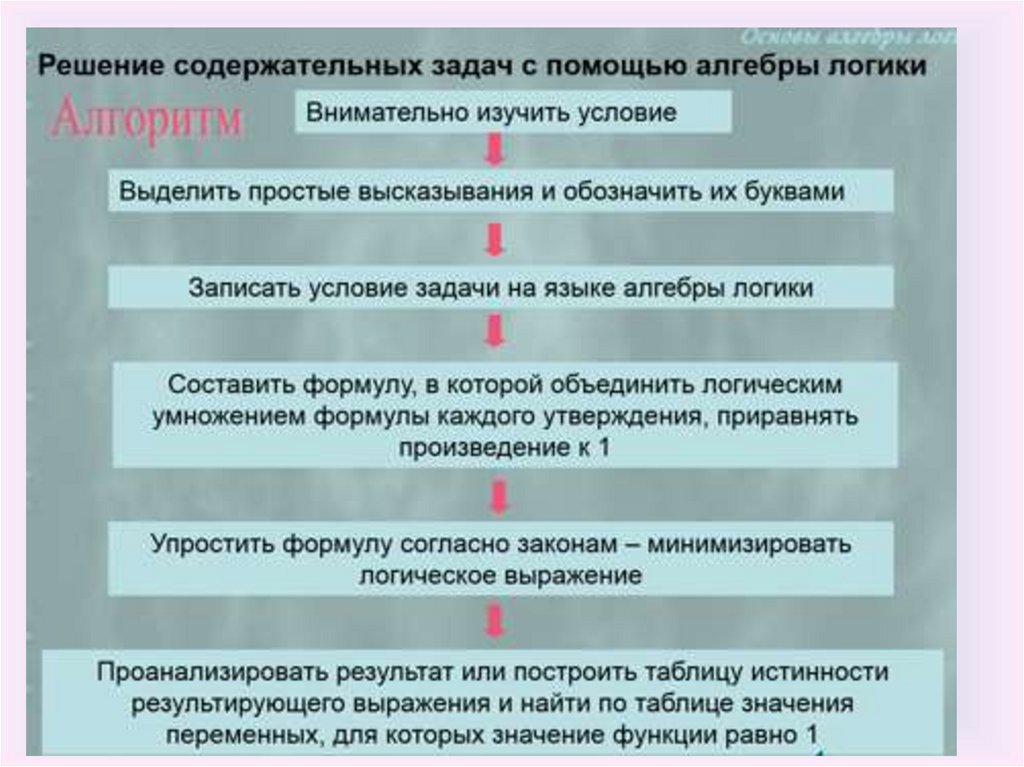
Решение содержательных задач
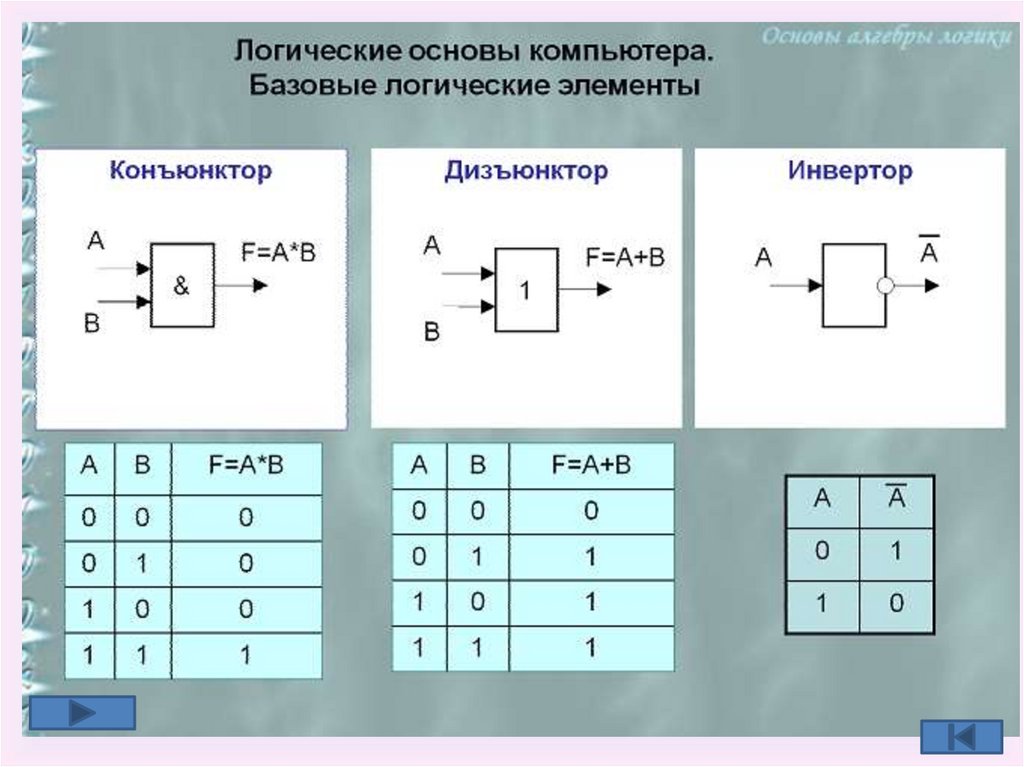
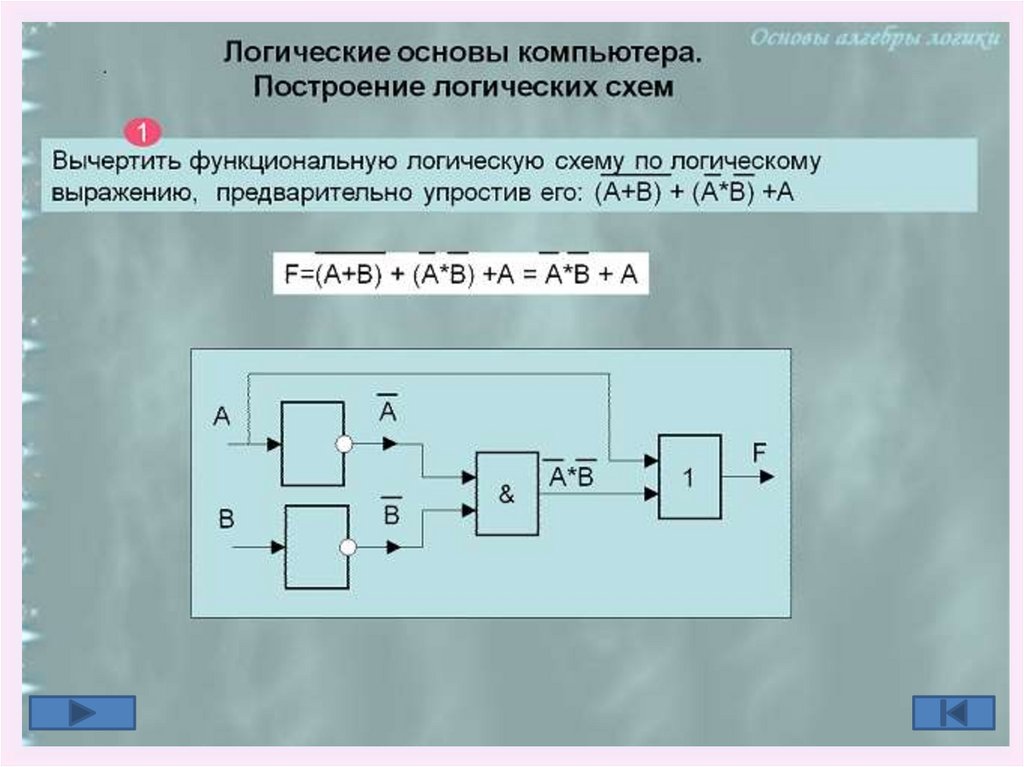
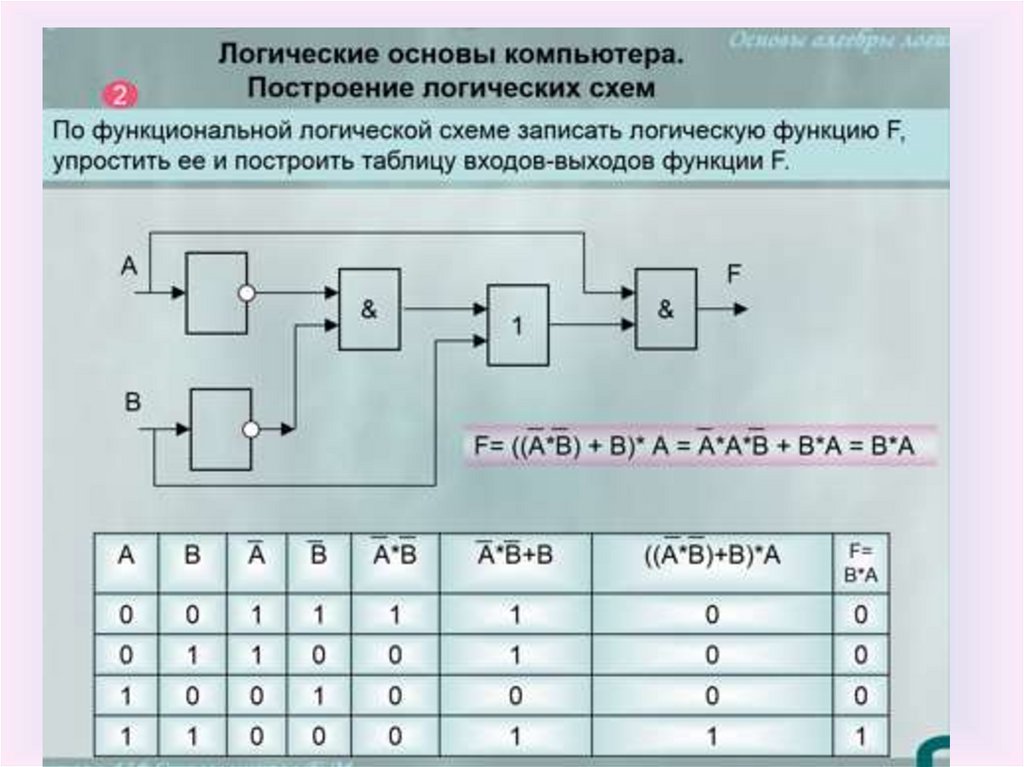
Логические основы компьютера
Построение логических схем
Вопросы для самопроверки
Темы для исследований
3. ЛОГИКА
НАУКА О ФОРМАХ ИСПОСОБАХ
МЫШЛЕНИЯ
4.
1 этап –формальная
логика
Основатель –
Аристотель
(384 -322гг. до н.э. )
Ввёл основные формулы
абстрактного
мышления
5.
• 2 этап – математическаялогика
• Основатель – немецкий
ученый и философ
Лейбниц(1642 -1716),
предпринял попытку
логических вычислений.
6.
• 3 этап - Алгебра высказываний(Булева алгебра)
Основатель - английский математик
Джордж Буль (1815 – 1864),ввёл алфавит,
орфографию и грамматику для
математической логики(1842).
Спустя 100 лет алгебра логики стала
основой теории цифровых ВМ, ее
используют в компьютерной логике,
электронике, в основе всех
микропроцессорных операций.
7. Алгебра логики – это математический аппарат с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают
8. ПОНЯТИЕ
форма мышления, которая выделяетсущественные признаки предмета или
класса предметов, позволяющие отличать
их друг от друга
(Пример: Прямоугольник - геометрическая
фигура у которой все углы прямые и
противоположные стороны равны)
9. ВЫСКАЗЫВАНИЕ
формулировка своего пониманияокружающего мира
(повествовательное предложение в
котором что-либо утверждается или
отрицается)
(Пример: Париж – столица Франции)
10. ВЫСКАЗЫВАНИЕ
ИСТИННОЕ(Пример: Буква «А» гласная)
ЛОЖНОЕ
(Пример: Компьютер
был изобретен до
нашей эры)
11.
1) Здравствуй!2) Аксиома не требует доказательств.
3) Идёт дождь.
4) Какая температура на улице?
5) Число 2 является делителем числа 9.
6) Число х не больше двух.
7) Уходя гасите свет.
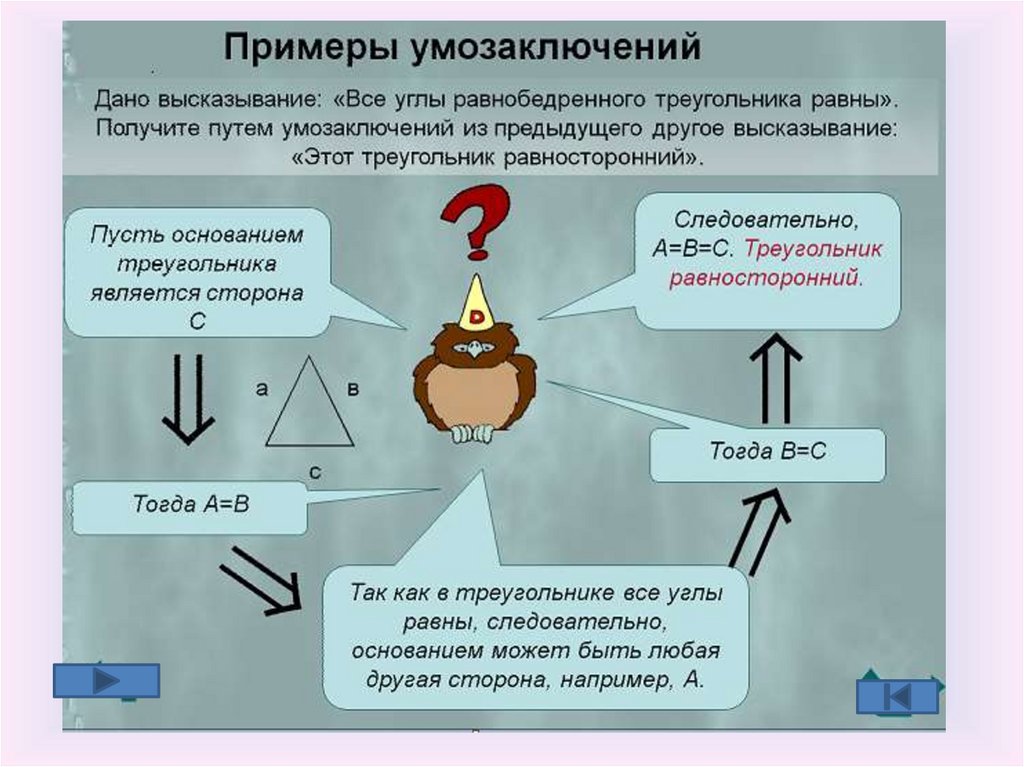
12. УМОЗАКЛЮЧЕНИЕ
форма мышления, с помощью которойиз одного или нескольких суждений
может быть получено новое
суждение
(знание или вывод)
(Пример: любая теорема)
13.
14. АЛГЕБРА ЛОГИКИ(ВЫСКАЗЫВАНИЙ)
наука об общих операциях, аналогичныхсложению и умножению, которые
выполняются над высказываниями
Смысл
высказывания
Истинность
или ложность
высказывания
15. Понятия алгебры логики:
• Логическая переменная – это простоевысказывание, содержащее только одну мысль
– Обозначение: латинская буква (А, В, Х …)
– Значение: ИСТИНА (1) или ЛОЖЬ (0)
• Логическая функция – это составное
высказывание, которое содержит несколько
простых мыслей, соединенных между собой с
помощью логических операций
– Обозначение: F
• Логические операции – логическое действие
16.
1. Информатика изучается в курсе средней школы.2. «Е»- шестая буква алфавита.
3. Квадрат является ромбом.
4. Квадрат гипотенузы равен сумме квадратов
катетов.
5. Сумма углов треугольника равна 1900.
6. 12+14>30
7. Графическое изображение векторной графики
формируется из точек(пикселей).
8. 16-битные звуковые карты точнее кодируют и
воспроизводят звук, чем 8-битные.
17. Базовые логические операции
НазваниеОбозначе
ние
Союз в
естественном
языке
Пример
А – «Число 10 – четное»
В – «Число 10 – отрицательное»
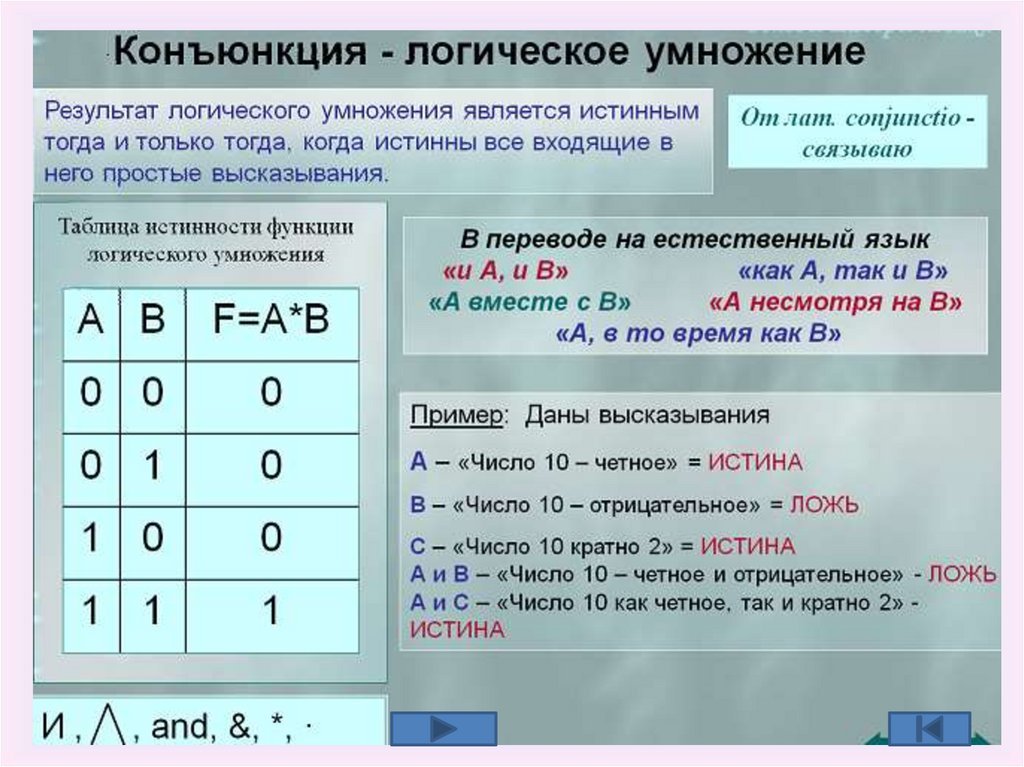
Конъюнкция
(логическое
умножение)
А^B
или
A&B
И
«Число 10 четное и
отрицательное» - ЛОЖЬ
Дизъюнкция
(логическое
сложение)
AvB
ИЛИ
«Число 10 четное или
отрицательно» - ИСТИНА
Инверсия
(отрицание)
¬A
или
Ā
НЕ
«Число 10 нечетное» – ЛОЖЬ
«Число 10 – не отрицательное» ИСТИНА
18. Таблица истинности
таблица определяющаязначение сложного
высказывания при всех
возможных значениях
простых высказываний
19.
20.
21.
22.
Если составное высказывание(логическую функцию) выразить в
виде формулы, в которую войдут
логические переменные и знаки
логических операций, то получится
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
истина
ложь
23. Порядок выполнения логических операций:
• Действия в скобках• Инверсия
• Конъюнкция
• Дизъюнкция
24. ПРИМЕР: Записать в виде логического выражения следующее высказывание: «Летом Петя поедет в деревню и будет ходить на рыбалку.
• Это составное высказывание состоит из 2-хпростых высказываний:
А = «Петя поедет в деревню»
В = «Будет ходить на рыбалку»
• Записываем высказывание в виде
логического выражения, учитывая порядок
действий
F=A^B
25. Упражнения:
1. Есть два простых высказывания:А = «Число 10 четное»
В = Волк – травоядное животное»
Составьте из них все возможные составные
высказывания и определите их истинность
2. Запишите следующие высказывания в виде
логических выражений:
Неверно, что корова – хищное животное
На уроке физики ученики выполняли
лабораторную работу и сообщали результаты
учителю.
Если Маша – сестра Саши, то Саша - брат Маши.
26.
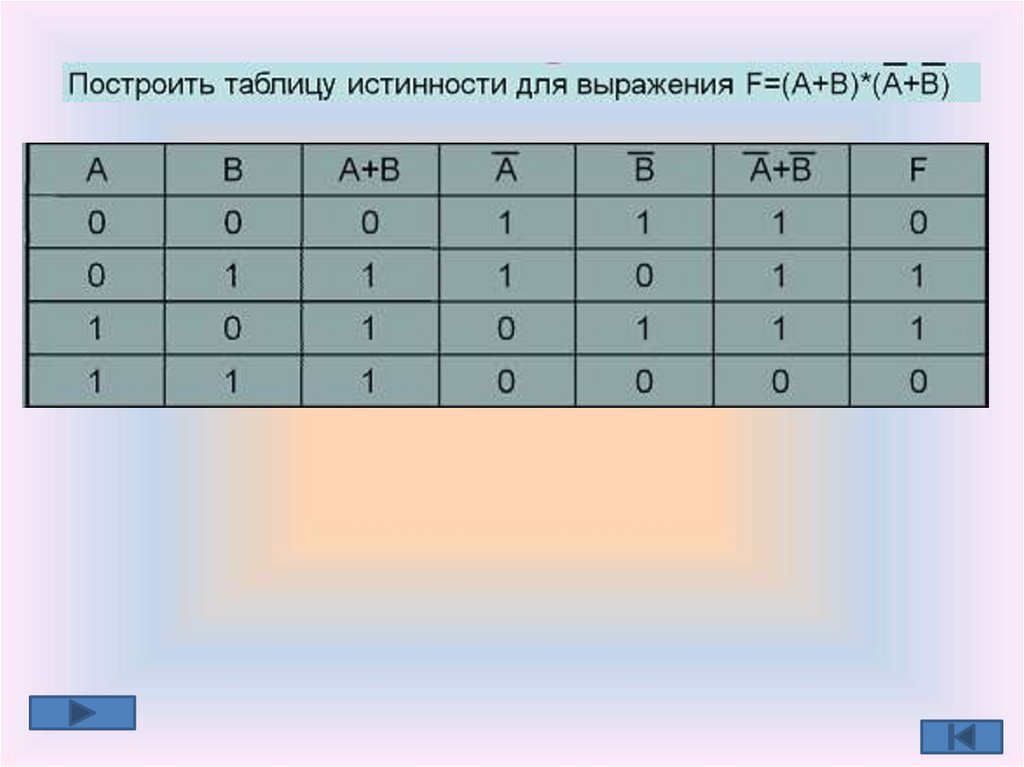
Алгоритм построения таблиц истинности• Определить количество наборов (строк в таблице)
по формуле Q=2n. (n-количество высказываний)
• Определить количество столбцов в таблице =
количество переменных+количество операций
• Разделить колонку значений первой переменной
пополам и заполнить верхнюю половину 0,
нижнюю половину 1.
• В следующей колонке для второй переменной
половину снова делить пополам и заполнить
четырьмя группами 0 и 1, вперемежку, начиная
опять с группы 0 и т.д.
27.
28.
29.
30.
31.
32.
Лекция 1133.
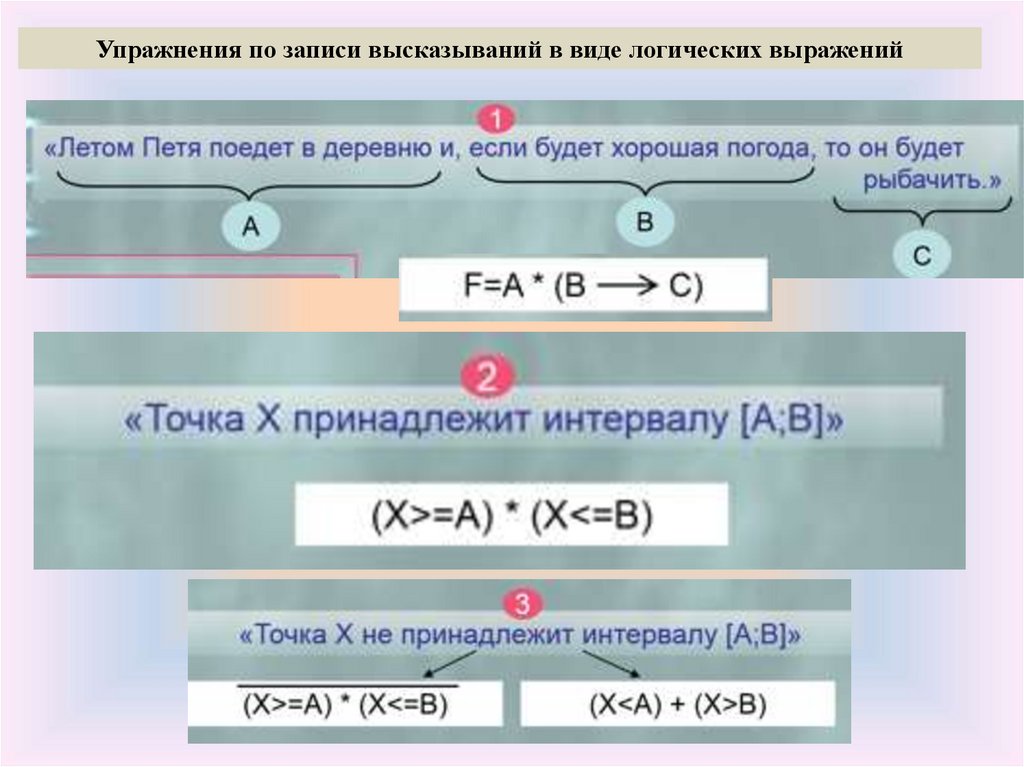
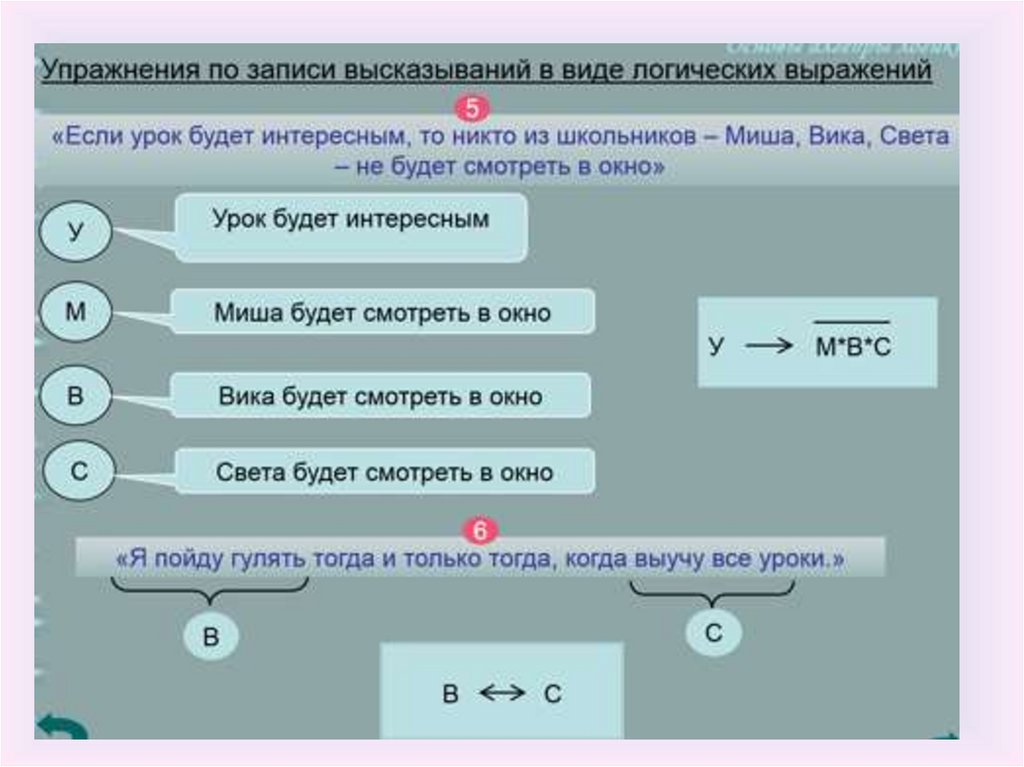
Упражнения по записи высказываний в виде логических выражений34.
35.
36.
37.
38.
39.
40.
41.
42.
• Кто является основателем формальной логики?• Дайте определение логики как науки. Каково её
назначение?
• Какие существуют основные формы мышления?
• Что
такое
высказывание?
Приведите
примеры
высказываний и предложений, не являющихся ими.
• Перечислите базовые логические операции.
• Для чего нужны таблицы истинности?
• Назовите базовые логические элементы?
























 Информатика
Информатика








