Занятие 3. Кодирование информации. Системы счисления

1.

МК
Занятие 3:
Кодирование информации.
Системы счисления
Информатика
1 курс СПО

2.

МК
Ключевые слова
• системы счисления
• позиционная система счисления
• непозиционная система счисления
• базис системы счисления
• схема Горнера

3.

МК
МК
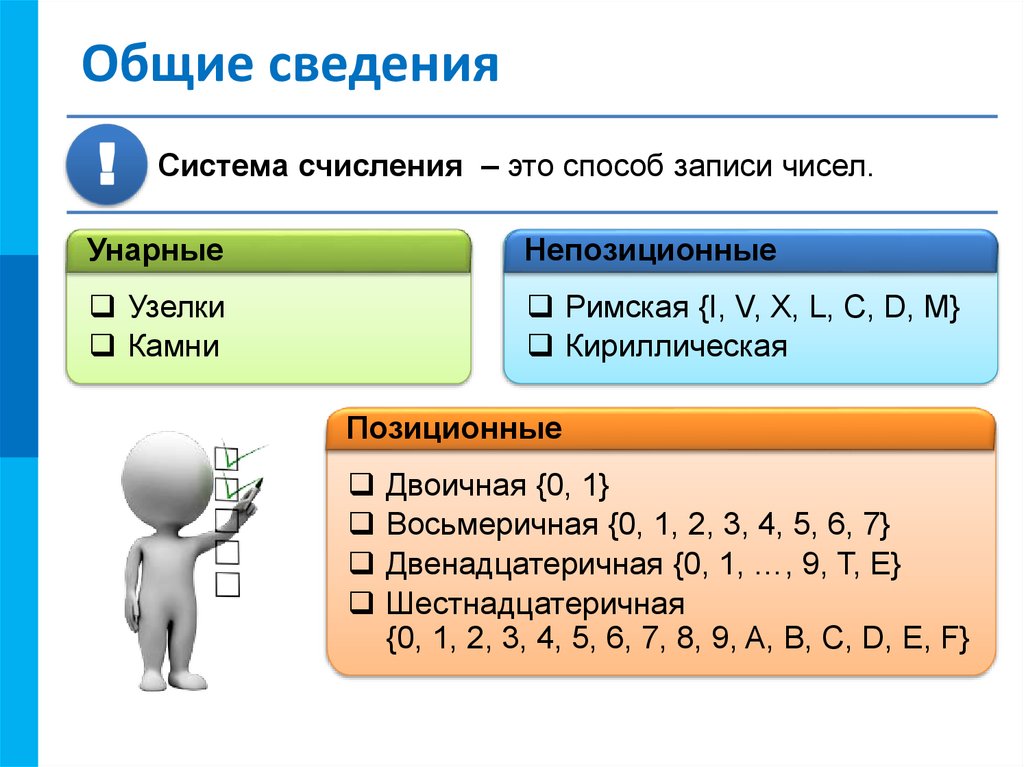
Общие сведения
!
Система счисления – это способ записи чисел.
Унарные
Непозиционные
Узелки
Камни
Римская {I, V, X, L, C, D, M}
Кириллическая
Позиционные
Двоичная {0, 1}
Восьмеричная {0, 1, 2, 3, 4, 5, 6, 7}
Двенадцатеричная {0, 1, …, 9, T, E}
Шестнадцатеричная
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}

4.

МК
Позиционные системы
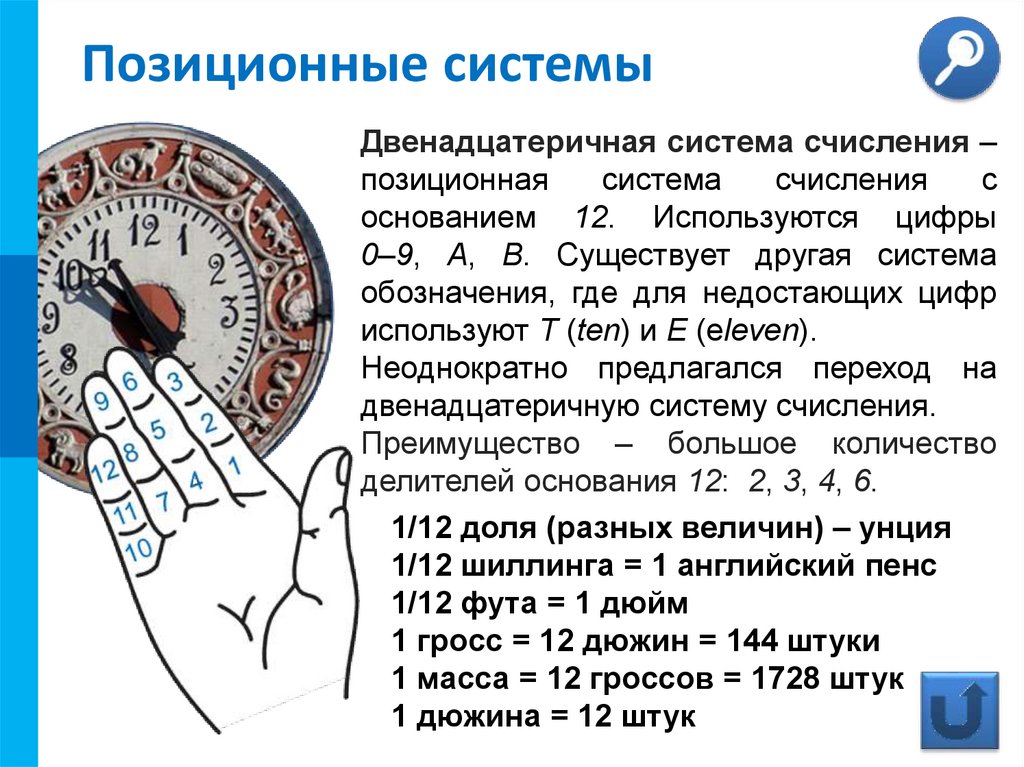
Двенадцатеричная система счисления –
позиционная
система
счисления
с
основанием 12. Используются цифры
0–9, A, B. Существует другая система
обозначения, где для недостающих цифр
используют T (ten) и E (eleven).
Неоднократно предлагался переход на
двенадцатеричную систему счисления.
Преимущество – большое количество
делителей основания 12: 2, 3, 4, 6.
1/12 доля (разных величин) – унция
1/12 шиллинга = 1 английский пенс
1/12 фута = 1 дюйм
1 гросс = 12 дюжин = 144 штуки
1 масса = 12 гроссов = 1728 штук
1 дюжина = 12 штук

5.

МК
Непозиционные системы
Часы (Суздаль)
Кириллическая система счисления основана на
алфавитной записи чисел с использованием кириллицы или
глаголицы. Применялась в России до начала XVIII века. В
настоящее время
используется в церковнославянском
языке.
Для отличия от букв над числовым значением писался
специальный знак – титло.

6.

МК
Система счисления
Система счисления – это способ записи чисел
по определенным правилам с помощью
специальных знаков – цифр.
Числа:
523
1010011
CXL
Цифры:
0, 1, 2, 3,…
0,1
I, V, X, L, …
Знаки (символы), используемые в СС для
обозначения чисел, называются цифрами.
Алфавит – это набор цифр. {0, 1, 2, …, 9}

7.

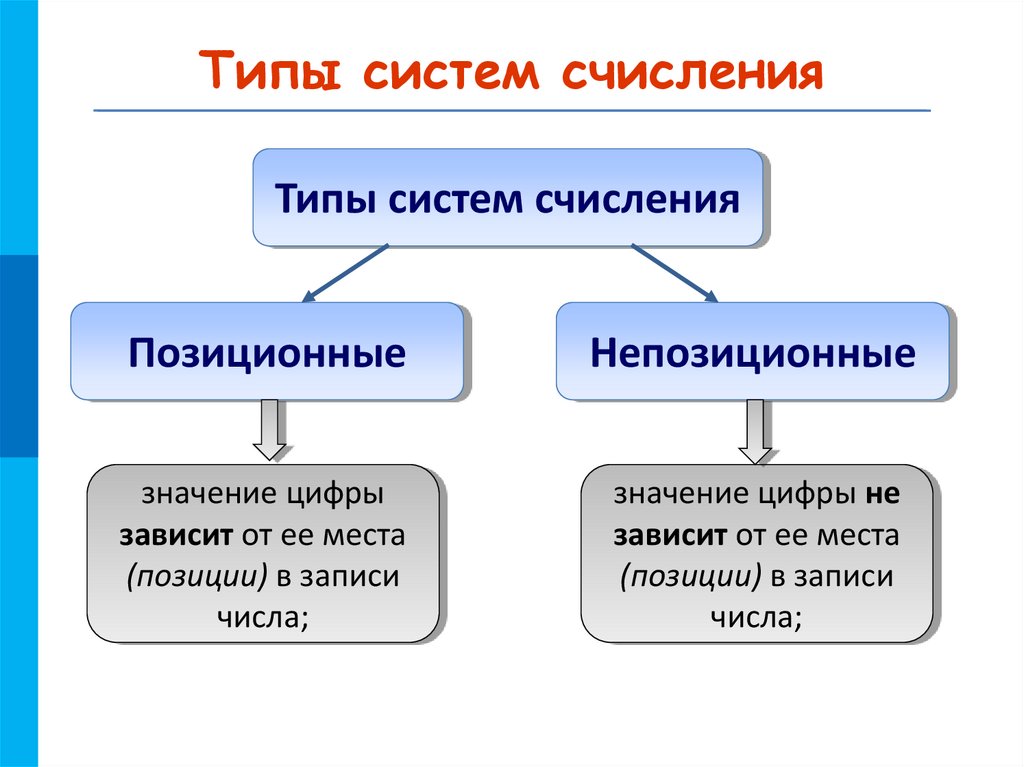
МК
Типы систем счисления
Типы систем счисления
Позиционные
Непозиционные
значение цифры
зависит от ее места
(позиции) в записи
числа;
значение цифры не
зависит от ее места
(позиции) в записи
числа;

8.

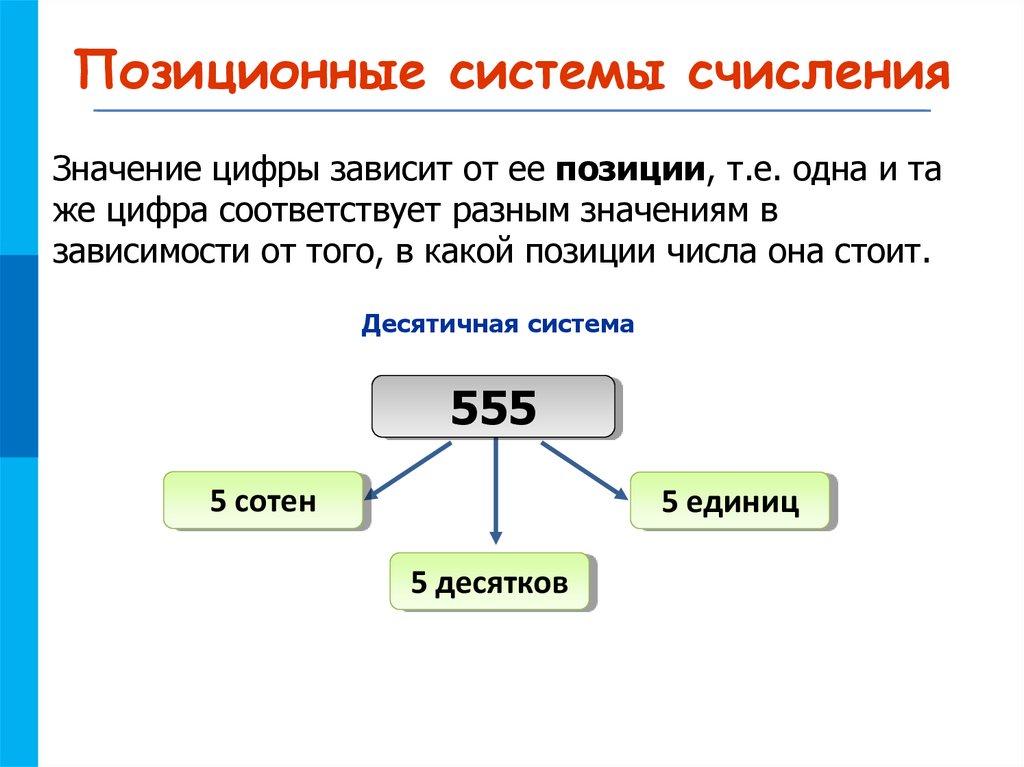
МК
Позиционные системы счисления
Значение цифры зависит от ее позиции, т.е. одна и та
же цифра соответствует разным значениям в
зависимости от того, в какой позиции числа она стоит.
Десятичная система
555
5 сотен
5 единиц
5 десятков

9.

МК
Позиционные системы счисления
Основание системы счисления (N) - количество
цифр (знаков), используемых для представления чисел
Основание
Алфавит
Пример
Двоичная система счисления
N=2
0, 1
10010112
Четверичная система счисления
N=4
0, 1, 2, 3
23014

10.

МК
Позиционные системы счисления
Основание
Алфавит
Пример
Восьмеричная система счисления
N=8
5278
0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная система счисления
N=16
10 11 12 13 14 15
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F
2F516

11.

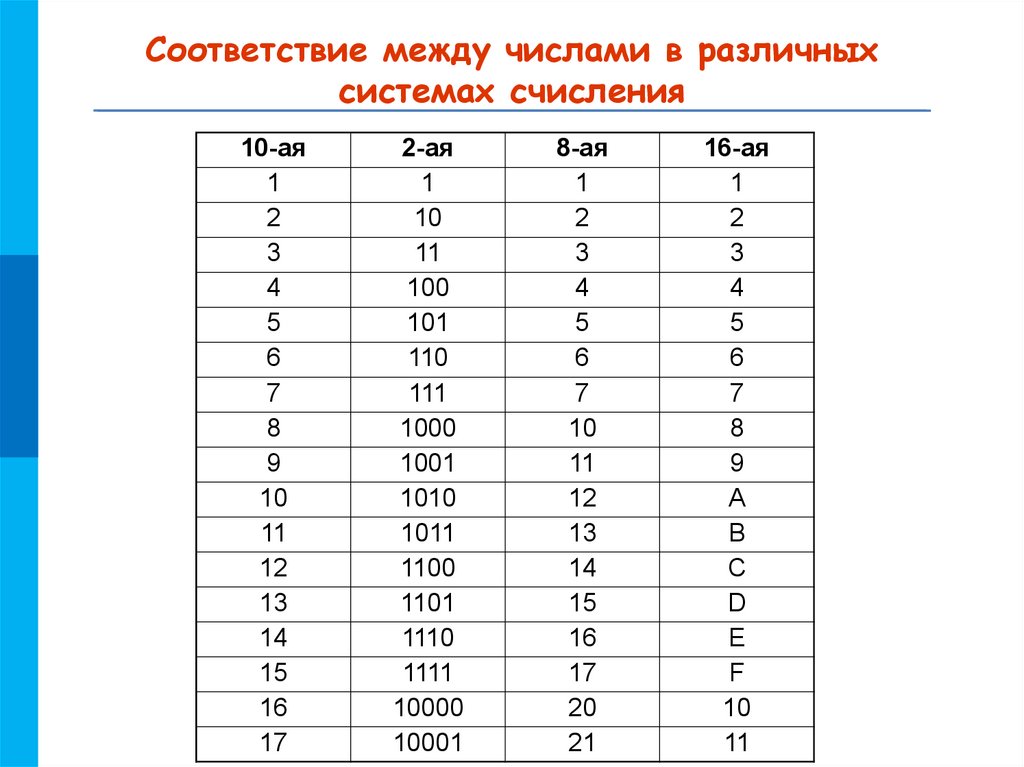
МК
Соответствие между числами в различных
системах счисления
10-ая
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2-ая
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
10000
10001
8-ая
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
20
21
16-ая
1
2
3
4
5
6
7
8
9
А
В
С
D
E
F
10
11

12.

МК
Перевод чисел из 10-й СС в 2-ю СС
Правила перевода
Разделить десятичное число на 2. Получится
частное и остаток.
Частное опять разделить на 2. Выполнять деление
до тех пор, пока последнее частное не станет
меньшим 2.
Записать последнее частное и все остатки в
обратном порядке. Полученное число и будет
двоичной записью исходного десятичного числа.

13.

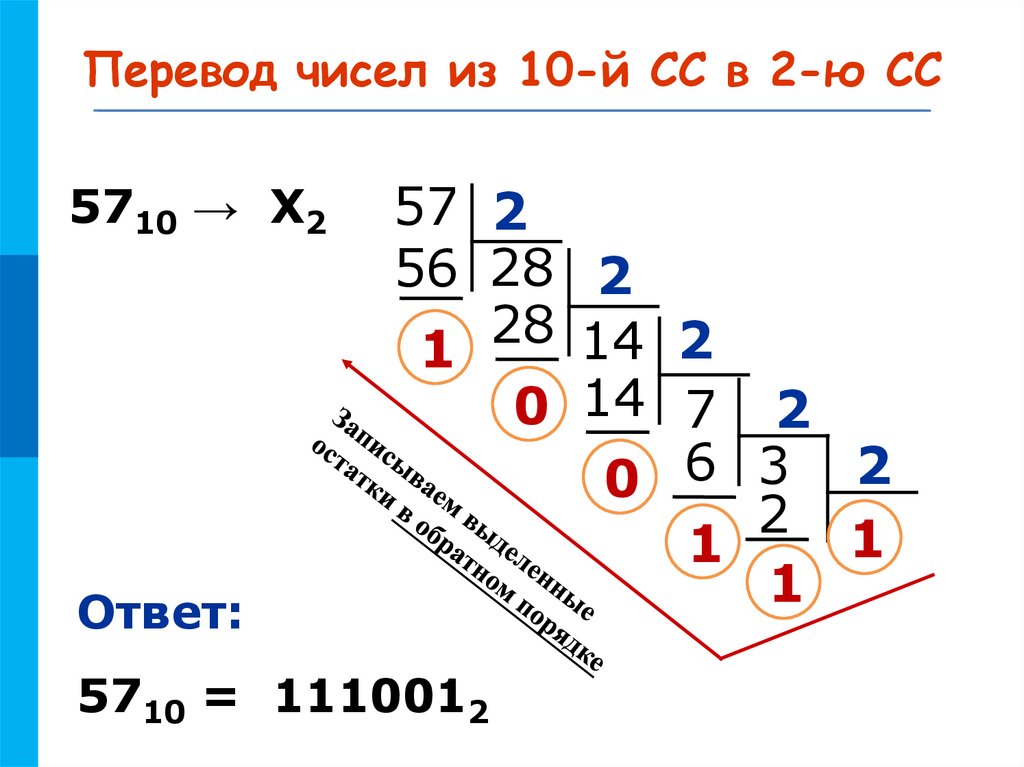
МК
Перевод чисел из 10-й СС в 2-ю СС
5710 → Х2
Ответ:
57 2
56 28 2
28
14 2
1
0 14 7 2
0 6 3 2
2 1
1
1
5710 = 1110012

14.

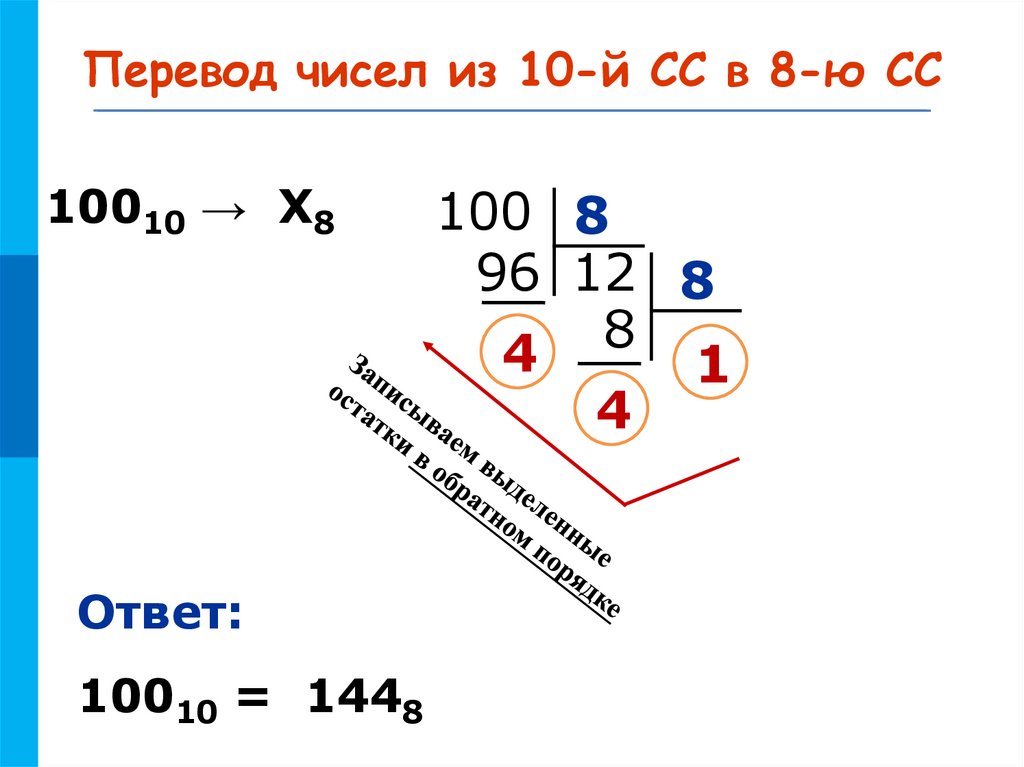
МК
Перевод чисел из 10-й СС в 8-ю СС
10010 → Х8
Ответ:
10010 = 1448
100 8
96 12 8
8
4
1
4

15.

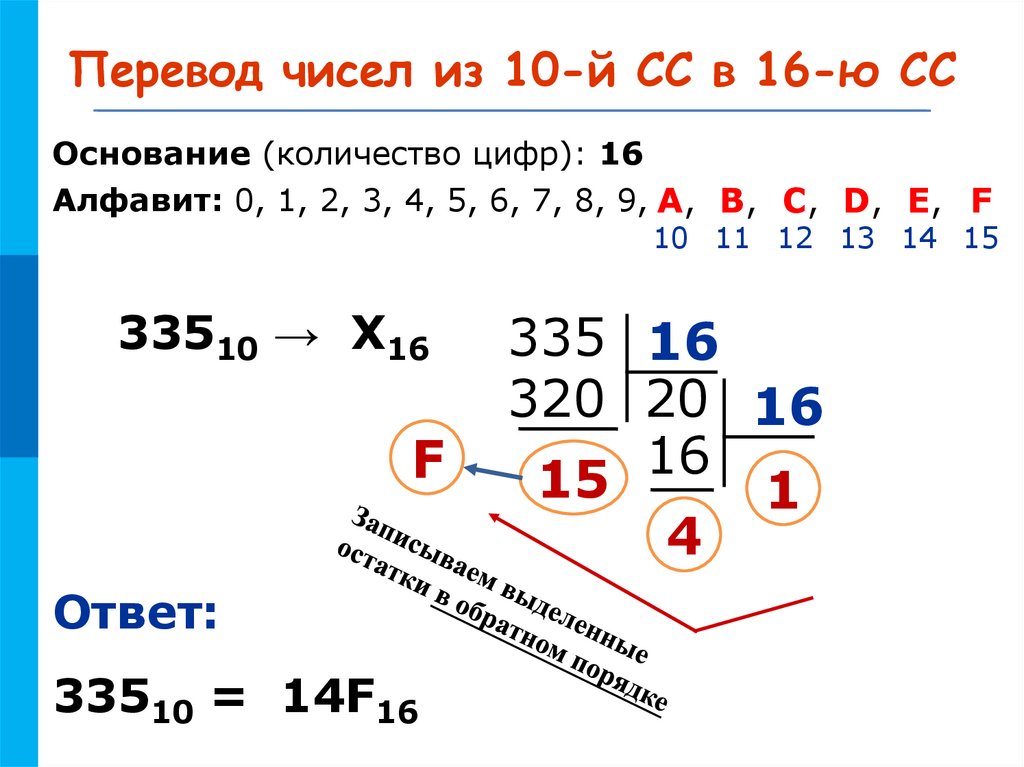
МК
Перевод чисел из 10-й СС в 16-ю СС
Основание (количество цифр): 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
10 11 12 13 14 15
33510 → Х16
F
Ответ:
33510 = 14F16
335 16
320 20 16
16
15
1
4

16.

МК
Решение задач
В двоичную систему:
В четверичную систему:
18510 = 101110012
7810 = 10324
185 2
184 24 2
1 24 12 2
0 12 6 2
0 6 3 2
02 1
1
78 4
76 19 4
2 16 4 4
3 4 1
0

17.

МК
Решение задач
Восьмеричная система:
7510 = 1138
13210 = 2048
27910 = 4278
75 8
72 9 8
3 8 1
1
132 8
128 16 8
4 16 2
0
279 8
272 34 8
7 32 4
2

18.

МК
Решение задач
Шестнадцатиричная система:
10710 = 6В16
25010 = FA16
72110 = 2D116
107 16
96 6
11
250 16
240 15
10
721 16
720 45 16
1 32 2
13

19.

МК
Перевод в десятичную СС
Любое позиционное число можно представить в виде
суммы степеней основания системы.
Формы записи числа
Свернутая
Развернутая
27510 =2*100+7*10+5*1 =
=2*102+7*101+5*100

20.

МК
Перевод из 2-ой в 10-ую СС
Для перехода из двоичной системы счисления в
десятичную необходимо двоичное число представить в
виде суммы степеней двойки и найти ее десятичное
значение.
Разряд цифры
3 2 1 0
11012=1*23+1*22+0*21+1*2=
Основание системы
=8+4+1 = 13

21.

МК
Решение задач
43 21 0
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 1910
7 6 5 4 3 210
11011100 = 1*27 + 1*26 + 1*24 +
+ 1*23 + 1*22 =
= 128 + 64 + 16 + 8 + 4 =22010

22.

МК
Перевод из 8-ой в 10-ую СС
1 0
718
2 1 0
1
0
2
1
= 7*8 +1*8 = 56+1= 5710
0
1448 = 1·8 + 4·8 + 4·8 =
= 64 + 32 + 4 = 10010

23.

МК
Перевод из 16-ой в 10-ую СС
1 0
7А16
2 1 0
1
0
= 7·16 + 10·16 =
= 112 + 10 = 12210
2
1
0
2С616= 2·16 + 12·16 + 6·16 =
= 512 + 192 + 6 = 71010
2 10
1C516 = 1·162 + 12·161 + 5·160
= 256 + 192 + 5 = 453

24.

МК
Самое главное
Система счисления – это способ записи чисел.
Система счисления называется позиционной, если
количественный эквивалент цифры зависит от её положения
в записи числа.
Существует бесконечно много позиционных систем
счисления. Каждая из них определяется целым числом q > 1,
называемым основанием системы счисления.
Для записи чисел в позиционной системе счисления с
основанием q нужен алфавит из q цифр: 0, 1, 2, …, q – 1.

25.

МК
Самое главное
Представление числа в виде конечной суммы степеней
числа q (суммы разрядных слагаемых) называется
развёрнутой формой записи числа в системе счисления с
основанием q.
Для перевода числа Aq в десятичную систему счисления
достаточно:
1. Записать развёрнутую форму числа Aq .
2. Представить все числа, фигурирующие в развёрнутой
форме, в десятичной системе счисления.
3. Вычислить значение полученного выражения по
правилам десятичной арифметики.

26.

МК
Домашнее задание
?
Перевести число из десятичной системы
счисления
в
двоичную,
восьмеричную,
шестнадцатеричную системы:
196=
Перевести числа в десятичную систему
счисления:
1011012=
1728=
5B716=

27.

МК
МК
Информационные источники
http://i4.fastpic.ru/big/2011/0316/17/763de43b420e65f3bd5a5f475597e617.png
http://www.rzd-expo.ru/images/history/Railways_of%20_the_Crimea/20.jpg
http://alkerz.ru/uploads/posts/2015-04/stati-vdomim-abo-yak-postaviti-galochku-v-kontakt_653.png
https://goo.gl/dtQ7ly
http://windowsmir.ru/wp-content/uploads/2016/06/GIMP_logo.jpg
http://gabrielecirulli.github.io/2048/