Похожие презентации:
Начертательная геометрия. Курс лекций. Электронный вариант пособия
1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ КУРС ЛЕКЦИЙ
В.И. АЛЕКСЕЕВНАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
КУРС ЛЕКЦИЙ
2. ЭЛЕКТРОННЫЙ ВАРИАНТ ПОСОБИЯ СООТВЕТСТВУЕТ УЧЕБНОМУ ПОСОБИЮ:
Алексеев В.И.Начертательная геометрия: курс лекций
учеб. пособие.
– Владивосток:
Мор. гос. ун-т,
2018.
– 162 с.
3.
Начертательная геометрия –это одно из направлений геометрии
Все геометрии отличаются МЕТОДОМ РЕШЕНИЯ ЗАДАЧ
в начертательной геометрии при решении задач используют
МЕТОД ПРОЕЦИРОВАНИЯ
ЗАДАЧИ РЕШАЮТ НЕ С САМИМИ
ГЕОМЕТРИЧЕСКИМИ ОБЪЕКТАМИ,
А С ИХ ИЗОБРАЖЕНИЯМИ НА ПЛОСКОСТИ
4. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
П - плоскость проекцийS - центр проецирования
А – объект проецирования
В
А'
sA - проецирующий луч
А' - проекция точки на
плоскости проекций П
А
s
В - объект проецирования
sВ – проецирующий луч
Точка В не имеет проекций на поле П, так как sB || П
П
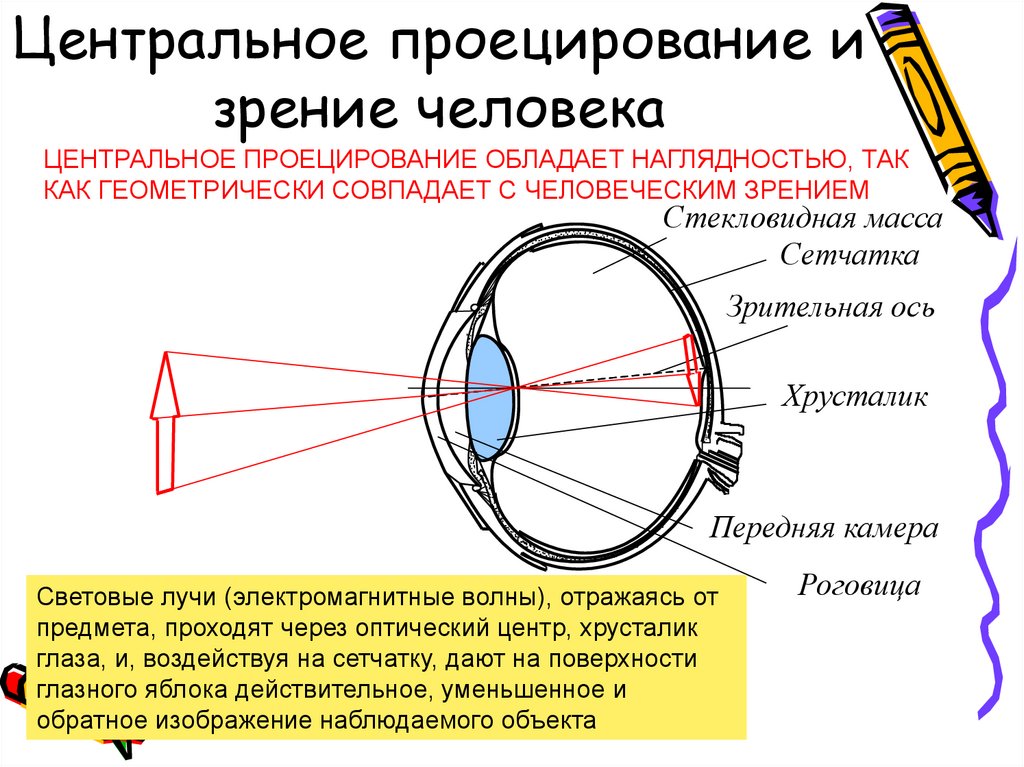
5. Центральное проецирование и зрение человека
ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ ОБЛАДАЕТ НАГЛЯДНОСТЬЮ, ТАККАК ГЕОМЕТРИЧЕСКИ СОВПАДАЕТ С ЧЕЛОВЕЧЕСКИМ ЗРЕНИЕМ
Стекловидная масса
Сетчатка
Зрительная ось
Хрусталик
Передняя камера
Световые лучи (электромагнитные волны), отражаясь от
предмета, проходят через оптический центр, хрусталик
глаза, и, воздействуя на сетчатку, дают на поверхности
глазного яблока действительное, уменьшенное и
обратное изображение наблюдаемого объекта
Роговица
6. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ В МОРЕХОДНОЙ АСТРОНОМИИ
ЦЕНТР ПРОЕЦИРОВАНИЯ (точка М)РАСПОЛОЖЕН НА ПОВЕРХНОСТИ
ЗЕМЛИ
C
C
C1
Небесная
сфера
C1
C1
C
C
М
C1
М
Небесная
сфера
Земля
Земля
ЦЕНТР ПРОЕЦИРОВАНИЯ (точка М)
РАСПОЛОЖЕН В ЦЕНТРЕ ЗЕМЛИ
7. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ В ПРОЕКЦИОННОЙ АППАРАТУРЕ
ЭКРАНЦЕНТР
ПРОЕЦИРОВАНИЯ
ИСТОЧНИК СВЕТА
ОБЪЕКТ
ПРОЕЦИРОВАНИЯ
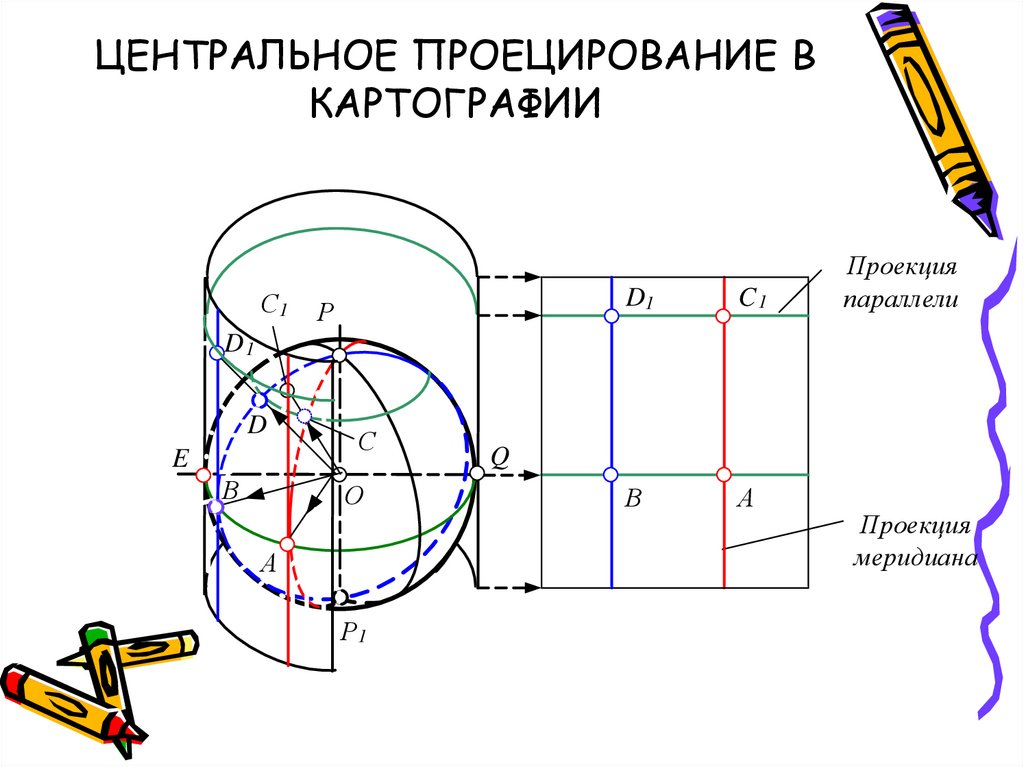
8. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ В КАРТОГРАФИИ
С1Р
D1
C1
В
А
Проекция
параллели
D1
D
E
В
С
О
А
Р1
Q
Проекция
меридиана
9. ПРОЕЦИРОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
Для построения проекцийпрямой
достаточно
спроецировать
две ее точки
многогранника
достаточно
спроецировать его
вершины
S
плоскости
достаточно
спроецировать
три точки
S
S
A
B
a
b
b A
пирамида
А
B
C
B
D
C
А'
b'
А'
В'
П
П
В' b'
C'
В'
A'
П
a'
C'
D'
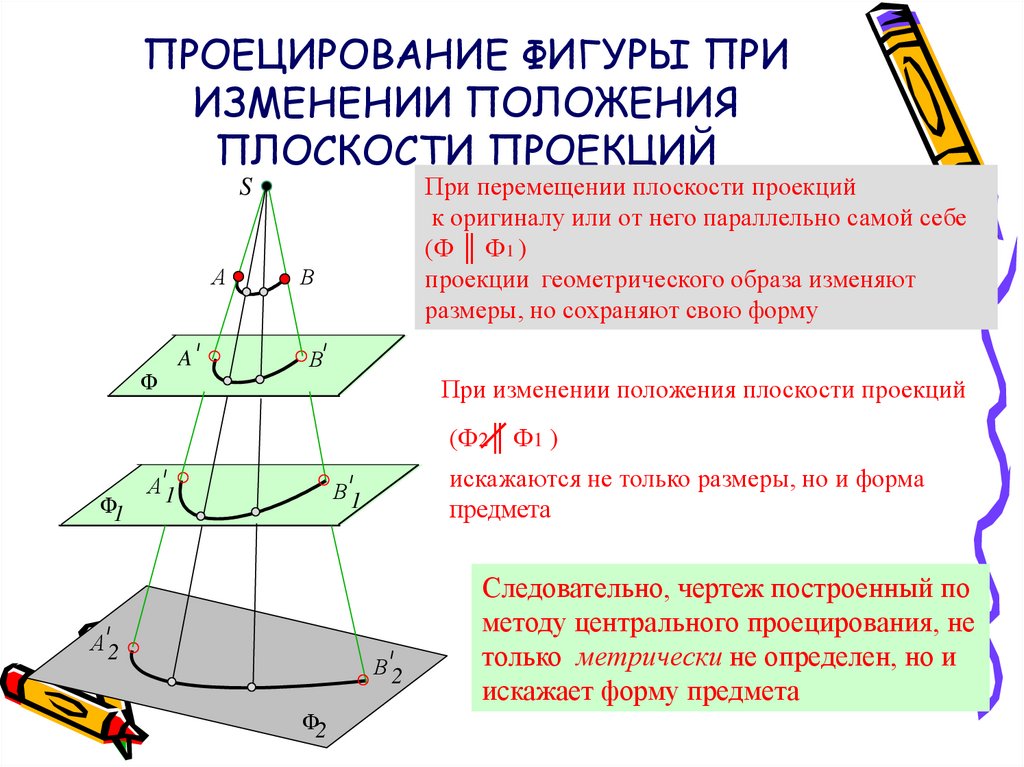
10. ПРОЕЦИРОВАНИЕ ФИГУРЫ ПРИ ИЗМЕНЕНИИ ПОЛОЖЕНИЯ ПЛОСКОСТИ ПРОЕКЦИЙ
При перемещении плоскости проекцийк оригиналу или от него параллельно самой себе
(Ф ║ Ф1 )
проекции геометрического образа изменяют
размеры, но сохраняют свою форму
S
А
Ф
A
В
В
При изменении положения плоскости проекций
(Ф2║ Ф1 )
Ф1
А1
искажаются не только размеры, но и форма
предмета
В1
А2
В2
Ф2
Следовательно, чертеж построенный по
методу центрального проецирования, не
только метрически не определен, но и
искажает форму предмета
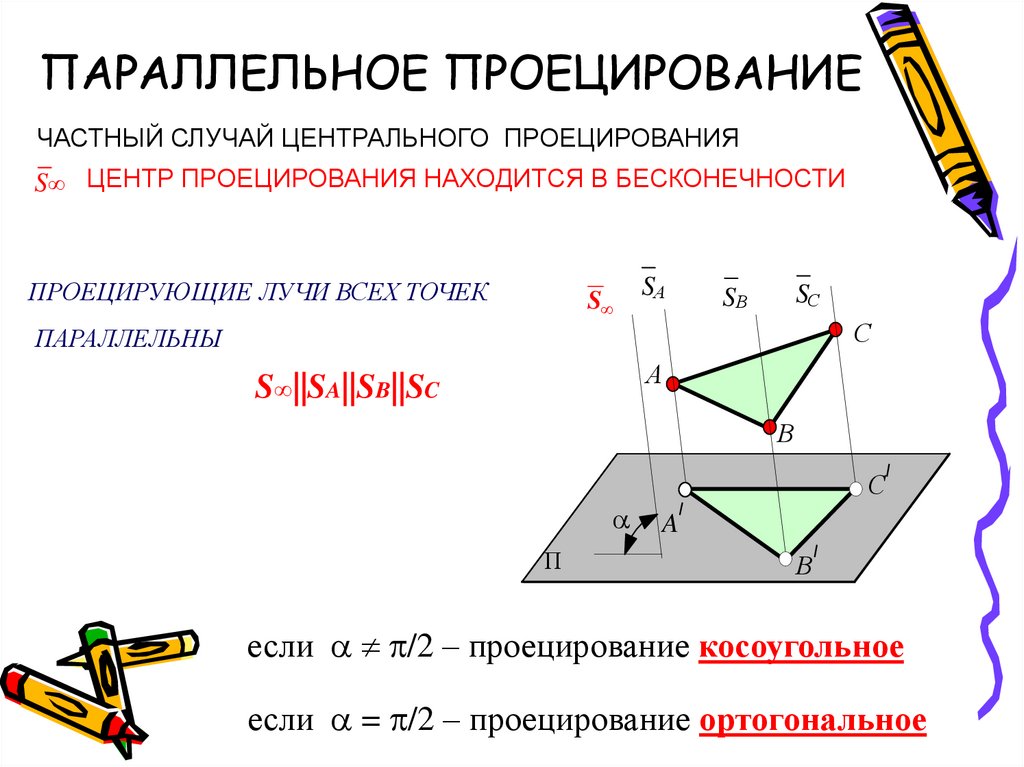
11. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
ЧАСТНЫЙ СЛУЧАЙ ЦЕНТРАЛЬНОГО ПРОЕЦИРОВАНИЯS∞ ЦЕНТР ПРОЕЦИРОВАНИЯ НАХОДИТСЯ В БЕСКОНЕЧНОСТИ
ПРОЕЦИРУЮЩИЕ ЛУЧИ ВСЕХ ТОЧЕК
S∞
SА
SС
SВ
С
ПАРАЛЛЕЛЬНЫ
А
S∞||SA||SB||SC
В
П
С
A
В
если /2 – проецирование косоугольное
если = /2 – проецирование ортогональное
12. ЗАВИСИМОСТЬ ФОРМЫ ПРОЕКЦИИ ОТ ПОЛОЖЕНИЯ ПЛОСКОСТИ ПРОЕКЦИЙ
S∞SВ
А
SК
SА
В
ИЗМЕНИМ ПОЛОЖЕНИЕ
ПЛОСКОСТИ ПРОЕКЦИЙ
К
A
В
К
Чем больше отклоняется от
прямого угла, тем больше проекция
отличается от оригинала
П
П1
В1
A1
К1
Следовательно, косоугольные проекции не
обеспечивают метричность чертежа
МЕТРИЧНОСТЬ ЧЕРТЕЖА ОБЕСПЕЧИВАЮТ
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
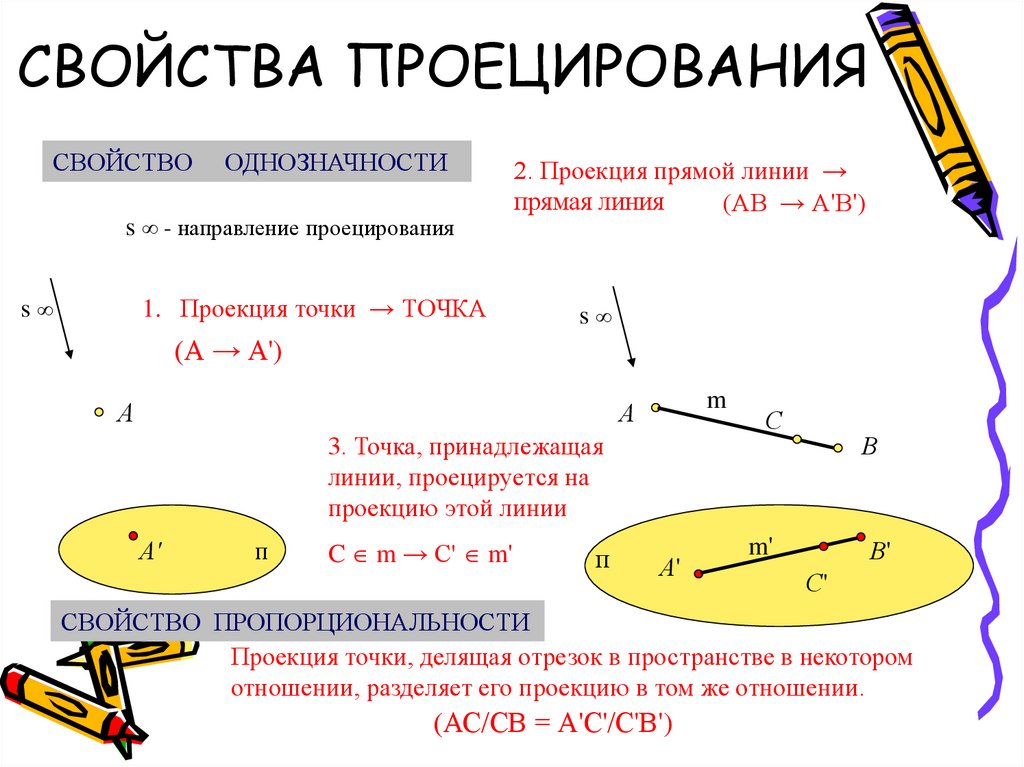
13. СВОЙСТВА ПРОЕЦИРОВАНИЯ
СВОЙСТВООДНОЗНАЧНОСТИ
s ∞ - направление проецирования
1. Проекция точки → ТОЧКА
s∞
2. Проекция прямой линии →
прямая линия
(АВ → А'В')
s∞
(А → А')
m
А
А
3. Точка, принадлежащая
линии, проецируется на
проекцию этой линии
А'
п
C m → C' m'
п
А'
С
В
В'
m'
С'
СВОЙСТВО ПРОПОРЦИОНАЛЬНОСТИ
Проекция точки, делящая отрезок в пространстве в некотором
отношении, разделяет его проекцию в том же отношении.
(АС/СВ = А'С'/С'В')
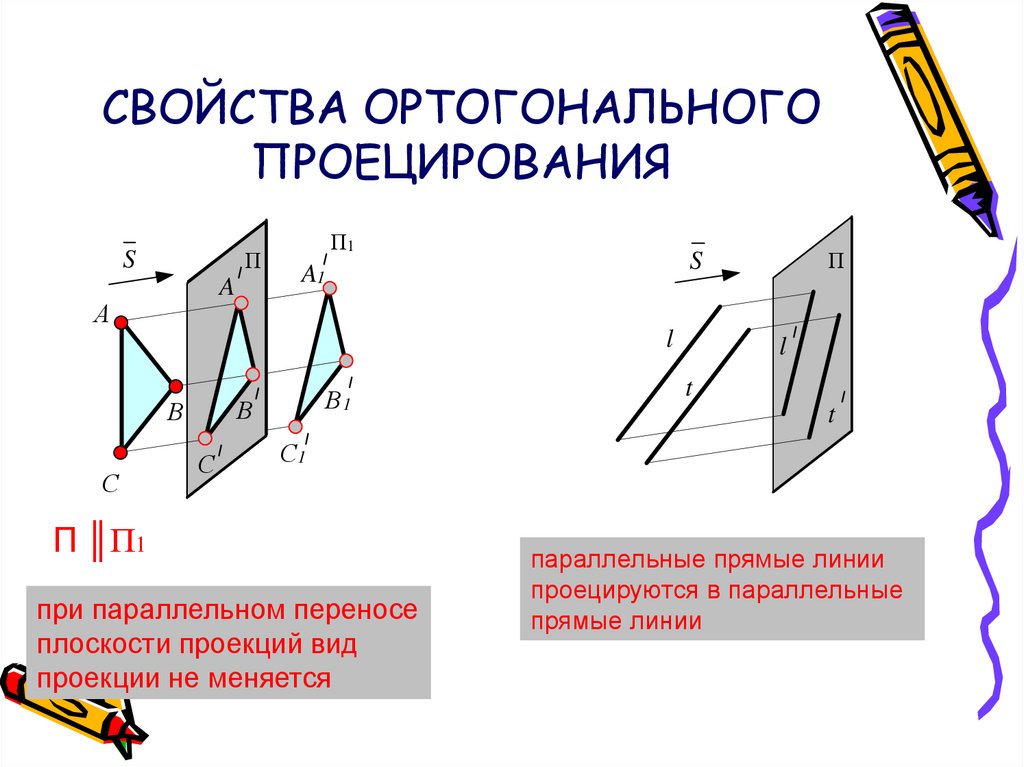
14. СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
ПS
A
А
П1
l
В
В
С
В1
С
П
S
A1
l
t
t
С1
П ║П1
при параллельном переносе
плоскости проекций вид
проекции не меняется
параллельные прямые линии
проецируются в параллельные
прямые линии








 Инженерная графика
Инженерная графика








