Digital Logic Design

1.

Digital Logic Design
Lecture – 3:
Combining Logic Gates
Konakbayev Olzhas, senior-lecturer,

2.

Lecture base
Digital Electronics: Principles & Applications, 9th edition by Roger
Tokheim & Patrick E. Hoppe:
• Chapter 4
2

3.

Topics to cover
• Constructing Circuits from Boolean Expressions
• Minterm and Maxterm Boolean Expressions
• Boolean Expression from a Truth Table
• Truth Tables and Boolean Expressions
• Simplifying Boolean Expressions
• Karnaugh Maps
• Using NAND Logic
• Using DeMorgan’s Theorem
3

4.

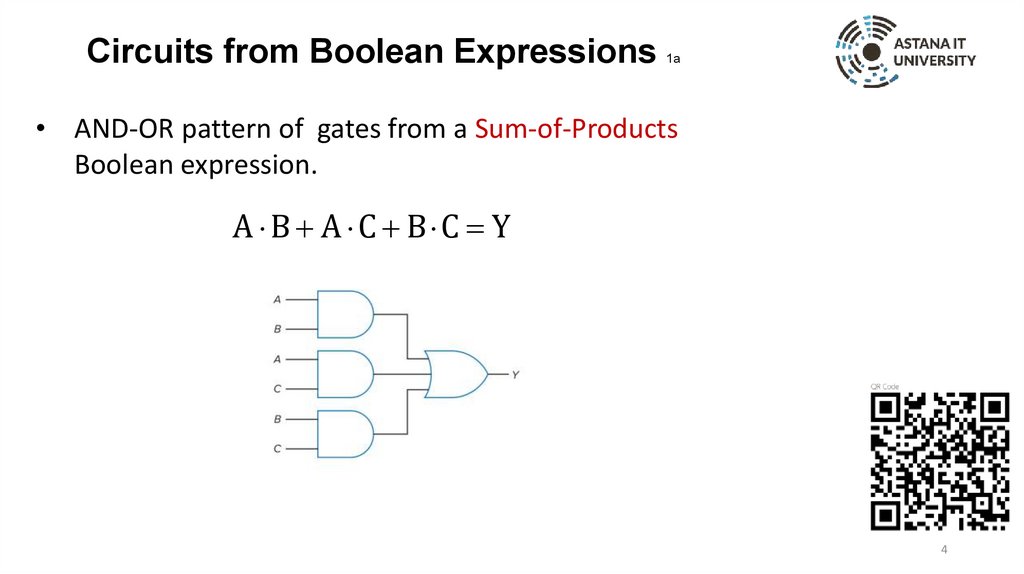
Circuits from Boolean Expressions
1a
• AND-OR pattern of gates from a Sum-of-Products
Boolean expression.
A B A C B C Y
4

5.

Circuits from Boolean Expressions
2
• OR-AND pattern of gates from a Product-of-Sums
Boolean expression.
(A B) (A B C) Y
5

6.

Circuits from Boolean Expressions
3
• Step 1: Identify pattern of operation
6

7.

Circuits from Boolean Expressions
4
• Step 2: Add the first OR gate with inputs
7

8.

Circuits from Boolean Expressions
5
• Step 3: Add the second OR gate with inputs
8

9.

Minterm and Maxterm Boolean Expressions
1
• Maxterm Boolean Expression
C+B+A C+B+A C+B+A =Y
(Product-of-Sum Expression)
9

10.

Minterm and Maxterm Boolean Expressions
2
• Minterm Boolean Expression
C B A C B A C B A Y
(Sum-of-Product Expression)
10

11.

Boolean Expression from a Truth Table
• Step 1: Write an AND
expression for each
instance Y = 1.
• Step 2: OR the
expressions together
to form a Boolean
expression.
11

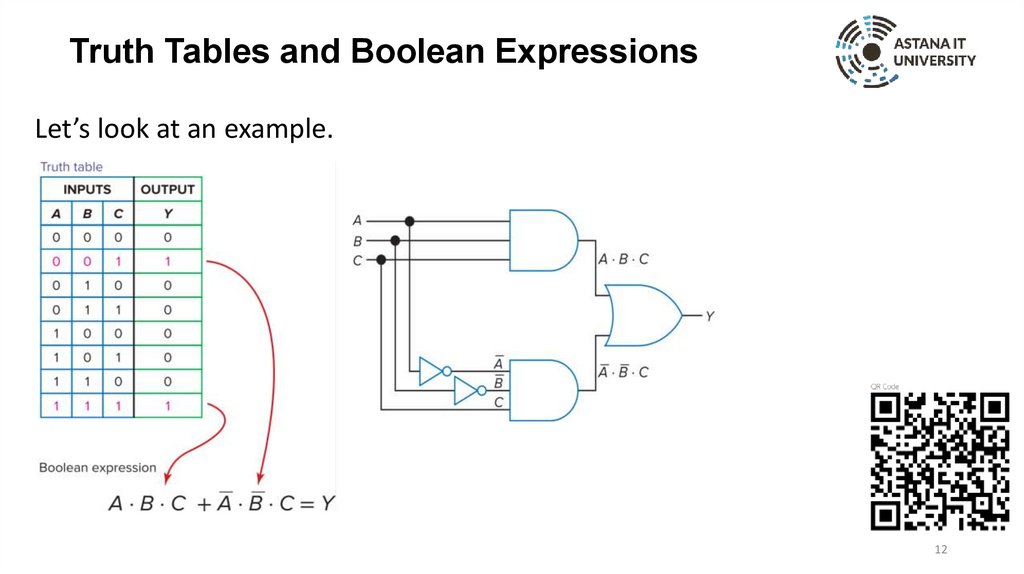
12.

Truth Tables and Boolean Expressions
Let’s look at an example.
12

13.

Simplifying Boolean Expressions
1
• Original Boolean Expression
13

14.

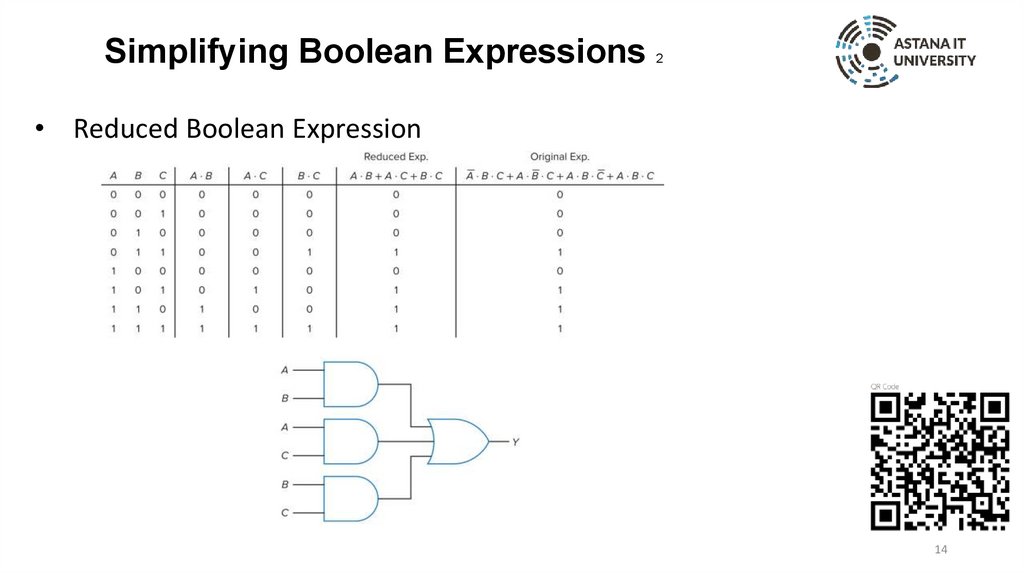
Simplifying Boolean Expressions
2
• Reduced Boolean Expression
14

15.

Single-variable Boolean Theorems
1
• The first Boolean theorem states that X ANDed with
0 is 0.
X 0 0
15

16.

Single-variable Boolean Theorems
2
• The second Boolean theorem states that X ANDed
with 1 is X.
X 1 X
16

17.

Single-variable Boolean Theorems
3
• The third Boolean theorem states that X ANDed with
X is X.
X X X
17

18.

Single-variable Boolean Theorems
4
• The fourth Boolean theorem states that X ANDed
with ഥ
X is 0.
X X 0
X
18

19.

Single-variable Boolean Theorems
5
The fifth Boolean theorem states that X ORed with 0 is X.
X+0=0
19

20.

Single-variable Boolean Theorems
6
• The sixth Boolean theorem states that X ORed with 1
is 1.
X+1=1
20

21.

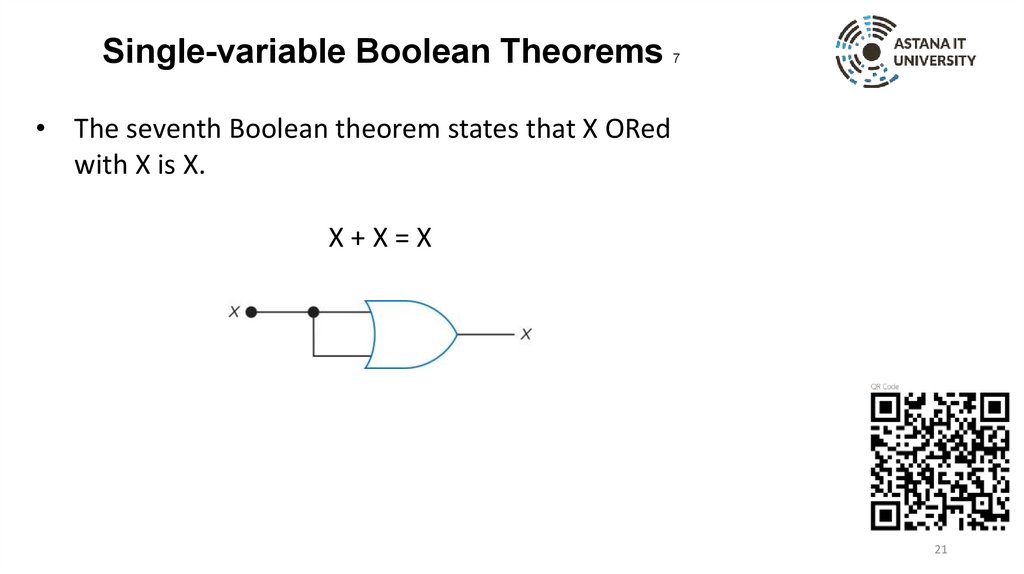
Single-variable Boolean Theorems
7
• The seventh Boolean theorem states that X ORed
with X is X.
X+X=X
21

22.

Single-variable Boolean Theorems
8
• The eighth Boolean theorem states that X ORed with
ഥ
X is 1
X X 1
22

23.

Single-Variable Boolean Theorems
9
23

24.

Multivariable Boolean Theorems
1
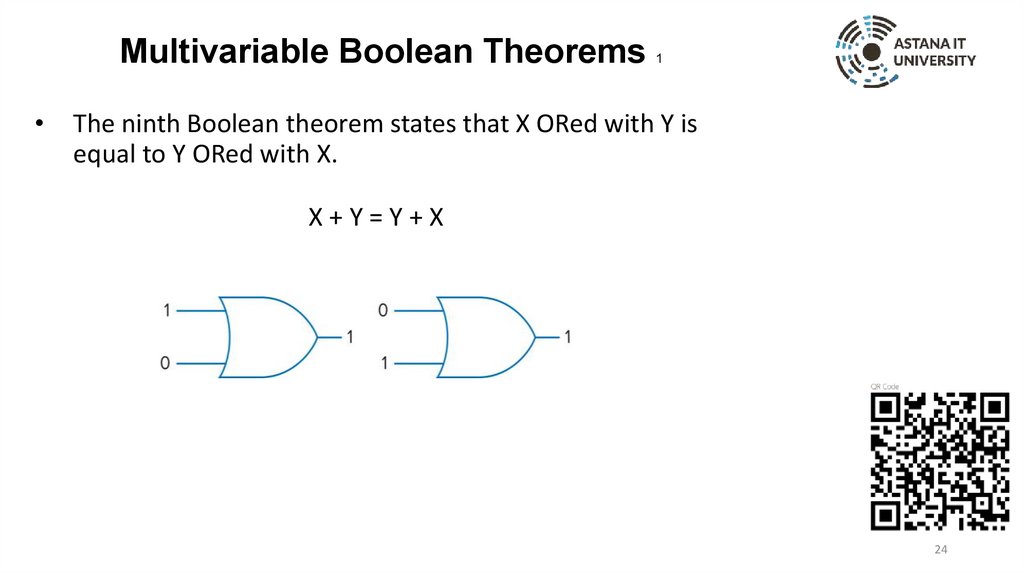
The ninth Boolean theorem states that X ORed with Y is
equal to Y ORed with X.
X+Y=Y+X
24

25.

Multivariable Boolean Theorems
2
• The tenth Boolean theorem states that X ANDed with
Y is equal to Y ANDed with X.
X Y Y X
25

26.

Multivariable Boolean Theorems
3
• The eleventh Boolean theorem demonstrates when
ORing multiple inputs, the order of operation does
not matter.
X Y Z X Y Z X Y Z
26

27.

Multivariable Boolean Theorems
4
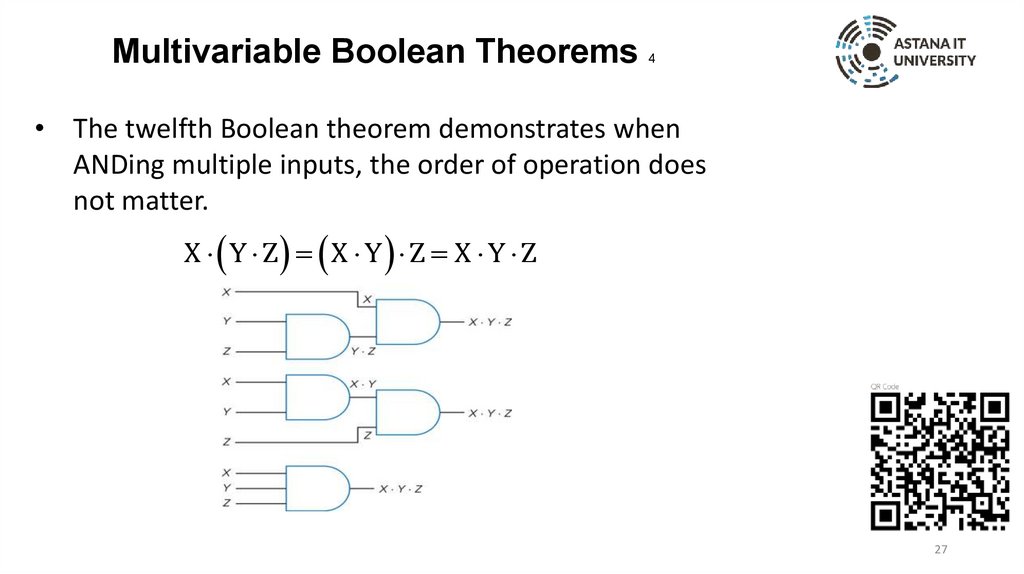
• The twelfth Boolean theorem demonstrates when
ANDing multiple inputs, the order of operation does
not matter.
X Y Z X Y Z X Y Z
27

28.

Multivariable Boolean Theorems
5
• The thirteenth Boolean theorem is sometimes called
the distributive theorem.
X Y Z X Y X Z
28

29.

Multivariable Boolean Theorems
6
• The fourteenth Boolean theorem states X ORed with
X ANDed with Y is equal to X.
X X Y X
29

30.

Multivariable Boolean Theorems
7
• The fifteenth Boolean theorem states X ORed with ഥ
X
ANDed with Y is equal to X ORed with Y.
X X Y X Y
Access the text alternative for slide images.
30
30

31.

Multivariable Boolean Theorems
8
31

32.

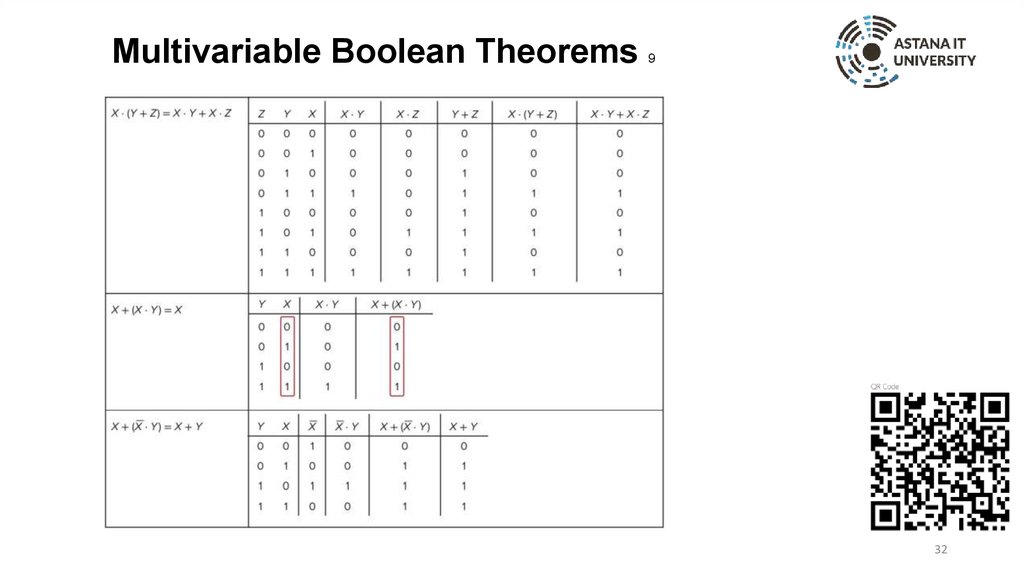
Multivariable Boolean Theorems
9
32

33.

Boolean Reduction with Two Variables
1
33

34.

Boolean Reduction with Two Variables
2
• Let’s check our answer.
34

35.

Boolean Reduction with Three Variables
1
35

36.

Boolean Reduction with Three Variables
2
• Let’s check our answer.
36

37.

Karnaugh Maps
• The columns and rows of the two and three input
Karnaugh maps must be laid out in this manner.
37

38.

Karnaugh Maps with Three Variables
1
Step 1: Write the minterm for each input
combination that produces a 1 on the
output.
38

39.

Karnaugh Maps with Three Variables
2
Step 2: Write the Sum of Product expression
using the minterms.
39

40.

Karnaugh Maps with Three Variables
3
Step 3: Fill in the 1’s for each minterm in
The Sum of Product expression
40

41.

Karnaugh Maps with Three Variables
4
Step 4: Loop adjacent 1’s in groups of
two, four, or eight.
41

42.

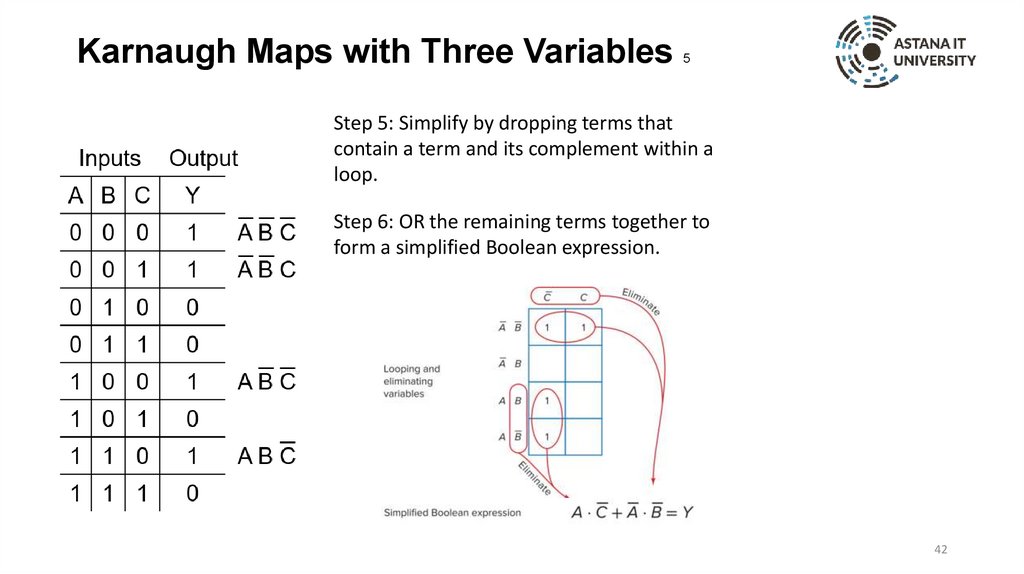
Karnaugh Maps with Three Variables
5
Step 5: Simplify by dropping terms that
contain a term and its complement within a
loop.
Step 6: OR the remaining terms together to
form a simplified Boolean expression.
42

43.

Karnaugh Maps with Three Variables
6
43

44.

Boolean Reduction with Three Variables
• Let’s check our answer.
44

45.

Karnaugh Maps with Four Variables
1
45

46.

Karnaugh Maps with Four Variables
2
46

47.

Other Looping Possibilities
1
• Consider the Karnaugh map as a vertical cylinder.
47

48.

Other Looping Possibilities
2
• Consider the Karnaugh map as a horizontal cylinder.
48

49.

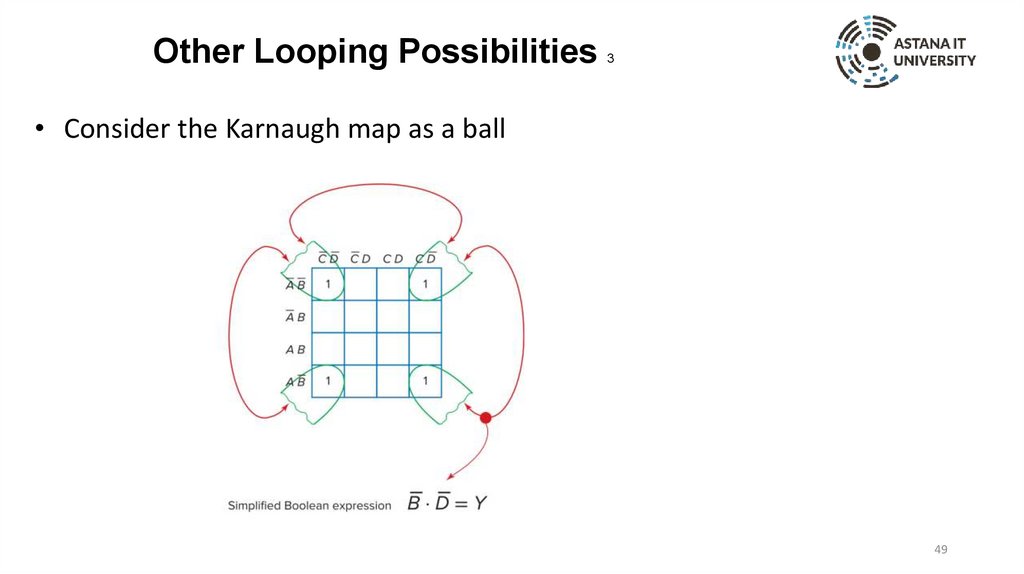
Other Looping Possibilities
3
• Consider the Karnaugh map as a ball
49

50.

Using NAND Logic
1
• Start with a minterm (sum-of-products) Boolean
expression.
• Draw the AND-OR logic diagram using AND, OR, and
NOT symbols.
• Substitute NAND symbols for each AND and OR
symbol, keeping all connections the same.
• Substitute NAND symbols with all inputs tied
together for each inverter.
• Test the logic circuit containing all NAND gates to
determine if generates the proper truth table.
50

51.

Using NAND Logic
2
• Start with a minterm (sum-of-products) Boolean
expression.
• Draw the AND-OR logic diagram using AND, OR, and
NOT symbols.
51

52.

Using NAND Logic
3
• Substitute NAND symbols for each AND and OR
symbol, keeping all connections the same.
• Substitute NAND symbols with all inputs tied together
for each inverter.
52

53.

De Morgan’s Theorem
1
• First Theorem
53

54.

De Morgan’s Theorem
2
Change OR to AND
Compliment each individual
variable
• Compliment the entire
function
• Eliminate all groups of
double overbars.
• Final expression
54

55.

De Morgan’s Theorem
3
• Second Theorem
55

56.

De Morgan’s Theorem
4
Change AND to OR
Compliment each
individual variable
Compliment the entire
function
Eliminate all groups of
double overbars.
• Final expression
56

57.

De Morgan’s Theorem 5
Break the line, change the sign
A B A gB
A gB A B
57

58.

De Morgan’s Theorem
6
Let’s do an example
58

59.

Review
1
• Draw the circuit for the Boolean expression shown.
A B A C B C Y
59

60.

Review
2
• Draw the circuit for the Boolean expression shown.
A gB A gC BgC Y
60

61.

Review
5
• Write the Sum of Product expression for the truth table
shown.
61

62.

Review 6
• Write the Sum of Product expression for the truth
table shown.
62

63.

Review
11
• Label the rows and columns of the Karnaugh maps.
63

64.

Review
12
• Label the rows and columns of the Karnaugh maps.
64

65.

Review
13
• Use the Karnaugh mapping to determine the reduced
Sum of Product expression.
65

66.

Review
14
• Use the Karnaugh mapping to determine the reduced
Sum of Product expression.
66

67.

Review
21
• Use De Morgan’s Theorem to simplify this Boolean
expression.
A B C A B C Y
67

68.

Review
22
• Use De Morgan’s Theorem to simplify this Boolean
expression.
A B C A B C Y
A B C A B C Y
68

69.

Thank you!
69