Похожие презентации:
SAT and model checking
1. SAT and Model Checking
2. Bounded Model Checking (BMC)
Biere, Cimatti, Clarke, Zhu, 1999A.I. Planning problems: can we reach a
desired state in k steps?
Verification of safety properties: can we
find a bad state in k steps?
Verification: can we find a counterexample
in k steps ?
3. What is SAT?
Given a propositional formula in CNF, find ifthere exists an assignment to Boolean variables
that makes the formula true:
literals
1 = (b c)
clauses
2 = ( a d)
3 = ( b d)
= 1 2 3
A = {a=0, b=1, c=0, d=1}
SATisfying
assignment!
4. BMC idea
Given: transition system M, temporal logic formula f, anduser-supplied time bound k
Construct propositional formula W(k) that is satisfiable iff f is valid
along a path of length k
k 1
Path of length k:
I ( s0 ) R( si , si 1 )
i 0
Say f = EF p and k = 2, then
W(2) I ( s0 ) R( s0 , s1 ) R( s1 , s2 ) ( p0 p1 p2 )
What if f = AG p ?
5. BMC idea (cont’d)
AG p means p must hold in every state along any path of length kWe take
k 1
k
i 0
i 0
W(k ) ( I ( s0 ) R( si , si 1 )) pi
So
k 1
k
i 0
i 0
W(k ) I ( s0 ) R( si , si 1 ) pi
That means we look for counterexamples
6. Safety-checking as BMC
p is preserved up to k-th transition iff W(k) is unsatisfiable:k 1
k
i 0
i 0
W(k ) I ( s0 ) R( si , si 1 ) p
p
p
p
s0
s1
s2
...
p
sk-1
p
sk
If satisfiable, satisfying assignment gives counterexample to the
safety property.
7. Example: a two bit counter
Initial state: I : l r00
11
l ' (l r )
Transition: R :
r ' r
01
10
Safety property: AG ( l r )
(l 0 r0 )
l1 (l 0 r0 ) r1 r0
(l1 r1 )
W(2) : ( l 0 r0 )
l 2 (l1 r1 ) r2 r1 (l r )
2 2
W(2) is unsatisfiable. W(3) is satisfiable.
8. Example: another counter
0011
01
10
l' l
l ' (l r )
I : l r
R:
r' r
r ' r
l
r
Liveness property: AF (l r )
Check: EG ( l r )
W(2) I ( s0 ) R( si , si 1 ) ( li ri ) loop
where
1
2
i 0
i 0
loop R( s2 , s3 ) ( s3 s0 s3 s1 s3 s2 )
W(2) is satisfiable
Satisfying assignment gives counterexample to the liveness property
9. What BMC with SAT Can Do
• All LTL• ACTL and ECTL
• In principle, all CTL and even mu-calculus
– efficient universal quantifier elimination or
fixpoint computation is an active area of
research
10. How big should k be?
• For every model M and LTL propertythere exists k s.t.
• The minimal such k is the Completeness
Threshold (CT)
11. How big should k be?
• Diameter d = longest shortest path from aninitial state to any other reachable state.
• Recurrence Diameter rd = longest loop-free
path.
• rd ¸ d
d=2
rd = 3
12. How big should k be?
• Theorem: for Gp properties CT = dp
s0
Arbitrary path
13. How big should k be?
• Theorem: for Fp properties CT= rdp
p
p
p
p
s0
Open Problem: The value of CT for general
Linear Temporal Logic properties is unknown
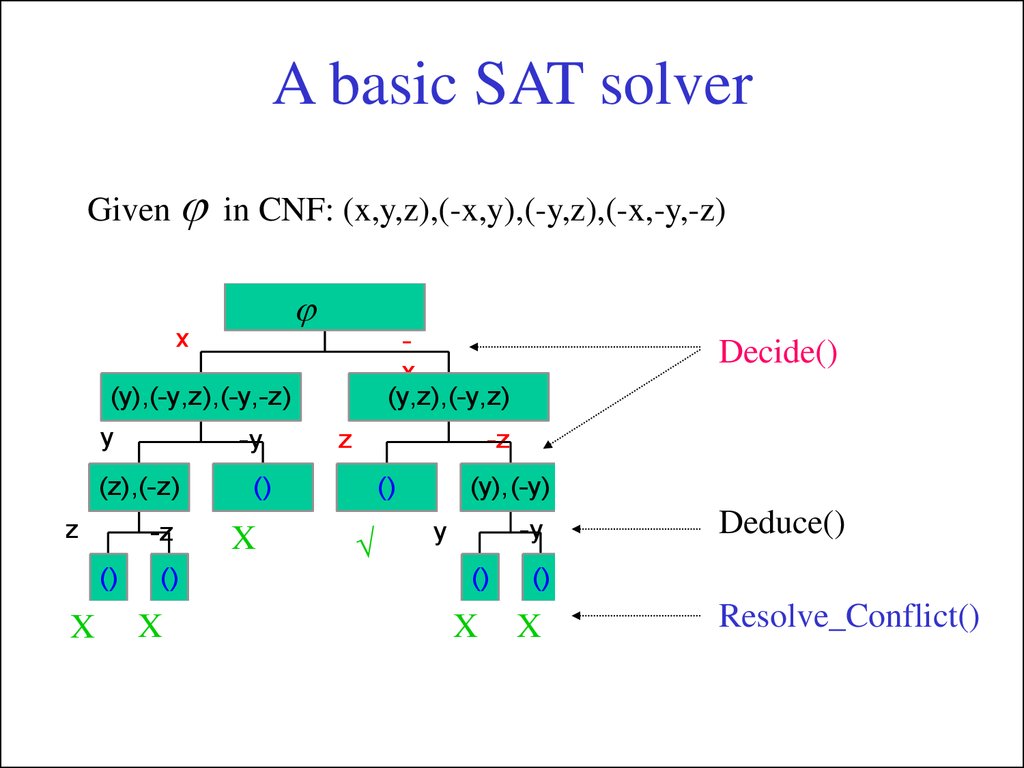
14. A basic SAT solver
Given in CNF: (x,y,z),(-x,y),(-y,z),(-x,-y,-z)x
x
(y,z),(-y,z)
(y),(-y,z),(-y,-z)
y
-y
(z),(-z)
z
-z
()
X
()
X
z
-z
()
X
Decide()
()
(y),(-y)
-y
y
()
X
Deduce()
()
X
Resolve_Conflict()
15.
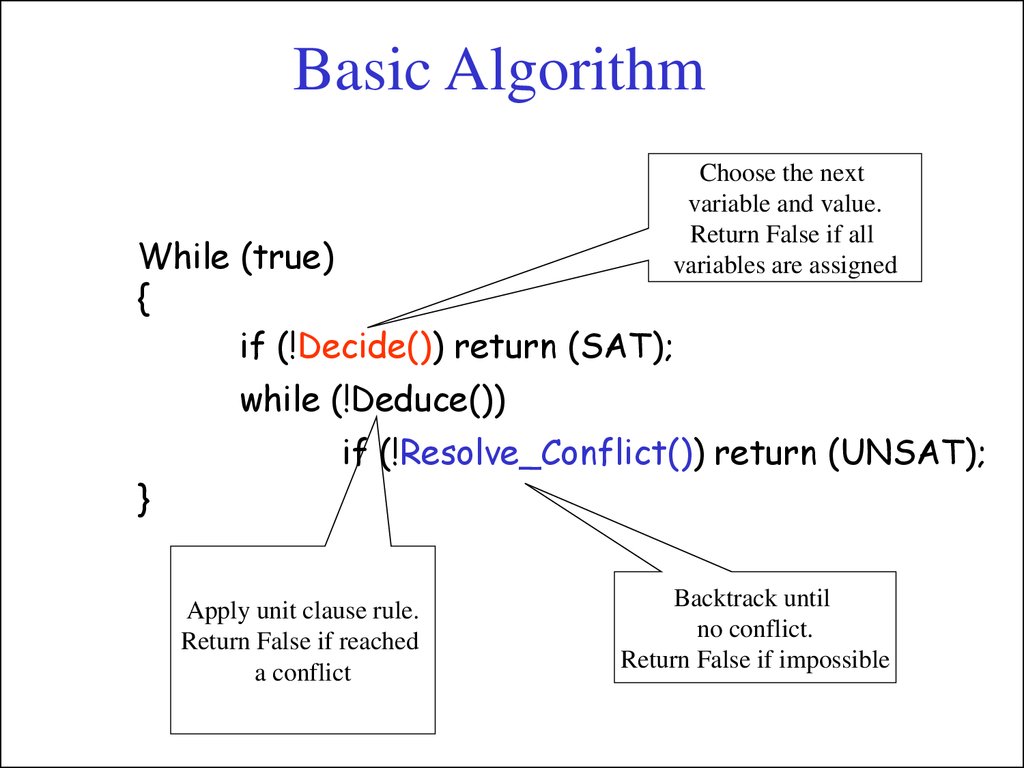
Basic AlgorithmChoose the next
variable and value.
Return False if all
variables are assigned
While (true)
{
if (!Decide()) return (SAT);
while (!Deduce())
}
if (!Resolve_Conflict()) return (UNSAT);
Apply unit clause rule.
Return False if reached
a conflict
Backtrack until
no conflict.
Return False if impossible
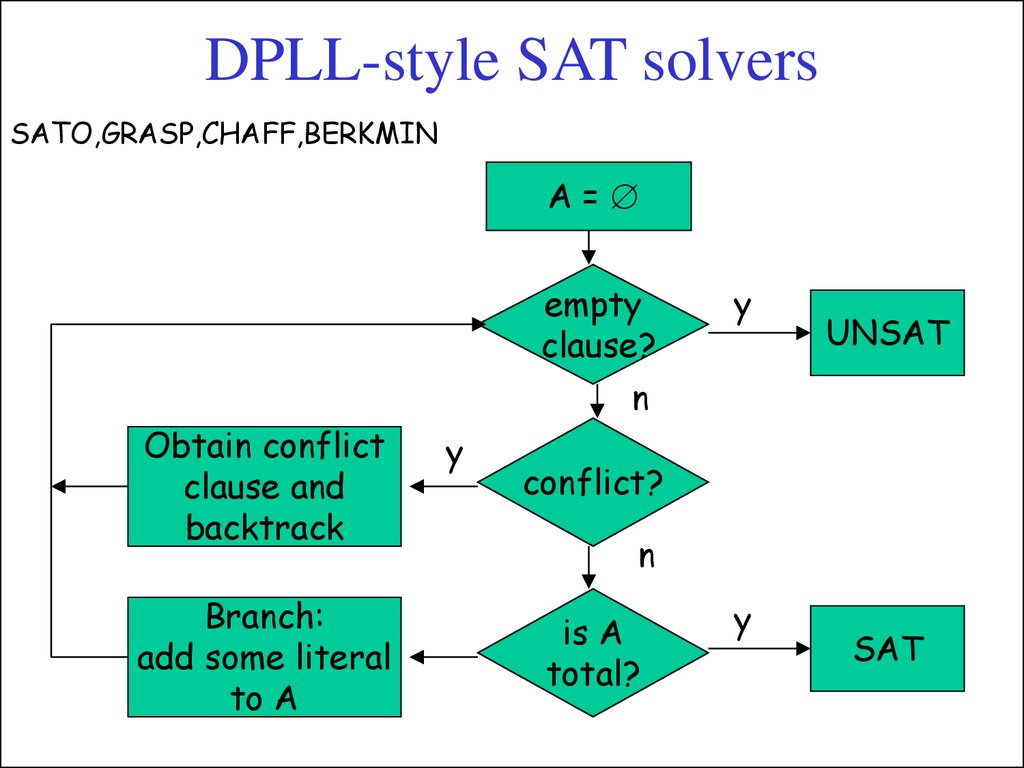
16. DPLL-style SAT solvers
SATO,GRASP,CHAFF,BERKMINA=
empty
clause?
y
UNSAT
n
Obtain conflict
clause and
backtrack
Branch:
add some literal
to A
y
conflict?
n
is A
total?
y
SAT
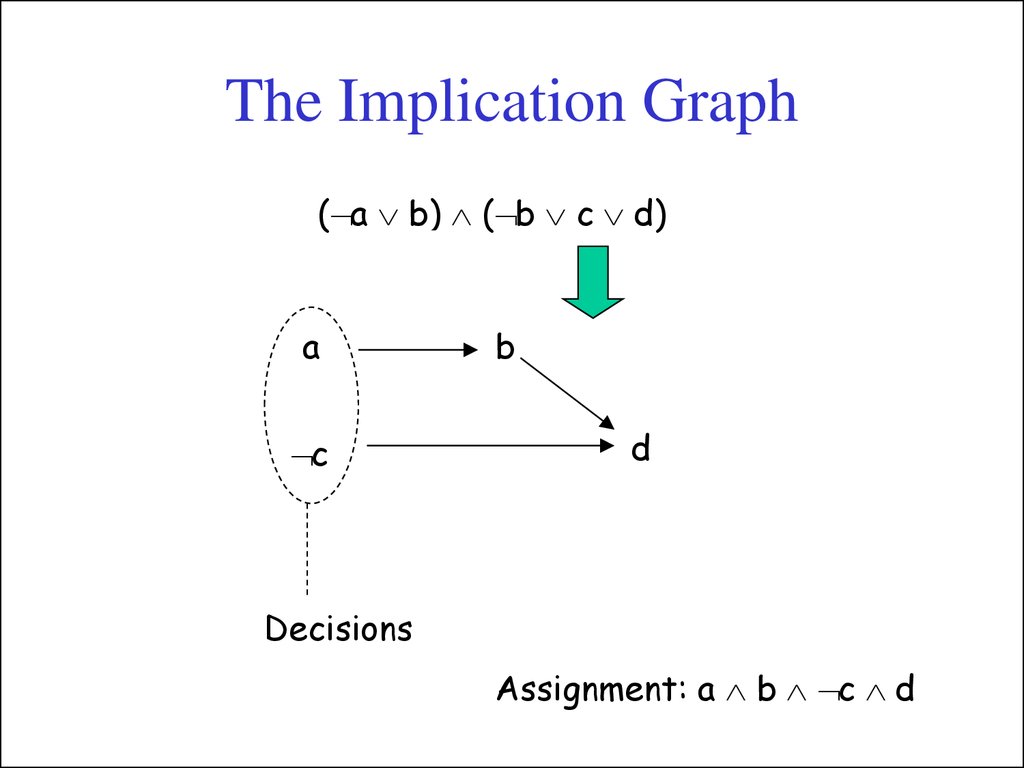
17. The Implication Graph
( a b) ( b c d)a
c
b
d
Decisions
Assignment: a b c d
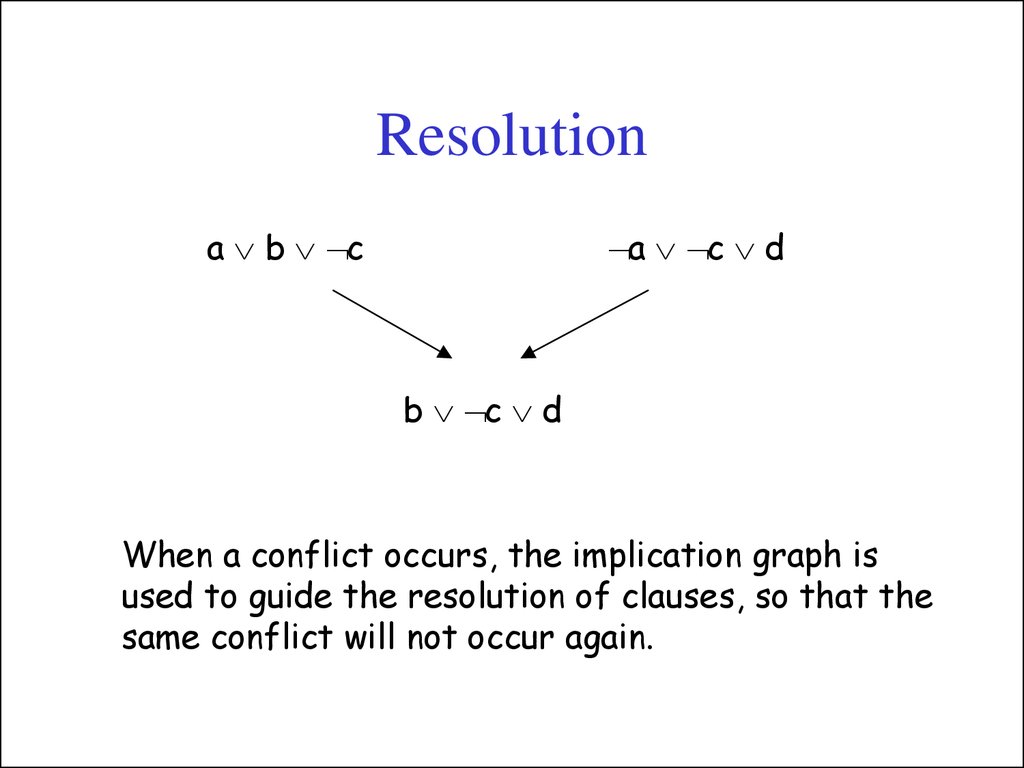
18. Resolution
a b ca c d
b c d
When a conflict occurs, the implication graph is
used to guide the resolution of clauses, so that the
same conflict will not occur again.
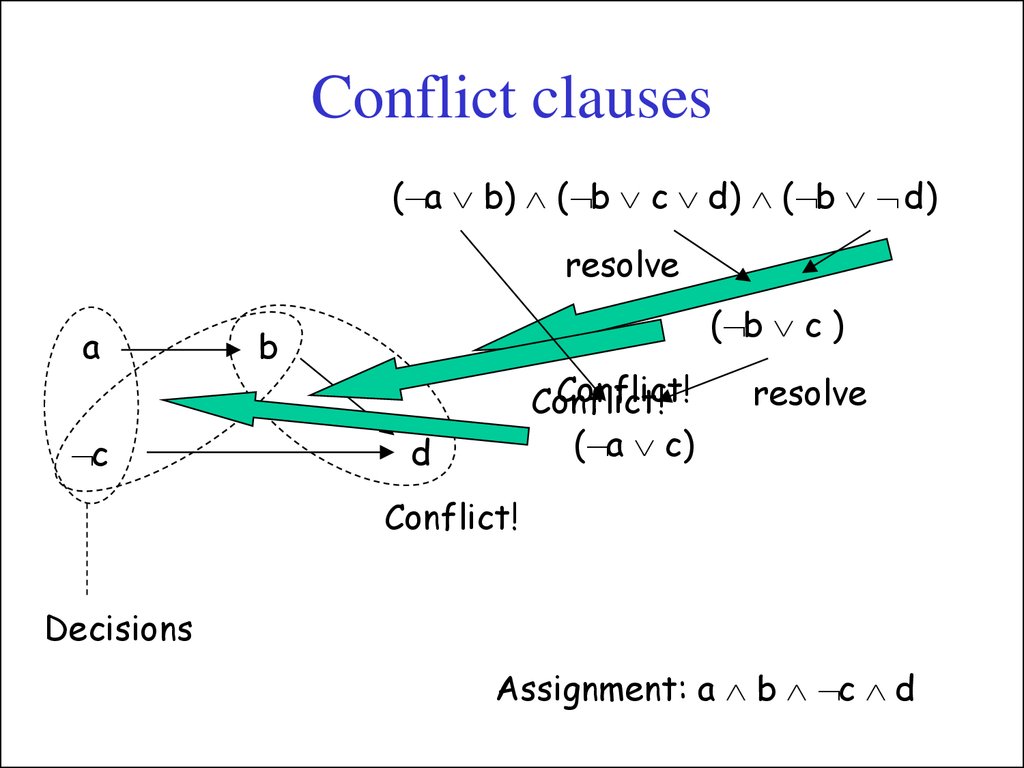
19. Conflict clauses
( a b) ( b c d) ( b d)resolve
a
c
( b c )
b
Conflict!
Conflict!
( a c)
d
resolve
Conflict!
Decisions
Assignment: a b c d
20. Conflict Clauses (cont.)
• Conflict clauses:–
–
–
–
Are generated by resolution
Are implied by existing clauses
Are in conflict with the current assignment
Are safely added to the clause set
Many heuristics are available for determining
when to terminate the resolution process.
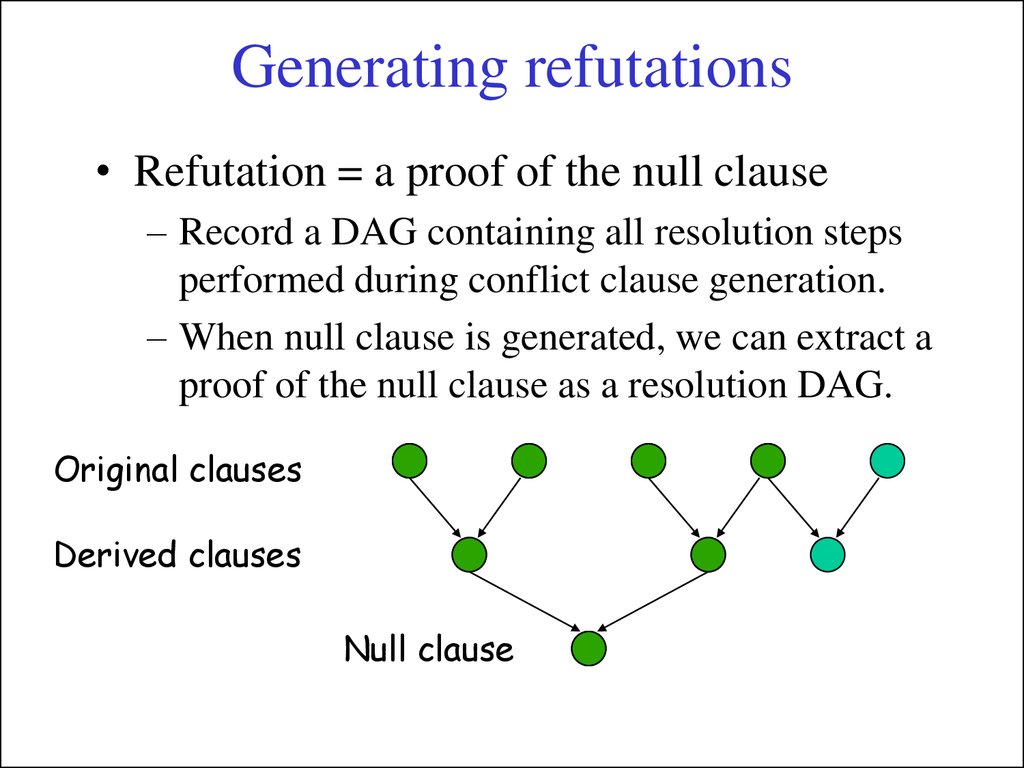
21. Generating refutations
• Refutation = a proof of the null clause– Record a DAG containing all resolution steps
performed during conflict clause generation.
– When null clause is generated, we can extract a
proof of the null clause as a resolution DAG.
Original clauses
Derived clauses
Null clause
22. Unbounded Model Checking
• A variety of methods to exploit SAT andBMC for unbounded model checking:
–
–
–
–
Completeness Threshold
k - induction
Abstraction (refutation proofs useful here)
Exact and over-approximate image
computations (refutation proofs useful here)
– Use of Craig interpolation
23. Conclusions: BDDs vs. SAT
• Many models that cannot be solved by BDDsymbolic model checkers, can be solved
with an optimized SAT Bounded Model
Checker.
• The reverse is true as well.
• BMC with SAT is faster at finding shallow
errors and giving short counterexamples.
• BDD-based procedures are better at proving
absence of errors.
24. Acknowledgements
“Exploiting SAT Solvers in Unbounded Model Checking” byK. McMillan, tutorial presented at CAV’03
“Tuning SAT-checkers for Bounded Model Checking” and
“Heuristics for Efficient SAT solving” by O. Strichman
Slides originally prepared for 2108 by Mihaela Gheorghiu.

















 Математика
Математика








