Двойственные задачи ЛП

1.

Лекция
Двойственные задачи ЛП
Домашова Д.В.
1

2.

Определение двойственной задачи
Рассмотрим задачу ЛП в общей форме
F c1x1 ... cn xn max
a11 x1 a12 x2 ... a1n xn b1
.
ak1 x1 ak 2 x2 ... akn xn bk
.
am1 x1 am 2 x2 ... amn xn bm
(1)
x j 0, j 1, l , l n
Определение: Задача
F * b1 y1 ... bm ym min
a11 y1 a21 y2 ... am1 ym c1
.
a
y
a
y
...
a
y
c
1l 1 2l 2
ml m
l
.
a1n y1 a2 n y2 ... amn ym cn
yi 0, i 1, k , k m
называется
задаче (1).
двойственной
к
2

3.

Определение двойственной задачи
Прямая задача
1 n - переменных
2 m - ограничений
3 Целевая функция – ищется max
4 c – вектор коэффициентов
целевой функции
5 b – вектор свободных членов
системы ограничений
6 A – матрица коэффициентов
системы ограничений
7 xj >=0, j=1,k
8 xj – не ограничена в знаке,
j=k+1,n
9 i-ое ограничение «<=»,i=1,l
10 i-ое ограничение «=»,i=l+1,m
Двойственная задача
m - переменных
n - ограничений
Целевая функция – ищется min
b – вектор коэффициентов
целевой функции
c – вектор свободных членов
системы ограничений
Aт – матрица коэффициентов
системы ограничений
j-ое ограничение «>=»,j=1,k
j-ое ограничение «=»,j=k+1,n
yi >=0, i=1,l
yi, – не ограничена в знаке,
i=l+1,m
3

4.

Пример постановки двойственной задачи
F = x1 – 4x2 – 3x3 min
3x1 4 x2 x3 7
x1 2 x2 x3 6
x 4
3
xj ≥ 0, j 1,3
F = - x1 + 4x2+ 3x3 max
3x1 4 x2 x3 7
x3 4
x 2x x 6
2
3
1
xj ≥ 0, j 1,3
F *= 7y1 – 4y2 + 6y3 min
3 y1 y3 1
4 y1 2 y3 4
y y y 3
2
3
1
y1,2 ≥ 0
4

5.

Симметричная пара двойственных задач
Симметричная пара двойственных задач:
F c, x max
Ax b
x 0
F b, y min
*
AT y C
y 0
5

6.

Основные теоремы двойственности
Теорема 1. Если одна из пары двойственных задач имеет
оптимальное решение, то и другая имеет оптимальное решение,
причем значения целевых функций задач при их оптимальных
планах равны между собой: F(x*) = F*(y*). Если же целевая
функция одной из пары двойственных задач не ограничена, то
другая задача вообще не имеет планов (ОДР пуста).
Теорема2: x ( x1 ,..., xn ) и y
прямой и двойственной задач
*
*
*
*
( y1* ,...., ym* ) - оптимальные решения
n
( aij x*j bi ) yi* 0, i 1, m
j 1
m
( aij yi* c j ) x*j 0, j 1, n
i 1
6

7.

Основные теоремы двойственности
*
1
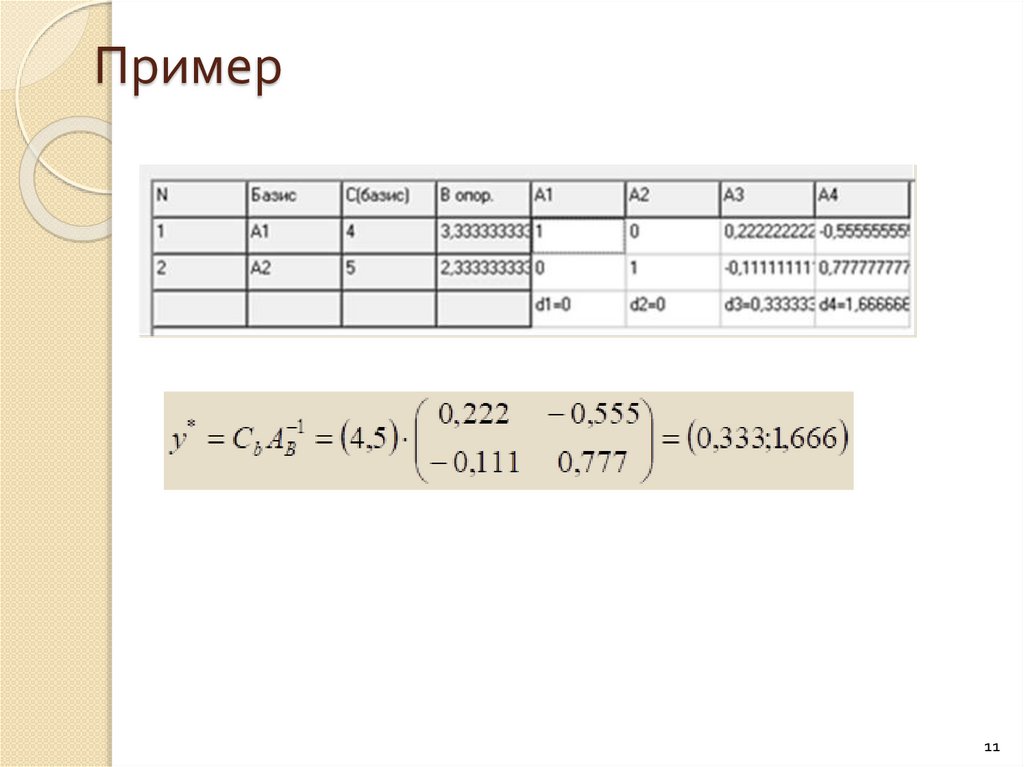
Теорема 3. y = Cb AB
Доказательство.
Пусть прямая задача:
F c, x max
Ax b
x 0
Тогда двойственная:
F * y, b min
AT y C
Пусть x* - оптимальное решение прямой.
Тогда ABx*b = b, AB 1 AB xb* AB 1b, xb* AB 1b .
Подставим x* в целевую функцию:
F = <c,x*> = cbx*b = Cb AB 1b ,
Cb AB 1b = y*b тогда y* = Cb AB 1 ,
где Cb – коэффициенты при базисных переменных;
AB 1 - обратная матрица к матрице, составленной из компонент векторов,
вошедших в оптимальных базис (расположена в первых m строках
последней (оптимальной) симплекс-таблицы, в столбцах векторов,
представляющих начальный базис.
При этом y* = Cb AB 1 - находится в строке Δ
7

8.

Основные теоремы двойственности
Установим соответствие между переменными прямой и двойственной
задач в симплекс-таблице:
x1...xn
xn 1...xn m
основные
дополнительные
y 1... ym n
m
y1... y m
дополнительные
основные
8

9.

Пример
9

10.

Пример
10

11.

Пример
11

12.

Экономическая интерпретация
двойственных задач
12

13.

Экономическая интерпретация
двойственных задач
Задача об оптимальном плане производства продукции
n – видов продукции, ;
m – видов ресурсов (сырья), ;
aij – количество ресурса i-го вида, требующегося для
производства единицы продукции j-го вида;
bi – запасы ресурса i-го вида ;
cj – доход (прибыль) от реализации единицы продукции
j-го вида.
13

14.

Экономическая интерпретация
двойственных задач
Задача об оптимальном плане производства продукции
Необходимо найти такой план производства продукции, при
котором достигается максимальная прибыль, для
реализации которого достаточно имеющихся ресурсов.
Оценить каждый из видов сырья, используемых для
производства продукции. Оценки, приписываемые каждому
из видов сырья должны быть такими, чтобы оценка всего
используемого сырья была минимальна, а суммарная
оценка сырья, используемого на производство единицы
продукции любого вида, - не меньше цены единицы
продукции данного вида.
Найти интервалы устойчивости двойственных оценок по
отношению к изменениям ресурсов каждого типа.
14

15.

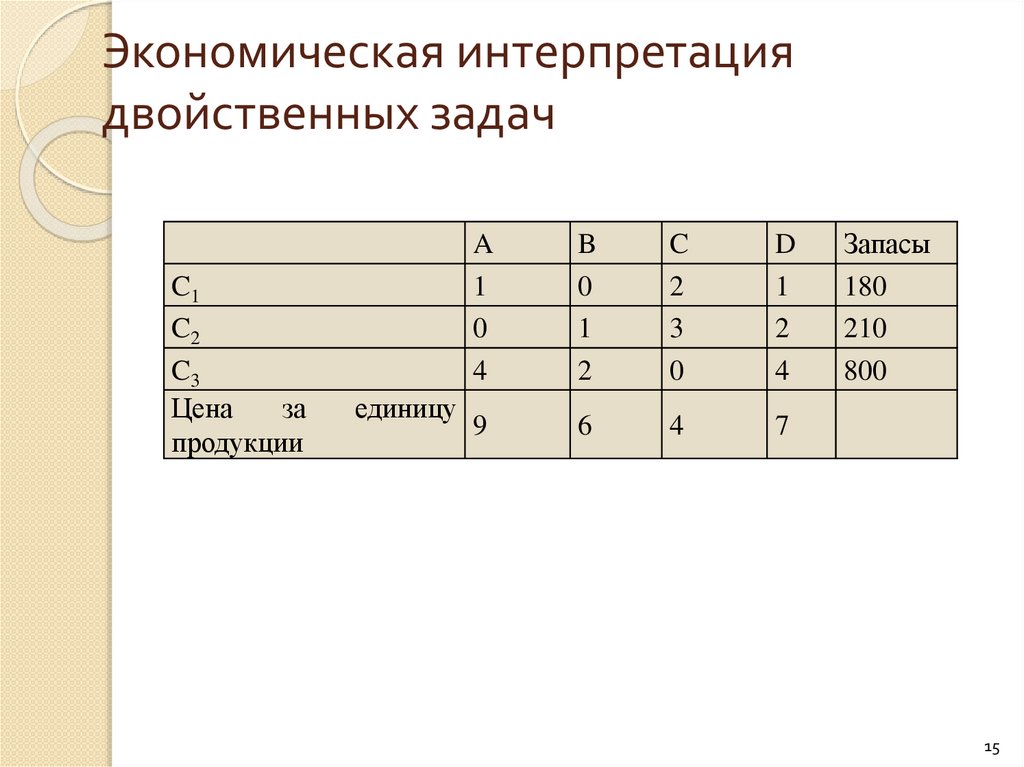
Экономическая интерпретация
двойственных задач
C1
C2
C3
Цена
за
продукции
единицу
A
1
0
4
B
0
1
2
C
2
3
0
D
1
2
4
9
6
4
7
Запасы
180
210
800
15

16.

Экономическая интерпретация
двойственных задач
Построим модели
16

17.

Экономическая интерпретация
двойственных задач
Построим модели
F 9 x1 6 x 2 4 x3 7 x4 max
x1 2 x3 x4 180
x2 2 x3 x4 210
4 x 2 x 4 x 800
2
4
1
x j 0, j 1,4
17

18.

Экономическая интерпретация
двойственных задач
Построим модели
F 9 x1 6 x 2 4 x3 7 x4 max
x1 2 x3 x4 180
x2 2 x3 x4 210
4 x 2 x 4 x 800
2
4
1
x j 0, j 1,4
F * 180 y1 210 y2 800 y3 min
y1 4 y3 9
y 2y 6
2
3
2 y1 3 y2 4
y1 2 y2 4 y3 7
yi 0, i 1,3
18

19.

Экономическая интерпретация
двойственных задач
Приведем к канонической форме
F 9 x1 6 x 2 4 x3 7 x 4 max
x1 2 x3 x 4 x5 180
x 2 3x 3 2 x 4 x6 210
4 x 2 x 4 x x 800
2
4
7
1
x j 0, j 1,7
19

20.

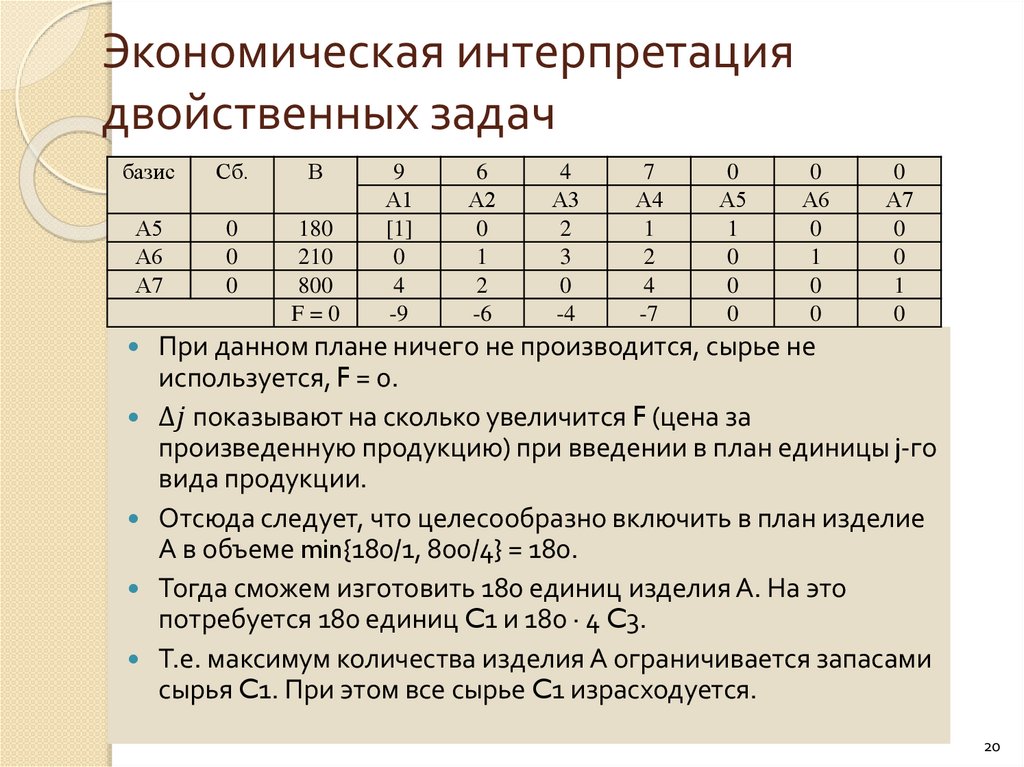
Экономическая интерпретация
двойственных задач
базис
Сб.
В
А5
А6
А7
0
0
0
180
210
800
F=0
9
А1
[1]
0
4
-9
6
А2
0
1
2
-6
4
А3
2
3
0
-4
7
А4
1
2
4
-7
0
А5
1
0
0
0
0
А6
0
1
0
0
0
А7
0
0
1
0
При данном плане ничего не производится, сырье не
используется, F = 0.
∆