Динамика материальной точки. Динамика твердого тела

1.

Сегодня: 29.09.2024
Лекция 3
Механика:
Динамика материальной точки
Динамика твердого тела
Бажин Игорь Вадимович
[email protected]

2.

Сегодня: 29.09.2024
Лекция 3
Механика:
Динамика материальной точки
Динамика твердого тела
Динамикой называется раздел механики, в котором изучаются законы
движения материальных тел под действием сил

3.

~F
Исаак Ньютон
(1643-1727)
Галилео
Галилей
(1564–1642))
F mg sin( ) mg
sin( )
(sin(30 ) 0,5
0
0.523599
6
sin( ) 0.024)
F
~ F t t
m
«Математичес
кие начала
натуральной
философии»
1687г.

4.

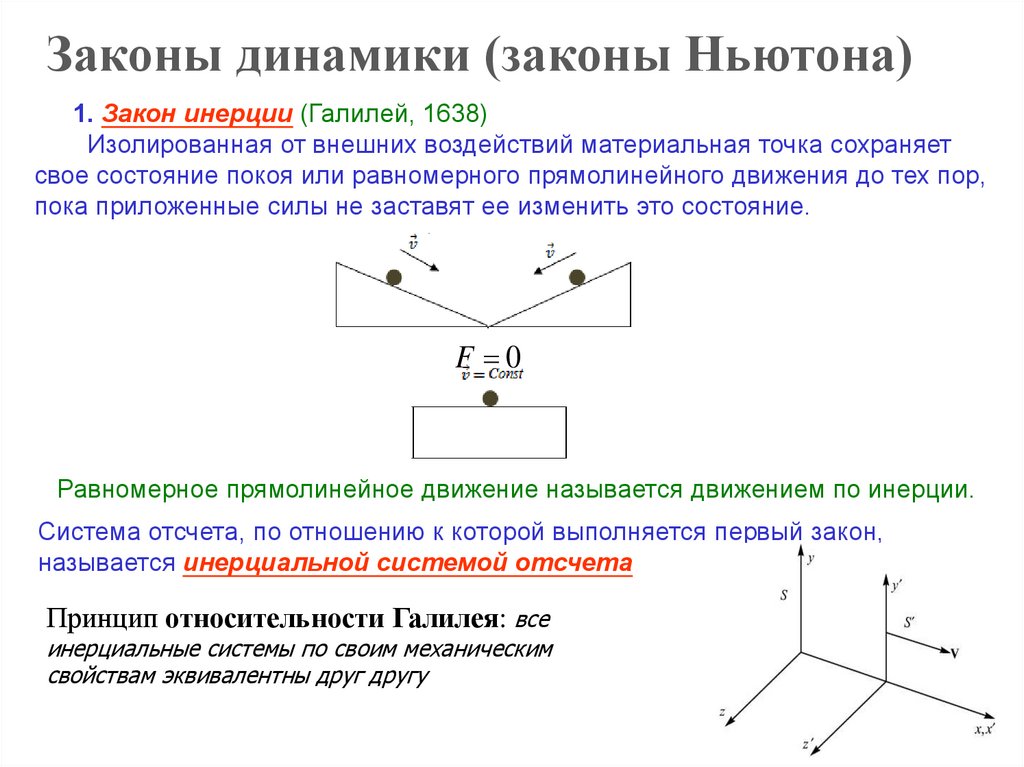
Законы динамики (законы Ньютона)
1. Закон инерции (Галилей, 1638)
Изолированная от внешних воздействий материальная точка сохраняет
свое состояние покоя или равномерного прямолинейного движения до тех пор,
пока приложенные силы не заставят ее изменить это состояние.
F 0
Равномерное прямолинейное движение называется движением по инерции.
Система отсчета, по отношению к которой выполняется первый закон,
называется инерциальной системой отсчета
Принцип относительности Галилея: все
инерциальные системы по своим механическим
свойствам эквивалентны друг другу

5.

Законы динамики (законы Ньютона)
2. Основной закон динамики (Галилей, Гук, 1650-1660е годы).
Произведение массы точки на ускорение, которое она получает под
действием данной силы, равно по модулю этой силе, а направление ускорения
совпадает с направлением силы.
F
d
d dt m
F
m
dt
ma F
dp
p m
F
p F
dt
dp
m
2
1 2
c
d p
F grad U
dt

6.

Первая (основная) задача динамики:
определение сил по заданному закону движению
r (t ) r(t ) n r(t )
d r d
a 2
dt
dt
2
2
dr 1
an
dt R R
ma F
2
F F 2 Fn2
ma F
man Fn

7.

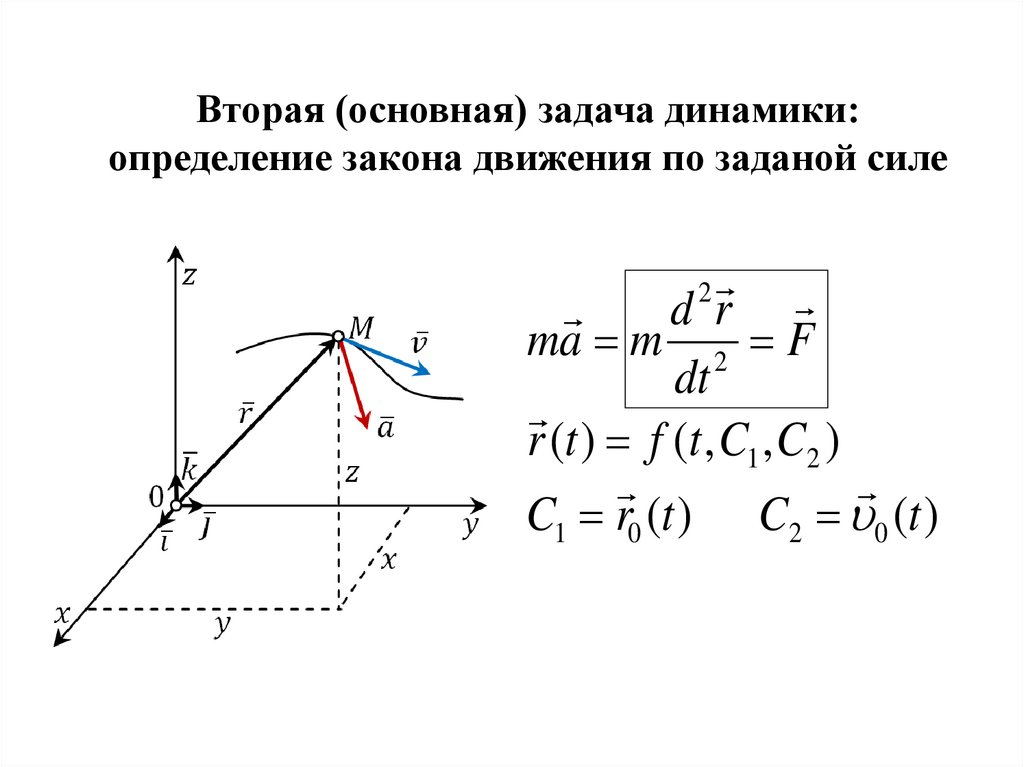
Вторая (основная) задача динамики:
определение закона движения по заданой силе
d r
ma m 2 F
dt
r (t ) f (t , C1 , C2 )
C1 r0 (t ) C2 0 (t )
2

8.

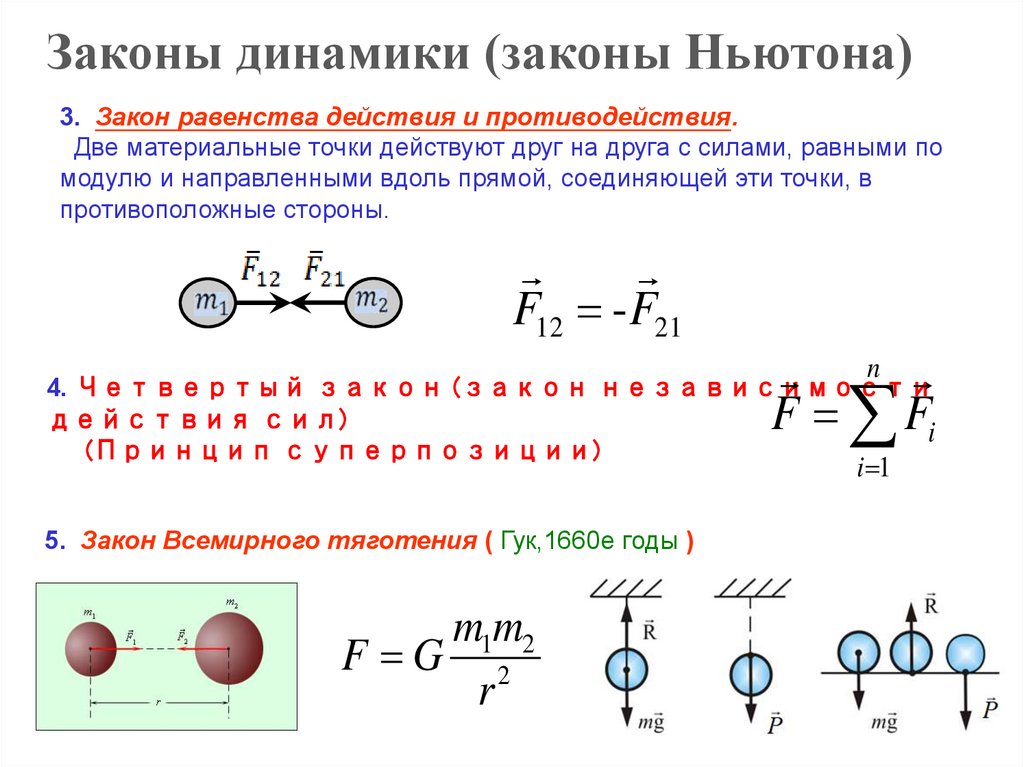
Законы динамики (законы Ньютона)
3. Закон равенства действия и противодействия.
Две материальные точки действуют друг на друга с силами, равными по
модулю и направленными вдоль прямой, соединяющей эти точки, в
противоположные стороны.
F12 - F21
n
F F
4. Четвертый закон (закон независимости
действия сил)
i
(Принцип суперпозиции)
i 1
5. Закон Всемирного тяготения ( Гук,1660е годы )
m1m2
F G 2
r

9.

Первая космическая скорость
2
1
mM
GM
m G 2 ; g 2
R
R
R
км
1 gR 9.81 6471 7.97
с
2
m 2
mM
G
2
R
км
2 2 gR 2 9.81 6471 11.23
с

10.

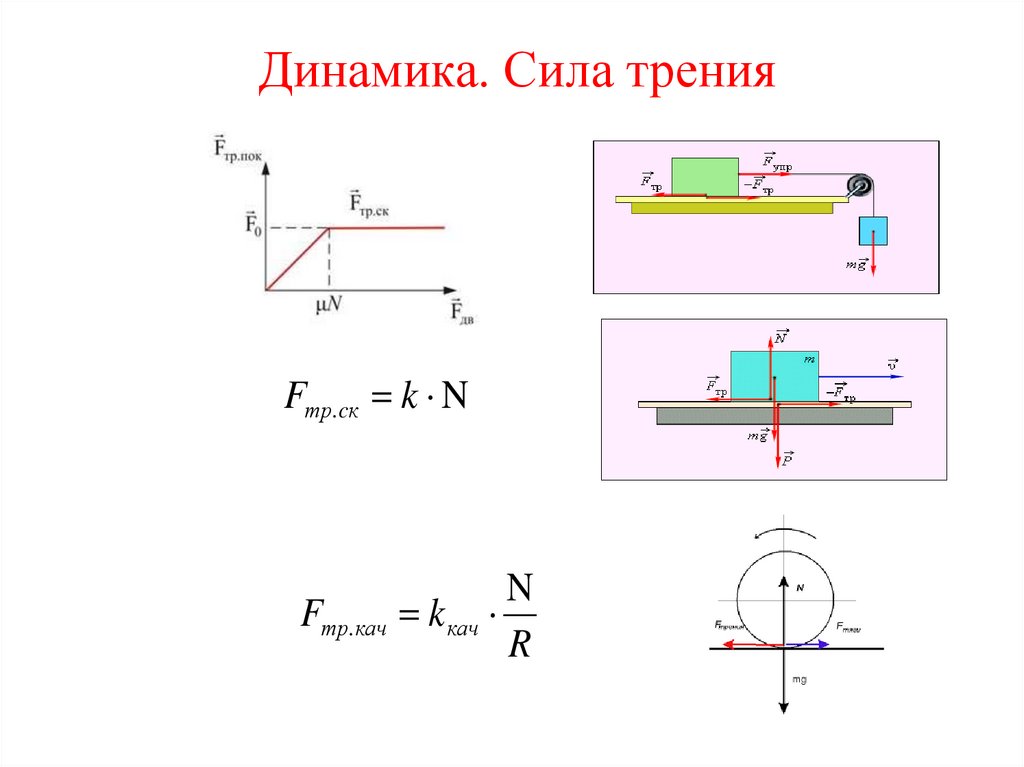
Динамика. Сила трения
Fтр.cк k N
N
Fтр. кач k кач
R

11.

Силы инерции
Уравнение Ньютона для неинерциальных
систем отсчета
Законы инерции выполняются в инерциальной системе отсчета. А как описать
движение тела в неинерциальной системе?
Рассмотрим пример: вы стоите в автобусе спокойно. Вдруг автобус резко
трогается, и вы невольно отклонитесь назад. Что произошло? Кто вас толкнул?
С точки зрения наблюдателя на Земле (в инерциальной системе отсчета), в тот
момент, когда автобус тронулся, вы остались стоять на месте – в соответствии с
первым законом Ньютона.
С точки зрения сидящего в автобусе – вы начали двигаться назад, как если бы
кто-нибудь вас толкнул. На самом деле, никто не толкнул, просто ваши ноги,
связанные силами трения с троллейбусом «поехали» вперед из-под вас и вам
пришлось падать назад.
Можно описать ваше движение в инерционной системе отсчета. Но это не
всегда просто, так как обязательно нужно вводить силы, действующие со стороны
связей.

12.

Они могут быть самыми разными и ведут себя по разному
– нет единого подхода к их описанию.
Можно и в неинерциальной системе воспользоваться
законами Ньютона, если ввести силы инерции. Они
фиктивны. Нет тела или поля под действием которого вы
начали двигаться в автобусе. Силы инерции вводят
специально, чтобы воспользоваться уравнениями Ньютона в
неинерциальной системе.
Силы инерции обусловлены не взаимодействием тел, а
свойствами самих неинерциальных систем отсчета. На силы
инерции законы Ньютона не распространяются.

13.

выражение для силы инерции при
поступательном
движении
неинерциальной
отсчета.
системы
Введем обозначения:
–
ускорение
тела
относительно
неинерциальной
системы;
– ускорение неинерциальной
системы
относительно
инерциальной
(относительно
Земли).
Тогда
ускорение
тела
относительно
инерциальной
системы:
a'
a
a a a '.

14.

Ускорение в инерциальной
системе можно выразить через
второй закон Ньютона
F
a a'
m
F
a a .
m
где m – масса движущегося тела, и
*
a
Мы
можем
и
соответствии
с
(формально)
F Fин
a
,
–
уравнение
представить
в
законом
Ньютона
maНьютона
' F F
для
m m системы отсчета.
неинерциальной
Здесь
–
фиктивная
сила,
обусловленная
свойствами
системы
F
отсчета, необходимая нам для того,
чтобы иметь возможность описывать
движения
тел
в
неинерциальных
ин
ин

15.

относительно перехода
из
одной
системы
отсчета в другую. Они не
подчиняются
закону
действия
и
противодействия.
Движения
тела
под
действием сил инерции
аналогично движению во
внешнем силовом поле.
Силы
инерции
всегда
являются
внешним
по
отношению
к
любому
движению
системы

16.

Принцип Даламбера:
«Если к заданным (активным) силам,
действующим на точку, и реакциям
наложенных связей
присоединить силу инерции,
то получится уравновешенная система
сил»
ma Ф;
ma P N ; P N ma 0;
Pi Ni Фi 0

17.

Динамика. Сила упругости
E
F
l
; ; l l l0
S
l0
S
l
2
S
l
ES
F
l k l
l0

18.

Закон сохранения импульса
F12 - F21
dp j
dt
F jk
dp j
dt
j
k
F jk 0;
j
F jk Fkj
k
d
dP
pj
0 P const
dt j
dt
Закон сохранения импульса связан с однородностью пространства.
Однородность пространства заключается в том, что при параллельном переносе в пространстве
замкнутой системы тел как целого её физические законы и законы движения не изменяются (не
зависят от выбора положения начала координат инерциальной системы отсчета).

19.

Законы сохранения энергии, импульса и момента импульса связаны
с фундаментальными свойствами времени и пространства.
Закон сохранения энергии связан с однородностью времени, а
законы сохранения импульса и момента импульса − соответственно с
однородностью и изотропностью пространства.
Однородность времени означает, что все моменты времени
эквивалентны и физические законы не изменяются со временем, т.е.
не зависят от начала отсчета времени.
Однородность пространства заключается в том, что при
параллельном переносе в пространстве замкнутой системы тел как
целого её физические законы и законы движения не изменяются (не
зависят от выбора положения начала координат инерциальной
системы отсчета).
Изотропность пространства означает одинаковость свойств
пространства по всем направлениям, т.е. независимость физических
законов от выбора направления координат системы отсчета.

20.

Динамика механической системы
1 n
m mi ;
rc mi ri
m i 1
i 1
n
dri 1
dri 1 n
c mi mi i
dt m i 1 dt m i 1
n
mi i m c
n
i 1

21.

Система центра масс
Система отсчёта, движущаяся со скоростью
центра масс, называется системой центра
масс(с.ц.м). В этой системе отсчёта начало системы
координат помещается в центр масс, поэтому r 0 ,
c
drc
следовательно,
c
dt
0
Это означает, что полный импульс системы
частиц равен нулю, и наблюдается только
относительное движение частиц, поэтому она удобна
для анализа столкновения частиц.

22.

Механическая работа. Мощность.
Изменение механического движения тела вызывается силами,
которые действуют на него со стороны других тел.Чтобы
количественно характеризовать процесс обмена энергии между
взаимодействующими телами, в механике вводится понятие
работы силы.
Если тело движется
прямолинейно и на него действует
постоянная сила F , которая составляет некоторый угол
с направлением перемещения, то работа этой силы равна
произведению проекции силы Fs F F cos
s
на перемещение точки приложения силы
A ( FS S ) FS S cos( )

23.

Работа силы на участке траектории от точки 1
до точки 2 равна алгебраической сумме
элементарных работ на отдельных бесконечно
малых участках пути.
Эта сумма равна определенному интегралу:
2
2
1
1
A F cos ds Fs ds
Единица работы – джоуль [ Дж]
1Дж = 1Н·м

24.

Чтобы охарактеризовать скорость совершения работы,
вводят понятие мощности
dA
N
dt
За время dt сила F совершает работу Fdr , и
мощность, развиваемая этой силой в данный момент
времени:
Fdr
N
F v
dt
то есть равна скалярному произведению силы на вектор
скорости, с которой движется точка приложения силы.
Мощность N - величина скалярная.
Единица мощности – ватт [Вт] 1Вт = 1Дж/с

25.

Кинетическая энергия
Кинетическая энергия механической системы – это
энергия механического движения этой системы.
Имеем покоящееся тело. На него действует сила F , под
действием которой тело начинает двигаться.
При этом сила совершает работу, а энергия движущегося
тела возрастает на величину затраченной работы.
Работа dA силы F на пути, который тело прошло за
время возрастания скорости от 0 до V , идет на
увеличение кинетической энергии. Покажем это.

26.

dP .
A1 2 F FdS
Vdt
dt
1
1
2
2
dP
или
dS Vdt F
dt
d d
dV
F
P mV m
dt
dt
dt
Здесь
V2
2
2
2
mV2 mV1
A1 2 F m VdV m VdV
2
2
1
V1
Выражение
2
mV
K
2
кинетическая
энергия

27.

Консервативные и неконсервативные и
диссипативные силы
Консервативными называются силы, работа которых
не зависит от того, по какой траектории произошло
перемещение тела, а зависит только от его начального и
конечного положений. Примеры таких сил : упругие силы
и гравитационные силы. Работа упругих сил была
рассмотрена ранее.
Определим работу, совершаемую силой тяготения
при перемещении ею материальной точки массой m .
На расстоянии R на данное тело действует сила:
Mm
F G 2
R

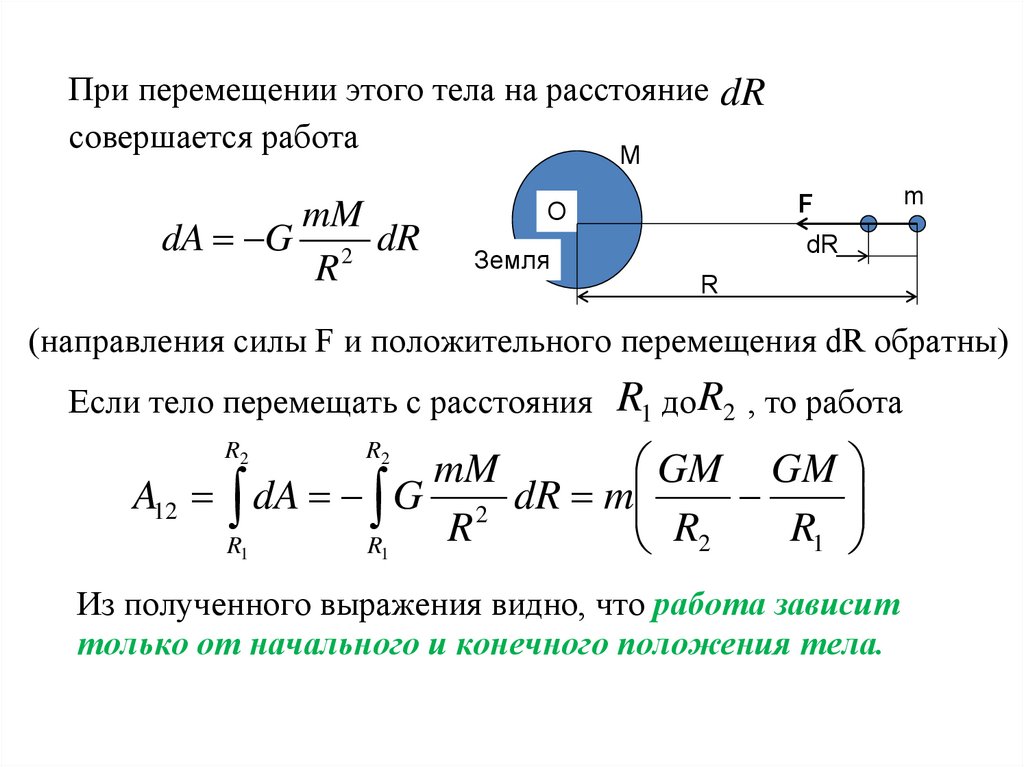
28.

При перемещении этого тела на расстояние dR
совершается работа
M
mM
dA G 2 dR
R
F
О
m
dR
Земля
R
(направления силы F и положительного перемещения dR обратны)
Если тело перемещать с расстояния
R1 до R2 , то работа
GM GM
mM
A12 dA G 2 dR m
R
R1
R2
R1
R1
R2
R2
Из полученного выражения видно, что работа зависит
только от начального и конечного положения тела.

29.

30.

31.

32.

Математическая запись этого утверждения может быть
представлена, исходя из определения работы, следующим
образом:
F
d
r
A
A
A
A
0
12
21
12
12
S
Интеграл по замкнутому контуру S :
называется циркуляцией вектора F.
Fdr
S
Введение нового математического понятия векторного
анализа
позволяет
дать
еще
одно
определение
консервативной силы:
Если циркуляция какого-либо вектора силы равна нулю,
то эта сила консервативна.

33.

Неконсервативные силы. К ним относятся прежде
всего, так называемые, диссипативные силы:
трение, сила вязкого сопротивления. Эти силы
зависят не только от конфигурации тел, но и от
относительных скоростей движения.
Сила трения направлена против скорости тела,
поэтому работа сил трения отрицательна.
Отсюда определение:
Диссипативными называются такие силы,
полная работа которых при любых движениях в
замкнутой системе всегда отрицательна.

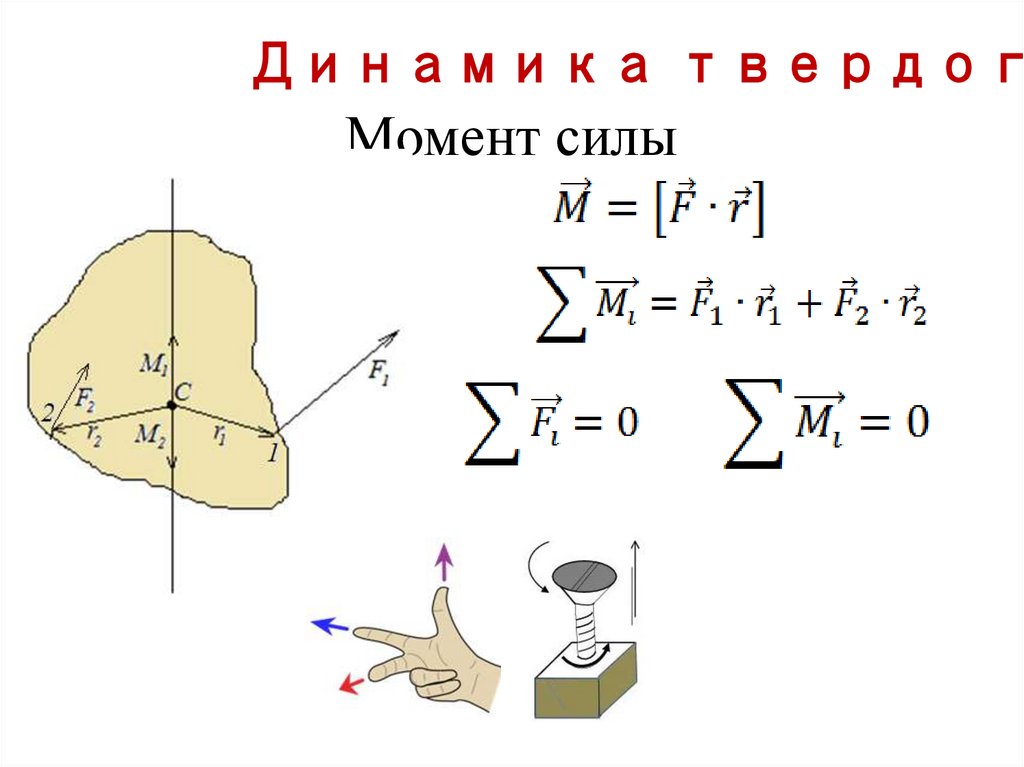
34. Момент силы

Динамика твердог
Момент силы
Состояние покоя

35.

Момент импульса
Материальная точка
dp
F
dt

36.

с другой стороны

37.

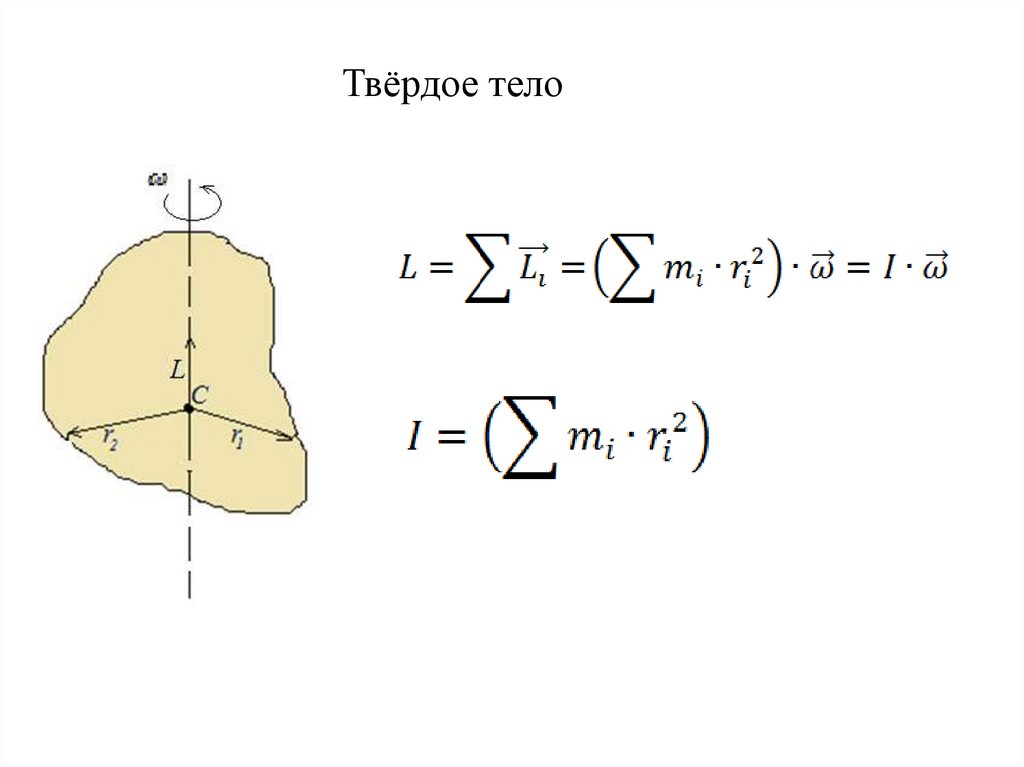
Твёрдое тело

38. Момент инерции твердого тела – физическая величина характеризующая массу тела и характер распределения её относительно оси

вращения

39. Кинетическая энергия вращающегося твёрдого тела

материальная точка
твёрдое тело

40.

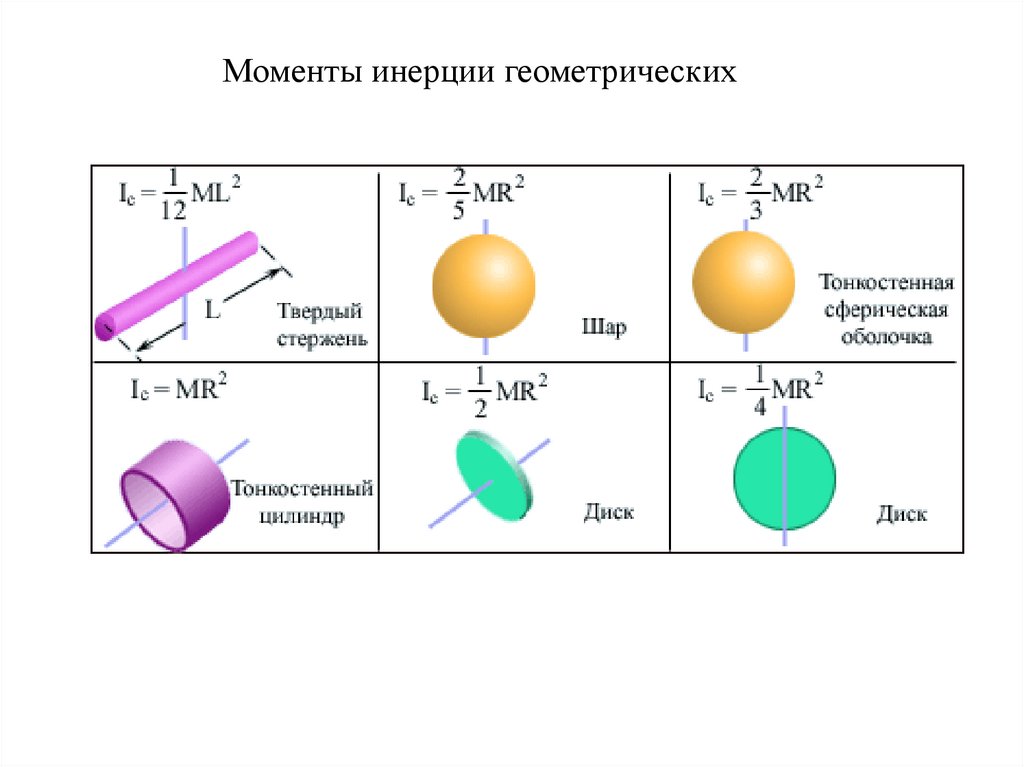
Моменты инерции геометрических тел.

41.

Теорема Гюйгенса-Штейнера.
Момент инерции тела относительно произвольной оси равен сумме моменту инерции тела
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения
массы тела на квадрат расстояния между осями.
I m d IC
2

42.

Любой набор взаимодействующих тел именуется
системой тел.
Если на тела, входящие в систему, не действуют
другие тела, не входящие в эту систему (или действие
других тел на каждое тело скомпенсировано), то такая
система тел называется замкнутой.
Если суммарный момент сил действующий на
систему равен нулю, то такая система также будет
замкнутой. Закон сохранения момента импульса

43.

Момент импульса замкнутой системы всегда
остаётся неизменным.

44.

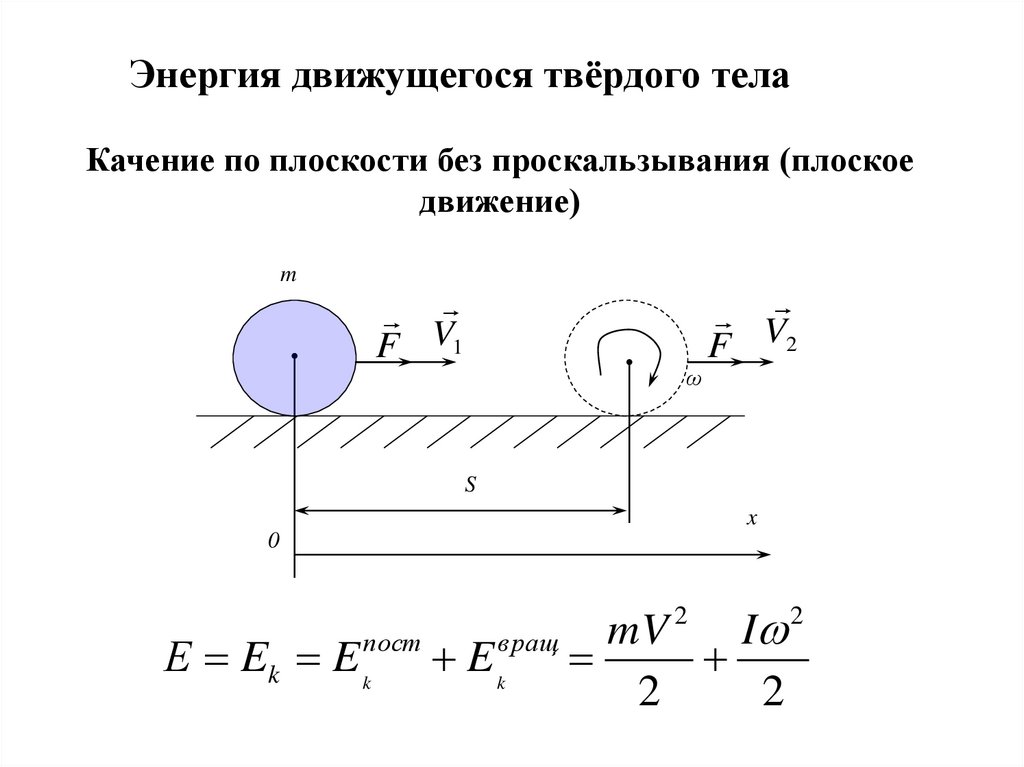
Энергия движущегося твёрдого тела
Качение по плоскости без проскальзывания (плоское
движение)
m
F V1
ω
V
F 2
S
x
0
Е Ek E k
пост
Ek
вращ
mV
I
2
2
2
2

45.

Поступательное
движение
Вращательное движение
вокруг неподвижной оси
Масса m
Момент инерции J
Перемещение dr
Скорость
dr dt
Угловое перемещение d
Угловая скорость
Ускорение
a d dt
d dt
Угловое ускорение d
dt
p m
Момент импульса
Сила
Импульс
dp
F
dt
F
ma F
Момент силы M
dL
M
dt
L J
J M