Построение сечений тетраэдра и параллелепипеда

1.

Уроки геометрии в 10 классе
КЕНЦИС Н.В.

2.

Содержание:
1.
Цель и задачи
2.
Введение
3.
Понятие секущей плоскости и определение сечения многогранника
4.
Основные аксиомы и теоремы, необходимые для построения сечений
5.
Правила построения сечений, возможные ошибки при построении сечений
6.
Виды сечений тетраэдра и параллелепипеда
7.
Задачи на построение сечения тетраэдра и параллелепипеда с объяснением
8.
Задача на построение сечения параллелепипеда с предложенными на выбор
вариантами построений
9.
Задача на построение сечения тетраэдра с комментариями
10. Задачи повышенной сложности на построение сечения тетраэдра и
параллелепипеда
11. Задача для самостоятельного построения сечения параллелепипеда (с
ответом – выполненным построением)
12. Заключение

3.

Цель уроков:
Сформировать умения у учащихся строить сечения
тетраэдра и параллелепипеда заданной плоскостью.
Задачи:
Дать определение секущей плоскости и определение сечения
многогранника.
Познакомить с правилами построения сечений тетраэдра и
параллелепипеда.
Рассмотреть возможные варианты сечений тетраэдра и параллелепипеда.
Выработать навыки построения сечений тетраэдра и параллелепипеда при
различных случаях задания секущей плоскости.
Способствовать формированию у учащихся пространственного
воображения.
Развивать умения у учащихся анализировать, сравнивать, обобщать, делать
выводы.
Способствовать развитию умения пользоваться чертежными
инструментами и умению выполнять построения более четко, наглядно и
аккуратно.

4.

Вспомним сказку “Маленький принц”.
Помните, какую картинку (первую в
своей жизни) нарисовал в детстве
Экзюпери? Посмотрите на нее, что там
изображено?
Как ни странно все думают, что это
шляпа. Но на самом деле это был удав,
проглотивший слона. Чтобы другие это
поняли, юный художник выразился
конкретнее и нарисовал второй рисунок.
Он был уверен, что теперь-то все
поймут, так как он объяснил взрослым
свою картинку не только снаружи, но и
изнутри.
Как же это удалось шестилетнему
художнику — будущему знаменитому
писателю и летчику?
Он мысленно разрезал удава-шляпу и
показал, что содержится внутри.

5.

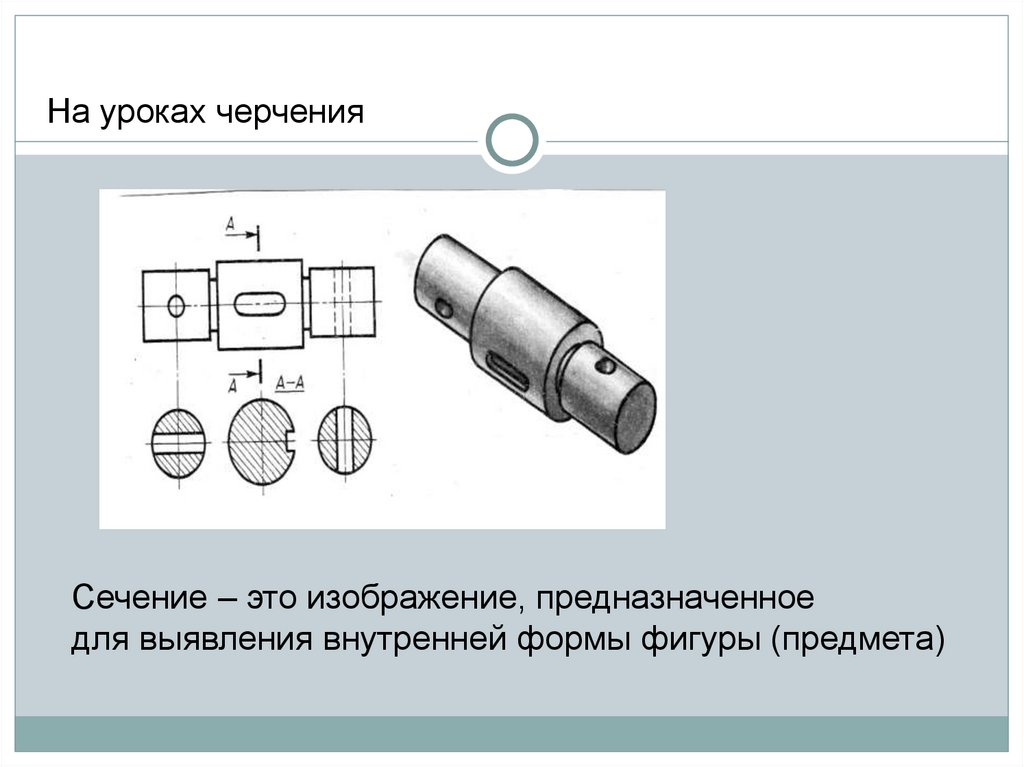
На уроках черчения
Сечение – это изображение, предназначенное
для выявления внутренней формы фигуры (предмета)

6.

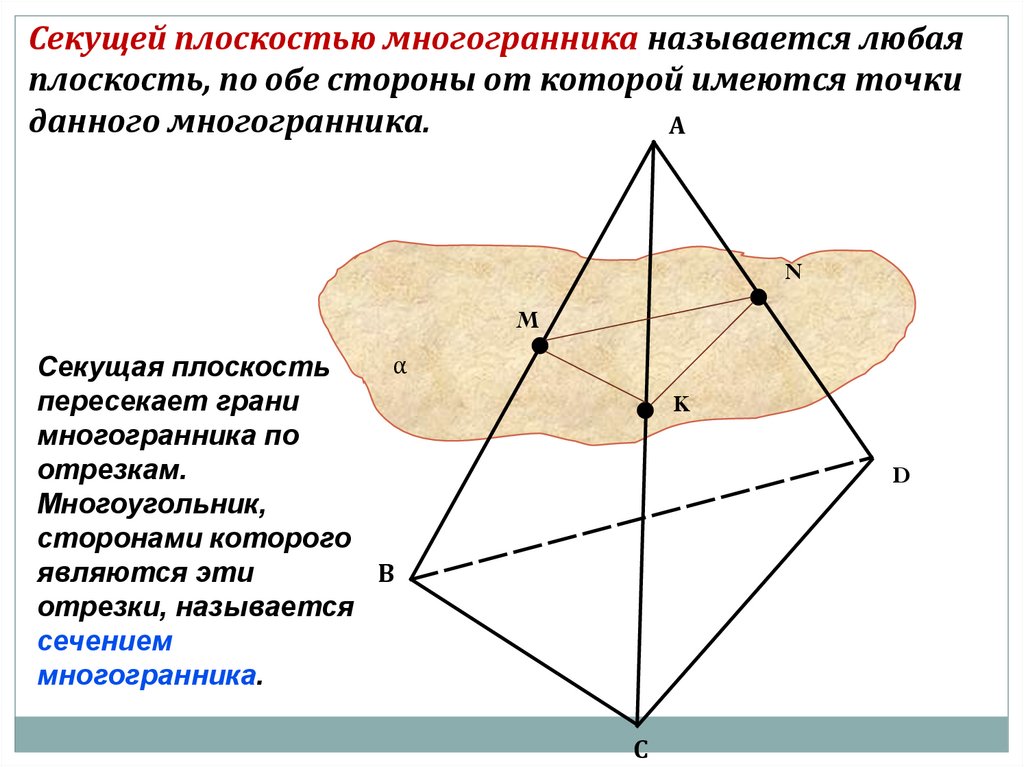
Секущей плоскостью многогранника называется любая
плоскость, по обе стороны от которой имеются точки
данного многогранника.
А
N
M
α
Секущая плоскость
пересекает грани
многогранника по
отрезкам.
Многоугольник,
сторонами которого
являются эти
В
отрезки, называется
сечением
многогранника.
K
D
С

7.

Аксиомы и теоремы стереометрии
В
А
α
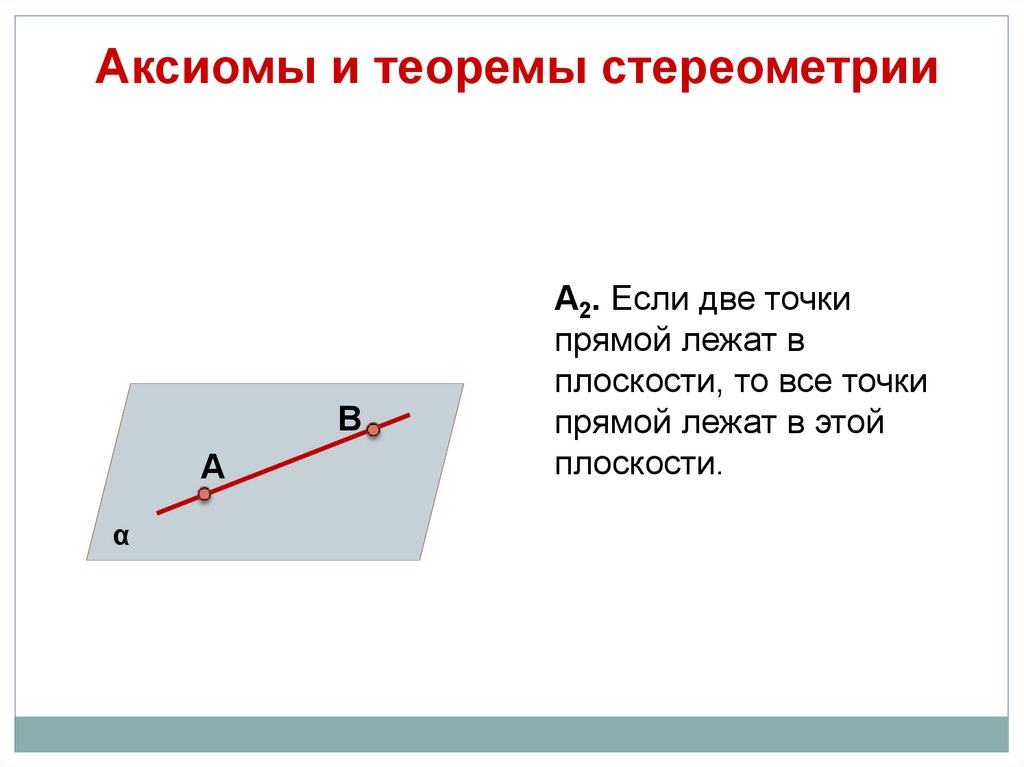
А2. Если две точки
прямой лежат в
плоскости, то все точки
прямой лежат в этой
плоскости.

8.

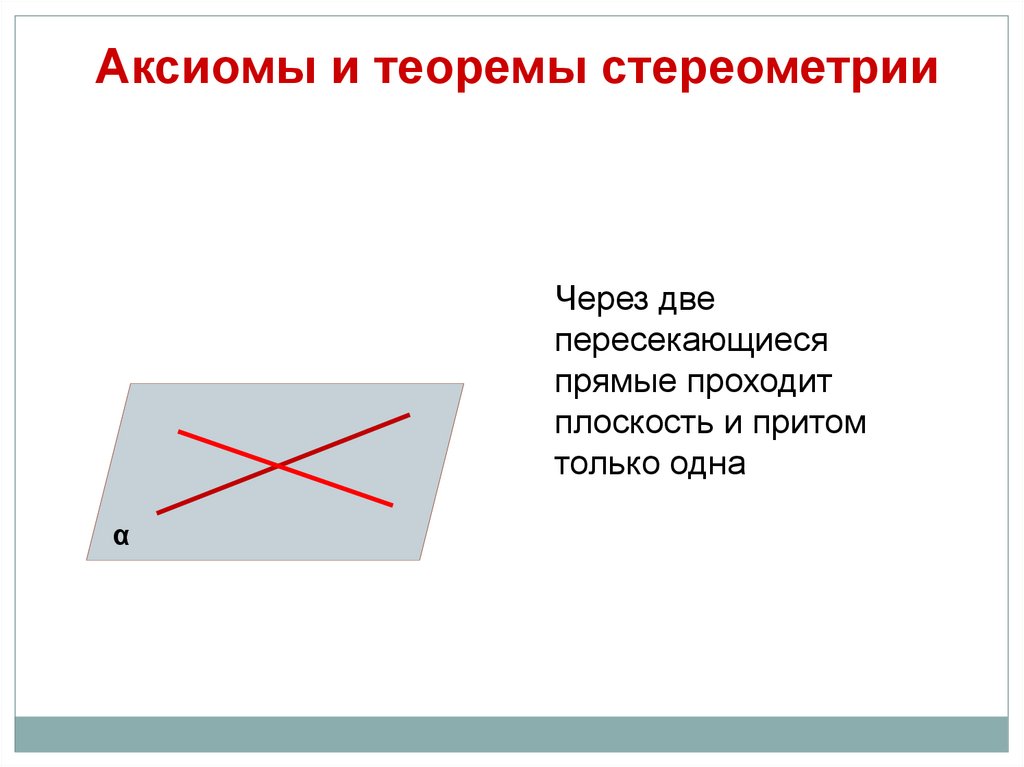
Аксиомы и теоремы стереометрии
Через две
пересекающиеся
прямые проходит
плоскость и притом
только одна
α

9.

Аксиомы и теоремы стереометрии
β
А
α
a
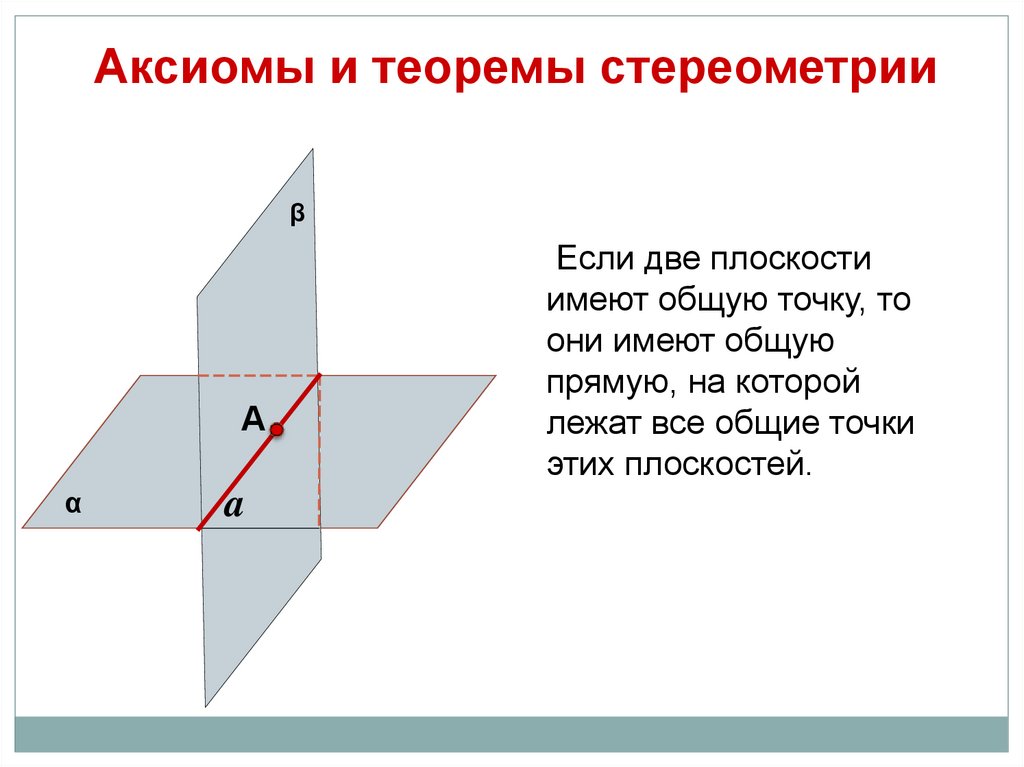
Если две плоскости
имеют общую точку, то
они имеют общую
прямую, на которой
лежат все общие точки
этих плоскостей.

10.

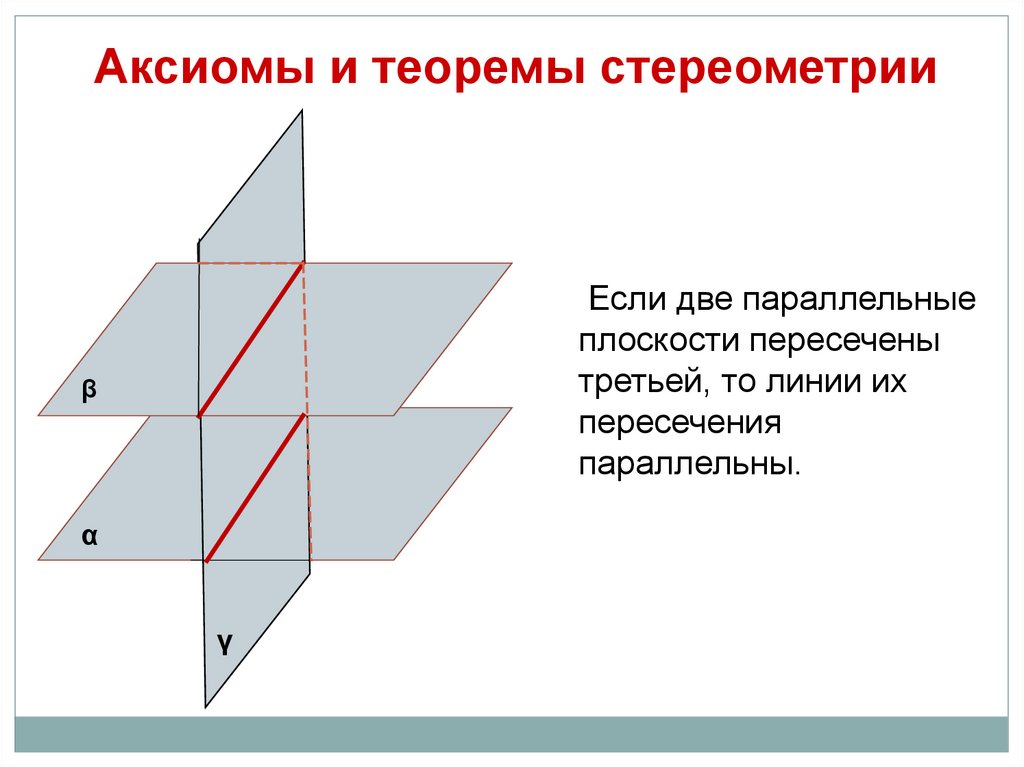
Аксиомы и теоремы стереометрии
Если две параллельные
плоскости пересечены
третьей, то линии их
пересечения
параллельны.
β
α
γ

11.

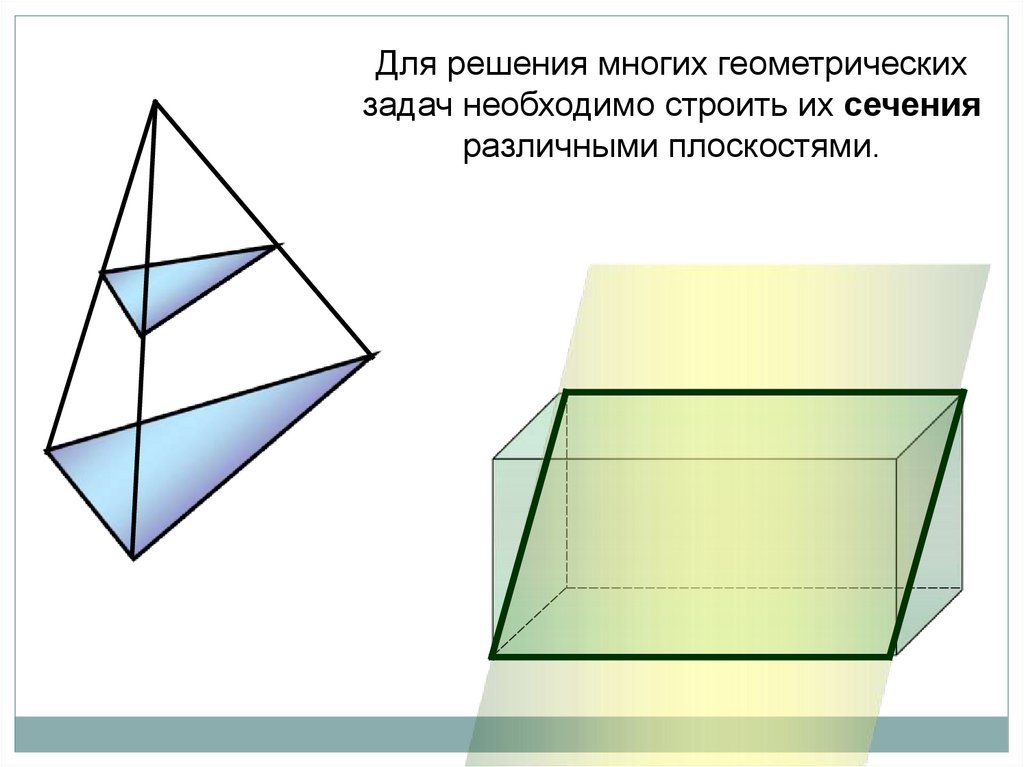
Для решения многих геометрических
задач необходимо строить их сечения
различными плоскостями.

12.

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
1. Соединять можно только две точки, лежащие в
плоскости одной грани.
2. Секущая плоскость пересекает
грани по параллельным отрезкам.
параллельные
3. Если в плоскости грани отмечена только одна точка,
принадлежащая плоскости сечения, то надо построить
дополнительную точку. Для этого необходимо найти
точки пересечения уже построенных прямых с другими
прямыми, лежащими в тех же гранях.

13.

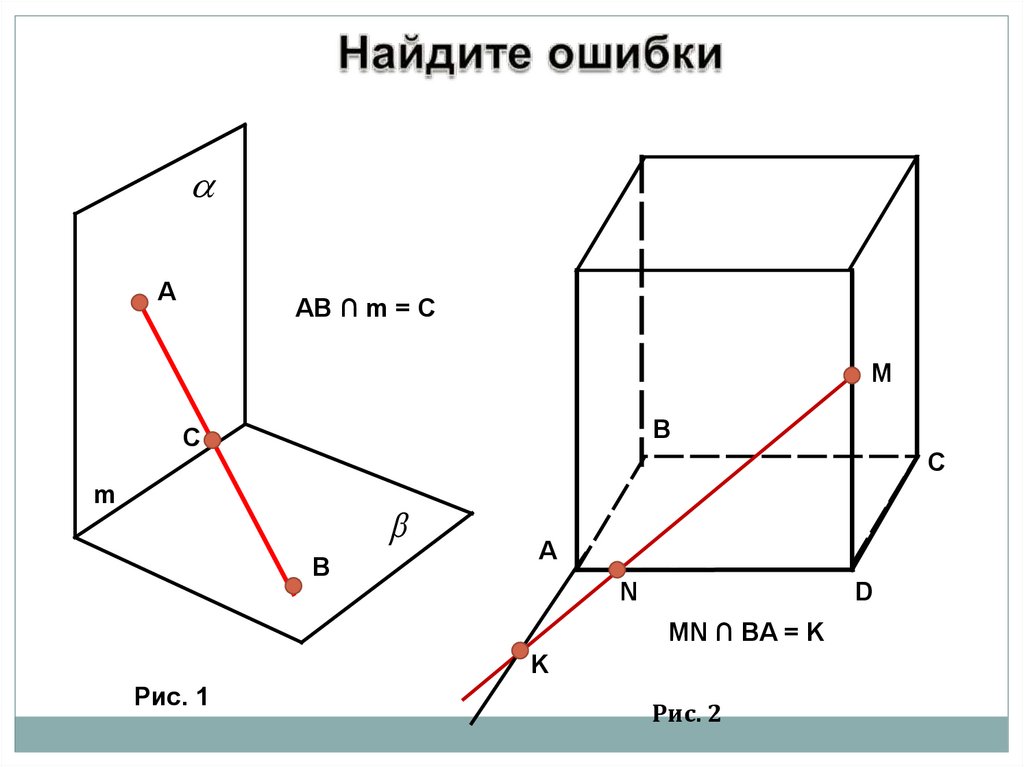
A
AB ∩ m = C
M
B
C
C
m
B
A
N
D
MN ∩ BA = K
K
Рис. 1
Рис. 2

14.

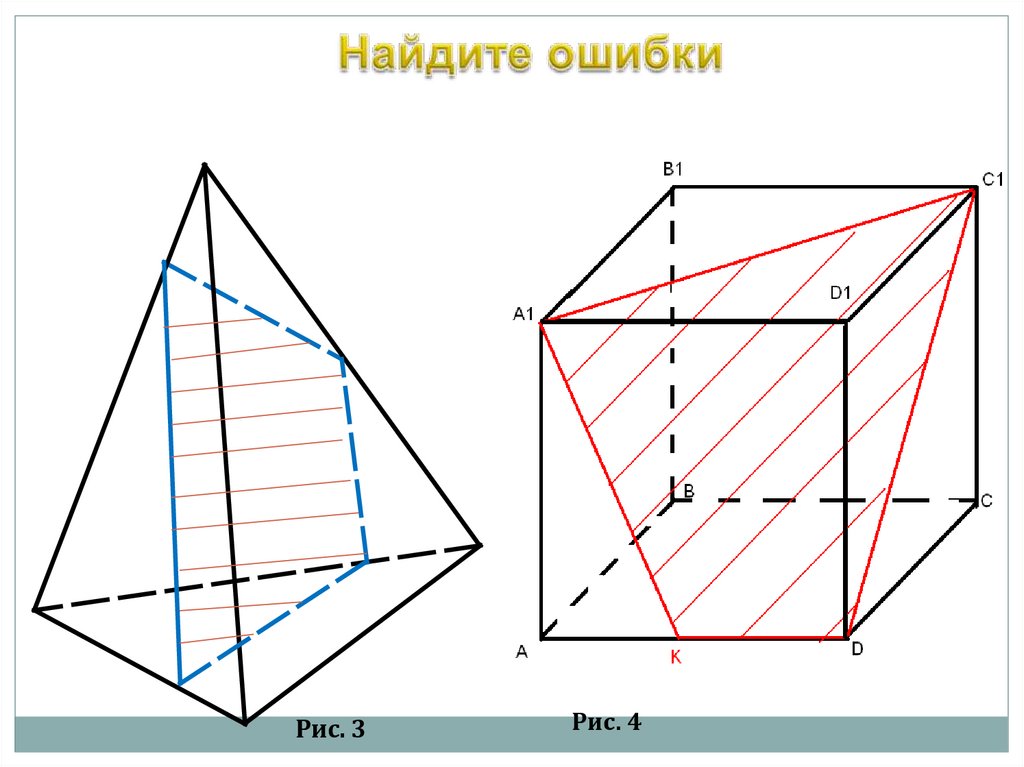
Рис. 3
Рис. 4

15.

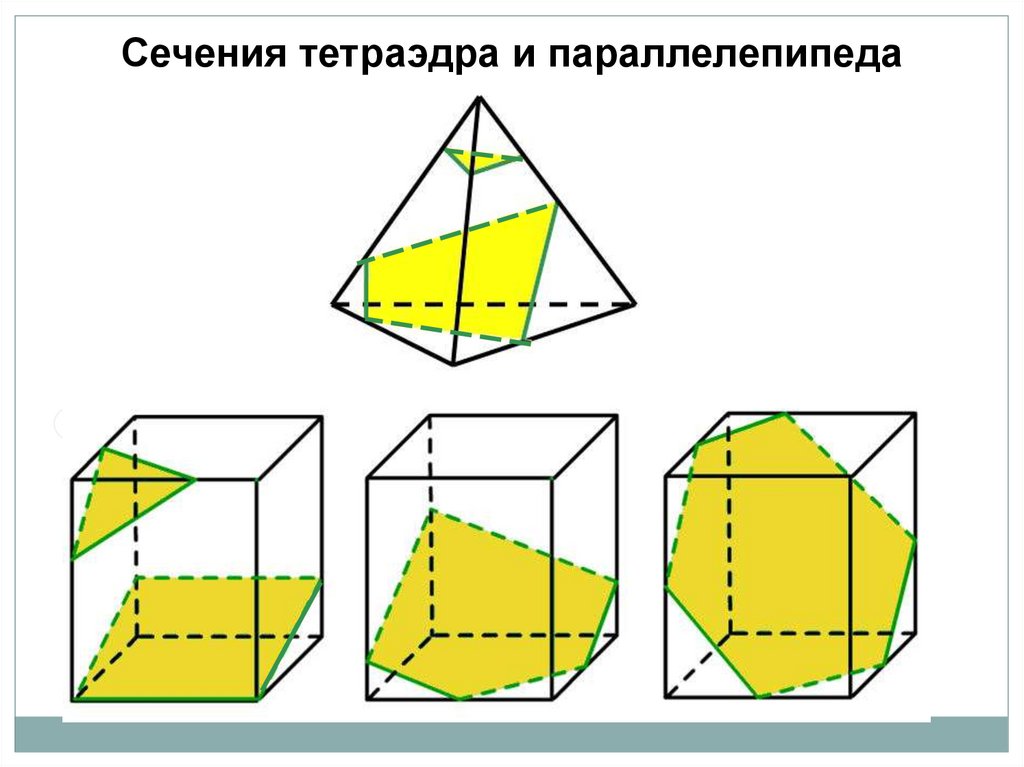
Сечения тетраэдра и параллелепипеда

16.

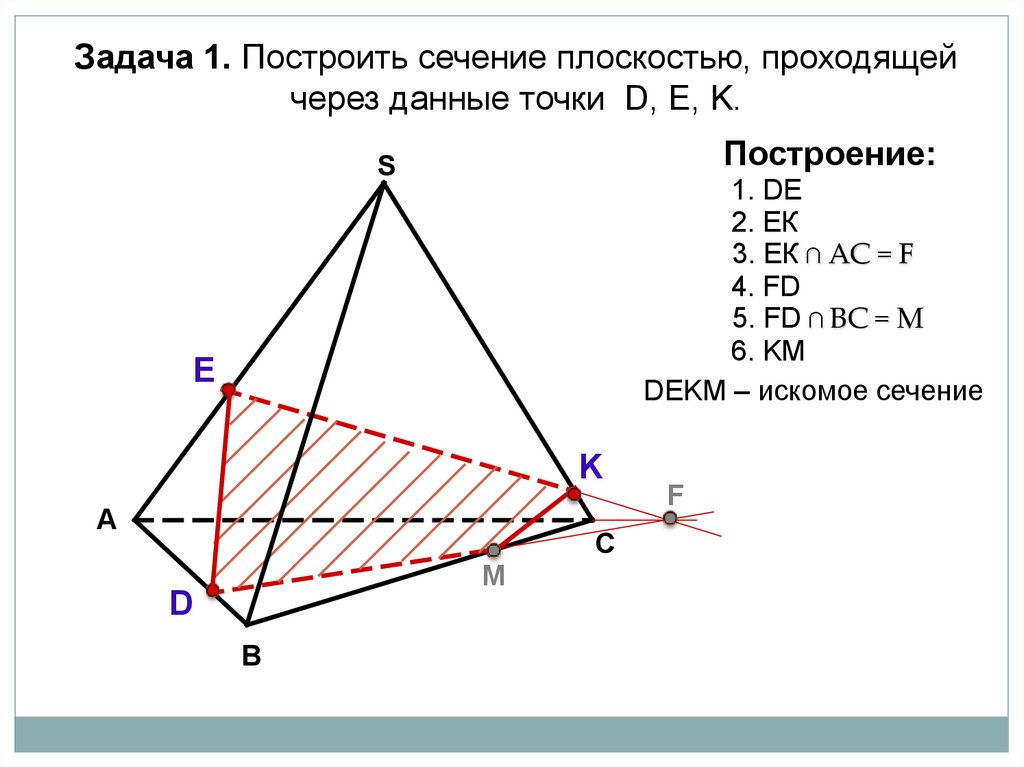
Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F

17.

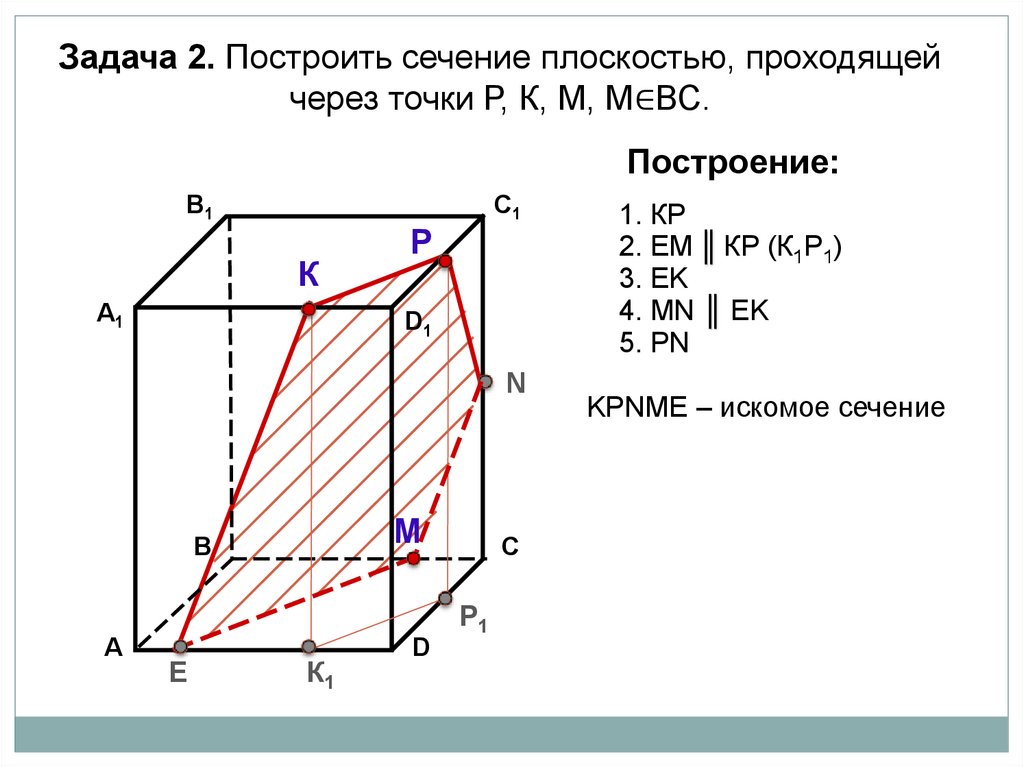
Задача 2. Построить сечение плоскостью, проходящей
через точки Р, К, М, М∈ВС.
Построение:
В1
К
А1
C1
Р
D1
N
М
В
А
С
Р1
E
К1
D
1. КP
2. EM ║ КP (К1Р1)
3. EK
4. МN ║ EK
5. РN
KРNМE – искомое сечение

18.

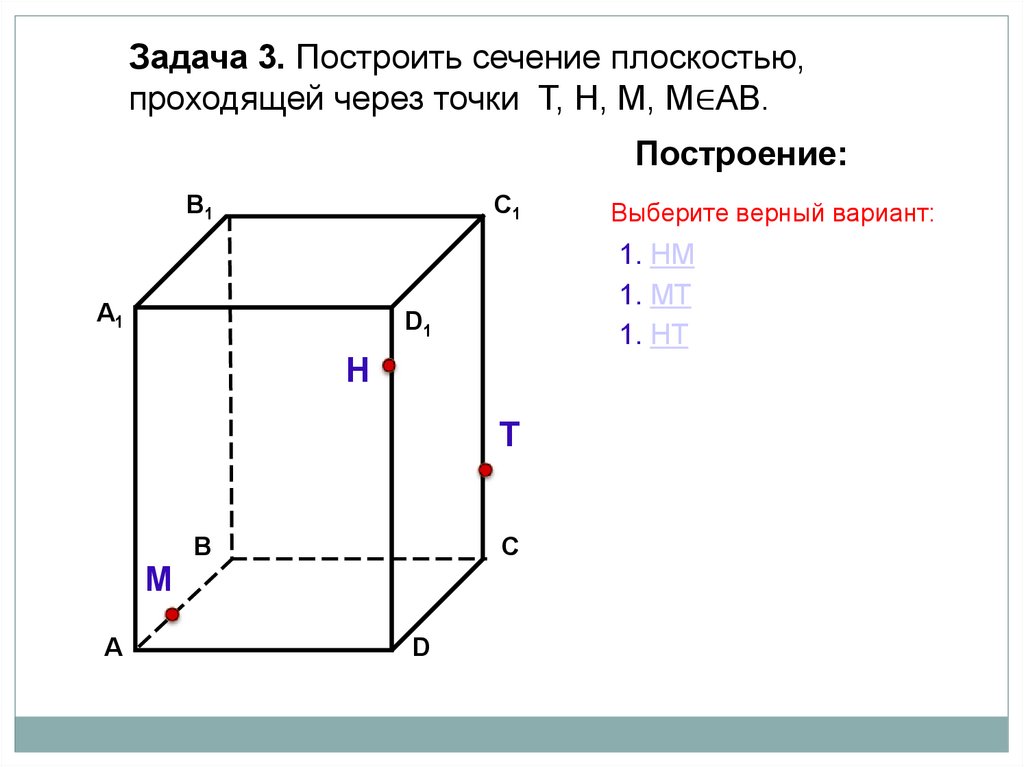
Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
1. НМ
1. МТ
1. НT
D1
Н
Т
М
А
В
С
D
Выберите верный вариант:

19.

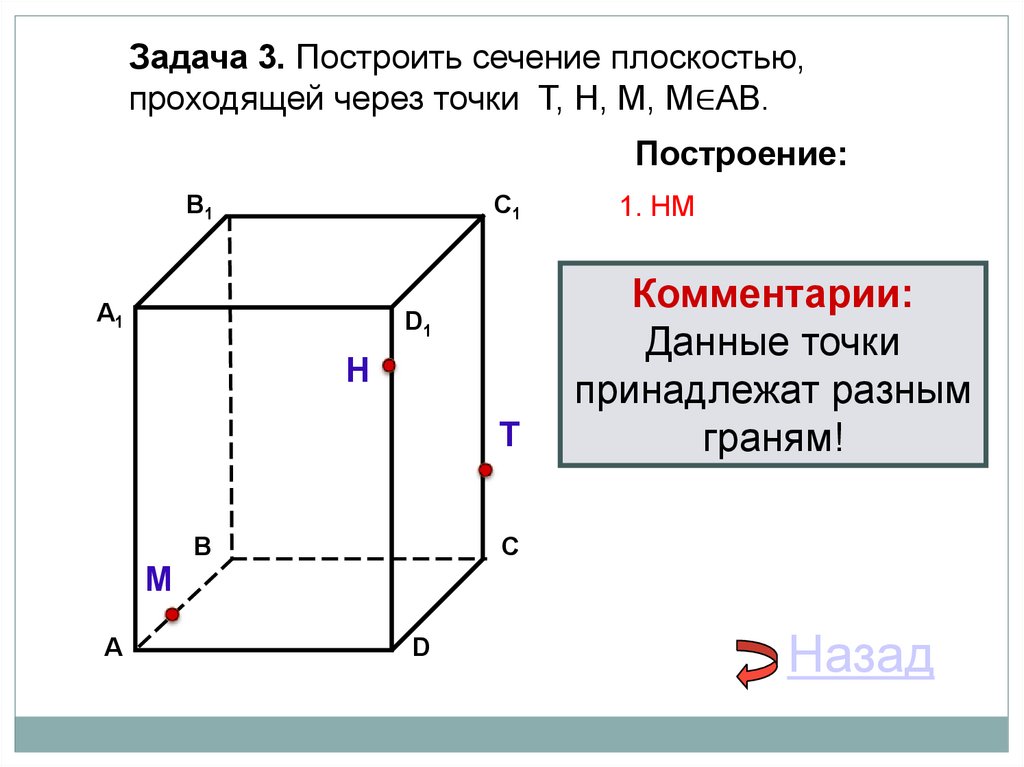
Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. НМ
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад

20.

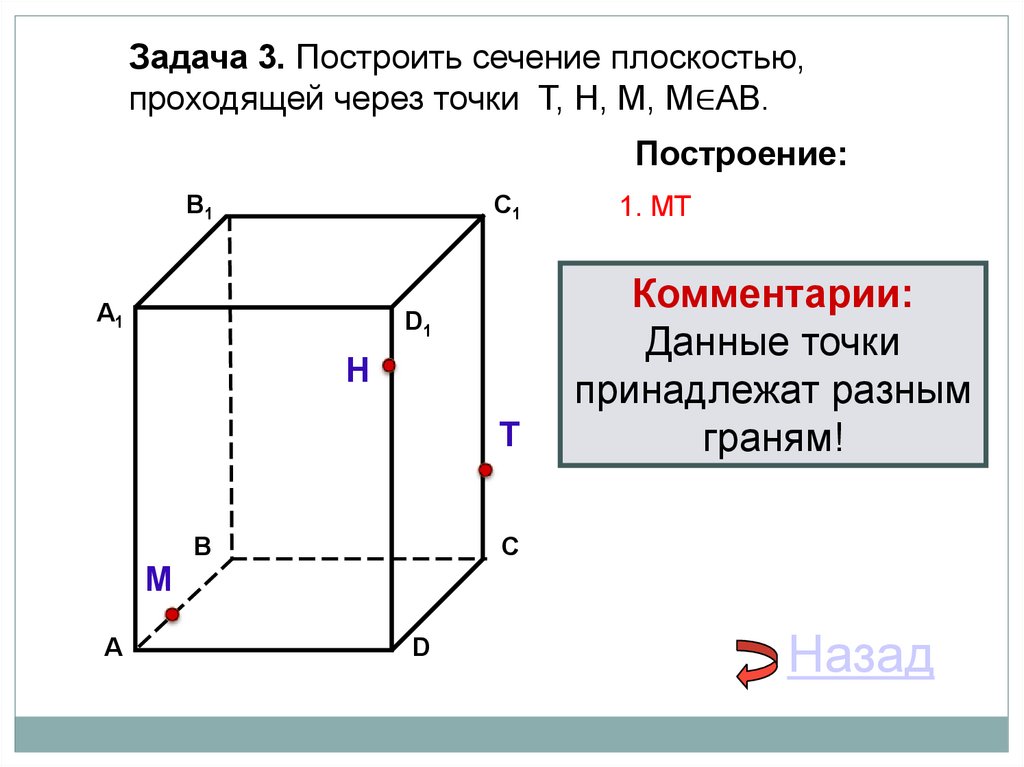
Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. МT
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад

21.

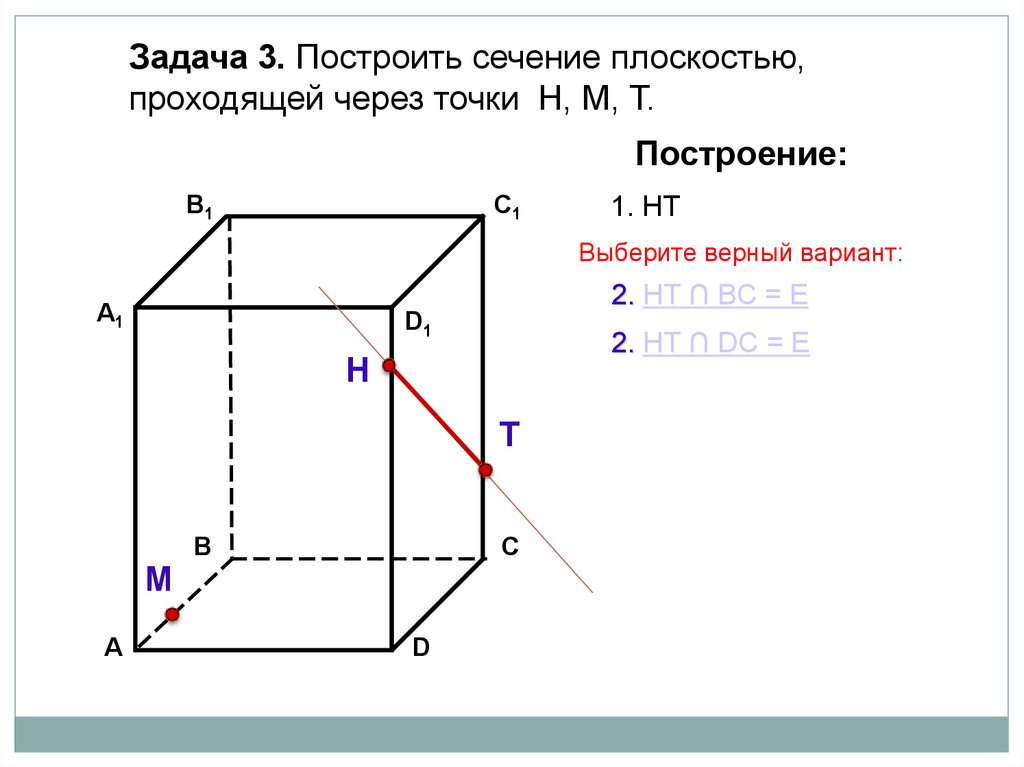
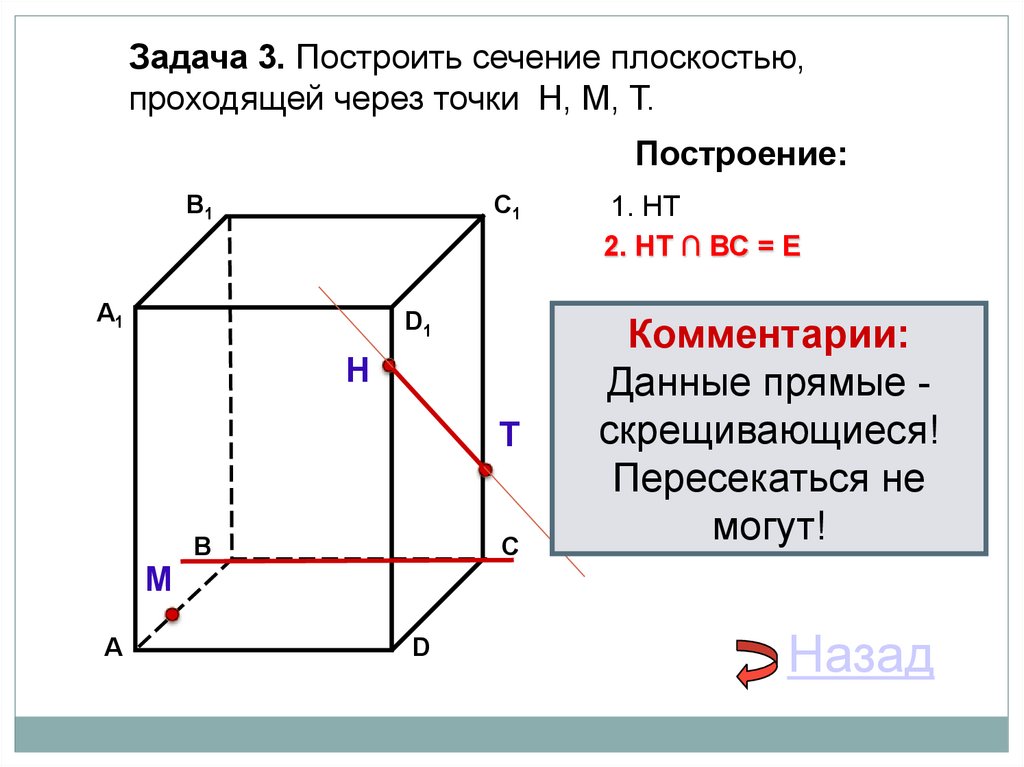
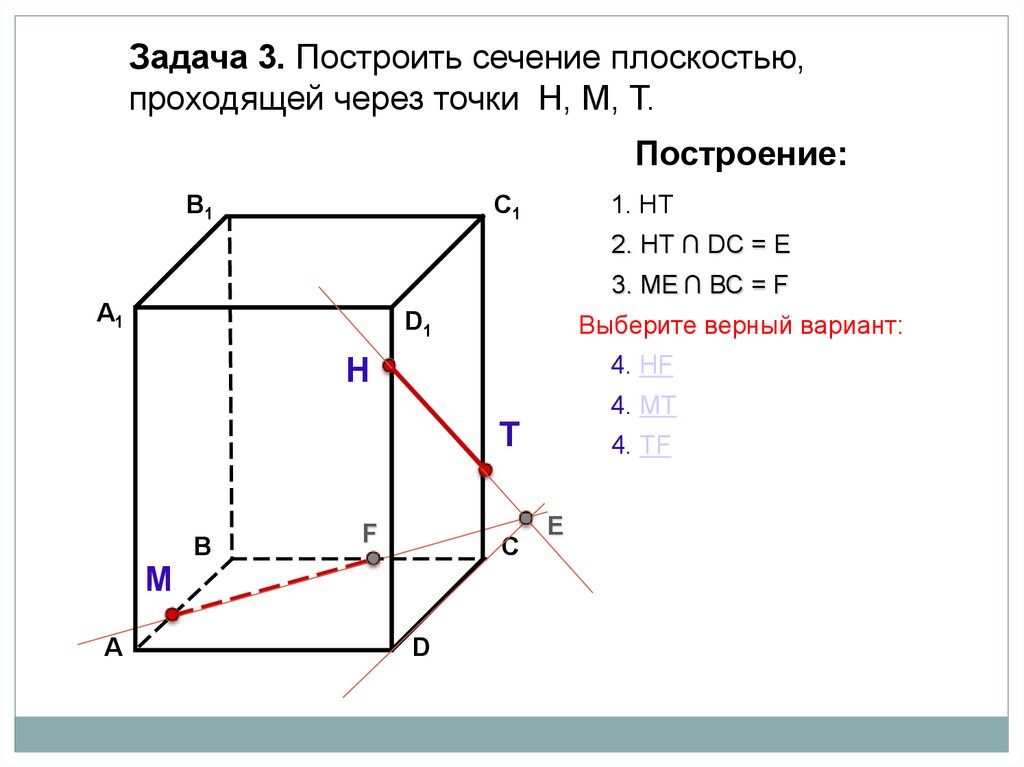
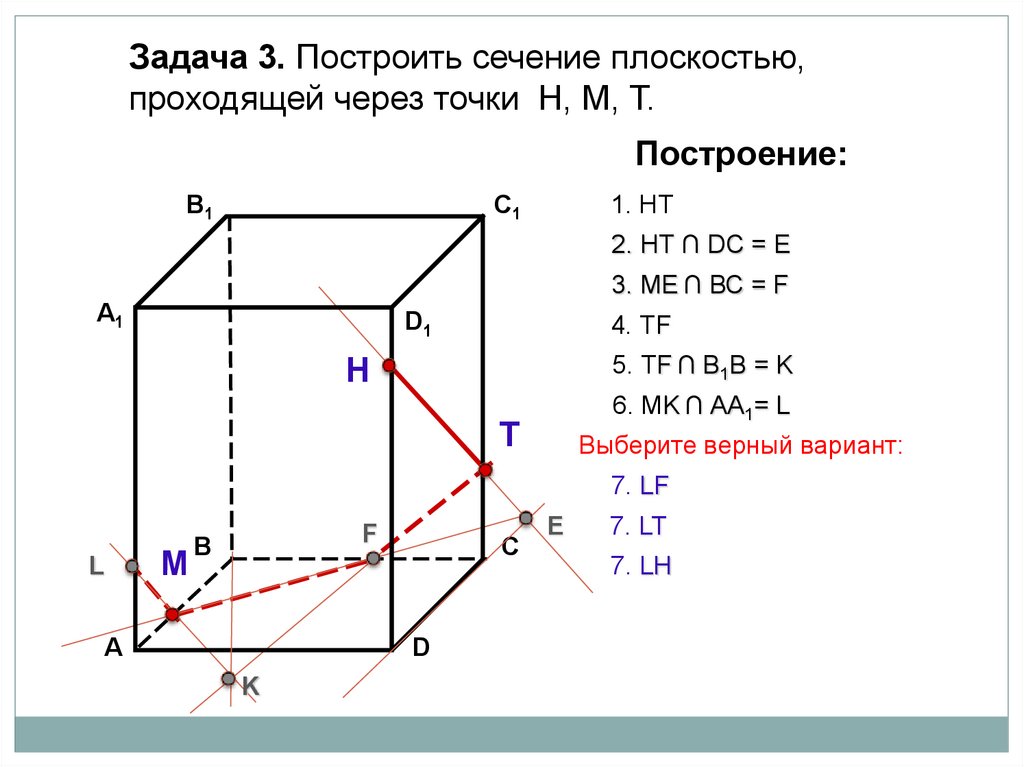
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
1. НТ
Выберите верный вариант:
2. НТ ∩ BС = Е
А1
D1
2. НТ ∩ DС = Е
Н
Т
М
А
В
С
D

22.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. НТ
2. НТ ∩ ВС = Е
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

23.

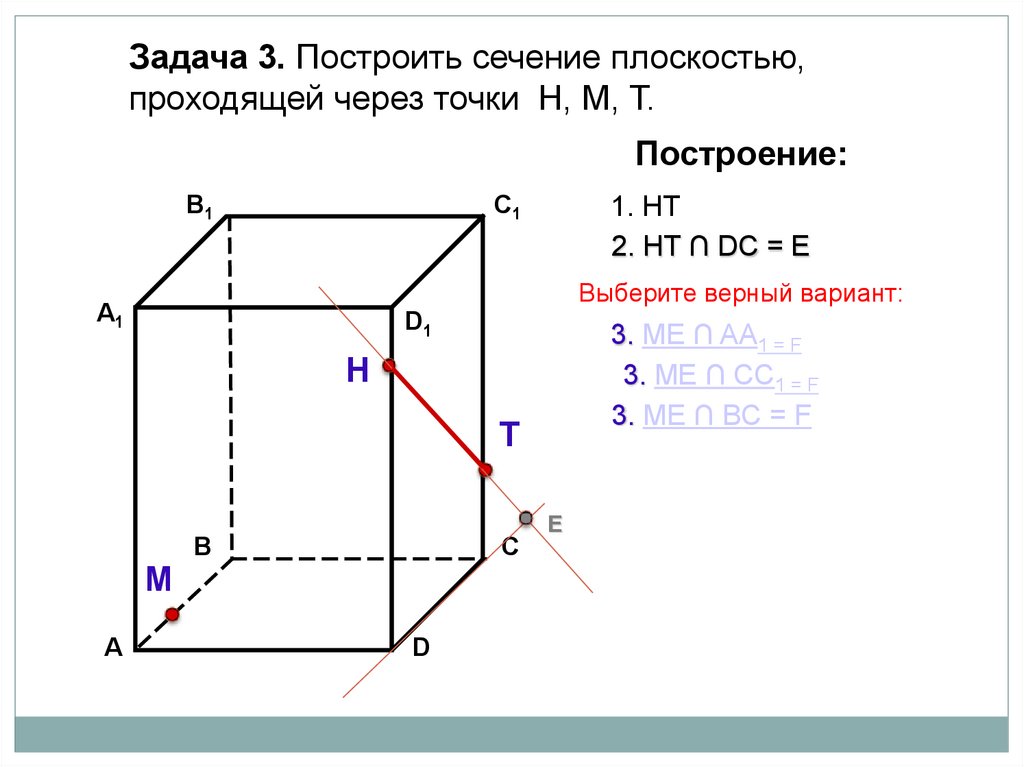
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = Е
C1
Выберите верный вариант:
А1
D1
3. ME ∩ AA1 = F
3. ME ∩ CC1 = F
3. ME ∩ BС = F
Н
Т
М
А
В
С
D
Е

24.

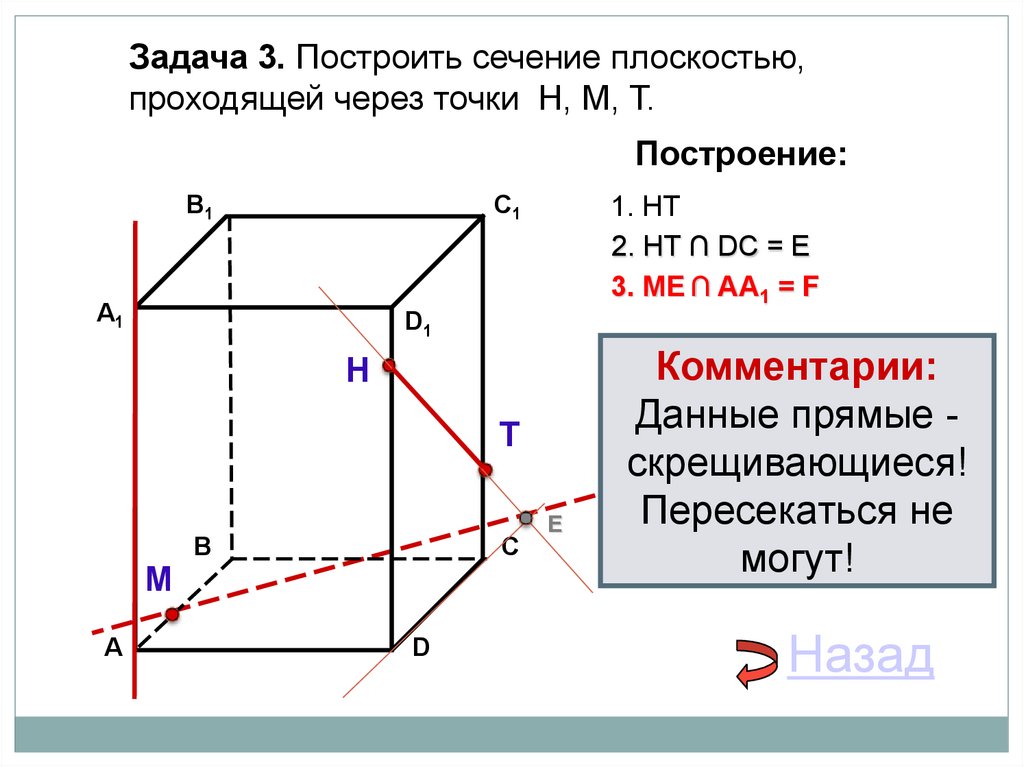
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ AA1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

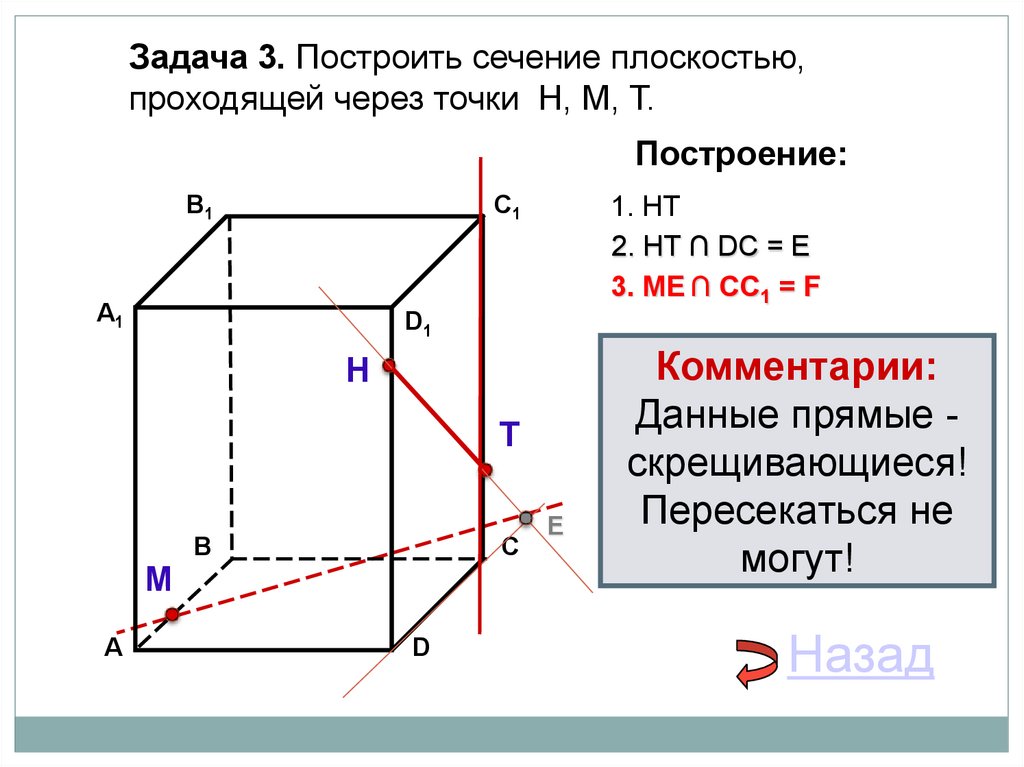
25.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ CC1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

26.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
Выберите верный вариант:
D1
4. НF
Н
4. МТ
Т
М
А
В
F
С
D
4. ТF
E

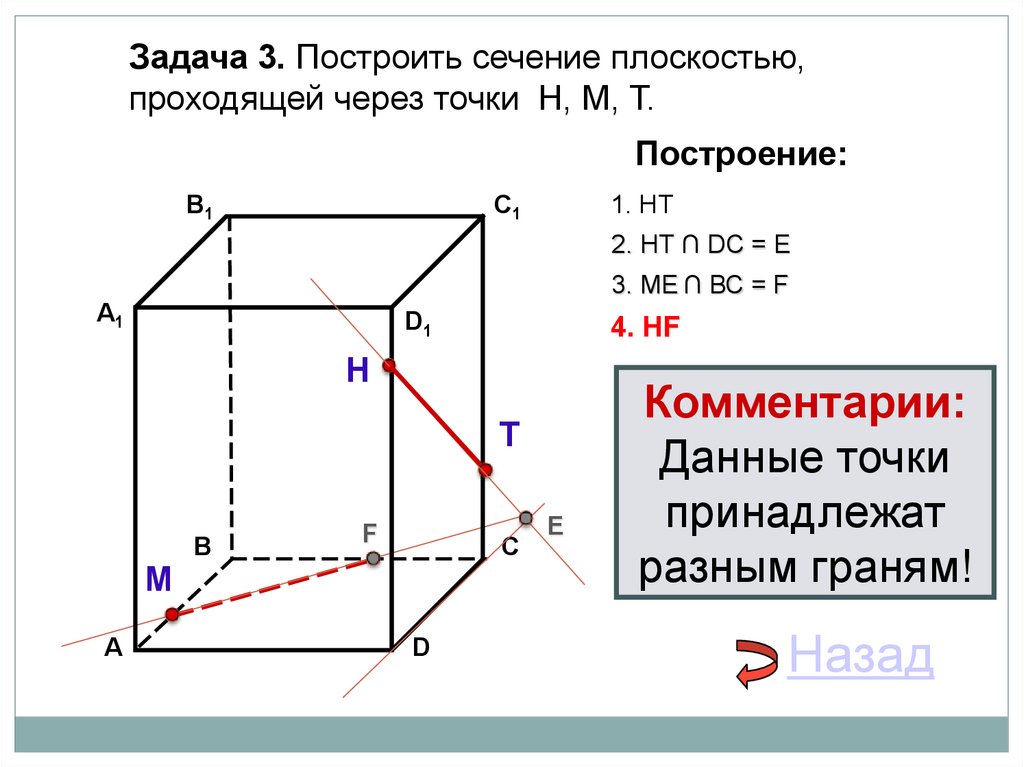
27.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. НF
D1
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

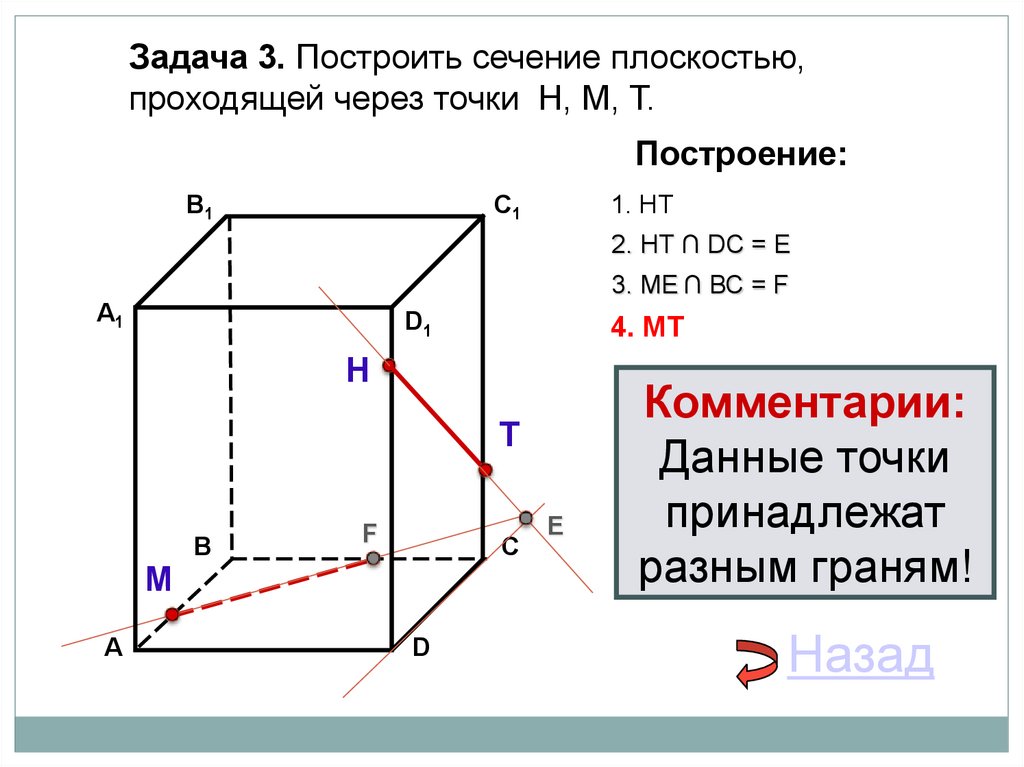
28.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
D1
4. MT
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

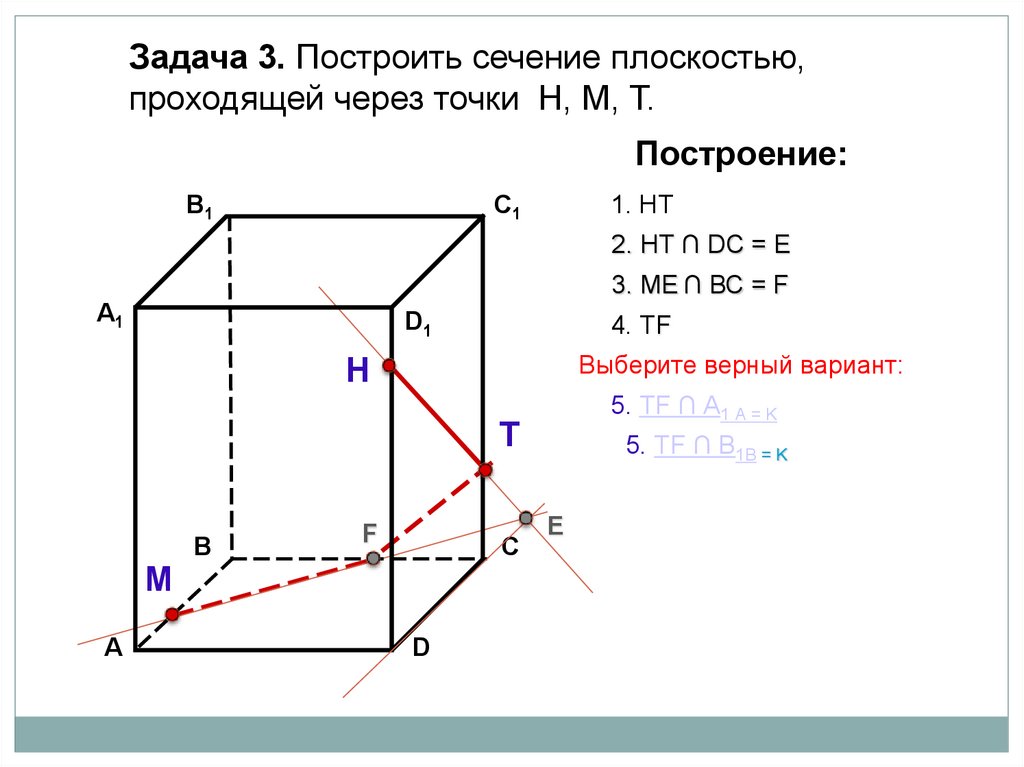
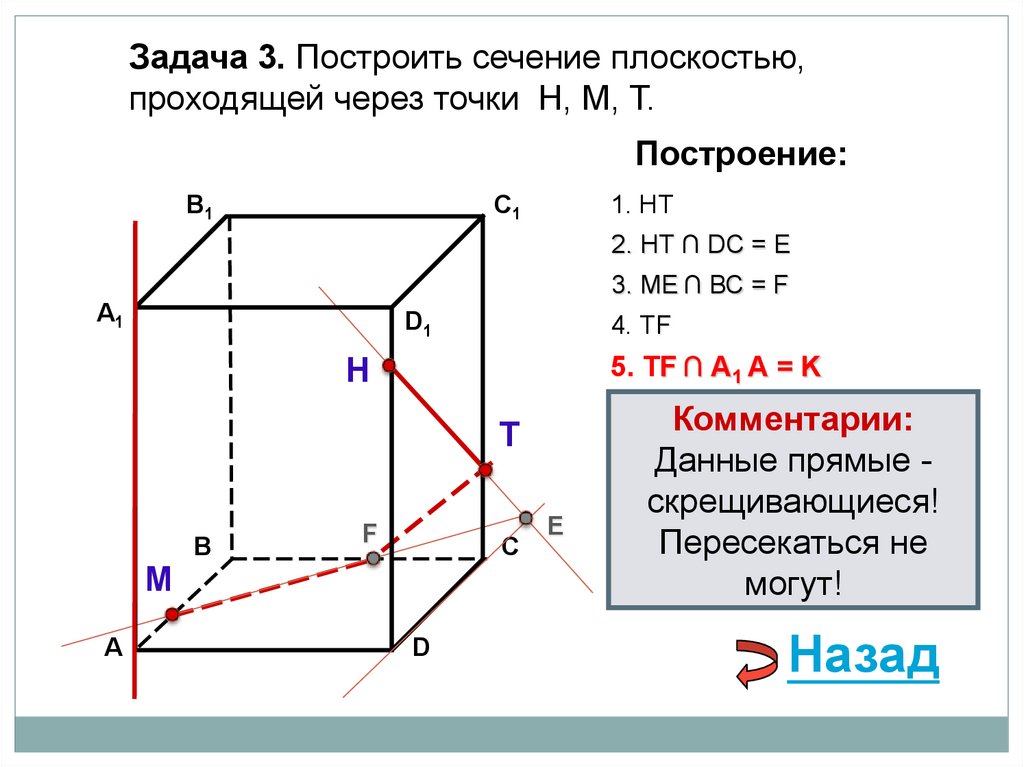
29.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
Выберите верный вариант:
Н
5. ТF ∩ А1 А = K
Т
М
А
В
F
С
D
5. ТF ∩ В1В = K
E

30.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ А1 А = K
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

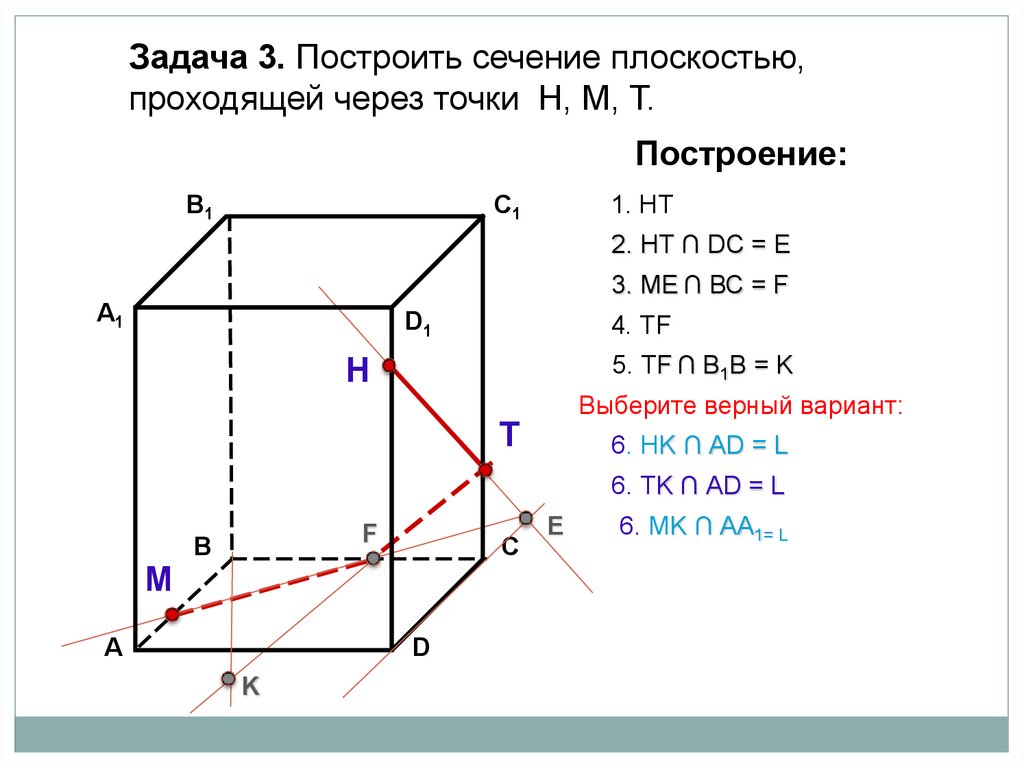
31.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
Выберите верный вариант:
Т
6. НK ∩ АD = L
6. ТK ∩ АD = L
М
F
В
А
С
D
K
E
6. МK ∩ АА1= L

32.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
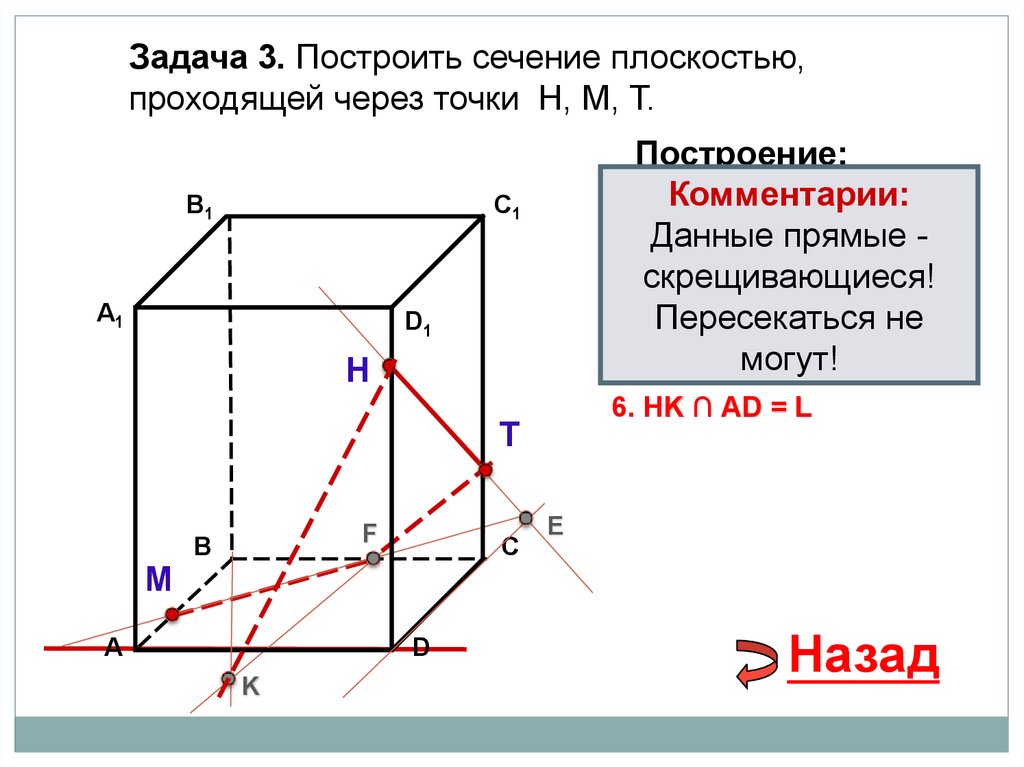
Н
6. НK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад

33.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
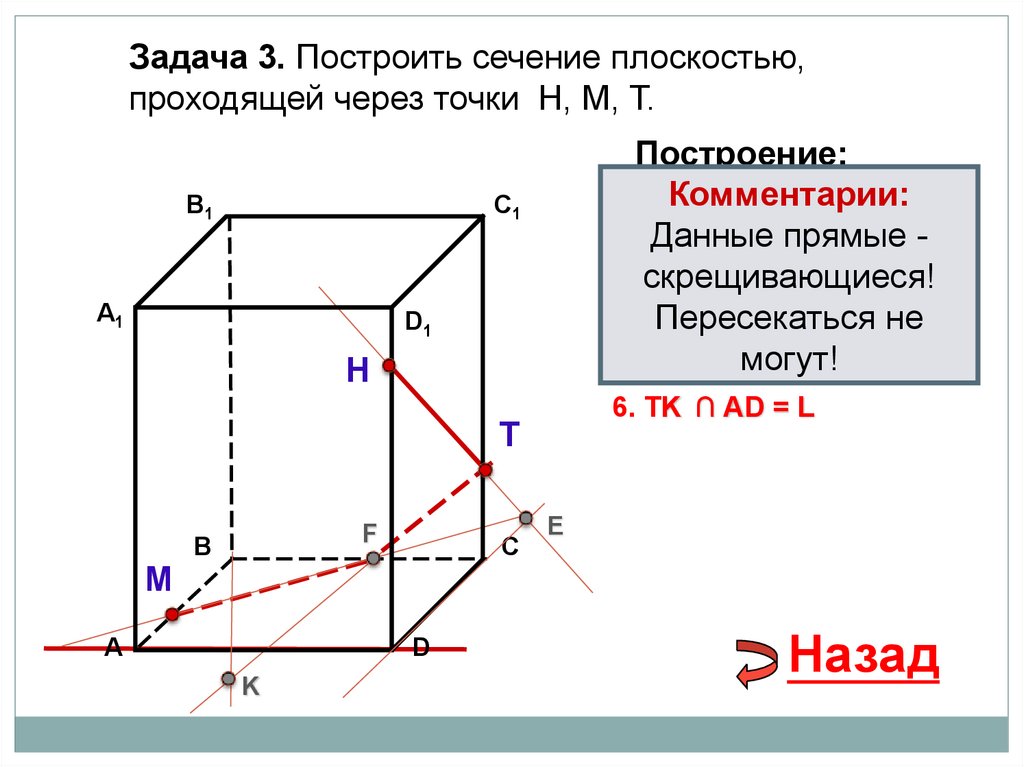
Н
6. TK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад

34.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
Выберите верный вариант:
7. LF
М
L
F
В
А
С
D
K
E
7. LT
7. LH

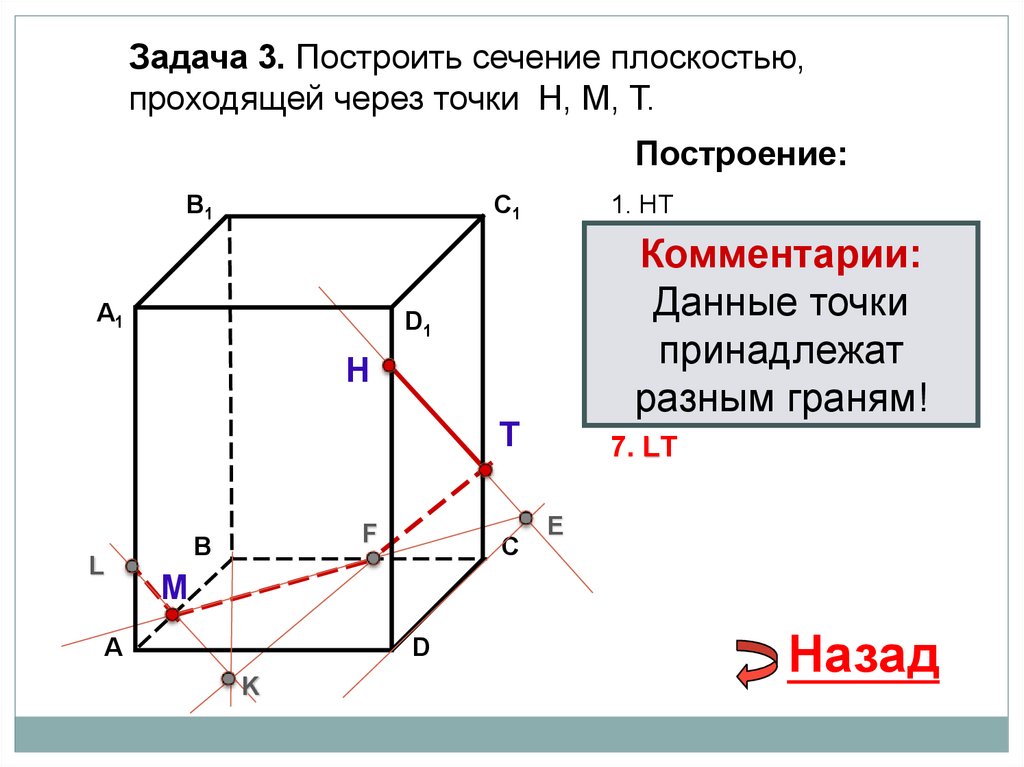
35.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
принадлежат
5. ТF
∩ В1 В = K
6.разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LТ
E
М
А
D
K
Назад

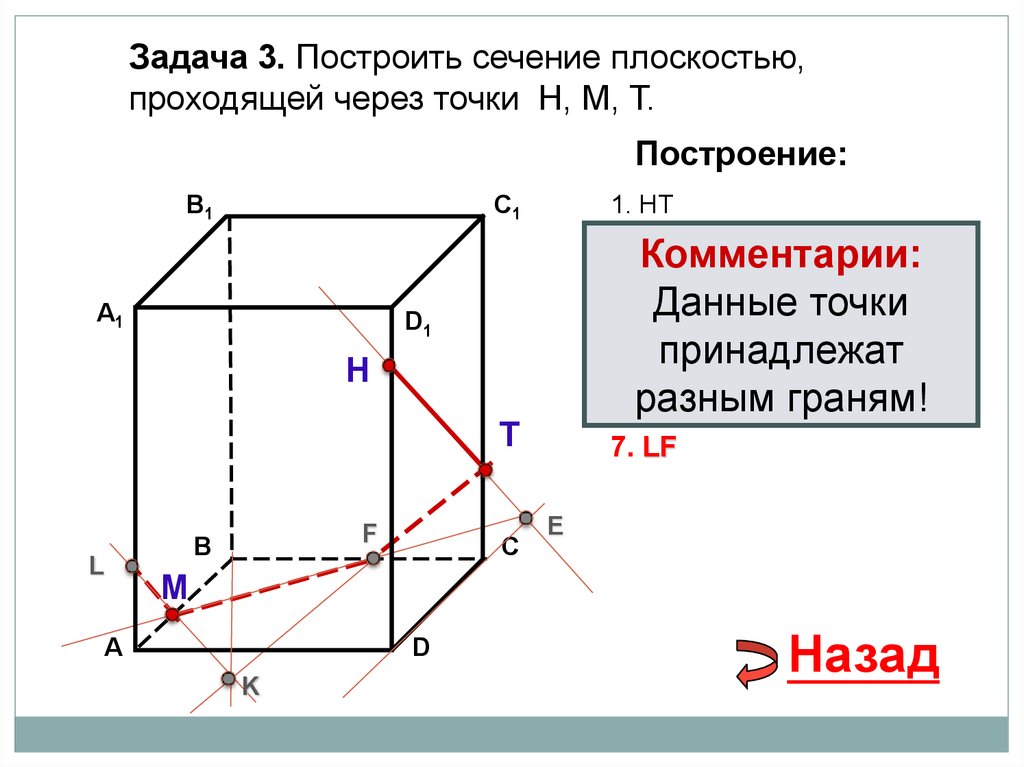
36.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
принадлежат
5. ТF
∩ В1 В = K
6.разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LF
E
М
А
D
K
Назад

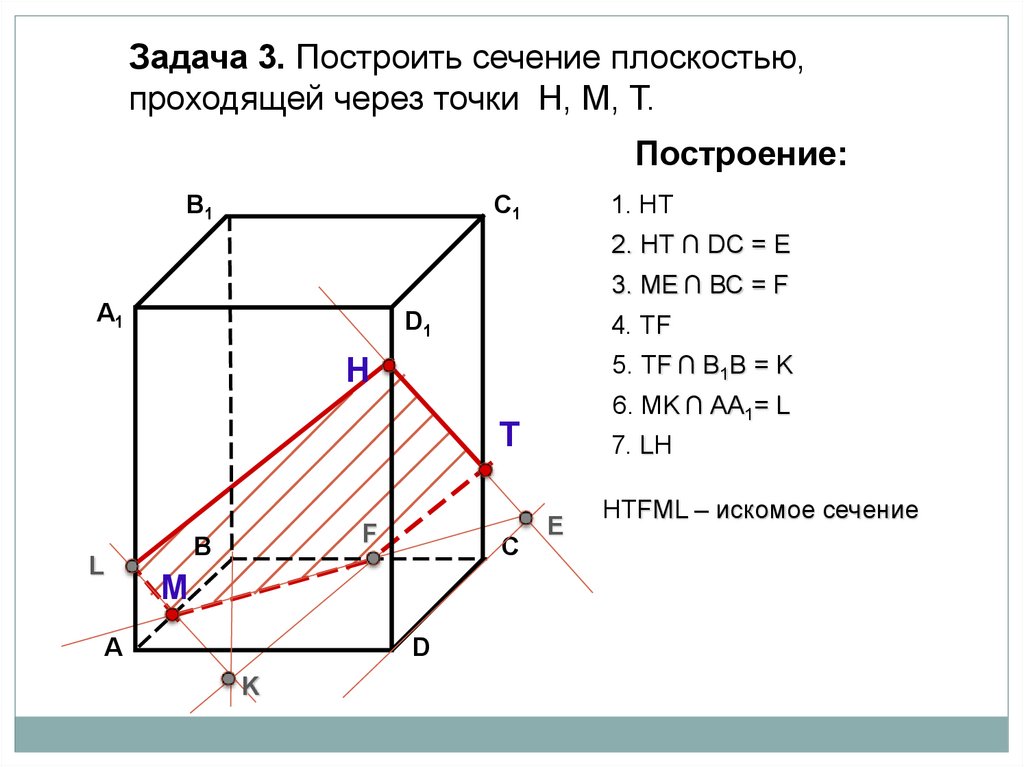
37.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
F
В
L
С
М
А
D
K
7. LН
E
НТFМL – искомое сечение

38.

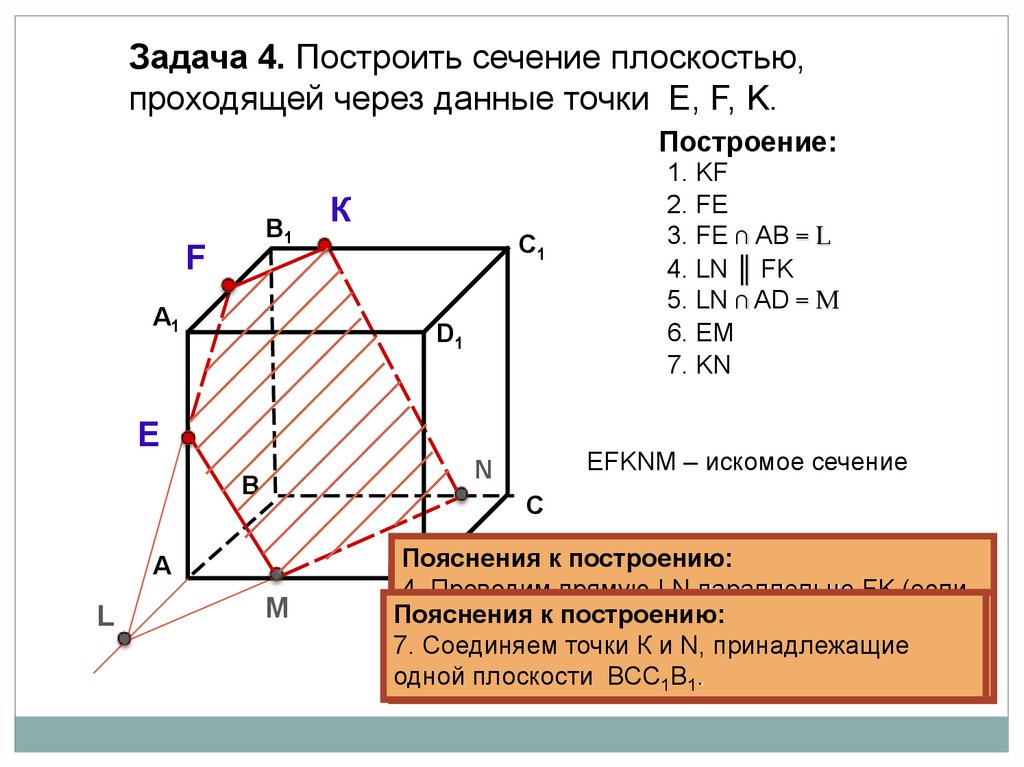
Задача 4. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
В1
F
А1
К
C1
D1
E
С
А
L
EFKNM – искомое сечение
N
В
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
М
Пояснения к построению:
4.
Проводим
LN параллельно FK (если
Пояснения
кпрямую
построению:
Пояснения
к построению:
Пояснения
Пояснения
кккпостроению:
построению:
секущая
плоскость
3.DПрямые
FE
и АВ,пересекает
лежащие
в принадлежащие
одной
плоскости
Пояснения
построению:
1. Соединяем
2.
точки
K и E,
F
F,
принадлежащие
7.
6.
Соединяем
точки
точкиграни,
КЕиивN,
М,то
принадлежащие
принадлежащие
противоположные
она
их
АА
В, пересекаются
L пересекает
. в точке M.
5.Соединяем
Прямая
LN
пересекает
AD
1В1одной
плоскости
А1точке
АА
Вребро
В
11С
1В.
1D1.
одной
одной
плоскости
плоскости ВСС
АА
по параллельным
отрезкам).
1D
1В
1D.
1.

39.

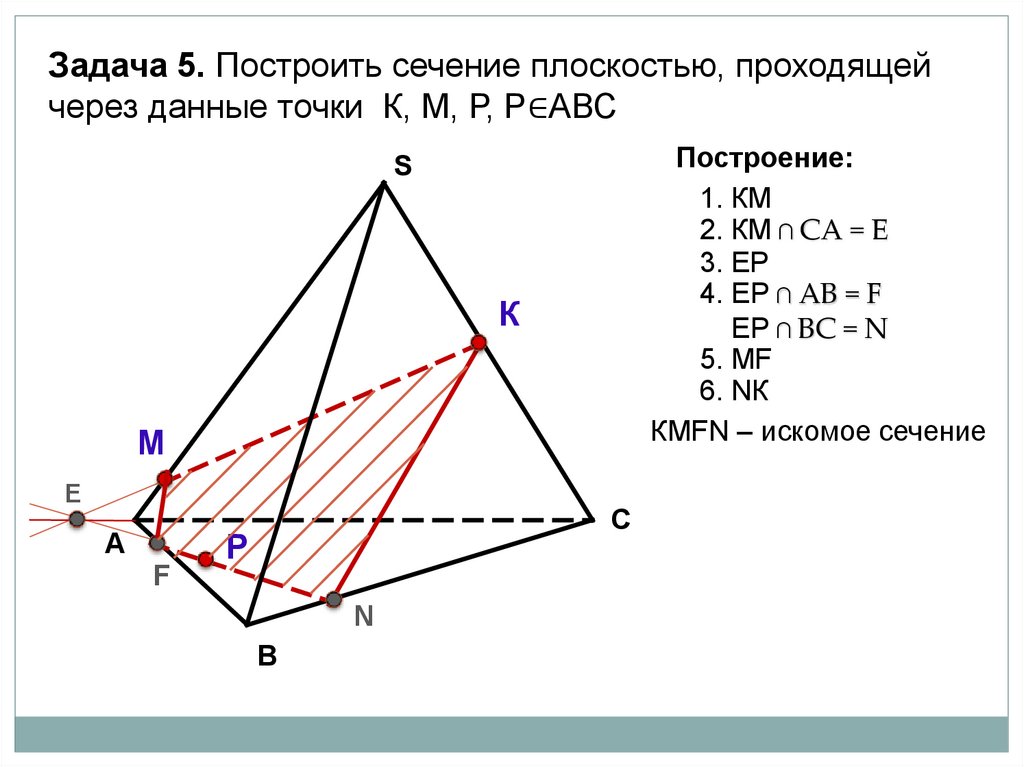
Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
S
К
М
Е
А
F
С
Р
N
В

40.

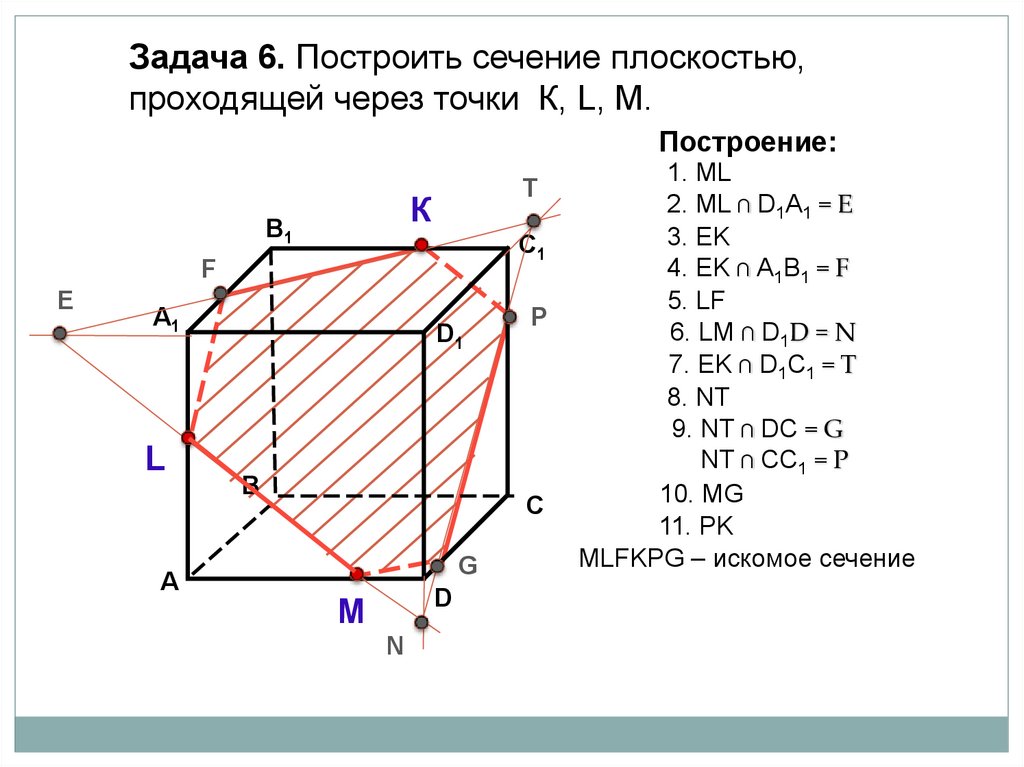
Задача 6. Построить сечение плоскостью,
проходящей через точки К, L, М.
Построение:
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение

41.

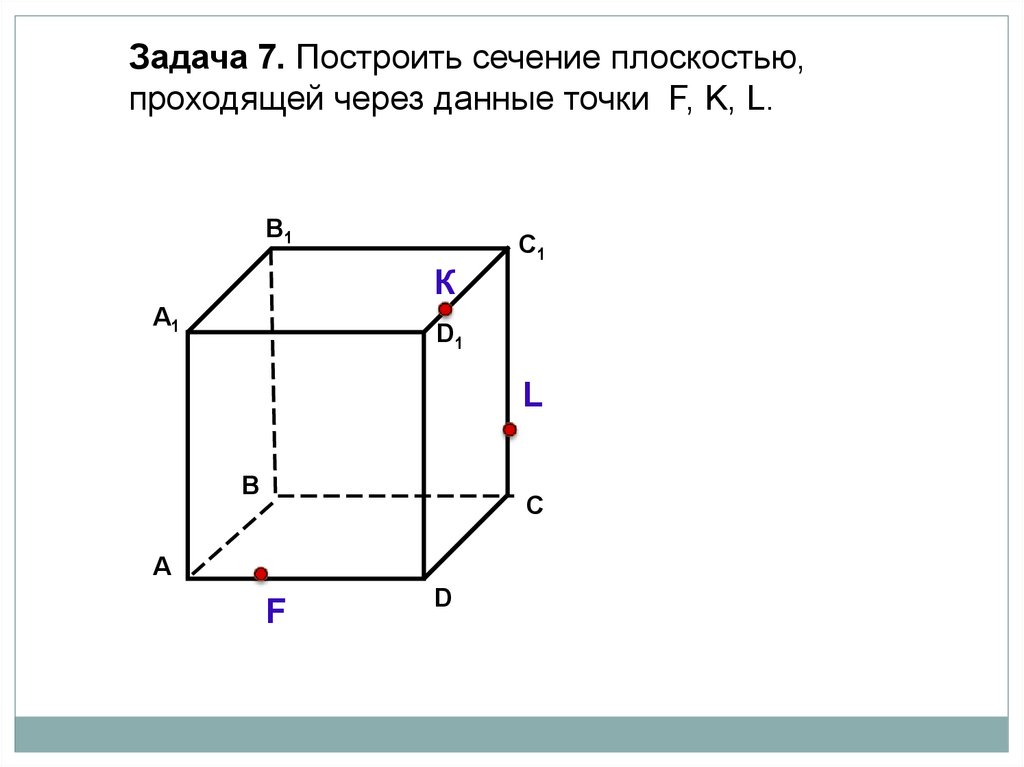
Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
В1
К
А1
C1
D1
L
В
С
А
F
D

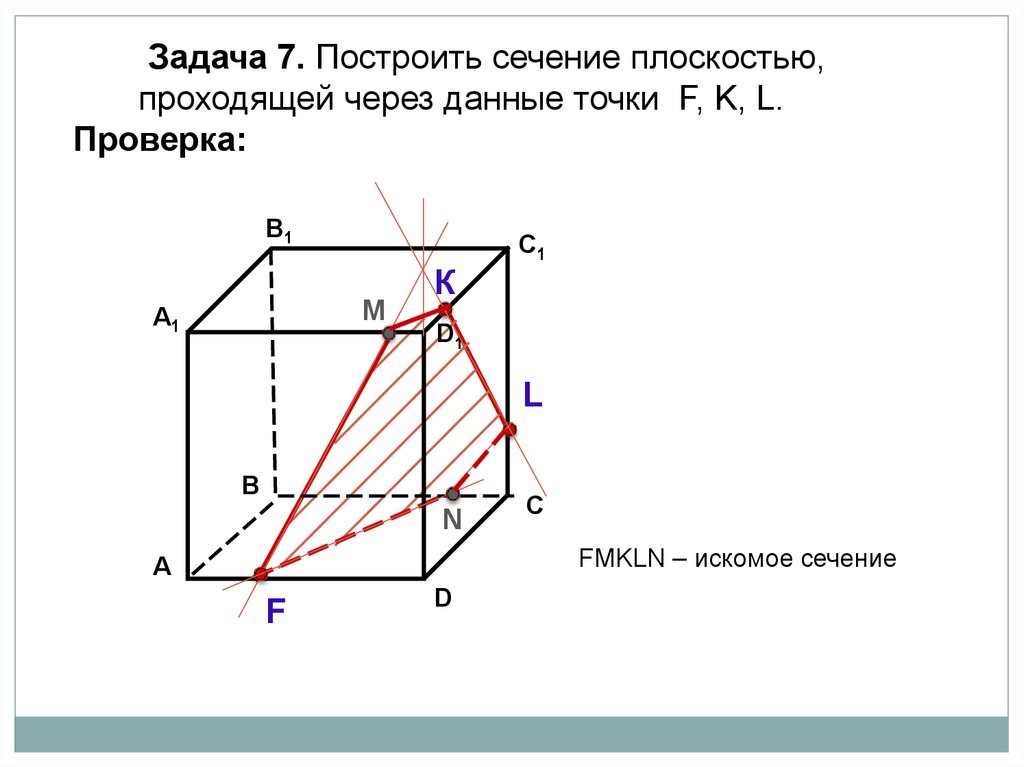
42.

Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
Проверка:
В1
М
А1
К
C1
D1
L
В
N
С
FМKLN – искомое сечение
А
F
D