7d998c9005c44c1c8381010e96eb8e8b

1. Построение сечений тетраэдра и параллелепипеда

2.

Цель работы:
Развитие пространственных представлений у учащихся.
Задачи:
Познакомить с правилами построения сечений.
Выработать навыки построения сечений тетраэдра и
параллелепипеда при различных случаях задания
секущей плоскости.
Сформировать умение применять правила
построения сечений при решении задач по темам
«Многогранники».

3.

Аксиомы и теоремы стереометрии
В
А
α
А2. Если две точки прямой
лежат в плоскости, то все
точки прямой лежат в этой
плоскости.

4.

Аксиомы и теоремы стереометрии
β
А
α
a
А3. Если две плоскости
имеют общую точку, то
они имеют общую прямую,
на которой лежат все
общие точки этих
плоскостей.

5.

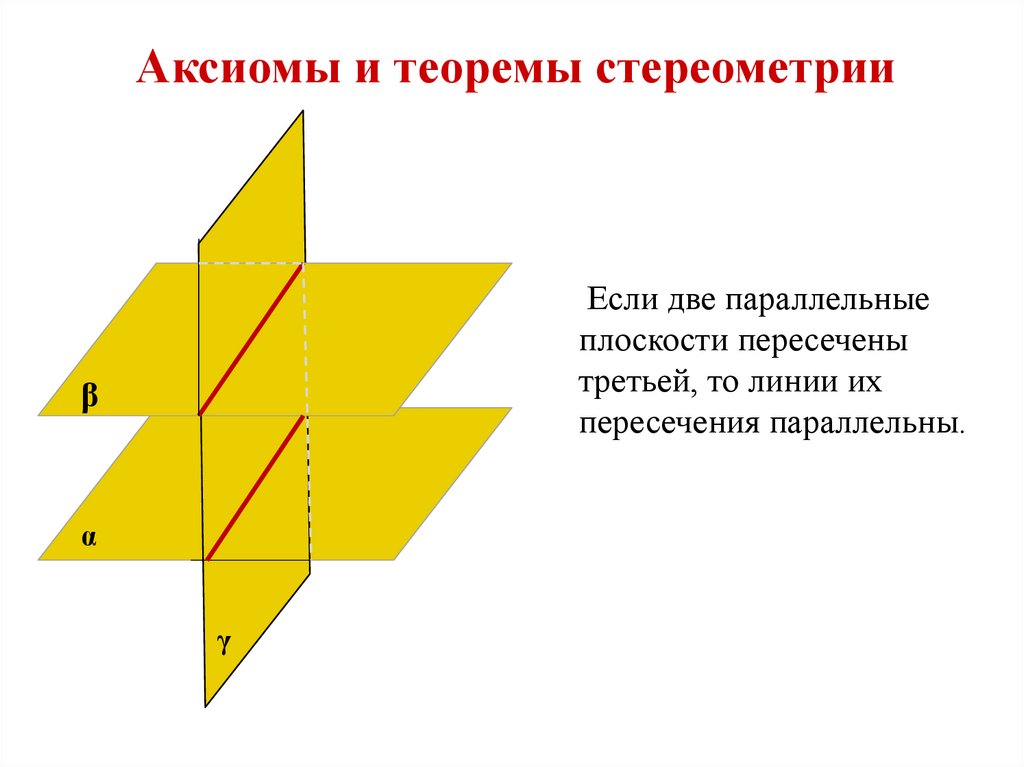
Аксиомы и теоремы стереометрии
Если две параллельные
плоскости пересечены
третьей, то линии их
пересечения параллельны.
β
α
γ

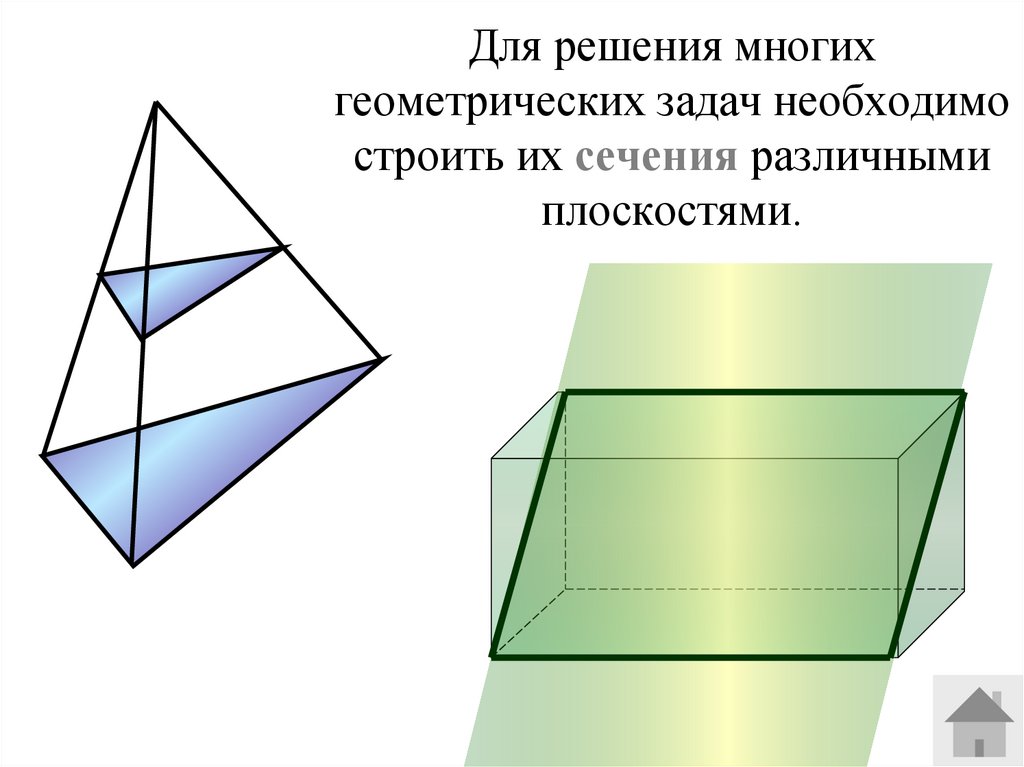
6. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.

7.

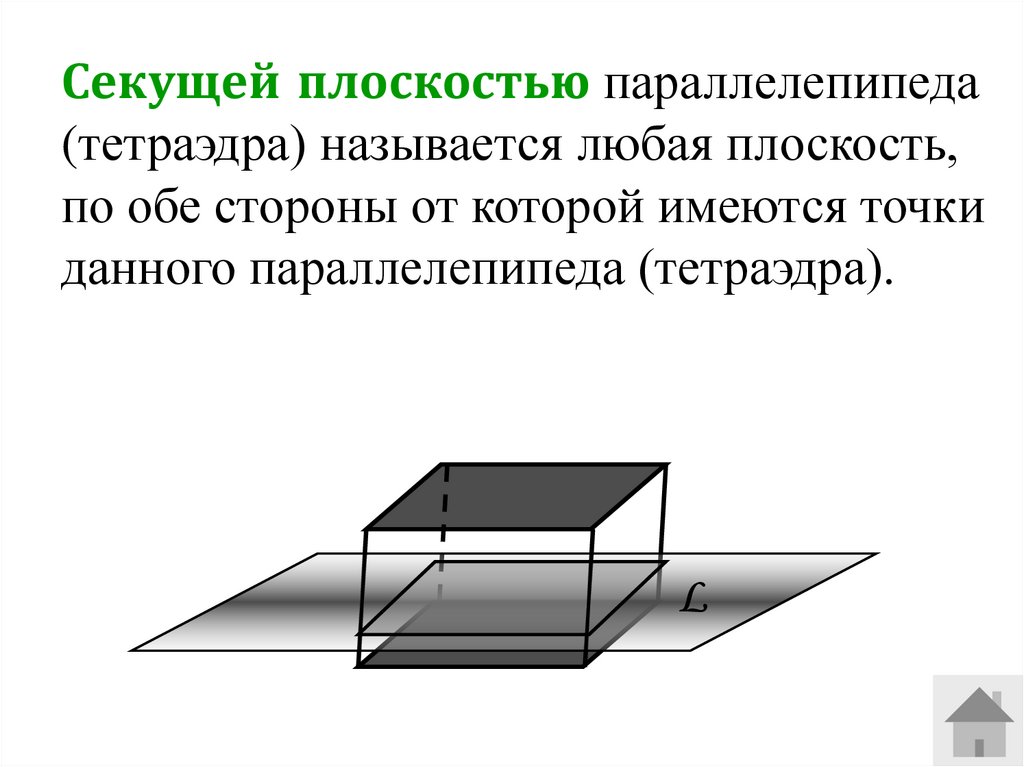
Секущей плоскостью параллелепипеда
(тетраэдра) называется любая плоскость,
по обе стороны от которой имеются точки
данного параллелепипеда (тетраэдра).
L

8.

Секущая плоскость пересекает грани
тетраэдра (параллелепипеда) по
отрезкам.
L
Многоугольник, сторонами
которого являются данные
отрезки, называется
сечением тетраэдра
(параллелепипеда).

9. При этом необходимо учитывать следующее:

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие
в плоскости одной грани.
2. Секущая плоскость пересекает
параллельные
грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна
точка, принадлежащая плоскости сечения, то надо
построить дополнительную точку. Для этого
необходимо найти точки пересечения уже
построенных прямых с другими прямыми,
лежащими в тех же гранях.

10. Сечение тетраэдра

11.

12.

13.

Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях могут получиться:
Треугольники
Четырехугольники

14.

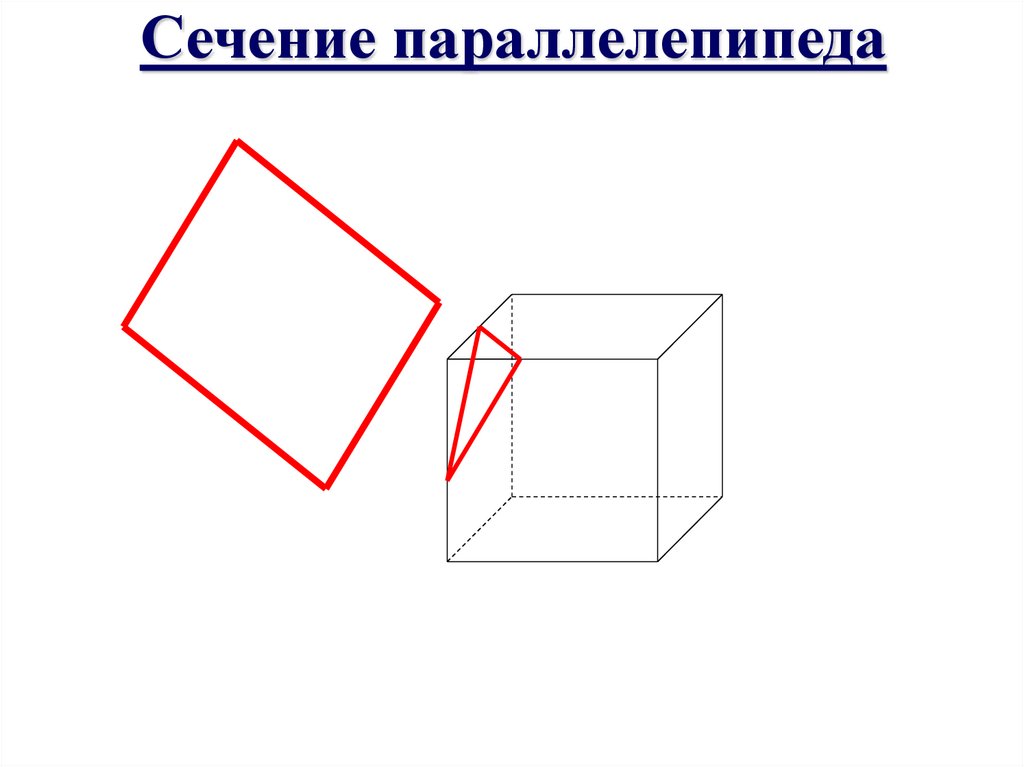
Сечение параллелепипеда

15.

16.

17.

18.

Параллелепипед имеет 6 граней
Треугольники
Пятиугольники
В его сечениях
могут получиться:
Четырехугольники
Шестиугольники

19.

Построить сечение тетраэдра DABC плоскостью, проходящей
через точки M,N,K
D
M
AA
1. Проведем прямую через
точки М и К, т.к. они лежат
в одной грани (АDC).
N
K
BB
C
C
2. Проведем прямую через
точки К и N, т.к. они лежат
в одной грани (СDB).
3. Аналогично рассуждая,
проводим прямую MN.
4. Треугольник MNK –
искомое сечение.

20.

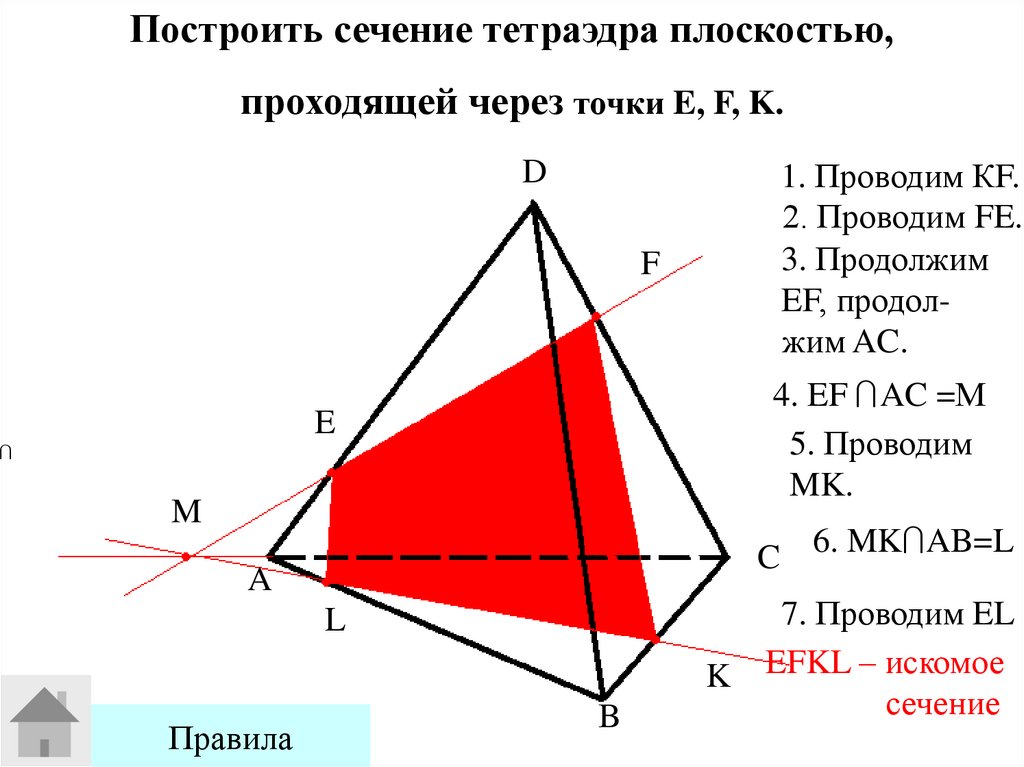
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
1. Проводим КF.
2. Проводим FE.
3. Продолжим
EF, продолжим AC.
D
F
4. EF AC =М
5. Проводим
MK.
E
M
C 6. MK AB=L
A
L
K
Правила
B
7. Проводим EL
EFKL – искомое
сечение

21.

Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F

22.

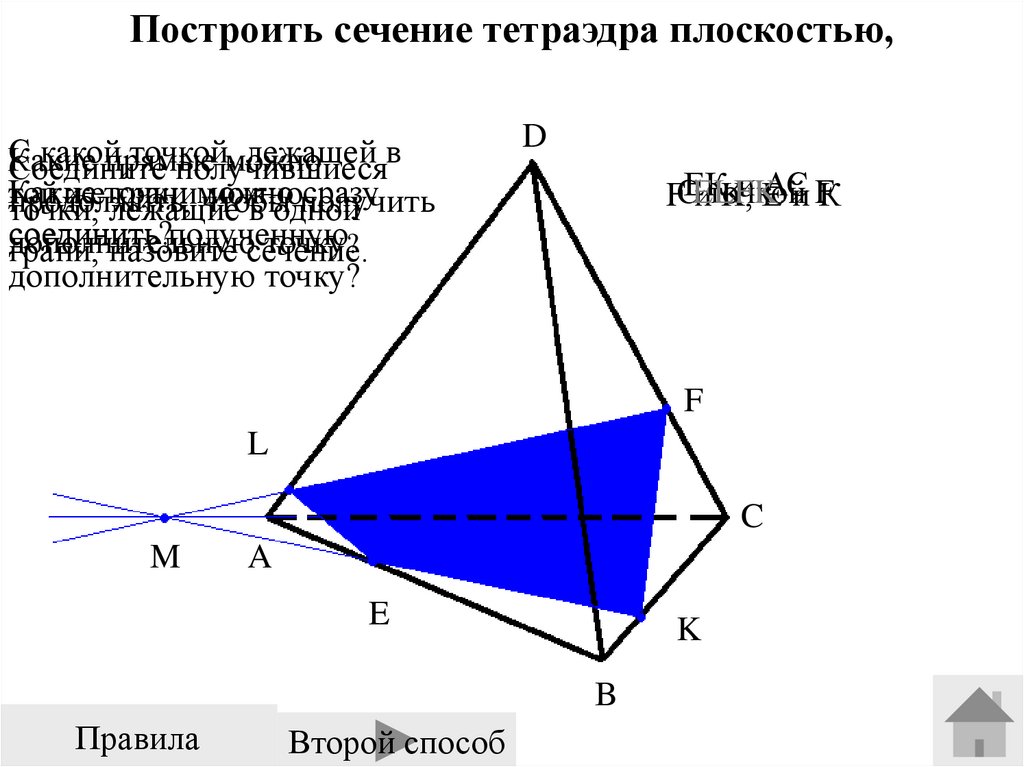
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
С
какойпрямые
точкой,
лежащей в
Какие
можно
Соедините
получившиеся
Какие
сразу
той
жеточки
граниможно
можно
продолжить,
чтобы
получить
точки,
лежащие
в одной
соединить?
соединить
полученную
дополнительную
точку?
грани, назовите
сечение.
дополнительную точку?
D
иЕ
АС
ЕLFK
FСЕК
иточкой
K,
и FК
F
L
C
M
A
E
K
B
Правила
Второй способ

23.

Построить сечение
тетраэдра плоскостью,
проходящей через
точки E, F, K.
D
F
L
C
A
E
K
B
Правила
Первый способ
О

24.

Способ №1.
Способ №2.
Вывод: независимо от способа
построения сечения одинаковые.

25.

Построить сечение параллелепипеда плоскостью,
проходящей через точки M,A,D.
В1
D1
E
A1
С1
В
А
1. AD
2. MD
3. ME//AD, т.к. (ABC)//(A1B1C1)
4. AE
5. AEMD – сечение.
М
D
С

26.

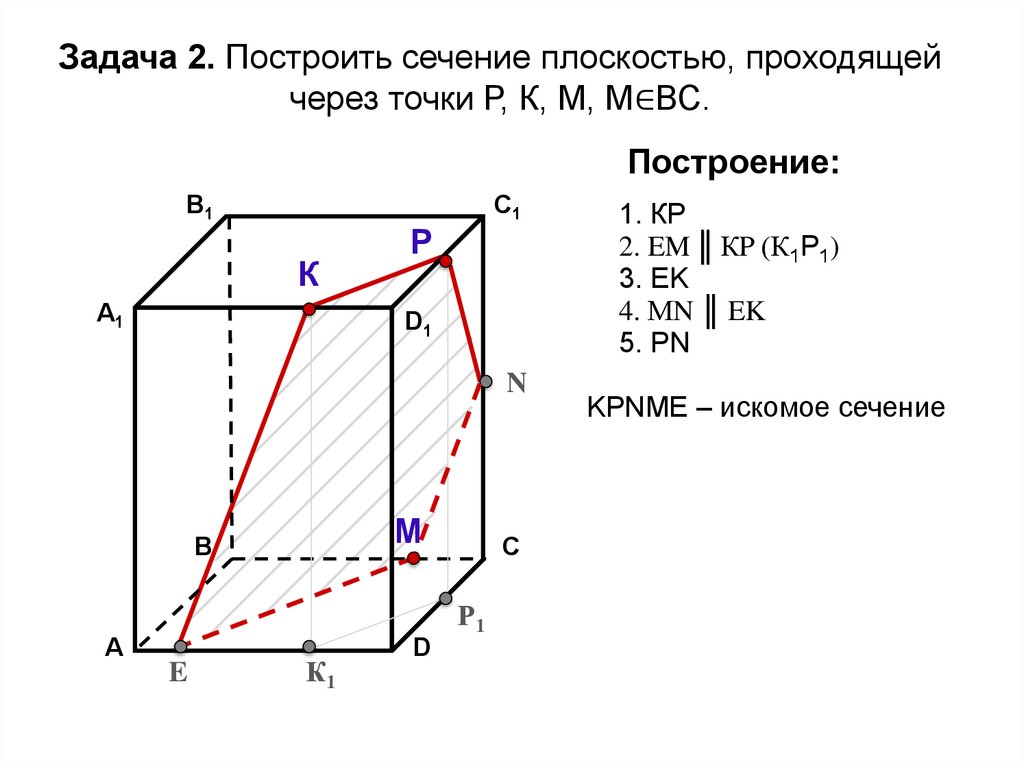
Задача 2. Построить сечение плоскостью, проходящей
через точки Р, К, М, М∈ВС.
Построение:
В1
К
А1
C1
Р
D1
N
М
В
С
Р1
А
E
К1
D
1. КP
2. EM ║ КP (К1Р1)
3. EK
4. МN ║ EK
5. РN
KРNМE – искомое сечение

27.

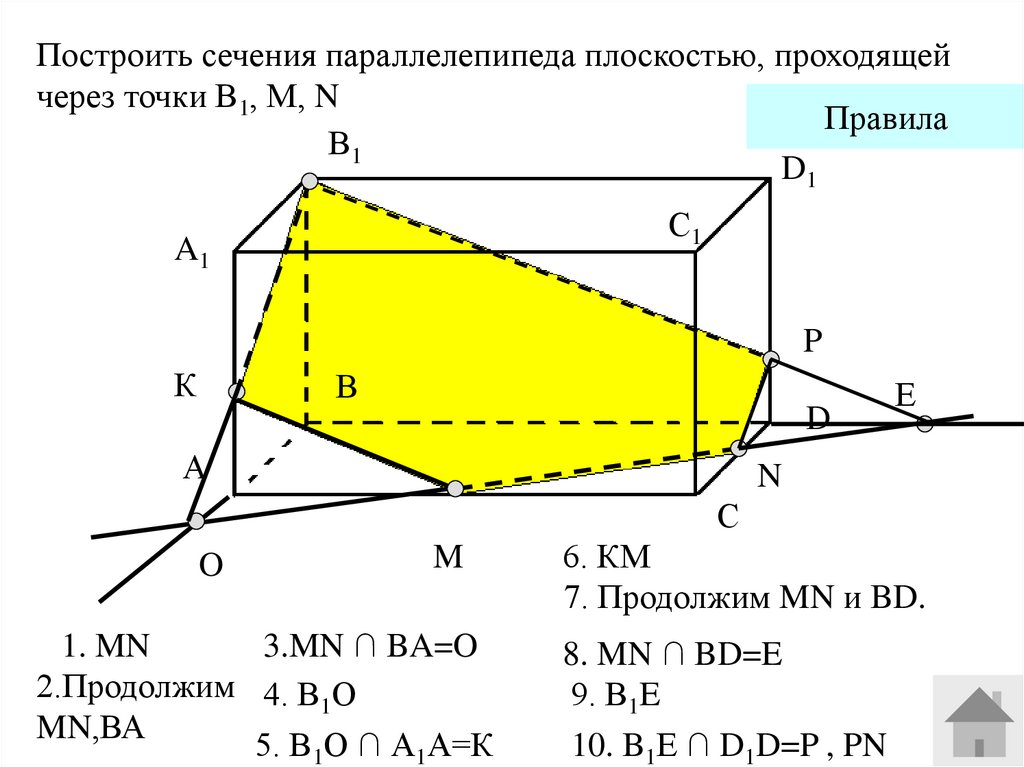
Построить сечения параллелепипеда плоскостью, проходящей
через точки В1, М, N
Правила
В1
D1
С1
A1
P
К
В
D
А
Е
N
С
O
M
1. MN
3.MN ∩ BA=O
2.Продолжим 4. В1О
MN,ВА
5. В1О ∩ А1А=К
6. КМ
7. Продолжим MN и BD.
8. MN ∩ BD=E
9. В1E
10. B1Е ∩ D1D=P , PN

28.

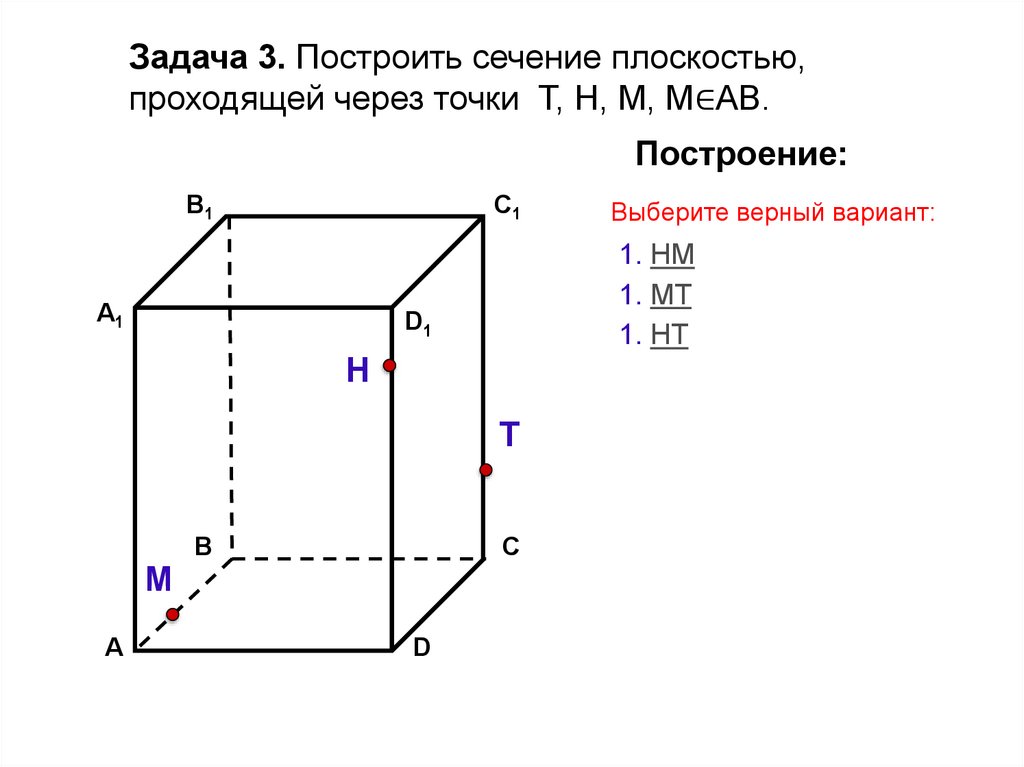
Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
1. НМ
1. МТ
1. НT
D1
Н
Т
М
А
В
С
D
Выберите верный вариант:

29.

Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. НМ
Комментарии:
Данные точки
принадлежат разным
граням!

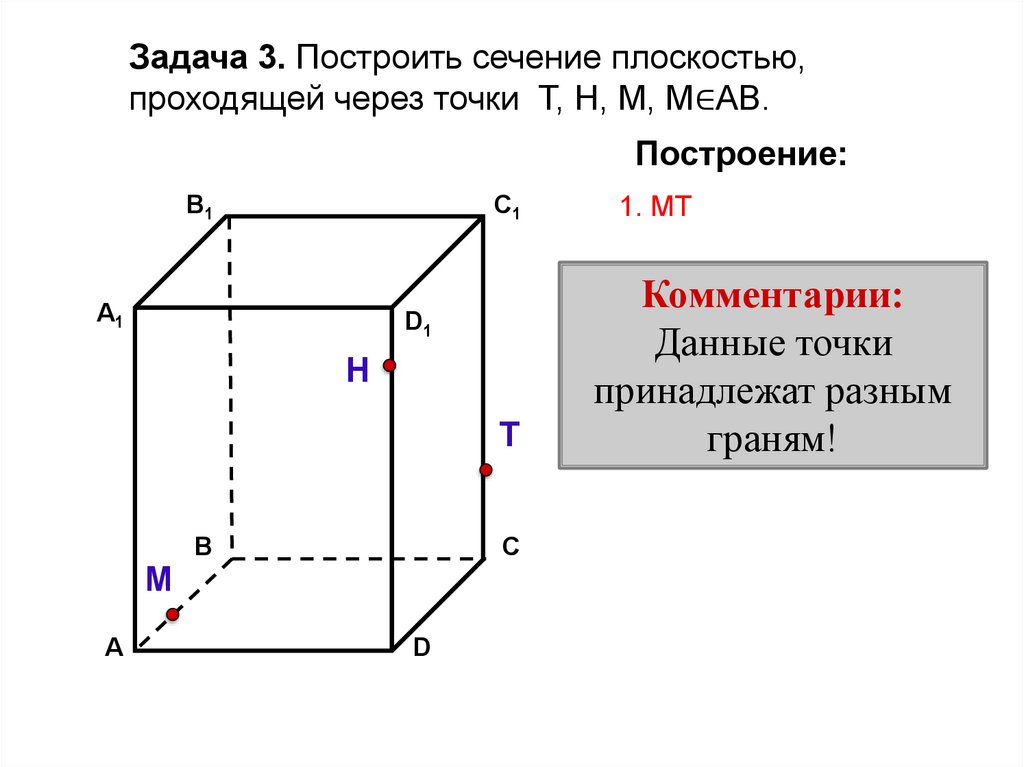
30.

Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. МT
Комментарии:
Данные точки
принадлежат разным
граням!

31.

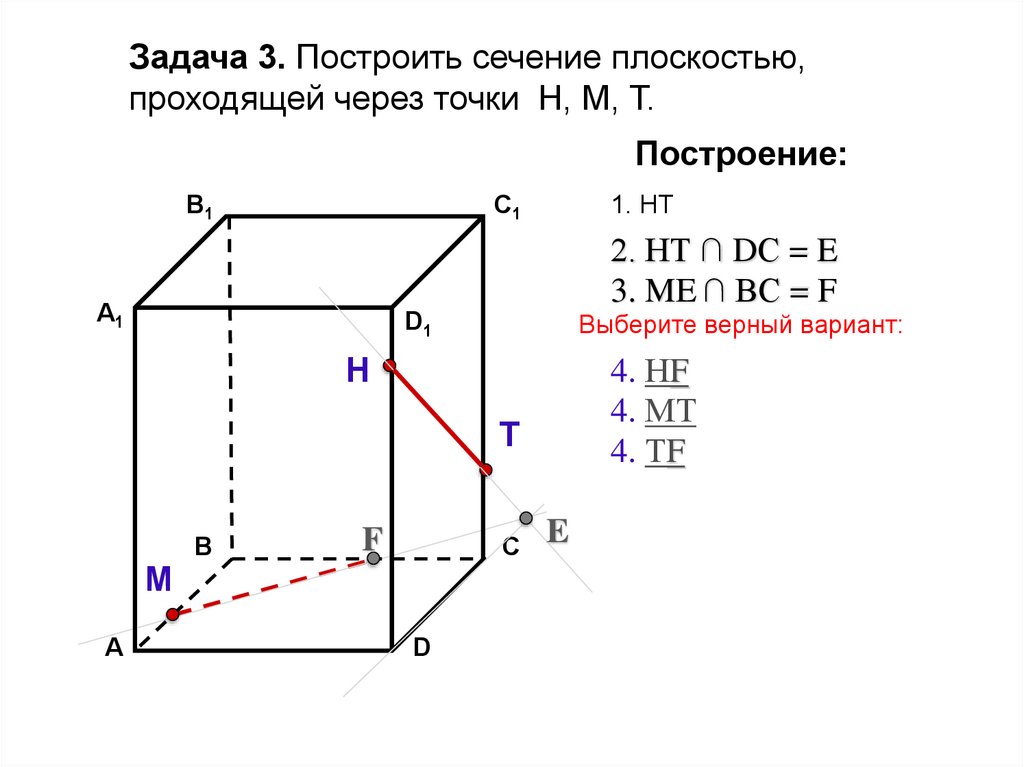
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
1. НТ
Выберите верный вариант:
2. НТ ∩ BС = Е
А1
D1
2. НТ ∩ DС = Е
Н
Т
М
А
В
С
D

32.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. НТ
2. НТ ∩ ВС = Е
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не могут!

33.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = Е
C1
Выберите верный вариант:
А1
D1
3. ME ∩ AA1 = F
3. ME ∩ CC1 = F
3. ME ∩ BС = F
Н
Т
М
А
В
С
D
Е

34.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ AA1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!

35.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ CC1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!

36.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
Выберите верный вариант:
D1
Н
4. НF
4. МТ
4. ТF
Т
М
А
В
F
С
D
E

37.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. НF
D1
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!

38.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
D1
4. MT
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!

39.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
А1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
4. ТF
D1
Выберите верный вариант:
Н
5. ТF ∩ А1 А =
5. ТF ∩ В1В = K
K
Т
М
А
В
F
С
D
E

40.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
А1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
4. ТF
D1
5. ТF ∩ А1 А = K
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не могут!

41.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
А1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
4. ТF
5. ТF ∩ В1В = K
D1
Н
Выберите верный вариант:
Т
М
F
В
А
С
D
K
E
6. НK ∩ АD = L
6. ТK ∩ АD = L
6. МK ∩ АА1= L

42.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТ Комментарии:
Данные
2. НТ
∩ DС прямые
=E
скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться
не могут!
4.
ТF
C1
А1
D1
Н
5. ТF ∩ В1В = K
6. НK ∩ АD = L
Т
М
F
В
А
С
D
K
E

43.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТ Комментарии:
Данные
2. НТ
∩ DС прямые
=E
скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться
не могут!
4.
ТF
C1
А1
D1
Н
5. ТF ∩ В1В = K
6. TK ∩ АD = L
Т
М
F
В
А
С
D
K
E

44.

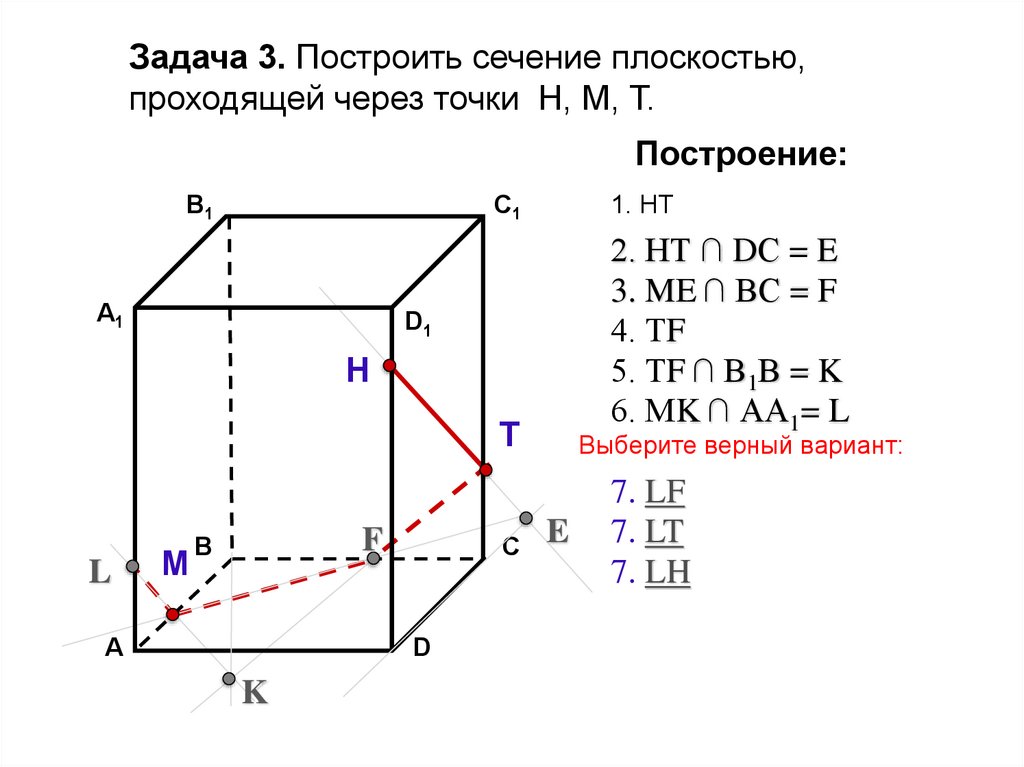
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
А1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
4. ТF
5. ТF ∩ В1В = K
6. МK ∩ АА1= L
D1
Н
Т
L
М
F
В
А
С
D
K
Выберите верный вариант:
E
7. LF
7. LT
7. LH

45.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
А1
2. НТ
∩ DС = E
Комментарии:
3. ME
∩ ВС =точки
F
Данные
4. ТF
принадлежат
разным
5. ТF ∩ В1В = K
6. МK ∩граням!
АА1= L
D1
Н
Т
L
F
В
С
М
А
D
K
7. LТ
E

46.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
А1
2. НТ
∩ DС = E
Комментарии:
3. ME
∩ ВС =точки
F
Данные
4. ТF
принадлежат
разным
5. ТF ∩ В1В = K
6. МK ∩граням!
АА1= L
D1
Н
Т
L
F
В
С
М
А
D
K
7. LF
E

47.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
L
F
В
С
М
А
D
K
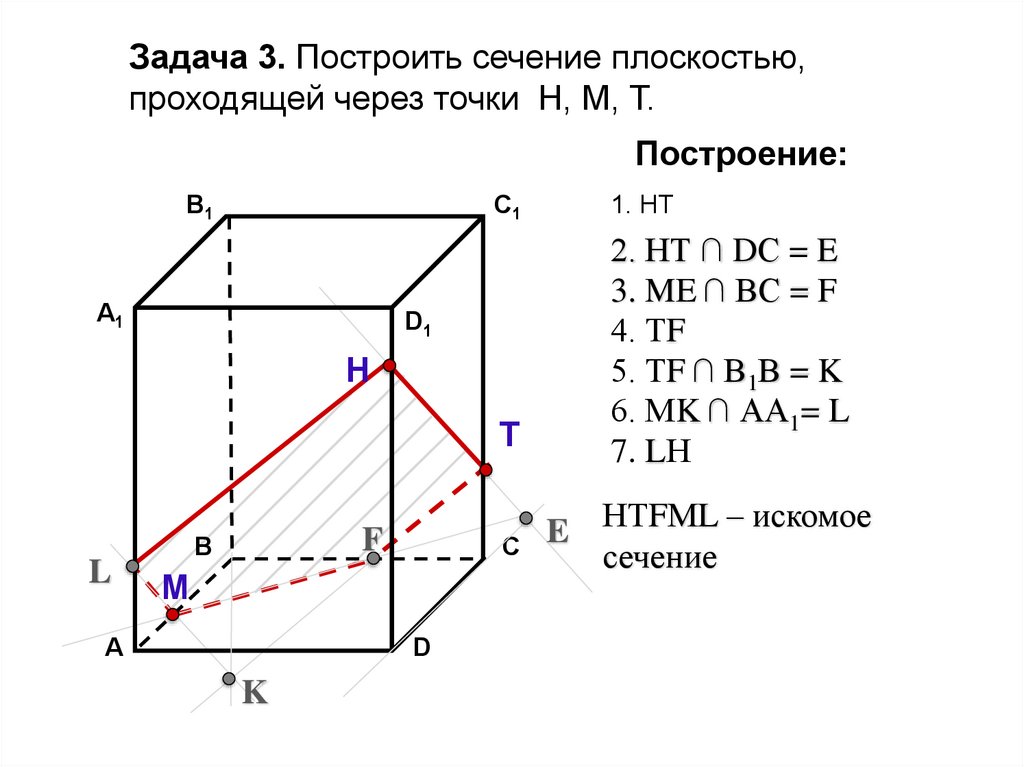
1. НТ
2. НТ ∩ DС = E
3. ME ∩ ВС = F
4. ТF
5. ТF ∩ В1В = K
6. МK ∩ АА1= L
7. LН
E НТFМL – искомое
сечение

48.

Задача 4. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
В1
F
А1
1. KF
2. FE
К
C1
D1
E
N
В
А
L
М
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD =
6. EM
M
7. KN
EFKNM – искомое сечение
С
Пояснения к построению:
Пояснения
кпрямую
построению:
Пояснения
к построению:
4.
Проводим
LN
D
Пояснения
Пояснения
к
к
построению:
построению:
Пояснения
к построению:
3.
Прямые
FE
и АВ,
лежащие
в
1.
2.
Соединяем
точки
K
F
и
E,
F,
параллельно
FK
(если
секущая
7.
6.
Соединяем
точки
точкиАА
КЕииВ
N,
М,В,
5. Соединяем
Прямая
LN
пересекает
ребро AD
одной
плоскости
принадлежащие
1 одной
1
плоскость
пересекает
принадлежащие
принадлежащие
одной
одной
плоскости
плоскости
в точке
M.
пересекаются
в
точке
Lто
.. она
плоскости
А
АА
В
В
С
В.
D
противоположные
грани,
1
1
1
1
1
1
ВСС
АА DВD.
.
1 1 11

49.

Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
S
К
М
Е
А
F
С
Р
N
В

50.

Задача 6. Построить сечение плоскостью,
проходящей через точки К, L, М.
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
D
М
N
G
Построение:
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение

51.

Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
В1
К
А1
C1
D1
L
В
С
А
F
D

52.

Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
Проверка:
В1
М
А1
К
C1
D1
L
В
N
С
FМKLN – искомое сечение
А
F
D