Похожие презентации:
Непрерывно-стохастические модели
1.
Раздел 1.Анализ систем методами теории
массового обслуживания
Тема 4.
Непрерывно-стохастические модели
2.
УЧЕБНЫЕ ВОПРОСЫ:1. Марковские
дискретными
случайные
состояниями
процессы
и
с
непрерывным
временем.
2. Предельные вероятности состояний.
3.
Вопрос 1.Марковские случайные процессы
с дискретными состояниями
и непрерывным временем
4.
Процессы в системах с дискретными состояниями,меняющимися
в
случайные
моменты
времени,
называются случайными процессами с дискретными
состояниями и непрерывным временем.
Рассмотрим особенности построения математических
моделей данных систем.
5.
Вместопереходных
вероятностей
Pij
вводятся плотности вероятностей перехода λij.
Пусть система S в момент времени t находится
в состоянии Si.
Рассмотрим
элементарный
промежуток
времени ∆t, за который система может перейти в
состояние Sj с вероятностью Pij.
Δt
0
t
t+Δt
6.
Плотностьвероятности
перехода
λij
описывается выражением:
ij lim
t 0
Pij t
t
(1)
где Pij(∆t) – вероятность того, что система,
находившаяся в момент t в состоянии
время ∆t перейдет в состояние Sj.
Si, за
7.
Из (1) следует, что при малом ∆tPij t ij t
Это выражение справедливо для стационарных
процессов,
когда
вероятность
перехода
Pij
определяется только длинной отрезка ∆t
и не
определяется местоположением отрезка на оси
времени t.
8.
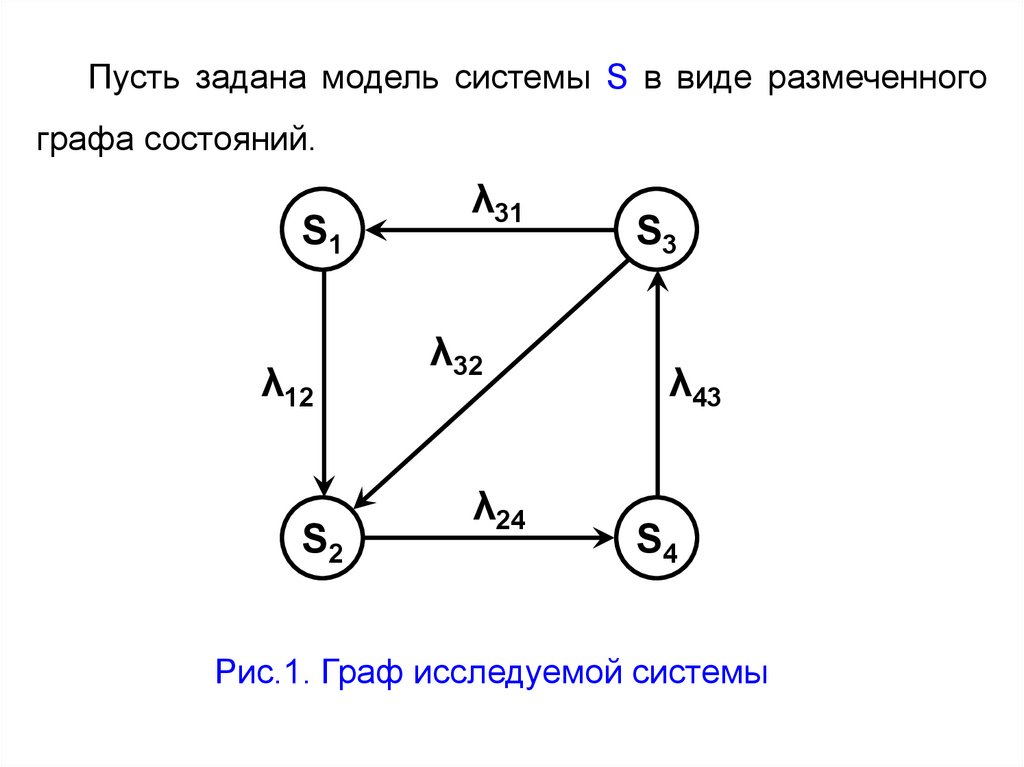
Пусть задана модель системы S в виде размеченногографа состояний.
S1
λ12
S2
λ31
λ32
λ24
S3
λ43
S4
Рис.1. Граф исследуемой системы
9.
Рассмотрим момент времени t.Придадим t малое приращение ∆t и найдем
P1(t+∆t) – вероятность того, что
времени
t+∆t
состоянии S1.
система
будет
в момент
находится
в
10.
Это может произойти в двух случаях(см.
рис. 1):
1) в момент t система была в состоянии S1 и
за время ∆t из него не вышла;
2) в момент t система была в состоянии S3 и
за время ∆t перешла в S1.
11.
Вероятностьпервого
случая
найдем
как
произведение вероятности Р1(t) того, что в
момент t система была в S1, на условную
вероятность того, что, будучи в состоянии S1,
система за время ∆t не перейдет в S2:
P1 t 1 12 t
12.
Вероятностьвторого
случая
равна
вероятности того, что в момент t система была в
S3,
умноженной
на
условную
вероятность
перехода за время ∆t в состояние S1:
P3 t 31 t
13.
Применим правило сложения вероятностей:P1 t t P1 t 1 12 t P3 t 31 t
Раскроем скобки в правой части, перенесем
Р1(t) в левую и разделим обе части равенства на
∆t:
P1 t t P1 t
12 P1 t 31P3 t
t
14.
Устремим ∆t к нулю и перейдем к пределу:P1 t t P1 t
lim
12 P1 t 31P3 t
t 0
t
Левая часть – производная функции Р1(t):
d P1 t
12 P1 t 31P3 t
dt
(2)
15.
Длявероятностей
остальных
состояний
такие уравнения получим аналогично.
Запишем
их,
отбросив
аргумент t у функции Рi(t):
для
краткости
16.
dP1P
P
12
1
31
3
dt
dP2 P P P
24 2
12 1
32 3
dt
(3)
dP
3 P P P
31 3
32 3
43 4
dt
dP
4 43P4 24 P2
dt
17.
Уравнения (3) называют уравнениямиКолмогорова.
Интегрирование
данной
системы
уравнений даст нам искомые вероятности
состояний как функции времени.
18.
Андрей НиколаевичКолмого́ров
(12.04.1903 -20.10.1987)
А.Н. Колмлгоров - один из
крупнейших математиков XX века.
Один
из
основоположников
современной теории вероятности, им
получены
фундаментальные
результаты в топологии, геометрии,
математической логике, классической
механике, теории турбулентности,
теории сложности алгоритмов, теории
функций, теории информации, теории
тригонометрических рядов, теории
меры, теории приближения функций,
теории множеств,
теории дифференциальных
уравнений,
теории
динамических систем, функциональном
анализе
и
др.
областях
математики.
19.
Начальныеусловия
определяются
исходным состоянием системы.
Например, если при t = 0 система была в
состоянии Sк, то полагают:
Pk(0)=1;
Pi(0)=0 при i ≠ к.
20.
Одноиз
дифференциальных
уравнений
в
системе (3) может быть заменено на балансное
алгебраическое уравнение:
P1 P2 P3 P4 1
так как система может находиться только в
одном состоянии.
21.
Правила составления уравненийКолмогорова
1. В
левой
производная
части
уравнения
вероятности
стоит
состояния
системы по времени.
2. В правой части стоит столько слагаемых,
сколько
стрелок
состоянием.
связано
с
данным
22.
3. Каждое слагаемое равно произведениюплотности вероятности перехода, записанной
возле стрелки, умноженной на вероятность того
состояния, из которого стрелка исходит.
4. Слагаемое имеет знак «+», если стрелка
направлена в состояние, и знак «–», если
стрелка исходит из него.
23.
Вопрос 2.Предельные вероятности
состояний
24.
Если:1)
число
состояний
системы
конечно;
2) из каждого состояния можно
перейти в любое другое,
то при t существуют предельные
(финальные) вероятности состояний
(ПВС),
которые
начальных условий.
не
зависят
от
25.
Для вычисления ПВС необходимо:в
системе
положить
левые
1)
уравнений
Колмогорова
части
(производные
вероятностей состояний) равными нулю;
2) одно из уравнений системы необходимо
заменить на балансное;
3)
решить
полученную
алгебраических уравнений.
систему
26.
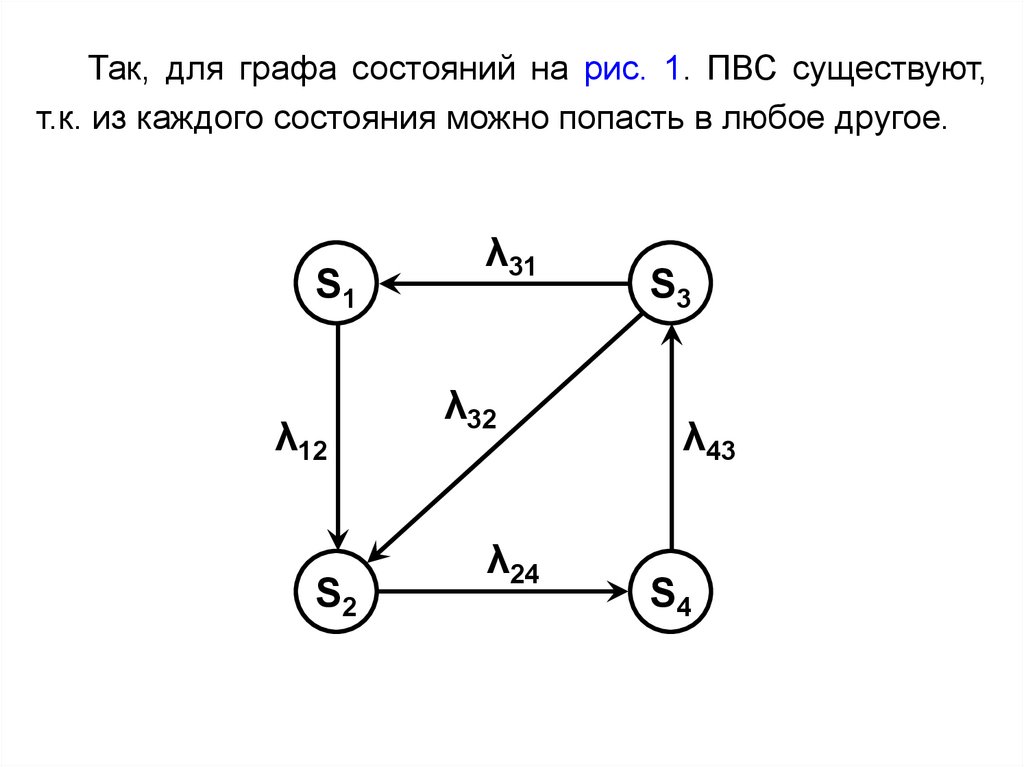
Так, для графа состояний на рис. 1. ПВС существуют,т.к. из каждого состояния можно попасть в любое другое.
S1
λ12
S2
λ31
λ32
λ24
S3
λ43
S4
27.
Приравняем левые части уравнений системы(3)
нулю
и
перенесем
туда
отрицательные
слагаемые:
12 P1 31P3
P P P
24 2
12 1
32 3
P
P
P
31
3
32
3
43
4
43P4 24 P2
(4)
28.
Длярешения
системы
(4)
одно
уравнений заменим на балансное.
12 P1 31P3
P P P
24 2
12 1
32 3
P
P
P
31
3
32
3
43
4
P1 P2 P3 P4 1
Решив ее, получим значения ПВС.
из
ее
29.
Физический смысл ПВС – среднеевремя
пребывания
системы
в
данном
состоянии (в долевом отношении).
Т.О.,
предполагаем,
что
при
t
в
системе S устанавливается предельный
стационарный режим.













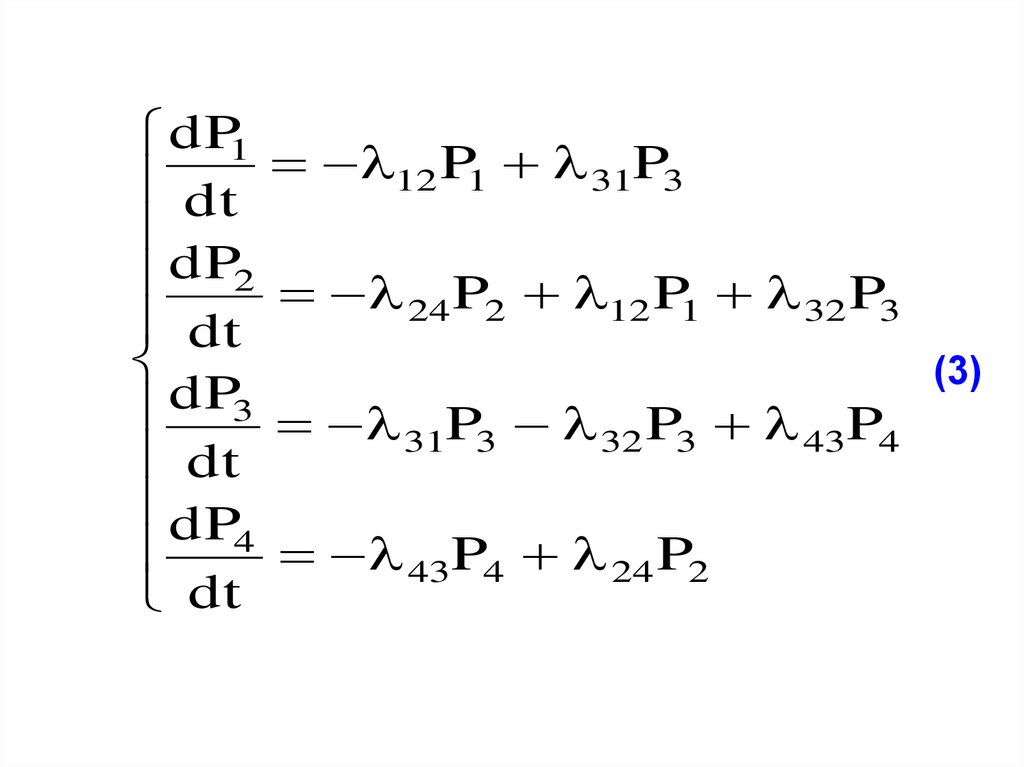












 Математика
Математика








