Похожие презентации:
Ключевое понятие квантовой механики - понятие «состояния системы»
1.
Ключевое понятие квантовой механики – понятие «состояния системы».Пример. Когда говорят, что атом водорода находится в «таком-то» (например, “s”)
состоянии, то это означает, что с вероятностью равной единице при измерении энергии
будет получено значение, отвечающее невозбужденному (основному) состоянию атома
водорода:
E E1
Если в этом состоянии попытаться измерить координату электрона, то окажется, что
результаты измерений будут меняться от эксперимента к эксперименту (существенно, что
атом водорода в каждый раз должен находиться в одном и том же состоянии!).
Обнаружение электрон в окрестности данной точки пространства оказывается
вероятностным событием. Если нас интересует плотность распределения x этой
вероятности, то мы, в соответствии с правилами квантовой механики, должны найти
зависящую от координат волновую функцию электрона основного состояния атома
водорода
1 x
Плотность распределения вероятности связана с волновой функцией равенством
x 1 x
2
2.
I ВАЖНЫЙ МОМЕНТВ рассмотренном примере основного состояния атома водорода энергия имеет
определённое значение (т.е., при повторных измерениях энергия будет иметь одно и то же
значение!). В то же время, при повторных измерениях координаты мы будем «ловить»
электрон в разных точках пространства. В такой ситуации говорят, что энергия и
координата не измеримы одновременно!
II ВАЖНЫЙ МОМЕНТ
Если мы будем измерять импульс электрона в том же самом основном состоянии атома
водорода, то нам необходимо знать зависящую от импульса волновую функцию этого
состояния
1 p
Волновые функции 1 x и 1 p - волновые функции основного состояния атома
водорода в координатном и импульсном представлениях!
3.
ПРИНЦИП СУПЕРПОЗИЦИИРассмотрим два состояния атома водорода – основное и возбуждённое. Соответствующие
этим состояниям волновые функции обозначим как 1 x и 2 x . Измерения
энергии в основном состоянии всегда будут давать значение E1 , в возбуждённом
состоянии - E2 . Предположим, что нам удалось «приготовить» состояние, которое в
координатном представлении описывается волновой функцией
x C1 1 x C2 2 x ,
C1 C2 1
2
2
Тогда при измерении энергии в новом состоянии с вероятностью C1 2 мы будем получать
2
значение E E1 , а с вероятностью C2 - E E2.
4.
Собственные функцииРассмотрим физическую величину f, которая принимает дискретные значения. Пусть этой
величине соответствует оператор fˆ . Напишем уравнение на собственные значения этого
оператора в координатном представлении
fˆ n x f n n x
Собственные значения f являются значениями физической величины f, измеряемыми в
n
эксперименте. Собственные функции n x описывают состояния системы, в которых
величина f имеет определённое значение
f fn
Приготовим состояние системы, описывающееся волновой функцией x . Произведём
измерения величины f. В результате, с разными вероятностями будут получены значения
f fn
Вопрос: как определить вероятности измерения различных значений f f n ?
5.
«КОНСТРУКТИВНЫЙ» ПРИНЦИП СУПЕРПОЗИЦИИПусть состояние системы описывается волновой функцией x . Разложим эту
функцию по собственным функциям оператора fˆ
x an n x
n
Величина
wn an
2
равна вероятности получить при измерении величины f значение f f n
Набор чисел an a f n - волновая функция рассматриваемого состояния в fпредставлении!
6.
Вычисление коэффициентов разложенияЗакон сохранения вероятности
*
*
dx
x
x
a
n an
n
Подставить разложение
* x an* *n x
n
В левую часть первого равенства. Результат?
7.
Вычисление коэффициентов разложения*
*
*
*
dx
x
x
a
dx
x
x
a
n n
n an
n
Формула для коэффициентов разложения
an dx *n x x
n
8.
Условия, которым должны подчиняться собственные функцииУсловие полноты
Подставить формулу для коэффициентов разложения
an dx *n x x
в разложение
x an n x
n
Результат?
9.
Промежуточная формула*
x dx x n x n x
n
Условие полноты
*
n x n x x x
n
10.
Условия, которым должны подчиняться собственные функцииУсловие ортогональности
Подставить разложение
x an n x
n
в условие нормировки
*
*
dx
x
x
a
n an
n
Результат?
11.
Промежуточная формула*
*
*
*
dx
x
x
a
a
dx
x
x
a
n m n
n an
m
n ,m
Условие ортогональности
*
dx
n x m x nm
n
12.
Дискретный спектрfˆ n x f n n x
x an n x , an dx *n x x
n
Условие ортогональности
*
dx
n x m x nm
Условие полноты
*
n x n x x x
n
13.
Непрерывный спектрfˆ f x f f x
x dx a f *f x , a f dx *f x x
Условие ортогональности
*
dx
n x m x nm
*
dx
f x f x f f
Условие полноты
*
n x n x x x
n
*
df
f x f x x x










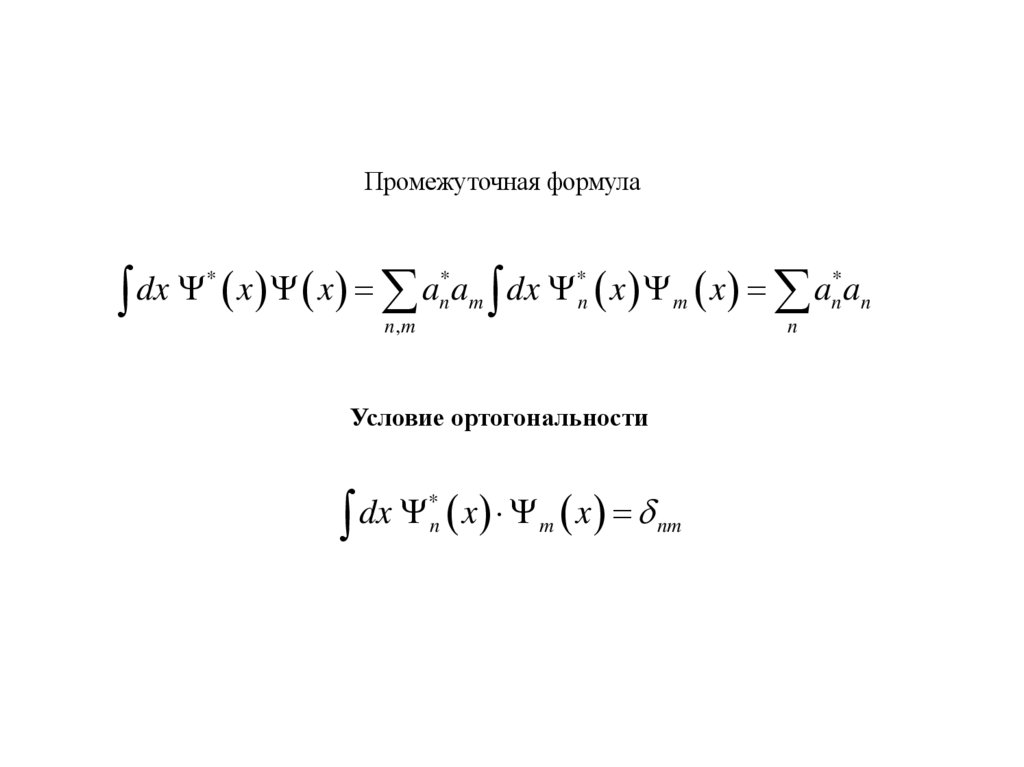
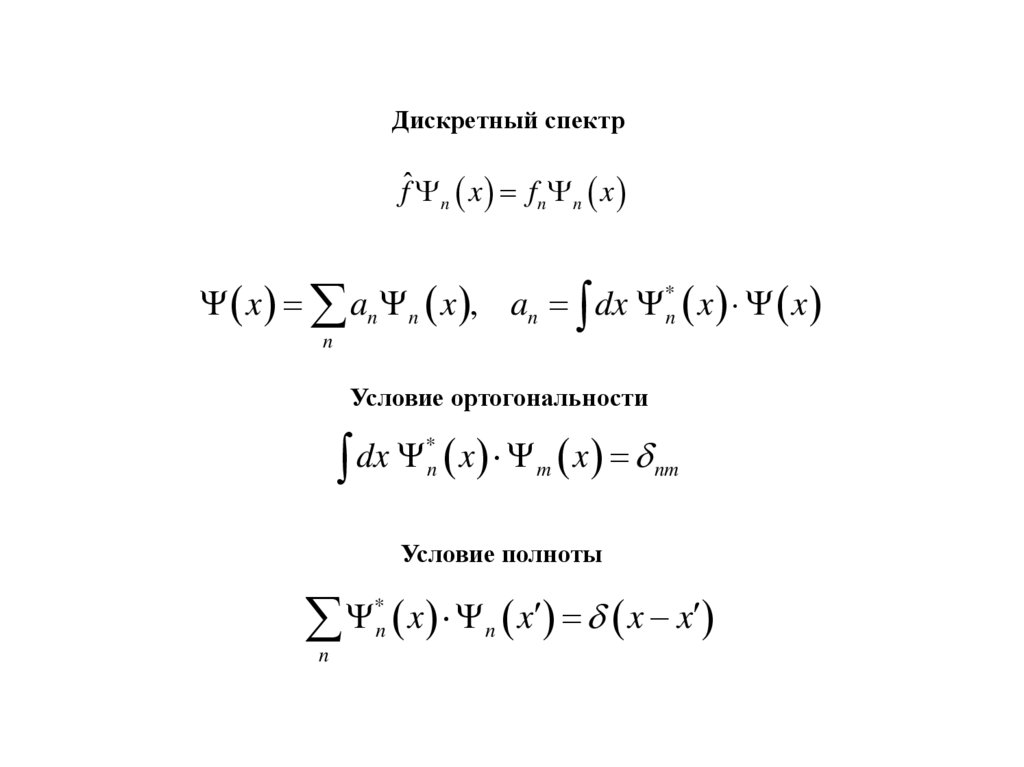

 Физика
Физика








