Похожие презентации:
Задачи по квантовой механике для химиков
1.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТимени М.В. Ломоносова
Л.А. Головань, Е.А. Константинова, П.А. Форш
ЗАДАЧИ ПО КВАНТОВОЙ МЕХАНИКЕ
ДЛЯ ХИМИКОВ
Допущено Научно-методическим советом по физике
Министерства образования и науки Российской Федерации
в качестве учебного пособия
для естественнонаучных, педагогических и технических
направлений и специальностей высших учебных заведений
Москва
Физический факультет МГУ
2010
1
2.
§1. Операторы в квантовой механике. Коммутационные соотношенияББК 22.314
Г61
УДК 530.145
Рецензенты:
профессор, доктор физико-математических наук Н.Ф. Степанов
профессор, доктор физико-математических наук Ю.В. Грац
Л.А.Головань, Е.А.Константинова, П.А.Форш
Г61
Задачи по квантовой механике для химиков: Учебное пособие. – М.
Физический факультет МГУ, 2010. – 154 с., ил.
Настоящее учебное пособие содержит задачи, которые в течение ряда
лет предлагались на семинарских занятиях по квантовой механике студентам
химического факультета МГУ имени М.В.Ломоносова. В пособии рассмотрены задачи по всем основным темам нерелятивистской квантовой механики,
предусмотренным программой учебной дисциплины для студентов естественных специальностей вузов и университетов. Для облегчения работы с задачником в каждом разделе кратко изложены основы теории, а в приложении приведены сведения по математике, необходимые для решения задач.
Пособие предназначено в первую очередь студентам университетов, для
которых физика не является профилирующим предметом, но может быть также полезно студентам вузов, обучающихся по специальности физика.
ББК 22.314
УДК 530.145
© Л.А.Головань, Е.А.Константинова, П.А.Форш, 2010
© Физический факультет МГУ, 2010
2
3.
§1. Операторы в квантовой механике. Коммутационные соотношенияОглавление
Предисловие ............................................................................................................. 4
§ 1. Операторы в квантовой механике. Коммутационные соотношения ........... 5
§ 2. Волновая функция. Среднее значение и дисперсия физических величин 15
§ 3. Собственные функции и собственные значения эрмитовых операторов . 20
§ 4. Уравнение Шрёдингера. Изменение квантовых состояний во времени ... 32
§ 5. Одномерное движение. Непрерывный спектр ............................................. 42
§ 6. Частицы в потенциальных ямах .................................................................... 51
§ 7. Гармонический осциллятор ........................................................................... 61
§ 8. Элементы теории момента импульса ............................................................ 70
§ 9. Движение в центральном поле ...................................................................... 80
§ 10. Элементы теории представлений................................................................ 90
§ 11. Спин микрочастицы ................................................................................... 101
§ 12. Стационарная теория возмущений. Невырожденный случай ............... 108
§ 13. Стационарная теория возмущений. Вырожденный случай ................... 117
§ 14. Нестационарная теория возмущений ....................................................... 126
§ 15. Вариационный метод ................................................................................. 133
Приложение 1. Комплексные числа .................................................................. 139
Приложение 2. Некоторые определенные интегралы ..................................... 140
Приложение 3. Дельта-функция Дирака ........................................................... 142
Приложение 4. Полиномы Эрмита .................................................................... 144
Приложение 5. Присоединенные функции Чебышева-Лагерра ..................... 147
Литература............................................................................................................ 149
3
4.
§1. Операторы в квантовой механике. Коммутационные соотношенияПРЕДИСЛОВИЕ
Содержание пособия составляют задачи, которые в течение ряда лет
предлагались на семинарских занятиях по квантовой механике студентам химического факультета МГУ имени М.В.Ломоносова. В настоящее время существует большое количество сборников задач по квантовой механике. Однако
все они преимущественно ориентированы на студентов физических специальностей, т.е. содержат большой объем материала, при изложении которого часто используется сложный математический аппарат. В данном пособии с одной
стороны охвачены практически все темы, предусмотренные программой учебной дисциплины, а с другой, оно примерно соответствует тому ограниченному
объему часов, который выделен на физику учебным планом для студентов естественных специальностей вузов и университетов, для которых физика не является профилирующим предметом.
Пособие состоит из пятнадцати параграфов, в которых рассматриваются
задачи практически по всем основным разделам нерелятивистской квантовой
механики. В начале каждого параграфа приводятся основные теоретические
сведения, необходимые для решения задач. Затем представлены подробные
решения типичных задач по изучаемой теме. Окончания решения задач отмечены знаком ♦. В заключение параграфа даны задачи для самостоятельного
решения с ответами. При подборе задач использовались различные источники,
список которых дан в разделе “Литература”. Пособие снабжено состоящим из
пяти частей приложением, в котором излагаются сведения по математике, необходимые для решения задач.
Авторы выражают самую искреннюю благодарность доценту физического факультета МГУ имени М.В.Ломоносова К.А. Казакову за ценные замечания и полезные советы, способствовавшие заметному улучшению данного
пособия.
4
5.
§1. Операторы в квантовой механике. Коммутационные соотношения§ 1. ОПЕРАТОРЫ В КВАНТОВОЙ МЕХАНИКЕ.
КОММУТАЦИОННЫЕ СООТНОШЕНИЯ
Под оператором понимают правило, по которому одной функции ψ сопоставляется другая функция ϕ . Формально это можно записать в виде
Fψ = ϕ .
Оператор принято обозначать буквой со «шляпкой» над ней. Например: F , G ,
M , x и т.д.
Линейным оператором называется оператор, обладающий следующими
свойствами:
1. F (ψ + ϕ ) = Fψ + Fϕ ,
2. F (αψ ) = α Fψ ,
(1.1)
где ψ и ϕ – произвольные функции, а α – произвольное комплексное число*.
Объектами применения операторов могут быть функции одной или нескольких переменных как непрерывных, так и прерывных, принимающих только определенные значения. Непрерывные переменные могут принимать либо
все значения, либо меняться в определенном промежутке. Независимые переменные мы будем всегда предполагать вещественными, а функции, к которым
применяются операторы, в общем случае считать комплексными. Под аргументом q функции ψ (q) , если это не оговорено особо, будем понимать одну или
несколько непрерывных переменных. В случае одной переменной аргумент q
часто будем обозначать посредством x .
Рассмотрим некоторые из возможных операторов. Оператор возведения
в квадрат Q , действуя на функцию ψ , даёт её квадрат ψ 2 :
Qψ = ψ 2 .
Оператор дифференцирования D =
(1.2)
d
действует на функцию ψ ( x ) и дает ее
dx
производную ψ '( x) :
d
ψ ( x) = ψ '( x) .
dx
Оператор инверсии I определяется равенством
Iψ ( x ) = ψ ( − x ) .
Dψ ( x) =
(1.3)
(1.4)
В квантовой механике радиусу-вектору частицы r ставится в соответст*
Некоторые сведения о комплексных числах изложены в приложении 1.
5
6.
§1. Операторы в квантовой механике. Коммутационные соотношениявие оператор r :
rψ (r ) = rψ (r ) ,
(1.5)
а обобщенному импульсу частицы p – оператор p :
p ψ (r ) = − i ∇ψ (r ) ,
где i - мнимая единица,
ратор Гамильтона «набла»:
(1.6)
- постоянная Планка, ∇ – дифференциальный опе-
∂ψ (r )
∂ψ (r )
∂ψ (r )
ex +
ey +
ez .
∂x
∂y
∂z
Здесь x, y, z - декартовы координаты частицы, а e x , e y , e z - орты осей x, y, z соответственно.
Из написанных соотношений следует, что оператор координаты x = x , а
∂
. Часто в дальнейшем,
оператор проекции обобщенного импульса p x = −i
∂x
где это не может привести к недоразумению, обобщенный импульс будем называть просто импульсом.
Задача 1.1. Проверить линейность операторов (1.2)-(1.6).
Решение. Чтобы определить является оператор линейным или нет, необходимо проверить удовлетворяет ли он условиям (1.1). Проверяя линейность
∇ψ (r ) =
оператора возведения в квадрат Q , подействуем им на сумму функций ψ и ϕ :
Q(ψ + ϕ ) = (ψ + ϕ ) = ψ 2 + ϕ 2 + 2ψϕ ≠ ψ 2 + ϕ 2 = Qψ + Qϕ .
2
Таким образом, данный оператор линейным не является.
Все остальные операторы линейны. Действительно,
d
d
d
d
D (ψ + ϕ ) = ψ + ϕ = Dψ + Dϕ , D αψ = (αψ ) = α ψ = α Dψ ;
dx
dx
dx
dx
I (ψ ( x) + ϕ ( x) ) = ψ ( − x ) + ϕ ( − x ) = Iψ ( x) + Iϕ ( x), Iαψ ( x) = αψ (− x) = α Iψ ( x);
r (ψ + ϕ ) = r (ψ + ϕ ) = rψ + rϕ = rψ + rϕ , r (αψ ) = α rψ = α rψ ;
p (ψ + ϕ ) = − i ∇ (ψ + ϕ ) = − i ∇ ψ − i ∇ ϕ = pψ + p ϕ ,
p (αψ ) = −i ∇(αψ ) = α (−i ∇ψ ) = α pψ . ♦
Суммой двух операторов F и G называется оператор F + G , действующий на функцию ψ согласно правилу
( F + G ) ψ = Fψ + Gψ .
Задача 1.2. Доказать, что F + G = G + F .
Решение. Согласно определению (1.7) имеем:
( F + G )ψ = Fψ + Gψ = Gψ + Fψ = (G + F )ψ ,
6
(1.7)
7.
§1. Операторы в квантовой механике. Коммутационные соотношенияоткуда следует, что
F + G = G + F .♦
Назовём произведением двух операторов их последовательное применение. Записывая F Gψ , мы понимаем, что на функцию ψ сначала действует
оператор G , а затем на результат действия оператора G действует оператор F
. В самом общем случае G Fψ ≠ F Gψ . Если GF = FG , то говорят, что операторы G и F коммутируют.
Введём специальный оператор F G − G F , который называется коммутатором операторов F и G и обозначается ⎡ F , G ⎤ , т.е.*:
⎣
⎦
⎡ F , G ⎤ = FG − GF .
⎣
⎦
Для коммутирующих операторов
⎡ F , G ⎤ = 0.
⎣
⎦
Укажем основные свойства коммутаторов:
⎡ A, A⎤ = 0 ,
⎣
⎦
(1.8)
⎡ A, B ⎤ = − ⎡ B, A⎤ ,
⎣
⎦
⎣
⎦
(1.9)
⎡ A + B, C ⎤ = ⎡ A, C ⎤ + ⎡ B, C ⎤ ,
⎣
⎦ ⎣
⎦ ⎣
⎦
(1.10)
⎡ ⎡ A, B ⎤ , C ⎤ + ⎡ ⎡ B , C ⎤ , A⎤ + ⎡ ⎡C , A⎤ , B ⎤ = 0 .
(1.11)
⎦ ⎦ ⎣⎣
⎦ ⎦ ⎣⎣
⎦ ⎦
⎣⎣
Как видно из формул (1.8) - (1.11) коммутатор, как и векторное произведение или скобки Пуассона в классической механике, является кососимметрической операцией и обладает теми же свойствами.
Задача 1.3. Показать, что операторы координат коммутируют между собой.
(тождество Якоби)
Решение .Рассмотрим, например, коммутатор ⎡ x, y ⎤ и подействуем им
⎣
⎦
на функцию ψ . Получим:
⎡ x, y ⎤ψ = x yψ − y xψ = xyψ − yxψ = 0 ,
⎣
⎦
откуда заключаем, что ⎡ x, y ⎤ =0. ♦
⎣
⎦
Задача 1.4. Показать, что операторы проекций импульса коммутируют
между собой.
*
В классической механике аналогом коммутатора являются скобки Пуассона.
7
8.
§1. Операторы в квантовой механике. Коммутационные соотношенияРешение. Рассмотрим, например, операторы p x и p y . Имеем:
(
)
⎡ p x , p y ⎤ψ = p x p y − p y p x ψ = −
⎣
⎦
=−
2
⎛ ∂ ⎛ ∂ψ
⎜ ⎜
⎝ ∂x ⎝ ∂y
2
⎞ ∂ ⎛ ∂ψ
⎟ − ∂y ⎜ ∂x
⎝
⎠
⎞⎞
⎟⎟ =
⎠⎠
⎛ ∂ 2ψ
∂ 2ψ ⎞
−
⎜
⎟.
x
y
y
x
∂
∂
∂
∂
⎝
⎠
∂ 2ψ
∂ 2ψ
и
равны, то ⎡ p x , p y ⎤ = 0 . ♦
Поскольку смешанные производные
⎣
⎦
∂x∂y
∂y∂x
Задача 1.5. Показать, что оператор координаты и оператор проекции
импульса на другую координату коммутируют.
Решение. Рассмотрим, например,
⎡ x, p y ⎤ψ = x p yψ − p y xψ = −i ⎜⎛ x ∂ψ − ∂ ( xψ ) ⎟⎞ = −i ⎜⎛ x ∂ψ − x ∂ψ
⎣
⎦
∂y
⎝ ∂y ∂y
⎠
⎝ ∂y
следовательно, ⎡ x, p y ⎤ = 0. ♦
⎣
⎦
⎞
⎟ = 0,
⎠
Задача 1.6. Найти коммутатор ⎡ x , p x ⎤ .
⎣
⎦
Решение. Действуя оператором ⎡ x , p x ⎤ на функцию ψ , находим:
⎣
⎦
⎡ x, p x ⎤ψ = x p xψ − p x xψ = −i ⎛⎜ x ∂ψ − ∂ ( xψ ) ⎞⎟ = −i ⎛⎜ x ∂ψ − x ∂ψ −ψ ⎞⎟ = i ψ ,
⎣
⎦
∂x
⎝ ∂x ∂x
⎠
⎝ ∂x
⎠
или
⎡ x, p x ⎤ = i . ♦
(1.12)
⎣
⎦
Задача 1.7. Доказать тождество
⎡ A, BC ⎤ = B ⎡ A, C ⎤ + ⎡ A, B ⎤ C .
⎣
⎦
⎣
⎦ ⎣
⎦
Решение. По определению
⎡ A, BC ⎤ = ABC − BC A .
⎣
⎦
В правую часть равенства добавим и вычтем оператор B AC . Получим
⎡ A, BC ⎤ = B AC − BC A + ABC − B AC = B AC − C A + AB − B A C =
⎣
⎦
(
) (
)
= B ⎡ A, C ⎤ + ⎡ A, B ⎤ C. ♦
⎣
⎦ ⎣
⎦
Для многих (но далеко не для всех) операторов можно найти обратные
операторы. Назовём оператор F
равенства
−1
обратным оператору F , если выполняются
FF
−1
8
−1
= F F = 1,
(1.13)
9.
§1. Операторы в квантовой механике. Коммутационные соотношениягде 1 - единичный оператор, действие которого на произвольную функцию ψ
оставляет её неизменной: 1ψ = ψ .
Задача 1.8. Найти операторы обратные операторам а) сдвига Ta :
Taψ ( x ) = ψ ( x + a ) ( a – вещественное число) и б) инверсии I
(1.4) :
Iψ ( x ) = ψ ( − x ) .
Решение. а) Согласно (1.13), должно выполняться равенство
−1
Ta Taψ ( x) = ψ ( x).
−1
Поскольку Taψ ( x ) = ψ ( x + a ) , то Ta ψ ( x + a) = ψ ( x) , откуда следует, что
−1
Ta = T − a .
Легко проверить, что для найденного оператора Ta
−1
выполняется первое
из равенств цепочки (1.13). Действительно,
−1
Ta Ta ψ ( x) = Taψ ( x − a) = ψ ( x) ,
−1
а значит Ta Ta = 1 .
б) Аналогично случаю а):
−1
−1
I Iψ ( x) = I ψ (− x) = ψ ( x) ,
−1
откуда заключаем, что I = I . ♦
Об n -кратном произведении операторов говорят, как о возведении оператора в степень n :
n
F = F …F .
n раз
(
)
2
Задача 1.9. Найти вид оператора x + D .
Решение. Было бы грубой ошибкой работать с операторами как с обычными числами и утверждать, что искомый оператор имеет вид x 2 + 2 x
(
)
d
d2
.
+
dx dx 2
В данном случае оператор x + D действует на функцию ψ ( x ) дважды:
d ⎞⎛
d ⎞
d ⎞⎛
dψ ( x ) ⎞
⎛
⎛
⎜ x + ⎟⎜ x + ⎟ψ ( x ) = ⎜ x + ⎟⎜ xψ ( x) +
⎟ =.
dx ⎠⎝
dx ⎠
dx ⎠⎝
dx ⎠
⎝
⎝
dψ ( x) d 2ψ ( x)
.
= ( x + 1)ψ ( x) + 2 x
+
dx
dx 2
Таким образом, для данного оператора мы можем записать:
2
9
10.
§1. Операторы в квантовой механике. Коммутационные соотношения2
d ⎞
d
d2
⎛
2
x
+
=
x
+
1
+
2
x
+
) dx dx2 . ♦
⎜
⎟ (
dx ⎠
⎝
Пусть функция f ( z ) допускает разложение в ряд Тейлора в окрестности
нуля, т.е.
∞
f ( z ) = ∑ cn z n ,
n =0
где коэффициенты
∞
1 dn f
cn = ∑
n
n =0 n ! d z
( )
.
z =0
Тогда оператор вида f F следует понимать как оператор, равный
( )
∞
n
f F = ∑ cn F .
n =0
(1.14)
()
( )
Задача 1.10. Найти явный вид оператора, f I = exp iaI , где a – действительная постоянная, а I – оператор инверсии (1.4).
Решение. В соответствии с определением (1.14) разложим экспоненту в
ряд Тэйлора:
∞
(ia ) n n
(1.15)
f I = exp iaI = ∑
I .
n =0 n !
()
( )
2
Легко показать, что I = 1 . Действительно, пользуясь определением (1.4),
имеем:
2
I ψ ( x) = I Iψ ( x) = Iψ (− x) = ψ ( x) .
Следовательно, все четные степени оператора I будут равны 1 , а нечетные – I .
С учетом этого, перепишем (1.15) в виде
⎛ a2 a4 a6
⎞ ⎛
⎞
a3 a5 a 7
f I = exp iaI = ⎜1 − + − + ... ⎟ + i ⎜ a − + − + ... ⎟ I .
2! 4! 6!
3! 5! 7!
⎝
⎠ ⎝
⎠
(Единичный оператор, который должен умножаться на первую скобку в правой части равенства для простоты записи опущен). В первой скобке справа
данного равенства стоит разложение в ряд функции cosa , а во второй скобке –
функции sin a .
Таким образом, в явном виде
()
( )
( )
exp iaI = cos a + i (sin a ) I . ♦
Эрмитово-сопряженным линейному оператору F называется оператор
10
11.
§1. Операторы в квантовой механике. Коммутационные соотношения+
F , для которого выполняется равенство:
∫ ϕ (q) Fψ (q)dq = ∫ ( F ϕ (q) ) ψ (q)dq,
*
+
*
(1.16)
где интегрирование производится по всей области изменения переменных q .
Символом dq обозначен элемент объема области интегрирования, а звездочкой помечены комплексно-сопряженные величины. Функции ψ (q ) и ϕ (q) в
(1.16) должны быть такими, чтобы написанные интегралы имели смысл, т.е.
были сходящимися. Кроме того, они должны обладать интегрируемым квадратом модуля:
∫ ϕ (q)
2
∫ ψ (q )
dq < ∞,
2
dq < ∞.
Отметим, что при этом сам оператор F может действовать на функции (в частности иметь собственные функции – см. далее) и не обладающие интегрируемым квадратом модуля.
Условие эрмитова сопряжения оператора часто записывают также в виде
(
)
*
+
*
*
∫ ϕ (q) Fψ (q)dq = ∫ψ (q) F ϕ (q)dq ,
где учтено, что правую часть равенства (1.16) можно представить как
∫(
)
(
*
+
)
*
+
F ϕ (q) ψ (q)dq = ∫ψ * (q ) F ϕ (q)dq .
Если оператор F совпадает со своим эрмитово-сопряженным оператором, т.е.
+
F=F ,
то он называется эрмитовым, или самосопряженным.
Задача 1.11. Найти эрмитово-сопряженный оператор для оператора дифd
ференцирования D =
.
dx
Решение. Рассмотрим для нашего оператора интеграл, стоящий в левой
части равенства (1.16) и проинтегрируем его по частям:
∞
∞
∞
∞
dψ ( x )
dϕ * ( x )
*
∫−∞ ϕ ( x) Dψ ( x)dx = −∞∫ ϕ ( x) dx dx = ϕ ( x)ψ ( x) −∞ − −∞∫ ψ ( x) dx dx =
*
*
∞
=
∫(
−∞
)
*
− Dϕ ( x) ψ ( x)dx.
(1.17)
В выражении (1.17) учтено, что в силу интегрируемости квадрата модуля
функций ϕ ( x) и ψ ( x) их значения на бесконечности стремятся к нулю, и, сле11
12.
§1. Операторы в квантовой механике. Коммутационные соотношениядовательно, внеинтегральное слагаемое обращается в нуль. Сравнивая (1.17) с
d
(1.16), приходим к заключению, что оператор D + = − D = − . ♦
dx
Тем самым оператор дифференцирования D не является эрмитовым.
Однако отметим, что с помощью абсолютно аналогичных рассуждений, можно
d
доказать эрмитовость оператора i . Отсюда, в частности, следует, что операdx
торы p x , p y и p z , а следовательно, и оператор p эрмитовы.
( )
+
+
Задача 1.12. Покажите, что cF = c* F , где c – произвольное комплексное число.
Решение. Данное равенство следует из определения (1.16) и следующей
цепочки равенств:
∫ (( cF )
+
)
( )
*
ϕ ( q) ψ ( q)dq = ∫ ϕ * ( q) cF ψ ( q)dq = c ∫ ϕ * ( q) F ψ ( q)dq =
(
)
(
*
+
)
*
+
= c ∫ F ϕ ( q) ψ ( q)dq = ∫ c F ϕ ( q) ψ ( q)dq.
*
( )
+
+
Сравнивая два крайних интеграла, видим, что cF = c* F . ♦
Задача 1.13. Доказать, что для произведения операторов FG
(FG)
+
+
+
=G F .
(1.18)
Для доказательства воспользуемся определением эрмитова сопряжения
(1.16). С одной стороны, имеем:
( )
( )
*
⎛ FG + ϕ (q) ⎞ ψ ( q)dq.
ϕ
(
q
)
FG
ψ
(
q
)
dq
=
⎟
∫
∫ ⎜⎝
⎠
С другой стороны, можно записать
*
∫ ϕ (q) ( FG )ψ (q)dq = ∫ ϕ (q) F ( Gψ (q) )dq = ∫ ( F ϕ (q) ) Gψ (q)dq =
*
+
*
(
+
+
)
*
(1.19)
*
(1.20)
= ∫ G F ϕ (q) ψ (q)dq.
Поскольку левые части (1.19) и (1.20) одинаковы, то, приравнивая их правые
части, получаем равенство (1.18). ♦
Задача 1.14. Доказать, что для некоммутирующих эрмитовых операторов F и G выполняется равенство:
⎡ F , G ⎤ = iD ,
⎣
⎦
12
(1.20)
13.
§1. Операторы в квантовой механике. Коммутационные соотношениягде D – тоже эрмитов оператор.
Решение. Из (1.20) следует, что оператор
D = −i ⎡ F , G ⎤ .
⎣
⎦
Докажем теперь, что этот оператор эрмитов:
(
+
D = −i ⎡ F , G ⎤
⎣
⎦
(
)
+
+
{(
= i ⎡F ,G⎤ = i F G
⎣
⎦
)
) ( ) }=
+
− GF
+
= i G F − FG = −i ⎡ F , G ⎤ = D.
⎣
⎦
Здесь мы воспользовались результатами задач 1.12 и 1.13. ♦
Оператор U называется унитарным, если
+
+
UU = U U = 1 .
Преобразование, при котором функции ψ
+
сопоставляется функция
+
ϕ = U ψ , а оператору A – оператор a = U AU , называется унитарным преобразованием.
Задача 1.15. Доказать, что унитарное преобразование сохраняет коммутационные соотношения.
Решение. Пусть ⎡ A, B ⎤ = C . В случае унитарного преобразования опера⎣
⎦
+
тору A ставится в соответствие оператор a = U AU , оператору B - оператор
+
+
b = U BU и оператору C - оператор c = U CU . Вычисляя коммутатор ⎡ a, b ⎤ ,
⎣ ⎦
имеем:
+
+
+
+
+
+
+
⎡ a, b ⎤ = U AUU BU − U BUU AU = U ABU − U B AU = U CU = c ,
⎣ ⎦
что и требовалось доказать. ♦
1.16.
Задачи для самостоятельного решения
Существует ли оператор, обратный оператору дифференцирования
d
?
dx
1.17. Доказать свойства коммутаторов (1.8)-(1.11).
1.18. Найти:
D=
3
⎛ d
⎞
а) ⎜ + x ⎟ ;
⎝ dx
⎠
б) ( A − B)( A + B) ;
13
14.
§1. Операторы в квантовой механике. Коммутационные соотношения3
⎛ d 1⎞
в) ⎜ + ⎟ .
⎝ dx x ⎠
2
2
2
2
1.19. Рассчитать ⎡ x , p x ⎤ , ⎡ x , p x ⎤ , ⎡ x , p x ⎤ .
⎣⎢
⎦⎥ ⎣⎢
⎦⎥ ⎣⎢
⎦⎥
1.20. Доказать, что
⎡ p x , f x ⎤ = −i ∂f ,
⎣
⎦
∂x
⎡ x, f ( p x )⎤ = i ∂f .
⎣
⎦
∂px
()
1.21. Доказать, что, если два эрмитовых оператора F и G коммутируют, то их
произведение также является эрмитовым.
1.22. Показать, что, если операторы F и G являются эрмитовыми операторами, то таким же будет и оператор
1
S = FG + GF .
2
(
)
d2
1.23. Показать, что оператор − 2 является эрмитовым.
dx
1.24. Доказать, что F
++
= F.
1.25. Доказать, что для эрмитова оператора F оператор ei F будет унитарным.
1.26. Доказать, что произведение унитарных операторов также будет унитарным оператором.
Ответы к задачам для самостоятельного решения
1.16. Нет.
1.18.
а)
d3
d2
d
+ 3 x 2 + ( 3 x 2 + 3) + ( x 3 + 3 x );
3
dx
dx
dx
d3 3 d2
в) 3 +
.
dx
x dx 2
1.19. 2i p x , 2i x , 2i
(x p
x
)
+ px x .
14
б)
2
2
A − B + ⎡ A, B ⎤ ;
⎣
⎦
15.
§2. Волновая функция. Среднее значение и дисперсия физических величин§ 2. ВОЛНОВАЯ ФУНКЦИЯ. СРЕДНЕЕ ЗНАЧЕНИЕ И
ДИСПЕРСИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
В квантовой механике состояние системы описывается волновой функцией Ψ ( q, t ) . В общем случае волновая функция является комплекснозначной.
Физический
смысл
имеет
квадрат
модуля
волновой
функции
Ψ ( q, t ) =Ψ * ( q, t )Ψ ( q, t ) , который определяет плотность вероятности обна2
ружения частицы в момент времени t в точке с координатой q .
Ограничимся пока лишь теми волновыми функциями, которые могут
быть проинтегрированы с квадратом модуля, то есть для которых интеграл
∞
∫ Ψ (q, t )
2
dq сходится. Поскольку вероятность обнаружить частицу во всём
−∞
пространстве равна 1, то это накладывает определённое условие нормировки на
волновую функцию Ψ ( q, t ) , а именно для каждого момента времени t должно
выполняться равенство:
∞
∫ Ψ ( q, t )
2
dq = 1.
(2.1)
−∞
В связи с тем, что время в квантовой механике играет роль параметра,
часто, где это не может привести к недоразумению, параметр t будем опускать.
Скалярное произведение двух функций ϕ (q) и ψ (q) определяется соотношением
ϕ ψ ≡ ∫ ϕ * ( q )ψ ( q ) dq .
Обозначение скалярного произведения посредством ϕ ψ
(2.2)
называется дира-
ковским.
Скалярное произведение функции ϕ и результата действия оператора F
на функцию ψ часто также записывается в виде
ϕ Fψ ≡ ϕ F ψ .
Условие нормировки функции Ψ в дираковских обозначениях запишется
как
Ψ Ψ = 1,
а определение эрмитово-сопряжённого оператора (см § 1):
15
16.
§2. Волновая функция. Среднее значение и дисперсия физических величин+
+
*
ϕ F ψ = F ϕψ = ψ F ϕ .
Если известна волновая функция квантовой системы Ψ ( q, t ) , то среднее
значение (математическое ожидание) физической величины F может быть
вычислено по формуле:
*
F = Ψ F Ψ ≡ ∫Ψ (q, t ) FΨ (q, t )dq.
(2.3)
Здесь волновая функция Ψ ( q, t ) предполагается нормированной на единицу в
соответствии с (2.1).
Задача 2.1. Показать, что необходимым и достаточным условием вещественности среднего значения величины F является эрмитовость (самосопряженность) ее оператора F .
Решение. Докажем сначала достаточность, т.е. докажем вещественность
среднего значения F , считая F эрмитовым оператором. Пользуясь определениями среднего значения и эрмитова оператора, имеем:
*
F = Ψ FΨ
*
= Ψ FΨ = F .
Теперь перейдем к доказательству необходимости. Пусть
F
*
= F .
Обозначим посредством F1 среднее значение величины F в состоянии ψ , а
посредством F2 - среднее значение величины F в состоянии ϕ , т.е.
F1 = ψ F ψ , а F2 = ϕ F ϕ .
Рассмотрим функцию Ψ = C (ψ + λϕ ) , где λ – произвольное комплексное
число, C – константа, позволяющая нормировать функцию Ψ на 1. Среднее
значение величины F в состоянии ψ есть
(
2
2
F = Ψ F€ Ψ = C
F1 + λ F2 + λ ψ F ϕ + λ * ϕ F ψ
Перейдем к комплексно-сопряженному выражению для
F
*
= F и F1
*
= F1 , F2
F =C
2
(F
1
*
2
*
F2 + λ * ψ F ϕ + λ ϕ F ψ
*
).
Вычитая из данного равенства равенство (2.4), получаем:
*
*
0 = λ * ψ F€ ϕ − ϕ F ψ + λ ϕ F ψ − ψ F ϕ .
(
(2.4)
F , учитывая, что
= F2 :
+λ
).
) (
)
(2.5)
Поскольку равенство (2.5) должно выполняться при произвольных λ , то
оба выражения в скобках должны по отдельности равняться нулю:
ϕ Fψ = ψ Fϕ
*
и
16
*
ψ Fϕ = ϕ Fψ .
17.
§2. Волновая функция. Среднее значение и дисперсия физических величин+
Следовательно, F = F . ♦
Задача 2.2. Найти связь между средними значениями координаты и импульса двух частиц, волновые функции которых Ψ 1 и Ψ 2 связаны соотношением
Ψ 2 ( x ) =Ψ 1 ( x + a ) ,
a = const .
Решение. Среднее значение координаты первой частицы
x1 = Ψ 1 x Ψ 1 ≡ ∫Ψ 1* ( x ) xΨ 1 ( x ) dx.
Учитывая полученное соотношение, найдем среднее значение координаты
второй частицы:
x2 = Ψ 2 x Ψ 2 ≡ ∫Ψ 2* ( x ) xΨ 2 ( x ) dx = ∫Ψ 1* ( x + a ) xΨ 1 ( x + a ) dx =
= ∫Ψ 1* ( x )( x − a )Ψ 1 ( x ) dx = x1 − a.
Для среднего значения импульса первой частицы имеем:
d
p1 = Ψ 1 p Ψ 1 ≡ −i ∫Ψ 1* ( x ) Ψ 1 ( x ) dx.
dx
Тогда среднее значение импульса второй частицы
d
d
p2 = Ψ 2 p€ Ψ 2 ≡ −i ∫Ψ 2* ( x ) Ψ 2 ( x ) dx = −i ∫Ψ 1* ( x + a ) Ψ 1 ( x + a ) dx =
dx
dx
d
= −i ∫Ψ 1* ( x ) Ψ 1 ( x ) dx ≡ p1 . ♦
dx
Дисперсия физической величины F определяется формулой:
(ΔF )
2
=
(F −
F
)
2
≡ F2 − F
2
.
Задача 2.3. Коммутатор операторов A и B двух физических величин
⎡ A, B ⎤ = iC,
⎣
⎦
где C - некоторый эрмитов оператор. Докажите, что
( ΔA )
2
( ΔB )
2
2
C
≥
.
4
(2.6)
Решение. Введем операторы
ΔA = A − A и ΔB = B − B ,
где A и B – средние значения величин A и B в состоянии Ψ . Поскольку
средние значения A и B вещественные, то операторы ΔA и ΔB – эрмитовы. Путем прямого вычисления найдем, что коммутатор
⎡ ΔA,ΔB ⎤ = AB − B A = iC.
⎣
⎦
Рассмотрим вспомогательный интеграл
17
(2.7)
18.
§2. Волновая функция. Среднее значение и дисперсия физических величин(
) (
)
(
)
2
I (α ) = α ΔA − i ΔB Ψ α ΔA − i ΔB Ψ ≡ ∫ α ΔA − i ΔB Ψ ( q ) dq ≥ 0.
(2.8)
Раскроем скобки, стоящие под знаком интеграла (2.8) и учтем коммутационное соотношение (2.7):
(α ΔA + i ΔB ) (α ΔA − i ΔB ) = α ( ΔA) − iα ( ΔAΔB − ΔBΔA) + ( ΔB )
= α ( ΔA ) + α C + ( Δ B ) .
2
2
2
2
2
=
(2.9)
2
Подставляя (2.9) в (2.8) и используя определение среднего значения (2.3), находим:
I (α ) = α 2
( ΔA )
2
( ΔB )
+α C +
2
≥ 0.
(2.10)
Неравенство (2.10) должно выполняться при произвольных значениях α . По-
( ΔA )
скольку коэффициент при α 2 в (2.10)
2
≥ 0, то квадратный трехчлен
α 2 ( ΔA ) + α C + ( Δ B )
2
2
будет неотрицателен, если дискриминант соответствующего квадратного
уравнения меньше либо равен нулю, т.е.
C
2
− 4 ( ΔA )
2
( ΔB )
2
≤ 0,
откуда непосредственно следует неравенство (2.6). ♦
Часто в качестве характеристики разброса получаемых при измерении
значений физической величины относительно среднего берут среднеквадратичное отклонение
ΔF =
(ΔF )
2
.
В данных обозначениях неравенство (2.6) примет вид:
C
Δ AΔB ≥
.
(2.11)
2
Неравенство (2.11) носит название соотношения неопределенностей.
Задача 2.4. Запишите соотношение неопределенностей для координаты и
проекции импульса .
Решение. Коммутатор операторов x и p x равен (см. задачу 1.6)
⎡ x, p x ⎤ = i .
⎣
⎦
В соответствии с (2.11) имеем:
Δ px Δ x ≥ . ♦
2
18
19.
§2. Волновая функция. Среднее значение и дисперсия физических величинЗадачи для самостоятельного решения
2.5. Доказать, что определённое соотношением (2.2) скалярное произведение обладает следующими свойствами:
ϕψ
*
= ψ ϕ ,
ϕ1 + ϕ 2 ψ = ϕ1 ψ + ϕ 2 ψ ,
ϕ αψ = α ϕ ψ ,
α ϕ ψ = α* ϕ ψ ,
где α – произвольное комплексное число.
2.6. Показать, что функции ϕ и φ = ϕ e iδ описывают одно и то же физическое состояние.
2.7. Найти связь между средними значениями координаты и импульса двух
частиц, волновые функции которых Ψ1 и Ψ 2 связаны соотношениями:
⎛ ip0 x ⎞
⎟ , p0 = const.
⎝
⎠
Ψ 2 ( x ) =Ψ 1 ( x ) exp ⎜
+
+
2.8. Доказать, что средние значения эрмитовых операторов F F и F F в
произвольном состоянии неотрицательны.
2.9. Доказать, что если в одном и том же состоянии среднее значение величины A равно A , а среднее значение величины B равно B , то среднее
значение суммы
A+ B = A + B .
2.10. Найти x , p , x 2 , p 2 ,
( Δx )
тель C для волновой функции Ψ = C e
2.7. x2
2.10. C =
−
2
x2
2a2
,
( Δp )
2
и нормировочный множи-
( a – вещественный параметр).
Ответы к задачам для самостоятельного решения
= x1 , p2 = p1 + p0 .
1
a π
, x = 0, p = 0, x
2
2
a2
2
= , p = 2,
2
2a
( Δx )
2
a2
= ,
2
( Δp )
2
=
2
2a 2
.
Указание. Значения вычисляемых в задаче интегралов можно найти в приложении 2.
19
20.
§3. Собственные функции и собственные значения эрмитовых операторов§ 3. СОБСТВЕННЫЕ ФУНКЦИИ И СОБСТВЕННЫЕ
ЗНАЧЕНИЯ ЭРМИТОВЫХ ОПЕРАТОРОВ
Пусть F – эрмитовый оператор. Все те числа F , при которых уравнение
F ψ = Fψ
(3.1)
имеет ненулевые (нетривиальные) решения ψ , называются собственными значениями оператора F , а соответствующие функции ψ – собственными функциями этого оператора, отвечающими значению F . Совокупность всех собственных значений оператора F называется его спектром. Реальные состояния
физических систем описываются однозначными, непрерывными и конечными
решениями уравнения (3.1).
В квантовой механике каждой физической величине сопоставляется эрмитов оператор. Один из основополагающих постулатов квантовой механики
состоит в том, что физическая величина F в любом квантово-механическом
состоянии, т.е. в состоянии, описываемом произвольной волновой функцией
Ψ ( q ) , может принимать только те значения, которые принадлежат спектру ее
оператора F .
Если множество собственных значений оператора F не более чем счетно, то говорят о дискретном спектре. В этом случае собственные значения
будем обозначать посредством Fn ( n = 0,1, 2,...) , а волновую функцию, соответствующую собственному значению Fn – посредствомψ Fn ≡ ψ n .
Если собственному значению Fn соответствует s линейно независимых
собственных функций ψ n1 ,ψ n2 ,...ψ ns , то собственное значение Fn называется s кратно вырожденным. Выбор собственных функций в этом случае неоднозначен. Очевидно, что любая линейная комбинация
s
ϕnm = ∑ cmi ψ ni ,
(3.2)
i =1
где c
i
m
– произвольные комплексные числа, также будет собственной функцией
оператора F , соответствующей значению Fn . Число линейно независимых комбинаций (3.2) равно s – кратности вырождения уровня. Поэтому вместо функций
ψ n1 ,ψ n2 ,...ψ ns можно выбрать любые s независимых линейных комбинаций (3.2).
Если собственные значения F являются произвольными комплексными
числами (пробегают непрерывный ряд в некотором интервале), то спектр опе20
21.
§3. Собственные функции и собственные значения эрмитовых операторовратора F называется непрерывным. Собственные значения оператора F в
случае непрерывного спектра будем обозначать просто той же буквой F (без
индекса), а соответствующие им собственные функции будем обозначать ψ F .
Очевидно, что собственные функции непрерывного спектра зависят от F как
от параметра, т.е. ψ F ( q ) ≡ ψ ( F , q ) .
Возможны операторы, имеющие спектр, состоящий из дискретных значений и значений, непрерывно изменяющихся в некоторых интервалах.
Отметим основные свойства собственных значений и собственных
функций линейных эрмитовых (самосопряженных) операторов.
1) Собственные значения эрмитова оператора вещественны. То есть, если
F – эрмитов оператор, то F = F * (в случае дискретного спектра) или F = F *
n
n
(в случае непрерывного спектра).
2) Собственные функции эрмитова оператора ортогональны.
Рассмотрим сначала дискретный спектр. Пусть F – эрмитов оператор, а ψ n
и ψ m его собственные функции, соответствующие собственным значениям Fn
и Fm (n, m = 0,1,...) :
F ψ n = Fn ψ n , ..., F ψ m = Fm ψ m .
Ортогональность собственных функций означает, что
ψ n ψ m ≡ ∫ψ n* ( q )ψ m ( q ) dq = 0, при n ≠ m.
Собственные функции дискретного спектра можно выбрать так, чтобы
выполнялось условие нормировки (2.1)
ψ n ψ n ≡ ∫ ψ n ( q ) dq = 1.
2
Два последних соотношения можно записать как
ψ n ψ m = δ nm ,
(3.3)
где δ nm – символ Kронекера:
⎧1, если n = m,
⎩0, если n ≠ m.
δ nm = ⎨
Выражение (3.3) называют условием ортонормированности, а удовлетворяющие (3.3) волновые функции – ортонормированными.
В случае вырождения собственного значения Fn эрмитова оператора F
нельзя гарантировать, что любые функции, соответствующие одному и тому
же значению Fn , ортогональны. Однако, используя формулу (3.2), всегда можно построить соответствующую ортонормированную систему собственных
21
22.
§3. Собственные функции и собственные значения эрмитовых операторовфункций
ϕ n1 , ϕ n2 ,...ϕ ns ,
для которых
ϕ nk ϕ nl = δ kl
( k , l = 0,1, 2,... ) .
Для построения такой ортонормированной системы можно положить
ϕ n1 = ψ n1 ,
ϕ n2 = a (ψ n1 + c22ψ n2 ),
где a – комплексная постоянная. Коэффициент c22 определяется из условия ортогональности
(
ϕ n1 ϕ n2 = ϕ n1 a (ψ n1 + c22ψ n2 ) = a ψ n1 ψ n1 + c22 ψ n1 ψ n2
) = 0,
откуда, считая функцию ψ n1 нормированной, получаем:
c22 = −
1
ψ n1 ψ n2
.
Постоянная a определяется из условия нормировки
ϕ n2 ϕ n2 = 1 .
Аналогично, полагая
ϕ n3 = b(ψ n1 + c32ψ n2 + c33ψ n3 ), b = const,
получим систему из двух линейных уравнений ϕ n1 ϕ n3 = 0 и ϕ n2 ϕ n3 = 0 для
определения c32 и c33 . Константа b определяется из условия нормировки. Пользуясь данной процедурой можно получить все s ( s – кратность вырождения)
линейно независимых ортонормированных функций. Такую процедуру называют ортогонализацией по Шмидту.
В том случае, если оператор F обладает непрерывным спектром собственных значений, функции ψ F нельзя нормировать обычным образом, так как
интеграл
∫ |ψ
F
|2 dq расходится. Для непрерывного спектра условие ортонор-
мированности, аналогичное условию (3.3) для дискретного спектра, записывается в виде
(3.4)
ψ F ψ F ′ ≡ ∫ψ F* ( q )ψ F ′ ( q ) dq = δ ( F ′ − F ),
где ψ F и ψ F ′ собственные функции, соответствующие собственным значениям
F и F ′ , а δ ( F ′ − F ) – дельта-функция Дирака∗.
3) Совокупность всех собственных функций оператора F образует полную
∗
Основные свойства дельта-функции Дирака приведены в приложении 3.
22
23.
§3. Собственные функции и собственные значения эрмитовых операторовили замкнутую систему функций, т.е. любая другая функция Ψ (q) , зависящая
от тех же переменных и удовлетворяющая тем же граничным условиям, что и
собственные функции оператора F , может быть представлена в случае дискретного спектра собственных значений оператора F в виде ряда
Ψ ( q ) = ∑ anψ n ( q ) ,
(3.5)
n
и в случае непрерывного спектра собственных значений оператора F в виде
интеграла
(3.6)
Ψ ( q ) = ∫ a ( F ) ψ F ( q ) dF .
Суммирование в (3.5) и интегрирование в (3.6) производятся по всем возможным значениям n и F .
Чтобы найти коэффициенты an и функцию a(F ) , умножим выражения
(3.5) и (3.6) на ψ n* ( q ) и ψ F* ( q ) соответственно и проинтегрируем по всему рассматриваемому пространству. В результате, учитывая ортогональность функций ψ n ( q ) и ψ F ( q ) , получим:
an = ∫ψ n* ( q )Ψ ( q ) dq ≡ ψ n Ψ ,
a F ≡ a ( F ) = ∫ψ F* ( q )Ψ ( q ) dq ≡ ψ F Ψ .
Пусть система, описываемая волновой функцией Ψ , находится в таком
состоянии, что величина F не имеет определенного значения. Это означает,
что при многократных измерениях (под измерением в квантовой механике
подразумевается всякий процесс взаимодействия между классическим прибором и квантовой системой) получается некоторый разброс наблюдаемых значений F . Величина an
2
определяет вероятность наблюдения значения Fn ве-
личины F в случае дискретного спектра, а a F
2
есть плотность распределения
2
вероятности величины F (т.е. произведение a F dF есть вероятность обнаружить F в интервале [ F , F + dF ] ) в случае непрерывного спектра. В силу
сказанного очевидно, что
∑a
2
n
= 1,
n
и
∫a
2
F
dF = 1 .
Если у оператора наряду с дискретным имеется также и непрерывный
спектр, то разложение функции Ψ по собственным функциям такого оператора записывается как
23
24.
§3. Собственные функции и собственные значения эрмитовых операторовΨ ( q ) = ∑ anψ n ( q ) + ∫ a ( F ) ψ F ( q ) dF .
n
Задача 3.1. Найти собственные значения и собственные функции оператора проекции момента импульса на ось z, который в сферических координатах имеет вид
∂
L z = −i
,
∂ϕ
где ϕ – полярный угол.
Решение. Уравнение на собственные значения и собственные функции
(3.1) в данном случае запишется как
dψ (ϕ )
−i
= Lzψ (ϕ ) .
dϕ
Это дифференциальное уравнение первого порядка, решением которого является функция
ψ (ϕ ) = C e
i
Lz ϕ
,
где C – некоторая константа. Для того чтобы функция ψ (ϕ ) была однозначной
необходимо выполнение условия
ψ (ϕ + 2π ) = ψ (ϕ ) ,
т.е.
e
i
Lz
2π
= 1,
откуда
Lz = m (m = 0, ± 1, ± 2,...).
При этом
ψ m (ϕ ) = Ceimϕ .
Таким образом, спектр оператора L z дискретный и невырожденный. Константу C находим из условия нормировки:
2π
ψ m ψ m = ∫ ψ m dϕ = 1 .
Получаем
2
0
*
1
,
2π
C=
и, следовательно, собственные функции
*
Нормировочная константа определяется с точностью до фазового множителя вида
, где
– любое вещественное число, поскольку физический смысл в квантовой механике имеет
только | | (см. задачу 2.6).
24
25.
§3. Собственные функции и собственные значения эрмитовых операторов1 imϕ
e . ♦
2π
Задача 3.2. Найти собственные значения и собственные функции оператора проекции импульса
∂
p x = −i
.
∂x
Решение. Уравнение на собственные значения и собственные функции
имеет вид:
dψ
−i
= pxψ .
dx
Отсюда
ψ m (ϕ ) =
ψ p ( x) = C e
x
i
px x
,
(3.7)
где C – нормировочная константа. Решение (3.7) удовлетворяет требованиям
однозначности, непрерывности и ограниченности при любом действительном
значении p x , то есть оператор p x обладает непрерывным спектром.
Для определения константы C воспользуемся условием (3.4):
*
∫ψ p′x ( x)ψ px ( x) dx = δ ( p′x − px ).
(3.8)
Преобразуем правую часть (3.8), используя интегральное представление δ функции (см. приложение 3). Имеем:
∫ψ ( x)ψ p ( x) dx =| C |
*
p′x
2
x
∞
∫e
i
( px − p′x ) x
dx = 2π | C |2 δ ( p′x − px ) .
−∞
Сравнивая данное выражение с (3.8), находим:
2π | C |2 = 1 ,
откуда
1
C=
.
2π
Таким образом, собственными функциями оператора проекции импульса
на ось x являются функции
i
px x
1
ψ px ( x ) =
e . ♦
2π
Задача 3.3. Найти собственные функции оператора координаты
r = r.
Решение. Уравнение на собственные значения и собственные функции
оператора r есть
25
26.
§3. Собственные функции и собственные значения эрмитовых операторовrψ ( r ) = r 0ψ (r ).
(3.9)
Здесь посредством r 0 обозначены конкретные значения координаты в отличие
от переменной r . Видно, что при r ≠ r 0 функция ψ (r ) должна быть равна нулю, а при r = r 0 функция ψ (r ) не определена. Из (3.9) следует:
∫ rψ (r ) dr = r ∫ψ (r ) dr.
0
(3.10)
Под dr в последнем равенстве понимается элемент объема dr = dxdydz . Решение уравнения (3.10) можно представить в виде
ψ r0 ( r ) = C δ ( r − r0 ) ,
где C – нормировочная константа, которую определяем из условия (3.4)
(спектр оператора координаты r очевидно является непрерывным):
∫ψ
*
r0′
(r )ψ r0 (r ) dr = δ (r0′ − r0 ) .
Имеем (см. приложение 3):
C
2
∫ δ (r − r0′ ) δ (r − r0 ) dr = C δ (r0′ − r0 )= δ (r0′ − r0 ) ,
2
откуда следует, что C = 1 .
Таким образом, собственные функции оператора r суть
ψ r0 ( r ) = δ ( r − r0 ) .
(3.11)
Функции (3.11) являются обобщенными функциями и не принадлежат к классу
рассматривавшихся до сих пор классических функций. ♦
Задача 3.4. Считая, что функция f ( z) разложима в ряд Тейлора, найти
собственные функции и собственные значения f ( F ) , если известны собственные функции и спектр оператора F .
Решение. Пусть Fn и ψ n – собственные значения и собственные функции оператора F соответственно. Операторная функция f ( F ) понимается как
разложение в формальный степенной ряд (см. § 1):
( )
∞
f F = ∑ ck F ,
k
k =0
где ck – коэффициенты разложения. Учитывая данное разложение, подействуем f ( F ) на функцию ψ n :
( )
∞
k
∞
f F ψ n = ∑ ck F ψ n = ∑ ck ( Fn ) ψ n = f ( Fn )ψ n .
k =0
k
k =0
Отсюда видно, что собственные функции f ( F ) совпадают с ψ n , а собствен26
27.
§3. Собственные функции и собственные значения эрмитовых операторовные значения есть f ( Fn ) .♦
Задача 3.5. Система описывается волновой функцией
Ψ (ϕ ) = C (1 + cos 3ϕ ) ,
где – полярный угол. Найти нормировочную константу C и наблюдаемые
значения проекции момента импульса в этом состоянии.
Решение. Пользуясь формулой Эйлера (см. приложение 1), запишем волновую функцию Ψ (ϕ ) в виде:
⎛ ei 3ϕ + e−i 3ϕ
Ψ (ϕ ) = C ⎜ 1 +
2
⎝
⎞
⎟.
⎠
(3.12)
Собственные функции оператора L z (см. задачу 3.1) есть
1 imϕ
ψ m (ϕ ) =
e .
2π
С учетом этого из (3.12) следует:
⎛
⎞
2π
2π
ψ 3 (ϕ ) +
ψ −3 (ϕ ) ⎟ .
2
2
⎝
⎠
Данное выражение есть не что иное как разложение (3.5) с отличными от нуля
коэффициентами
Ψ (ϕ ) = C ⎜ 2π ψ 0 (ϕ ) +
2π
C.
2
a0 = 2π C , a3 = a− 3 =
Из условия нормировки
2π
∫ Ψ (ϕ ) dϕ = 1
2
0
имеем:
C=
Функция
1
.
3π
тогда запишется в виде
2
1
1
ψ 0 (ϕ ) + ψ 3 (ϕ ) + ψ −3 (ϕ ) .
3
6
6
Таким образом, при измерении будут наблюдаться следующие значения
Lz (напомним, что Lz = m , см. задачу 3.1): Lz =0 с вероятностью a0 2 = 2 и
3
Ψ (ϕ ) =
Lz = ±3 с одинаковыми вероятностями a±3 2 = 1 .
6
Видно, что
∑a
2
n
2
2
2
= a0 + a3 + a − 3 = 1 . ♦
n
27
28.
§3. Собственные функции и собственные значения эрмитовых операторовЗадача 3.6. Пусть состояние системы описывается нормированной
функцией Ψ , которая раскладывается по собственным функциям ψ n эрмитова
оператора F : Ψ = ∑ a n ψ n . Выразить среднее значение оператора F через коn
эффициенты разложения an .
Решение. По определению
F = Ψ F Ψ = ∫ ∑ am*ψ m* F ∑ anψ n dq.
m
n
Отсюда, принимая во внимание ортонормированность функций ψ n , и то, что
функции ψ n суть собственные функции оператора F , находим:
F
=
∑a
*
m
m ,n
=
a n ∫ψ
∑
*
m
Fψ ndq =
∑a
m ,n
a m* a n F n δ m n =
m ,n
∑
*
m
a n F n ∫ ψ m* ψ n d q =
2
a n Fn .
♦ (3.13)
n
Задача 3.7. Для задачи 3.5 найти среднее значение проекции момента
импульса .
Решение.
По
формуле
(3.13)
вычисляем,
что
2
1
1
Lz = ⋅ 0 + 3 + ( −3 ) = 0. ♦
3
6
6
Задача 3.8. Показать, что два эрмитовых оператора F и G имеют общий
полный набор собственных функций тогда и только тогда, когда их коммутатор равен нулю.
Решение. Доказательство проведем для дискретного спектра. Сначала
докажем необходимость. Пусть функции ψ n , n = 0,1,2... образуют общий полный набор собственных функций операторов F и G , т.е.
F ψ n = Fn ψ n ,
Gψ n = Gn ψ n .
(3.14)
Произвольную функцию из общей области определения операторов F и G
можно представить в виде (3.5):
Ψ = ∑ anψ n .
n
Учитывая последние соотношения, получим для коммутатора операторов F и
G:
(
⎡ F , G ⎤Ψ = FG − GF
⎣
⎦
)∑a ψ
n
n
n
Следовательно,
28
= ∑ an ( FnGn − Gn Fn )ψ n = 0.
n
29.
§3. Собственные функции и собственные значения эрмитовых операторов⎡F,G⎤ = 0 ,
⎣
⎦
(3.15)
что и требовалось доказать.
Перейдем теперь к доказательству достаточности. Предположим для
простоты, что спектры операторов F и G невырожденны. Пусть Fn и ψ n
(n = 0,1,2...) – собственные значения и собственные функции оператора F .
Учитывая (3.15), получим:
G ( Fψ n ) = F (Gψ n ).
С другой стороны
G ( Fψ n ) = Fn (Gψ n ) .
Из последних двух соотношений заключаем, что
F (Gψ n ) = Fn (Gψ n ) .
Отсюда следует, что функция G ψ n является собственной функцией оператора
F , соответствующей собственному значению Fn . Поскольку собственное значение Fn не вырождено, то G ψ n может отличаться от собственной функции
ψ n только числовым множителем. Обозначив этот множитель посредством Gn ,
имеем:
G ψ n = Gn ψ n .
Отсюда следует, что функции ψ n являются собственными функциями оператора G .
Если операторы имеют вырожденные собственные значения, то из собственных функций ψ ni ( i = 0,1, 2,...s , s – кратность вырождения) оператора F
всегда можно составить линейные комбинации вида (3.2), которые будут собственными функциями оператора G (хотя сами функции ψ ni не являются собственными функциями оператора G ). ♦
Наличие общего полного набора собственных функций у операторов означает, что соответствующие таким операторам физические величины могут
быть одновременно измерены.
Задача 3.9. Доказать, что собственные значения унитарных операторов
по модулю равны единице.
Решение. Проведем доказательство для функции ψ , нормированной на
единицу. Запишем задачу на собственные функции и собственные значения
унитарного оператора U :
29
30.
§3. Собственные функции и собственные значения эрмитовых операторовU ψ = λψ .
(3.16)
+
Подействуем на обе части (3.16) оператором U . Получим:
+
+
+
U Uψ = U λψ = λ U ψ .
Умножим обе части этого выражения на ψ * и проинтегрируем по всему пространству:
+
+
*
*
∫ψ U Uψ dq = λ ∫ψ U ψ dq.
(3.17)
Пользуясь определением эрмитово-сопряженного оператора, преобразуем
правую часть равенства (3.17):
+
( )
*
λ ∫ψ * U ψ dq = λ ∫ Uψ ψ dq =λλ * ∫ψ *ψ dq = λλ * = λ .
2
С другой стороны, интеграл, стоящий в (3.17) слева, равен единице, поскольку
+
2
для унитарного оператора по определению U U = 1 . Следовательно, λ = 1 .
Для ненормированных функций решение проводится аналогично.♦
Задачи для самостоятельного решения
3.10. Доказать, что собственные значения эрмитова оператора вещественны.
3.11. Доказать, что собственные функции эрмитова оператора ортогональны.
3.12. Найти собственные значения и собственные функции оператора комплексного сопряжения K :
Kψ = ψ * .
3.13. Найти собственные значения и собственные функции оператора импульса p = −i ∇ .
3.14. Найти собственные значения и собственные функции оператора F , представляющего собой линейную комбинацию операторов одноименных компонент импульса и координаты:
F = α px + β x ,
где α , β – вещественные параметры. Доказать полноту системы собственных
функций.
3.15. Найти собственные значения и собственные функции оператора
d
F = sin
,
dϕ
где ϕ – полярный угол.
3.16. Найти собственные значения эрмитова оператора F , удовлетворяющего
соотношению
30
31.
§3. Собственные функции и собственные значения эрмитовых операторов3
F = c2 F ,
где c – вещественный параметр.
3.17. Показать, что если невырожденные собственные значения эрмитова оператора F располагаются симметрично относительно нуля, то собственные
2
значения оператора F будут двукратно вырождены.
3.18. Найти собственные значения и собственные функции оператора инверсии I (см. (1.4)). Какова кратность вырождения собственных значений? Разложить произвольную волновую функцию Ψ по собственным функциям оператора I .
3.19. Доказать, что в случае, когда система находится в собственном состоянии измеряемой величины, среднее значение совпадает с собственным значением в этом состоянии.
Ответы к задачам для самостоятельного решения
3.12. ψ K = e f , K = e −2 iα , f – произвольная вещественная функция, α – проiα
извольное вещественное число.
3.13. p – произвольный вещественный вектор, ψ p ( r ) =
1
( 2π )
i
e
32
3.14. F – произвольные вещественные числа,
ψ F ( x) =
1
2πα
e
−
i ( β x− F )
2αβ
3.15. F = sin(im), ψ F (ϕ ) =
3.16. F1 = 0, F2,3 = ±c
2
.
1 imϕ
e ; m = 0, ± 1, ± 2,...
2π
3.18. I1 = +1, ψ I1 ( r ) ≡ ψ + ( r ) – произвольная чётная функция,
I 2 = −1, ψ I2 ( r ) ≡ ψ − ( r ) – произвольная нечётная функция,
1
1
Ψ (r ) = ψ + (r ) + ψ − (r ) .
2
2
31
( p ,r )
.
32.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времени§ 4. УРАВНЕНИЕ ШРЁДИНГЕРА. ИЗМЕНЕНИЕ
КВАНТОВЫХ СОСТОЯНИЙ ВО ВРЕМЕНИ
Волновая функция Ψ (q, t ) системы удовлетворяет уравнению Шрёдингера
i
∂Ψ ( q, t )
= HΨ ( q, t ),
∂t
(4.1)
где H - оператор Гамильтона, или гамильтониан. Если имеется всего одна
частица, то совокупность координат квантовой системы q есть просто радиусвектор частицы r = { x, y , z} . В простейшем случае (без учета релятивистских
поправок) Гамильтониан H в квантовой механике получается в соответствии
с общими правилами из классической функции Гамильтона H ( r , p, t ) путем
замены координат и декартовых компонент обобщенного импульса соответствующими операторами, т.е. r → r ≡ r и p → p ≡ −i ∇ . В случае одной частицы,
находящейся в потенциальном поле, оператор
2
2
p
+ U ( r, t ) = −
Δ + U ( r, t ) ,
H=
(4.2)
2M
2M
где U ( r , t ) – потенциальная энергия частицы, M – масса частицы, а Δ – опе-
ратор Лапласа:
∂2
∂2
∂2
Δ=∇ = 2 + 2 + 2 .
∂x
∂y
∂z
частиц волновая функция Ψ (r1 , r2 ,..., rn , t ) удовлетворяет урав2
В случае
нению (4.1) с гамильтонианом (в случае потенциального поля)
2
2
n
pi
H =∑
+ U ( r1 , r2 ,..., rn , t ) = −∑
Δ ri + U ( r1 , r2 ,..., rn , t ) ,
i =1 2 M i
i =1 2 M i
n
где M i - масса i -ой частицы, Δ ri - оператор Лапласа, в котором дифференцирование осуществляется по координатам i -ой частицы, а U ( r1 , r2 ,..., rn , t ) – потенциальная энергия системы, включающая энергию взаимодействия между
частицами.
Из эрмитовости оператора p следует, что оператор H также является
эрмитовым.
Задача 4.1. Построить гамильтониан атома гелия.
Решение. Пусть M 1 – масса каждого из двух электронов, а M 2 - масса
ядра атома гелия. Радиус-вектор ядра обозначим посредством R , а радиусы32
33.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во временивекторы электронов – посредством r1 и r2 . Потенциальная энергия системы
будет складываться из энергий взаимодействий электронов с ядром и друг с
другом (заряд ядра Z = 2 ):
2e 2
2e 2
e2
U ( r1 , r2 ) = −
−
+
,
R − r1 R − r2 r1 − r2
где e - заряд электрона.
В соответствии с (4.2) гамильтониан атома гелия имеет вид
2
2
2e 2
2e 2
e2
.♦
H =−
ΔR −
Δ r 1 + Δ r2 ) −
−
+
R − r1 R − r2 r1 − r2
2M 2
2M1
(
Задача 4.2. Доказать, что для средних значений координаты x и импульса p x частицы массы M выполняется соотношение
p
d x
= x .
(4.3)
dt
M
Решение. Продифференцируем выражение для среднего значения координаты
x = ∫Ψ * xΨ dx
по времени:
d x
∂Ψ *
∂Ψ
=∫
xΨ dx + ∫Ψ * x
dx .
dt
∂t
∂t
(4.4)
Из (4.1) следует, что комплексно-сопряженная функция Ψ * удовлетворяет
уравнению
*
∂Ψ *
(4.5)
−i
= H Ψ *.
∂t
∂Ψ *
∂Ψ
Выражая производные
в (4.4) с помощью (4.1) и (4.5), имеем:
и
∂t
∂t
*
d x
i
i
= ∫ H Ψ * xΨ dx − ∫Ψ * xHΨ dx.
(4.6)
dt
Пользуясь тем, что оператор H эрмитов, перепишем (4.6) в виде
d x
i
i
i
= ∫Ψ * H xΨ dx − ∫Ψ * xHΨ dx = ∫Ψ * ⎡ H , x ⎤Ψ dx.
⎣
⎦
dt
2
Используя выражение для гамильтониана (4.1) и учитывая, что p x = −
найдем:
33
(4.7)
2
∂2
,
∂x 2
34.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времени∂ 2 ( xΨ )
⎡ H , x ⎤Ψ = H ( xΨ ) − xHΨ = −
+
⎣
⎦
2 M ∂x 2
(4.8)
2
2
∂ 2Ψ
∂Ψ
+U xΨ +
− xUΨ = −
.
x
M ∂x
2 M ∂x 2
С учетом (4.8) из (4.7) получаем:
d x
∂Ψ
1
i
= − ∫Ψ *
dx ≡ ∫Ψ * p xΨ dx ,
(4.9)
∂x
dt
M
M
что и требовалось доказать. ♦
Аналогично доказывается, что в трехмерном случае
d
1
Ψ * rΨ dr = ∫Ψ * pΨ dr ,
∫
dt
M
т.е.
d r
p
=
.
(4.10)
dt
M
Задача 4.3. Доказать, что для средних значений координаты x и про2
екции силы Fx выполняется соотношение
d2 x
M
= Fx ,
dt 2
(4.11)
где M - масса частицы.
Решение. Продифференцируем выражение (4.9) по времени:
d2 x
∂Ψ *
∂Ψ
*
=
+
M
p
dx
p
dx.
Ψ
Ψ
x
x
∫ ∂t
∫
∂t
dt 2
(4.12)
Используя (4.1) и (4.5), а также, учитывая то, что H – эрмитов оператор, перепишем (4.12) в виде:
*
d2 x
i M
H
Ψ * p xΨ dx + ∫Ψ * p x HΨ dx = ∫Ψ * ⎡⎣ p x , H ⎤⎦Ψ dx.
=
−
2
∫
dt
Далее, находим:
3
3
⎡ p x , H ⎤Ψ = p x HΨ − H p xΨ = p x Ψ + p x (UΨ ) − p x Ψ −
⎣
⎦
2M
2M
∂Ψ
∂U
∂Ψ
∂U
− p xUΨ = −i U
−i
= −i
Ψ +i U
Ψ.
∂x
∂x
∂x
∂x
Тогда из (4.13) следует, что
d2 x
* ⎛ ∂U ⎞
M
Ψ
=
∫ ⎜⎝ − ∂x ⎟⎠Ψ dx.
dt 2
По определению
34
(4.13)
35.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времениFx = −
∂U
,
∂x
и, следовательно,
d2 x
M
= ∫Ψ * FxΨ dx. ♦
2
dt
В трехмерном случае равенство (4.11) принимает вид:
d2 r
M
= ∫Ψ * ( −∇U )Ψ dr ≡ F .
(4.14)
2
dt
Равенства (4.3), (4.10), (4.11) и (4.14) составляют содержание теорем
Эренфеста, утверждающих, что средние значения величин (координат, импульса, энергии), характеризующих движение частицы в квантовой механике,
а также среднее значение силы, действующей на частицу, связаны между собой уравнениями, аналогичными соответствующим уравнениям классической
механики. Соотношения между средними значениями, аналогичные классическим, приведены также в задачах 4.9 и 4.10.
Задача 4.4. Получить выражение, описывающее изменение плотности
вероятности Ψ
2
частицы с течением времени (уравнение непрерывности в
квантовой механике).
Решение. Рассмотрим интеграл
∫Ψ
2
dr,
V
взятый не по всему бесконечному объему, а по некоторому конечному объему
V . Этот интеграл представляет собой вероятность нахождения частицы в данном объеме. Вычислим производную от этой вероятности по времени:
⎛ * ∂Ψ
d
d
∂Ψ * ⎞
2
*
Ψ dr = ∫Ψ Ψ dr = ∫ ⎜Ψ
+Ψ
⎟dr.
dt V∫
dt V
t
t
∂
∂
⎝
⎠
V
(4.15)
В соответствии с выражениями (4.1), (4.2) и (4.5) перепишем (4.15) в виде
d
1
2
*
*
Ψ
=
−
Ψ
Δ
Ψ
−
Ψ
Δ
Ψ
+
Ψ *UΨ −Ψ UΨ * dr.
d
r
d
r
∫
∫
∫
dt V
2Mi
i V
V
(
)
(
)
Второй интеграл здесь очевидно равен нулю. Первый интеграл можно записать так:
−∫
V
(Ψ
2Mi
ΔΨ −Ψ ΔΨ * ) dr = −∫
*
V
2Mi
∇ (Ψ *∇Ψ −Ψ ∇Ψ * ) dr.
Действительно, по правилам дифференцирования
∇ (Ψ *∇ Ψ −Ψ ∇ Ψ * ) = Ψ *∇ 2Ψ + ∇ Ψ *∇ Ψ −Ψ ∇ 2Ψ * − ∇ Ψ ∇ Ψ * =
35
36.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времени=Ψ *∇2Ψ −Ψ ∇2Ψ * =Ψ *ΔΨ −ΨΔΨ * .
Таким образом,
d
2
⎡
Ψ
Ψ *∇Ψ −Ψ ∇Ψ * )⎤⎥ dr.
dr = − ∫ ∇ ⎢
(
∫
dt V
⎣ 2 Mi
⎦
V
(4.16)
По теореме Остроградского-Гаусса правую часть этого соотношения можно
заменить интегралом по замкнутой поверхности S , ограничивающей объем V .
Это приведет к формуле
d
2
Ψ dr = − ∫ ⎡⎢
Ψ *∇Ψ −Ψ ∇Ψ * )⎤⎥ d s .
(
∫
2 Mi
dt V
⎦
S ⎣
Отсюда видно, что стоящий справа поверхностный интеграл определяет скорость убывания вероятности нахождения частицы в объеме V и, следовательно, представляет собой поток вероятности через поверхность S . В связи с
этим вектор
j=
(Ψ
2Mi
∇Ψ −Ψ ∇Ψ * )
*
(4.17)
можно трактовать как плотность потока вероятности.
Воспользовавшись обозначением (4.17), запишем формулу (4.16) следующим образом:
2
∂Ψ
d
2
d
Ψ
=
r
∫V ∂t dr = −V∫ ∇ ⋅ j dr.
dt V∫
Ввиду произвольности объема интегрирования V в каждой точке пространства
должно выполняться условие (учитываем, что скалярное произведение
∂j ∂j ∂j
∇ ⋅ j ≡ div j = x + y + z , где jx , j y , jz - проекции вектора j на оси декарто∂x ∂y ∂z
вой системы координат)
∂ρ
+ div j = 0 ,
∂t
2
где введено обозначение ρ ≡ Ψ . Полученное соотношение называется уравнением непрерывности. Оно аналогично классическим уравнениям непрерывности. Так, например, в электродинамике уравнение непрерывности имеет вид
∂ρ
+ div j = 0,
∂t
где ρ – плотность заряда, а j – плотность электрического тока. ♦
Задача 4.5. Производную по времени от величины F в квантовой механике определяют как величину, среднее значение которой равно производной
по времени от среднего значения, т.е. должно выполняться равенство
36
37.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времениdF
d
=
F .
dt
dt
Исходя из данного определения, найти оператор F€ .
Решение. По определению
d
d
∂Ψ *
∂F
∂Ψ
*
F = ∫Ψ FΨ dq = ∫
FΨ dq + ∫Ψ * Ψ dq + ∫Ψ * F
dq.
∂t
∂t
∂t
dt
dt
∂F
есть оператор, получающийся дифференцированием оператора F по
∂t
времени, от которого последний может зависеть как от параметра.
С учетом соотношений (4.1) и (4.5)
Здесь
d
i
∂F
i
F = ∫ ( H€*Ψ * ) FΨ dq + ∫Ψ * Ψ dq − ∫Ψ * FH€Ψ dq.
∂t
dt
Поскольку оператор H эрмитов,
∫ (H Ψ
*
*
) FΨ dq = ∫Ψ * H FΨ dq,
и, следовательно,
⎛ ∂F i
d
+ HF − FH
F = ∫Ψ * ⎜
⎜ ∂t
dt
⎝
(
⎞
) ⎟⎟Ψ dq.
⎠
(4.18)
С другой стороны
dF
= ∫Ψ * FΨ dq.
dt
Приравнивая (4.18) и (4.19), получаем
F=
(
)
∂F i
∂F i ⎡
+ HF − FH =
+ H , F ⎤.
⎣
⎦
∂t
∂t
(4.19)
(4.20)
Из (4.20) следует, что если оператор F физической величины F не зависит явно от времени и коммутирует с гамильтонианом, то F = 0, а значит
dF
d
=
F = 0,
dt
dt
откуда F = const. Другими словами, среднее значение величины остается постоянным во времени. При этом можно также утверждать, что если в данном
состоянии величина F имеет определенное значение, то и в дальнейшие моменты времени она будет иметь то же самое значение. ♦
Пусть гамильтониан системы не зависит явно от времени. Тогда в соответствии с (4.20) H = 0 и можно заключить, что функция Гамильтона сохраня37
38.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времениется. Как известно из классической физики, это означает сохранение обобщенной энергии системы. В отличие от классической механики, энергия в квантовой механике не обязана иметь определенное значение. Смысл закона сохранения энергии в этом случае состоит в том, что если в данном состоянии энергия
имеет определенное значение, то это значение остается постоянным во времени.
Состояния, в которых энергия имеет определенные значения, называются стационарными состояниями системы. Стационарные состояния удовлетворяют уравнению
HΨ ( q, t ) = EΨ ( q, t ) ,
где Ψ ( q , t ) - волновые функции стационарных состояний, а E - собственные
значения энергии. Соответственно этому, уравнение (4.1) для волновых функций Ψ ( q , t ) стационарных состояний
∂Ψ ( q, t )
= HΨ ( q, t ) = EΨ ( q, t )
∂t
может быть непосредственно проинтегрировано по времени. В результате интегрирования имеем
⎛ i ⎞
Ψ (q, t ) = exp ⎜ − Et ⎟ψ (q),
⎝
⎠
где ψ (q) – функция только координат.
i
Малой буквой мы будем обозначать волновые функции стационарных
состояний без временного множителя. Эти функции, а также сами собственные значения энергии, определяются уравнением
Hψ ( q ) = Eψ ( q ) .
(4.21)
Уравнение (4.21) называется уравнением Шрёдингера для стационарных состояний или, короче, стационарным уравнением Шрёдингера. Уравнение
(4.21) представляет собой задачу на собственные значения и собственные
функции оператора H и, следовательно, для него справедливы все свойства,
собственных функций и собственных значений эрмитова оператора, перечисленные в § 3.
Если известны решения стационарного уравнения Шрёдингера 4.21 , то
решение уравнения (4.1) можно записать в виде
i
Ψ n ( q, t ) = ∑ an exp ⎛⎜ − En t ⎞⎟ψ n ( q)
(4.22)
⎝
⎠
n
в случае дискретного спектра, или в виде
38
39.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времениΨ ( q, t ) = ∫ aE exp ⎛⎜ − Et ⎞⎟ψ E ( q)dE
i
⎝
⎠
(4.23)
в случае непрерывного спектра.
Коэффициенты в (4.22) и (4.23) однозначно определяются заданием волновой функции в начальный момент времени
an ( E ) = ∫ψ n*( E ) ( q )Ψ ( q, t = 0) dq.
(4.24)
Задача 4.6. Стационарные состояния частицы в одномерной бесконечно
глубокой потенциальной яме шириной a описываются волновыми функциями
⎧ 2
⎛πn ⎞
x ⎟ , при 0 < x < a,
sin ⎜
⎪
ψ n ( x) = ⎨ a
⎝ a ⎠
⎪0, при x ≤ 0 или x ≥ a ,
⎩
которые соответствуют собственным значениям энергии
En =
π 2 2n2
(n = 1,2,...),
2 Ma 2
где M – масса частицы. Пусть в начальный момент времени волновая функция частицы
4
πx
sin 3
.
Ψ ( x, t = 0) =
a
5a
Найти волновую функцию в произвольный момент времени.
Решение. В произвольный момент времени волновая функция определяется равенством (4.22). Коэффициенты разложения a n в данном случае проще
определить не прямым вычислением интеграла (4.24), а воспользовавшись
тригонометрической формулой
⎛ π n ⎞ 3 ⎛ π x ⎞ 1 ⎛ 3π x ⎞
sin 3 ⎜ ⎟ = sin ⎜
⎟ − sin ⎜
⎟.
⎝ a ⎠ 4 ⎝ a ⎠ 4 ⎝ a ⎠
Тогда
4
πx
3
πx
1
3π x
sin 3
sin
sin
.
Ψ ( x, t = 0) =
=
−
(4.25)
a
a
a
5a
5a
5a
С другой стороны, согласно (4.22),
2
⎛πn ⎞
sin ⎜
x ⎟.
(4.26)
a
a
⎝
⎠
n
n
Сравнивая (4.25) и (4.26) видим, что отличными от нуля являются только коэффициенты
3
1
a1 =
и a3 =
.
10
10
Ψ ( x, t = 0) = ∑ anψ n ( x ) = ∑ an
39
40.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времениСоответствующие значения энергии
E1 =
π2
2
2 Ma 2
9π 2 2
и E3 =
.
2 Ma 2
Таким образом,
⎛ iπ 2 ⎞ ⎛ π x ⎞
⎛ 9iπ 2 ⎞ ⎛ 3π x ⎞
3
1
t sin ⎜ ⎟ −
t sin ⎜
exp ⎜ −
exp ⎜ −
Ψ ( x, t ) =
⎟. ♦
2 ⎟
2 ⎟
Ma
a
Ma
a
2
2
5a
5
a
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
Задачи для самостоятельного решения
4.7. Построить гамильтониан двумерного изотропного гармонического осциллятора в декартовой системе координат. Масса осциллятора M , а частота ω .
4.8. Построить гамильтониан атома водорода, перейдя в систему центра масс.
Масса ядра атома равна M 1 , а масса электрона M 2 .
4.9. Показать, что для пространственных средних момента импульса L = [rp ] и
момента силы M = [rF ] выполняется соотношение
d L
= M .
dt
4.10. Пусть F – среднее значение не зависящего явно от времени оператора
F в состоянии Ψ (q, t ) . Показать, что
d F
i
= ⎡H , F ⎤ .
⎣
⎦
dt
Пользуясь данным результатом, доказать соотношения
d px
d x
∂H
∂H
,
.
=
=−
dt
∂px
dt
∂x
4.11. Состояние частицы массой M задается волновой функцией
pr − Et ⎞
Ψ (r, t ) = C exp ⎛⎜ i
⎟,
⎝
⎠
2
где p – импульс частицы, E = p
- энергия частицы, C - нормировочная
2M
константа. Найти плотность вероятности распределения и поток вероятности
этой частицы.
4.12. Доказать, что если гамильтониан стационарной системы зависит от параметра λ , то в произвольном стационарном состоянии энергии E
Ψ
∂H
Ψ
∂λ
где Ψ – волновая функция системы.
40
=
∂E
,
∂λ
41.
§4. Уравнение Шрёдингера. Изменение квантовых состояний во времени4.13. Показать, что средние значения плотности вероятности и плотности потока вероятности в стационарных состояниях не зависят от времени.
4.14. Показать, что для частицы заряда e в однородном электрическом поле
напряженности E 0 оператор F = p − E0t является оператором сохраняющейся
величины. Указание. Гамильтониан частицы H = p
2
− eE0r.
2M
4.15. Стационарные состояния одномерного движения свободной частицы
описываются волновыми функциями
1
⎛i
⎞
ψ px ( x ) =
exp ⎜ px x ⎟ ,
2π
⎝
⎠
которые соответствуют собственным значениям энергии
p x2
E=
.
2M
Пусть в начальный момент времени волновая функция свободной частицы
⎧ ip0 x x 2 ⎫
exp ⎨
− 2 ⎬,
Ψ ( x.t = 0) =
1
2 4
2a ⎭
⎩
(π a )
где a > 0, p0 - вещественные параметры. Найти волновую функцию в произ1
вольный момент времени.
Ответы к задачам для самостоятельного решения
4.7 H = −
⎛ ∂2
∂ 2 ⎞ M ω 2 ( x2 + y 2 )
.
+
⎜
⎟+
2M ⎝ ∂x2 ∂y 2 ⎠
2
2
e2
M r + M 2r2
∇ −
∇ − ; R= 11
4.8 H = −
,
r
2( M1 + M 2 )
2M
M1 + M 2
2
M=
2
R
2
2
r
r = r1 − r2 ,
M 1M 2
, r1 , r2 – радиусы-векторы ядра и электрона соответственно.
M1 + M 2
4.11 j = C
2
p
.
m
4.15 Ψ ( x, t ) =
( a 2π )
1
4
⎛ 2
it 2 2 ⎞
2 p0
−
+
x
2
ia
x
p0 a ⎟
⎜
1
M
⎟.
exp ⎜ −
t ⎞
2⎛
t ⎞
⎜
⎟
⎛
2a ⎜ 1 + i
2 ⎟
⎜
⎟
⎜1 + i
2 ⎟
Ma ⎠
⎝
⎝
⎠
Ma ⎠
⎝
41
42.
§5. Одномерное движение. Непрерывный спектр§ 5. ОДНОМЕРНОЕ ДВИЖЕНИЕ. НЕПРЕРЫВНЫЙ СПЕКТР
Одномерным называется движение системы, имеющей одну степень
свободы. Обозначим пространственную координату, описывающую движение
системы, посредством . Пусть гамильтониан системы не зависит явно от времени. В этом случае задача определения волновой функции системы сводится
к решению уравнение Шрёдингера (4.21), которое при наличии потенциального поля
можно записать в виде:
d 2ψ 2M
+ 2 ⎡⎣ E − U ( x )⎤⎦ψ ( x ) = 0.
(5.1)
dx 2
Решение этого уравнения – волновая функция
– удовлетворяет
всем свойствам собственных функций, отмеченным в §3. В частности, она
должна быть непрерывной, однозначной и ограниченной. Кроме того, если понигде не обращается в бесконечность, непрерывтенциальная энергия
dψ ( x)
ными в каждой точке также должны оставаться производные
≡ ψ ′( x) .
dx
В данном разделе мы рассмотрим задачи на движение частицы, характеризуемой непрерывным энергетическим спектром. В классической механике
аналогом этого случая является инфинитное движение.
Задача 5.1. Найти значения энергии и волновые функции стационарных
состояний одномерного свободного движения частицы массы .
2
p
Решение. Поскольку движение свободное, то U ( x) = 0 , H = T =
и из
2m
уравнения (5.1) имеем:
d 2ψ ( x ) 2M
+ 2 Eψ ( x ) = 0.
dx2
Частные решения этого уравнения можно записать в виде
⎛
⎝
ψ (1,2)
( x ) = C1,2 exp ⎜ ±i
p
x
px ⎞
x ⎟,
⎠
(5.2)
где C1,2 - произвольные константы, а px = 2ME представляет собой импульс
частицы вдоль оси движения .
⎛ p ⎞
Решение C1 exp ⎜ i x x ⎟ соответствует частице, движущейся вправо (ось
⎜
⎟
⎝
⎠
42
43.
§5. Одномерное движение. Непрерывный спектр⎛ p ⎞
считаем направленной вправо), а решение C2 exp ⎜ −i x x ⎟ описывает части⎜
⎟
⎝
⎠
цу, движущуюся влево. Таким образом, стационарные состояния c энергией E
будут двукратно вырождены.
Решения (5.2) будут однозначными, непрерывными и ограниченными
при любых действительных значениях импульса p x , а следовательно, и при
0. Это означает, что спектр свободного
любых действительных значениях
движения частицы является непрерывным.
С учетом нормировочной константы, найденной в задаче 3.2, волновая
функция для свободной частицы, движущейся вправо, запишется в виде:
ψ p ( x) =
x
1
⎛ p ⎞
exp ⎜ i x x ⎟.
2π
⎝
⎠
Эта функция также является собственной функции оператора проекции импульса p x (см. задачу 3.2). Данный факт есть следствие возможности одно2
временного измерения кинетической энергии свободной частицы T =
px
2M
и
ее импульса p x (операторы T и p x коммутируют). ♦
Предположим, что зависимость потенциальной энергии от координаты
имеет один максимум и
имеет вид, показанный на рис. 5.1, т.е. функция
монотонно убывает влево и вправо от этого максимума. Такую зависимость
принято называть потенциальным барьером. Пусть слева из бесконечности на потенциальный барьер падает однородный поток частиц. В квантовой
механике в общем случае всегда есть вероятность того, что частица отразится
от барьера (даже, если энергия частиц
), и вероятность того, что частица пройдёт сквозь барьер (даже, если энергия частиц
). Таким образом,
при прохождении через потенциальный барьер имеются три потока частиц:
падающий, прошедший и отраженный. Рассматриваемый процесс удобно характеризовать следующими величинами: коU
эффициентом отражения
U0
j
j
R=
пад
jотр
(5.3)
jпад
и коэффициентом прохождения
D=
jпрош
jпад
прош
jотр
.
(5.4)
43
0
Рис. 5.1
x
44.
§5. Одномерное движение. Непрерывный спектрВ формулах (5.3) и (5.4) jпад , jотр , jпрош – плотности потока вероятности, определяемые формулой (4.17), для падающих, отраженных и прошедших частиц
соответственно. Причем, пад и отр вычисляются при x → −∞ , а прош – при
∞. В рассматриваемом здесь стационарном случае (в случае установившегося потока частиц) плотность потока вероятности не зависит от времени и
определяется волновыми функциями стационарных состояний
:
⎛ * dψ
dψ * ⎞
−
ψ
ψ
(5.5)
⎜
⎟.
dx ⎠
2Mi ⎝ dx
Таким образом, для определения коэффициентов отражения и прохождения необходимо решить стационарное уравнение Шрёдингера и найти jпад ,
jотр , jпрош . Из физических соображений очевидно, что сумма коэффициента
j=
отражения и прохождения должна быть равна единице:
R + D = 1.
Задача 5.2. Найти коэффициент отражения частицы, налетающей на
“потенциальную ступеньку”
I
U
U0
U
II
(x) =
⎧ 0, при x < 0,
⎨
⎩U 0 , п р и x > 0 .
Энергия частицы E < U 0 (рис. 5.2).
Решение. Обозначим область слева от
ступеньки ( x < 0 ) цифрой I и все решения
для этой области будем отмечать индексом
E
0) обо1. Область справа от ступеньки (
x значим цифрой II и будем отмечать соот0
ветствующие ей решения индексом 2.
Рис. 5.2
Уравнение Шрёдингера (5.1) для частицы в таком силовом поле имеет вид:
d 2ψ1 ( x ) 2M
+ 2 Eψ1 ( x ) = 0 (в области I),
dx2
и
d 2ψ 2 ( x ) 2M
− 2 (U0 − E )ψ 2 ( x ) = 0 (в области II).
dx2
Введем обозначения
k1 =
2ME
и k2 =
2M (U 0 − E )
,
и запишем уравнения Шрёдингера для областей I и II в новых обозначениях:
44
45.
§5. Одномерное движение. Непрерывный спектрd 2ψ 1 ( x )
+ k12ψ 1 ( x ) = 0 ,
2
dx
d 2ψ 2 ( x )
− k22ψ 2 ( x ) = 0.
2
dx
Решениями данных уравнений являются
ψ 1 ( x ) = A1 exp ( ik1 x ) + B1 exp ( −ik1 x ) ,
ψ 2 ( x ) = A2 exp ( k 2 x ) + B2 exp ( − k 2 x ) .
Первое слагаемое в волновой функции
описывает плоскую волну,
распространяющуюся вдоль оси из −∞ к ступеньке, т.е. слева направо (падающая волна). Аналогично, второе слагаемое описывает плоскую волну, распространяющуюся вдоль оси в отрицательном направлении (отражённая волна).
Поскольку волновая функция должна быть ограниченной, а первое слагаемое в выражении для волновой функции
неограниченно возрастает
при
∞, то необходимо потребовать, чтобы коэффициент
перед этим
слагаемым был равен нулю.
В силу того, что потенциальная ступенька имеет конечную высоту, волновая функция на границе раздела областей I и II должна быть не только непрерывной, но и гладкой, т.е. иметь непрерывную производную. Приравнивание волновых функций и их производных на границе раздела двух областей, в
которых волновая функция имеет разный вид, получило название условий
сшивания. В данном случае условия сшивания имеют вид
dψ 1
dψ 2
ψ 1 (0) =ψ 2 (0) и
x =0 =
x =0 ,
dx
dx
или
A1 + B1 = B2 и ik1 A1 − ik1B1 = −k2 B2 .
(5.6)
Уравнения (5.6) позволяют выразить коэффициенты B1 и
через коэф-
фициент
– амплитуду падающей волны. Поскольку в подобных задачах все
имеющие физический смысл величины, такие, например, как коэффициенты
отражения, прохождения и т.д., выражаются через отношения коэффициентов
B1 и B2 (или аналогичных им) к A1 , то без потери общности можно положить
=1. При этом для
и
из (5.6) получаем:
k − ik2
2k1
B1 = 1
.
, B2 =
k1 + ik2
k1 + ik2
Таким образом, волновые функции частицы равны:
k − ik2
ψ 1 ( x ) = exp ( ik1 x ) + 1
exp ( −ik1 x ) , x < 0,
k1 + ik2
45
46.
§5. Одномерное движение. Непрерывный спектрψ 2 ( x) =
2k1
exp ( −k2 x ) , x > 0.
k1 + ik2
Отметим, что система уравнений (5.6) имеет решения при любых значениях k1 и k2 , т.е. при любых значениях энергии . Это означает, что частица
обладает непрерывным энергетическим спектром.
Используя (5.5), найдем плотности потоков вероятности:
jотр
*
⎛ * dψ пад
⎞
dψ пад
k1
−ψ пад
jпад =
,
⎜ψ пад
⎟=
2Mi ⎝
dx
dx ⎠ M
*
⎛ * dψ отр
⎞
dψ отр
k1 k1 − ik2
k
=
−ψ отр
= 1,
⎜⎜ψ отр
⎟⎟ =
2Mi ⎝
dx
dx ⎠ M k1 + ik2 M
где
ψ пад = exp ( ik1 x ) , ψ отр ( x ) =
k1 − ik2
exp ( −ik1 x ) .
k1 + ik2
Коэффициент отражения примет значение:
R=
jотр
jпад
= 1.
Полученный результат означает, что как и в классической механике,
частицы со стопроцентной вероятностью отразятся от потенциальной ступеньки. Отличие от классического случая в данной задаче заключается в том, что
частица с отличной от нуля вероятностью может оказаться в области II, т.е.
, а с ней и плотность
под барьером. Действительно, волновая функция
вероятности нахождения частицы в области барьера ψ 2 ( x ) , отличны от нуля
2
и убывают по экспоненциальному закону с возрастанием . Поэтому хоть отражение и является полным, оно не обязательно происходит на границе раздела областей I и II. С определенной вероятностью частица может проникнуть в
область II и затем выйти из нее*. ♦
Задача 5.3. Найти коэффициенты отражения и прохождения частицы в
случае прямоугольного потенциального барьера высотой U 0 и шириной :
U
(x ) =
⎧ 0, при x < 0 или x > a ,
⎨
⎩ U 0 , при 0 < x < a.
Энергия частицы E < U 0 (рис. 5.3).
Решение. Обозначим цифрой I область слева от барьера, цифрой II – об*
Аналогом этого эффекта является полное внутреннее отражение в оптике, при котором
световая волна выходит за границы раздела сред.
46
47.
§5. Одномерное движение. Непрерывный спектри цифрой III – область справа
ласть 0
от барьера. Соответствующие указанным областям волновые функции снабдим индексами 1, 2
и 3. Будем считать, что частица приближается к
барьеру со стороны отрицательных значений ,
т.е. движется слева направо.
Уравнения Шрёдингера для областей I, II
и III имеют вид:
U
I
U0
II
III
E
d ψ1 ( x)
+ k12ψ 1 ( x ) = 0 , область I,
2
dx
d 2ψ 2 ( x )
− k22ψ 2 ( x ) = 0 , область II,
2
dx
d 2ψ 3 ( x )
+ k12ψ 3 ( x ) = 0 , область III,
2
dx
2
a
0
Рис. 5.3
x
где
k1 =
2ME
и k2 =
2M (U 0 − E )
.
Волновые функции, являющиеся решениями данных уравнений, запишем следующим образом:
ψ 1 ( x ) = A1 exp ( ik1 x ) + B1 exp ( −ik1 x ) ,
ψ 2 ( x ) = A2 exp ( k 2 x ) + B2 exp ( − k 2 x ) ,
ψ 3 ( x ) = A3 exp ( ik1 x ) + B3 exp ( −ik1 x ) .
Первое слагаемое в волновой функции
соответствует падающей на
барьер волне. Не снижая общности задачи, положим A1 = 1 (см. задачу 5.2).
Член
представляет собой отраженную волну, а член A3 exp ( ik1 x ) –
прошедшую. Второе слагаемое в выражении для волновой функции
есть
плоская волна, движущаяся справа налево. Однако, принимая во внимание,
что в области III может распространяться только прошедшая волна, коэффициент
необходимо выбрать равным нулю (т.к. нет барьеров на пути прошедшей волны).
Условия непрерывности волновых функций и их производных на грани0и
, приводят к системе четырех уравнений с
цах барьера, т.е. при
четырьмя неизвестными – коэффициентами B1 , A2 , B2 , A3 :
47
48.
§5. Одномерное движение. Непрерывный спектр1 + B1 = A2 + B2 ,
⎧
⎪ ik − ik B = k A − k B ,
⎪
1
1 1
2 2
2 2
(5.7)
⎨
k2 a
− k2 a
ik1a
A
e
+
B
e
=
A
e
,
2
2
3
⎪
k2 a
− k2 a
⎪⎩ k2 A2e − k2 B2e
= ik1 A3eik1a .
и , а следовательно, и
Эта система имеет решения при любых значениях
при любых значениях энергии частицы , т.е. энергетический спектр частицы
является непрерывным.
прошедшей волны,
Решая систему уравнений (5.7) для амплитуды
имеем:
4ik1k2 exp ( −ik1a )
A3 =
.
2
2
+
−
−
−
k
ik
k
a
k
ik
k
a
exp
exp
( 1 2)
( 2 ) ( 1 2)
( 2 )
Теперь рассчитаем плотности потоков вероятности для падающей на
барьер и прошедшей через него волн:
k
k
2
jпад = 1 , jпрош = 1 A3 .
M
M
Коэффициент прохождения частицы через барьер:
D=
jпрош
jпад
−1
2
= A3
⎡ ⎛ k 2 + k 2 ⎞2
⎤
2
k
a
= ⎢1 + ⎜ 1
sh
⎥ .
(
)
2
⎟
k
k
2
⎢⎣ ⎝ 1 2 ⎠
⎥⎦
Коэффициент отражения
R = 1− D .
В случае, когда ширина барьера a удовлетворяет условию k2 a
exp ( − k2 a )
1,
1 и гиперболический синус можно заменить экспонентой
1
sh ( k2 a ) ≈ exp ( k2 a ) ,
2
коэффициент прохождения частицы через барьер примет вид:
D=
16k12 k22
(k
2
1
+k
)
2 2
2
exp ( −2k2 a ) .
, получим:
⎡ 2a
⎤
2M (U 0 − E ) ⎥ ,
D = D0 exp ⎢ −
⎣
⎦
Подставляя сюда выражения для
и
где коэффициент
D0 = 16
E⎛
E⎞
1
−
⎜
⎟
U0 ⎝ U0 ⎠
48
(5.8)
49.
§5. Одномерное движение. Непрерывный спектрявляется медленно изменяющейся функцией отношения E U 0 , значение которой в практически важных случаях близко к единице.
Таким образом, основной вклад в коэффициент дает экспонента в выражении (5.8). Отсюда следует, что коэффициент прохождения сильно (экспоненциально) зависит от ширины барьера a , массы частицы M и разности
(U 0 − E ) .
Прохождение частицы через потенциальный барьер, высота которого
превышает энергию частицы, получило название туннельного эффекта. ♦
Задача 5.4. Используя формулу (5.8) получить приближенное выражение для коэффициента прохождения частицы через потенциальный барьер
U
произвольной формы.
Решение. Представим потенциальный
барьер в виде последовательности большого
числа узких прямоугольных потенциальных
барьеров, расположенных один за другим E
(рис. 5.4). Будем считать, что барьер имеет достаточно плавную форму, т.е. полагать, что его
x2
x1
x
0
высота на расстоянии, сравнимом с длиной
Рис. 5.4
2π
( p = 2ME – импульс частицы), изменяется
волны де Бройля частицы λ =
p
незначительно. Кроме того, пренебрежем надбарьерным отражением частицы.
Волна де Бройля, прошедшая через i-й прямоугольный барьер, представляет собой волну, падающую на
1 -й барьер и т.д. Вероятность прохождения частицы через цепочку последовательно расположенных потенциальных
барьеров равна произведению вероятностей прохождения через каждый из
равен произведению
барьеров. Таким образом, коэффициент прохождения
коэффициентов прохождения для каждого барьера:
⎡ 2Δxi
⎤
D = ∏ Di ≈ ∏ exp ⎢ −
2 M (U ( xi ) − E ) ⎥ =
⎣
⎦
i
i
2Δxi
⎡
⎤
2 M (U ( xi ) − E ) ⎥ ,
= exp ⎢ −∑
⎣ i
⎦
где Δxi - ширина i -го барьера, а U ( xi ) - его высота. Переходя в последней
формуле в пределе Δxi → 0 от суммирования к интегрированию, получаем:
⎡ 2 x2
⎤
D = exp ⎢ − ∫ 2M (U ( x ) − E )dx ⎥ ,
x1
⎣⎢
⎦⎥
49
50.
§5. Одномерное движение. Непрерывный спектргде x1 и x2 - значения координат, при которых U ( x ) = E (см. рис. 5.4). ♦
Задачи для самостоятельного решения
5.5. Для свободной частицы, движение которой ограничено непроницаемой
стенкой
(x) =
U
⎧ 0, при x > 0,
⎨
⎩∞ , при x < 0,
найти волновые функции стационарных состояний.
5.6. Найти коэффициенты отражения и прохождения частицы, налетающей на
“потенциальную ступеньку”
U
(x) =
⎧ 0, при x < 0,
⎨
⎩U 0 , п р и x > 0 .
Энергия частицы E > U 0 .
5.7. Найти коэффициент прохождения частицы в случае прямоугольного потенциального барьера высотой U 0 и шириной a :
U
(x ) =
⎧ 0, при x < 0 или x > a ,
⎨
⎩ U 0 , при 0 < x < a.
Энергия частицы E > U 0 . Определить также значения энергии частицы, при
которых она будет проходить через данный барьер без отражения.
5.8. Доказать независимость значения коэффициента отражения при данной
энергии от направления падения частицы на силовой центр.
Ответы к задачам для самостоятельного решения
1
⎛ 2M ⎞ 4 ⎛ 2ME
5.5. ψ ( x ) = ⎜ 2 2 ⎟ sin ⎜
⎝π E ⎠
⎝
⎞
x⎟.
⎠
2
⎛
U
U0 ⎞
1− 0
⎜1− 1−
⎟
E ⎟ , D=4
E
5.6. R = ⎜
⎛
U0 ⎟
⎜
U0 ⎞
⎜1+ 1−
⎟
⎜1 + 1 −
⎟
E ⎠
⎝
E ⎠
⎝
2M ( E − U 0 )
⎡ U 02 sin 2 ( ka ) ⎤
π 2 2n2
+ U0
5.7. D = ⎢1 +
; D = 1 при E =
⎥ , k=
2
Ma
2
E
E
U
4
−
(
)
0
⎣
⎦
−1
(n = 1,2,3...).
50
51.
§6. Частицы в потенциальных ямах§ 6. ЧАСТИЦЫ В ПОТЕНЦИАЛЬНЫХ ЯМАХ
В этой и следующей главах мы рассмотрим тот случай, когда спектр
значений энергии частицы является дискретным. Аналогом этого состояния в
классической механике является финитное движение.
Задача 6.1. Найти собственные значения энергии и собственные функции частицы, находящейся в потенциальной яме шириной с бесконечно высокими стенками:
U
(x ) =
⎧∞ , при x < 0 или x > a,
⎨
0, при 0 < x < a.
⎩
Решение. Внутри потенциальной ямы ( 0 < x < a ) уравнение Шрёдингера
имеет вид
d 2ψ ( x )
+ k 2ψ ( x) = 0, k 2 = 2ME /
2
dx
Его решение можно записать следующим образом:
ψ ( x ) = A sin kx + B cos kx,
где A и B – подлежащие определению константы.
2
.
Бесконечно высокие потенциальные стенки моделируют физическую ситуацию, в которой за счет сил отталкивания частица не может оказаться вне
области 0 < x < a . Поэтому волновая функция частицы в точках x = 0 и x = a
должна обращаться в нуль. Из условия
ψ (0) = 0
следует, что B = 0 . Условие
ψ (a ) = 0
приводит к равенству
sin ka = 0,
откуда
ka = π n (n = 1,2,3,...).
Значение n = 0 здесь отброшено, поскольку при этом волновая функция частицы тождественно равна нулю. Учитывая, что
k 2 = 2 ME / 2 ,
находим собственные значения энергии частицы:
2 2 2
π n
En =
.
2 Ma 2
51
(6.1)
52.
§6. Частицы в потенциальных ямахψn
Таким образом, энергетический
спектр частицы оказывается дискретным
с бесконечным количеством уровней
энергии. Число n , определяющее энергию частицы в потенциальной яме, называется квантовым числом, а соответствующее ему значение E n – уровнем
E3
E2
энергии.
Состояние частицы, в котором она
x обладает наименьшей энергией, называется основным состоянием. В данной задаче
E1
0
a
Рис. 6.1
энергия основного состояния:
E1 =
π2
2
.
2 Ma 2
Все остальные состояния являются возбужденными: значение n = 2 отвечает первому возбужденному состоянию, значение n = 3 – второму возбужденному состоянию и т.д.
Для определения константы A воспользуемся условием нормировки волновых функций дискретного спектра. Имеем:
a
∫| A|
2
0
⎛πn ⎞
x ⎟ dx = 1.
sin 2 ⎜
⎝ a ⎠
Отсюда
2
,
a
и, следовательно, нормированные волновые функции частицы
A=
2 ⎛πn ⎞
x ⎟.
sin ⎜
(6.2)
a
⎝ a ⎠
Волновые функции первых трех состояний схематично показаны на рис. 6.1. ♦
Задача 6.2. Найти дисперсии координаты x и импульса p в случае частицы, находящейся в потенциальной яме шириной a с бесконечно высокими
стенками.
Решение. Используя определение среднего значения, и учитывая, что
волновая функция частицы в бесконечно глубокой потенциальной яме имеет
вид (6.2), находим:
ψn =
x = ψn x ψn
2
a
⎛πn ⎞
x ⎟ dx = ,
= ∫ψ n xψ n dx = ∫ x sin 2 ⎜
a0
2
⎝ a ⎠
0
a
a
52
53.
§6. Частицы в потенциальных ямахx = ψn x ψn
2
2
2 2 2 πn
a2
a2
= ∫ x sin ( x) dx = − 2 2 .
3 2π n
a0
a
a
Дисперсия координаты
a2
a2
( Δ x) = x − x = − 2 2 .
12 2π n
Теперь найдем, что
2
p = ψn p ψn
p
2
2
2
2
⎛ π n ⎞ d ⎡ ⎛ π n ⎞⎤
x⎟
x ⎟ dx = 0,
= −i ∫ sin ⎜
sin ⎜
a 0 ⎝ a ⎠ dx ⎢⎣ ⎝ a ⎠ ⎥⎦
a
2
2
π 2 2n2
⎛ π n ⎞ d ⎡ ⎛ π n ⎞⎤
sin ⎜
sin ⎜
,
x⎟
x ⎟ dx =
a ∫0 ⎝ a ⎠ dx 2 ⎢⎣ ⎝ a ⎠⎥⎦
a2
a
= ψn p ψn = −
2
и, значит,
( Δp )
2
= p − p
2
=
π 2 2n2
. ♦
a2
Задача 6.3 Найти собственные значения энергии связанных состояний
частицы, находящейся в потенциальной яме с конечными стенками (рис. 6.2):
⎧U , при x < 0 или x > a,
U ( x) = ⎨ 0
0, при 0 < x < a.
⎩
2
Решение. Для существования связанных состояний частицы (состояний
дискретного спектра), полная энергия
последней должна быть меньше U 0 .
U
Разобьем потенциал на три области
I, II и III так, как показано на рисунке.
U0
E
Волновые функции частицы в областях I,
II, III будем обозначать индексами 1 2, 3
0
соответственно. Уравнения Шредингера
Рис. 6.2
в каждой из областей имеют вид:
d 2ψ 1 ( x)
− k12ψ 1 ( x) = 0, в области I,
2
dx
2
d ψ 2 ( x)
+ k22ψ 2 ( x) = 0, в области II,
2
dx
2
d ψ 3 ( x)
− k12ψ 3 ( x) = 0, в области III,
2
dx
где
k1 =
2M (U 0 − E )
53
и k2 =
2ME
III
II
I
.
a
x
54.
§6. Частицы в потенциальных ямахРешения этих уравнений – волновые функции частицы – можно записать
следующим образом:
ψ 1 ( x) = A1e k1x + B1e− k1x ,
ψ 2 ( x) = A2eik x + B2e− ik x ,
2
2
ψ 3 ( x) = A3ek x + B3e− k x .
1
1
Поскольку волновые функции должны быть ограниченными, следует положить B1 = 0 и A3 = 0 . Действительно, в области I при x → −∞ неограниченно
возрастает член B1e − k1x , а в области III к бесконечности стремится A3e k1x при
x → +∞ .
Далее воспользуемся условиями непрерывности волновой функции и ее
первой производной на границах областей I и II, II и III, т.е. при x = 0 и при
x = a . Выпишем эти условия:
ψ 1 x=0 = ψ 2 x=0 , ψ 1′ x=0 = ψ 2′ x=0 ,
ψ 2 x =a = ψ 3 x =a ,
ψ 2′ x=a = ψ 3′ x=a ,
или
A1 = A2 + B2 ,
(6.3)
k1 A1 = ik2 A2 − ik2 B2 ,
(6.4)
A2 eik2 a + B2e − ik2a = B3e − k1a ,
ik 2 A2eik2a − ik 2 B2e − ik2a = − k1 B3e − k1a .
(6.5)
(6.6)
Из (6.3) и (6.4) получаем:
B2 =
ik2 − k1
A2 .
ik2 + k1
С другой стороны уравнения (6.5) и (6.6) приводят к равенству:
ik + k
B2 = 2 1 e2ik2a A2 .
ik2 − k1
(6.7)
(6.8)
Приравнивая правые части равенств (6.7) и (6.8), имеем
ik2 − k1 ik2 + k1 2ik2a
=
e ,
ik2 + k1 ik2 − k1
или, что то же самое,
ik2 − k1 −ik2a ik2 + k1 ik2a
e
=
e .
ik2 + k1
ik2 − k1
Отсюда после простых алгебраических преобразований можно получить:
2k k
tg ( k2 a ) = − 2 1 2 2 .
(6.9)
k1 − k2
54
55.
§6. Частицы в потенциальных ямахС учетом введенных обозначений для k1 и k2 соотношение (6.9) принимает вид
2 E (U 0 − E )
⎛ 2ME ⎞
tg ⎜
a⎟ = −
.
U
2
E
−
0
⎝
⎠
Из этого уравнения определяются собственные значения энергии системы E . Данное уравнение – трансцендентное. Его решения можно найти, например, графически. Для этого удобнее воспользоваться уравнением (6.9). Используя тригонометрическую формулу, перепишем левую часть (6.9) следующим образом:
⎛k a⎞
2 tg ⎜ 2 ⎟
⎝ 2 ⎠ .
tg ( k2 a ) =
⎛k a⎞
1 − tg 2 ⎜ 2 ⎟
⎝ 2 ⎠
⎛k a⎞
Разрешая теперь уравнение (6.9) относительно tg ⎜ 2 ⎟ , находим два решения:
⎝ 2 ⎠
⎛k a⎞ k
tg ⎜ 2 ⎟ = 1 ,
⎝ 2 ⎠ k2
(6.10)
k
⎛k a⎞
ctg ⎜ 2 ⎟ = − 1 .
k2
⎝ 2 ⎠
Далее воспользуемся равенствами
(6.11)
⎛k a⎞
cos ⎜ 2 ⎟ = ±
⎝ 2 ⎠
2 2 k2 a
,
=±
=±
2
2
2
2
MU
a
k
a
k
k
+
⎛
⎞
0
1
2
1 + tg 2 ⎜ 2 ⎟
⎝ 2 ⎠
⎛k a⎞
sin ⎜ 2 ⎟ = ±
⎝ 2 ⎠
2 2 k2 a
,
=±
=±
MU 0 a 2 2
k12 + k22
2 ⎛ k2 a ⎞
1 + ctg ⎜
⎟
⎝ 2 ⎠
1
k2
1
k2
и введем обозначения
2 2
ξ=
MU 0 a 2
и
z=
k2 a
.
2
В результате из (6.10) и (6.11) получаем
cos z = ±ξ z ,
sin z = ±ξ z .
(6.12)
(6.13)
Причем, в силу (6.10) и (6.11) корни первого уравнение должны браться в области, где tg z > 0 , а корни второго уравнения – в области tg z < 0 . Схематично
графические решения (в области z ∈ [ 0, 2π ] ) уравнений (6.12) и (6.13) пред55
56.
§6. Частицы в потенциальных ямахставлены на рис. 6.3 (а) и (б) соответственно. Нечетные уровни (первый, третий, пятый и т.д.) определяются уравнением (6.12), а четные (второй, четвертый, шестой и т.д.) - уравнением (6.13). Из рисунка 6.3 (а) следует, что в одномерном случае всегда (при любых параметрах ямы – ширине и высоте) имеется, по крайней мере, один энергетический уровень (одно решение). Кроме того, число уровней (при ξ ≠ 0 ) конечно.
f
f
f=sinz
f=ξz
0
π
z1
2π z
π
0
z2 2π
z
f = - ξz
f=cosz
б
а
Рис. 6.3
Если zn ( n = 1,2,3,... – корни уравнений (6.12) и (6.13), то в соответствии
с введенными обозначениями собственные значения энергии частицы
2 2 zn2
En =
. ♦
Ma 2
Одномерная потенциальная яма
⎧0, при x < 0 или x > a,
U ( x) = ⎨
⎩ −U 0 , при 0 < x < a.
2 MU 0 a 2
при условии
1 может быть аппроксимирована потенциалом δ -ямы:
2
U ( x) = −γδ ( x) , где
+∞
−γ = ∫ U ( x)dx < 0 .
−∞
Задача 6.4. Найти энергию связанного состояния и соответствующую
волновую функцию для частицы в δ -образной потенциальной яме
U ( x) = −γδ ( x) .
Решение. Поскольку нас интересуют связанные состояния, то полная
энергия частицы должна быть меньше нуля. При этом уравнение Шредингера
для частицы
d 2ψ 2M
+ 2 ( − E + γδ ( x) )ψ = 0
(6.14)
dx 2
56
57.
§6. Частицы в потенциальных ямахвсюду, за исключением точки
0, имеет вид
d 2ψ
− k 2ψ = 0 ,
2
dx
(6.15)
где
2M E
k=
.
Решение уравнения (6.15) есть
ψ = Aekx + Be− kx .
Поскольку волновая функция должна быть ограниченной, следует положить A = 0 в области x > 0 , а в области x < 0 необходимо, чтобы B = 0 . Таким
образом,
ψ = Be − kx , если x > 0 ,
ψ = Ae kx , если x < 0 .
Непрерывность волновой функции приводит к следующему условию
сшивания в точке x = 0 :
ψ (+0) = ψ (−0) ,
откуда находим, что
(6.16)
A= B.
dψ ( x)
Однако первая производная волновой функции
≡ ψ ′( x) в данной задаче
dx
не будет непрерывной, так как в точке x = 0 потенциальная энергия обращается в бесконечность (см. § 5). Для нахождения условия, накладываемого на
производную волновой функции проинтегрируем (6.14) по ε -окрестности
точки x = 0 и устремим ε → 0 . Получим
2M γ
ψ ′ ( +0 ) − ψ ′ ( −0 ) = − 2 ψ (0) ,
или
− kA − kB = −
2M γ
2
A.
Учитывая (6.16), отсюда имеем
k=
Mγ
2
,
а, значит,
Mγ 2
.
2 2
Таким образом, в δ -яме всегда имеется один и только один энергетический уровень.
E=−
57
58.
§6. Частицы в потенциальных ямахВыражение для волновой функции справедливое и в области x > 0 , и в
области x < 0 можно записать следующим образом:
ψ = Ae − k x .
Для нахождения A воспользуемся условием нормировки
+∞
∫
2
A e
−2 k x
dx = 1.
−∞
Поскольку
+∞
∫
−∞
2
2
A e
−2 k x
+∞
⎛ 0 2 kx
⎞ A
dx = A ⎜ ∫ e dx + ∫ e −2 kx dx ⎟ =
,
k
0
⎝ −∞
⎠
2
то
A = k.
Следовательно, волновая функция частицы
Mγ
⎛ Mγ ⎞
exp ⎜ − 2 x ⎟ . ♦
⎝
⎠
К одномерной сводится задача о движении системы в пространстве, если
ее потенциальная энергия может быть разбита на сумму функций, каждая из
которых зависит только от одной из координат, т.е.
U ( x, y, z ) = U ( x) + U ( y ) + U ( z ).
В этом случае собственные значения энергии системы равны сумме собственных значений E x , E y , E z вдоль каждой из координат:
ψ = ke− k x =
E = Ex + E y + Ez ,
(6.17)
а волновые функции системы определяются произведением одномерных волновых функций ψ ( x), ψ ( y ), ψ ( z ) :
ψ = ψ ( x)ψ ( y )ψ ( z ) .
(6.18)
Отметим, что данное свойство верно как для дискретного, так и для непрерывного спектров.
Задача 6.5. Найти собственные значения энергии и собственные функции частицы, находящейся в трехмерной потенциальной яме с бесконечно высокими стенками ( U = 0 при 0 < x < a, 0 < y < b, 0 < z < c , и U = ∞ вне этой
области).
Решение. В соответствии с формулами (6.1) и (6.2)
2 2 2
2 2 2
2 2 2
π n1
π n2
π n3
Ex ≡ En1 =
E
E
E
E
,
≡
=
,
≡
=
;
y
n
z
n
2
3
2Ma 2
2Mb 2
2 Mc 2
ψ n ( x) =
1
2 ⎛ π n1 ⎞
2 ⎛ π n2
x ⎟ , ψ n2 ( y ) =
sin ⎜
sin ⎜
a ⎝ a ⎠
b ⎝ b
58
2 ⎛ π n3 ⎞
⎞
y ⎟ , ψ n3 ( z ) =
z⎟.
sin ⎜
c
⎠
⎝ c ⎠
59.
§6. Частицы в потенциальных ямахИспользуя (6.17) и (6.18), находим собственные значения энергии и волновые функции системы:
π 2 ⎛ n12
n22 n32 ⎞
En1n2n3 = En1 + En2 + En3 =
⎜ + + ⎟,
2M ⎝ a 2 b2 c 2 ⎠
ψ n n n ( x, y , z ) = ψ n ( x )ψ n ( y )ψ n ( z ) =
2
1 2 3
=
1
8
⎛πn ⎞ ⎛πn
sin ⎜ 1 x ⎟ sin ⎜ 2
abc ⎝ a ⎠ ⎝ b
2
3
⎞ ⎛πn ⎞
y ⎟ sin ⎜ 3 z ⎟ . ♦
⎠ ⎝ c ⎠
Задачи для самостоятельного решения
6.6. Доказать, что в случае одномерного движения состояния дискретного
спектра не вырождены.
6.7. Показать, что если гамильтониан системы с дискретным спектром удовлетворяет условию
H (− x) = H ( x) ,
то волновые функции системы обладают определенной четностью, т.е. могут
быть либо только четными, либо только нечетными.
6.8. Частица находится в одномерной потенциальной яме с конечными стенками:
⎧U , при x < 0 или x > a,
U ( x) = ⎨ 0
0, при 0 < x < a.
⎩
Построить волновые функции частицы ψ ( x) и распределения плотности веро2
ятности ψ ( x) для первых трех энергетических уровней.
6.9. Частица находится в потенциале
⎧ ∞, при x < 0,
⎪
U ( x) = ⎨0, при 0 < x < a,
⎪U , при x > a.
⎩ 0
Найти энергии связанных состояний частицы.
6.10. Найти средние значения потенциальной и кинетической энергии для частицы, находящейся в потенциальной δ -яме
U ( x) = −γδ ( x) (γ > 0).
6.11. Частица массы m находится в потенциале
∞, при x < 0 и x > a,
⎧
⎪
U ( x) = ⎨
a⎞
⎛
−
−
αδ
x
⎜
⎟ , при 0 < x < a (α > 0).
⎪
2
⎝
⎠
⎩
59
60.
§6. Частицы в потенциальных ямахНайти, при каком значении ширины a не будет связанного состояния с энергией E<0 (т.е. в δ -яме отсутствет энергетический уровень).
6.12. Найти кратность k вырождения 5-го квантового уровня для частицы в а)
двумерной квадратной и б) трехмерной кубической потенциальных ямах с
бесконечно высокими стенками.
6.13. Частица находится во втором возбужденном состоянии в двумерной
квадратной потенциальной яме с абсолютно непроницаемыми стенками (U = 0
при 0 < x < a, 0 < y < a, и U = ∞ вне этой области). Найти вероятность P обнаружения частицы в области 0 < x < a , 0 < y < a .
3
3
Ответы к задачам для самостоятельного решения
2 2
n
z
, n = 0,1, 2,...; где zn - корень уравнения
2M
z
.
tg( za ) = −
2 MU 0
2
−z
2
6.9. En =
6.10. U = −
Mγ 2
2
,
Mγ 2
.
T =
2 2
⎛ βa ⎞
mα ⎛ ⎛
a⎞
⎞
th
,
x
E
β
αδ
=
−
−
где
⎜
⎟
⎜
⎟
2
2 ⎜
⎟.
2⎠
⎝ ⎝
⎠
⎝ 2 ⎠
6.12. а) k = 2; б) k = 1.
6.11. β =
mα
2
⎛1
3⎞
6.13. P = ⎜ +
⎟ .
3
8
π
⎝
⎠
60
61.
§7. Гармонический осциллятор§ 7.
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
Гармоническим осциллятором называется частица массы M , совершающая одномерное движение в потенциальном поле
kx 2 M ω 2 x 2
=
,
U ( x) =
2
2
где k – коэффициент квазиупругой силы, ω = k M – собственная частота осциллятора.
Задача 7.1. Найти собственные значения энергии и волновые функции
гармонического осциллятора.
Решение. Поскольку при x → ±∞ потенциальная энергия обращается в
бесконечность, то частица будет совершать финитное движение, а следовательно, энергетический спектр осциллятора является дискретным.
Уравнение Шредингера в данном случае имеет вид:
d 2ψ 2M ⎛
M ω 2 x2 ⎞
+
−
E
⎟ψ = 0 .
2 ⎜
2
dx 2
⎝
⎠
Введем вместо координаты
безразмерную переменную
x
ξ= ,
x0
(7.1)
где x0 – некоторая величина, задающая масштаб координаты*
.
x0 =
(7.2)
Mω
В результате получим дифференциальное уравнение
d 2ψ ⎛ 2 E
⎞
(7.3)
+⎜
− ξ 2 ⎟ψ = 0 .
2
dξ
⎝ ω
⎠
Для больших значений ξ ( ξ → ±∞ ) асимптотическими решениями дан-
ного уравнения являются функции e
подстановкой. Действительно,
±ξ
2
2
. В этом можно убедиться прямой
⎛ ±ξ ⎞
d ⎜e 2 ⎟
2
2
⎝
⎠ = ξ 2 ± 1 e±ξ 2 ≈ ξ 2e±ξ 2 .
( )
dξ 2
2
2
Здесь мы учли, что ξ 2
*
1 при ξ → ±∞ . Теперь, пренебрегая в (7.3) членом
Величина x0 имеет смысл классической границы для основного состояния осциллятора.
61
62.
§7. Гармонический осциллятор2E
ω
по сравнению с ξ 2 , получаем тождество:
ξ2
ξ2
d 2ψ ⎛ 2 E
2⎞
2 ± 2
2 ± 2
+⎜
− ξ ⎟ψ ≈ ξ e
−ξ e
= 0.
dx 2 ⎝ ω
⎠
Поскольку нас интересуют только конечные решения, экспонента со
знаком плюс в показателе должна быть отброшена. Таким образом, решение
уравнения (7.3) ведет себя при ξ → ±∞ как e
вольном ξ будем искать решение в виде
ψ =e
−ξ
2
2
−ξ
2
f (ξ ) .
2
. В связи с этим при произ-
(7.4)
Подставляя (7.4) в (7.3), получаем:
d 2 f (ξ )
df (ξ )
(7.5)
− 2ξ
+ λ f (ξ ) = 0 ,
2
dξ
dξ
где введено обозначение
⎛ 2E ⎞
λ =⎜
− 1⎟ .
(7.6)
⎝ ω ⎠
Из требования конечности ψ следует, что функция f (ξ ) должна быть конечной при всех конечных значениях ξ . Поскольку движение частицы финитное,
то на бесконечности волновая функция (7.4) должна обращаться в нуль. Удовлетворяющие указанным выше условиям решения уравнения (7.5) существуют
лишь при (см. приложение 4)
λ = 2n (n = 0,1,2,...).
Из (7.6) следует, что собственные значения энергии при этом равны
1⎞
⎛
En = ω ⎜ n + ⎟ (n = 0,1,2,...) .
(7.7)
2
⎝
⎠
Энергетические уровни гармонического осциллятора эквидистантны,
т.е. расстояния между любыми соседними уровнями одинаковы и равны
Δ E = En+1 − En = ω.
Можно отметить следующие отличия энергетического спектра квантового
осциллятора от классического:
1. энергетический спектр квантового осциллятора является дискретным, т.е. в
отличие от классического случая частица не может иметь произвольные
значения энергии;
2. энергия основного состояния квантового осциллятора отлична от нуля и
равна ω ;
2
3. энергия квантового осциллятора в отличие от классического зависит от час62
63.
§7. Гармонический осциллятортоты, а не от амплитуды, которая в квантовой теории вообще не определена.
Собственными функциями уравнения (7.5) являются полиномы Эрмита, определяемые формулой (П4.12)
n
2
n ξ2 d
(n = 0,1, 2,...).
H n (ξ ) = (−1) e
e −ξ
n
dξ
В соответствии с (7.4) собственные функции осциллятора имеют вид:
( )
−ξ
2
(7.8)
ψ n = Cn e 2 H n (ξ ) ,
где C n – нормировочные постоянные.
Функции (7.8) выражены через безразмерную переменную ξ . Возвращаясь к переменной x , находим:
2
−x
2
⎛ x⎞
ψ n = Cne 2 x0 H n ⎜ ⎟ .
⎝ x0 ⎠
Так как спектр гармонического осциллятора является дискретным, собственные функции ψ n должны быть нормированы на единицу, т.е.
+∞
∫C
2
n
e
−x
2
2
x02
−∞
⎛ ⎛ x ⎞⎞
⎜ H n ⎜ ⎟ ⎟ dx = 1.
⎝ ⎝ x0 ⎠ ⎠
Используя (П4.14), получаем
Cn =
1
2 n! x0 π
n
.
Таким образом, волновые функции гармонического осциллятора
ψn =
1
2n n! x0 π
e
−x
2
2 x02
⎛ x⎞
Hn ⎜ ⎟ .
⎝ x0 ⎠
Поскольку каждому значению энергии En соответствует только одна волновая функция ψ n , то уровни энергии осциллятора являются невырожденными. ♦
Задача 7.2. Найти энергетические уровни и волновые функции плоского
изотропного осциллятора, т.е. частицы движущейся в потенциальном поле
mω 2 2
U ( x, y ) =
x + y 2 ).
(
2
Какова кратность вырождения уровней?
Решение. Поскольку потенциальная энергия представляет собой сумму
функций, каждая из которых зависит только от одной из координат, т.е.
U ( x, y ) = U ( x) + U ( y ),
где
63
64.
§7. Гармонический осцилляторmω 2 x 2
mω 2 y 2
и U ( y) =
,
U ( x) =
2
2
то собственные значения энергии осциллятора равны сумме собственных значений En1 и En2 , вдоль координат и соответственно, а волновые функции сис-
темы – произведению одномерных волновых функций ψ ( x) и ψ ( y ) (см. §6).
Используя результаты задачи 7.1, можно записать:
1⎞
1⎞
⎛
⎛
En1 = ω ⎜ n1 + ⎟ , En2 = ω ⎜ n2 + ⎟ (n1 , n2 = 0,1,2,...) ;
2⎠
2⎠
⎝
⎝
ψ n ( x) =
1
ψ n ( y) =
2
1
2n1 n1 ! x0 π
1
2n2 n2 ! x0 π
e
−x
e
2
−y
2 x02
⎛ x⎞
H n1 ⎜ ⎟ ,
⎝ x0 ⎠
2
2 x02
⎛ y⎞
H n2 ⎜ ⎟ .
⎝ x0 ⎠
Тогда значения энергии плоского изотропного осциллятора равны
EN = En1 + En2 = ω ( N + 1) , N = n1 + n2 ,
а его волновые функции есть
(x +y )
2
ψ n n ( x, y ) = ψ n ( x)ψ n ( y ) =
1 2
1
2
1
1
x0 π
2n1 + n2 n1 !n2 !
e
−
2
2 x02
⎛ x⎞
⎛ y⎞
H n1 ⎜ ⎟ H n2 ⎜ ⎟ .
⎝ x0 ⎠
⎝ x0 ⎠
Уровню EN с заданным значением N соответствует ( N + 1) независимая
собственная функция ψ n1n2 с n1 = 0,1,2,..., N (при этом n2 = N − n1 ) . Поэтому
уровень EN является ( N + 1) -кратно вырожденным. ♦
Введем два оператора:
p ⎞
1 ⎛ x
⎜⎜ + i x ⎟⎟ ,
p0 ⎠
2 ⎝ x0
и эрмитово-сопряжённый ему оператор
a=
+
a =
(7.9)
p ⎞
1 ⎛ x
⎜⎜ − i x ⎟⎟ ,
p0 ⎠
2 ⎝ x0
(7.10)
Mω .
(7.11)
где*
p0 =
+
Оператор a называется оператором понижения, а оператор a - оператором
*
Аналогично величине x0 величина p0 имеет смысл максимального значения импульса для состояния с энер-
гией E = 1 2 ω в классической задаче о гармоническом осцилляторе.
64
65.
§7. Гармонический осцилляторповышения, оба эти оператора иногда именуют лестничными операторами.
Задача 7.3. Выразить гамильтониан гармонического осциллятора через
+
операторы понижения a и повышения a .
+
Решение. Отметим, что x0 p0 = . Рассмотрим произведение a a :
2
p x ⎞⎛ x
p x ⎞ 1 ⎛ x2 p x i
1⎛ x
a a = ⎜ − i ⎟⎜ + i ⎟ = ⎜ 2 + 2 + x p x − p x x
p0 ⎟⎜
p0 ⎟⎠ 2 ⎜ x0 p0
2 ⎜⎝ x0
⎠⎝ x0
⎝
(
+
)
⎞
⎟.
⎟
⎠
Поскольку коммутатор ⎡ x, p x ⎤ ≡ x p x − p x x = i (см. задачу 1.6), то для произ⎣
⎦
+
ведения a a можно записать
2
⎞
1 ⎛ x2 p x
a a = ⎜ 2 + 2 − 1⎟ ,
⎟
2 ⎜ x0 p0
⎝
⎠
или, учитывая явные выражения (7.2) и (7.11) для x0 и p0 ,
+
2
1 ⎛ p x M ω 2 x2 ⎞ 1
⎜
⎟− .
+
a a=
ω ⎜ 2M
2 ⎟ 2
⎝
⎠
В круглых скобках полученного выражения стоит оператор Гамильтона
+
+
гармонического осциллятора H . Выражая H через a a , получаем
1⎞
⎛ +
H = ω⎜a a + ⎟. ♦
2⎠
⎝
Задача 7.4. Доказать следующие соотношения:
(7.12)
+
a ψ n = n + 1ψ n+1 , aψ n = nψ n−1 ,
где ψ n - волновые функции гармонического осциллятора.
Решение. Вновь введем вместо координаты величину в соответствии
с формулой (7.1), а p0 выразим с помощью (7.11). Операторы повышения и
понижения при этом можно представить в виде
1 ⎛
d ⎞
1 ⎛
d ⎞
⎜ ξ − dξ ⎟ , a =
⎜ ξ + dξ ⎟ .
2⎝
2⎝
⎠
⎠
Запишем теперь, используя (П4.12), в явном виде волновые функции (7.8):
+
a =
ξ2
ψ n = (−1) Cn e
n
+
2
2
d n e −ξ
.
dξ n
Действуя оператором повышения a на функцию (7.13), имеем
65
(7.13)
66.
§7. Гармонический осцилляторn −ξ 2
n −ξ 2
ξ2
ξ2
⎡
⎛
C
1 ⎛
d ⎞
d
e
d
d
e
n
n
−
a ψn =
⎢ξ e 2
⎜⎜ e 2
⎜ ξ − d ξ ⎟ψ n = ( −1)
n
dξ
dξ ⎝
dξ n
2⎝
2 ⎢⎣
⎠
+
⎞⎤
⎟⎟ ⎥ =
⎠ ⎥⎦
ξ2
Cn ⎡ ξ 2 2 d n +1e −ξ ⎤
d n +1e −ξ
n +1 Cn
2
= ( −1)
.
e
⎢ −e
⎥ = ( −1)
d ξ n +1 ⎦
d ξ n+1
2⎣
2
Согласно задаче 7.1 отношение
Cn +1
1
.
=
Cn
2( n + 1)
2
2
n
С учетом этого можно записать
2
d n+1e−ξ
= n + 1ψ n+1.
a ψ n = n + 1(−1) Cn+1e
dξ n+1
Таким образом, первое соотношение доказано.
Для доказательства второго соотношения подействуем на функцию ψ n
+
ξ2
n +1
2
(7.13) оператором понижения a :
⎡ ξ 2 d n e −ξ 2 d ⎛ ξ 2 d n e −ξ 2
1 ⎛
d ⎞
n Cn
+
aψ n =
⎢ξ e 2
⎜⎜ e 2
⎜ ξ + d ξ ⎟ψ n = ( −1)
n
ξ
ξ
d
d
dξ n
2⎝
2 ⎢⎣
⎠
⎝
ξ2
ξ2
Cn ⎡
d n e −ξ
dn
2
2
2
= ( −1)
+
ξ
e
e
⎢
dξ n
dξ n
2 ⎢⎣
2
n
⎛ de −ξ
⎜⎜
⎝ dξ
2
⎞⎤
⎟⎟ ⎥ =
⎠ ⎥⎦
ξ2
ξ2
⎤
Cn ⎡
d n e −ξ
dn
−ξ 2
2
2
2
= ( −1)
−
ξ
e
e
⎢ 2ξ e
⎥=
dξ n
dξ n
2⎣
⎦
2
1
−
n
ξ
2
d
ξ e −ξ .
= ( −1) n −1 2Cn n e 2
n −1
dξ
В последнем равенстве данной цепочки мы учли, что
2
(
n
(
2
)
)
2
2
dn
d n e −ξ
d ξ d n −1e −ξ
n( n − 1) d 2ξ d n− 2e −ξ
−ξ 2
=ξ
+n
+
+
ξe
dξ n
dξ n
d ξ d ξ n −1
2! d ξ 2 d ξ n − 2
(
)
2
2
2
n
n( n − 1)( n − 2) d 3ξ d n −3e −ξ
d n e −ξ
d n−1e −ξ
−ξ 2 d ξ
+
+
+
e
=
+
n
ξ
...
.
d ξ 3 d ξ n −3
dξ n
dξ n
d ξ n −1
3!
Так как
Cn−1 Cn = 2n ,
то легко находим
(
)
2
d n −1
ξ e −ξ = nψ n−1.
n −1
dξ
Тем самым доказано и второе соотношение. ♦
aψ n = n ( −1) Cn −1e
n −1
ξ2
2
66
⎞⎤
⎟⎟ ⎥ =
⎠ ⎥⎦
67.
§7. Гармонический осциллятор+
Задача 7.5. С помощью операторов a и a найти собственные значения
и волновые функции гармонического осциллятора.
Решение. Стационарное уравнение Шрёдингера для гармонического осциллятора имеет вид
Hψ n = Enψ n .
(7.14)
Используя выражение (7.12), запишем уравнение Шрёдингера следующим образом:
1⎞
⎛ +
ω ⎜ a a + ⎟ψ n = Enψ n .
2⎠
⎝
Умножим обе части данного уравнения на ψ n* и проинтегрируем по всей области изменения координаты x гармонического осциллятора:
1⎞
⎛ +
ψ n ω ⎜ a a + ⎟ ψ n = ψ n En ψ n .
(7.15)
2⎠
⎝
Воспользовавшись условием нормировки волновых функций гармонического
осциллятора на единицу ψ n ψ n = 1 , находим правую часть уравнения (7.15):
ψ n En ψ n = En ψ n ψ n = En .
Теперь распишем левую часть уравнения (7.15):
+
1⎞
ω
⎛ +
ψn ω⎜a a + ⎟ψn = ω ψn a a ψn +
ψn ψn =
2⎠
2
⎝
ω
ω
1⎞
⎛
= ω ⎜ n + ⎟.
2
2
2⎠
⎝
Таким образом, собственные значения энергии гармонического осциллятора
1⎞
⎛
En = ω ⎜ n + ⎟ .
2⎠
⎝
Для нахождения волновых функций гармонического осциллятора подей+
= ω n ψ n a ψ n−1 +
= ωn ψn ψn +
ствуем оператором понижения a на волновую функция основного состояния
ψ 0 . Поскольку состояний с меньшей энергией не существует (другими словами, не существует волновых функций ψ n с отрицательными ), то
aψ 0 = 0 ,
или
⎛ x
p ⎞
⎜⎜ + i x ⎟⎟ψ 0 = 0 .
p0 ⎠
⎝ x0
Учитывая явный вид оператора p x , представим (7.16) в виде
67
(7.16)
68.
§7. Гармонический осцилляторdψ 0
x
= − 2 ψ 0.
dx
x0
Интегрируя данное уравнение, находим волновую функцию основного состояния:
⎛
x2 ⎞
,
2 ⎟
x
2
⎝
0 ⎠
где константа C0 определяется из условия нормировки.
Далее, поскольку
ψ 0 = C0 exp ⎜ −
+
a ψ n = n + 1ψ n+1 ,
+
то, применяя к ψ 0 оператор a n раз, определяем волновую функцию ψ n . ♦
Задача 7.6. Доказать, что для оператора координаты отличными от нуля
будут только следующие интегралы:
ψ n+1 x ψ n = x0
n +1
n
и ψ n−1 x ψ n = x0
,
2
2
n +1
n
, ψ n−1 p x ψ n = −ip0
,
2
2
где ψ n – волновые функции гармонического осциллятора.
ψ n+1 p x ψ n = ip0
Решение. Из формул (7.9) и (7.10) находим, что
+
x
x= 0 a +a .
2
Рассмотрим интеграл
ψk x ψn .
(
)
Используя (7.19), имеем
+
+
x
x
x
ψk x ψn = 0 ψk a + a ψn = 0 ψk a ψn + 0 ψk a ψn =
2
2
2
n +1
n
n +1
n
ψ k ψ n+1 + x0
ψ k ψ n−1 = x0
δ k ,n+1 + x0 δ k ,n−1 ,
2
2
2
2
откуда следует (7.17).
Абсолютно аналогично имеем
ip +
px = 0 a − a .
2
Значит,
+
+
ip
ip
ip
ψ k px ψ n = 0 ψ k a − a ψ n = 0 ψ k a ψ n − 0 ψ k a ψ n =
2
2
2
= x0
(
68
)
(7.17)
(7.18)
(7.19)
69.
§7. Гармонический осцилляторn +1
n
n +1
n
ψ k ψ n +1 − ip0
ψ k ψ n−1 = ip0
δ k ,n +1 − ip0 δ k ,n −1 ,
2
2
2
2
что приводит к соотношению (7.18). ♦
= ip0
Задачи для самостоятельного решения
7.7. Гармонический осциллятор находится в основном состоянии. Найти вероятность P обнаружения частицы вне пределов классической области, т.е. вне
области − x0 < x < x0 .
7.8. Найти дисперсии координаты и импульса гармонического осциллятора.
7.9. Гармонический осциллятор находится в первом возбужденном состоянии.
Найти средние значения потенциальной U и кинетической T энергий ос-
циллятора.
7.10. На гармонический осциллятор массы M и заряда e действует вдоль линии колебаний постоянное однородное электрическое поле напряженности E .
Найти энергии стационарных состояний гармонического осциллятора и соответствующие им волновые функции.
7.11. Найти кратность вырождения k n -го энергетического уровня трехмерного изотропного осциллятора, т.е. частицы движущейся в потенциальном поле
mω 2 2
U ( x, y , z ) =
x + y 2 + z 2 ).
(
2
7.12. Доказать, что
⎡ a, a + ⎤ = 1 .
⎢⎣
⎥⎦
Ответы к задачам для самостоятельного решения
7.7.
2
π
∞
−ξ
∫ e dξ ≈ 0.157 .
2
1
1⎞
⎛
⎜ n + ⎟,
Mω ⎝
2⎠
3
7.9. U = T = ω.
4
7.8.
( Δx )
2
=
(Δ p)
2
1⎞
⎛
= M ω ⎜ n + ⎟ (n = 0,1,2,...).
2⎠
⎝
1
1⎞
eE
⎛
M ω ⎞ 4 осц ⎛ M ω
⎛
, ψn = ⎜
7.10. En = ω ⎜ n + ⎟ −
⎟ ψn ⎜
2 ⎠ 2M ω 2
⎝
⎝
⎠
⎝
eE ⎞ ⎞
⎛
x
−
⎜
⎟⎟,
2M ω 2 ⎠ ⎠
⎝
n = 0,1, 2..., ψ nосц − волновые функции незаряженного осциллятора.
7.11. k =
( n + 1) (n + 2) .
2
69
70.
§8. Элементы теории момента импульса§ 8. ЭЛЕМЕНТЫ ТЕОРИИ МОМЕНТА ИМПУЛЬСА
В классической механике момент импульса L определяется как векторное произведение радиуса-вектора частицы на ее импульс, т.е. L = r × p . В соответствии с общими принципами построения операторов в квантовой механике ( p → p, r → r ) оператор момента импульса есть
L = r × p = − i r × ∇.
Операторы проекций момента импульса на координатные оси x, y и z
задаются выражениями:
⎛ ∂
∂ ⎞
L x = y p z − z p y = −i ⎜ y − z ⎟ ,
∂y ⎠
⎝ ∂z
∂⎞
⎛ ∂
L y = z p x − x p z = −i ⎜ z − x ⎟ ,
∂z ⎠
⎝ ∂x
⎛ ∂
∂⎞
Lz = x p y − y p x = −i ⎜ x − y ⎟ .
∂x ⎠
⎝ ∂y
Квадрат оператора момента импульса
2
2
2
2
L = Lx + L y + Lz .
Задача 8.1. Найти следующие коммутаторы: а) ⎡ L x , L y ⎤ , б) ⎡ L y , L z ⎤ ,
⎣
⎦
⎣
⎦
в) ⎡ L z , L x ⎤ .
⎣
⎦
Решение. а) Используя правила раскрытия коммутаторов, имеем:
⎡Lx , L y ⎤ = ⎡ y pz − z p y , z px − x pz ⎤ = ⎡ y pz , z px − x pz ⎤ −
⎣
⎦ ⎣
⎦ ⎣
⎦
(8.1)
− ⎡z p y , z px − x pz ⎤ = ⎡ y pz , z px ⎤ − ⎡ y pz , x pz ⎤ −
⎣
⎦ ⎣
⎦ ⎣
⎦
− ⎡z p y , z px ⎤ + ⎡z p y , x pz ⎤.
⎣
⎦ ⎣
⎦
Второй и третий из четырёх членов в правой части (8.1) оказываются
равными нулю, поскольку оператор координаты и оператор проекции импульса на другую координату коммутируют между собой, а также коммутируют
друг с другом операторы проекций импульса (см. задачи 1.4 и 1.5).
Найдем теперь значения первого и последнего членов в правой части равенства (8.1):
(
)
⎡ y p z , z p x ⎤ = y p z z p x − z p x y p z = y −i + z p z p x − z p x y p z =
⎣
⎦
= −i y p x + zy p z p x − zy p z p x = −i y p x .
70
(8.2)
71.
§8. Элементы теории момента импульса(
)
⎡ z p y , x p z ⎤ = z p y x p z − x p z z p y = z p y x p z − x −i + z p z p y =
⎣
⎦
= xz p z p y + i x p y − xz p z p y = i x p y .
В равенствах (8.2) и (8.3) мы учли, что ⎡ p z , z ⎤ = −i .
⎣
⎦
Таким образом, окончательно получаем:
⎡Lx , L y ⎤ = i
⎣
⎦
(xp
y
)
− y px = i Lz.
(8.3)
(8.4)
Аналогично получаем:
б) ⎡ L y , L z ⎤ = i L x .
⎣
⎦
(8.5)
(8.6)
в) ⎡ L z , L x ⎤ = i L y .
⎣
⎦
Формулы (8.4)-(8.6) показывают, что операторы проекций момента импульса на разные координаты не коммутируют друг с другом. ♦
Задача 8.2. Показать, что каждый из операторов проекций момента импульса коммутирует с оператором квадрата момента импульса.
2
Решение. Рассмотрим, например, коммутатор ⎡ L x , L ⎤ :
⎣⎢
⎦⎥
⎡ L x , L 2 ⎤ = ⎡ L x , L 2x + L 2y + L 2z ⎤ = ⎡ L x , L 2x ⎤ + ⎡ L x , L 2y ⎤ + ⎡ L x , L 2z ⎤ .
⎥⎦ ⎢⎣
⎥⎦ ⎢⎣
⎥⎦ ⎢⎣
⎥⎦
⎢⎣
⎥⎦ ⎢⎣
Коммутаторы, стоящие в правой части этого выражения, равны:
⎡ L x , L 2x ⎤ = 0 ,
⎢⎣
⎥⎦
⎡ L x , L 2y ⎤ = L x L 2y − L 2y L x = L x L y L y − L y L x L y + L y L x L y − L y L y L x =
⎢⎣
⎥⎦
= ⎡Lx , L y ⎤ L y + L y ⎡Lx , L y ⎤ = i Lz L y + i L y Lz = i
⎣
⎦
⎣
⎦
(L L
y
z
)
+ Lz L y ,
⎡ L x , L 2z ⎤ = L x L 2z − L 2z L x = L x L z L z − L z L x L z + L z L x L z − L z L z L x =
⎢⎣
⎥⎦
(
)
= ⎡ L x , L z ⎤ L z + L z ⎡ L x , L z ⎤ = −i L y L z − i L z L y = −i L y L z + L z L y .
⎣
⎦
⎣
⎦
Следовательно,
⎡ L x , L 2 ⎤ = i L y L z + L z L y − i L y L z + L z L y = 0.
⎢⎣
⎥⎦
Аналогично можно показать, что
⎡ L y , L 2 ⎤ = 0 и ⎡ L z , L 2 ⎤ = 0. ♦
⎢⎣
⎥⎦
⎢⎣
⎥⎦
При решении ряда задач квантовой механики удобно бывает пользовать-
(
) (
)
ся операторами L + и L − , представляющими собой комплексные линейные
71
72.
§8. Элементы теории момента импульсакомбинации операторов L x и L y :
L+ = L x + iL y ,
L− = L x − iL y .
Задача 8.3. Вычислить коммутаторы: а) ⎡ L + , L z ⎤ , б) ⎡ L − , L z ⎤ , в) ⎡ L + , L − ⎤ .
⎣
⎦
⎣
⎦
⎣
⎦
Решение.
а) ⎡ L + , L z ⎤ = ⎡ L x + iL y , L z ⎤ = ⎡ L x , L z ⎤ + i ⎡ L y , L z ⎤ = −i L y − L x = − L + .
⎣
⎦ ⎣
⎦ ⎣
⎦ ⎣
⎦
б) ⎡ L − , L z ⎤ = ⎡ L x − iL y , L z ⎤ = ⎡ L x , L z ⎤ − i ⎡ L y , L z ⎤ = −i L y + L x = L − .
⎣
⎦ ⎣
⎦ ⎣
⎦ ⎣
⎦
в) ⎡ L + , L − ⎤ = ⎡ L x + iLy , L x − iLy ⎤ = ⎡ L x , L x ⎤ + i ⎡ L y , L x ⎤ − i ⎡ L x , L y ⎤ +
⎣
⎦ ⎣
⎦ ⎣
⎦ ⎣
⎦ ⎣
⎦
+ ⎡ L y , L y ⎤ = −2i ⎡ L x , L y ⎤ = 2 Lz .
⎣
⎦
⎣
⎦
♦
2
Поскольку операторы L x и L y коммутируют с оператором L , то
⎡ L + , L 2 ⎤ = ⎡ L x , L 2 ⎤ + i ⎡ L y , L 2 ⎤ = 0,
⎢⎣
⎥⎦ ⎢⎣
⎥⎦ ⎢⎣
⎥⎦
⎡ L − , L 2 ⎤ = ⎡ L x , L 2 ⎤ − i ⎡ L y , L 2 ⎤ = 0.
⎢⎣
⎥⎦ ⎢⎣
⎥⎦ ⎢⎣
⎥⎦
2
Задача 8.4. Найти явный вид операторов L x , L y , L z , L+ , L− , L в сферических координатах.
Решение. Запишем формулы связывающие декартовы и сферические координаты:
x = r sin θ cos ϕ ; y = r sin θ sin ϕ ; z = r cosθ .
Рассмотрим функцию ψ ( x, y, z ) и найдём ее частную производную по азимутальному углу ϕ :
∂ψ ∂ψ ∂x ∂ψ ∂y ∂ψ ∂z
∂ψ
∂ψ
=
+
+
=−
r sin θ sin ϕ +
r sin θ cos ϕ =
∂ϕ ∂x ∂ϕ ∂y ∂ϕ ∂z ∂ϕ
∂x
∂y
∂ψ
∂ψ
=x
−y
.
∂y
∂x
(8.7)
Действуя оператором L z на функцию ψ ( x, y, z ) , в соответствии с (8.7) имеем:
⎛ ∂ψ
∂ψ ⎞
∂ψ
L zψ = −i ⎜ x
−y
= −i
.
⎟
∂
∂
∂
ϕ
y
x
⎝
⎠
Таким образом, в сферической системе координат
∂ψ
L z = −i
.
∂ϕ
Далее, найдём частную производную функции ψ ( x, y, z ) по полярному углу θ :
72
73.
§8. Элементы теории момента импульса∂ψ ∂ψ ∂x ∂ψ ∂y ∂ψ ∂z
∂ψ
∂ψ
=
+
+
= r cosθ cos ϕ
+ r cosθ sin ϕ
−
∂θ
∂x ∂θ ∂y ∂θ ∂z ∂θ
∂x
∂y
∂ψ
− r sin θ
= ctgθ
∂z
⎛ ∂ψ
∂ψ ⎞
∂ψ
+
−
θ
x
y
z
tg
.
⎜ ∂x
∂y ⎟⎠
∂z
⎝
Действие оператора L+ сводится к следующему:
⎛ ∂ψ
∂ψ ⎞
∂ψ
⎛ ∂ψ
−z
+ ⎜z
−x
L +ψ = ( L x + iL y )ψ = −i ⎜ y
⎟
∂y ⎠
∂z
⎝ ∂x
⎝ ∂z
⎛ ∂ψ
∂ψ
∂ψ
= ⎜ iz
+z
− ( x + iy )
∂x
∂z
⎝ ∂y
Воспользуемся тем, что
⎞
⎟=
⎠
⎞
⎟.
⎠
(8.8)
.
x + iy = r sinθ ( cosϕ + i sin ϕ ) = reiϕ sin θ ,
x − iy = r sin θ ( cosϕ − i sin ϕ ) = re−iϕ sin θ .
Тогда
⎛
∂ψ
∂ψ
∂ψ
L +ψ = eiϕ ⎜ ire − iϕ cosθ
+ re − iϕ cosθ
− r sin θ
∂y
∂x
∂z
⎝
⎛
∂ψ
∂ψ
∂ψ
= eiϕ ⎜ i ( x − iy ) ctgθ
+ ( x − iy )ctgθ
− r sin θ
∂y
∂x
∂z
⎝
⎡
⎛ ∂ψ
∂ψ
= eiϕ ⎢ctgθ ⎜ x
+y
∂y
⎝ ∂x
⎣
⎞
⎟=
⎠
⎞
⎟=
⎠
(8.9)
⎞
⎛ ∂ψ
∂ψ
∂ψ
⎟ − tgθ z ∂z + i ctgθ ⎜ x ∂y − y ∂x
⎠
⎝
Учитывая (8.7) и (8.8), в выражении (8.9) легко можно выделить
⎞⎤
⎟⎥ .
⎠⎦
∂ψ
и ∂ψ и
∂ϕ
∂θ
получить, таким образом, что в сферических координатах оператор
⎛ ∂
∂ ⎞
L + = eiϕ ⎜
+ ictgθ
⎟.
∂
∂
θ
ϕ
⎝
⎠
Аналогичный расчёт даёт, что
⎛ ∂
∂ ⎞
L− = − e−iϕ ⎜
− ictgθ
⎟.
∂
∂
θ
ϕ
⎝
⎠
(8.10)
(8.11)
С помощью (8.10) и (8.11) можно получить выражения для операторов L x и L y :
⎛
L+ + L−
∂
∂ ⎞
,
= i ⎜ sin ϕ
+ ctgθ cosϕ
∂θ
∂ϕ ⎟⎠
2
⎝
⎛
L − L−
∂
∂ ⎞
.
Ly = +
= −i ⎜ cosϕ
− ctgθ sinϕ
∂θ
∂ϕ ⎟⎠
2i
⎝
Lx =
Наконец, для оператора квадрата момента импульса получим:
73
74.
§8. Элементы теории момента импульса⎧ 1 ∂ ⎛
1 ∂2 ⎫
∂ ⎞
L =L +L +L =− ⎨
⎬. ♦
⎜ sin θ
⎟+
∂θ ⎠ sin 2 θ ∂ϕ 2 ⎭
⎩ sin θ ∂θ ⎝
Полученные в задачах 8.1 и 8.2 коммутационные соотношения означают,
что невозможно одновременно точно измерить две проекции момента импульса*, зато можно одновременно точно определить величины одной проекции
момента импульса и квадрата момента импульса. В качестве одной из проек2
2
x
2
y
2
z
2
ций момента импульса обычно выбирают L z . Равенство нулю коммутатора
⎡ L z , L 2 ⎤ означает, что эти два оператора обладают общей системой собствен⎢⎣
⎥⎦
ных функций.
В сферической системе координат задача на определение общих собст2
венных значений и собственных функций операторов L z и L имеет вид:
∂Y (θ ,ϕ )
L zY (θ ,ϕ ) = −i
= LzY (θ ,ϕ ) ,
(8.12)
∂ϕ
2
L Y (θ ,ϕ ) = −
2
⎧ 1 ∂ ⎛
∂Y (θ ,ϕ ) ⎞
1 ∂ 2Y (θ ,ϕ ) ⎫
sin
θ
+
⎨
⎬ = λY (θ ,ϕ ) . (8.13)
⎜
⎟
2
2
sin
sin
θ
θ
θ
θ
ϕ
∂
∂
∂
⎝
⎠
⎩
⎭
2
где Lz и λ – собственные значения операторов L z и L соответственно, а посредством Y (θ ,ϕ ) обозначены общие функции рассматриваемых операторов.
Данная задача допускает разделение переменных, позволяя искать решение в
виде произведения двух функций Y (θ ,ϕ ) = Θ (θ ) Φ (ϕ ) , одна из которых, Θ (θ ) ,
зависит только от полярного угла θ , а другая, Φ (ϕ ) , – только от азимутального угла ϕ . При этом уравнение (8.12) запишется как
d Φ (ϕ )
−i
= Lz Φ (ϕ ) .
dϕ
Собственные значения и нормированные собственные функции данного уравнения найдены в задаче 3.1. и равны соответственно:
Lz = m (m = 0, ±1, ± 2,...) ,
Φ m (ϕ ) =
1 imϕ
e .
2π
Подставляя теперь в (8.13) Y (θ ,ϕ ) = Θ (θ )
*
1 imϕ
e , получаем:
2π
За исключением случая L = 0 , когда точно известно, что все три проекции момента импульса равны нулю.
74
75.
§8. Элементы теории момента импульса1 d ⎛
d Θ(θ ) ⎞
m2
λ
(8.14)
⎜ sin θ
⎟ − 2 Θ(θ ) + 2 Θ(θ ) = 0 .
sin θ dθ ⎝
dθ ⎠ sin θ
Решения уравнения (8.14) должны быть однозначными, ограниченными и подчиняющимися условию нормировки
π
∫ Θ (θ ) sinθ dθ = 1.
2
0
Можно показать, что такие решения существуют лишь при
λ = 2l (l + 1), l = 0,1,2,... ,
и определяются равенством
Θlm (θ ) = ( −1)
m+ m
2
( 2l + 1) ( l − m )!
2 ( l + m )!
Pl m ( cosθ ) ,
(8.15)
где
d l + m ( cos2 θ − 1)
1
m
Pl (cos θ ) = l sin θ
,
l+ m
2 l!
d
cos
θ
(
)
l
m
причем m ≤ l . Функции Pl (cosθ ) называются присоединенными полиномами
m
Лежандра.
Общие собственные функции операторов L z и L
Ylm (θ ,ϕ ) = Θlm (θ ) Φ m (ϕ ) = ( −1)
m+ m
2
( 2l + 1) ( l − m )!
4π ( l + m )!
2
Pl m ( cosθ ) eimϕ
( m ≤ l)
носят название шаровых (или сферических) функций. Шаровые функции ортонормированны:
2π π
∫ ∫Y
*
l ′m′
Ylm sin θ dθ dϕ = δ ll′δ mm′ .
0 0
Число m часто называют магнитным квантовым числом, а l – азимутальным квантовым числом. В табл. 8.1. выписаны шаровые функции для состояний
с l = 0 и l = 1 *, а также приведены значения Lz , Lx , Ly ( Lx , Ly – собственные значения операторов L x и L y соответственно) и λ для данных состояний. Полярные
диаграммы функций Yl m (θ ) для l = 0 и l = 1 приведены на рис. 8.1.
2
*
Состояния с l = 0 часто называются s-состояниями, а состояния с l = 1 – p-состояниями.
75
76.
§8. Элементы теории момента импульсаТаблица 8.1.
Состояние
s
p
Шаровые
Вид шаровых
функции
функций
0
Y0,0
1
4π
1
-1
Y1,-1
1
0
Y1,0
1
1
Y1,1
l
m
0
−
3
sin θ e − iϕ
8π
Lz
L2
Lx , Ly
0
0
0, 0
−
2
2
Не определены
3
cosθ
4π
0
2
2
Не определены
3
sin θ eiϕ
8π
+
2
2
Не определены
Рис. 8.1.
Задача 8.5. Найти энергетический спектр и волновые функции стационарных состояний пространственного ротатора с моментом инерции I. Какова
кратность вырождения уровней?
Решение. Ротатор представляет собой частицу, движущуюся по сфере
заданного радиуса r = a = const . Примером ротатора может служить двухатомная молекула, атомы которой находятся на неизменном расстоянии a
друг от друга. Момент инерции такой молекулы равен I = Ma2 ( M – приведённая масса атомов). В классической механике функцию Гамильтона ротатора можно представить в виде
L2
H= .
2I
76
77.
§8. Элементы теории момента импульсаПо общему правилу построения операторов в квантовой механике гамильтониан ротатора
2
L
H=
.
2I
Следовательно, стационарное уравнение Шредингера для ротатора имеет вид
2
L
ψ = Eψ .
2I
2
Зная собственные значения и собственные функции оператора L , легко
найти, что уровни энергии ротатора
E=
2
l (l + 1)
,
2I
а собственные функции
ψ lm = Ylm (θ ,ϕ ) (l = 0,1,2,...; m = l , l − 1,...., −l ) .
Поскольку при фиксированном l число m может принимать 2l + 1 значений, то все состояния, кроме основного ( l = 0 ), являются (2l + 1) -кратно вырожденными. ♦
Задача 8.6. Волновая функция, описывающая состояние ротатора, имеет
вид:
ψ = C ( 2 sin θ sin ϕ + 3i ) .
Найти нормировочный множитель C , величины Lz , λ (собственные значения
2
оператора L ) и E , которые могут быть найдены при измерении и вероятности
PLz , Pλ , PE их появления.
Решение. Разложим данную функцию по собственным функциям опера2
тора L :
⎡ ⎛ 8π
⎢⎣ ⎝ 3
ψ = C ⎢2 ⎜
3
1
8π
sin θ eiϕ −
8π
2i
3
⎞
3
1
sin θ e − iϕ ⎟ + 3i 4π
8π
2i
⎠
⎡
⎤
8π
8π
Y1,1 + i
Y1,−1 + 3i 4π Y0,0 ⎥ .
= C ⎢ −i
3
3
⎣
⎦
Из условия нормировки
77
1
4π
⎤
⎥=
⎥⎦
78.
§8. Элементы теории момента импульсаТаблица 8.2.
Lz
−
0
λ
PLz
2/31
2/31
2
2
27/31
Pλ
0
2π π
∫ ∫ψ
2
4/31
27/31
E
2
I
0
PE
4/31
27/31
sin θ dθ dϕ = 1
0 0
находим, что C =
3
. Нормированная функция ψ имеет вид:
124π
2
2
27
Y1,1 + i
Y1,−1 + i
Y0,0 .
31
31
31
Набор собственных функций, по которым возможно разложение функции ψ ,
определяет те значения величин Lz , λ и E , которые могут быть найдены в экс-
ψ = −i
перименте. Напомним, что эти величины суть собственные значения соответствующих операторов, отвечающие тем собственным функциям, которые входят
в функцию ψ . Вероятности обнаружения в эксперименте той или иной величины определяются квадратами модуля коэффициентов в разложении по собственным функциям. Значения величин и их вероятности приведены в табл. 8.2. ♦
Задача 8.7. Показать, что при действии операторов L+ и L− , на собственные функции Φ m оператора L z , получаются также собственные функции
оператора L z .
Решение. Используя коммутационные соотношения из задачи 8.3, можно
записать
L z L + Φ m = L + L z Φ m + L + Φ m = L + mΦ m + L + Φ m =
( m + 1) L + Φ m .
Данное равенство свидетельствует, что функция L + Φ m также является собственной функцией оператора L z , которой соответствует собственное значение
Lz =
( m + 1) . Таким образом, оператор L+ действует как повышающий опера-
тор. Аналогичным образом можно показать, что функция L − Φ m является собственной функцией оператора L z , описывающей состояние с Lz =
78
( m − 1) . ♦
79.
§8. Элементы теории момента импульсаЗадачи для самостоятельного решения
8.8. Найти коммутаторы:
а) ⎡ L x , x ⎤ , б) ⎡ L x , y ⎤ , в) ⎡ L x , z ⎤ .
⎣
⎦
⎣
⎦
⎣
⎦
8.9. Найти коммутаторы:
а) ⎡ L x , p x ⎤ , б) ⎡ L x , p y ⎤ , в) ⎡ L x , p z ⎤ .
⎣
⎦
⎣
⎦
⎣
⎦
8.10. Вычислить следующие коммутаторы:
2
2
а) ⎡ L x , r ⎤ , б) ⎡ L x , p ⎤ .
⎢⎣
⎥⎦
⎢⎣
⎥⎦
8.11. Показать, что
2
2
L = L− L+ + L z + L z .
8.12. Пользуясь операторами L+ и L− найти собственные значения и собствен2
ные функции оператора L .
8.13. Найти энергетический спектр и волновые функции стационарных состояний плоского ротатора с моментом инерции I . Какова кратность k вырождения уровней?
8.14. Волновая функция, описывающая состояние пространственного ротатора, имеет вид ψ = С ( 3sin θ cosϕ + 2i ) . Найти нормировочный множитель С , ве2
личины Lz , λ (собственные значения оператора L ) и E , которые могут быть
найдены при измерении и вероятности их появления.
8.15. Найти cos θ и cos 2 θ в s -состоянии пространственного ротатора.
8.16. Найти cos 2 θ в p -состоянии пространственного ротатора.
Ответы к задачам для самостоятельного решения
8.8. а) 0, б) i z , в) − i y. 8.9. а) 0, б) i p z , в) − i p y . 8.10. а) 0, б) 0 .
8.13. Φ m =
1 imϕ
e
( m = 0, ±1, ±2,...); k = 2 (при m ≠ 0) и k = 1 (при m = 0) .
2π
8.14. С = 1
28π , Lz принимает значения + ,0, − с вероятностями 3/14, 4/7 и
3/14 соответственно; λ принимает значения 2 2 , 0 с вероятностями 3/7 и 4/7
соответственно; E принимает значения
ветственно.
1
8.15. 0 и .
3
8.16.
2
I
, 0 с вероятностями 3/7 и 4/7 соот-
3
1
для m = 0 ; для m = ±1.
5
5
79
80.
§9. Элементы теории представлений§ 9. ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ
Потенциальная энергия частицы в центральном поле зависит только от
расстояния частицы до силового центра, т.е. U = U (r ) . Следовательно, ее гамильтониан имеет вид
H =−
2
Δ + U (r ) .
2M
В случае движения частицы в указанном поле зависимость волновой функции
от сферических углов не связана с конкретным выбором вида потенциальной
энергии. Угловая часть волновой функции в случае центрального поля задается шаровыми функциями Ylm (θ , ϕ ) .
Вследствие центральной симметрии силового поля гамильтониан целесообразно записать в сферических координатах:
⎛1 ∂⎛ 2 ∂⎞ 1⎧ 1 ∂ ⎛
∂ ⎞
1 ∂2 ⎫ ⎞
H =−
⎬ ⎟ + U (r ). (9.1)
⎜
⎜r
⎟+ ⎨
⎜ sinθ ⎟ + 2
∂θ ⎠ sin θ ∂ϕ 2 ⎭ ⎠
2M ⎝ r 2 ∂r ⎝ ∂r ⎠ r 2 ⎩ sinθ ∂θ ⎝
2
В фигурных скобках выражения (9.1) стоит оператор квадрата углового мо2
мента L , деленный на −
дующим образом:
2
. Поэтому гамильтониан можно представить сле2
⎛ ∂2 2 ∂ ⎞ L
H =−
+
+ U (r ).
⎜
⎟+
2M ⎝ ∂r 2 r ∂r ⎠ 2Mr 2
2
(9.2)
2
Можно легко показать, что операторы L и L z коммутируют с оператором H частицы, находящейся в поле центральных сил. Следовательно, такая
частица может обладать одновременно определенными значениями и энергии,
и квадрата углового момента, и проекции этого момента на выделенное направление z. Волновые функции этих состояний являются одновременно собственными функциями всех трех вышеперечисленных операторов. Требова2
ние, чтобы ψ была собственной функцией операторов L и L z определяет ее
зависимость от углов, а именно, угловая часть волновой функции частицы в
центральном поле описывается шаровыми функциями Ylm (θ , ϕ ) .
Решение уравнения Шрёдингера с гамильтонианом (9.2) можно искать в
виде:
ψ (r,θ ,ϕ ) = R(r) Ylm (θ ,ϕ ) ,
80
(9.3)
81.
§9. Движение в центральном полегде R( r ) – радиальная волновая функция, которая определяется видом потенциальной энергии U (r ) . Очевидно, что функция (9.3) является также и собст2
венной функцией операторов L , L z .
Подставляя (9.3) в стационарное уравнение Шредингера с гамильтониа2
ном (9.2) и учитывая, что L ψ =
2
l ( l + 1)ψ (см. § 8), получаем так называемое
радиальное уравнение Шрёдингера:
d 2R 2 d
2M
+
R+ 2
2
dr
r dr
2
l ( l + 1) ⎤
⎡
⎢ E − U (r) − 2M r 2 ⎥ R = 0 .
⎣
⎦
(9.4)
Если потенциальная энергия U (r ) везде конечна, то и функция R( r )
должна иметь конечное значение в области r от 0 до ∞. На бесконечном удалении от силового центра граничное условие определяется конкретной постановкой задачи.
Для решения уравнения (9.4) часто бывает удобным перейти к новой
функции χ (r ) = rR(r ) . При этом уравнение (9.4) принимает вид:
2
l ( l + 1) ⎤
⎡
(9.5)
⎢ E − U ( r ) − 2 M r 2 ⎥ χ = 0.
⎣
⎦
Поскольку функция R( r ) конечна (см. выше), то χ (r ) должна при r = 0 обращаться в нуль:
χ (0) = 0.
Уравнение (9.5) по своей структуре совпадает с уравнением Шрёдингера
в одномерном случае с «эффективной» потенциальной энергией
2
l (l + 1)
U eff (r ) = U (r ) +
.
2Mr 2
Задача 9.1. Найти волновую функцию для свободной частицы в sсостоянии.
Решение. Запишем уравнения (9.5) для свободной частицы ( U = 0 ) с l = 0 :
d2 (χ )
+ k 2χ = 0 ,
2
dr
где
2ME
k2 = 2 .
d 2 χ 2M
+ 2
dr 2
Решение этого уравнения есть
χ = A sin(kr ) + B cos(kr ) .
Из условия χ (0) = 0 следует, что B = 0 . Таким образом, для радиальной части
волновой функции получаем:
81
82.
§9. Движение в центральном полеsin ( kr )
.
r
Никаких дополнительных условий на функцию R(r ) не накладывается. ПоэтоRk (r ) = A
му k , а значит, и энергия E могут принимать любые (неотрицательные) действительные значения. Следовательно, частица обладает непрерывным спектром. Коэффициент A находится из условия нормировки для непрерывного
спектра
∞
∞
sin(kr ) sin(k ′r ) 2
r dr = δ ( k ′ − k ) .
∫
r
r
0
0
Интеграл в (9.6) можно записать в виде
∫ R (r )Rk′ (r )r dr = A
*
k
2
∞
2
∞
∞
1
1
∫0 sin(kr )sin(k ′r ) dr = 2 ∫0 cos[(k − k ′)r ]dr − 2 ∫0 cos[(k + k ′)r ]dr =
∞
∞
1
1
= ∫ cos [ (k − k ′)r ] dr − ∫ cos [ (k + k ′)r ] dr.
4 −∞
4 −∞
∞
Поскольку
∫ cos[(k + k′)r ] dr
(9.6)
.
не расходится при k = k ′ , в условии нормировки
−∞
его можно опустить. Согласно (П3.10)
∞
1
π 1
′
−
=
cos
(
k
k
)
r
dr
[
]
∫
4 −∞
2 2π
∞
∫ cos[(k − k′)r ] dr =
−∞
π
2
δ (k − k ′) .
Здесь мы воспользовались равенством
sin(kr ) = −
i ikr
e − e − ikr ) .
(
2
Тогда из (9.6) находим
A=
2
π
.
Учёт угловой части волновой функции Y0,0 =
частицы
1
даёт волновую функцию
4π
1 sin ( kr )
.♦
r
2π
Задача 9.2. Найти возможные значения энергии и волновые функции
частицы массы М, находящейся в сферически симметричной потенциальной
яме
⎧ 0, при r < a,
U (r ) = ⎨
⎩∞, при r > a,
ψ k 00 ( r,θ ,ϕ ) =
82
83.
§9. Движение в центральном поледля s-состояния.
Решение. Внутри ямы ( r < a ) уравнение (9.5) имеет вид
d2 (χ )
+ k 2χ = 0 ,
2
dr
где
k2 =
2ME
2
,
а его решение есть χ = A sin(kr ) + B cos(kr ) .
Условие χ (0) = 0 дает B = 0 . Поскольку частица не может проникнуть в
область r > a , необходимо положить
χ (a ) = A sin(ka) = 0.
Отсюда получаем, что
ka = π n
(n = 1, 2,...).
Значение n = 0 мы отбросили, поскольку оно ведет к тождественно равной нулю волновой функции. Принимая во внимание связь между k и E , находим
значения энергии частицы:
π2
2
En =
2
n 2 (n = 1,2,...).
2Ma
Таким образом, спектр частицы является дискретным.
Константу A ищем из условия нормировки
a
∫ R (r )
2
0
a
r dr = ∫ χ (r ) dr = A
2
2
0
2
a
∫ sin (kr )dr = 1.
2
(9.7)
0
Так как
a
a
∫ sin (kr )dr = ∫ sin
2
0
0
то из (9.7) заключаем, что A =
2
a
⎛πn ⎞
⎜ r ⎟dr = ,
2
⎝ a ⎠
2
. Тем самым радиальная волновая функция
a
частицы
⎛πn ⎞
sin ⎜
r⎟
2
a ⎠
⎝
.
Rn (r ) =
a
r
Учитывая, что угловая часть волновой функции Y0,0 =
тельно для волновой функции частицы получаем выражение
83
1
, оконча4π
84.
§ Движение в центр§9.
ральном полле
⎛πn ⎞
siin ⎜
r⎟
1
a ⎠
⎝
ψ n 00 ( r , θ , ϕ ) =
. ♦
r
2π a
Заадача 9.3.. Найти собственн
с
ные значеения энерргии и воолновые функции
ф
связанны
ых состояяний часттицы с заарядом e , движущ
щейся в ккулоновскком поле
Ze2
притяжеения U (r ) = −
(водородоподобны
ый атом).
r
Реешение. В этом слуучае уравнение Шр
рёдингераа для радиальной функции
ф
(9.4) естть
⎡ 2M ⎛
d 2R 2 d
Ze2 ⎞ l ( l + 1) ⎤
R+⎢ 2 ⎜E +
+
⎥ R = 0.
⎟−
2
dr 2 r dr
r
r
⎠
⎝
⎦
⎣
(9.8)
Зави
исимость эффекттивной потенцип
а
альной
эн
нергии отт r схематично представп
л
лена
на рис.
р
9.1 Видно,
В
чтто связан
нные сос
стояния
частицы могут
м
сущ
ществоватть только
п E < 0.
при
Перепишем уравнение
у
е (9.8) в виде:
в
d 2 R 2 dR ⎡
2B l ( l + 1) ⎤
+
+
−
A
−
+
⎢
⎥ R = 0,
r
r2 ⎦
dr 2 r dr ⎣
г
где
Рис. 9.1
9
MZe2
2
≡ B > 0,
2
2ME
2
≡ A < 0.
В
Вводя
новвую перем
менную
ρ = 2 A r,
получаем уравнен
ние:
l ( l + 1) ⎤
d 2 R 2 dR ⎡ 1
B
⎥ R = 0.
⎢
+
+ − +
−
(9.9)
2
ρ
dρ2 ρ dρ ⎢ 4
A
ρ
⎥
⎣
⎦
Наайдем сн
начала решения эттого ураввнения в случаях,, когда ρ → ∞ и
ρ → 0 . При ρ → ∞ из (9.9) следуеет уравнение (в кввадратныхх скобкахх уравнения (9.9)) пренебррегаем всееми членаами, содеержащими
и в знамен
нателе ρ ):
)
d 2 R∞ 1
(9.10)
− R∞ = 0 ,
dρ2 4
где посрредством R∞ обоззначено асимптоти
а
ическое решение
р
((9.9) при
и ρ → ∞.
⎛ρ⎞
⎛ ρ⎞
Решенияями (9.100) являютсся две фуункции: eexp ⎜ ⎟ и exp ⎜ − ⎟ , однакко экспо⎝ 2⎠
⎝2⎠
84
85.
§9. Движение в центральном полененту со знаком “+” в показателе нужно отбросить, так как она неограниченно
возрастает при ρ → ∞ . Таким образом,
⎛ ρ⎞
R∞ = exp ⎜ − ⎟ .
⎝ 2⎠
Для нахождения асимптотического решения R0 при ρ → 0 на основании
(9.9) запишем уравнение, в котором мы пренебрегаем членами
сравнению с
l ( l + 1)
ρ2
1
и
4
B
Aρ
по
:
l ( l + 1)
d 2 R0 2 dR0
R0 = 0.
+
+−
2
dρ
ρ dρ
ρ2
Решение этого уравнения будем искать в виде
R0 = ρ q .
(9.11)
(9.12)
Подставляя (9.12) в (9.11), находим
q ( q + 1) − l ( l + 1) = 0.
Данное уравнение имеет два решения:
q1 = l , q2 = − ( l + 1) .
Поэтому частными решениями (9.11) являются R0 = ρ l и R0 = ρ
ку решение R0 = ρ
−( l +1)
−( l +1)
. Посколь-
неограниченно возрастает при ρ → 0 , его необходимо
исключить из дальнейшего рассмотрения. Тем самым окончательно получаем
R0 = ρ l .
Теперь займемся нахождением решения уравнения (9.9) для произвольного ρ . Сделав в нем замену χ = ρ R , имеем:
l ( l + 1) ⎤
d 2χ ⎡ 1
B
⎥ χ = 0.
+ ⎢− +
−
dρ2 ⎢ 4 ρ A
ρ2 ⎥
⎣
⎦
Решение этого уравнения будем искать в виде:
⎛ ρ⎞
χ = ρ R∞ R0u ( ρ ) = ρ l +1 exp ⎜ − ⎟ u ( ρ ) ≡ ν ( ρ )u ( ρ ),
⎝ 2⎠
(9.13)
(9.14)
⎛ ρ⎞
где u ( ρ ) - подлежащая определению функция, а ν ( ρ ) ≡ ρ l +1 exp ⎜ − ⎟ . По⎝ 2⎠
∞
скольку интеграл
∫ R( ρ )
0
2
∞
ρ d ρ = ∫ χ ( ρ ) d ρ должен быть конечен (иначе
2
2
0
волновую функцию рассматриваемой частицы невозможно будет нормировать
85
86.
§9. Движение в центральном полена единицу, как это необходимо для дискретного спектра), то функция u( ρ )
должна удовлетворять условию
∞
∫ρ
2l + 2 − ρ
e u ( ρ )d ρ < ∞ .
(9.15)
0
Подставляя (9.14) в (9.13), получаем:
l ( l + 1) ⎤
v′ ⎡ v′′ 1
B
⎥u = 0,
−
u′′ + 2u′ + ⎢ − +
ρ2 ⎥
v ⎢v 4 ρ A
⎣
⎦
где штрих обозначает дифференцирование по ρ .
Заметим, что
1
ln v = − ρ + ( l + 1) ln ρ ,
2
v′
1 l +1
,
= ( ln v )′ = − +
ρ
v
2
тогда
т.е.
⎛ 1 l +1⎞
v′ = ⎜ − +
⎟v .
⎝ 2 ρ ⎠
Далее
(9.16)
имеем
⎛ 1 l +1⎞
v ′′ 1 l + 1 l ( l + 1)
v′′ = − 2 v + ⎜ − +
v
,
и
.
= −
+
ρ
ρ ⎟⎠
v 4
ρ
ρ2
⎝ 2
Пользуясь найденными формулами, преобразуем (9.16) к виду:
⎡ B
⎤
ρ u′′ + ⎡⎣ 2 ( l + 1) − ρ ⎤⎦ u′ + ⎢
− l − 1⎥ u = 0.
⎢⎣ A
⎥⎦
B
+ l , имеем
Отсюда, введя обозначения: k = 2l + 1, λ =
A
l +1
2
ρ u′′ + [ k + 1 − ρ ] u′ + [λ − k ] u = 0.
(9.17)
Уравнение (9.17) представляет собой присоединенное дифференциальное
уравнение Лагерра (см. приложение 5). Данное уравнение может иметь решение, удовлетворяющее условию (9.15), только, если
λ = n′ и n′ ≥ k ,
где, вообще говоря, n′ может принимать значения 0,1,2 и т.д. Однако, условие
n′ ≥ k = 2l + 1 исключает из рассмотрения n′ = 0 . Вместо n′ обычно удобно использовать главное квантовое число, определяемое равенством n′ = n + l . Видно, что главное квантовое число может принимать значения n = 1,2,... .
Из условия λ = n′ определяются уровни энергии частицы:
B
+l =n+l,
A
отсюда
86
87.
§9. Движение в центральном поле1 Z 2 e2
En = −
,
2 n 2 a0
(9.18)
2
где a0 =
– так называемый боровский радиус (для атома водорода
Me2
a0 ≈ 0,529 Å). Заметим, что значения энергии частицы в рассматриваемом поле зависят только от главного квантового числа. При n = 1 энергия минимальна, поэтому состояние с главным квантовым числом равным единице является
основным.
Неравенство n′ ≥ k показывает, что n ≥ l + 1 . Значит при фиксированном
n возможные значения l = 0,1,2,..., n − 1 .
Решением (9.17) является функция (вместо n′ и k используем их выражения через n и l )
u = CL2nl++l1 ( ρ ) ,
где L2nl++l1 ( ρ ) - присоединенные полиномы Чебышева-Лагерра (см. приложение
5), а C - произвольная константа.
Радиальная волновая функция частицы
χ ( ρ ) ν ( ρ )u ( ρ )
⎛ ρ⎞
=
= C ρ l +1 exp ⎜ − ⎟ L2nl++l1 ( ρ ) ,
R( ρ ) =
ρ
ρ
⎝ 2⎠
или, возвращаясь к переменной r ,
l
⎛ 2Zr ⎞
⎛ Zr ⎞ 2l +1 ⎛ 2Zr ⎞
Rnl (r ) = C ⎜
⎟ exp ⎜ −
⎟ Ln+l ⎜
⎟.
na
na
0 ⎠
⎝ 0⎠
⎝
⎝ na0 ⎠
В последнем равенстве мы снабдили радиальную волновую функцию индексами “ n ” и “ l ”, чтобы подчеркнуть ее зависимость от главного квантового
числа и азимутального квантового числа.
Константу C находим из условия нормировки для радиальной волновой
функции
2
2l
⎛ 2Zr ⎞
⎛ 2 Zr ⎞ ⎧⎪ 2l +1 ⎛ 2 Zr ⎞ ⎫⎪ 2
2
=
(
)
exp
R
r
r
dr
C
∫0
∫0 ⎜⎝ na0 ⎟⎠ ⎜⎝ − na0 ⎟⎠ ⎨⎪ Ln+l ⎜⎝ na0 ⎟⎠ ⎬⎪ r dr = 1.
⎩
⎭
Используя значение интеграла (П5.6), из (9.19) легко найти
∞
2
2
∞
⎛ 2Z ⎞
C =⎜
⎟
⎝ na0 ⎠
3
2
(n − l − 1)!
2n {(n + l )!}
3
(9.19)
.
Учитывая, что угловая часть волновой функции определяется шаровыми
функциями Ylm (θ ,ϕ ) , окончательно для волновой функции частицы получаем
87
88.
§9. Движение в центральном полеψ nlm ( r,θ ,ϕ ) =
⎛ 2Z ⎞
=⎜
⎟
⎝ na0 ⎠
3
2
l
⎛ Zr ⎞ 2 l +1 ⎛ 2 Zr ⎞
( n − l − 1)! ⎛ 2 Zr ⎞
exp
⎜
⎟
⎜−
⎟ Ln+l ⎜
⎟ Ylm (θ ,ϕ ).
3
2n {( n + l )!} ⎝ na0 ⎠
⎝ na0 ⎠
⎝ na0 ⎠
(9.20)
Полученные волновые функции, а также значения энергии (9.18) описывают состояния атома водорода (в этом случае Z = 1) и водородоподобных атомов – ионизированных атомов He+ ( Z = 2 ), Li++ ( Z = 3 ) и тому подобных. ♦
Задача 9.4. Для основного состояния атома водорода найти:
1) наиболее вероятное расстояние между электроном и ядром;
2) среднее значение модуля кулоновской силы, действующей на электрон;
3) среднее значение потенциальной энергии электрона в поле ядра.
Решение. Из (9.20) следует, что волновая функция атома водорода в основном состоянии
⎛ r ⎞
1
exp ⎜ − ⎟ .
ψ 100 (r ) =
π a03
⎝ a0 ⎠
1) Вероятность того что, частица находится в области от r до r+dr, определяется выражением:
2
dP = 4π ψ 1,0,0 ( r ) r 2 dr .
Тогда наиболее вероятное расстояние между электроном и ядром соответству2
ет максимуму функции 4π ψ 1,0,0 ( r ) r 2 . Дифференцируя ее по r и приравнивая
производную нулю, получим rвер = a0 .
e2
2) Среднее значение кулоновской силы F ( r ) = 2 , действующий на электрон,
r
определяется следующей формулой:
∞
F (r ) = 4π e ∫ψ
2
0
2
1,0,0
∞
⎛ 2 ⎞
4e2
2e2
(r )dr = 3 ∫ exp ⎜ − r ⎟dr = 2 .
a0 0
a0
⎝ a0 ⎠
e2
3) Среднее значение потенциальной энергии электрона в поле ядра U ( r ) = −
r
вычисляется аналогично
∞
U = −4π e ∫ψ
2
0
2
1,0,0
∞
⎛ 2 ⎞
4e2
e2
(r) rdr = − 3 ∫ exp ⎜ − r ⎟ rdr = − . ♦
a0 0
a
⎝ a0 ⎠
88
89.
§9. Движение в центральном полеЗадачи для самостоятельного решения
9.5. Частица находится в сферически-симметричном потенциальном поле в
⎛ r⎞
exp ⎜ − ⎟
1
⎝ a ⎠ , где r – расстояние от центра
стационарном состоянии ψ =
r
2π a
поля. Найти среднее значение r .
9.6. Для водородоподобного атома найти кратность вырождения k уровня с
номером n .
9.7. Для водородоподобного атома найти явный вид волновых функций состояний со значением главного квантового числа n = 2 . Показать, что эти
функции нормированы на единицу.
9.8. Найти среднее значение r k ( k = −1,0,1,2,... ) в 2s-состоянии водородоподобного атома.
Ответы к задачам для самостоятельного решения
a
.
2
9.6. k = n2 .
9.5. r =
⎧ψ 2,0,0 ( r ) = R2,0 ( r ) Y0,0 (θ ,ϕ )
R2,0 ( r ) =
⎪
⎪ψ 2,1,1 ( r ) = R2,1 ( r ) Y1,1 (θ ,ϕ )
9.7. ⎨
;
,
r
R
r
Y
ψ
=
θ
ϕ
(
)
(
)
(
)
2,1
1,0
⎪ 2,1,0
⎪ψ
R2,1 ( r ) =
⎩ 2,1,−1 ( r ) = R2,1 ( r ) Y1,−1 (θ ,ϕ )
n
1⎛ a ⎞
9.8. ⎜ 0 ⎟ ( k 2 + 3k + 4 ) ( k + 2 )!.
8⎝ Z ⎠
89
3
2
⎛ Zr ⎞⎛
1 ⎛Z⎞
Zr ⎞
⎜ ⎟ exp ⎜ −
⎟⎜ 1 −
⎟
2 ⎝ a0 ⎠
⎝ 2a0 ⎠⎝ 2a0 ⎠
3
2
⎛ Zr ⎞⎛ Zr ⎞
1 ⎛Z⎞
exp
⎜ ⎟
⎜−
⎟⎜
⎟
2 6 ⎝ a0 ⎠
⎝ 2a0 ⎠⎝ 2a0 ⎠
.
90.
§11. Спин микрочастицы§ 10. ЭЛЕМЕНТЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
В предыдущих параграфах мы описывали состояние квантовой системы,
используя зависящую от координат волновую функцию. Это, однако, не является единственным способом описания состояния. Зачастую в задачах следует
найти вероятности того, что система примет то или иное значение импульса,
энергии, любой другой физической величины. При этом удобно рассматривать
волновую функцию как функцию этой физической величины. Квадрат модуля
волновой функции даст нам плотность распределения вероятности по данной
физической величине.
Рассмотрим частицу в состоянии, описываемом волновой функцией
ψ ( r ) , где r – радиус-вектор частицы. Пусть F – эрмитовый оператор, обладающий, для определенности, дискретным спектром и действующий в том же
пространстве, в котором определена функция ψ ( r ) . Обозначим собственные
функции оператора F посредством ϕFn ( r ) , Fn – собственные значения оператора F . Согласно свойству (3.5) эрмитова оператора функцию ψ ( r ) можно
разложить по функциям ϕFn ( r ) :
ψ ( r ) = ∑ aF ϕ F ( r ) ,
n
n
n
где коэффициенты разложения
a Fn ≡ a ( Fn ) = ∫ ϕ F*n (r )ψ (r ) dr .
(10.1)
Коэффициенты разложения a( Fn ) можно рассматривать в качестве вол-
новой функции частицы в F -представлении, в то время как функция ψ ( r ) яв-
ляется волновой функцией системы в координатном или r -представлении.
2
Квадрат модуля волновой функции в F -представлении a ( Fn ) определяет вероятность наблюдения величины Fn .
Все сказанное выше справедливо и для оператора F , обладающего непрерывным спектром, а именно (см. формулу (3.6))
ψ ( r ) = ∫ a F ϕ F ( r ) dF ,
a F ≡ a ( F ) = ∫ ϕ F* (r )ψ (r ) dr ,
(10.2)
где ϕ F ( r ) - собственные функции оператора F , а a ( F ) - волновая функция
2
состояния в F -представлении. Величина a( F ) дает плотность распределения
вероятности величины F .
90
91.
§11. Спин микрочастицыТаким образом, одно и то же состояние частицы может описываться различными волновыми функциями в зависимости от выбранного представления.
При этом знание волновой функции в каком-нибудь одном представлении однозначно определяет ее вид в любом другом представлении (формулы (10.1),
(10.2)). Наиболее важными представлениями являются импульсное ( F = p ),
энергетическое ( F = E ) и представление z -компоненты момента импульса (
F = Lz ).
Поскольку в случае дискретного спектра оператора F волновая функция
a( Fn ) в F -представлении зависит от дискретной переменной, то в определении скалярного произведения функций (2.2) интегрирование по непрерывным
переменным q должно быть заменено суммированием по Fn , т.е. скалярное
произведение функций a( Fn ) и b( Fn ) определяется соотношением
a b = ∑ a * ( Fn )b ( Fn ) .
(10.3)
n
Задача 10.1. Собственная функция оператора координаты частицы x в
координатном представлении, отвечающая собственному значению x0 ,
ψ x ( x ) =δ ( x − x0 ) (см. задачу 3.3). Найти собственную функцию ax ( px ) опе0
0
ратора x в импульсном представлении.
Решение. Собственная функция оператора p x в координатном представлении (см. задачу 3.2)
i
px x
1
ϕ px ( x ) =
e .
2π
С учетом этого по формуле (10.2) получаем
i
i
− px x
− px x0
1
1
*
ax0 ( px ) = ∫ ϕ px ( x)ψ x0 ( x) dx = ∫
e
δ ( x − x0 ) dx =
e
.♦
2π
2π
Задача 10.2. Собственная функция оператора проекции импульса частицы p x в координатном представлении, отвечающая собственному значению
i 0
px x
1
e
(см. задачу 3.2). Найти собственную функцию
p , ψ p0 ( x ) =
x
2π
a p0 ( p x ) оператора p x в импульсном представлении.
0
x
x
Решение. Поскольку
i
px x
1
ϕ px ( x ) =
e ,
2π
то по формуле (10.2) находим
91
92.
§11. Спин микрочастицыa p0 ( px ) = ∫ ϕ ( x )ψ p0 ( x ) dx =
*
px
1
∫e
−
i
( px − px ) x
0
dx = δ ( px − px0 ) .
2π
В последнем равенстве учтены формула (П3.8) и (П3.9). ♦
Задача 10.3. Состояние системы описывается волновой функцией в координатном представлении
2
⎛
1
1⎛ x⎞ ⎞
exp ⎜ ik0 x − ⎜ ⎟ ⎟ ,
ψ ( x) =
⎜
2 ⎝ a ⎠ ⎟⎠
a π
⎝
k0 , a = const
(волновой пакет). Найти для данного состояния волновую функцию в импульсном представлении и распределение вероятности по импульсу.
Решение. В соответствии с (10.2) получаем для функции a ( px ) , описывающей волновой пакет в импульсном представлении,
x
x
1
a ( px ) =
2π
∫
1
1⎛ x ⎞
ik0 x − ⎜ ⎟
2⎝ a ⎠
e
a π
Выделив в показателе экспоненты полный квадрат
2
e
i
− px x
dx .
2
2
(10.4)
2
⎛x ⎛p
⎛ x⎞
⎛ px
⎞
⎞ ⎞ ⎛p
⎞
− k0 ⎟ x = ⎜ + i ⎜ x − k0 ⎟ a ⎟ + ⎜ x − k0 ⎟ a 2 ,
⎜ ⎟ + 2i ⎜
⎝a⎠
⎝
⎠
⎠ ⎠ ⎝
⎠
⎝a ⎝
x ⎛p
⎞
и сделав замену η = + i ⎜ x − k0 ⎟ a , перепишем (10.4) в виде:
a ⎝
⎠
1
2
⎛ 1⎛ p
− η2
1
⎞ 2⎞ a
x
exp ⎜ − ⎜
dη e 2 .
− k0 ⎟ a ⎟
⎜
⎟
2π
⎠
⎝ 2⎝
⎠ a π
Принимая во внимание, что
∫
∞
∫η
d
1
− η2
e 2
= 2π (см. приложение 2),
−∞
окончательно получаем вид волновой функции в импульсном представлении
2
⎛ 1⎛ p
x0
⎞ 2⎞
x
exp ⎜ − ⎜
a ( px ) =
− k0 ⎟ a ⎟ ,
⎜ 2⎝
⎟
⎠
π
⎝
⎠
а также гауссовское распределение вероятности для импульса
2
⎛ ⎛p
2
x0
⎞ 2⎞
a ( px ) =
exp ⎜ − ⎜ − k0 ⎟ a ⎟ .♦
⎜ ⎝
⎟
π
⎠
⎝
⎠
При изменении представления, помимо волновой функции, изменяется
также вид операторов физических величин. До сих пор мы рассматривали операторы, как функции координат, т.е. в r –представлении. Пусть в координат92
93.
§11. Спин микрочастицыном представлении задан оператор K , который, действуя на функцию ψ (r ) ,
дает функцию ψ (r) :
ψ (r ) = Kψ (r ) .
(10.5)
Найдем вид оператора K в F -представлении. Вначале будем считать, что
оператор F обладает дискретным спектром, а его собственные функции попрежнему будем обозначать посредством ϕ Fn (r ) . Умножим обе части (10.5) на
ϕ F* (r) и проинтегрируем по всему объему dr :
n
∫ϕ
(r )ψ (r )dr = ∫ ϕ F*n (r ) Kψ (r )dr .
*
Fn
(10.6)
В левой части данного равенства, согласно (10.1), стоит получающаяся в результате действия оператора K волновая функция a( Fn ) в F -представлении.
Используя разложение ψ ( r ) = ∑ a ( Fm )ϕ Fm ( r ) , правую часть (10.6) запишем в
m
виде
∫ϕ
*
Fn
(r ) Kψ (r ) dr = ∑ a ( Fm ) ∫ ϕ F*n (r ) Kϕ Fm (r ) dr .
m
Тогда, имеем
a ( Fn ) = ∑ a ( Fm ) ∫ ϕ F*n (r ) Kϕ Fm (r ) dr ,
m
или, используя дираковские обозначения ∫ ϕ F*n (r ) Kϕ Fm (r )dr ≡ ϕ Fn K ϕ Fm ,
a ( Fn ) = ∑ ϕ Fn K ϕ Fm a ( Fm ) .
(10.7)
m
Данное равенство есть не что иное, как равенство (10.5) в F представлении. Тем самым, зная все величины ϕ Fn K ϕ Fm , мы можем по
формуле (10.7) найти волновую функцию a( Fn ) по заданным a ( Fm ) . Поэтому
совокупность всех величин ϕ Fn K ϕ Fm
следует рассматривать, как оператор
K в F -представлении.
Введем обозначения ϕ Fn K ϕ Fm ≡ K nm , a( Fn ) ≡ a n , a ( Fm ) ≡ am . Тогда равенство (10.7) принимает вид:
a n = ∑ K nm a m .
(10.8)
m
Совокупность величин K nm , представляющая оператор K , может быть записана в виде квадратной матрицы, вообще говоря, с бесконечным числом строк
и столбцов:
93
94.
§11. Спин микрочастицы⎛ K11
⎜K
⎜ 21
K = ⎜ ...
⎜
⎜ K n1
⎜ ...
⎝
... K1m ... ⎞
... K 2 m … ⎟
⎟
... … … ⎟ .
⎟
... K nm … ⎟
... ... ... ⎟⎠
K12
K 22
...
Kn 2
...
(10.9)
Величины K nm суть матричные элементы. Каждый матричный элемент имеет
два индекса. Первый есть номер строки, второй – номер столбца.
В случае матричной записи совокупности величин a n и an следует рассматривать как векторы-столбцы, т.е.
⎛ a1 ⎞
⎛ a1 ⎞
⎜ ⎟
⎜a ⎟
⎜ a2 ⎟
⎜ 2⎟
⎜
⎟
an =
an = ⎜ ⎟ .
,
⎜ ⎟
⎜ ⎟
⎜ an ⎟
⎜ an ⎟
⎜ ⎟
⎜⎜ ⎟⎟
⎝ ⎠
⎝ ⎠
При этом выражение (10.8) принимает вид:
⎛ a1 ⎞ ⎛ K11
⎜ ⎟ ⎜
⎜ a 2 ⎟ ⎜ K 21
⎜ ⎟ = ⎜ ...
⎜ ⎟ ⎜
⎜ a n ⎟ ⎜ K n1
⎜ ⎟ ⎜ ...
⎝ ⎠ ⎝
K12
... K1m
K 22 ... K 2 m
... ... …
K n 2 ... K nm
...
...
...
... ⎞⎛ a1 ⎞
⎟
… ⎟⎜
⎟⎜ a2 ⎟
… ⎟⎜ ⎟ ,
⎟⎜ ⎟
… ⎟⎜ an ⎟
⎟
... ⎟⎜
⎠⎝ ⎠
а скалярное произведение (10.3) функций an и bn можно записать как
a b = ( a1*
a2* … an*
⎛ b1 ⎞
⎜b ⎟
⎜ 2⎟
…) ⎜ ⎟ .
⎜ ⎟
⎜ bn ⎟
⎜ ⎟
⎝ ⎠
Задача 10.4. Показать, что оператор F в F -представлении имеет вид
диагональной матрицы, все диагональные элементы которой представляют собой собственные значения оператора F .
Решение. Пусть ϕn – собственные функции оператора F в координатном представлении, а Fm - его собственные значения. Тогда матричный элемент
94
95.
§11. Спин микрочастицыFnm = ϕ n F ϕ m = ϕ n Fm ϕ m = Fm ϕ n ϕ m = Fm δ mn . ♦
Задача 10.5. Записать матрицы операторов Гамильтона, координаты и
импульса одномерного гармонического осциллятора в энергетическом представлении.
Решение. Обозначим собственные функции гармонического осциллятора
в координатном представлении посредством ψ n , т.е.
Hψ n = Enψ n ,
(10.10)
где En – значения энергии осциллятора. Учитывая (10.10), находим:
H nm = ψ n H ψ m = ψ n Emψ m = Em ψ n ψ m = Emδ nm .
1⎞
⎛
Так как (см. задачу 7.1) Em = ω ⎜ m + ⎟ , то оператор Гамильтона в энер2⎠
⎝
гетическом представлении имеет вид бесконечной диагональной матрицы:
⎛ ω
⎞
0
0
0
…
⎜ 2
⎟
⎜
⎟
⎜ 0 3 ω 0
0
…⎟
⎜
⎟
2
H =⎜ 0
0
…
…⎟.
⎜
⎟
⎜
⎟
1
⎛
⎞
ω ⎜ n + ⎟ …⎟
0
⎜ 0
2⎠
⎝
⎜
⎟
⎜
⎟
⎝
⎠
Поскольку для гармонического осциллятора нумерация уровней энергии En
начинается с n = 0 , то первая строка и первый столбец матрицы оператора Гамильтона соответствуют значениям n = 0, m = 0 .
Найдём теперь операторы координаты и импульса. В задаче (7.6) были
получены выражения для матричных элементов координаты и импульса:
ψ n+1 x ψ n = x0
n +1
,
2
ψ n−1 x ψ n = x0
n
;
2
n +1
n
, ψ n−1 p x ψ n = −ip0
.
2
2
С помощью этих соотношений получаем:
ψ n+1 p x ψ n = ip0
95
96.
§11. Спин микрочастицы⎛
⎜
⎜
⎜
⎜
⎜
⎜
x = x0 ⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜⎜
⎝
0
1
2
0
0
1
2
0
1
0
0
1
0
3
2
0
0
⎞
…⎟
⎟
…
…⎟
⎟
⎟
⎟
…
…⎟
,
⎟
n +1
⎟
…⎟
2
⎟
⎟
…⎟
0
⎟⎟
⎠
…
3
2
n
2
и
⎛
⎜
⎜
⎜
⎜
⎜
⎜
p x = p0 ⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
0
i
2
0
0
i
2
−
0
…
0
−i
…
i
0
…
0
0
i
n
2
⎞
…⎟
⎟
… ⎟⎟
0
⎟
…⎟
0
⎟. ♦
n +1
…⎟
−i
⎟
2
⎟
…⎟
0
⎟
⎟
⎠
0
Задача 10.6. Записать оператор L z в Lz -представлении в случае системы
с орбитальным квантовым числом l = 1 .
Решение. Если l = 1 , то существует всего три собственные функции оператора L z , которые в координатном представлении суть Y1,−1 , Y1,0 и Y1,1 . Действие оператора L z на эти функции сводится к следующему (см. § 8):
L z Y1,−1 = − Y1,−1 ,
L z Y1,0 = 0Y1,0 ,
L z Y1,1 = + Y1,1 .
Учитывая данные соотношения и условие ортогональности шаровых функций,
находим:
96
97.
§11. Спин микрочастицыY1,n lz Y1,m = m δ nm ; n, m = −1,0,1 .
Таким образом, оператор L z представляется в виде матрицы
⎛− 0 0 ⎞
Lz = ⎜ 0 0 0 ⎟ . ♦
⎜
⎟
⎜ 0 0 + ⎟
⎝
⎠
F
Если оператор
обладает непрерывным спектром, то для
F-
представления оператора K справедливо выражение аналогичное (10.7)
(10.11)
a ( F ) = ∫ K ( F , F ′ ) a ( F ′ )dF ′ ,
где
K ( F , F ′ ) = ϕ F K ϕ F ′ ≡ ∫ ϕ F* (r ) Kϕ F ′ (r )dr .
(10.12)
Таким образом, здесь мы имеем дело с интегральным преобразованием.
K ( F , F ′ ) называется ядром интегрального преобразования. Заданием
K ( F , F ′ ) определяется оператор K в F -представлении.
Задача 10.7. Найти вид оператора импульса p x в импульсном представлении.
Решение. Согласно (10.12) ядро оператора p x в импульсном представлении
ϕ p p x ϕ p′ = ϕ p p′xϕ p′ = p′x ϕ p ϕ p′ = p′xδ ( p x − p′x ) , (10.13)
x
x
x
x
x
x
где ϕ px -собственные функции оператора импульса p x в координатном представлении. Таким образом оператор p x в p x -представлении можно задать соотношением (10.13).
Воспользуемся теперь формулой (10.11). Имеем:
a ( p x ) = ∫ p′xδ ( p x − p′x ) a ( p′x )dp′x ,
или, вычисляя интеграл
a ( px ) = px a ( px ) .
Поскольку по определению a ( px ) = p x a ( px ) , то оператор проекции импульса
p x в импульсном представлении сводится просто к умножению на p x . ♦
Задача 10.8. Найти вид оператора координаты x в импульсном представлении.
Решение. Аналогично предыдущей задаче ядро x в импульсном представлении
97
98.
§11. Спин микрочастицыϕ p x ϕ p′ =
x
x
∞
1
∫
2π
∂ ⎛ 1
=
⎜
i ∂p′x ⎝ 2π
e
i
− px x
i
xe
p′x x
dx =
−∞
∞
∫e
−
i
( px − p′x ) x
−∞
∞
1
∫
2π
i
xe
( p′x − px ) x
dx =
−∞
⎞
∂
dx ⎟ = −i
δ ( p′x − p x ) .
′
∂
p
x
⎠
.
(10.14)
Здесь мы учли, что собственные функции оператора p x в координатном предi
px x
1
e , а также воспользовались свойставлении (см. задачу 3.2) ψ px ( x ) =
2π
ствами δ -функции (П3.8) и (П3.9).
Далее, по формуле (10.11), находим:
+∞
⎛
⎞
∂
a( px ) = ∫ ⎜ −i
δ ( p′x − px ) ⎟ a( p′x )dp′x .
(10.15)
′
∂
p
⎠
x
−∞ ⎝
Интегрируя (10.15) по частям, получаем:
a( px ) = −i a ( p′x ) δ ( p′x − px )
∞
−∞
∞
∫ δ ( p′x − px )
+i
−∞
∂
a ( p′x ) dp′x .
∂p′x
(10.16)
В силу особенностей δ -функции подстановки в (10.16) дают 0, и в результате
∂
a( px ) = i
a ( px ) .
∂p x
Таким образом, оператор x в импульсном представлении может быть
∂
.♦
дан либо в виде (10.14), либо в виде дифференциального оператора i
∂px
Задачи для самостоятельного решения
10.9. Записать волновую функцию основного состояния водородоподобного
атома в импульсном представлении.
10.10. Доказать, что для матричных элементов эрмитова оператора K выполняется равенство:
*
.
K nm = K mn
10.11. Доказать, что матричные элементы
K L определяются равенством
( KL )nm
( KL )nm = ∑ K nk Lkm .
k
98
произведения операторов
99.
§11. Спин микрочастицы10.12. Используя матрицы операторов координаты x и импульса p одномерного гармонического осциллятора в энергетическом представлении (см. задачу
2
p
Mω2 2
+
x = H.
10.5), найти операторы x и p . Проверить, что
2M
2
+
1 ⎛ x
p⎞
1 ⎛ x
p⎞
i
,
a
i
+
=
−
10.13. Записать операторы a =
⎜
⎟
⎜
⎟ в энергетиp0 ⎟⎠
p0 ⎟⎠
2 ⎜⎝ x0
2 ⎜⎝ x0
ческом представлении гармонического осциллятора.
2
2
10.14. Записать операторы L x и L y в Lz -представлении для системы с орбитальным моментом l = 1.
10.15. Записать операторы L+ и L− в L z -представлении для системы с орбитальным моментом l = 1.
Ответы к задачам для самостоятельного решения
8⎛ a ⎞
10.9. a1,0,0 ( p ) = ⎜ 0 ⎟
π ⎝2 Z ⎠
3/2
1
(1 + ( a p
0
Z)
)
2 2
, a0 =
2
Me 2
.
10.12.
⎛
⎜
⎜
⎜
2
x02 ⎜
x = ⎜
2
⎜
⎜
⎜
⎜
⎝
⎛ 1
⎜
⎜ 0
⎜
2
p02 ⎜ − 2
p =
2 ⎜ 0
⎜
⎜
⎜
⎜
⎝
0
…
0
6
…
0
5
0
…
6
0
1
0
0
3
2
0
2
0
2n + 1
n ( n − 1)
0
− 2
0
3
0
− 6
0
5
0
− 6
0
0
⎞
⎟
…
…
⎟
⎟
…
…
⎟
⎟.
− ( n + 1)( n + 2 ) ⎟
0
⎟
2n + 1
0
⎟
⎟
0
⎠
…
− n ( n − 1)
n = 0,1,2,...
99
⎞
⎟
…
⎟
⎟
…
⎟
⎟,
n
n
+
1
+
2
( )(
)⎟
⎟
0
⎟
⎟
⎠
…
…
100.
§11. Спин микрочастицы10.13.
⎛0
⎜
⎜0
⎜0
a=⎜
⎜0
⎜
⎜0
⎜
⎝
1
0
0
⎛0
⎜1
⎜
⎜0
+
a =⎜
⎜0
⎜
⎜0
⎜0
⎝
2
0
0
0
0
0
0
0
0
3 0
0 …
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
3 0
0
0
0
0
2
0
n
… ⎞
⎟
… ⎟
… ⎟⎟
,
… ⎟
⎟
n +1⎟
⎟
⎠
…⎞
… ⎟⎟
…⎟
⎟,
…⎟
⎟
0⎟
⎟
⎠
n = 0,1,2,...
10.14.
⎛
⎜
⎜
⎜
Lx = ⎜ −
⎜
⎜
⎜
⎝
0
−
2
2
0
2
2
0
−
2
2
⎞
⎛
⎟
⎜ 0
⎟
⎜
⎜ 2
2 ⎟
i
−
⎟ , Ly = ⎜
2 ⎟
2
⎜
⎟
⎜
0 ⎟
⎜ 0
⎠
⎝
0
−
2
i
2
0
2
i
2
⎞
⎟
⎟
2 ⎟
i ⎟.
−
2 ⎟
⎟
0 ⎟
⎠
0
10.15.
⎛0 − 2
⎜
L− = ⎜ 0
0
⎜0
0
⎜
⎝
0 ⎞
⎛ 0
⎟
⎜
− 2 ⎟ ; L+ = ⎜ − 2
⎜ 0
0 ⎟⎟
⎝
⎠
100
0
0
− 2
0⎞
⎟
0⎟ .
0 ⎟⎠
101.
§11. Спин микрочастицы§ 11. СПИН МИКРОЧАСТИЦЫ
Ряд экспериментальных фактов указывает на существование у микрочастиц специфической внутренней степени свободы. Этой степени свободы
приписывают собственный момент импульса микрочастицы, не связанный с ее
движением в пространстве и получивший название спина. Спин является неотъемлемым свойством микрочастицы (как, например, масса, заряд и т.п.) и
имеет сугубо квантовый и, строго говоря, релятивистский характер. При переходе к классической механике он обращается в нуль. Спин частицы является
вектором. Как и момент импульса спин будем измерять в единицах ħ. В соответствии с общими принципами квантовой механики спину ставят в соответствие линейный эрмитовый оператор, который обозначим посредством S .
Коммутационные соотношения для оператора спина имеют такой же вид, как
для оператора момента импульса (см. § 9). В частности,
⎡S 2 , S z ⎤ = 0 .
(11.1)
⎢⎣
⎥⎦
Однако, в отличие от оператора момента импульса, оператор спина действует не на обычные координаты r , а на некоторые “особые”, так называемые, спиновые переменные. Обозначим их буквой σ . Будем предполагать, что
волновую функцию частицы ψ ( r , σ ) можно представить в виде
ψ ( r , σ ) = ϕ ( r ) χ (σ ) .
В этом случае функцию ϕ ( r ) называют координатной волновой функцией, а
χ (σ ) - спиновой волновой функцией. В данном параграфе нас будет интересовать только спиновая волновая функция.
Из (11.1) следует, что собственные значения квадрата спина и проекции
спина на ось z могут быть одновременно измерены. Собственные значения
2
оператора S равны
2
s ( s + 1) , где s может быть любым целым (включая зна-
чение ноль), либо полуцелым числом. При этом проекция спина (собственное
значение оператора
S z ) S z = ms , где ms
может пробегать значения
s, s − 1,..., −s - всего 2s + 1 значений. Величина ms называется магнитным спиновым квантовым числом. Так, например, для электрона, протона, нейтрона s=
1
1
, а ms может принимать только два значения ± .
2
2
Оператор спина удобно записывать в S z -представлении. При этом аргу-
ментом волновой функции χ (σ ) будет являться индекс, нумерующий собст101
102.
§11. Спин микрочастицывенные значения оператора S z (см. § 10). В качестве этого индекса принято
использовать значения магнитного спинового квантового числа ms . Таким образом, спиновая переменная σ является дискретной и может принимать значения (при заданном s ) s, s − 1,..., −s .
1
Рассмотрим частицу со спином s = . Поскольку в этом случае число
2
наблюдаемых значений проекции спина электрона равно двум, то спиновая
⎛1⎞
⎛ 1⎞
волновая функция частицы имеет две компоненты χ ⎜ ⎟ и χ ⎜ − ⎟ . В даль⎝2⎠
⎝ 2⎠
нейшем, для удобства, будем обозначать эти компоненты посредством
⎛1⎞
⎛ 1⎞
a ≡ χ ⎜ ⎟ и b ≡ χ ⎜ − ⎟ Формально такую двухкомпонентную волновую
⎝2⎠
⎝ 2⎠
⎛a⎞
⎝b⎠
функцию можно записать в виде матрицы-столбца (спинора) χ = ⎜ ⎟ . Стандартные условия, налагаемые на спиноры, сводятся к тому, что их элементы
должны быть однозначны и ограничены.
1
Оператор спина для s = в S z -представлении имеет следующий вид:
2
S=
2
σ,
где σ – вектор, компоненты которого
⎛ 0 1⎞
⎛ 0 −i ⎞
⎛1 0 ⎞
=
σ
z
,
⎜ 0 −1⎟ .
0 ⎟⎠
⎝
⎠
σx =⎜
⎟, σ y = ⎜ i
⎝ 1 0⎠
⎝
Матрицы σ x , σ y , σ z называются матрицами Паули.
1
Задача 11.1. Найти для частицы со спином s = собственные значения и
2
собственные функции операторов а) S x , б) S y , в) S z .
Решение. а) Обозначим собственные значения оператора S x посредством
S x , а его собственные функции запишем в виде
ны находятся из уравнения
S x χ Sx = S x χ Sx :
102
⎛a⎞
χ S = ⎜ ⎟ . Искомые величи⎝b⎠
x
103.
§11. Спин микрочастицы⎛ 0 1 ⎞⎛ a ⎞
⎛a⎞
⎜ 1 0 ⎟⎜ b ⎟ = S x ⎜ b ⎟ ,
2⎝
⎠⎝ ⎠
⎝ ⎠
или
⎛b⎞
⎛a⎞
=
S
x
⎜ ⎟
⎜b⎟.
2⎝a⎠
⎝ ⎠
Отсюда следует, что S x равно ± . При этом a = b , если S x = и a = −b , при
2
2
Sx = − .
2
Из условия нормировки имеем:
a
( a* b* ) ⎛⎜ b ⎞⎟ = a 2 + b 2 = 2 a 2 = 1,
⎝ ⎠
1
.
и, следовательно, a = b =
2
Таким образом, для собственных значений S x =
соответственно, следующие собственные
1 ⎛ 1⎞
1 ⎛1⎞
и χ
χ
=
=
⎜
⎟
⎜ −1⎟ .
Sx =
S x =−
1
2
2
⎝ ⎠
⎝ ⎠
2
2
2
и Sx = −
функции
2
получаем,
оператора
Sx :
Абсолютно аналогично находим:
б) χ
S
в) χ
y=
Sz =
1 ⎛1⎞
1 ⎛1⎞
=
χ
⎜ ⎟ и S y =−
⎜ ⎟;
2 ⎝i⎠
2 ⎝ −i ⎠
2
⎛1⎞
⎛0⎞
=⎜ ⎟ и χ
= ⎜ ⎟. ♦
S z =−
⎝0⎠
⎝1⎠
2
=
2
2
Задача 11.2. Указать вид оператора проекции спина на произвольное
направление, задаваемое единичным вектором n .
Решение. Оператор проекции спина на направление, задаваемое единич-
ным вектором n , можно записать в виде скалярного произведения S n = nS , где
{
}
n = {nx , n y , nz } = {sin θ cosϕ ,sin θ sin ϕ ,cosθ } и S = S x , S y , S z . Тогда получим:
103
104.
§11. Спин микрочастицы1
(sin θ cosϕσ x + sin θ sin ϕσ y + cosθσ z ) =
2
0
sin θ cosϕ ⎞ ⎛
0
−i sin θ sin ϕ ⎞ ⎛ cosθ
1 ⎡⎛
= ⎢⎜
+
⎟ ⎜ i sin θ sin ϕ
⎟+⎜ 0
0
0
2 ⎣⎝ sin θ cosϕ
⎠ ⎝
⎠ ⎝
Sn =
0 ⎞⎤
=
cosθ ⎟⎠⎥⎦
e−iϕ sin θ ⎞
⎟.
cosθ ⎠
1 ⎛ cosθ
=
⎜
2 ⎝ eiϕ sin θ
Задача 11.3. Частица со спином s =
♦
1
находится в состоянии с опреде2
ленным значением проекции спина Sz = . Определить вероятности возмож2
ных значений проекции спина на ось z′ , если угол между осями z и z′ равен
θ.
Решение. Согласно предыдущей задаче оператор
⎛ cosθ
e −iϕ sin θ ⎞
S z′ = ⎜ iϕ
⎟.
2 ⎝ e sin θ
cosθ ⎠
Спиновая волновая функция частицы со значением Sz =
2
есть (см. зада-
чу 11.1 (в))
⎛1⎞
=⎜ ⎟
Sz =
⎝0⎠
2
По определению среднее значение спина в направлении оси z′
⎛ cosθ
e− iϕ sin θ ⎞ ⎛ 1 ⎞
S z′ = χ 1 S z′ χ 1 = (1 0 ) ⎜ iϕ
⎟ ⎜ ⎟ = cosθ .
Sz =
Sz =
2
sin
cos
e
θ
θ
2
2
⎝
⎠⎝ 0⎠ 2
χ
С другой стороны,
⎛ ⎞
Sz′ = w+ + ⎜ − ⎟ w− ,
2
⎝ 2⎠
где w+ и w− — вероятности проекций спина вдоль и противоположно направ-
лению оси z′ соответственно.
Из последних двух уравнений следует, что
w+ − w− = cos θ .
(11.2)
Кроме того, очевидно, равенство
w+ + w− = 1 .
2
Из (11.2) и (11.3) получаем: w+ = cos
θ
2
и w− = sin 2
104
(11.3)
θ
2
. ♦
105.
§11. Спин микрочастицыЗадача 11.4. Спиновая часть гамильтониана для частицы со спином
1
, находящейся в однородном стационарном магнитном поле, направлен2
ном вдоль оси z , имеет вид: H = − μH σ z , где H – напряженность магнитного поля, а μ = const – магнитный момент частицы. Найти зависимость от времени спиновой волновой функции и средних значений компонент вектора
спина такой частицы.
∂χ ( t )
= H χ ( t ) для спиновой волноРешение. Уравнение Шредингера i
∂t
⎛ a(t ) ⎞
вой функции χ ( t ) = ⎜
⎟ сводится к уравнениям:
⎝ b(t ) ⎠
s=
d
d
a (t ) = iω a (t ) , b(t ) = −iωb(t ) ,
dt
dt
где ω =
μH
. Отсюда находим:
a(t ) = a(0)exp ( iωt ) , b(t ) = b(0) exp ( −iωt ) ,
где a(0) и b(0) определяются начальными условиями. Причем, из условия
нормировки волновой функции
⎛ a(t ) ⎞
2
2
χ (t ) χ (t ) = ( a* (t ) b* (t ) ) ⎜
= a(t ) + b(t ) = 1
⎟
⎝ b(t ) ⎠
2
2
следует, что a (0) + b(0) = 1 .
Среднее значение
s x (t ) = χ ( t )
2
σ x χ (t ) =
( a (t )
2
*
⎛ 0 1 ⎞⎛ a (t ) ⎞
b * (t ) ) ⎜
⎟⎜ b(t ) ⎟ =
1
0
⎝
⎠⎝
⎠
= b* (t ) a (t ) + a* (t )b(t ) = b* (0) a (0)e 2iωt + a* (0)b(0)e −2iωt =
2
2
=
( b (0)a(0) + a (0)b(0) ) cos 2ωt + i 2 ( b (0)a(0) − a (0)b(0) ) sin 2ωt.
2
*
*
*
*
Учитывая, что
sx (0) = χ (0)
=
2
σ x χ (0) =
( a (0)
2
*
( b (0)a(0) + a (0)b(0) )
2
*
*
и
105
⎛ 0 1 ⎞⎛ a(0) ⎞
b* (0) ) ⎜
⎟⎜
⎟=
⎝ 1 0 ⎠⎝ b(0) ⎠ ,
(11.4)
106.
§11. Спин микрочастицыs y (0) = χ (0)
=i
2
σ y χ (0) =
( a (0)
2
*
( b (0)a(0) − a (0)b(0) )
2
*
⎛ 0 −i ⎞⎛ a(0) ⎞
b* (0) ) ⎜
⎟⎜ b(0) ⎟ =
i
0
⎝
⎠⎝
⎠ ,
*
перепишем (11.4) в виде
sx (t ) = sx (0) cos 2ωt + s y (0) sin 2ωt .
(11.5)
Аналогично (11.5) получаем
s y (t ) = s y (0) cos 2ωt − sx (0) sin 2ωt ,
s z (t ) = s z (0) = const . ♦
Задача 11.5. Вычислить скалярное произведение S1S 2 спинов двух час1
1
тиц ( s1 = , s2 = ) в состояниях, в которых суммарный спин S = S1 + S 2 имеет
2
2
определенные значения s = 1 (триплетное состояние) и s = 0 (синглетное состояние).
Решение. Оператор суммарного спина системы имеет вид
S = S1 + S 2 .
Возводя обе части данного равенства в квадрат и учитывая, что коммутатор
⎡S1, S2 ⎤ = 0 (поскольку операторы S1 , S 2 действуют на спиновые координаты
⎣
⎦
разных частиц), имеем
2
2
2
S = S1 + S 2 + 2S1S 2 .
Отсюда
(
)
2
2
1 2
S − S1 − S 2 ,
2
или, переходя к собственным значениям,
S1S 2 =
S1S2 =
2
{s(s + 1) − s1(s1 + 1) − s2 (s2 + 1)} =
2
Согласно (11.6), в триплетном состоянии ( s = 1 )
S1S2 =
а в синглетном состоянии ( s = 0 )
2
4
,
3 2
S1S2 = −
.♦
4
106
2
3⎫
⎧
⎨s(s + 1) − ⎬ .
2⎩
2⎭
(11.6)
107.
§11. Спин микрочастицыЗадачи для самостоятельного решения
11.6. Нормировать спиновые волновые функции:
⎛a⎞
а) χ = A⎜ ⎟ ( a, b ≠ 0 );
b
⎝ ⎠
⎛3⎞
б) χ = A ⎜ ⎟ .
⎝ 4i ⎠
11.7. Пользуясь явным видом матриц Паули, проверить справедливость следующих выражений:
а) ⎡σ x , σ y ⎤ = 2iσ z ,
⎣
⎦
б) σ i σ j + σ j σ i = 2δ ij 1 , где i,j= x, y, z,
2
в) σ = 31 .
( )
n
11.8. Упростить выражение a ⋅ σ , где n – целое неотрицательное число, a –
вещественный числовой вектор.
11.9. Найти собственные значения оператора F = a + b ⋅ σ , где a – вещественное число, b - вещественный числовой вектор.
11.10. Атом водорода помещен в направленное вдоль оси z внешнее магнитное поле напряженности H . Для электрона найти
11.11. Вычислить квадрат проекции спина
2
d sx
d sy
и
.
dt
dt
на произвольное направление.
Ответы к задачам для самостоятельного решения
1
2
2 −1/2
11.6. а) A = a + b
; б) A = .
5
(
)
( )
11.8. a n - для четных n и a n −1 a ⋅ σ - для нечетных n .
11.9. F1,2 = a ± b.
11.10.
d sx
d sy
= μH s y ,
= − μH s x ; μ = const – магнитный момент электрона.
dt
dt
2
11.11.
4
.
107
108.
§12. Стационарная теория возмущений. Вырожденный случай§ 12. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ.
НЕВЫРОЖДЕННЫЙ СЛУЧАЙ
Точное аналитическое решение уравнения Шрёдингера и определение
энергии стационарных состояний системы возможно только для некоторых
простых систем (например, прямоугольная потенциальная яма с бесконечно
глубокими стенками, линейный гармонический осциллятор, атом водорода). В
большинстве случаев для определения собственных значений и собственных
функций гамильтониана необходимо использовать приближенные методы вычисления. Одним из таких методов является теория возмущений. Она применима в тех случаях, когда отклонение рассматриваемой системы от системы,
допускающей точное решение, можно представить в виде малой добавки (возмущения) к гамильтониану невозмущенной системы:
H = H0 +V
где H 0 — гамильтониан задачи, допускающей точное аналитическое решение, а V - некоторая малая добавка, называемая возмущением (оператором
возмущения). Теория возмущений подразделяется на стационарную и нестационарную. Стационарная теория (или теория возмущений для стационарных состояний) имеет дело с возмущениями, не зависящими от времени
(гамильтониан H 0 также предполагается не зависящим явно от времени).
Нестационарная теория (или метод вариации постоянных), рассматривает
системы, в которых оператор возмущения явно зависит от времени.
Предположим, что известны точные решения уравнения “невозмущенной” системы с гамильтонианом H 0
H 0 ψ n(0) = En(0) ψ n(0) .
(12.1)
Задачей стационарной теории возмущений является определение энергии и
волновых функций полного гамильтониана H через известные значения энергии En (0) и волновые функции ψ n (0) . В данном параграфе рассматривается случай систем с дискретным спектром энергии, для которых собственные значения оператора H 0 не вырождены.
Если возмущение V мало, то спектр En и собственные функции ψ n оператора H мало отличаются от En (0) и ψ n (0) . В этом случае решения возмущенного уравнения Шрёдингера (12.1) ищутся в виде разложения в ряд:
En = En
(0)
+ E n + En
(1)
(2)
108
∞
+ ... = ∑ En ( k ) ,
k =0
(12.2)
109.
§12. Стационарная теория возмущений. Невырожденный случайψ n =ψ n
+ψ n +ψ n
(0)
(1)
(2)
∞
+ ... = ∑ψ n ( k ) ,
(12.3)
k =0
где En (1) и ψ n (1) – поправки того же порядка малости, что и возмущение V ,
En (2) и ψ n (2) – поправки, квадратичные по возмущению, En ( k ) и ψ n ( k ) - поправки
k-го порядка малости по возмущению. Метод теории возмущений представляет собой метод последовательных приближений: сначала вычисляют поправки
того же порядка малости, что и возмущение, затем поправки, квадратичные по
возмущению и т. д.
Задача 12.1. Найти общий вид поправок к волновой функции и энергии
в первом порядке теории возмущений.
Решение. Подставляя (12.2) и (12.3) в стационарное уравнение Шрёдингера Hψ = Eψ , получим
(H
)
+ V (ψ n(0) + ψ n(1) + ψ n(2) + ...) =
0
= (E
(0)
n
+E +E
(1)
n
(2)
n
+ ...)(ψ
(0)
n
+ψ
(1)
n
+ψ
(2)
n
+ ...) .
(12.4)
Ограничимся в (12.4) членами, порядок малости которых не превышает первого, т.е. членами, содержащими H 0 , V , En(0) , En(1) , ψ n(0) , ψ n(1) . Тогда из (12.4) имеем:
H 0ψ n(0) + Vψ n(0) + H 0ψ n(1) + Vψ n(1) = En(0)ψ n(0) + En(1)ψ n(0) + En(0)ψ n(1) + En(1)ψ n(1) .
Отметим, что члены Vψ n(1) и En(1)ψ n(1) содержат по два множителя первого порядка малости, являясь, тем самым, членами второго порядка малости, и, следовательно, ими также надо пренебречь. Принимая также во внимание уравнение Шрёдинегра для невозмущенной системы (12.1), получим:
(H
0
)
(
)
− En(0) ψ n(1) = − V − En(1) ψ n(0) .
(12.5)
Волновую функцию ψ n(1) будем искать в виде разложения по собственным функциям ψ k (0) невозмущенного оператора H 0 :
ψ n(1) = ∑ Cnkψ k (0) .
(12.6)
k
Подставим (12.6) в (12.5), умножим полученное равенство на ψ m(0)* и проинтегрируем по всему пространству. Уравнение (12.5) в этом случае примет вид:
(E
(0)
m
− En(0) ) Cnm = En(1)δ mn − Vmn .
(12.7)
Отсюда для m = n получаем:
En(1) = Vnn ,
109
(12.8)
110.
§12. Стационарная теория возмущений. Невырожденный случайа для m ≠ n :
Cnm =
Vmn
,
En (0) -Em (0)
где
Vmn = ψ m(0) V ψ n(0) = m V n = ∫ψ m(0)*Vψ n(0) dq
представляет собой матричный элемент оператора V по невозмущенным волновым функциям (оператор V предполагается эрмитовым, т.е. Vnm = Vmn* ). Отметим, что E n (1) равняется среднему значению «возмущения» в состоянии
ψ n (0) .
Уравнение (12.7), однако, не позволяет найти коэффициент Cnn , и нам
придётся определить его из условия нормировки волновой функции
ψ n = ψ n(0) + ψ n(1) :
ψ n ψ n = 1 = ψ n(0) + Cnnψ n(0) + ∑ ' Cnkψ k (0) ψ n(0) + Cnnψ n(0) + ∑ ' Cnmψ m (0) =
k
m
*
= 1 + Cnn ψ n(0) ψ n(0) + (1 + Cnn ) ∑ ' Cnk* ψ k (0) ψ n(0) + (1 + Cnn
) ∑ 'Cnm ψ n(0) ψ m(0) .
2
k
m
Здесь штрих у знака суммы означает пропуск слагаемого с m=n или k=n. В силу ортонормированности функций ψ n(0) все суммы во втором и третьем членах
равны нулю. Отсюда получаем, что
2
2
*
1 + Cnn = 1 + Cnn + Cnn
+ Cnn = 1.
Ограничиваясь первым порядком малости, мы должны пренебречь членом
2
Cnn , который является величиной второго порядка малости. Отсюда получаем, что C nn = 0 . Таким образом,
ψ n(1) = ∑ '
m
Vmn
ψ m(0) , ♦
(0)
(En -Em )
(0)
(12.9)
Аналогично образом можно найти поправку второго порядка для энергии:
En
(2)
=∑
2
'
m
Vnm
.
(En (0) -Em (0) )
(12.10)
(2)
и коэффициенты С nm
в разложении поправки второго порядка ψ n( 2) к волновой
функции:
(2)
Cnm
=
⎛ ' VmkVkn
1
VnnVkn ⎞
'
−
⎜
⎟.
∑
∑
En (0) -Em (0) ⎝ k En (0) -Ek (0) k En (0) -Ek (0) ⎠
110
111.
§12. Стационарная теория возмущений. Невырожденный случайУсловие применимости теории возмущений записывается в следующем
виде:
Vnm
En (0) - Em (0)
(12.11)
для всех т≠п, т.е. недиагональные элементы матрицы оператора возмущения
V должны быть малы по сравнению с разностью значений энергии соответствующих невозмущенных состояний.
Задача 12.2. Показать, что поправка второго порядка к энергии основного состояния всегда отрицательна.
Решение. Энергия основного состояния минимальна. Поэтому, если индекс п примет значение, отвечающее основному состоянию, то во всех слагаемых выражения (12.10) будет E n (0) < Em (0) . Поэтому, поправка второго порядка
к энергии основного состояния всегда отрицательна. ♦
Задача 12.3. Для заряженной частицы, находящейся в одномерной бесконечно глубокой потенциальной яме в основном состоянии найти сдвиги
энергетических уровней в однородном электрическом поле (направленном
вдоль оси x ) в первых двух порядках теории возмущений.
Решение. Оператор возмущения определяется потенциальной энергией
частицы в однородном электрическом поле:
V = − eE x.
Зная вид волновых функций невозмущенного гамильтониана для данного слу(1)
чая ψ n(0) (см. задачу 6.1), можем определить En по формуле (12.8):
En(1) = Vnn = − eE ψ n(0) x ψ n(0) = − eE
2 a 2 ⎡ π ( n + 1) ⎤
a
sin ⎢
x ⎥ xdx = − eE ,
∫
a 0
2
⎣ a
⎦
(2)
где n=0,1,2…. Величину En определим по формуле (12.10). Для этого снача-
ла вычислим матричный элемент координаты (для n ≠ 0 ):
a
4 ⎡⎣(−1)n − 1⎤⎦
2
⎡ π ⎤ ⎡ π (n + 1) ⎤
(n + 1)a .
x0n = ∫ sin ⎢ x ⎥ sin ⎢
x ⎥ ⋅ xdx = 2 2
2
(
2)
+
a 0 ⎣a ⎦ ⎣ a
n
n
π
⎦
Это выражение отлично от нуля лишь для нечетных значений n . Далее, учитывая вид невозмущенного энергетического спектра частицы в яме (см. задачу
6.1), находим поправку второго приближения к основному уровню:
(2)
0
E
∞
=∑
n =1
e2E 2 x02n
⎡ π2 2 π2 2
2⎤
⎢ 2 Ma 2 − 2 Ma 2 ( n + 1) ⎥
⎣
⎦
=
512 Ma 4 e2E
111
π6
2
2
(k + 1)2
.
∑
5
5 ♦
k =0 (2k + 1) (2k + 3)
∞
112.
§12. Стационарная теория возмущений. Невырожденный случайЗадача 12.4. Частица находится вблизи дна одномерной потенциальной
ямы произвольной формы. Найти приближенные значения энергии частицы.
Решение. Пусть частица находится в потенциальной яме с потенциальной энергией U ( x ) . Совместим начало координат с минимумом потенциальной энергии и будем вести отсчет потенциальной энергии так, чтобы в точке
x = 0 она обращалась в нуль. Тогда, раскладывая потенциальную энергию в
ряд, имеем:
x2
x3
x4
U ( x) = U (0) + xU ′(0) + U ′′(0) + U ′′′(0) + U ′′′′(0) + ... ,
2
3!
4!
где штрих означает дифференцирование по x . Учтем, что U (0) = U ′(0) = 0 , и
U ′′′(0)
U ′′′′(0)
введем обозначения U ′′(0) = k ,
= ε1 ,
= ε 2 . Поскольку частица на3!
4!
ходится вблизи дна потенциальной ямы, то можно ограничиться лишь первыми членами разложения потенциальной энергии U ( x) . Ограничиваясь четвертым порядком малости по x , можем записать
kx2
U ( x) =
+ ε1 x 3 + ε 2 x 4 .
(12.12)
2
Первый член в (12.12) представляет собой потенциальную энергию гармонического осциллятора. Собственные значения энергии и волновые функции
kx 2
частицы, движущейся в потенциале U ( x ) =
найдены в задаче 7.1 и равны
2
соответственно
1⎞
⎛
En(0) = ω ⎜ n + ⎟ ( n = 0,1, 2,...) ,
2⎠
⎝
ψ
(0)
n
1
( x) =
2n n! x0 π
e
−x
2
2 x02
⎛ x⎞
Hn ⎜ ⎟ .
⎝ x0 ⎠
Рассмотрим оставшиеся члены в (12.12) как возмущение
V = ε1 x3 + ε 2 x 4 .
В первом порядке теории возмущений сдвиг уровней частицы определяется
диагональными матричными элементами:
+∞
En =
(1)
2
3
4
(0)
∫ (ε1x + ε 2 x ) ψ n ( x) dx .
−∞
Так как ψ n(0)
2
- четная функция x , то член x 3 не дает вклада в первую поправ-
ку E n (1) . Тогда первая поправка равна:
112
113.
§12. Стационарная теория возмущений. Невырожденный случай+∞
2
En = ε 2 ∫ x 4 ψ n(0) ( x) dx
(1)
−∞
и ее можно вычислить, заменив полином Эрмита в подынтегральном выражении согласно формуле (П4.12) и производя n-кратное интегрирование по частям. В результате получим:
En =
(1)
+∞
ε 2 x04
2n n! π
∫e
−ξ 2
−∞
dn 4
(ξ H n (ξ ))dξ .
dξ n
Здесь для удобства мы перешли к переменной ξ =
x
. Многочлен степени
x0
n + 4 под знаком интеграла, который требуется продифференцировать n раз,
начинается с членов:
⎛
⎝
ξ 4 H n (ξ ) = 2 n ⎜ ξ n + 4 −
1 n n+ 2 3 n n
⎞
ξ +
ξ + ... ⎟ ,
22
44
⎠
поэтому
dn
3 n⎞
⎛ (n + 4)! 4 (n + 2)! 1 n 2
ξ 4 H n (ξ ) ) = 2 n ⎜
ξ −
ξ + n! ⎟ .
n (
dξ
2! 2 2
4 4⎠
⎝ 4!
Учитывая значения интегралов (см. Приложение 2)
+∞
∫e
−ξ 2
dξ = π ,
−∞
+∞
∫ξ e
2 −ξ 2
−∞
1
π,
dξ =
2
+∞
4 −ξ
∫ ξ e dξ =
2
−∞
3
π,
2
получим в результате следующее выражение:
En(1) =
3x04
ε 2 (2n2 + 2n + 1) .
4
Во втором порядке теории возмущений поправка от ε 1 x 3 будет того же
порядка малости, что и поправка от ε 2 x 4 . Поэтому рассчитаем поправку от
ε 1 x 3 во втором порядке теории возмущений. Согласно (12.10)
En (2) = ∑ '
m
< n ε1 x 3 m >
2
En (0) − Em(0)
.
(12.13)
Вычисление матричных элементов в выражении (12.13) аналогично рассмотренному выше случаю для En(1) . Отличны от нуля только следующие недиагональные матричные элементы:
3
< ψ n(0)
⎛ n +1⎞2
x3 ψ n(0)+1 >= 3x03 ⎜
⎟ ,
⎝ 2 ⎠
113
114.
§12. Стационарная теория возмущений. Невырожденный случай3
⎛ n ⎞2
= 3x03 ⎜ ⎟ ,
⎝2⎠
ψ n(0) x 3 ψ n(0)−1
1
< ψ n(0)
⎤2
3 ⎡1
>=
+
+
+
x 3 ψ n(0)
x
n
n
n
(
3)(
2)(
1)
0 ⎢
+3
⎥⎦ ,
⎣8
1
⎤2
3 ⎡1
< ψ n(0) x 3 ψ n(0)
−3 >= x0 ⎢ n ( n − 1)( n − 2) ⎥ .
⎣8
⎦
Подставляя вычисленные значения матричных элементов в (12.13), имеем:
ε 2 15 6 ⎛ 2
11 ⎞
En(2) = − 1
x0 ⎜ n + n + ⎟.
ω 4 ⎝
30 ⎠
Таким образом, приближенные значения энергии частицы (учитываем,
что x0 =
Mω
)
1⎞
⎛
En = En (0) + En (1) + En (2) = ω ⎜ n + ⎟ +
2⎠
⎝
2
♦
3
ε 15 ⎛
3 ⎛
11 ⎞
⎞
⎞ ⎛ 2
2
+ ε2 ⎜
⎜
⎟ ⎜ n + n + ⎟.
⎟ (2n + 2n + 1) −
ω 4 ⎝ Mω ⎠ ⎝
4 ⎝ Mω ⎠
30 ⎠
Задача 12.5. Определить в первом неисчезающем порядке теории возмущений сдвиг энергии и изменение волновой функции стационарного состояния гармонического осциллятора с частотой ω, массой M и зарядом e, помещенного в однородное электрическое поле напряженности E, направленное
вдоль оси Ox. Указать условие применимости теории возмущений.
Решение. Оператор возмущения определяется потенциальной энергией
осциллятора в однородном электрическом поле:
2
1
V = − eE x .
Учитывая результаты задачи 7.6, матричный элемент
⎛ m
⎞
m +1
δ m,n+1 +
δ m,n−1 ⎟ .
⎜
2
Mω ⎝ 2
⎠
Следовательно, поправка в первом порядке теории возмущений
En(1) = −eE Vnn = 0
Во втором порядке теории возмущений
Vmn = −eE m x n = −eE
2
(2)
n
E
Vmn
e2E 2
= ∑ (0)
=
(0)
2M ω2
m≠n En − Em
1
∑
m ≠n n − m
(
mδ m ,n+1 + m + 1δ m,n−1
)
2
e2E 2
=−
.
2M ω2
Используя формулу (12.9), можно вычислить поправку первого порядка
к волновым функциям:
114
115.
§12. Стационарная теория возмущений. Невырожденный случайVnmψ m(0)
1
eE
mδ m ,n+1 + m + 1δ m ,n−1 ψ m(0) =
ψ = ∑ (0)
=−
∑
(0)
3
m ≠ n En − Em
2 M ω m ≠n n − m
eE
(0)
=
n + 1ψ n(0)
+1 − nψ n −1 .
3
2M ω
Согласно формуле (12.11) для применимости теории возмущений поле E
должно быть достаточно слабым, т.е.
(
(1)
n
(
E
)
)
M ω3
. ♦
e
Задачи для самостоятельного решения
12.6. Показать, что поправка к энергии во втором порядке теории возмущений
определяется формулой (12.10).
12.7. Для частицы с массой M, находящейся в бесконечно глубокой прямоугольной потенциальной яме ширины a, найти в первом порядке теории возмущений смещение энергетических уровней под действием возмущения вида
(0 ≤x≤ a):
а)V(x) = (V 0 / a ) ( a - │ 2 x - a │ ) ;
б) V(x)=V0, b≤x≤a-b; и V(x)=0, 0 < x < b , a - b < x < a .
Указать условие применимости теории возмущений.
12.8. Для частицы с массой M, находящейся в бесконечно глубокой прямоугольной потенциальной яме ширины a, найти в первых двух порядках
теории возмущений смещение энергетических уровней под действием
возмущения вида V(x) = V0δ(x - a/2).
12.9. Показать, что поправка первого порядка En(1) к энергетическим уровням
частицы из предыдущей задачи для произвольного возмущения V(x) при достаточно больших значениях n не зависит от n.
12.10.На осциллятор массы m и частоты ω наложено возмущение
1
V = − αω 2 x 2 .
2
В первом неисчезающем порядке теории возмущений найти энергии и волновые функции стационарных состояний осциллятора. Указать условие применимости теории возмущений.
115
116.
§12. Стационарная теория возмущений. Невырожденный случай12.11. Используя результат задачи 12.4, построить графически для ангармонического осциллятора энергетические уровни (n=0, 1, 2, 3) в координатах
En
ω
ε1,2
для асимметричного (ε1ξ3) и симметричного возмущения (ε2ξ4).
ω
Ответы к задачам для самостоятельного решения
12.7. а) En
(1)
n
⎧ 1 1 + (−1) ⎫
= V0 ⎨ + 2
2⎬
⎩ 2 π (n + 1) ⎭
б) En (1) =
V0 ⎧
a
2π (n + 1)b ⎫
sin
⎨a − 2b +
⎬
a⎩
π (n + 1)
a
⎭
условие применимости теории возмущений: V0
π2
2
Ma 2
( n + 1) , n= 0,1,...
2V0
2 MV02
(2)
12.8. для четных n: E =
, En = − 2 2
;
a
π ( n + 1) 2
для нечетных n: Еn(1) = En(2) = 0;
(1)
n
2
условие применимости теории возмущений: V0
M π 2a
n = 0,1,...
a
12.9. En
(1)
1
= n V ( x) n ≈ ∫ V ( x)dx
a0
α ⎞⎛
1⎞
⎛
(0)
(1)
12.10. En = En + En = M ⎜ 1 +
⎟⎜ n + ⎟ ;
2⎠
⎝ 2m ⎠⎝
ψ n ( x) =ψ n(0) ( x) , n=0,1,…
условие применимости теории возмущений: α
116
m.
( n + 1) ,
,
117.
§13. Cтационарная теория возмущений. Вырожденный случай§ 13. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ.
ВЫРОЖДЕННЫЙ СЛУЧАЙ
Рассмотрим случай, когда энергетические уровни систем, имеющих дискретный спектр, вырождены или расположены достаточно близко, так что для
данного оператора возмущения V не удовлетворяется условие (12.11). Примером может служить g-кратно вырожденный уровень, при наличии которого
соответствующие знаменатели в (12.9) и (12.10) обращаются в нуль. Чтобы избежать возникающих трудностей, волновую функцию уже в нулевом приближении необходимо искать в виде линейной комбинации невозмущенных волновых функций, соответствующих данному вырожденному состоянию или
системе близких уровней:
ψ
(0)
g
= ∑ cmψ m(0) ,
(13.1)
m=1
где g — кратность вырождения уровня, либо число близких уровней, которые
нумеруются индексом m, ψ m — волновые функции, соответствующие невоз(0)
(0)
мущенным уровням энергии Em и удовлетворяющие уравнению Шрёдингера:
H€0ψ m(0) = Em(0)ψ m(0) .
(13.2)
(0)
(0)
(0)
(0)
(0)
Если ψ m соответствует вырожденному уровню, то E1 = E2 = ...Em = E .
Будем считать функции ψ m ортонормированными (это всегда можно сделать):
(0)
∫ψ
(0)*
k
(ξ )ψ m(0) (ξ )d ξ = δ km .
(13.3)
Коэффициенты разложения в (13.1) неизвестны и подлежат определению.
Также как и в предыдущем параграфе, нам необходимо решить уравнение
Шрёдингера при наличии возмущения:
( H€ + V€)ψ
(0)
0
= Eψ (0) .
Вместо ψ (0) в данное уравнение необходимо подставить разложение (13.1).
Затем умножим скалярно левую и правую части получившегося уравнения на
ψ k(0)* и проинтегрируем по всему конфигурационному пространству. Тогда с
учетом (13.2) и (13.3) получим:
g
∑ ⎣⎡( E
m=1
(0)
m
− E ) δ km + Vkm ⎦⎤ cm = 0,
k = 1, 2,...g ,
(13.4)
где Vkm = ∫ψ k(0)* (ξ )V€ψ m(0)* (ξ )dξ . Полученные уравнения представляют собой
117
118.
§13. Стационарная теория возмущений. Вырожденный случайсистему g линейных однородных алгебраических уравнений с g неизвестными
коэффициентами cm. Система (13.4) имеет нетривиальное решение (все cm одновременно не равны нулю), когда равен нулю детерминант:
det ( Em(0) − E ) δ km + Vkm = 0
(13.5)
Это уравнение называется секулярным и определяет энергию в первом порядке по возмущению. Левая часть (13.5) представляет собой многочлен степени
g относительно Е. В общем случае уравнение (13.5) имеет g корней (среди которых могут быть и кратные).
Если в невозмущенной задаче уровень E (0) g-кратно вырожден, а уравнение (13.5) имеет g различных корней, то говорят, что возмущение V€ полностью снимает вырождение. Если среди корней (13.5) встречаются кратные, то
вырождение снимается частично.
Для каждого корня (13.5) существует нетривиальное решение системы (13.4),
представляющее собой набор коэффициентов cm. Если их нормировать условием:
g
∑c
m=1
m
2
=1
(13.6)
и подставить в (13.1), то для значения Е мы получим правильные функции нулевого приближения.
Для нахождения поправок к энергии во втором порядке теории возмущений в секулярном уравнении (13.5) элементы Vkm необходимо заменить на
Vkm(2) = ∑
i
VV
.
E −E
ki im
(0)
(0)
m
i
Здесь сумма не распространяется на близко расположенные состояния (или,
при наличии вырождения, на вырожденные состояния).
Задача 13.1. Определить изменение двух близких уровней энергии Е1 и
Е2=Е1+∆ (∆>0) под действием возмущения V , матричные элементы которого
по базису невозмущенных состояний известны. Найти правильные волновые
функции нулевого приближения.
Решение. Пусть в отсутствие возмущения уровню Е1 соответствует волновая функция Ψ1, а E2 — Ψ2. Будем искать решение уравнения Шредингера
при наличии возмущения в виде:
ψ = c1ψ 1 + c2ψ 2
(13.7)
Тогда с учетом (13.4) получаем систему уравнений:
⎧( E1 − E + V11 )c1 + V12c2 = 0,
(13.8)
⎨
V
c
(
E
E
V
)
c
0.
+
−
+
=
2
22
2
⎩ 21 1
Решение соответствующего секулярного уравнения
118
119.
§13. Стационарная теория возмущений. Вырожденный случайE1 − E + V11
V12
V21
E2 − E + V22
=0
дает 2 корня:
2
E + V + E2 + V22
2
⎛ E + V − E1 − V11 ⎞
E± = 1 11
± ⎜ 2 22
⎟ + V12 .
2
2
⎝
⎠
Как следует из (13.9), при V€ → 0 : E → E и E → E .
+
−
2
(13.9)
1
Подставляя полученные значения энергии в систему (13.8), найдем выражение, связывающее коэффициенты c1 и c2 (достаточно решить только первое уравнение):
2V12
(13.10)
c1± =
c .
2
2 2±
Δ + V11 − V22 ∓ ( Δ + V22 − V11 ) + 4 V12
Для определения c1 и c2 дополним выражение (13.10) условием нормировки
(13.6), т.е.
2
2
c1± + c2± = 1.
Тогда получим:
⎧
⎪⎪
⎨
⎪ ⎡Δ + V − V ∓
11
22
⎩⎪ ⎢⎣
⎫
⎪⎪
4 V12
2
+
1
⎬ c2± = 1.
2
2
2
( Δ + V22 − V11 ) + 4 V12 ⎤⎥ ⎪⎪
⎦
⎭
2
Проводя несложные алгебраические преобразования, найдем коэффициент c2:
⎧
⎪
c2± = ⎨
⎪⎩
( Δ + V22 − V11 ) + 4 V12 ± ( Δ + V11 − V22 ) ⎫⎪
⎬
2
2
2 ( Δ + V22 − V11 ) + 4 V12
⎪⎭
2
2
1
2
.
Проанализируем полученные результаты при различных предельных соотношениях между диагональными и недиагональными матричными элементами
оператора V€ . Рассмотрим следующие случаи.
1) Большие диагональные матричные элементы:
|V11|, |V22| >> |V12|;
|V12|<< |∆ + V22 - V11|.
С учетом данных соотношений по формулам (13.9) и (13.7) получим предельные выражения для энергий стационарных состояний при наличии вырождения и правильные функции нулевого приближения:
E+ ≈ E2 + V22 ,
ψ + ≈ψ 2,
E− ≈ E1 + V11 ;
ψ − ≈ −ψ 1.
В состоянии с энергией E + доминирует ψ 2 , с энергией E− — ψ 1 . Такие же результаты дает и теория возмущений для невырожденных уровней в первом по119
120.
§13. Стационарная теория возмущений. Вырожденный случайрядке (убедиться самостоятельно).
2) Большие недиагональные матричные элементы:
|V11|, |V22| <<|V12|;
|V12|>> |∆ + V22 - V11|.
Как и в предыдущем случае, используя формулы (13.9) и (13.7), получим:
1
1
E+ = ( E1 + E2 ) + V12 ; E− = ( E1 + E2 ) − V12
2
2
1
1
ψ+ =
(ψ 2 + ψ 1 ) ; ψ − = (ψ 2 −ψ 1 )
2
2
В данном случае сильно недиагональное возмущение приводит к “раздвиганию” близких уровней. “Невозмущенные” состояния вносят одинаковый вклад
в формирование “возмущенных” уровней.
Таким образом, анализ предельных случаев показывает, что теорией возмущений для близких уровней нужно пользоваться в том случае, если в матрице
оператора возмущения недиагональные элементы доминируют над диагональными и по величине существенно превышают межуровневые расстояния. ♦
Задача 13.2. Определить расщепление первого возбужденного энергетического уровня и волновые функции атома водорода в однородном электрическом поле напряженности E (эффект Штарка).
Решение. Пусть поле, действующее на атом водорода, направлено вдоль
оси z. Тогда оператор возмущения, описывающий взаимодействие электрона с
внешним однородным электрическим полем, имеет следующий вид:
V = − eE z = − eE r cos θ .
Матричные элементы оператора (13.11) запишутся в виде:
(13.11)
(0)
Vnlm ,nl′m′ = − ψ nlm
− eEr cosθ ψ nl(0)′m′ =
∞
= −eE ∫ Y Y cosθ sin θ dθ dϕ ∫ Rnl Rnl ' r ⋅ r 2 dr.
*
lm l ′m′
(13.12)
0
Отметим, что для основного состояния атома водорода эффект Штарка
первого порядка отсутствует. Действительно, поскольку основное состояния
(0)
является невырожденным, то функция ψ 1,0,0
будет правильной и, соответст-
венно, имеем:
(0)
(0)
E1(1) = V100,100 = ψ 1,0,0
− eE r cos θ ψ 1,0,0
=
=−
.
⎛ 2r ⎞
1
2
exp
−
e
E
r
cos
θ
r
sin
θ
drd
θ
d
ϕ
=
0.
⎜
⎟
π a03 ∫
⎝ a0 ⎠
Первое возбужденное состояние атома водорода (n = 2) четырехкратно вырождено, т.е энергии E2 соответствуют следующие функции:
120
121.
§13. Стационарная теория возмущений. Вырожденный случай1
4 2π
ψ 200 =
3
2
⎛1⎞
⎛ r ⎞⎛
r ⎞
⎜ ⎟ exp ⎜ −
⎟⎜2 − ⎟
a0 ⎠
⎝ a0 ⎠
⎝ 2 a0 ⎠ ⎝
5
⎛ r ⎞
1 ⎛ 1 ⎞2
ψ 211 = −
exp
⎜ ⎟
⎜−
⎟ r exp(iϕ )sin θ
8 π ⎝ a0 ⎠
⎝ 2 a0 ⎠
1
4 2π
ψ 210 =
(13.13)
5
2
⎛1⎞
⎛ r ⎞
⎜ ⎟ exp ⎜ −
⎟ r cos θ
2
a
a
0 ⎠
⎝ 0⎠
⎝
5
2
⎛ r ⎞
1 ⎛1⎞
⎜ ⎟ exp ⎜ −
⎟ r exp( −iϕ )sin θ
2
a
8 π ⎝ a0 ⎠
0 ⎠
⎝
Из шестнадцати матричных элементов Vnlm,nl′m′ , которые можно получить с по-
ψ 21−1 =
мощью функций (13.13), отличны от нуля только два, отвечающие l ≠ l ′ и
m ≠ m′ . В этом можно убедиться непосредственной проверкой. Кроме того,
можно воспользоваться следующими соображениями. Поскольку четность
функции Ylm (θ , ϕ ) совпадает с четностью квантового числа l , то при замене:
θ → π − θ , ϕ → ϕ + π функция Ylm (θ , ϕ ) умножается на (-1)l. Радиальная функция Rnl ( r ) является четной (при инверсии r не изменяется). Функция cosθ является нечетной. Следовательно, четность подынтегральной функции в выражении (13.12) равна l + l′ + 1 . Интегрирование нечетной функции углов по
dΩ = sinθ dθ dϕ в пределах полного телесного угла 4π дает нуль. Таким образом, интеграл (13.12) отличен от нуля лишь для четных значений l + l′ + 1 , т.е.
для l ≠ l′ . Далее, при m ≠ m′ выражение (13.14) будет содержать множитель
2π
∫e
i ( m −m′ )ϕ
dϕ = 0 при m ≠ m′ .
0
Таким образом, отличны от нуля лишь элементы V200,210 и V210,200 . Они имеют
следующее значение:
V200,210 = V210,200 =
∞π
1
32π a
⎛
r ⎞ r ⎛
r ⎞ 2
2
⎟ ⎜ 2 − ⎟ cos θ eEr ⋅ 2π r sin θ dθ dr = −3eEa0
a0 ⎠
0 ⎠ a0 ⎝
∫ ∫ exp ⎜⎝ − a
3
0 0 0
Запишем теперь секулярное уравнение:
0 − E −3eE a0
−3eE a0 0 − E
= 0.
0−E
0−E
Раскрывая определитель, получим:
121
(13.14)
122.
§13. Стационарная теория возмущений. Вырожденный случай( −E ) {( −E ) − ( −3eEa0 ) } = 0 .
2
2
2
Корни данного уравнения:
E1 = 3eE a0 , E 2 = − 3eE a0 , E3 = E 4 = 0 .
Подставив в (13.14) корень E1 , получим систему уравнений:
⎧−3eEa0c1 − 3eEa0c2 = 0,
⎪−3eEa c − 3eEa c = 0,
⎪
0 1
0 2
⎨
−3eEa0c3 = 0,
⎪
⎪⎩
−3eEa0c4 = 0,
откуда следует, что c1 = − c2 , c3 = c4 = 0. Таким образом, энергетическому уровню E0 + E1 соответствует в нулевом приближении функция (с учетом (13.6)):
32
⎛ r ⎞⎡
⎤
r
1
1 ⎛1⎞
(0)
(0)
−ψ 2,1,0
=
ψ 1 = c (ψ −ψ ) =
ψ 2,0,0
(
)
⎜ ⎟ exp ⎜ −
⎟ ⎢ 2 − (1 + cos θ ) ⎥
a0
2
8 π ⎝ a0 ⎠
⎝ 2 a0 ⎠ ⎣
⎦
Выражение для ψ 2 , соответствующей энергетическому уровню E0 + E2 , реко(0)
2,0,0
(0)
2,1,0
мендуем читателю получить самостоятельно.
Подставляя в (13.44) значение следующих корней E3 = E4 = 0 , получим
что c1 = c2 = 0 , остальные коэффициенты остаются неопределенными, так что
можно положить:
(0)
(0)
ψ 3 =ψ 2,1,1
и ψ 4 = ψ 2,1,
−1 .
Совокупность полученных функций ψ 1 −ψ 4 образует систему правильных
функций нулевого приближения для оператора возмущения (13.11).
Итак, из четырех вырожденных состояний, соответствующих n=2, в первом приближении два состояния вообще не изменяются при воздействии слабого электрического поля. Два других состояния, описываемые волновыми функциями ψ 1 и ψ 2 , приобретают добавочную энергию E1 = 3eE a0 и E 2 = − 3eE a0 .
Полученные результаты свидетельствуют о том, что атом водорода в первом
возбужденном состоянии ведет себя как диполь с моментом 3ea0 , способный
ориентироваться параллельно полю (первое состояние), антипараллельно полю
(второе состояние) и перпендикулярно к полю (третье и четвертое состояния). ♦
В качестве следующего примера на применение теории возмущений для
вырожденного случая рассмотрим эффект Зеемана для микрочастицы, подобной электрону, за исключением одного – ее спин равен нулю. Эффектом
Зеемана называется расщепление энергетических уровней (или спектральных
линий) атомов, находящихся во внешнем постоянном магнитном поле. Различают простой и сложный (аномальный) эффект Зеемана. В первом случае час122
123.
§13. Стационарная теория возмущений. Вырожденный случайтица не обладает спином, и совокупность расщепленных в магнитном поле
спектральных линий представляет собой триплет или дублет. Сложный эффект Зеемана (в случае s≠0) объясняется зависимостью величины расщепления
спектральных линий от множителя Ланде g (фактора спектроскопического
расщепления), т.е. существованием спина электрона. При этом число расщепленных линий оказывается больше трех.
Задача 13.3. Найти поправку к энергии в первом порядке теории возмущений для атома водорода без учета спина электрона, помещенного в однородное постоянное магнитное поле H . Масса частицы M .
Решение. Гамильтониан микрочастицы в поле ядра имеет вид:
2
e2
p
€
H0 =
− .
2M r
Собственные значения такого оператора определяются выражением (9.18), а собственные функции – выражением (9.20). Рассмотрим, как изменятся значения
энергии, если подействовать на нашу систему магнитным полем H . Функция
Гамильтона для частицы с зарядом e определяется следующим выражением:
2
1 ⎛
e ⎞
H=
⎜ p − Б ⎟ + eϕ ,
2M ⎝
c ⎠
где p — обобщенный импульс частицы, A и ϕ — векторный и скалярный потенциалы поля в точке, в которой находится частица. Согласно общему правилу построения операторов в квантовой механике гамильтониан атома водорода
1
H=
2M
2
e ⎞
⎛
⎜ p − Б ⎟ + eϕ .
c ⎠
⎝
Раскрыв скобки, получим:
1 2
e
e
e2
H=
p −
p⋅A −
A⋅p +
A 2 + eϕ
2
2M
2 Mc
2 Mc
2 Mc
Вычисляя значение коммутатора
(13.15)
⎡ p, A ⎤ = p ⋅ A − A ⋅ p = − i ∇ ⋅ A
⎣
⎦
и заменяя p ⋅ A через A ⋅ p − i ∇ ⋅ A , а также учитывая, что заряд электрона от-
рицательный, можно привести (13.15) к следующему виду:
e
e
1 2
e2
H=
p +
A ⋅p − i
∇A +
A 2 − e ϕ . (13.16)
2
2M
2 Mc
2 Mc
Mc
Направим ось z вдоль магнитного поля. Тогда векторный потенциал однородного постоянного поля H можно представить формулами:
1
1
(13.17)
Ax = − H y , Ay = H x, Az = 0.
2
2
123
124.
§13. Стационарная теория возмущений. Вырожденный случайЗаметим, что для однородного постоянного поля ∇⋅ A = 0 . Подставляя (13.17)
в (13.16), учитывая следующие результаты вычислений:
1
1
1
1
A ⋅ p = − H y p x + H x p y = H x p y − y p x = H Lz ∼ H ,
2
2
2
2
1
A2 = H 2 ( x2 + y 2 ) ∼ H 2 ,
2
и, ограничиваясь случаем слабых полей, т.е. пренебрегая членом, пропорциоe2
нальным
H 2 , запишем выражение (13.16) как
2
2 Mc
e
e
e
1 2
(13.18)
H=
p +
A⋅p − = H0 +
A⋅p,
2M
Mc
r
Mc
где подставлено значение ϕ для поля ядра. Как видно из (13.18) гамильтониан
(
)
распался на сумму невозмущенного гамильтониана H 0 =
1 2 e
p − , описы2M
r
вающего атом водорода, и оператора возмущения:
e
eH
V=
Lz .
A ⋅p =
Mc
2 Mc
Отметим, что n-му значению энергии соответствует несколько волновых
функций, отличающихся значениями квантовых чисел l и m (т.е. имеет место
вырождение по квантовым числам l и m). При наличии вырождения поправки
к энергии в первом приближении теории возмущений находятся из решения
секулярного уравнения (13.5). Чтобы составить данное уравнение необходимо
сначала вычислить матричные элементы:
(0)
Vnlm ,nl′m′ = ψ nlm
eH
L z ψ nl(0)′m′
2 Mc
,
(13.19)
(0)
где ψ nlm
- собственные функции невозмущенного гамильтониана H€0 . Как было
(0)
показано в §§ 9-10 функции ψ nlm
являются одновременно собственными функ-
циями оператора L€z , т.е. удовлетворяют уравнению
(0)
(0)
L€zψ nlm
= mψ nlm
.
Следовательно,
eH
mψ nl(0)′m′ .
2 Mc
Подстановка этого выражения в (13.19) дает:
eH
Vnlm ,nl′m′ =
mδ l ,l ′ δ m ,m′ .
2 Mc
Vψ nl(0)′m′ =
124
125.
§13. Стационарная теория возмущений. Вырожденный случайТем самым при любом n матрица (13.19) диагональна. Таким образом, по отношению к рассматриваемому возмущению V функции (9.20) являются правильными. В этом случае поправки к энергии в первом приближении равны
диагональным матричным элементам (13.19), т. е.
e
(1)
Enlm
=
H m.
2 Mc
Итак, при действии магнитного поля на атом без учета спина энергия атома
начинает зависеть от квантового числа m (поэтому его и называют магнитным).
Таким образом, магнитное поле снимает вырождение по m . Однако, поскольку
поправка к энергии не зависит от квантового числа l , вырождение по l остается,
так что в данном случае возмущение снимает вырождение только частично. ♦
Задачи для самостоятельного решения
13.4. В задаче 13.1 найти правильную волновую функцию нулевого приближения для энергетического уровня E0 + E2 .
13.5. Найти расщепление первого возбужденного уровня энергии плоского
гармонического осциллятора с массой M и частотой ω под действием возмущения V€ = α xy ((x, y) — плоскость колебаний). Указать правильные собственные функции нулевого приближения.
13.6. Определить расщепление стационарных уровней энергии плоского ротатора с m=±1 в однородном электрическом поле E, лежащем в плоскости вращения ротатора. Момент инерции ротатора I, электрический дипольный момент d.
13.7. Найти уровни энергии и волновые функции стационарных состояний заряженной частицы без спина, находящейся в однородном магнитном поле, направленном вдоль оси z, при следующей калибровке векторного потенциала:
Ax = 0 , Ay = H x , Az = 0 .
Ответы к задачам для самостоятельного решения
13.4. ψ 2 =
13.5.
⎛ r ⎞⎡
⎤
1
1 1
r
θ
−
−
−
exp
2
1
cos
(
)
(ψ 200 +ψ 210 ) =
⎜
⎟⎢
⎥
3/2
a0
2
8 π a0
⎝ 2 a0 ⎠ ⎣
⎦
α
1
(0)
E± = 2 ω ±
ψ 10(0) ± ψ 01(0)
;ψ± =
2M ω
2
(
13.6. ΔE = E+ − E− =
13.7.
ψ np p ( x, y , z ) =
y x
d 2E 2I
2
)
2
d 2E 2I ⎛
3⎞
, E± =
+
1± ⎟
2 ⎜
2I
3
2⎠
⎝
⎧⎪ i ( p y y + p z z ) ⎫⎪
cp y
осц ⎛
exp ⎨
⎬ψ n ⎜ x −
2π
eH
⎝
⎩⎪
⎭⎪
1
125
⎞
⎟
⎠
,
1 ⎞ p2
⎛
E np y pz = ω H ⎜ n + ⎟ + z
2 ⎠ 2M
⎝
126.
§14. Нестационарная теория возмущений§ 14. НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
Рассмотрим случай, когда на систему действует сравнительно слабое
возмущение, меняющееся во времени V ( r, t ) . По-прежнему будем считать, что
нам известны уровни энергии E n(0) и волновые функции ψ n(0) (r ) , являющиеся
решением невозмущённого уравнения Шрёдингера с гамильтонианом H 0 (r ) :
H 0ψ n(0) = En(0) ψ n(0) .
При учёте возмущения гамильтониан всей системы H = H 0 + V ( r, t ) зависит от времени. Поскольку энергия в этом случае не сохраняется, то говорить о поправках к собственным значениям энергии в этом случае нельзя. Задача здесь сосотоит в приближенном вычислении волновых функций Ψ (r , t )
нестационарного уравнения Шрёдингера
∂Ψ
= HΨ = H 0Ψ + V ( r , t )Ψ ,
(14.1)
i
∂t
по волновым функциям стационарных состояний ψ n(0) (r ) невозмущенной системы. Для этого, как и в случае стационарной теории возмущений, разложим
функцию Ψ ( r ,t ) по собственным функциям невозмущённой задачи:
∞
Ψ ( r , t ) = ∑ an ( t )ψ n(0) ( r )e − iω t ,
n
(14.2)
n =0
где зависимость от времени учтена экспоненциальным множителем и коэффициентами an (t ) , а ω n ≡ En(0) . Подставим волновую функцию (14.2) в нестационарное уравнение Шрёдингера (14.1). Получаем
∞
∞
dan (0)
− iωnt
i ∑ ψ n ( r )e
+ i ∑ ( −iωn ) anψ n(0) ( r ) e−iωnt =
n =0 dt
n =0
∞
∞
n =0
n =0
= ∑ an H 0ψ n(0) ( r ) e−iωnt + ∑ anV ( r, t )ψ n(0) ( r ) e−iωnt .
Учитывая, что H 0ψ n(0) = En(0)ψ n(0) и ω n = En(0) , имеем:
∞
∞
dan (0)
− iωnt
i ∑
ψ n ( r )e
= ∑ an V ( r, t )ψ n(0) ( r ) e − iωnt .
n =0 dt
n=0
(0)* iωmt
Умножим это уравнение на ψ m e и проинтегрируем по всему пространству.
Благодаря ортонормированности функций ψ n(0) находим для каждого из коэффициентов am
i
dam ∞
= ∑ an ( t )Vmn ( t )e − iωnmt ,
dt
n =0
126
(14.3)
127.
§14. Нестационарная теория возмущенийгде Vmn ( t ) = m V ( r , t ) n = ∫ψ m(0)* (r )V ( r , t )ψ n(0) (r ) dr – зависящие от времени
матричные элементы, а ω n m ≡ ω n − ω m = ( En(0) − Em(0) ) / .
Уравнения (14.3) образуют систему дифференциальных уравнений для
зависящих от времени коэффициентов an ( t ) . В общем случае эта система бесконечна. В случае малости матричных элементов оператора возмущения Vmn (t )
мы можем воспользоваться общим подходом, предлагаемым теорией возмущений, а именно разложим коэффициенты am в ряд по степени малости:
Коэффициенты a m(0)
am = am(0) + am(1) + am( 2) + ... .
определяются состоянием системы до начала дейст-
вия возмущения (или в бесконечно далёкий момент времени в прошлом). В
(1)
первом порядке теории возмущений коэффициенты am определяются из сис-
темы уравнений
∞
da m(1)
(14.4)
i
= ∑ a n(0) ( t )Vmn ( t )e − iωnm t .
dt
n =0
Задача 14.1. Система находится в состоянии, описываемом волновой
функцией ψ k(0) . В течение конечного временина на систему действует возму-
щение V ( r, t ) . Найти вероятность перехода системы в другие состояния.
Решение. Тот факт, что исходное состояние описывается волновой функцией ψ k(0) , означает, что из всех коэффициентов a m( 0 ) только лишь коэффициент
a k( 0 ) отличен от нуля и ak(0) = 1 . Все остальные коэффициенты am(0) = 0 ( m ≠ k ) .
Поскольку возмущение действует в течение конечного времени, то по его окончании система вновь окажется в стационарном состоянии, которое, однако, может не совпадать с первоначальным состоянием ψ k(0) . Вероятность того, что система под действием возмущения перешла из исходного состояния k в состояние
m , определяется квадратом модуля коэффициента am(1) :
2
wmk = am(1) .
Уравнения (14.4) в этом случае примут вид:
da m(1)
= Vmk ( t )eiωmk t .
i
dt
Интегрируя, получим:
1
a =
i
(1)
m
+∞
ω
∫ dt′ V ( t′)e
i
mk
−∞
127
mk t ′
.
(14.5)
128.
§14. Нестационарная теория возмущенийЧтобы рассчитать, с какой вероятностью после окончания действия возмущения система перейдёт в то или иное состояние, необходимо интегрировать до
времени завершения возмущения или до +∞ .
Таким образом,
1
wmk ( t ) =
i
2
+∞
∫ dt′ V ( t′)e
iωmk t ′
mk
. ♦
−∞
Задача 14.2. Найти коэффициенты am(1) , если в операторе возмущения
можно выделить пространственный и временной факторы, то есть оператор V
имеет вид
V ( r, t ) = W ( r ) f ( t ) .
Решение. В этом случае уравнение (14.4) принимает вид:
W
a = mk
i
(1)
m
+∞
ω
∫ f ( t′)e
i
mk t ′
dt′ . ♦
(14.6)
−∞
Подробнее рассмотрим случаи различных возмущений.
Задача 14.3. Найти вероятности переходов в случае, когда f ( t ) = δ ( t )
(импульсное возмущение).
Решение. Такой вид функции f годится для моделирования тех случаев,
когда возмущение действует весьма непродолжительное время. Интеграл в
(14.6) оказывается равен:
+∞
∫ δ ( t′) e
iωmk t ′
dt′ = 1 .
−∞
Отсюда получаем для вероятности переходов:
wmk =
Wmk
2
2
. ♦
Задача 14.4. Рассмотреть случай, когда возмущение, включившись в определённый момент времени (можем считать, что это произошло в момент
t = 0 ), осталось неизменным (не выключилось). При этом можно считать, что
f ( t ) = θ ( t ) , где θ ( t ) – тета-функция Хевисайда. Найти вероятности перехода
из исходного состояния в другие состояния.
Решение. Как и дельта-функция Дирака, тета-функция Хевисайда является обобщённой функцией. Она принимает следующие значения:
⎧0, t < 0,
θ (t ) = ⎨
⎩1, t > 0.
Отметим, что производная от тета-функции есть дельта-функция.
128
129.
§14. Нестационарная теория возмущенийt
Рассчитаем интеграл
∫ θ ( t′)e
iωmk t ′
dt ′. Его можно взять по частям:
−∞
t
∫ dt′ θ ( t′)e
iωmk t ′
−∞
Тогда при t > 0
⎛ eiωmk t′ ⎞′
eiωmk t′
= ∫ dt ′ θ ( t ′ )⎜
= θ ( t′)
⎜ iωmk ⎟⎟
iωmk
−∞
⎝
⎠
t
t
−∞
eiωmk t′
δ ( t′) .
− ∫ dt ′
i
ω
mk
−∞
t
Wmk ⎛ eiωmk t
1
a (t ) =
−
⎜
i ⎝ iωmk iωmk
⎞ Wmk
1 − eiωmk t ) .
(
⎟=
⎠ ωmk
Поправка к невозмущённой функции ψ k(0) имеет вид:
(1)
m
∞
∑a
(1)
n
n =0
ψ
(0)
n
(r ) e
− iωnt
∞
=∑
n =0
Wnk
(1 − e )ψ ( r ) e
⎡
⎛
iωnk t
ωnk
(0)
n
− iωnt
=
Wnk ⎞ (0) ⎤ −iωk t
⎟ψ n ( r ) ⎥ e .
ω
ω
n =0
nk
nk ⎠
⎣ n =0 ⎝
⎦
Вторая из сумм представляет собой не что иное, как поправку к волновой
функции исходного состояния, рассчитанную в рамках стационарной теории
возмущений. Вероятности перехода из исходного состояния k в другие состояния n определяются коэффициентами, стоящими в первой сумме. Таким
образом, для вероятностей переходов имеем:
∞
=∑
Wnk
∞
ψ n(0) ( r ) e−iω t + ⎢∑ ⎜ −
n
wmk =
Wmk
2
♦
(14.7)
.
2
ωmk
Задача 14.5. Пусть в момент времени t = 0 включается возмущение, зависящее от времени по гармоническому закону с частотой ω , например
t < 0,
⎧ 0,
f (t ) = ⎨
⎩sin ωt , t > 0.
Подобное возмущение описывает в частности взаимодействие вещества с электромагнитной волной. Найти скорости переходов между различными состояниями под действием такого возмущения.
Решение. В этом случае
t
t
t
⎤
Wmk
Wmk ⎡ iωt′ iωmk t′
iωmk t ′
− iωt ′ iωmk t ′
(1)
′
′
′
′
=
−
−
am (t ) =
t
e
dt
e
e
dt
e
e
dt
sin
ω
⎢
⎥=
∫0
i ∫0
2 ⎣ ∫0
⎦
2
⎡ ei(ωmk +ω )t − 1 ei(ωmk −ω )t − 1 ⎤ W ⎡ ei(ωmk −ω )t − 1 ei(ωmk +ω )t − 1 ⎤
⎢
⎥ = mk ⎢
⎥.
−
−
i
i
+
−
−
+
ω
ω
ω
ω
ω
ω
ω
ω
(
)
(
)
(
)
(
)
2
i
⎢⎣
⎥⎦
⎢⎣ mk
⎥⎦
mk
mk
mk
В случае, когда частота ω оказывается близка к частоте ω mk перехода между
W
= − mk
2
состояниями m и k , вклад первого члена с знаменателем ω mk − ω оказывается
129
130.
§14. Нестационарная теория возмущенийнамного больше, чем вклад второго члена с знаменателем ω mk + ω , поэтому
далее мы будем пренебрегать последним.
Для вероятности перехода под действием гармонического возмущения
получим:
2
wmk ( t ) = am(1) ( t )
2
i(ωmk −ω )t
2
−1
Wmk 1 e
.
= 2
4 (ωmk − ω )2
Стоящий в числителе этого выражения квадрат модуля e (
i ωmk −ω )t
2
− 1 можно
преобразовать следующим образом:
ei(ωmk −ω )t − 1 = ( cos (ωmk − ω ) t − 1) + sin 2 (ωmk − ω ) t =
2
2
⎛ω −ω ⎞
= 2 − 2cos (ωmk − ω ) t = 4sin 2 ⎜ mk
t⎟.
2
⎝
⎠
Тогда
⎛ω −ω ⎞
sin 2 ⎜ mk
t⎟
Vmk 1
2
⎝
⎠.
wmk = 2
2
4 ⎛ ωmk − ω ⎞
⎜
⎟
⎝ 2 ⎠
Для дельта-функции известно следующее соотношение (см. П3.15):
1 sin 2 α t
= δ (α ) .
lim
t →∞ π t
α2
Учитывая это, вероятность перехода из состояния k в состояние m запишется
как
2
2
2
V
1
⎛ ω − ω ⎞ Vmk π
wmk = mk2 π tδ ⎜ mk
tδ ( Em − Ek − ω ) .
⎟=
4
2
⎝ 2 ⎠
Здесь мы воспользовались свойством дельта-функции δ ( ax ) = (1 a ) δ ( x ) . Вероятность перехода оказывается пропорциональна времени. Следовательно, вероятность перехода в единицу времени (скорость перехода) оказывается равной
dwmk π
2
Vmk δ ( Em − Ek − ω ) . ♦
=
(14.8)
dt
2
Полученное выражение для скорости перехода часто называют золотым
правилом Ферми. Обратим внимание на то, что скорость перехода оказывается
2
пропорциональна квадрату матричного элемента Vmk . Например, при взаимодействии атома с электрическим полем напряжённостью E , в том числе с
электромагнитной волной, энергия этого взаимодействия равна V = −d ⋅E , где
d = er – дипольный момент внешнего электрона атома. Матричный элемент
130
131.
§14. Нестационарная теория возмущенийVmk пропорционален матричному элементу rmk = m r k , поэтому равенство
нулю последнего запрещает дипольный переход между состояниями k и m
под действием внешнего электрического поля; это обусловливает возникновение так называемых правил отбора. Присутствие же в выражении (14.8) дельта-функции представляет собой не что иное, как закон сохранения энергии:
переход между состояниями k и m под действием гармонического возмущения с частотой ω возможен лишь тогда, когда разность энергий этих состояний E m − E k в точности равна ω .
Задача 14.6. При внезапном изменении заряда ядра на единицу
Z → Z ± 1 (электронный и позитронный распад ядра) электрон из основного
состояния переходит в первое возбужденное состояние. В рамках теории возмущений найти вероятность этого перехода. Для упрощения расчётов предположить, что атом является водородоподобным, т. е. содержит один электрон в
поле внешнего заряда Z .
Решение. Пусть атом изначально находился в основном состоянии, описываемом волновой функцией
3
ψ 1,0,0
Z
1 ⎛ Z ⎞ 2 − a0 r
= R1,0 Y0,0 =
⎜ ⎟ e .
π ⎝ a0 ⎠
При больших величинах заряда Z изменение потенциальной энергии
при изменении заряда на единицу сравнительно мало. Поэтому это изменение
энергии можно рассматривать как возмущение V = ±e 2 / r . Для водородоподобного атома матричный элемент будет иметь вид
2π π
∞
e2
Vn′l′m′,nlm = ± ∫ r
Rnl Rn′l′dr ∫ ∫ Yl*′m′ Y00 sin θ dθ dϕ.
r
0
0 0
Ортонормированность шаровых функций требует, чтобы l′ = 0 . Другими словами, возбуждение при изменении заряда из основного состояния возможно
только в s-состояние. Радиальная часть волновой функции ψ 2,0,0
2
3
R2,0
Z
⎛ Z ⎞ 2⎛
Z ⎞ − 2 a0 r
r ⎟e
=⎜
−
.
2
⎟ ⎜
a0 ⎠
⎝ 2a0 ⎠ ⎝
Интеграл
3
∞
⎛ Z ⎞ 2⎛ Z ⎞
∫0 rR2,0 R1,0dr = 2 ⎜⎝ 2a0 ⎟⎠ ⎜⎝ a0 ⎟⎠
3
3
⎛ Z ⎞ 2⎛ Z ⎞ 2⎡ ∞
= 2⎜
⎟ ⎜ ⎟ ⎢ 2 ∫ re
⎝ 2a0 ⎠ ⎝ a0 ⎠ ⎢⎣ 0
3Z
r
−
2 a0
3
2 ∞
∫ re
0
−
Z
r
a0
⎛
Z
⎜2 −
a0
⎝
Z
⎞ − r
r ⎟ e 2 a0 dr =
⎠
3Z
∞
Z 2 − 2 a0 r ⎤ 4 2 Z
dr − ∫ r e
dr ⎥ =
.
a0 0
⎥⎦ 27 a0
131
132.
§14. Нестационарная теория возмущенийРазность уровней энергии основного и первого возбуждённого состояний равна
Z 2e2 ⎛ Z 2e2 ⎞ 3Z 2e2
−
−⎜−
.
⎟=
8a0 ⎝ 2a0 ⎠ 8a0
Таким образом, в соответствии с (14.7) мы получаем вероятность переходов из
основного в первое возбуждённое состояние
2
⎛ 4 2 Ze2 ⎞ ⎛ 8a0 ⎞ 2 211 1 2048 1
. ♦
w (1s → 2 s ) = ⎜
⎟ ⎜ 2 2⎟ = 8 2 =
2
27
a
3
Z
e
3
Z
6561
Z
⎝
⎠
0
⎝
⎠
Задачи для самостоятельного решения
14.7. Рассчитать вероятности перехода под действием включившегося постоянного электрического поля E из первого возбуждённого состояния одномерного гармонического осциллятора, обладающего зарядом e , в основное и второе возбуждённое состояния.
14.8. Частица находится в потенциальной яме с бесконечно высокими стенками:
x < − a / 2,
⎧∞,
⎪
U ( x ) = ⎨ 0, − a / 2 < x < a / 2,
⎪∞
x > a / 2.
⎩
В середине потенциальной ямы действует мгновенное возмущение вида
V ( x, t ) = W0 δ ( x ) δ ( t ) . Найти вероятности переходов под действием этого возмущения.
14.9. На частицу массы M с зарядом e , находящуюся в потенциальной яме с
бесконечно высокими стенками, действует электрическое поле E , меняющееся во времени по закону E ( t ) =E0 e
⎛t⎞
−⎜ ⎟
⎝T ⎠
2
. Найти, с какой вероятностью к момен-
ту завершения импульса (бесконечно далёкому моменту времени) произойдут
переходы между уровнями.
Ответы к задачам для самостоятельного решения
2
2
1 ⎛ eEx0 ⎞
3 ⎛ eEx0 ⎞
14.7. ⎜
⎟ и ⎜
⎟ соответственно.
2⎝ ω ⎠
2⎝ ω ⎠
2W0 2
14.8. w = 2 , переходы возможны лишь между нечётными состояниями.
a
14.9. Переходы возможны лишь между уровнями m и k разной чётности.
2
2
2
ω T
− mn
nm
⎛ eE ⎞ 2 256
2
w=⎜
T e 2 ,
⎟ a 3 2
2
2
π (n − m )
⎝
⎠
132
где
ωmn =
π2
2 Ma
2
(m
2
− n 2 ).
133.
§15. Вариационный метод§ 15. ВАРИАЦИОННЫЙ МЕТОД
Для вычисления первых дискретных уровней энергии квантовых систем
иногда бывает удобным воспользоваться вариационным методом. Данный метод, в отличие от теории возмущений, не требует наличия в задаче малых параметров. В основе его лежит следующее неравенство:
E 0 ≤ ∫ψ * Hψ dq ,
где E0 – энергия основного состояния квантовой системы (то есть состояния с
минимальной энергией), H – оператор Гамильтона, а ψ – произвольная
функция, удовлетворяющая условию нормировки:
∫ψ ψ dq = 1 .
*
Определение энергии основного состояния сводится к нахождению минимума
интеграла ∫ψ * Hψ dq на определённом классе функций ψ , которые называют
пробными функциями.
Решение задачи вариационным методом осуществляется следующим образом.
1) Выбирается нормированная пробная функция ψ , зависящая от ряда параметров, которые мы обозначим буквами α , β и т.д. Выбор пробной
функции базируется на качественном анализе решения с учетом симметрии задачи. Прежде всего, пробная функция должна удовлетворять стандартным условиям – быть непрерывной, однозначной и ограниченной.
2) Рассчитывается интеграл J (α , β ,... ) = ∫ψ * Hψ dq , который также будет
зависеть от этих параметров.
3) Находятся параметры α0 , β0 ,... , при которых интеграл J достигает своего минимума. Для этого необходимо решить систему уравнений вида:
∂J
∂J
= 0,
= 0.
∂α
∂β
4) Определяется энергия основного состояния
E0 = J (α 0 , β 0 ,...) .
При удачном выборе пробной функции получаемое значение E0 будет
близко к истинному значению, даже при сравнительно малом числе используемых параметров.
Указанный метод можно обобщить и для поиска энергий возбуждённых
состояний. Так, для расчёта первого возбуждённого состояния необходимо
найти условия достижения минимума интеграла
133
134.
§15. Вариационный метод∫ψ
Hψ 1dq ,
*
1
где ψ 1 – нормированная функция, ортогональная волновой функции основного состояния ψ 0 :
∫ψ ψ dq = 1,
∫ψ ψ dq = 0.
*
1
1
*
1
0
Для второго возбуждённого состояния минимум
∫ψ
*
2
Hψ 2 dq
ищется при выполнении условий
∫ψ ψ
*
2
2
dq = 1,
∫ψ ψ dq = ∫ψ ψ dq = 0 .
*
2
*
2
1
0
Задача 15.1. Вычислить с использованием вариационного метода энергию основного состояния одномерного гармонического осциллятора. Пробную
функцию выбрать в виде ψ 0 ( x,α ) = Ae
1
− α x2
2
, α > 0.
Решение. Условие нормировки для функции ψ ( x,α ) даёт нам:
∞
∫ψ
*
0
( x,α )ψ 0 ( x,α )dx = A
2
−∞
∞
∫e
−α x 2
−∞
dx =
A
2
α
π = 1,
или
1/4
⎛α ⎞
A=⎜ ⎟ .
⎝π ⎠
Теперь находим интеграл
∞
J (α ) = ∫ ψ ( x,α ) Hψ 0 ( x,α )dx =
*
0
−∞
α ∞ − 12α x
=
∫ e
π −∞
∞
∫
−∞
α − 12α x
e
π
2
2
⎛
d 2 M ω 2 x 2 ⎞ − 12α x2
+
dx =
⎜−
⎟e
2
2 ⎠
⎝ 2 M dx
2
⎛
M ω 2 x 2 ⎞ − 12α x2
2 2
(α x − α ) + 2 ⎟ e dx =
⎜−
⎝ 2M
⎠
2
⎤ −α x 2
α ∞ ⎡⎛ 2 2 M ω 2 ⎞ 2
=
+
⎢⎜ −α
⎥ e dx =
⎟x +α
∫
π −∞ ⎣⎝
2M
2 ⎠
2M ⎦
2
2
α ⎡⎛ 2 2 M ω 2 ⎞ π
π⎤
α Mω2
+
.
=
+
+α
⎢ −α
⎥=
⎟
π ⎣⎜⎝
2M α ⎦ 4M
4α
2M
2 ⎠ 2α 3/2
При вычислении данного интеграла мы использовали, что (здесь и далее в
этом параграфе значения многих вычисляемых интегралов приведены в приложении 2)
2
134
135.
§15. Вариационный метод∞
∫
e
−α x 2
−∞
J (α )
Минимум
J (α 0 ) = E0 =
ω
2
π
dx =
,
α
достигается
∞
∫
2
x 2 e−α x dx =
−∞
когда
α0 =
π
.
2α 3/2
Mω
,
при
этом
значение
, а волновая функция имеет вид:
1/ 4
Mω
−
x2
⎛ Mω ⎞
2
,
ψ0 = ⎜
⎟ e
⎝ π ⎠
что совпадает с точными значениями энергии и видом волновой функции основного состояния одномерного гармонического осциллятора (см. § 7). ♦
Задача 15.2. Найти энергию и волновую функцию основного состояния (
1s ) атома водорода. Пробную функцию выбрать в идее
ψ 0 ( r ,α ) = A exp( −α r ), α > 0.
Решение. Условие нормировки волновой функции приводит к выражению
π 2π ∞
∫ ∫ ∫ψ
*
0
(r ,α )ψ 0 (r ,α )r sin θ drdϕ dθ = 4π A
2
2
0 0 0
∞
A
∫ exp(−2α r )r dr = π α
2
2
3
= 1,
0
3
α 2
.
откуда A =
π
Гамильтониан атома водорода в сферических координатах имеет вид
(см. §9):
H€ = −
⎧1 ∂ ⎛ 2 ∂ ⎞
1
1
∂ ⎛
∂ ⎞
∂ 2 ⎫ e2
⎨
⎬ − , (15.1)
⎜r
⎟+
⎜ sinθ ⎟ + 2 2
2M ⎩ r 2 ∂r ⎝ ∂r ⎠ r 2 sinθ ∂θ ⎝
∂θ ⎠ r sin θ ∂ϕ 2 ⎭ r
2
где e - заряд электрона. Интеграл
π 2π ∞
J (α ) = ∫ ∫ ∫ψ 0* (r ,α ) Hψ 0 (r ,α )r 2 sin θ drdϕ dθ =
0 0 0
=−
2π
2
M
A
2 ∞
⎧d ⎛
∫ exp(−α r ) ⎨⎩ dr ⎜⎝ r
0
2
d ⎞
⎫
⎟ exp(−α r ) ⎬ dr −
dr ⎠
⎭
(15.2)
∞
− 4π A e ∫ r exp(−2α r )dr.
2
2
0
Первый интеграл в правой части (15.2) можно вычислить путем интегрирования по частям:
135
136.
§15. Вариационный метод∞
∞
⎧d ⎛ 2 d ⎞
⎫
2 d exp( −α r )
−
∫0 exp(−α r ) ⎨⎩ dr ⎜⎝ r dr ⎟⎠ exp(−α r )⎬⎭ dr = exp(−α r ) r
dr
0
2
∞
∞
1
⎛ d exp(−α r ) ⎞ 2
2
2
−∫ ⎜
⎟ r dr = −α ∫ exp(−2α r )r dr = − .
dr
4α
⎠
0⎝
0
Второй интеграл равен
∞
1
∫ r exp(−2α r )dr = 4α
2
.
.
0
α3
)
Теперь выражение (15.2) запишем как (учитываем, что A =
π
α2 2
J (α ) =
− α e2 .
2
2M
Из условия минимума J (α )
(15.3)
∂J (α )
= 0,
∂α
определяем, что α 0 =
Me 2
2
.
Подставляя α 0 в (15.3), имеем
Me4
e2
E0 = J (α 0 ) = − 2 = −
,
2
2a0
где a0 =
2
Me2 – боровский радиус.
Волновая функция основного состояния
ψ 0 (r ,α 0 ) = Ae −α r =
0
⎛ r ⎞
exp ⎜ − ⎟ .
π a03
⎝ a0 ⎠
1
Отметим, что полученные выражения для энергии и волновой функции
совпадают с точными (см. § 9). ♦
Задача 15.3. Найти энергию и волновую функцию первого возбуждённого состояния ( 2s ) атома водорода. В качестве пробной функции взять
2
⎛
⎛ αr ⎞
r ⎞
ψ 1 (r ,α , β ) = A ⎜1 − β ⎟ exp ⎜ − ⎟ , α , β > 0, a0 =
– боровский радиус.
2
a
a
Me
0 ⎠
⎝
⎝ 0⎠
Решение. Волновая функция основного состояния атома водорода ψ 0
найдена в задаче (15.2). Запишем условие ортогональности функций ψ 0 и ψ 1 :
π 2π ∞
∫ ∫ ∫ψ
*
0
(r )ψ 1 (r ,α , β )r 2 sin θ drdϕ dθ =
0 0 0
136
4A
(α + 1)
3
⎛
⎝
π a03 ⎜ 2 −
6β ⎞
= 0.
α + 1 ⎟⎠
137.
§15. Вариационный методОтсюда находим связь между параметрами α и β :
α +1
β=
.
3
Учитывая (15.4), из условия нормировки
π 2π ∞
∫ ∫ ∫ψ
*
1
(15.4)
(r ,α , β )ψ 1 (r ,α , β )r 2 sin θ drdϕ dθ =
0 0 0
2
∞
3
⎛
⎛ 2α r ⎞ 2
r ⎞
2 π a0
= 4π A ∫ ⎜1 − β ⎟ exp ⎜ −
α 2 − α + 1) = 1,
⎟ r dr = A
5(
a0 ⎠
3α
⎝ a0 ⎠
0⎝
находим, что
2
3α 5
.
A=
π a03 (α 2 − α + 1)
(15.5)
Далее, вычисляем интеграл
π 2π ∞
J (α , β ) = ∫ ∫ ∫ψ 1* (r ,α , β ) Hψ 1 (r ,α , β )r 2 sin θ drdϕ dθ
0 0 0
с гамильтонианом H (15.1). Имеем:
J (α , β ) =
2π
2
A
M
∞
2
⎛ α r ⎞ ⎞ ⎪⎫ 2
r ⎞
⎪⎧ d ⎛ ⎛
β
−
1
exp
⎜
⎨
⎜
⎟
⎜
∫0 ⎪ dr ⎝ ⎝ a0 ⎠ ⎝ − a0 ⎟⎠ ⎟⎠⎬⎪ r dr −
⎩
⎭
2 ∞
2
⎛
⎛ 2α r ⎞
r ⎞
− 4π A e2 ∫ r ⎜1 − β ⎟ exp ⎜ −
⎟ dr =
a
a
0 ⎠
0 ⎠
⎝
0 ⎝
2
2
π a02e2 A ⎛ β 2 − βα + α 2
3 β2 ⎞
=
− α + 2β −
⎜
⎟,
α3
α
2
2
⎝
⎠
или, выражая A и β через α с помощью выражений (15.4) и (15.5), получаем
⎞
e2 ⎛ 7α 2 α
α2
⎜
⎟.
− −
a0 ⎜ 6
2 2 (α 2 − α + 1) ⎟
⎝
⎠
Условие минимума J (α )
J (α ) =
∂J
=0
∂α
1
1
дает α 0 = . При этом в соответствии с (15.4) параметр β 0 также равен .
2
2
Искомая энергия
e2
E1 = J (α 0 ) = −
,
8a0
137
138.
§15. Вариационный метода волновая функция
⎛
⎛ r ⎞
r ⎞
⎜1 −
⎟ exp ⎜ −
⎟.
2
a
2
a
0 ⎠
0 ⎠
⎝
⎝
И в этой задаче, благодаря удачному выбору пробной функции, найденные значение энергии и волновая функция совпадают с точными (см. § 9). ♦
ψ 1 (r ) =
1
8π a03
Задачи для самостоятельного решения
15.4. Найти энергию и волновую функцию первого возбуждённого состояния
одномерного осциллятора. В качестве пробной функции взять ψ 1 = Bxe
1
− β x2
2
.
15.5. Используя вариационный метод, найти энергию основного состояния
частицы, если потенциальная энергия имеет вид:
⎧ Fx, x ≥ 0
U ( x) = ⎨
.
⎩∞, x < 0
В качестве пробных функции использовать:
а) ψ = Axe
−α x
, б) ψ = Bxe
1
− α x2
2
. Какая из функций дает лучшее приближение?
15.6. Найти энергию а) основного и б) первого возбуждённого состояний для
частицы в потенциальной яме шириной a с бесконечно высокими стенками. В
качестве пробных функций взять для основного состояния функию
ψ = Ax(a − x) , а для первого возбужденного состояния – функцию
⎛a
⎝
⎞
⎠
ψ = Bx ⎜ − x ⎟ (a − x ) .
2
Ответы к задачам для самостоятельного решения
1
3
Mω
3
⎛ 2 ⎞ 2 ⎛ M ω ⎞ 4 − 2 x2
15.4. E1 = ω , ψ 1 ( x ) = ⎜
xe
⎟
⎟ ⎜
2
⎠
⎝ π ⎠ ⎝
13
13
2 2
⎛ 243 ⎞ ⎛ F ⎞
15.5. а) ⎜
⎟ ⎜
⎟
⎝ 32 ⎠ ⎝ M ⎠
13
13
13
⎛ 2F 2 ⎞
≈ 1,966 ⎜
⎟ ,
M
⎝
⎠
13
2 2
⎛ 2F 2 ⎞
⎛ 81 ⎞ ⎛ F ⎞
1,861
≈
б) ⎜
⎟ ⎜
⎟
⎜
⎟ .
⎝ 4π ⎠ ⎝ M ⎠
⎝ M ⎠
Поскольку вариационный метод даёт оценку величины энергии сверху, имеет
смысл в качестве оценки брать меньший результат б).
2
5 2
15.6. а)
, б) 21
.
Ma 2
Ma 2
138
139.
ПриложенияПРИЛОЖЕНИЕ 1. КОМПЛЕКСНЫЕ ЧИСЛА
Используемые в квантовой механике
волновые функции в общем случае комплекснозначны. Поэтому вспомним свойства комплексных чисел.
Вводится мнимая единица i , квадрат
которой равен −1 . Число z = x + iy называется комплексным числом. Число x носит
название действительной части числа и
обозначается Re z , число y носит название мнимой части числа и обозначается
Im z . Комплексному числу соответствует
вектор на комплексной плоскости, по осям
которой откладываются действительная и
y
Im z
z
z
| |
ϕ
Re z
x
z
-ϕ
| |
-Im z
z
*
Рис. П1.1.
мнимая части числа (рис. П1.1). Модуль этого вектора равен
x 2 + y 2 и назы-
вается модулем комплексного числа z . Угол ϕ между осью x и вектором называется аргументом числа z : ϕ = arg z ; tgϕ =
Im z
.
Re z
Для произведения двух комплексных чисел имеем:
z1 z2 = ( x1 + iy1 )( x2 + iy2 ) = ( x1 x2 − y1 y2 ) + i ( x2 y1 + x1 y2 ) .
Комплексное число z * = x − iy называется комплексным сопряжённым
*
числу z = x + iy . Очевидно, что z = z , а arg z* = − arg z . Произведение
2
zz * = ( x + iy )( x − iy ) = x 2 + y 2 = z .
2
Равенство z = z 2 справедливо только для действительных чисел. Для ком2
плексных чисел в общем случае z ≠ z 2 . Отметим, что для произведения или
частного двух комплексных чисел ( z1 z2 ) = z1* z2* , ( z1 / z2 ) = z1* / z2* .
*
*
Действительная и мнимая части комплексного числа выражаются через
его модуль и аргумент:
Re z = z cos ϕ , Im z = z sin ϕ .
Используя формулу Эйлера для комплексной экспоненты
eiϕ = cos ϕ + i sin ϕ ,
можем записать комплексное число z в виде
z = z eiϕ
139
140.
ПриложенияДля комплексно сопряжённого числа z* = z e−iϕ .
Если вектор вращается в комплексной плоскости с частотой ω , то его
проекции на действительную и мнимую оси изменяются во времени как
Re z = cos ωt , Im z = sin ωt ,
что позволяет описывать вращение с помощью комплексной экспоненты eiωt .
Волну, бегущую вдоль оси x с волновым вектором k , тоже удобно описывать, используя комплексную экспоненту e−iωt +ikx . Для стоячих волн, напротив, удобнее использовать функции sin ω t и cos ωt .
ПРИЛОЖЕНИЕ 2. НЕКОТОРЫЕ ОПРЕДЕЛЕННЫЕ
ИНТЕГРАЛЫ
Докажем, что
∞
−x
∫ e dx = π .
2
(П2.1)
−∞
Рассмотрим произведение двух одинаковых интегралов
∞
∫e
−∞
− x2
∞
dx ∫ e
− y2
∞ ∞
dy =
−∞
∫∫
e
(
− x2 + y2
)
dxdy .
−∞ −∞
Перейдём в этом интеграле к полярной системе координат
∞ ∞
(
)
2π
∞
∞
1 −r2
e
dxdy
=
d
ϕ
e
rdr
=
π
e d (r2 ) = π .
2
∫−∞ −∞∫
∫0 ∫0
∫
20
Отсюда и получаем (П2.1).
Интеграл
− x2 + y 2
−r2
∞
−α x
∫ e dx =
2
−∞
π
.
α
(П2.2)
Все интегралы вида, где k – целое число
∞
∫x
2 k +1 −α x 2
e
dx = 0 ,
(П2.3)
−∞
поскольку подынтегральная функция нечётна. Интегралы вида
∞
∫
2
x 2 k e −α x dx
−∞
можно взять с помощью дифференцирования по параметру. Рассмотрим про∞
изводную
−α x
∫ e dx по параметру α :
2
−∞
140
141.
Приложения∞
∂
∂α
∫
e
−α x 2
−∞
∞
dx = − ∫ x 2 e −α x dx .
2
−∞
С другой стороны,
∂ π
1 π
=−
.
∂α α
2 α 32
Отсюда следует, что
∞
1 π
.
∫−∞
2 α 32
Последовательно дифференцируя по α , получим
2
x 2 e−α x dx =
∞
∫
x 4 e−α x dx =
∫
x6 e−α x dx =
3 π
,
4 α 52
(П2.5)
15 π
,
8 α 72
(П2.6)
2
−∞
∞
2
−∞
(П2.4)
∂ k ⎛ π ⎞ ( 2k − 1)!! π
(П2.7)
∫−∞ x e dx = ( −1) ∂α k ⎜⎝ α ⎟⎠ = 2k α 2k +12 ,
где n!! обозначает произведение всех чисел той же чётности, что и n , от 1 (или
2) до n .
В силу чётности подынтегрального выражения
∞
2k
k
−α x 2
∞
∫x
2k
e
−α x 2
0
∞
2
1
dx = ∫ x 2 k e −α x dx.
2 −∞
(П2.8)
Интегралы вида
∞
∫x
k
e −α x dx
(П2.9)
0
можно также легко взять методом дифференцирования по параметру. Интеграл
∞
∫e
−α x
dx =
0
1
α
.
(П2.10)
Последовательно дифференцируя по параметру α , получим
∞
∫ xe
0
∞
−α x
∫x e
2 −α x
0
∞
∫x
0
n
e
∞
∂
1
−α x
=
dx = −
e
dx
,
α2
∂α ∫0
∞
∂2
2
−α x
dx =
e
dx
=
,
α3
∂α 2 ∫0
−α x
(П2.11)
∞
∂n
n!
dx = ( −1)
e −α x dx = n+1
n ∫
∂α 0
α
n
141
(П2.12)
(П2.13)
142.
ПриложенияУкажем также на очевидную связь интеграла (П2.9) с гамма-функцией
Эйлера
∞
Γ( x ) = ∫ t x −1e − t dt ;
0
значение гамма-функции для целого числа представляет собой факториал
Γ( n + 1) = n !
ПРИЛОЖЕНИЕ 3. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
Дельта-функцией Дирака или δ -функцией называется функция, определенная следующим образом:
⎧0, при x ≠ 0,
δ ( x) = ⎨
⎩∞, при x = 0,
причем
+∞
∫ δ ( x)dx = 1.
(П3.1)
−∞
В интеграле (П3.1) пределы интегрирования не обязательно должны быть бесконечными. Достаточно, чтобы промежуток интегрирования включал в себя
точку x = 0 .
Важнейшее свойство дельта-функции заключается в том, что для произвольной непрерывной функции f ( x )
+∞
∫ δ ( x) f ( x)dx = f (0).
−∞
Очевидно, что функция δ ( x − a ) обладает в окрестности точки x = a теми же свойствами, что и функция δ ( x ) в окрестности точки x = 0 . В частности,
+∞
∫ δ ( x − a) f ( x)dx = f (a).
(П3.2)
−∞
Аналогично одномерной определяется трехмерная функция Дирака δ (r ) .
В декартовых координатах
δ (r ) = δ ( x)δ ( y )δ ( z ).
Свойство (П3.2) в случае трехмерной дельта-функции принимает вид:
(П3.3)
∫ δ ( r − r0 ) f (r )dr = f (r0 ) ,
где интегрирование производится по объему, содержащему точку, определяемую вектором r0 .
142
143.
ПриложенияОпределенная таким образом дельта-функция не относится к числу
функций, рассматриваемых в классическом анализе. Действительно, интеграл
(П3.1), взятый по любому отрезку, содержащему точку x = 0 , конечен, в то
время как функция δ ( x ) отлична от нуля лишь на множестве меры нуль.
Дельта-функция является представителем класса так называемых обобщенных
функций и определяется не заданием величины для всех значений аргумента, а
заданием правил интеграции ее произведений с непрерывными функциями.
Отметим некоторые основные соотношения, которым удовлетворяет
дельта-функция:
1)
δ (− x) = δ ( x),
(П3.4)
f ( x)δ ( x − a ) = f ( a)δ ( x − a ),
2)
(П3.5)
в частности, xδ ( x) = 0,
+∞
3)
∫ δ (a − x)δ ( x − b) = δ (a − b),
(П3.6)
−∞
n
4) δ ( f ( x)) = ∑
i =1
δ ( x − xi )
df ( x)
dx x= xi
,
(П3.7)
где xi – нули функции f ( x) , n - количество нулей на всей оси x , в частности,
1
(П3.8)
δ (α x ) = δ ( x ), α ≠ 0.
α
Дельта-функция допускает интегральное представление:
1
δ ( x) =
2π
+∞
∫e
− ikx
dk .
(П3.9)
−∞
Поскольку функция δ ( x ) четная, то формулу (П3.9) можно представить в эквивалентном виде
1
δ ( x) =
2π
+∞
∫ cos kxdk .
(П3.10)
−∞
В трехмерном случае интегральное представление аналогичное (П3.9)
имеет вид:
1
(П3.11)
δ (r ) =
e− ikr dk ,
3 ∫
( 2π )
где интегрирование производится по всему k -пространству.
Производные от δ -функции определяются равенством:
143
144.
Приложения+∞
∫δ
(n)
( x) f ( x)dx = (−1)n f ( n ) (0),
−∞
где n - любое целое число.
Дельта-функция может быть определена как предел последовательностей обычных функций. В частности,
⎛ x2 ⎞
δ ( x) = lim
exp ⎜ − 2 ⎟ ,
ε →0 π ε
⎝ ε ⎠
1 ε
δ ( x) = lim
,
2
2
ε →0 π ε + x
1 sin(ε x)
,
δ ( x) = lim
ε →0 π
x
1 sin 2 (ε x)
.
δ ( x) = lim
ε →∞ πε
x2
1
(П3.12)
(П3.13)
(П3.14)
(П3.15)
ПРИЛОЖЕНИЕ 4. ПОЛИНОМЫ ЭРМИТА
Рассмотрим уравнение
d 2 f ( x)
df ( x)
2
x
−
+ λ f ( x) = 0,
(П4.1)
dx 2
dx
в котором λ является некоторым параметром. Поставим задачу об определении решения этого уравнения, остающегося конечным при любых конечных
значениях x и стремящегося при x → ±∞ к бесконечности не быстрее конечной степени x . Будем искать это решение в виде ряда
∞
f ( x ) = ∑ ak x k .
(П4.2)
k =0
Первая и вторая производные f ( x) равны
df ( x ) ∞
= ∑ kak x k −1 ,
dx
k =0
(П4.3)
∞
d 2 f ( x) ∞
k −1
= ∑ k ( k − 1) ak x = ∑ k ( k − 1) ak x k −1 =
2
dx
k =0
k =2
∞
= ∑ ( k + 1)( k + 2) ak + 2 x k .
(П4.4)
k =0
В сумме (П4.3) мы сначала отбросили равные нулю члены, соответствующие
k = 0 и k = 1 , а затем заменили k на k + 2 .
Подставляя (П4.2) – (П4.4) в уравнение (П4.1), получаем
144
145.
Приложения∞
∑ (k + 1)(k + 2)a
k =0
k +2
∞
x − 2 x ∑ kak x
k
k =0
k −1
∞
+ λ ∑ ak x k = 0,
k =0
или, внося во втором члене x под знак суммы,
∞
∑ [(k + 1)(k + 2)a
k =0
k +2
−2kak + λ ak ] x k = 0.
Последнее соотношение должно выполняться для всех x . Этого можно добиться только положив равными нулю коэффициенты при всех степенях x , т.е.
должно быть справедливым следующее соотношение:
( k + 1)( k + 2) ak + 2 − 2 kak + λ ak = 0,
Откуда
2k − λ
ak +2 =
ak .
(П4.5)
(k + 1)(k + 2)
Тем самым мы получили рекуррентное соотношение для коэффициентов a k
ряда (П4.2). По формуле (П4.5) можно последовательно определить коэффициенты ak , причем первые два коэффициента a0 и a1 остаются произвольными. Представим функцию f ( x) в виде
f ( x ) = ( a0 + a2 x 2 + a4 x 4 + ...) + ( a1 x + a3 x 3 + a5 x 5 + ...) ≡ f 0 ( x ) + f1 ( x ) .
Здесь f0 ( x) – ряд, содержащий только четные, а f1 ( x) - ряд, содержащий только нечетные степени . Ряды f0 ( x) и f1 ( x) являются линейно-независимыми
решениями уравнения (П4.1).
При больших соотношение (П4.5) можно упростить:
2
ak +2 =
ak .
(П4.6)
k+2
Распространим формулу (П4.6) на любые . Имеем для четных коэффициентов
a
a
a2 k −6
1
a2 k = 2 k −2 = 2 k −4 =
= ... = a0 .
(П4.7)
k
k (k − 1) k (k − 1)(k − 2)
k!
С учетом (П4.7) ряд (П4.2) для четных коэффициентов запишется следующим
образом:
∞
1
f 0 ( x) = a0 ∑ x 2 k .
(П4.8)
k =0 k !
То обстоятельство, что по формуле (П4.6), справедливой для больших k , вычислены начальные коэффициенты ряда (П4.8) не играет заметной роли при
больших x , так как в этом случае вклад первых членов ряда не является существенным.
2
С другой стороны разложение функции e x в ряд имеет вид
145
146.
Приложения∞
1 2k
x .
k =0 k !
Сравнивая (П4.8) и (П4.9), замечаем, что при больших x
e =∑
x2
(П4.9)
2
f 0 ( x ) = a0e x .
Мы получили выражение при больших x для решения f0 ( x) в предположении, что отличны от нуля коэффициенты ak с четными номерами. Абсолютно аналогично можно получить такой же результат для решения f1 ( x) ,
рассмотрев коэффициенты с нечетными k .
2
Так как при x → ±∞ функция e x стремится к бесконечности быстрее
конечной степени x , то для получения искомых решений уравнения (П4.1)
число слагаемых в f0 ( x) ( f1 ( x) ) должно быть конечным. Для этого необходимо, чтобы коэффициенты , начиная с некоторого четного (нечетного) значения k , были равны нулю и a1 = 0 ( a0 = 0 ).
Пусть an ≠ 0 , а an+2 = 0 . Тогда в соответствии с (П4.5) 2n − λ = 0 . Отсюда
получаем значения λ , при которых уравнение (П4.1) имеет конечные решения:
λ = 2n ( n = 0,1,2,...) .
(П4.10)
Числа λ называются собственными значениями уравнения (П4.1), а его
решения - собственные функции – представляют собой многочлены
n
f n ≡ H n ( x ) = ∑ ak x k ,
k =0
коэффициенты которых удовлетворяют условию
2(k − n)
ak +2 =
ak .
(П4.11)
(k + 1)(k + 2)
Такие многочлены называются полиномами Эрмита.
Последним отличным от нуля коэффициентом полинома Эрмита H n ( x )
будет a n . Следовательно, при четном n в полиноме содержатся только четные
степени x , а при нечетном n - только нечетные степени x . Формула (П4.11)
позволяет выразить a k через a 0 при четном n , либо через a1 при нечетном n .
Значения a 0 или a 1 для каждого H n ( x ) определяются из условия нормировки.
Полиномы Эрмита часто представляют в виде
2
d ne− x
(П4.12)
H n ( x ) = ( −1) e
, n = 0,1, 2,...
dx n
Можно показать, что определяемые таким образом полиномы ортогональны с
n
x2
2
весом e− x , т.е.
146
147.
Приложения+∞
∫
2
H n ( x)H m ( x)e − x dx = 0,
n ≠ m.
(П4.13)
−∞
При n = m последний интеграл отличен от нуля и равен
+∞
n
−x
∫ [ H n ( x)] e dx = n!2
2
2
π.
(П4.14)
−∞
Первые два полинома Эрмита H 0 ( x ) и H 1 ( x ) легко вычислить непосредственно по формуле (П4.12):
H 0 ( x ) = 1,
H 1 ( x ) = 2 x.
Для вычисления следующих полиномов Эрмита удобно воспользоваться рекуррентным соотношением:
H n + 2 ( x ) = 2 xH n +1 ( x ) − 2( n + 1) H n ( x ).
Так, например,
H 2 ( x ) = 2 xH 1 ( x ) − 2 H 0 ( x ) = 4 x 2 − 2,
H 3 ( x ) = 2 xH 2 ( x ) − 4 H 1 ( x ) = 8 x 3 − 12 x,
H 4 ( x ) = 2 xH 3 ( x ) − 6 H 2 ( x ) = 16 x 4 − 48 x 2 + 12.
ПРИЛОЖЕНИЕ 5. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ
ЧЕБЫШЕВА-ЛАГЕРРА
Полином Lkn ( x ) , определяемый формулой
d k ⎛ x d n n −x ⎞
(x e ) ⎟,
L = k ⎜e
dx ⎝ dx n
⎠
k
n
(П5.1)
где n, k = 0,1,2,... (k ≤ n) , называется присоединенным полиномом ЧебышеваЛагерра порядка k . Например,
L10 ( x ) = 1 − x,
L02 ( x ) = x 2 − 4 x + 2,
L12 ( x ) = 2 x − 4,
L22 ( x ) = 2,
L13 ( x ) = −3 x 2 + 18 x − 18.
Присоединенные полиномы Чебышева-Лагерра Lkn ( x ) и Lkm ( x ) одного и
того же порядка k и различных степеней ( n ≠ m) ортогональны с весом
ρ ( x ) = x k e − x на интервале x ∈ ⎡⎣0, ∞ ) , т.е.
147
148.
Приложения∞
∫x e
k −x k
n
L ( x) Lkm ( x)dx = 0, n ≠ m.
(П5.2)
0
При n = m справедливо следующее условие нормировки для присоединенных полиномов Чебышева-Лагерра:
∞
(n!)3
∫0 x e ⎡⎣ L ( x) ⎤⎦ dx = (n − k )!.
k −x
k
n
2
(П5.3)
Уравнение
d2y
dy
x 2 + ( k + 1 − x ) + (λ − k ) y = 0
(П5.4)
dx
dx
называется присоединенным дифференциальным уравнением Лагерра. В математике доказывается следующая теорема: уравнение (П5.4) имеет нетривиальное решение y = y ( x ) конечное при x = 0 и имеющее степенной рост при
x → +∞ , т.е. удовлетворяющее условиям:
y ( x)
= 0,
x→+∞ x N
где N - натуральное число, только при λ = n ≥ k , (n = 0,1,2,...) . Таким решениy (0) ≠ 0,
lim
ем с точностью до константы C являются присоединенные полиномы Чебышева-Лагерра, т.е.
(П5.5)
y = CLkn ( x ).
Для вычисления нормировочной константы для радиальной функции
атома водорода нам пригодится значение следующего интеграла:
∞
(n!)3
∫0 x e ⎡⎣ L ( x)⎤⎦ dx = (n − k )! (2n − k + 1).
k +1 − x
k
n
2
148
(П5.6)
149.
ЛитератураЛитература
1. Блохинцев Д.И. Основы квантовой механики. М.: Наука, 1983.
2. Галицкий В.М., Карнаков Б.М., Коган В.И. Задачи по квантовой механике.
Ч. 1, М.: УРСС, 2001.
3. Гречко Л.Г., Сугаков В.И., Томасевич О.Ф., Федорченко А.М. Сборник задач по теоретической физике. М.: Высшая школа, 1972.
4. Гольдман И.И., Кривченков В.Д. Сборник задач по квантовой механике. М.:
Изд-во технико-теоретической литературы, 1957.
5. Давыдов А.С. Квантовая механика. М.: Наука, 1973.
6. Казаков К.А. Введение в теоретическую и квантовую механику. М.: Изд-во
МГУ, 2008. 232 с.
7. Копытин И.В., Корнев А.С. Задачи по квантовой механике. Ч. 1-3, Воронеж: Изд-во ВГУ, 2004.
8. Ландау Л.Д., Лифшиц Е.М. Квантовая механика. М.: Физматлит, 2004.
9. Мартинсон Л.К., Смирнов Е.В. Квантовая физика. М.: Изд-во МГТУ им.
Н.Э. Баумана, 2004.
10. Соколов А. А., Тернов И. М., Жуковский В.Ч. Квантовая механика. М.: Наука, 1979, 528 с.
11. Степанов Н.Ф. Квантовая механика и квантовая химия. М.: Мир и Изд-во
МГУ, 2001.
12. Флюгге З. Задачи по квантовой механике. Т. 1, М.: Мир, 1974.
13. Фок В.А. Начала квантовой механики. М.: УРСС, 2001.
14. Шпольский Э.В. Атомная физика, тт. I-II. М.: Наука, 1974.
149
150.
Учебное изданиеГОЛОВАНЬ Леонид Анатольевич
КОНСТАНТИНОВА Елизавета Александровна
ФОРШ Павел Анатольевич
ЗАДАЧИ ПО КВАНТОВОЙ МЕХАНИКЕ ДЛЯ ХИМИКОВ
УЧЕБНОЕ ПОСОБИЕ
Подписано в печать
. .2010 г.
Печать офсетная. Формат А5.
Объем 9 п.л. Тираж
экз. Заказ №
Физический факультет МГУ
Лицензия ЛР-021293 от 18.06.1998
119991 Москва, Ленинские Горы, МГУ им. М.В. Ломоносова
150



















































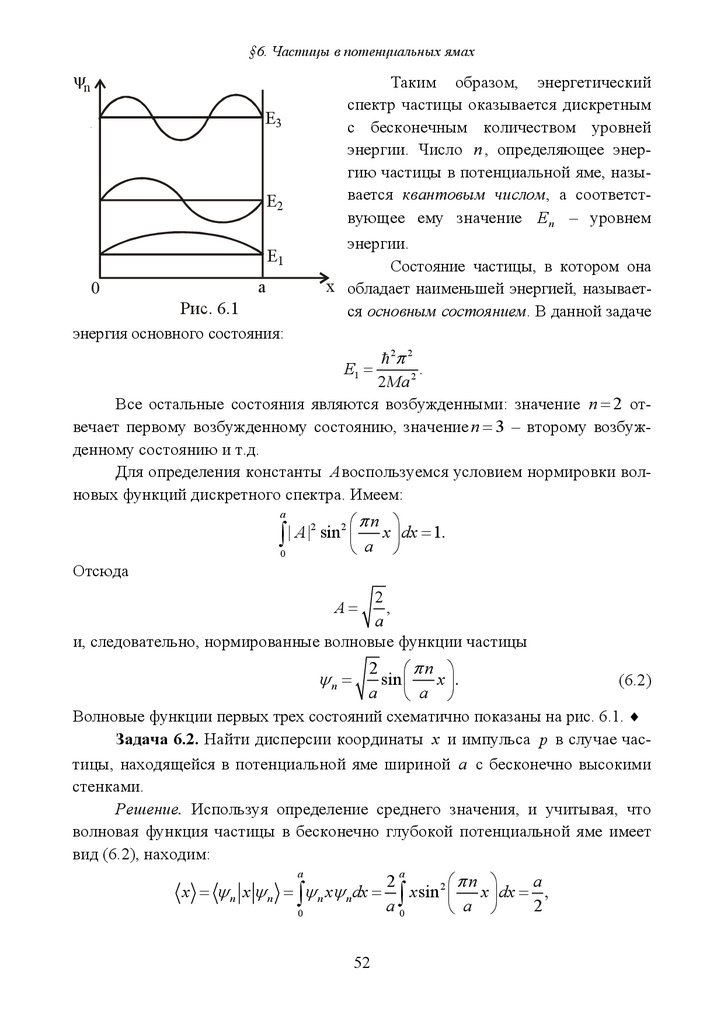



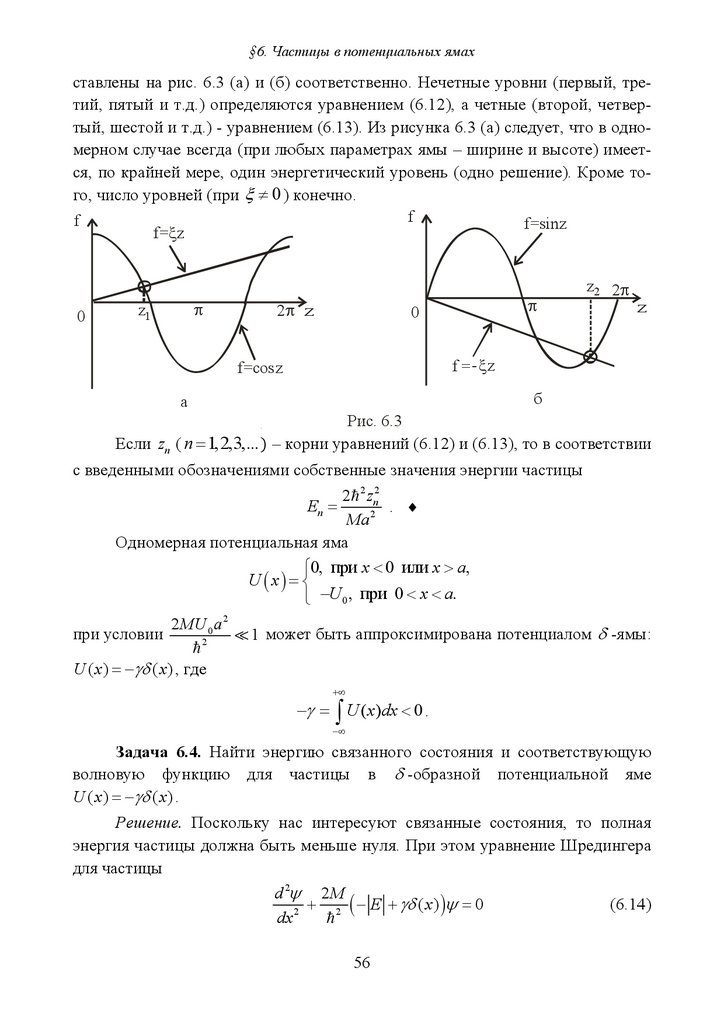



























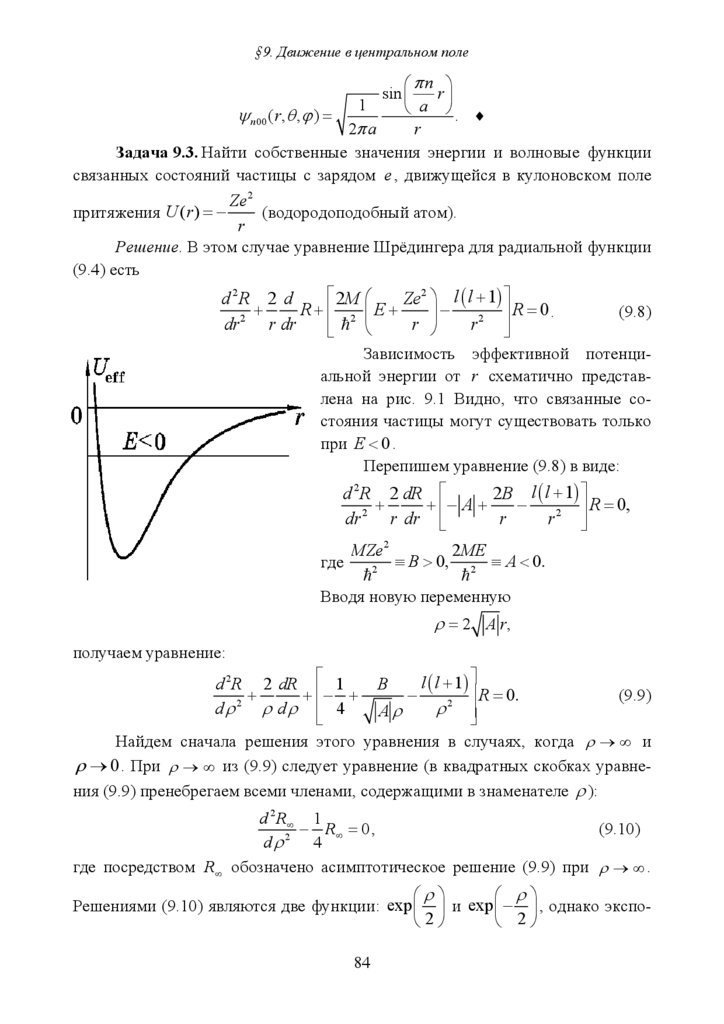















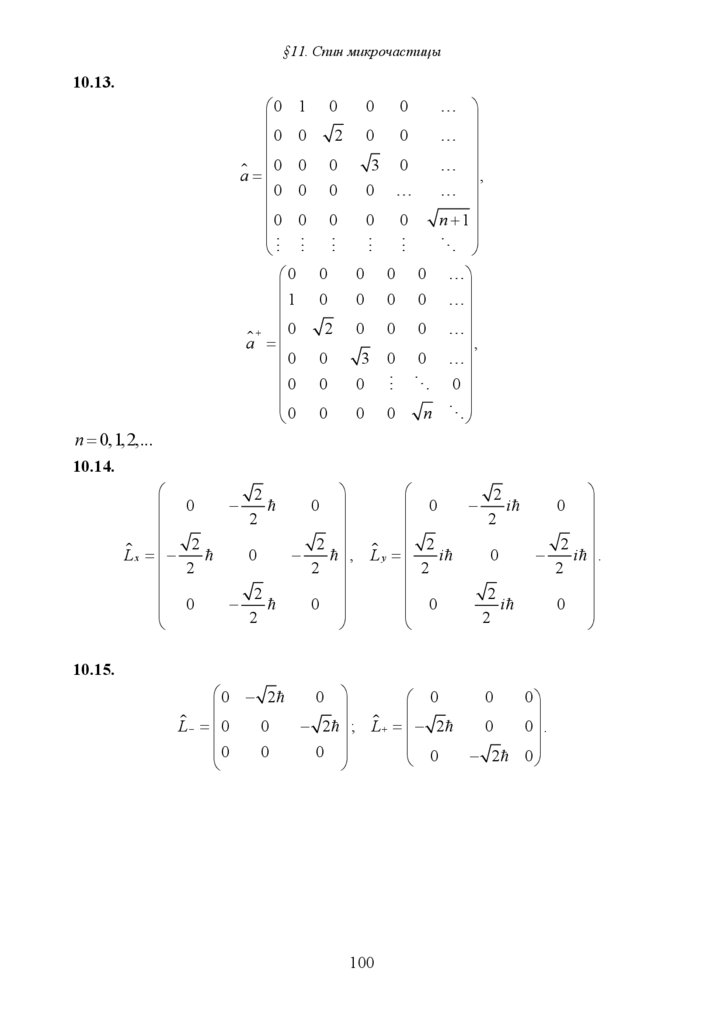


















































 Физика
Физика








