Похожие презентации:
Теория вероятностей
1.
2.
Теория вероятностей — раздел математики, изучающий закономерностислучайных явлений: случайные события, случайные величины, их свойства
и операции над ними.
Понятие вероятности восходит к древним временам; оно было известно
уже античным философам. Мысль о том, что законы природы проявляются
через множество
случайных событий,
впервые возникла
у древнегреческих
материалистов.
3.
Игральный кубик бросили один раз. Какова вероятность того, чтовыпадает не менее 4 очков?
Решение:
1.Бросаем игральный кубик один раз – 6исходов. Значит, у данного
действия (бросание одного игрального кубика 1 раз) всего имеется
n=6 возможных исходов.
2.Выписываем все благоприятные исходы: 4; 5; 6.
Значит, k = 3 – число благоприятных исходов.
3
1.По формуле классической вероятности имеем: Р( А) 0,5
6
Ответ: 0,5
4.
Задание B10 (№ 283441)В случайном эксперименте бросают две игральные кости. Найдите
вероятность того, что в сумме выпадет 5 очков. Результат округлите
до сотых.
Решение:
Бросаем первую игральную кость – 6 исходов, для каждого из
которых возможны ещё 6 исходов (когда мы бросаем вторую
кость) Значит у данного действия (бросание двух игральных костей)
всего имеется n=62=36 возможных исходов
Выписываем все благоприятные исходы в виде пар чисел:
(1;4), (2;3), (3;2), (4;1)
Значит, k=4 – число благоприятных исходов.
4 1
Р
(
А
)
0,11
По формуле классической вероятности имеем:
36 9
Ответ: 0,11
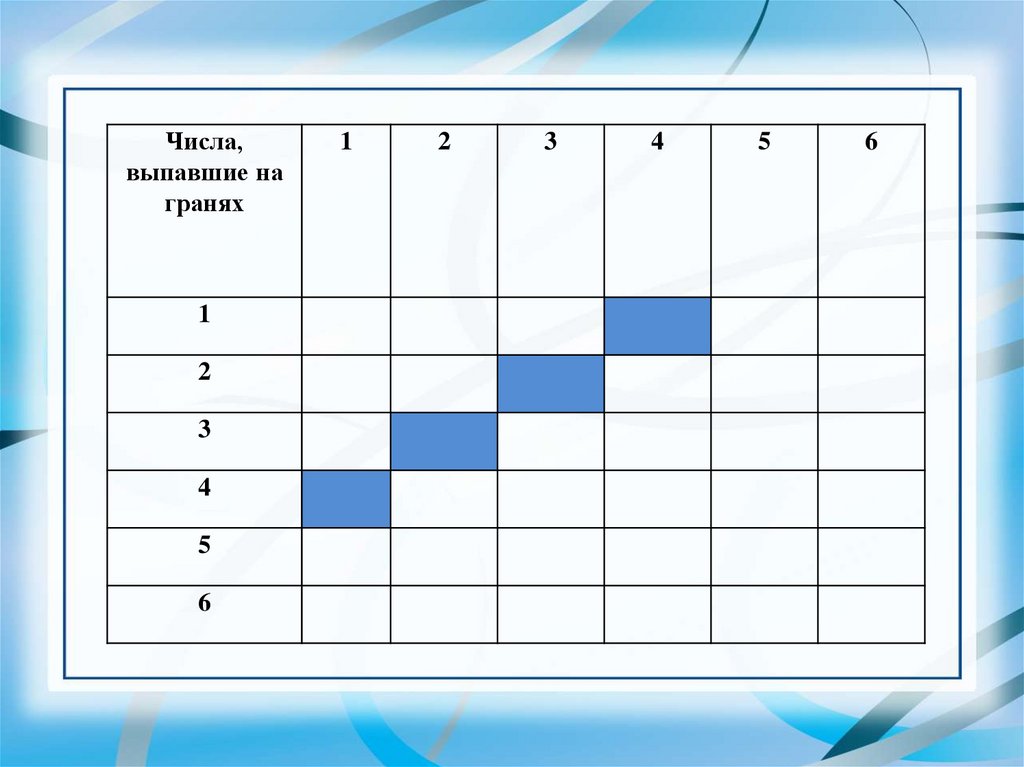
5.
Числа,выпавшие на
гранях
1
2
3
4
5
6
1
2
3
4
5
6
6.
Задача 4. В случайном эксперименте бросают дваигральных кубика. Найдите вероятность того, что в
сумме выпадет 8 очков.
Решение:
Множество элементарных исходов: N=36
Числа на
выпавших
сторонах
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
3 4 5 6 7
4 5 6 7 8
5 6 7 8 9
6 7 8 9 10
7 8 9 10 11
8 9 10 11 12
A= {сумма равна 8}
N(А)=5
N ( A)
P ( A)
N
5
P ( A)
36
Ответ:5/36
7.
Реши самостоятельно!Монету бросают три раза. Какова вероятность того, что
результаты двух первых бросков будут одинаковы?
1
2
3
О
О
О
О
О
Р
О
Р
О
О
Р
Р
Р
О
О
Р
О
Р
Р
Р
О
Р
Р
Р
4
P ( A) 0,5
8
Ответ: 0,5
8.
Задача 9. В чемпионате мира участвуют 16 команд. Спомощью жребия их нужно разделить на 4 группы по 4
команды в каждой. В ящике вперемешку лежат
карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова
вероятность того, что команда России окажется во
второй группе.
Решение:
Множество элементарных событий: N=16
A={команда России во второй группе}
С номером «2» четыре карточки: N(A)=4
N ( A) 4
P( A)
0,25
N
16
Ответ: 0,25
9. № 320181 В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами.
Турист А. хотел бы сходить в магазин, но онподчиняется жребию. Какова вероятность того, что А.
пойдёт в магазин?
Решение:
Возможные комбинации пар из 5 человек (1,2,3,4,5)
12 23 34 45
13 24 35
14 25
15
Всего - 10
У каждого 4 шанса
Р=4/10=0,4
08.10.2024
Ответ:0,4
9
10. № 320186 На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием.
№ 320186На рок-фестивале выступают группы — по одной от
каждой из заявленных стран. Порядок выступления
определяется жребием. Какова вероятность того, что
группа из Дании будет выступать после группы из Швеции и
после группы из Норвегии? Результат округлите до сотых.
Решение:
Возможные комбинации (независимо от количества
групп):
ДШН
ШНД
Благоприятных - 2
2 1
P 0,33
6 3
08.10.2024
ДНШ
НДШ
ШДН
НШД
6 - вариантов
Ответ:0,33
10
11.
Определение. События называют несовместными,если они не могут происходить одновременно в одном и
том же испытании.
Теорема. Вероятность суммы двух несовместных
событий А и В (появления хотя бы одного события)
равна сумме вероятностей этих событий:
P(A+ B) = P (A)+ P(B).
Следствие. Сумма вероятностей противоположных
событий А и A равна 1:
12.
Зачет по стрельбе курсант сдаст, если получит оценкуне ниже 4. Какова вероятность сдачи зачета, если
известно, что курсант получает за стрельбу оценку 5 с
вероятностью 0,3 и оценку 4 с вероятностью 0,6?
Решение. Данный опыт состоит в том, что проведены
стрельбы и по ним курсант получил оценку. В этом опыте
обозначим через А событие «по стрельбе курсант получил
оценку 5» и через В событие «по стрельбе курсант
получил оценку 4». Эти события несовместны. Событие С
«зачет сдан» является их суммой C = A + B . Из условия
задачи следует, что вероятности P(A) = 0,3 и P(B) = 0,6 . По
формуле сложения вероятностей несовместных событий
имеем:.
Р (C)= P (A+ B) = P (A) + P (B)= 0,3 +0, 6 =0,9
Ответ: 0,9.
13.
Задание B10 (№ 320385)На экзамене по геометрии школьнику достаётся один вопрос из списка
экзаменационных вопросов. Вероятность того, что это вопрос на
тему «Вписанная окружность», равна 0,1. Вероятность того, что это
вопрос на тему «Тригонометрия», равна 0,35. Вопросов, которые
одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по
одной из этих двух тем.
Решение:
1. А={ вопрос на тему «Вписанная окружность»}
В={ вопрос на тему «Тригонометрия»}
С={ вопрос по одной из двух тем}
2. События А и В несовместны, так как по смыслу задачи нет
C A B
вопросов, относящихся к двум темам одновременно. Значит
3. 3. По правилу сложения для несовместных событий имеем:
P C P A B P A B
Р(С)=0,1+0,35=0,45
Ответ: 0,45
14.
Определение. События называют совместными, если онимогут происходить одновременно.
Теорема. Вероятность суммы двух совместных событий
А и В (появления хотя бы одного события) равна сумме их
вероятностей без вероятности их совместного появления, то
есть
Р(A+ B) = P(A) - P(B) - P(AB).
Частным случаем приведенной формулы является
формула сложения вероятностей для несовместных
событий, так как их совместное наступление есть
невозможное событие и P(AB)= 0 .
Для случая трех совместных событий формула имеет
вид:
Р(A+ B+ C)= P( A)+ P( B)+ P( C) - P (АB) - P( AC) - P(
BC) + P( ABС).
15.
Прибор, состоящий из двух блоков, выходит из строя, если выходятиз строя оба блока. Вероятность безотказной работы за определенный
промежуток времени первого блока составляет 0,9, второго – 0,8,
обоих блоков – 0,75. Найти вероятность безотказной работы прибора в
течение указанного промежутка.
Решение. Обозначим через А событие «первый блок работает
безотказно в течение определенного промежутка времени», через В
событие «второй блок работает безотказно в течение определенного
промежутка времени», через АВ событие «оба блока работают
безотказно в течение определенного промежутка времени». Событие С
«прибор работает безотказно в течение определенного промежутка
времени» является суммой событий А и В: C = A + B . Из условия
задачи известны вероятности P(A) = 0,9 , P(B) = 0,8 и P(AB) = 0,75 . По
формуле сложения вероятностей имеем:
Р( C)= P (A+ B)= P( A)+ P( B) - P( AB)= 0,9+ 0,8 - 0, 75= 0,95.
Ответ: 0,95
16.
Событие В называетсяНЕЗАВИСИМЫМ от события А,
если появления события А не изменяет
вероятности события В.
Формула умножения вероятностей для
независимых событий:
P C P A B P A B
17.
Задание B10 (№ 320477)Биатлонист 4 раза стреляет по мишеням. Вероятность
попадания в мишень при одном выстреле равна 0,85. Найдите
вероятность того, что биатлонист первые 2 раза попал в
мишени, а последние два промахнулся. Результат округлите
до сотых.
Решение:
Вероятность попадания = 0,85
Вероятность промаха =1-0,85=0,15
А={попадание, попадание, промах, промах}
События независимые. По формуле умножения вероятностей:
P C 0,85 0,85 0,15 0,15 0,7225 0,0225 0,01625625 0,02
Ответ: 0,02
















 Математика
Математика








