Похожие презентации:
Алгоритмы перевода целых чисел
1. АЛГОРИТМЫ ПЕРЕВОДА ЦЕЛЫХ ЧИСЕЛ
из Р-ричной системысчисления в Q-ричную
2. Перевод в десятичную систему счисления
Двоичная система счисления, q=21011,012 1 23 0 22 1 21 1 20 0 2 1 1 2 2 11,2510
Восьмеричная система счисления, q=8
542,188 5 82 4 81 2 80 1 8 1 8 8 2 354,2510
Шестнадцатеричная система счисления, q=16
F 5C , E 616 F 16 2 5 161 C 160 E 16 1 6 16 2 3932,910
2
3. I. Перевод целого десятичного числа в систему с основанием q
1. При переводе целого десятичного числа всистему с основанием q его необходимо
последовательно делить на q до тех пор, пока
не останется остаток, меньший или равный q–1.
2. Число в системе с основанием q записывается
как последовательность остатков от деления,
записанных в обратном порядке, начиная с
последнего частного.
3. q = 2; 8; 16.
3
4.
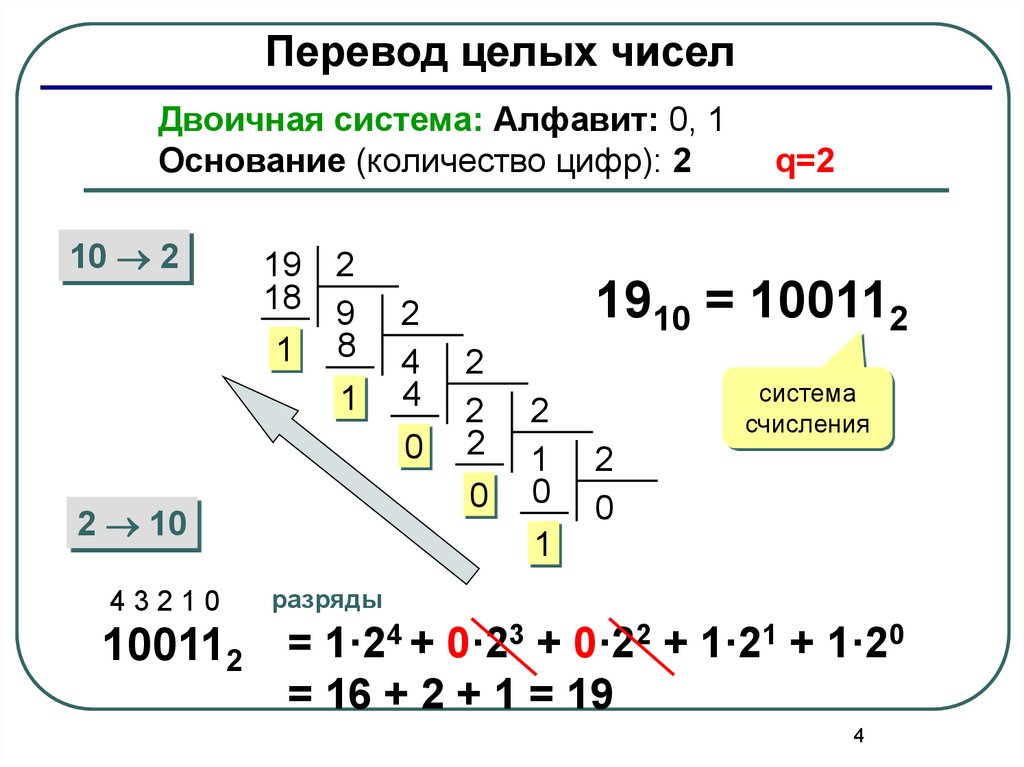
Перевод целых чиселДвоичная система: Алфавит: 0, 1
Основание (количество цифр): 2
10 2
19
18
1
2
9
8
1
2
4
4
0
43210
1910 = 100112
2
2
2
0
2 10
q=2
2
1
0
система
счисления
2
0
1
разряды
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19
4
5.
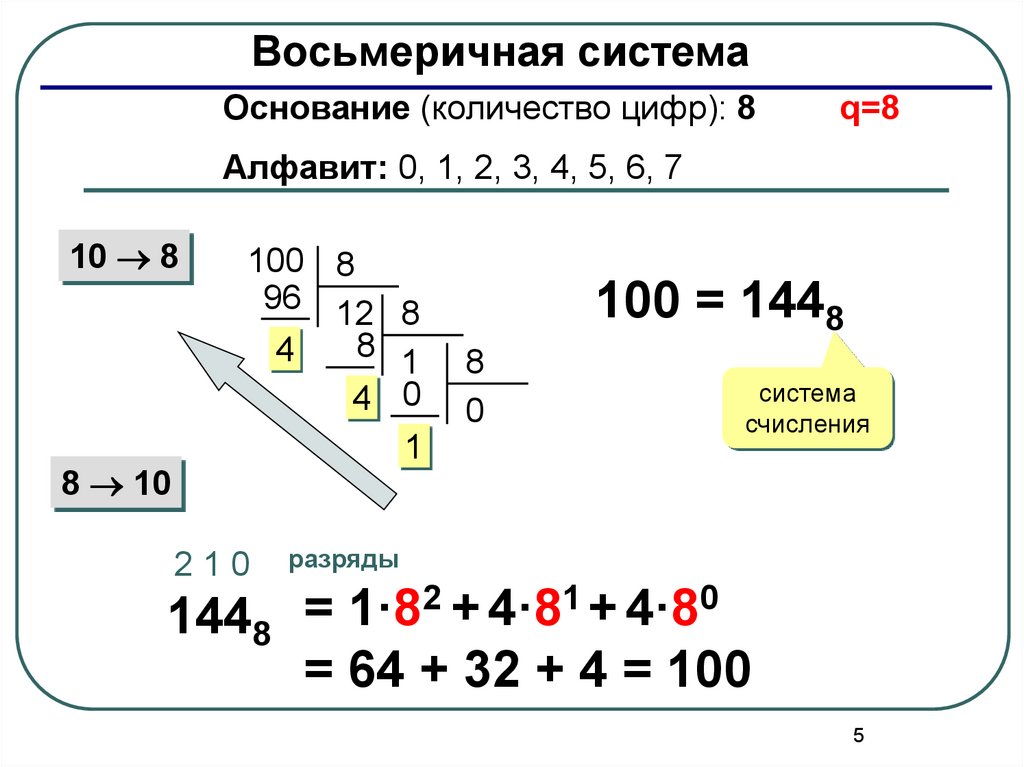
Восьмеричная системаОснование (количество цифр): 8
q=8
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
10 8
100 8
96 12 8
8 1
4
4 0
1
8 10
210
100 = 1448
8
0
система
счисления
разряды
2 + 4·81 + 4·80
=
1·8
1448
= 64 + 32 + 4 = 100
5
6.
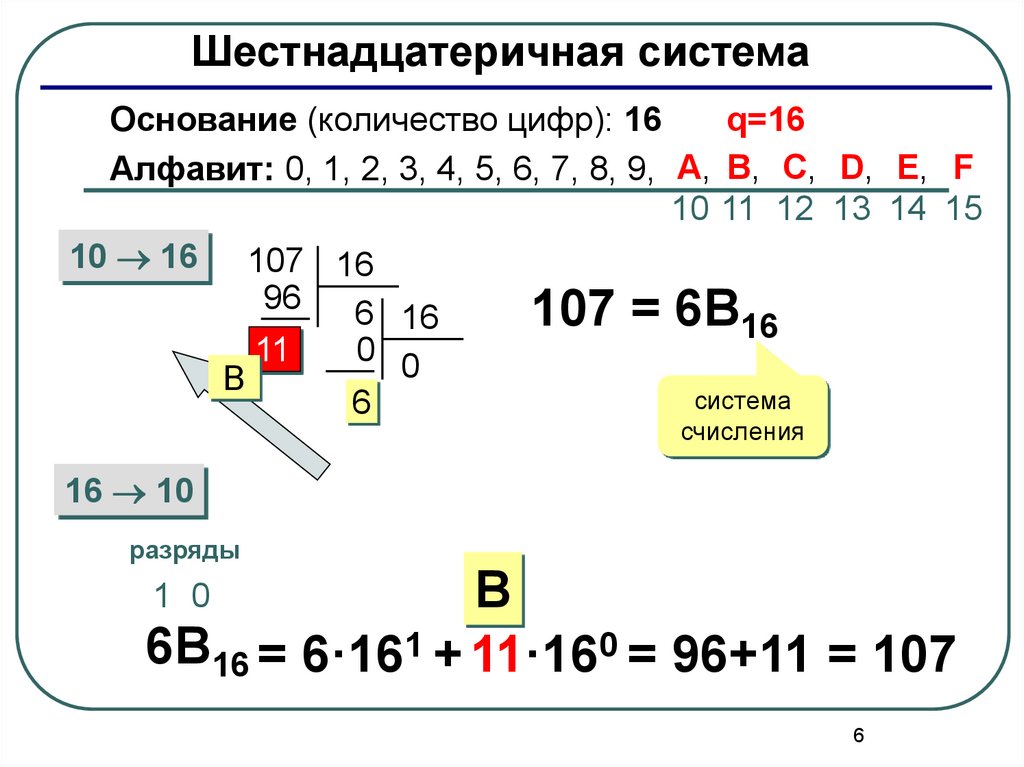
Шестнадцатеричная системаОснование (количество цифр): 16
q=16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
10 11 12 13 14 15
10 16 107 16
96
6 16
107 = 6B16
0 0
11
B
система
6
счисления
16 10
разряды
B
6B16 = 6·161 + 11·160 = 96+11 = 107
1 0
6
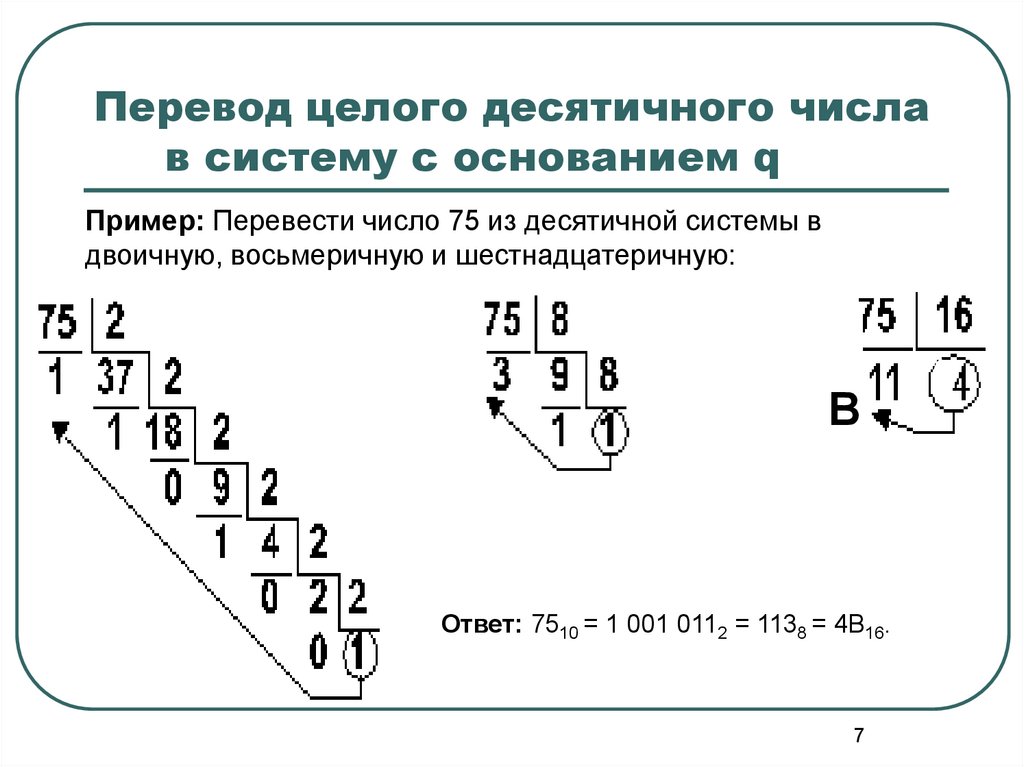
7. Перевод целого десятичного числа в систему с основанием q
Пример: Перевести число 75 из десятичной системы вдвоичную, восьмеричную и шестнадцатеричную:
B
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
7
8. Решение задач по переводу целого десятичного числа в систему с основанием q
Задача 1. Перевести число 523 из десятичной системысчисления в двоичную.
Ответ: 10000010112
Задача 2. Перевести число 856 из десятичной системы
счисления в восьмеричную.
Ответ: 15308
Задача 3. Перевести число 5012 из десятичной системы
счисления в шестнадцатеричную.
Ответ: 139416
8
9. Перевод целого двоичного числа в систему с основанием q=2n
Для того, чтобы целое двоичное число записать всистеме счисления с основанием q=2n, необходимо:
1) данное двоичное число разбить справа налево на
группы по n цифр в каждой;
2) если в последней левой группе окажется меньше n
разрядов, то ее надо дополнить слева нулями до
нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное
число и записать его соответствующей цифрой в
нужной системе счисления, воспользовавшись
таблицей систем счисления.
9
10. Перевод целого двоичного числа в систему с основанием q=2n
q = 2 = 21q = 8 = 23
q = 10 ≈ 23
q = 16 = 24
10
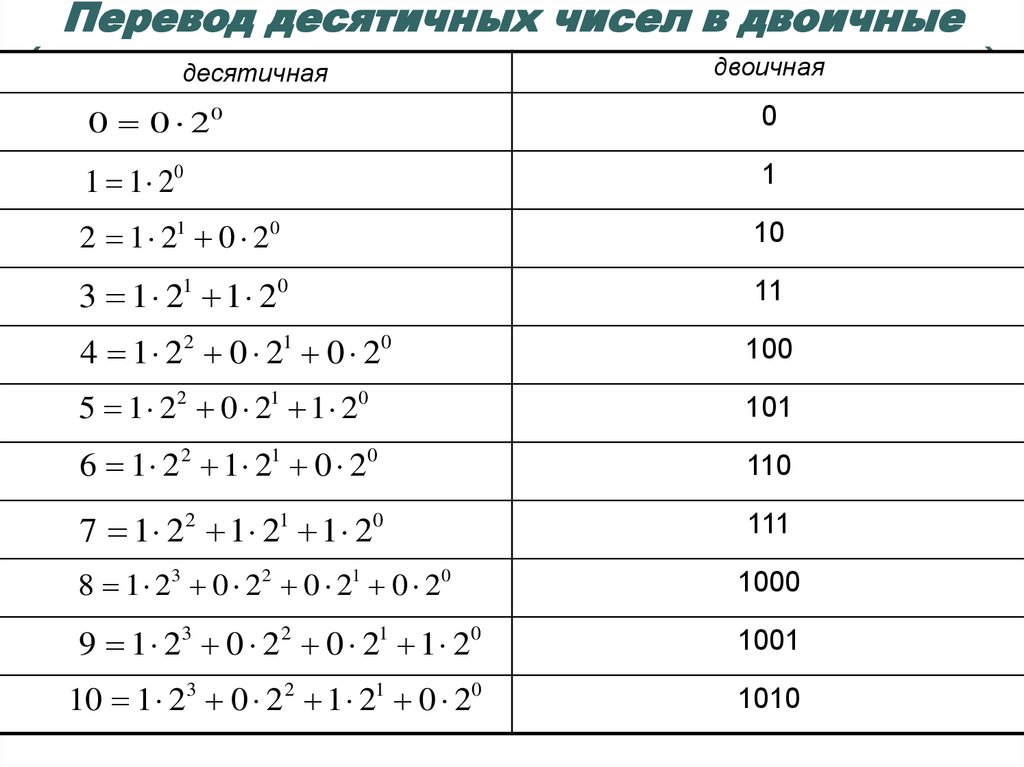
11. Перевод десятичных чисел в двоичные
десятичнаядвоичная
0 0 20
0
1 1 20
1
2 1 21 0 20
10
3 1 21 1 20
11
4 1 22 0 21 0 20
100
5 1 22 0 21 1 20
101
6 1 22 1 21 0 20
110
7 1 22 1 21 1 20
111
8 1 23 0 22 0 21 0 20
1000
9 1 23 0 22 0 21 1 20
1001
10 1 23 0 22 1 21 0 20
1010
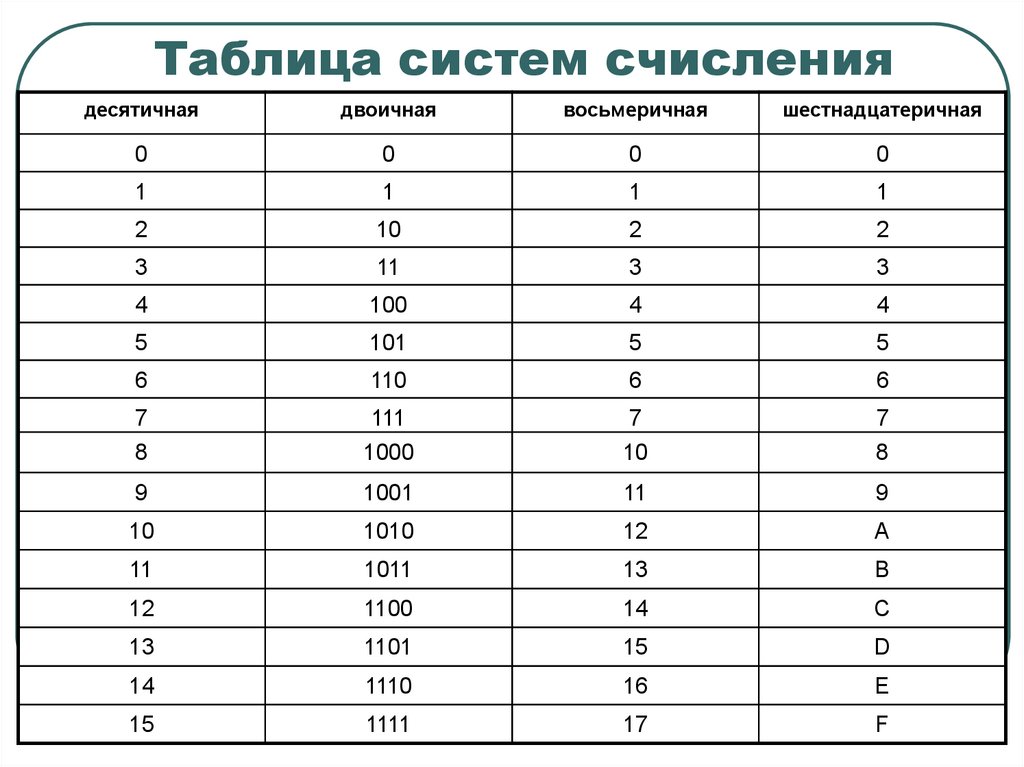
12. Таблица систем счисления
десятичнаядвоичная
восьмеричная
шестнадцатеричная
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
8
111
1000
7
10
7
8
9
1001
11
9
10
1010
12
А
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
12
F
13.
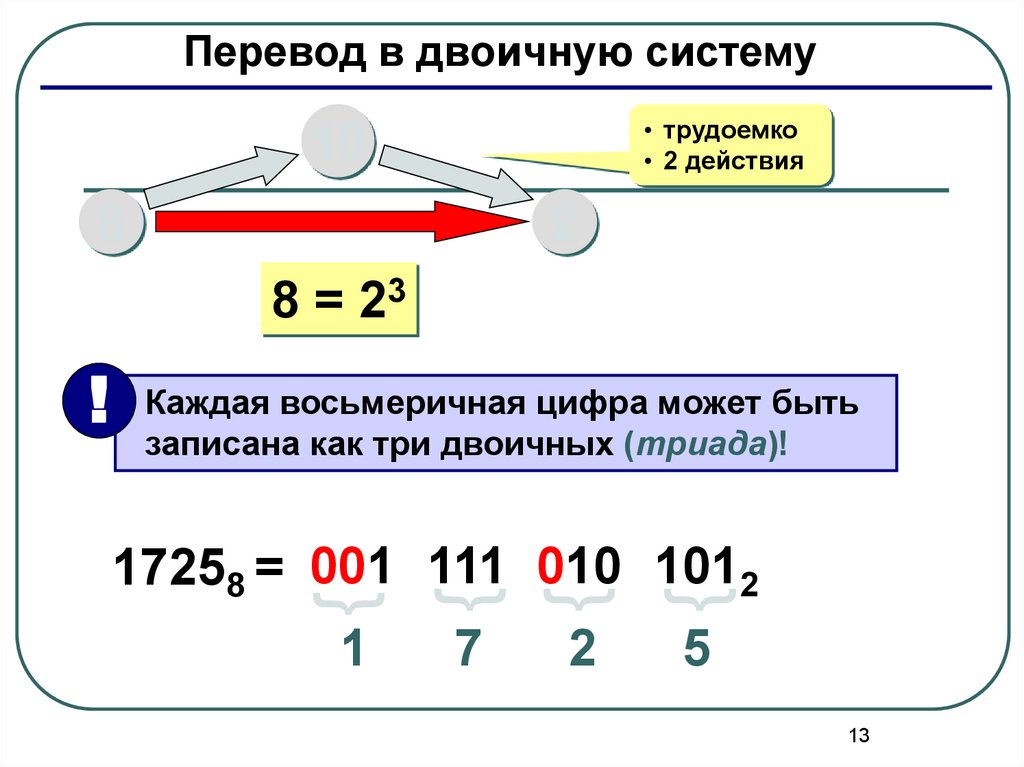
Перевод в двоичную систему• трудоемко
• 2 действия
10
8
2
8 = 23
! Каждая восьмеричная цифра может быть
записана как три двоичных (триада)!
{
{
{
{
17258 = 001 111 010 1012
1
7
5
2
13
14.
Обратный перевод в восьмеричную систему10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:
001 001 011 101 1112
1
1
3
5
7
Ответ: 10010111011112 = 113578
14
15.
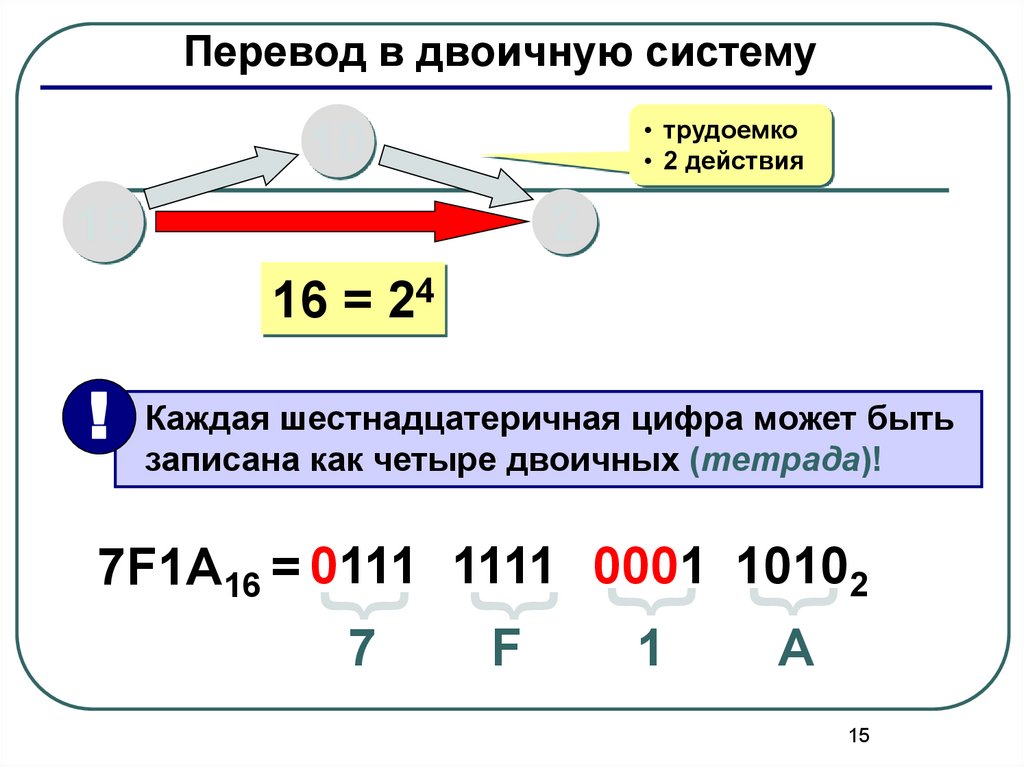
Перевод в двоичную систему• трудоемко
• 2 действия
10
16
2
16 = 24
! Каждая шестнадцатеричная цифра может быть
записана как четыре двоичных (тетрада)!
{
{
{
{
7F1A16 = 0111 1111 0001 10102
7
F
A
1
15
16.
Обратный перевод в шестнадцатеричную систему10010111011112
Шаг 1. Разбить на тетрады, начиная справа:
0001 0010 1110 11112
Шаг 2. Каждую тетраду записать одной
шестнадцатеричной цифрой:
0001 0010 1110 11112
1
2
E
F
Ответ: 10010111011112 = 12EF16
16
17.
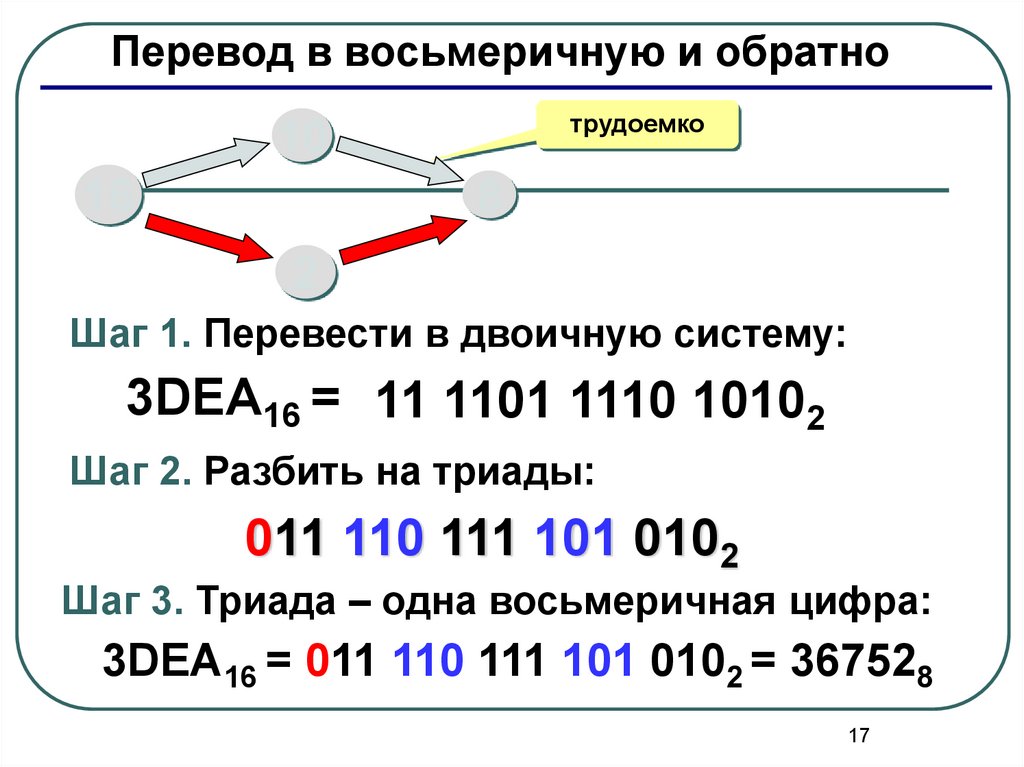
Перевод в восьмеричную и обратнотрудоемко
10
16
8
2
Шаг 1. Перевести в двоичную систему:
3DEA16 = 11 1101 1110 10102
Шаг 2. Разбить на триады:
011 110 111 101 0102
Шаг 3. Триада – одна восьмеричная цифра:
3DEA16 = 011 110 111 101 0102 = 367528
17
18. Решение задач
Пример: Перевести двоичное число110111101011101111 в шестнадцатеричную систему.
Решение: Разделим данное число на группы по четыре
цифры (тетрады), начиная справа. Так как в крайней
левой группе меньше четырех цифр, дополним ее
нулями 0011 0111 1010 1110 1111
А теперь глядя на двоично-шестнадцатеричную
таблицу, заменим каждую цифру на соответствующую
шестнадцатеричную цифру.
Ответ: 1101111010111011112 = 37АЕF16.
18
19. Решение задач
Задача 1. Перевести двоичное число 1010101 в восьмеричнуюсистему счисления.
Ответ: 1258
Задача 2. Перевести двоичное число 11011010001 в
шестнадцатеричную систему счисления.
Ответ: 6D116
Задача 3. Переведите в десятичную систему двоичные числа:
А) 1000011110101
Б) 1010010111011
Ответ: А) 1036510 ;
Б) 1227310
19
20. Решение задач
Задача 4. Перевести шестнадцатеричные числа в двоичную системусчисления: 1АС7; FACC. Примечание: Каждой шестнадцатеричной цифре
соответствует четверка двоичных цифр.
Ответ: 0001101011000111; 1111101011001100.
Задача 5. Перевести шестнадцатеричные числа в восьмеричную
систему счисления: А45; 54В.
Примечание: Сначала нужно перевести в двоичную систему, а
потом уже в восьмеричную.
Ответ: 101001000101 = 101001000101 = 51058;
010101001011 = 010101001011 = 25138.
Задача 6. Перевести восьмеричные числа в шестнадцатеричную
систему счисления: 774; 665. Примечание: Сначала нужно
перевести в двоичную систему, а потом уже в шестнадцатеричную .
Ответ: 111111100 = 000111111100 = 1FC16,
110110101 = 000110110101 = 1B516.
20
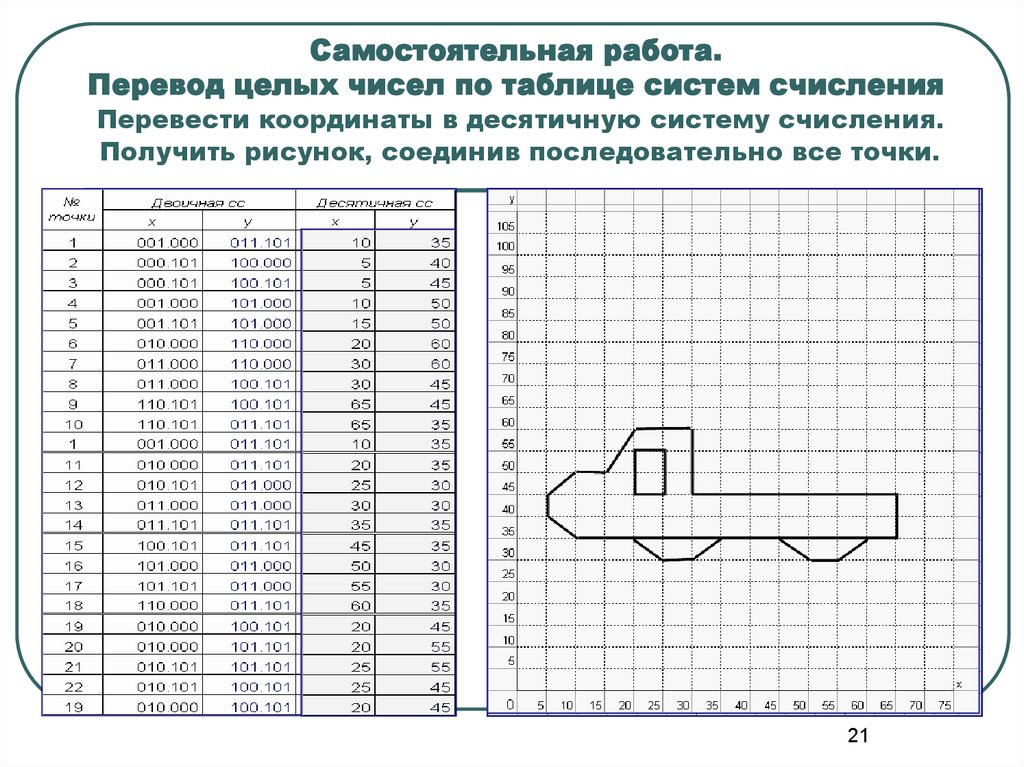
21. Самостоятельная работа. Перевод целых чисел по таблице систем счисления Перевести координаты в десятичную систему счисления.
Получить рисунок, соединив последовательно все точки.21
22. ДОМАШНЕЕ ЗАДАНИЕ
Перевод целого десятичного числа в систему с основанием q.1. Перевести число 365 из десятичной системы счисления в
шестнадцатеричную, восьмеричную и двоичную
систему счисления.
Перевод целого двоичного числа в систему с основанием q=2n.
2. Двоичное число 1110100 переведите в десятичную,
шестнадцатеричную и восьмеричную систему
счисления.
3. Перевести число 15АВ из шестнадцатеричной в
восьмеричную систему счисления.
4. Перевести число 452 из восьмеричной в
шестнадцатеричную систему счисления.
22












 Информатика
Информатика








