Похожие презентации:
Матрицы и определители
1.
Математика - наиболеесовершенный способ водить
самого себя за нос.
А. ЭЙНШТЕЙН
2.
3.
Матрицей размера m x n называетсяпрямоугольная таблица чисел,
содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются
элементами матрицы.
4.
Обозначение:A
( m n )
a ij
- матрица размерности m x n
- элемент матрицы i –ой строки и j -го
столбца
Где
i=1,2…m
j=1,2…n
5.
a11a21
A (aij )
m n
...
a
m1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
6.
Две матрицы называются равными, еслиу них одинаковая размерность и
совпадают строки и столбцы.
Если число строк матрицы равно числу ее
столбцов, то такая матрица называется
квадратной.
7.
0 21
A 2 4
5
0 3 1
- квадратная матрица размерности 3х3
8.
Элементы матрицы aij , у которых номерстолбца совпадает с номером строки,
называются диагональными.
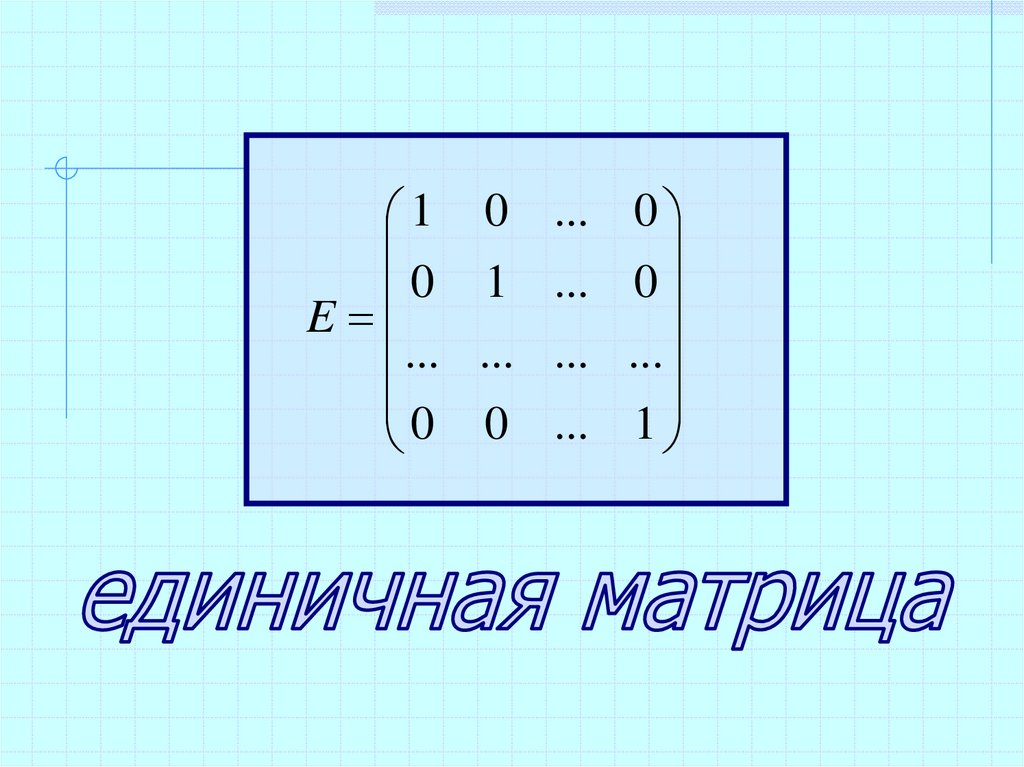
Если в квадратной матрице все
диагональные элементы равны 1, а
остальные элементы равны 0, то
она называется единичной.
9.
10
E
...
0
0
1
...
0
...
...
...
...
0
0
...
1
10.
Матрица любого размера называетсянулевой, если все ее элементы равны 0.
0
0
...
0
0
0
...
0
...
...
...
...
0
0
...
0
11.
Матрица, состоящая из одной строки,называется матрицей-строкой или
вектором-строкой.
A (a11 a12 ... a1n )
12.
Матрица, состоящая из одного столбца,называется матрицей-столбцом или
вектором-столбцом.
b11
b21
B
b
n1
13.
Спомощью матриц удобно
различного рода зависимости.
Например:
Распределение
экономики:
ресурсов
описывать
по
отраслям
Ресурсы
Промышленность
с/хозяйство
Эл.
энергия
Труд.
ресурсы
Водные
ресурсы
8
7.2
5
3
4.5
5.5
14.
Эту зависимость можно представить в видематрицы:
8 7.2
A 5
3
3 2
4.5 5.5
Где элемент aij показывает сколько i – го
ресурса потребляет j – отрасль.
Например, a32 показывает, сколько воды
потребляет сельское хозяйство.
15.
Чтобы умножить матрицу на число, надокаждый элемент матрицы умножить на
это число.
Полученные
произведения
итоговую матрицу.
образуют
16.
Пусть дана матрицаA (aij )
m n
Умножаем ее на число λ:
A B
Где каждый элемент матрицы В:
bij aij
Где:
i 1,2...m
j 1,2...n
17.
Например:Умножая матрицу
2 3 0
A
1 0 4
на число 2, получим:
2 2 3 2 0 2 4 6 0
A 2
1 2 0 2 4 2 2 0 8
18.
Складываются матрицы одинаковойразмерности. Получается матрица той же
размерности, каждый элемент которой
равен сумме соответствующих
элементов исходных матриц.
19.
Пусть даны матрицыСкладываем их:
A (aij )
B (bij )
A B C
Где каждый элемент матрицы С:
cij aij bij
Аналогично проводится вычитание матриц.
20.
Найти сумму и разность матриц:2 3 0
A
1 0 4
0 2 3
B
1 5 2
21.
2 1 3A B
2 5 6
2 5 3
A B
0 5 2
22.
Умножение матриц возможно, если числостолбцов первой матрицы равно числу строк
второй.
Тогда каждый элемент полученной матрицы
равен сумме произведений элементов i – ой
строки
первой
матрицы
на
соответствующие элементы j-го столбца
второй.
23.
Пусть даны матрицыУмножаем их:
A (aij )
m k
B (bij )
k n
A
B
C
m k k n
m n
Где каждый элемент матрицы С:
cij ai1b1 j ai 2b2 j ... aik bkj
i 1,2...m
j 1,2...n
24.
Найти произведение матриц:2 3 0
A
1 0 4
1 0
B 1 4
0 2
25.
Число столбцов первой матрицы равночислу строк второй, следовательно их
произведение существует:
2 1 3 1 0 0 2 0 3 4 0 2 5 12
A B
2 3 3 2
1 1 0 1 4 0 1 0 0 4 4 2 1 8
26.
Теперь перемножим матрицы в обратномпорядке:
1 2 0 1 1 3 0 0 1 0 0 4 2 3 0
B A 1 2 4 1 1 3 4 0 1 0 4 4 6 3 16
3 2 2 3
0 2 2 1 0 3 2 0 0 0 2 4 2 0 8
Умножение
матриц
некоммутативно:
в
A B B A
общем
случае
27.
Перечисленные операции над матрицамиобладают следующими свойствами:
1
А+В=В+А
2
(А+В)+С=А+(В+С)
28.
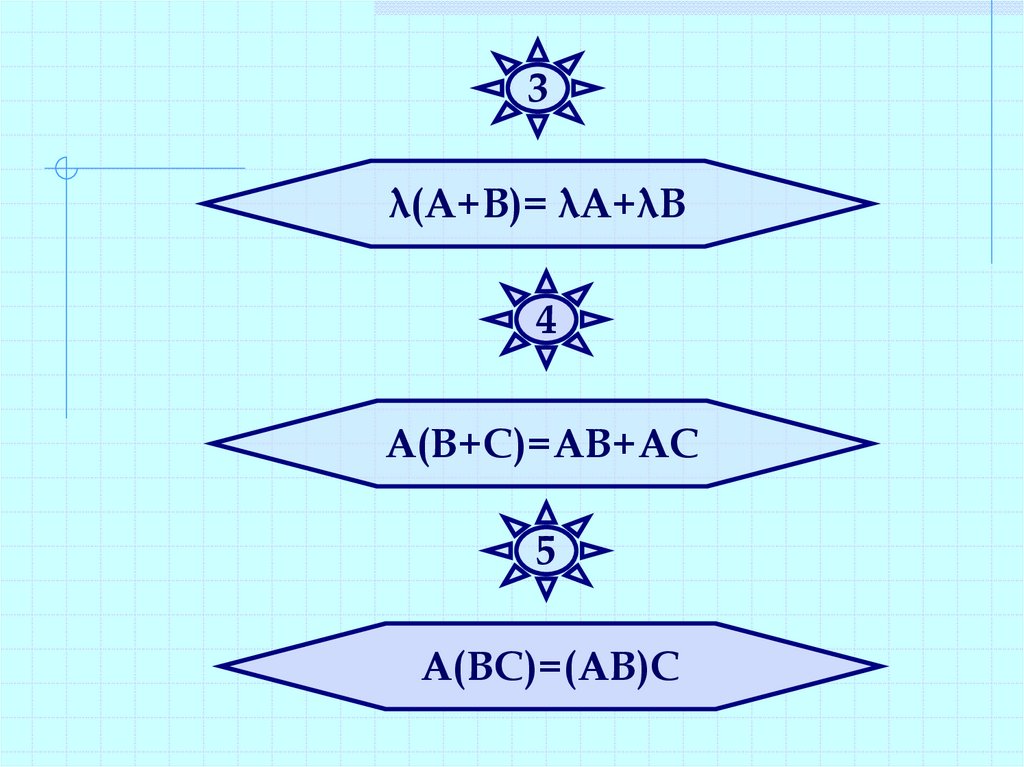
3λ(А+В)= λА+λВ
4
А(В+С)=АВ+АС
5
А(ВС)=(АВ)С
29.
Матрица АТ называетсятранспонированной к матрице А, если
в ней поменяли местами строки
и столбцы.
a11 a12
a21 a22
A
m n
...
...
a
m1 am 2
... a1n
... a2 n
... ...
... amn
a11 a21
a12 a22
T
A
... ...
n m
a1n a2 n
... am1
... am 2
... ...
... amn
30.
1(АТ)Т=А
2
(А+В)Т=АТ+ВТ
31.
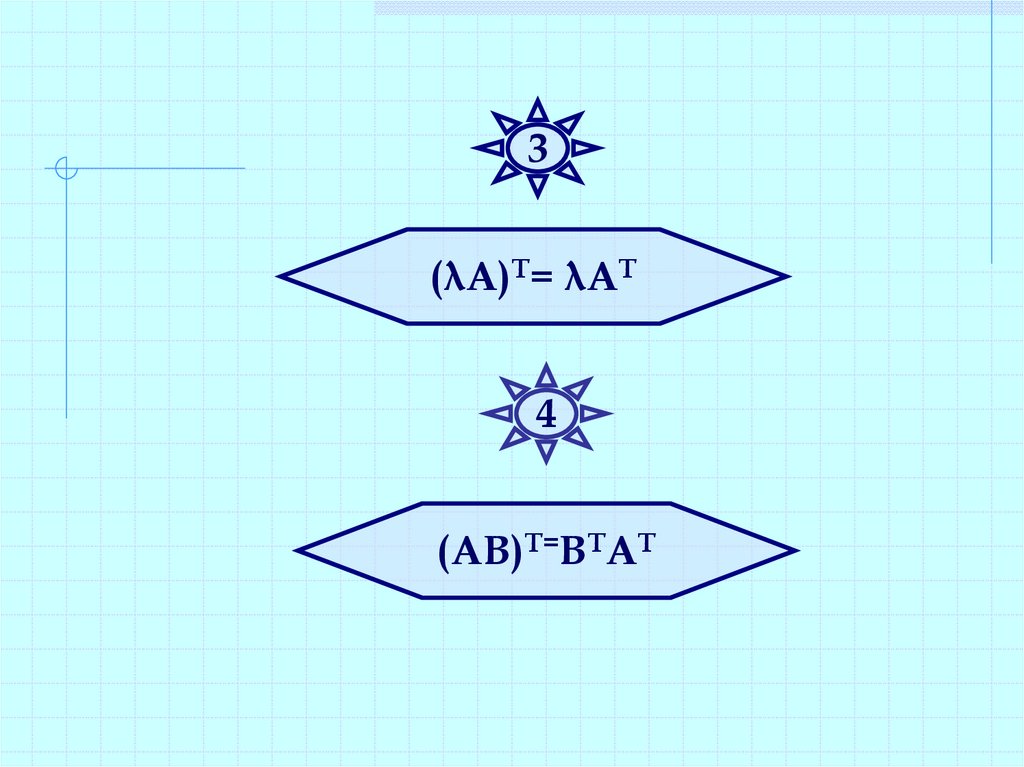
3(λА)Т= λАТ
4
(АВ)Т=ВТАТ
32.
Транспонировать матрицу:1 2 3
A 4 5 6
7 8 9
33.
1 4 7T
A 2 5 8
3 6 9






























 Математика
Математика








