Похожие презентации:
Сжатие и помехоустойчивое кодирование
1.
Центр дистанционного обученияСЖАТИЕ И ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
Старт 2-клик
Стоп - 1 клик
Практические занятия. Тема 1
Энтропийные коды
ФИО преподавателя: Смирнов
Александр Витальевич
e-mail: av_smirnov@mirea.ru
online.mirea.ru
2. Введение
Центр дистанционного обученияВведение
Выполнение заданий по данной теме рассчитано на два
практических занятия. По теме оформляется один отчет в
электронном виде. Рекомендуемый формат файла .pdf. Имя
файла должно содержать фамилию студента, номер группы
и номер работы. Текст и рисунки отчета могут выполняться
как на компьютере, так и на бумаге с последующим
сканированием или фотографированием.
При выполнении задания, относящегося к
арифметическому кодированию, используются программы
на языке программной среды Matlab, работающие и в
свободно распространяемой программе Octave.
online.mirea.ru
3. 2. Письменно ответить на вопросы
Центр дистанционного обучения2. Письменно ответить на вопросы
Для каждого математического соотношения необходимо
пояснить сущность входящих в него величин.
2.1. Дать определение источника информации без памяти.
2.2. Записать соотношение для расчета количества информации на
символ в случае алфавита из равновероятных символов.
2.3. Записать соотношение для расчета среднего количества
информации на символ в случае алфавита из равновероятных
символов (энтропия по Шеннону).
2.4. Записать определение избыточности источника информации.
2.5. Дать определение префиксного кода.
2.6. Записать формулировку теоремы Шеннона о кодировании
источника для случая двоичного кода.
2.7. Дать определение избыточности кода. Пояснить, как ее оценить
экспериментально.
online.mirea.ru
4. 3. Задание по коду Хаффмана
Центр дистанционного обучения3. Задание по коду Хаффмана
3.1. Сформировать алфавит из не менее 6 символов с разными
вероятностями появления. Сумма вероятностей должна быть 1.
3.2. Рассчитать энтропию алфавита.
3.3. Построить для своего алфавита код по алгоритму Хаффмана.
3.4. Составить 3 сообщения из не менее 20 символов каждое,
имеющие следующие характеристики:
– примерно соответствующее статистике алфавита;
– состоящее только из символов с высокими вероятностями;
– содержащее аномально большое число символов с низкими
вероятностями появления.
3.5. Закодировать сообщения построенным кодом Хаффмана.
Рассчитать для этих сообщений средние количества битов на
символ.
3.6. Проверить для одного из сообщений, возможно ли
декодирование. Для этого имитировать работу декодера, который
последовательно выделяет коды символов, сверяя принимаемые
биты с таблицей кода.
10.8.20
online.mirea.ru
5. Расчет энтропии источника
Центр дистанционного обученияРасчет энтропии источника
В случае не равновероятных и взаимно независимых
символов среднее количество информации на символ
определяется величиной, названной К.Шенноном
энтропией, которая равна:
M
H pi log 2 pi бит/символ.
i 1
где pi - вероятность появления i-го символа.
Расчет логарифма по основанию 2:
lg x
log 2 x
lg 2
online.mirea.ru
6. Пример построения кода Хаффмана
Центр дистанционного обученияПример построения кода Хаффмана
Установим правило: если на каком то шаге получились два
равных значения вероятностей, то та ветвь, которая образована
соединением ветвей на предыдущем шаге, остается ниже.
В примере символам соответствуют кодовые слова
0, 11, 100, 101.
online.mirea.ru
7. 4. Задание по коду Голомба
Центр дистанционного обучения4. Задание по коду Голомба
4.1. Записать правила формирования кода Голомба.
4.2. Записать символы алфавита по п. 3.1 в порядке убывания
вероятности и пронумеровать их, начиная с номера 1.
4.3. Записать коды Голомба символов алфавита, приняв параметр
m = 3.
4.4. Закодировать сообщения по п. 3.4. Посчитать средние
количества битов на символ.
4.5. Проверить для одного из сообщений, возможно ли
декодирование.
10.8.20
online.mirea.ru
8. Правила построения кода Голомба, часть1
Центр дистанционного обученияПравила построения кода Голомба, часть1
Код Голомба неотрицательного целого числа n с целочисленным
параметром m строится следующим образом.
1. Рассчитываются значения переменных
n 1
q
; r n 1 qm.
m
где [x] – целая часть числа x; r – остаток от деления n на m.
2. Значение q представляется унарным кодом, содержащим q единиц
и 0. Например, унарный код числа 4 имеет вид 11110.
3. Правило записи остатка r.
3.1. Если m – целая степень числа 2, то код остатка представляет
собой двоичную запись числа r , содержащую log2m битов.
10.8.20
online.mirea.ru
9. Правила построения кода Голомба, часть2
Центр дистанционного обученияПравила построения кода Голомба, часть2
3.2. Если m не является целой степенью числа 2, то вычисляется
переменная b = [log2m] + 1, и далее:
3.2.1. Если r < 2b – m, то код остатка представляет собой двоичную
запись числа r, содержащую b – 1 бит.
3.2.2. В противном случае код остатка представляет собой двоичную
запись числа r + 2b – m, содержащую b битов.
3.3. Например, при m = 3 возможные остатки 0, 1, 2 представляются
кодами 0, 10, 11, а при m = 5 возможные остатки 0, 1, 2, 3, 4
представляются кодами 00, 01, 100, 101, 110.
4. Код r приписывается справа к коду q. Например, код Голомба числа 4
при m = 3 имеет вид 100. Граница между кодами q и r находится после
первого слева нуля.
Если пронумеровать символы алфавита в порядке убывания вероятности,
то частым символам будут соответствовать короткие коды Голомба
10.8.20
online.mirea.ru
10. 5. Задание по арифметическому коду
Центр дистанционного обучения5. Задание по арифметическому коду
5.1. Закодировать первые 6 символов из сообщения, примерно
соответствующего статистике алфавита из п.3.4. Использовать метод
кодирования на основе целых десятичных чисел из Лекции 1.
5.2. Полученное десятичное число преобразовать в двоичную форму.
Определить среднее количество бит на символ.
5.3. Выполнить декодирование. Проверить правильность результата.
5.4. С помощью программы Arithcode_1.m закодировать сообщения,
составленные в п.3.4. Окна переменных для каждого случая
скопировать в отчет. Если массивы значений переменных seq и
decode не отображаются целиком в области переменных, получить их
отображения в отдельном окне. Двоичную последовательность code в
отчет помещать не надо. Проверить правильность декодирования.
5.5. Записать в отчет количества битов в кодированных сообщениях.
Рассчитать и записать в отчет средние количества битов на символ.
Сравнить их с результатом п.5.2.
10.8.20
online.mirea.ru
11. Принцип арифметического кода
Центр дистанционного обученияПринцип арифметического кода
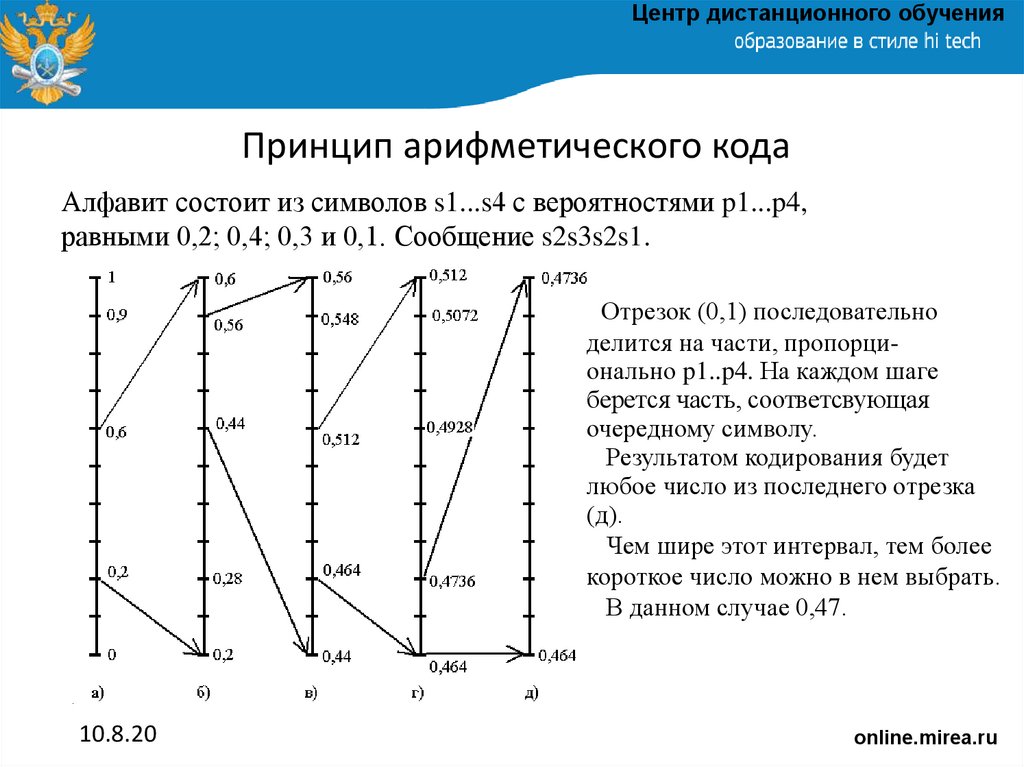
Алфавит состоит из символов s1...s4 с вероятностями p1...p4,
равными 0,2; 0,4; 0,3 и 0,1. Сообщение s2s3s2s1.
Отрезок (0,1) последовательно
делится на части, пропорционально p1..p4. На каждом шаге
берется часть, соответсвующая
очередному символу.
Результатом кодирования будет
любое число из последнего отрезка
(д).
Чем шире этот интервал, тем более
короткое число можно в нем выбрать.
В данном случае 0,47.
10.8.20
online.mirea.ru
12. Декодирование
Центр дистанционного обученияДекодирование
Закодированное сообщение имеет вид 47, "0," не передается.
Число символов в сообщении считаем известным. Цифра "4"
показывает, что первый символ s2. Затем вычисляются границы
интервала кода второго символа как и в кодере. Число 47
показывает, что второй символ s3, затем s2, затем s1.
Если число символов в сообщении не известно, то код должен
иметь вид, например 4700eof, где eof - символ конца сообщения.
Вместо нулей могут быть любые цифры.
10.8.20
online.mirea.ru
13. Реальный алгоритм
Центр дистанционного обученияРеальный алгоритм
Если сообщения длинные, то и числа получаются очень
длинные, и выполнять операции с ними практически
невозможно. Поэтому реальный алгоритм работает не так.
Цифры, которые одинаковы у обеих границ интервала,
записываются в выходной файл. Сами значения границ
представляются целыми числами.
После записи в файл цифры старшего разряда справа
дописывается 0 для нижней границы и 9 для верхней.
В реальности вычисления выполняются в двоичной форме.
Процесс декодирования описан в книге Д.Сэломона "Сжатие
данных, изображений и звука". М.: "Техносфера". - 2004.
10.8.20
online.mirea.ru
14. Пример кодирования
Центр дистанционного обученияПример кодирования
Продолжим пример. Сообщение s2s3s2s1s4s3.
Символ
Нижн.
Верхн.
В файл
Нижн.сдв.
Верхн. сдв.
s2
2000
6000
-
2000
6000
s3
4400
5600
-
4400
5600
s2
4640
5120
-
4640
5120
s1
4640
4736
4
6400
7369
s4
7272
7369
7
2720
3699
s3
3307
3601
3600
-
-
10.8.20
online.mirea.ru
15. Программное обеспечение
Центр дистанционного обученияПрограммное обеспечение
Арифметическое кодирование и декодирование выполняются
программой Arithcode_1.m, из которой вызываются функции
кодирования M_arithenco.m и декодирования M_arithdeco.m. Эти
функции представляют собой немного измененные для
совместимости с Octave функции arithenco.m и arithdeco.m из
модуля Comm (Communication Toolbox) Matlab. Для выполнения
программ необходимо установить версию Octave 6.3.0 или более
позднюю.
10.8.20
online.mirea.ru
16. Программа Arithcode_1.m
Центр дистанционного обученияПрограмма Arithcode_1.m
10.8.20
online.mirea.ru
17. Пояснения к программе
Центр дистанционного обученияПояснения к программе
- В строке 6 записаны символы алфавита из приведенного выше примера.
Помните, что в программе Octave кириллица отображается неправильно.
- В строке 9 записаны умноженные на 100 значения вероятностей символов
алфавита. Значения counts должны быть только целочисленными. Если
значения вероятностей при умножении на 100 не дают целых чисел, то надо
умножать на еще большее число.
- В строке 11 записана кодируемая последовательность символов в виде
последовательности номеров этих символов в алфавите.
- В строке 13 вызывается функция кодирования. В переменную code
записывается результат кодирования в виде последовательности нулей и
единиц. В строке 14 определяется длина кода, записываемая в переменную
code_len.
- В строке 17 определяется длина кодируемой последовательности len, то
есть число символов в ней. Этот параметр, как и массив значений
вероятностей counts, должны передаваться вместе с кодированной
последовательностью, чтобы ее можно было декодировать.
- В строке 18 вызывается функция декодирования. Результат сохраняется в
переменной decode в виде последовательности номеров символов в
алфавите.
10.8.20
online.mirea.ru
18. Работа с программой - 1
Центр дистанционного обученияРабота с программой - 1
Перед запуском программы необходимо изменить строки 6, 9 и
11 в соответствии со своим примером. При запуске в Matlab
значения переменных отображаются в окне «Workspace» (рис.1.4).
Если значения переменной не умещаются в этом окне, как в случае
переменной code, то следует сделать двойной клик на имени этой
переменной, и весь массив ее значений отобразится в отдельном
окне.
10.8.20
online.mirea.ru
19. Работа с программой - 2
Центр дистанционного обученияРабота с программой - 2
При работе в Octave после первой попытки запуска программы
может появиться сообщение (рис.1.5).
Это сообщение о том, что модуль Communication не загружен. Для
его загрузки надо ввести после >> команду pkg load communications
и нажать Enter. В следующих запусках программа будет работать
нормально.
10.8.20
online.mirea.ru
20. Работа с программой - 3
Центр дистанционного обученияРабота с программой - 3
Значения переменных будут отображаться в окне «Область
переменных» (рис.1.6). Если массив не отображается полностью,
надо действовать также, как в Matlab.
10.8.20
online.mirea.ru
21. 6. Анализ результатов
Центр дистанционного обучения6. Анализ результатов
6.1. Составить итоговую таблицу средних количеств бит/символ
для трех энтропийных кодов и трех сообщений. Рядом с
таблицей или в отдельной ее графе записать рассчитанное в
п.3.2 значение энтропии.
6.2. Сравнить результаты трех кодов между собой и с результатом
теоремы Шеннона о кодировании источника. Для каждого кода
рассчитать значение избыточности, усреднив количества
бит/символ по трем сообщениям. Записать выводы по
результатам сравнения.
10.8.20
online.mirea.ru
22.
Центр дистанционного обученияСпасибо за внимание!
online.mirea.ru





















 Программирование
Программирование








