СмирновАВ_СиПК_ЛК01

1.

Центр дистанционного обучения
СЖАТИЕ И ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
Старт 2-клик
Стоп - 1 клик
Лекция 1
Введение. Энтропийное кодирование.
Кодирование с предсказанием
ФИО преподавателя: Смирнов
Александр Витальевич
e-mail: [email protected]
online.mirea.ru

2. Введение

Центр дистанционного обучения
Введение
Программой предусмотрено 16 лекций, 16
практических занятий и 4 лабораторных занятия
В течение семестра необходимо выполнить 4
лабораторных работы и 8 домашних заданий
Форма промежуточной аттестации - экзамен
К экзамену допускаются студенты, выполнившие
все работы и задания
online.mirea.ru

3. Из списка литературы

Центр дистанционного обучения
Из списка литературы
1. Вернер М. Основы кодирования. Учебник для вузов. – М.:
Техносфера, 2004. – 286 с*. https://library.mirea.ru/books/6648.
2. Сэломон Д. Сжатие данных, изображений и звука. Учебное
пособие. – М.: Техносфера, 2006. – 368 с*.
5. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования.
Методы, алгоритмы, применение. Учеб. пособие для вузов. Пер.
с англ. — М.: Техносфера, 2005. — 319 с*.
https://library.mirea.ru/books/43713
6. Думачев В.Н. Теория информации и кодирование. Учебное
пособие. Воронеж: Воронежский институт МВД России, 2012. 200 с*.
8. Золотарев В.В., Овечкин Г.В. Помехоустойчивое кодирование.
Методы и алгоритмы: Справочник / Под ред. чл.-корр. РАН Ю.Б.
Зубарева. – М.: Горячая линия – Телеком, 2004. – 126 с*.
(*На кафедре есть электронные версии этих пособий)
online.mirea.ru

4. Основные понятия и термины

Центр дистанционного обучения
Основные понятия и термины
Информация - это не материя и не энергия,
а информация (Н.Винер).
Сообщение - это информация, представленная в
материальной форме.
Сообщение состоит из символов, например,
букв, отсчетов сигнала, пикселей.
Используемые символы образуют алфавит.
Кодирование - это преобразование сообщения
посредством замены одних символов или
групп символов другими.
10.8.20
online.mirea.ru

5. Зачем нужно кодирование

Центр дистанционного обучения
Зачем нужно кодирование
Кодирование - это преобразование формы представления
информации в сообщениях.
Как правило, кодирование используется в цифровых системах
передачи информации.
Основные виды кодирования:
1. Сжатие информации.
2. Кодирование для исправления ошибок
3. Шифровка
online.mirea.ru

6. Классификация методов сжатия информации

Центр дистанционного обучения
Классификация методов сжатия информации
1. Сжатие без потерь информации.
Применяется в случаях, когда потери не допустимы.
Например, при передаче числовых данных или текстов.
2. Сжатие с потерей части информации.
Применяется в основном при передаче видео и
звуковой информации. Основано на удалении не
воспринимаемых или слабо воспринимаемых
составляющих сообщения, потеря которых не ухудшает
или мало ухудшает качество изображения или звука.
online.mirea.ru

7. Количество информации

Центр дистанционного обучения
Количество информации
Единица измерения количества информации - бит
(binary digit). 1 бит - это ответ на один вопрос,
допускающий ответ да/нет.
Мера информации была предложена Хартли в 1928
году. В случае алфавита из M равновероятных
взаимно независимых символов количество
информации на символ равно:
I1 log 2 M бит/символ.
Определенная так информация - аддитивная величина.
Если сообщение можно представить как N ответов "Да"
или "Нет", то оно содержит N битов информации.
10.8.20
online.mirea.ru

8. Энтропия Шеннона

Центр дистанционного обучения
Энтропия Шеннона
В случае не равновероятных, но по-прежнему взаимно
независимых символов среднее количество информации
на символ определяется величиной, названной
К.Шенноном энтропией, которая равна:
M
H pi log 2 pi бит/символ.
i 1
где pi - вероятность появления i-го символа.
H максимальна, если все символы равновероятны,
и равна 0, если возможна передача только
одного символа. Чем более неравномерно распределение
вероятностей, тем меньше энтропия.
10.8.20
online.mirea.ru

9. Взаимно зависимые символы

Центр дистанционного обучения
Взаимно зависимые символы
Если рассматривать совместные вероятности соседства
двух символов xi, xj, энтропия будет равна
H p xi , x j log 2 p xi , x j
M
M
i 1 j 1
бит/символ
По мере увеличения числа учитываемых символов,
значение энтропии будет уменьшаться, так как
совместное распределение вероятностей групп
символов будет становиться все более
неравномерным.
10.8.20
online.mirea.ru

10. Энтропия английского языка

Центр дистанционного обучения
Энтропия английского языка
Пример: английский язык, 26 букв и пробел.
Простейший код - 5 бит/символ.
Считая буквы равновероятными - 4,76 бит/символ.
С учетом вероятности букв - 4,03 бит/символ.
Учитывая пары букв - 3,32 бит/символ.
Учитывая тройки букв - 3,1 бит/символ.
Учитывая частоту слов - 2,14 бит/символ.
Учитывая сочетания слов - 1,4 бит/символ.
10.8.20
online.mirea.ru

11. Избыточность

Центр дистанционного обучения
Избыточность
При кодировании мы представляем символы или
группы символов исходного алфавита кодовыми
словами, состоящими из символов другого алфавита,
обычно - двоичными цифрами.
Избыточность кода определяется как
R = Lср - H,
где Lср - средняя длина кодовых слов (бит/символ),
H - энтропия кодируемого сообщения.
10.8.20
online.mirea.ru

12. Принцип энтропийного кодирования

Центр дистанционного обучения
Принцип энтропийного кодирования
Для уменьшения избыточности необходимо строить
код так, чтобы часто встречающиеся символы имели
короткие кодовые слова, а редкие символы - длинные
кодовые слова. Такие коды называются энтропийными
или кодами переменной длины, а также неравномерными
кодами.
Для неравномерных кодов возникает задача
определения границ кодовых слов в потоке передаваемых
битов. Чтобы эта задача была решаемой, необходимо,
чтобы код был префиксным. Это означает, что никакое
кодовое слово не является началом (префиксом) другого
кодового слова.
10.8.20
online.mirea.ru

13. Теорема Шеннона о кодировании источника

Центр дистанционного обучения
Теорема Шеннона о кодировании источника
Для любого дискретного источника без памяти с
конечным алфавитом и энтропией H можно построить
D-ичный префиксный код, в котором средняя длина
кодового слова nср удовлетворяет неравенствам
H
H
nср
1
log 2 D
log 2 D
В случае двоичного кода log2 D = 1 и данное условие
принимает вид
H ≤ nср ≤ H + 1.
10.8.20
online.mirea.ru

14. Энтропийные коды

Центр дистанционного обучения
Энтропийные коды
Теорема Шеннона доказывает возможность
построения эффективного префиксного кода, но не дает
рецепта, как построить такой код.
По-видимому, самым первым энтропийным кодом
была азбука Морзе. Однако этот код не является
префиксным. В нем для разделения кодовых слов
используется пауза между ними.
С простыми энтропийным кодами - Хаффмана и
Голомба, мы поработаем на семинаре.
Сейчас же ознакомимся с наиболее совершенным
энтропийным кодом - арифметическим кодом. При
его использовании средняя длина кодовых слов для
достаточно длинных сообщений стремится к значению
энтропии. Лучше сделать нельзя.
10.8.20
online.mirea.ru

15. Принцип арифметического кода

Центр дистанционного обучения
Принцип арифметического кода
Алфавит состоит из символов s1...s4 с вероятностями p1...p4,
равными 0,2; 0,4; 0,3 и 0,1. Сообщение s2s3s2s1.
Отрезок (0,1) последовательно
делится на части, пропорционально p1..p4. На каждом шаге
берется часть, соответсвующая
очередному символу.
Результатом кодирования будет
любое число из последнего отрезка
(д).
Чем шире этот интервал, тем более
короткое число можно в нем выбрать.
В данном случае 0,47.
10.8.20
online.mirea.ru

16. Декодирование

Центр дистанционного обучения
Декодирование
Закодированное сообщение имеет вид 47, "0," не передается.
Число символов в сообщении считаем известным. Цифра "4"
показывает, что первый символ s2. Затем вычисляются границы
интервала кода второго символа как и в кодере. Число 47
показывает, что второй символ s3, затем s2, затем s1.
Если число символов в сообщении не известно, то код должен
иметь вид, например 4700eof, где eof - символ конца сообщения.
Вместо нулей могут быть любые цифры.
10.8.20
online.mirea.ru

17. Реальный алгоритм

Центр дистанционного обучения
Реальный алгоритм
Если сообщения длинные, то и числа получаются очень
длинные, и выполнять операции с ними практически
невозможно. Поэтому реальный алгоритм работает не так.
Цифры, которые одинаковы у обеих границ интервала,
записываются в выходной файл. Сами значения границ
представляются целыми числами.
После записи в файл цифры старшего разряда справа
дописывается 0 для нижней границы и 9 для верхней.
В реальности вычисления выполняются в двоичной форме.
Процесс декодирования описан в книге Д.Сэломона "Сжатие
данных, изображений и звука". М.: "Техносфера". - 2004.
10.8.20
online.mirea.ru

18. Пример кодирования

Центр дистанционного обучения
Пример кодирования
Продолжим пример. Сообщение s2s3s2s1s4s3.
Символ
Нижн.
Верхн.
В файл
Нижн.сдв.
Верхн. сдв.
s2
2000
6000
-
2000
6000
s3
4400
5600
-
4400
5600
s2
4640
5120
-
4640
5120
s1
4640
4736
4
6400
7369
s4
7272
7369
7
2720
3699
s3
3307
3601
3600
-
-
10.8.20
online.mirea.ru

19. Варианты реализации энтропийного кодирования

Центр дистанционного обучения
Варианты реализации энтропийного кодирования
1. Статический. Таблицы вероятностей символов
формируются на основе статистики большого числа
сообщений и хранятся в кодере и декодере.
2. Полуадаптивный. Сначала строится таблица
вероятностей для данного сообщения, а затем
выполняется кодирование этого сообщения. Таблица
должна передаваться вмести с ним.
3. Адаптивный. Кодирование выполняется за один
проход, в процессе которого накапливается
статистика и обновляется таблица вероятностей.
Декодер также строит таблицу в процессе приема.
10.8.20
online.mirea.ru

20. Кодирование источников с памятью

Центр дистанционного обучения
Кодирование источников с памятью
В реальных источниках сообщений, как правило,
передаваемые символы зависят от ранее переданных
символов. Энтропия источника с памятью оказывается
меньше, чем энтропия источника с таким же алфавитом
и независимыми символами.
Для эффективного сжатия информации источника
с памятью энтропийный код должен строиться не для
отдельных символов, а для блоков символов с длиной
L > r, где r - объем памяти источника. Чем больше L,
тем эффективнее кодирование.
Другой способ эффективного кодирования
источников с памятью - кодирование с предсказанием.
10.8.20
online.mirea.ru

21. Кодирование с предсказанием

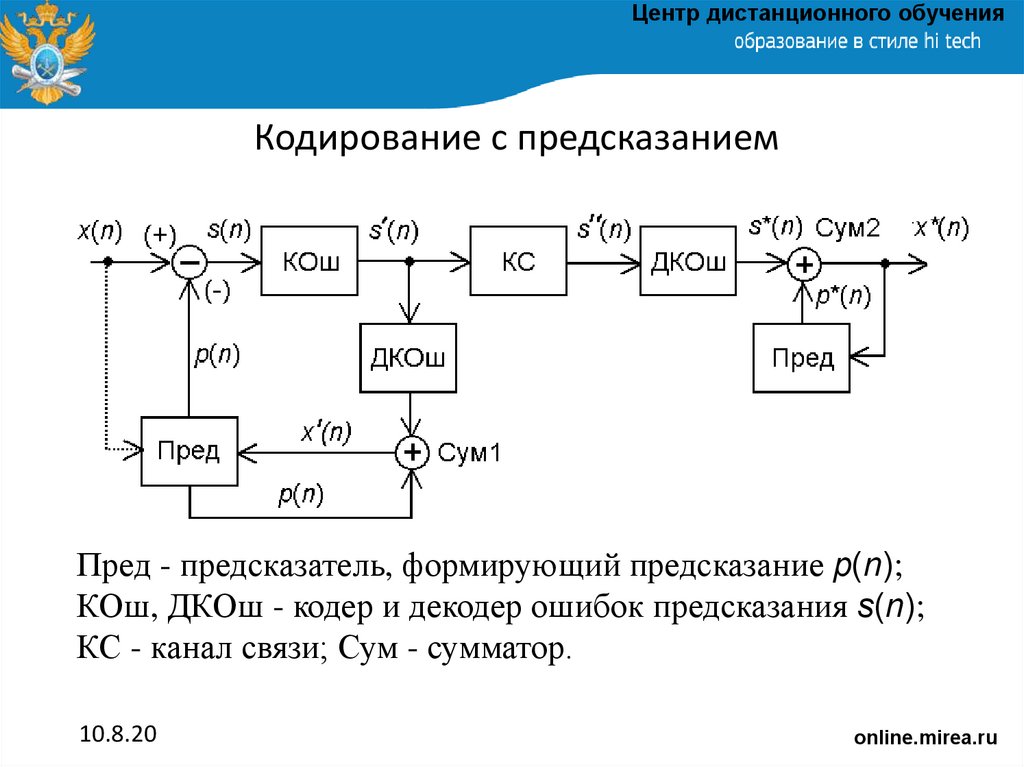
Центр дистанционного обучения
Кодирование с предсказанием
Пред - предсказатель, формирующий предсказание p(n);
КОш, ДКОш - кодер и декодер ошибок предсказания s(n);
КС - канал связи; Сум - сумматор.
10.8.20
online.mirea.ru

22. Кодирование и декодирование

Центр дистанционного обучения
Кодирование и декодирование
Для предсказания 1-го порядка p(n) = x(n-1). При этом предсказатель
должен содержать ЗУ для одного значения сигнала.
В вычитателе формируется ошибка предсказания
s(n) = x(n) - p(n),
которая кодируется в КОш. Результат кодирования s'(n) передается по
каналу связи. Принятый сигнал s''(n) декодируется и полученное
значение ошибки предсказания s*(n) суммируется с предсказанным в
декодирующей части системы значением p*(n):
x*(n) = p*(n) + s*(n).
Если кодирование ошибок предсказания и передача по каналу связи
не вносят необратимых потерь информации, то получается s*(n) = s(n).
Приняв p(1) = 0, в кодирующей части для предсказания 1-го порядка имеем:
p(1) = 0, s(1) = x(1); p(2) = x(1), s(2) = x(2) - x(1); … .
А в декодирующей части:
p*(1) = 0,
x*(1) = s*(1) = x(1);
p*(2) = x*(1),
x*(2) = p*(2) + s*(2) = x(2); … .
Сигнал на выходе системы такой же, как и на входе.
10.8.20
(1)
(2)
(3)
(4)
online.mirea.ru

23. Влияние ошибок в канале связи

Центр дистанционного обучения
Влияние ошибок в канале связи
Пусть в качестве предсказанного значения в приемнике используется
предыдущее декодированное значение
p*(k) = x*(k-1).
Предположим, что j-й принятый отсчет содержит ошибку r(j):
s*(j) = s(j) + r(j),
Эта ошибка перейдет в декодированное значение сигнала
x*(j) = p*(j) + s*(j) = x(j-1) + s(j) + r(j) = x(j) + r(j).
Далее ошибка переходит в предсказанное значение следующего отсчета
p*(j+1) = x*(j) = x(j) + r(j),
затем в декодированное значение следующего отсчета
x*(j+1) = p*(j +1) + s*(j +1) = x(j) + r(j) + s(j +1) = x(j +1) + r(j),
и т.д. То есть, ошибка попадет во все следующие отсчеты сигнала на
выходе системы. Следующие ошибки также будут накапливаться.
Для устранения этого эффекта периодически передают опорные
отсчеты. С каждого опорного отсчета прием начинается с начала, а все
накопившиеся ошибки «сгорают».
10.8.20
(5)
(6)
(7)
(8)
(9)
online.mirea.ru

24. Эффект кодирования с предсказанием

Центр дистанционного обучения
Эффект кодирования с предсказанием
Распределение вероятностей ошибок предсказания (справа)
обычно более неравномерно, чем распределение вероятностей
отсчетов сигнала (слева). Поэтому применение энтропийного
кода после предсказания часто дает хороший эффект.
10.8.20
online.mirea.ru

25. Дифференциальная ИКМ (ДИКМ)

Центр дистанционного обучения
Дифференциальная ИКМ (ДИКМ)
Если в качестве кодера ошибки предсказания применен
квантователь, то такой способ передачи называется
дифференциальная импульсно-кодовая модуляция (ДИКМ
или DPCM). Если скорость изменения сигнала ограничена,
то значения s(n) невелики и могут передаваться с
использованием меньшего числа битов, чем отсчеты сигнала.
Число битов для передачи s(n) или, что эквивалентно, шаг
квантования s(n), можно изменять в зависимости от свойств
передаваемого участка сигнала. Такой способ называется
адаптивная ДИКМ (АДИКМ или ADPCM).
Предельный случай, когда передаются однобитовые значения
изменений сигнала, называется дельта-модуляцией. При этом
частота отсчетов s(n) берется в несколько раз больше частоты
дискретизации передаваемого сигнала.
10.8.20
online.mirea.ru

26. Линейное предсказание

Центр дистанционного обучения
Линейное предсказание
M
p ( n) a m x ( n m)
m 1
LPC - Linear predictive coding.
Чем выше порядок M, тем точнее будет предсказание,
но больше объем вычислений и передаваемой информации о
коэффициентах am.
Важная задача - выбрать значения am так, чтобы получить
минимальную среднеквадратическую ошибку предсказания.
E s ( n ) x ( n ) a m x ( n m)
m 1
M
2
2
10.8.20
online.mirea.ru

27.

Центр дистанционного обучения
Спасибо за внимание!
online.mirea.ru