Лекция 1 Инжен.граф. Точка, прямая

1.

Лекция 1
по дисциплине
«Начертательная геометрия и
инженерная графика»
для направлений подготовки 07.03.01, 07.03.02, 07.03.04
Лектор - доцент кафедры Инженерной графики и компьютерного моделирования (ИГиКМ)
Фаткуллина Алина Алимовна
[email protected]
[email protected]
Тел. 8 (977) 266-27-42

2.

Структура дисциплины «Начертательная геометрия и
инженерная графика»
1. Инженерная графика. Знакомство с ГОСТами ЕСКД (Единая система конструкторской
документации) и СПДС (Система проектной документации для строительства), изучение общих
правил оформления строительных чертежей.
- ГОСТ 2.301-68 ЕСКД. Форматы.
- ГОСТ 2.303-68* ЕСКД. Линии.
- ГОСТ 2.304-81 ЕСКД. Шрифты чертёжные.
- ГОСТ 2.302-68 ЕСКД. Масштабы.
- ГОСТ 3.306-68 ЕСКД. Обозначения графические материалов и правила их нанесения
чертежах.
на
- Национальный стандарт РФ ГОСТ Р 21.101-2020 СПДС. Основные требования к проектной и
рабочей документации.
- ГОСТ 21.501 -2018 СПДС. Правила выполнения рабочей документации архитектурных и
конструктивных решений.
- ГОСТ 21.201-2011 СПДС. Условные графические изображения элементов зданий, сооружений и
конструкций.
Выполнение чертежей плана этажа, фасада и разреза здания.

3.

Структура дисциплины «Начертательная геометрия и
инженерная графика»
2.
Начертательная геометрия. Изучение следующих разделов предмета:
2.1. Ортогональные проекции. Проекции точки, прямой линии, плоскости, поверхностей. Их взаимное
положение. Решение метрических и позиционных задач. Построение развёрток поверхностей. Построение
теней.
Выполнение чертежа на тему «Пересечение поверхностей, построение развёрток поверхностей».
Выполнение чертежа на тему «Построение теней в ортогональных проекциях».
Решение задач в тетради упражнений.
2.2. Перспективные проекции. Вида перспективных проекций. Перспектива на вертикальной плоскости
(линейная перспектива). Аппарат линейной перспективы. Перспектива прямых, плоскости, окружности,
геометрических тел. Решение позиционных задач. Геометрические закономерности и приёмы, применяемые
в перспективе. Способы построения перспективы. Основы построения теней в перспективе.
Решение задач в тетради упражнений.
2.3. Проекции с числовыми отметками. Изображение прямых, плоскости, поверхностей. Решение
позиционных задач. Определение границы земляных работ при проектировании горизонтальной площадки и
наклонных дорог.
Решение задач в тетради упражнений.

4.

Методические материалы и задания.
Методические материалы будут размещаться по ходу изучения дисциплины на
диске
https://drive.google.com/drive/folders/1fdV3BMxNhU16UKgw9obaqvLvwMqUP48O
?usp=drive_link
Для решения задач по начертательной геометрии необходимо распечатать
страницы из тетрадей упражнений, которые можно найти в электронной
библиотеке МГСУ или на диске.
1. Начертательная геометрия. Сборник задач : методические указания к практических занятиям и
самостоятельной работе для обучающихся по направлениям подготовки 07.03.01 Архитектура, 07.03.02
Реконструкция и реставрация архитектурного наследия / Национальный исследовательский
Московский государственный строительный университет, кафедра инженерной графики и
компьютерного моделирования. - Москва : Изд-во МИСИ-МГСУ, 2022 - 2023. - (Архитектура)
. - URL: http://lib-04.gic.mgsu.ru/lib/metod2022/43.pdf. - Загл. с титул. экрана. - Электронные данные :
электронные.
Часть 1 / сост.: А. А. Фаткуллина, И. М. Гусакова ; [рец. А. Ю. Борисова]. - 2022. - Электрон. текстовые
дан. (3,3 Мб). Распечатать стр. 6-31 на формате А4 или А3.

5.

Методические материалы и задания.
2. Начертательная геометрия : методические указания к практическим занятиям и самостоятельной
работе для обучающихся по направлениям подготовки 07.03.01 Архитектура, 07.03.02 Реконструкция и
реставрация архитектурного наследия / Национальный исследовательский Московский государственный
строительный университет, каф. инженерной графики и компьютерного моделирования. - Москва : Издво МИСИ-МГСУ, 2022 - 2023. - (Архитектура)
. - URL: http://lib-06.edu.mgsu.ru/lib/Metod2023/81.pdf. - Загл. с титул. экрана. - Электронные данные :
электронные.
Часть 2 / сост.: А. А. Фаткуллина, И. М. Гусакова ; [рец. Н. С. Калинина]. - 2023. - Электрон. текстовые дан.
(4,03 Мб). Распечатать стр. 10-21 на формате А3.
В конце приведены список теоретических экзаменационных вопросов и перечень тем и вопросов для
подготовки к экзамену.

6.

Список рекомендуемой литературы по разделу
«Инженерная графика»
1. Каминский В.П., Георгиевский О.В., Будасов Б.В. Строительное
черчение. — 6-е изд., доп. и перераб. — Москва : Архитектура-С, 2004.
— 456 с.
2. Короев Ю.И. Черчение для строителей : учебник. — 8 изд., стереотип.
— Москва : Высшая школа, 2003. — 256 с.
3. Инженерно-строительное черчение : учеб. для вузов / ред. Ю.И.
Короев ; [П.В. Барсуков [и др.]. — 2-е изд., доп. и перераб. — Москва :
Высшая школа, 1976. — 256 с.
4. Георгиевский О.В. Единые требования по выполнению строительных
чертежей : справочное пособие для сред. и высш. учеб. Заведений. —
5-е изд., испр. и перераб. — Москва : Архитектура-С, 2011. — 143 с.

7.

Список рекомендуемой литературы по разделу
«Начертательная геометрия»
1.
2.
3.
4.
5.
6.
7.
8.
Короев Ю.И. Начертательная геометрия : учебник для вузов. — 2-е изд., перераб. и доп. — Москва :
Архитектура-С, 2015. — 424 с.
Климухин А.Г. Начертательная геометрия : учеб. пособие. — Москва : АрхитектураС, 2007. — 336 с.
Климухин А.Г. Тени и перспектива : учебник для вузов. — Москва : Архитектура-С, 2014. — 200 с.
Методы изображения в архитектурных и градостроительных чертежах : учебнометодическое пособие /
А.А. Фаткуллина и др. — Москва : Издательство МИСИ – МГСУ, 2020. — 73 c.
Начертательная геометрия. Сборник задач. Часть 1 : методические указания к практических занятиям и
самостоятельной работе для обучающихся по направлениям подготовки 07.03.01 Архитектура, 07.03.02
Реконструкция и реставрация архитектурного наследия / сост.: А.А. Фаткуллина, И.М. Гусакова — Москва :
Издательство МИСИ – МГСУ, 2022. — 38 с.
Ортогональные проекции : методические указания к практическим занятиям и самостоятельной работе
для обучающихся по направлениям подготовки 07.03.01 Архитектура, 07.03.02 Реконструкция и
реставрация архитектурного наследия / сост.: А.А Фаткуллина, И.М. Гусакова, Е.П. Знаменская. — Москва :
Издательство МИСИ – МГСУ, 2021. — 34 с.
Построение теней : методические указания для обучающихся бакалавриата по направлениям подготовки
07.03.02 Реконструкция и реставрация архитектурного наследия, 07.03.04 Градостроительство / сост.: Т.М.
Кондратьева, Т.В. Митина, А.А. Фаткуллина. — Москва : Издательство МИСИ – МГСУ, 2019. — 41 с.
Тени в ортогональных проекциях : методические указания к практическим занятиям и самостоятельной
работе для обучающихся по направлениям подготовки 07.03.01 Архитектура, 08.05.01 Строительство
уникальных зданий и сооружений, 23.05.01 Наземные транспортно-технологические средства / сост.: А.А.
Фаткуллина, Е.А. Гусарова. — Москва : Издательство МИСИ – МГСУ, 2020. — 28 с.

8.

8

9.

ВВЕДЕНИЕ
Начертательная геометрия изучает
методы изображения пространственных
форм на плоскости и способы решения
геометрических задач по этим
изображениям
По изображениям, построенным по правилам
начертательной геометрии , можно представить форму
предмета в пространстве, его размеры и расположение
относительно других предметов.
Начертательная геометрия является основой
инженерной графики.
Основателем начертательной геометрии является
французский геометр Гаспар Монж (1746 -1818)
9

10.

Введение
В курсе начертательной геометрии
изучаются:
Методы изображения пространственных
форм на плоском чертеже
Способы графического решения
различных геометрических задач
Способы преобразования и исследования
геометрических свойств изображенного
объекта
Способы геометрического
формообразования поверхностей
10

11.

Введение
Принятые обозначения
A, B, C, D или I, II, III… - точки , расположенные в пространстве
a, b, c, d или 1, 2, 3 … - горизонтальные проекции точек
a̕, b̕, c̕, d̕ или 1̕, 2̕, 3̕… - фронтальные проекции точек
a", b", c", d" или 1", 2" ,3"… - профильные проекции точек
H – горизонтальная плоскость проекций
V – фронтальная плоскость проекций
W – профильная плоскость проекций
P, S, Q, R… - плоскости в пространстве
PH , PV , PW , SH , SV , SW… - следы плоскости
α - угол наклона к горизонтальной плоскости проекций
β - угол наклона к фронтальной плоскости проекций
γ - угол наклона к профильной плоскости проекций
символы - ≡ – тождество ,r– перпендикуляр ,∩– пересечение
II – параллельность ,ϵ – принадлежность
11

12.

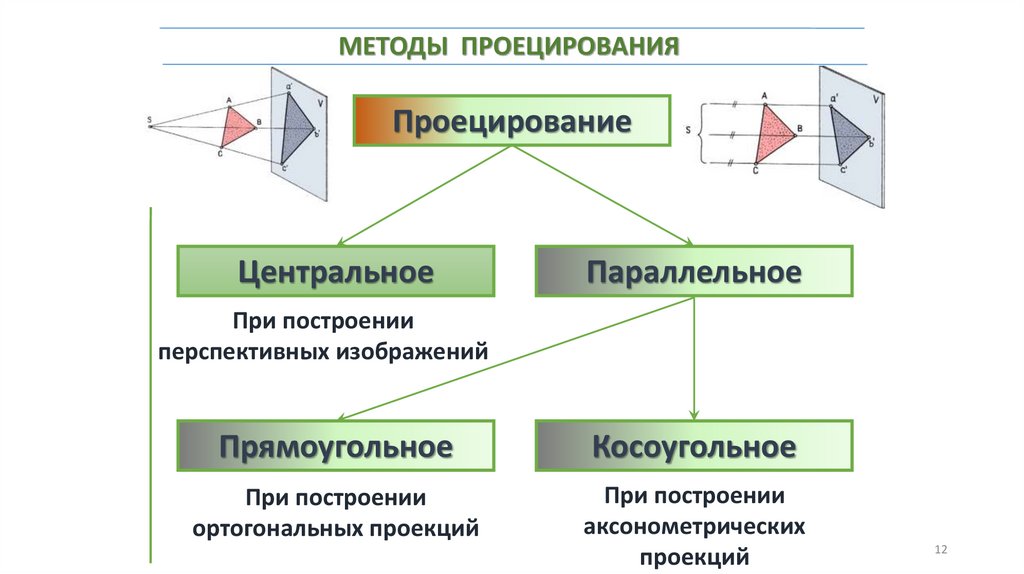
МЕТОДЫ ПРОЕЦИРОВАНИЯ
Проецирование
Центральное
Параллельное
При построении
перспективных изображений
Прямоугольное
Косоугольное
При построении
ортогональных проекций
При построении
аксонометрических
проекций
12

13.

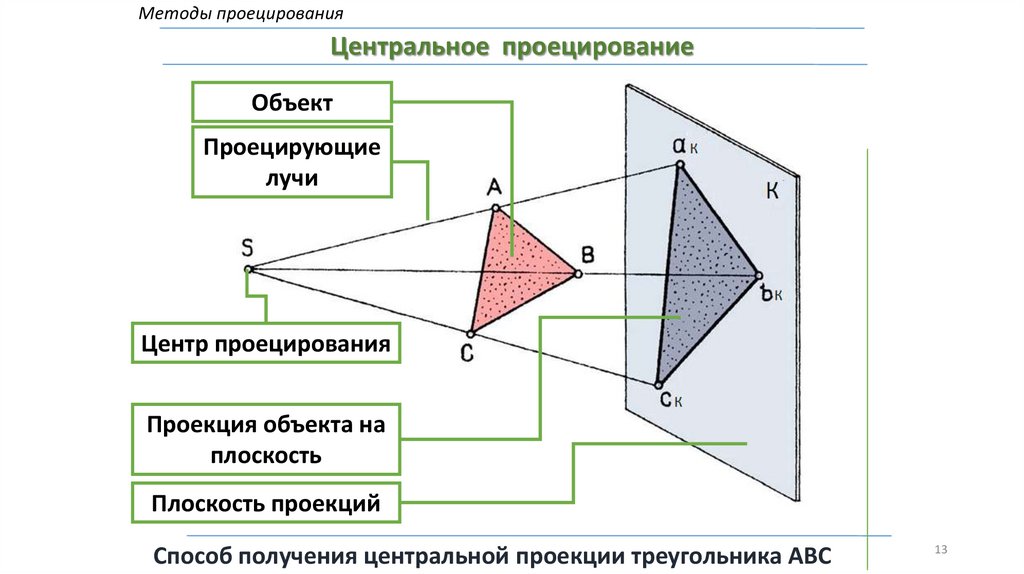
Методы проецирования
Центральное проецирование
Объект
Проецирующие
лучи
Центр проецирования
Проекция объекта на
плоскость
Плоскость проекций
Способ получения центральной проекции треугольника АВС
13

14.

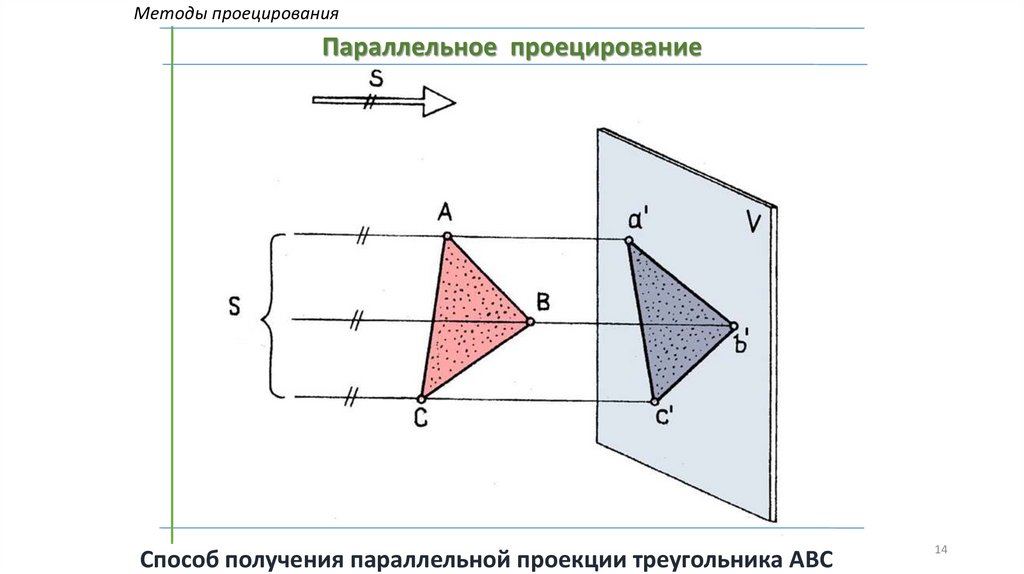
Методы проецирования
Параллельное проецирование
Способ получения параллельной проекции треугольника АВС
14

15.

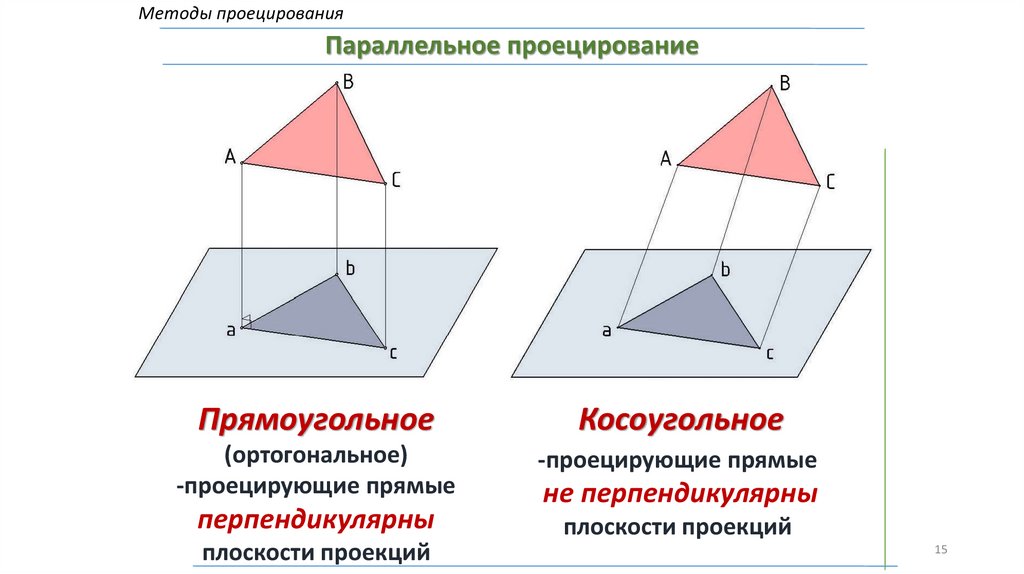
Методы проецирования
Параллельное проецирование
Прямоугольное
Косоугольное
(ортогональное)
-проецирующие прямые
-проецирующие прямые
перпендикулярны
плоскости проекций
плоскости проекций
не перпендикулярны
15

16.

Методы проецирования
Параллельное проецирование
Свойства параллельного проецирования
Проекция точки – точка
Проекция прямой – прямая
Если точка принадлежит прямой , то проекция
точки принадлежит проекции этой прямой
Отношение отрезков в пространстве
сохраняется на проекциях (
)
Если прямые в пространстве параллельны,
то параллельны и их проекции
( АВ II CD → ab II cd )
16

17.

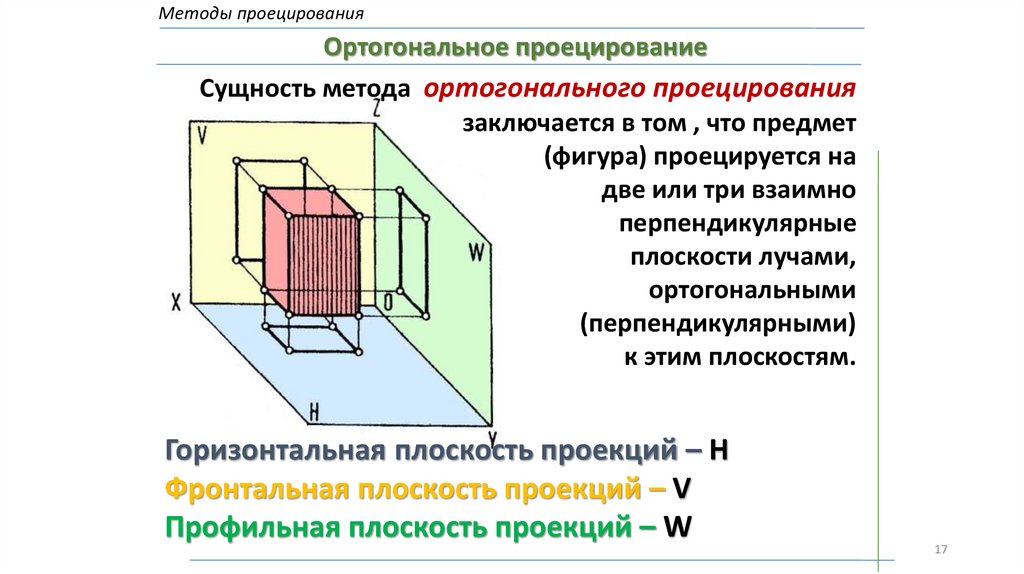
Методы проецирования
Ортогональное проецирование
Сущность метода ортогонального проецирования
заключается в том , что предмет
(фигура) проецируется на
две или три взаимно
перпендикулярные
плоскости лучами,
ортогональными
(перпендикулярными)
к этим плоскостям.
Горизонтальная плоскость проекций – H
Фронтальная плоскость проекций – V
Профильная плоскость проекций – W
17

18.

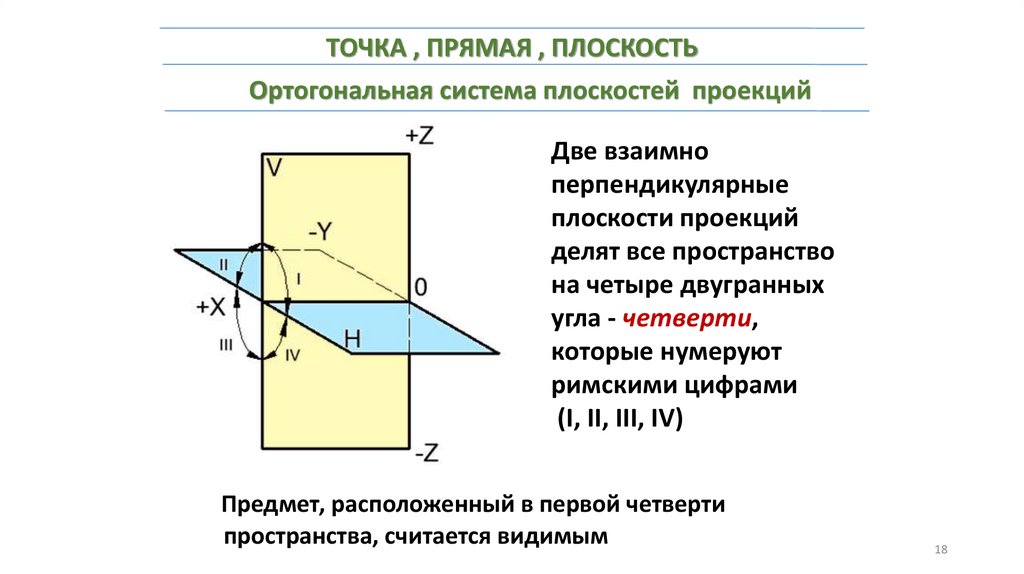
ТОЧКА , ПРЯМАЯ , ПЛОСКОСТЬ
Ортогональная система плоскостей проекций
Две взаимно
перпендикулярные
плоскости проекций
делят все пространство
на четыре двугранных
угла - четверти,
которые нумеруют
римскими цифрами
(I, II, III, IV)
Предмет, расположенный в первой четверти
пространства, считается видимым
18

19.

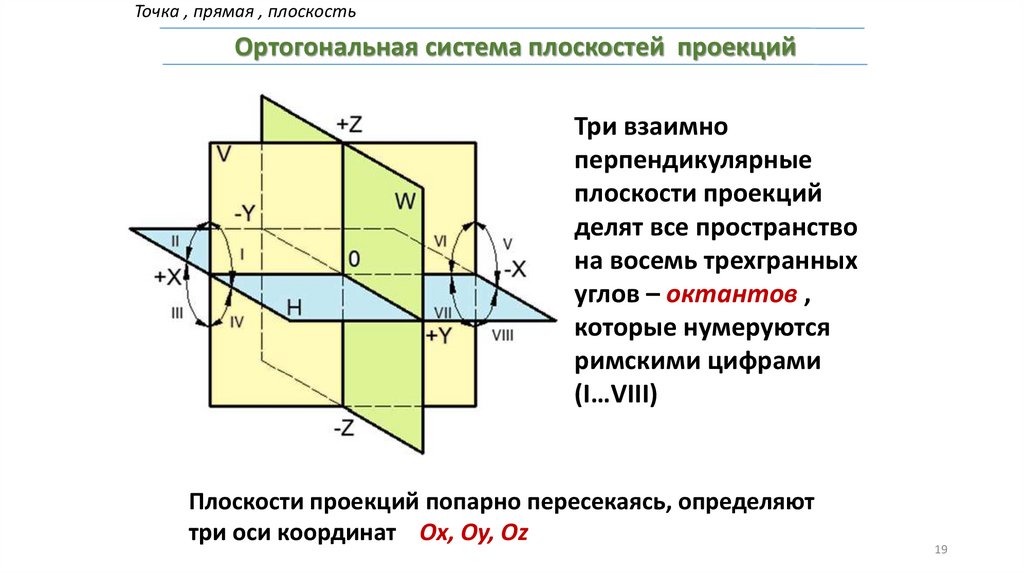
Точка , прямая , плоскость
Ортогональная система плоскостей проекций
Три взаимно
перпендикулярные
плоскости проекций
делят все пространство
на восемь трехгранных
углов – октантов ,
которые нумеруются
римскими цифрами
(I…VIII)
Плоскости проекций попарно пересекаясь, определяют
три оси координат Ox, Oy, Oz
19

20.

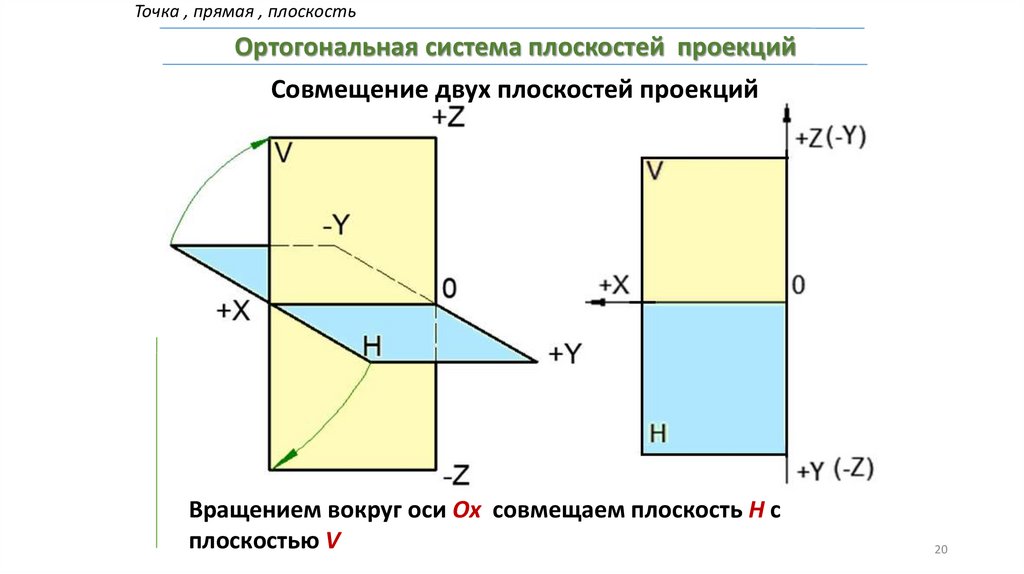
Точка , прямая , плоскость
Ортогональная система плоскостей проекций
Совмещение двух плоскостей проекций
Вращением вокруг оси Ох совмещаем плоскость Н с
плоскостью V
20

21.

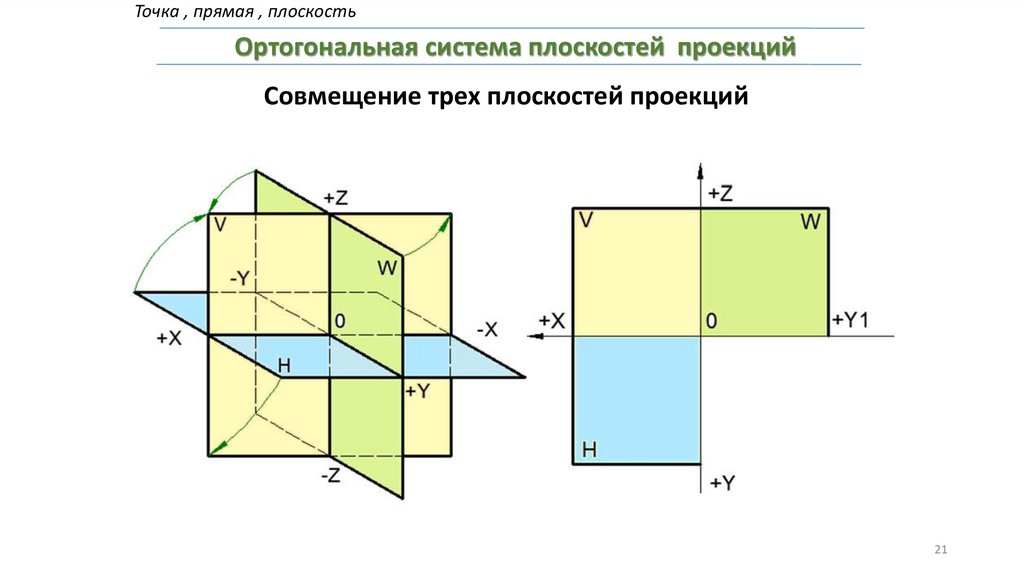
Точка , прямая , плоскость
Ортогональная система плоскостей проекций
Совмещение трех плоскостей проекций
21

22.

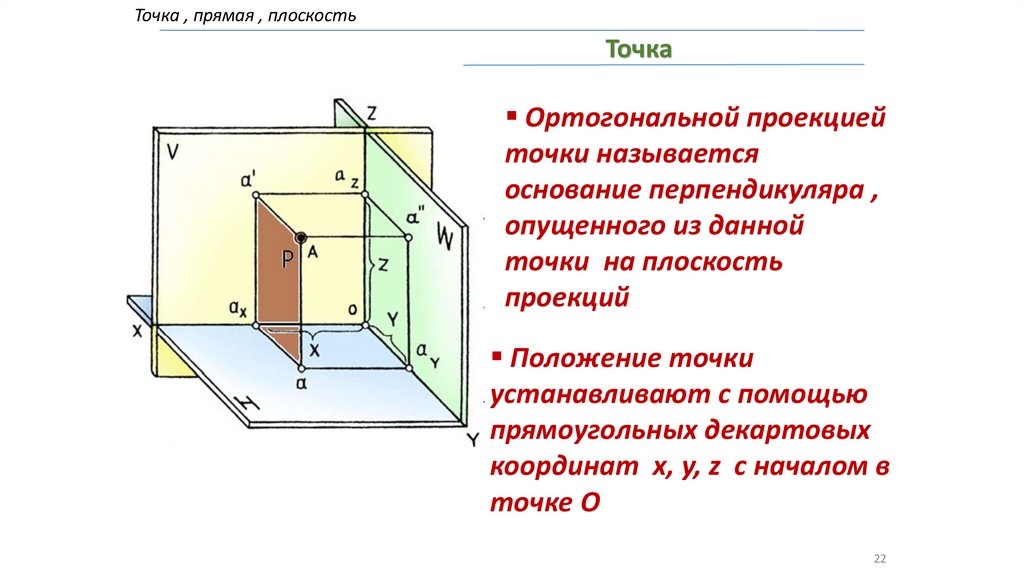
Точка , прямая , плоскость
Точка
Ортогональной проекцией
точки называется
основание перпендикуляра ,
опущенного из данной
точки на плоскость
проекций
Положение точки
устанавливают с помощью
прямоугольных декартовых
координат x, y, z с началом в
точке О
22

23.

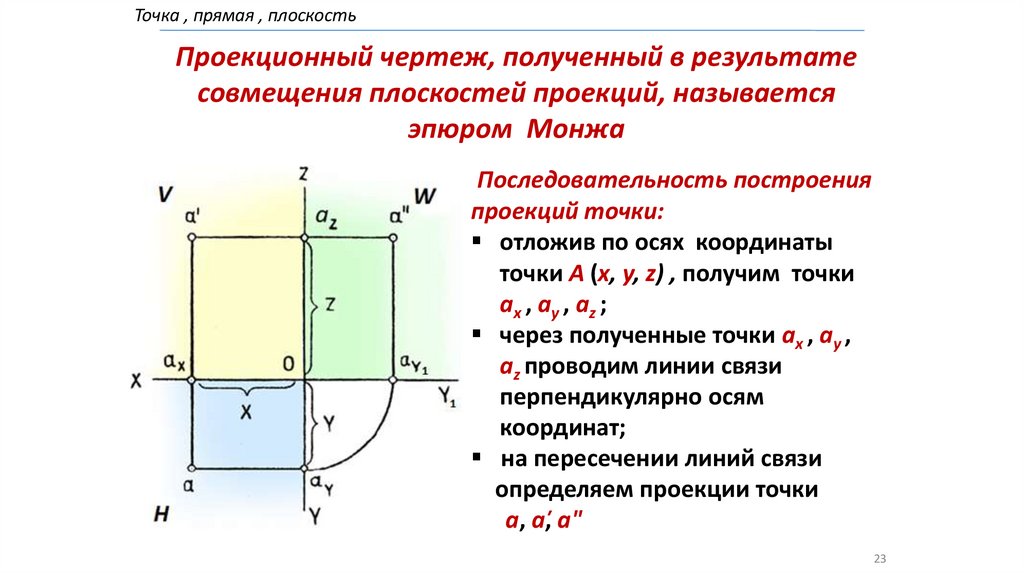
Точка , прямая , плоскость
Проекционный чертеж, полученный в результате
совмещения плоскостей проекций, называется
эпюром Монжа
Последовательность построения
проекций точки:
отложив по осях координаты
точки А (x, y, z) , получим точки
ax , ay , az ;
через полученные точки ax , ay ,
az проводим линии связи
перпендикулярно осям
координат;
на пересечении линий связи
определяем проекции точки
а, а̕, а"
23

24.

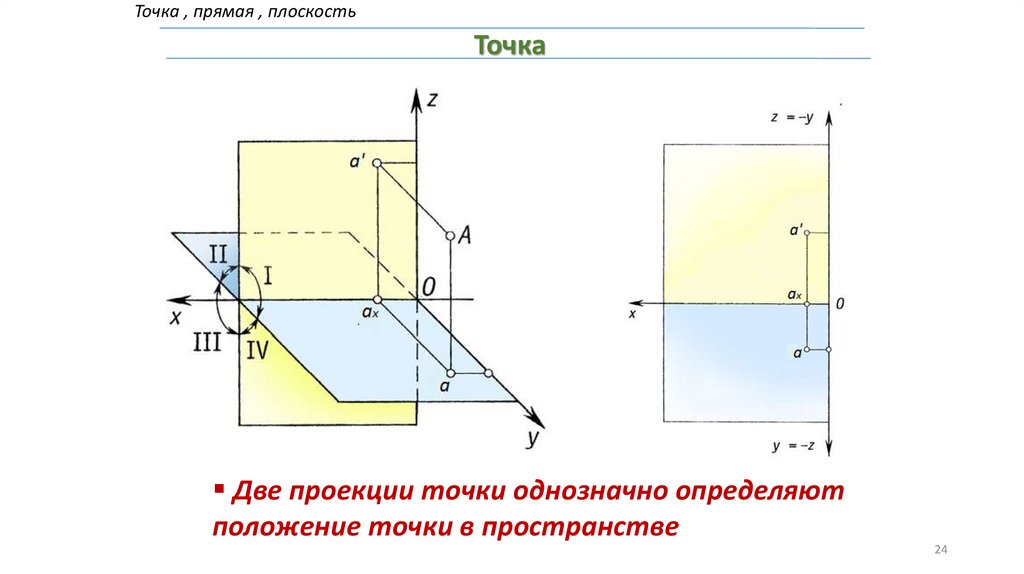
Точка , прямая , плоскость
Точка
Две проекции точки однозначно определяют
положение точки в пространстве
24

25.

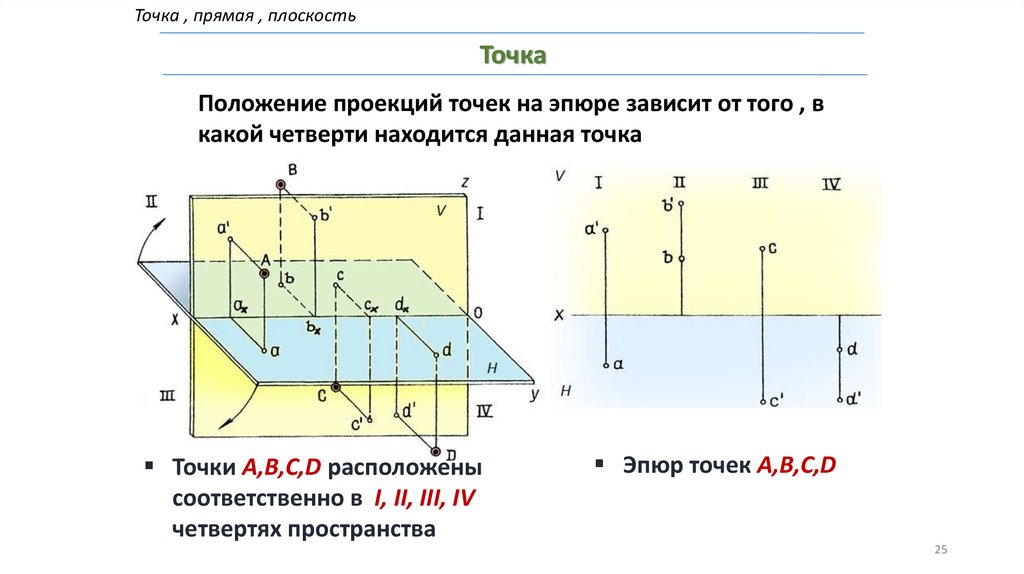
Точка , прямая , плоскость
Точка
Положение проекций точек на эпюре зависит от того , в
какой четверти находится данная точка
Точки A,B,C,D расположены
соответственно в I, II, III, IV
четвертях пространства
Эпюр точек A,B,C,D
25

26.

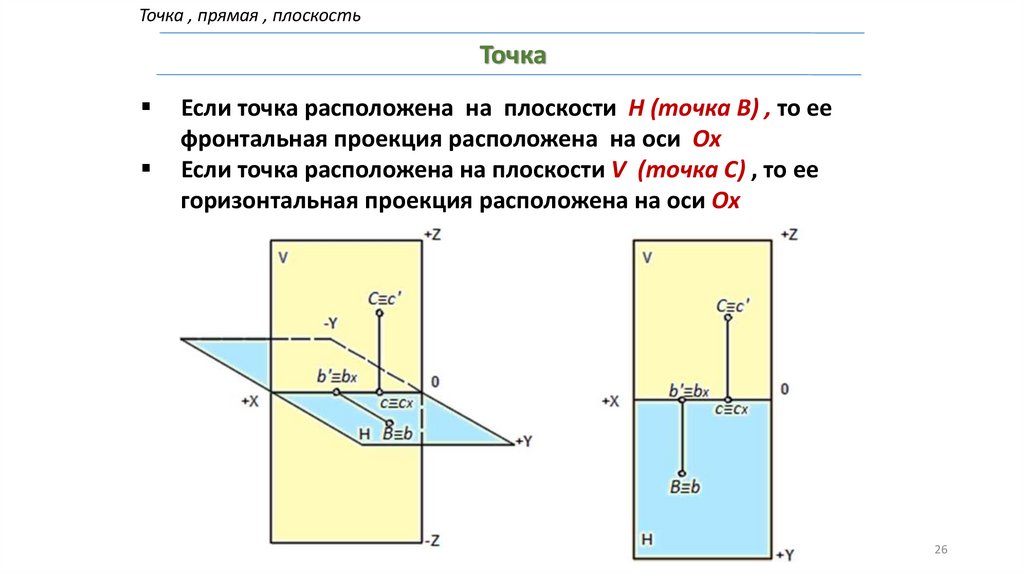
Точка , прямая , плоскость
Точка
Если точка расположена на плоскости H (точка В) , то ее
фронтальная проекция расположена на оси Ox
Если точка расположена на плоскости V (точка С) , то ее
горизонтальная проекция расположена на оси Ox
26

27.

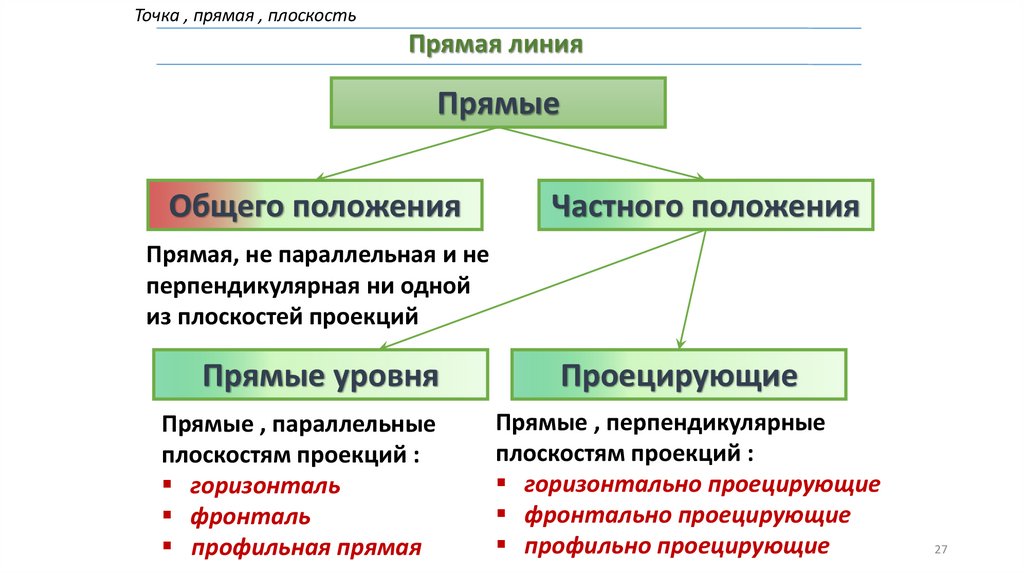
Точка , прямая , плоскость
Прямая линия
Прямые
Общего положения
Частного положения
Прямая, не параллельная и не
перпендикулярная ни одной
из плоскостей проекций
Прямые уровня
Прямые , параллельные
плоскостям проекций :
горизонталь
фронталь
профильная прямая
Проецирующие
Прямые , перпендикулярные
плоскостям проекций :
горизонтально проецирующие
фронтально проецирующие
профильно проецирующие
27

28.

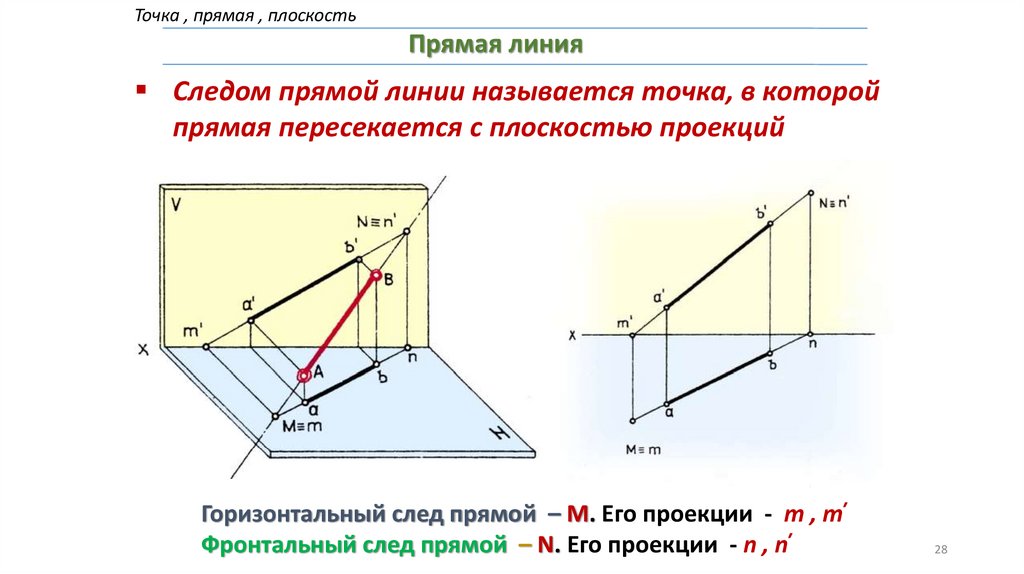
Точка , прямая , плоскость
Прямая линия
Следом прямой линии называется точка, в которой
прямая пересекается с плоскостью проекций
Горизонтальный след прямой – M. Его проекции - m , m̕
Фронтальный след прямой – N. Его проекции - n , n̕
28

29.

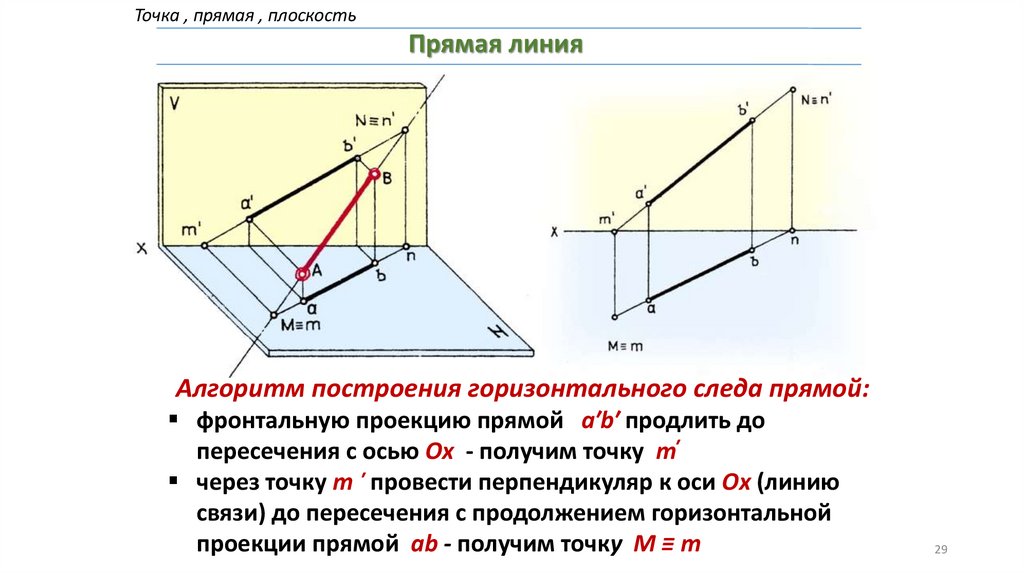
Точка , прямая , плоскость
Прямая линия
Алгоритм построения горизонтального следа прямой:
фронтальную проекцию прямой а′̕b′ продлить до
пересечения с осью Ох - получим точку m̕
через точку m ̕ провести перпендикуляр к оси Ох (линию
связи) до пересечения с продолжением горизонтальной
проекции прямой аb - получим точку М ≡ m
29

30.

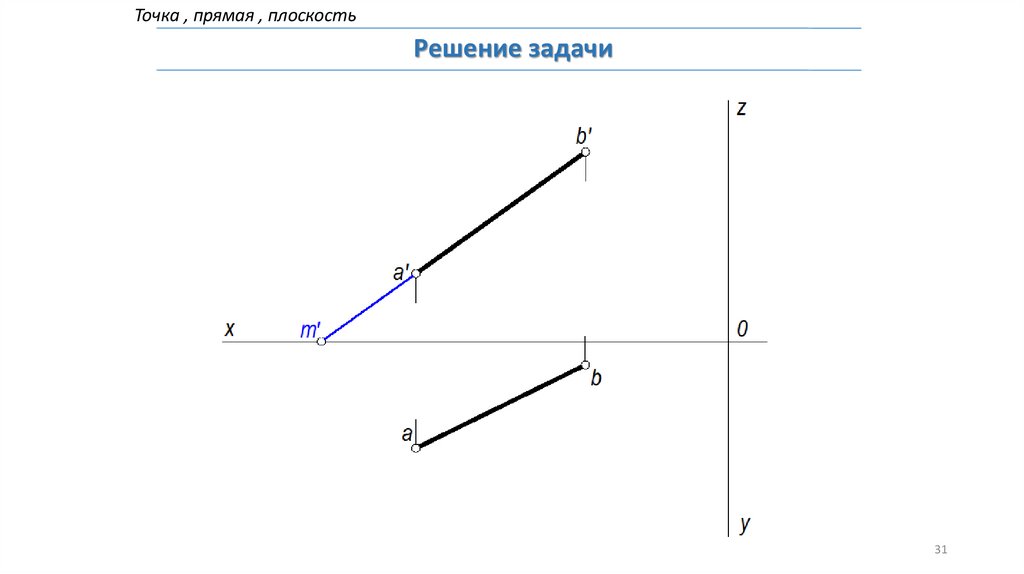
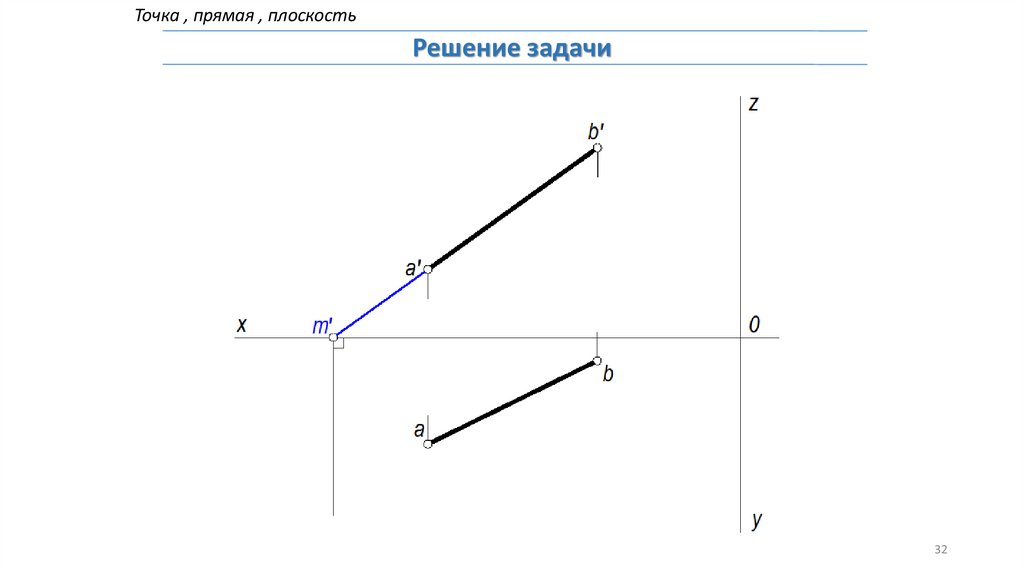
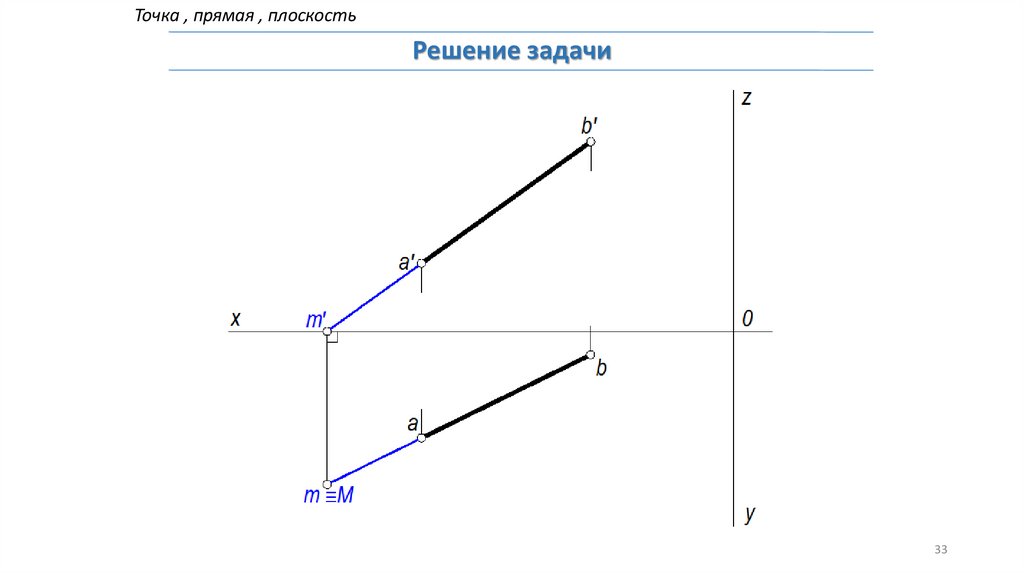
Точка , прямая , плоскость
Решение задачи
Задача: Построить следы прямой АВ
30

31.

Точка , прямая , плоскость
Решение задачи
31

32.

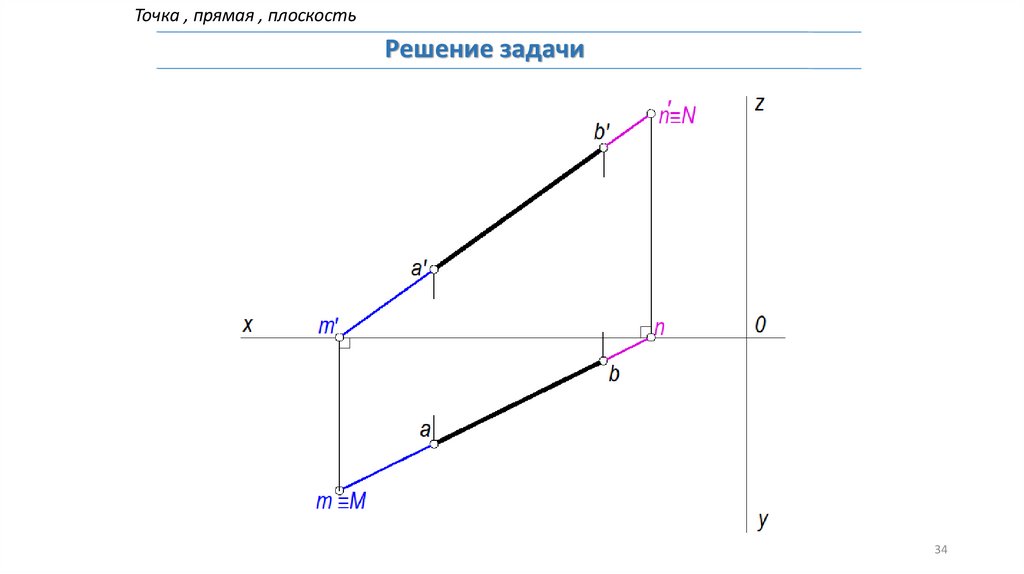
Точка , прямая , плоскость
Решение задачи
32

33.

Точка , прямая , плоскость
Решение задачи
33

34.

Точка , прямая , плоскость
Решение задачи
34

35.

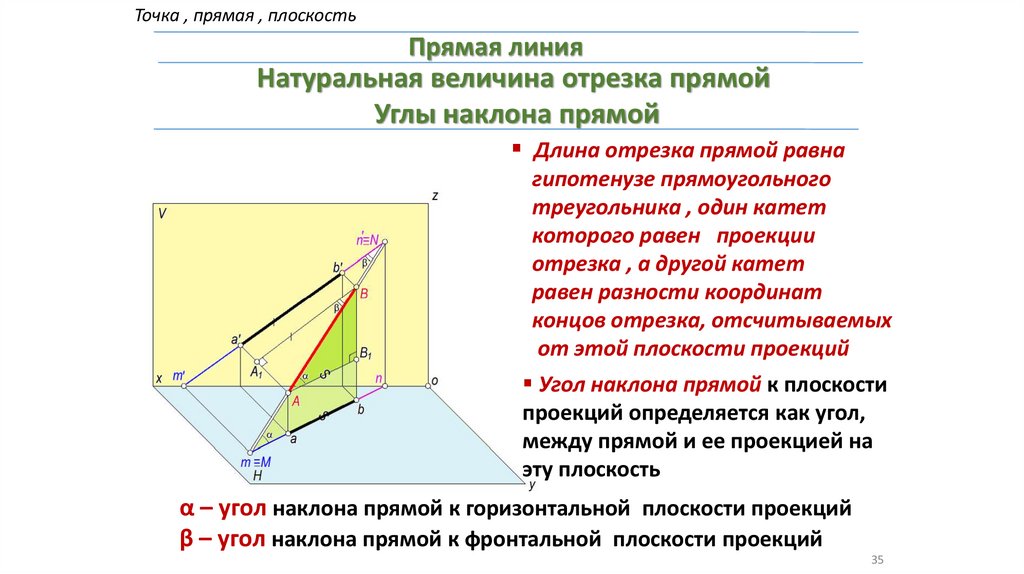
Точка , прямая , плоскость
Прямая линия
Натуральная величина отрезка прямой
Углы наклона прямой
Длина отрезка прямой равна
гипотенузе прямоугольного
треугольника , один катет
которого равен проекции
отрезка , а другой катет
равен разности координат
концов отрезка, отсчитываемых
от этой плоскости проекций
Угол наклона прямой к плоскости
проекций определяется как угол,
между прямой и ее проекцией на
эту плоскость
α – угол наклона прямой к горизонтальной плоскости проекций
β – угол наклона прямой к фронтальной плоскости проекций
35

36.

Точка , прямая , плоскость
Решение задачи
Задача: Определить длину отрезка АВ и угол его
наклона к плоскостям проекций
36

37.

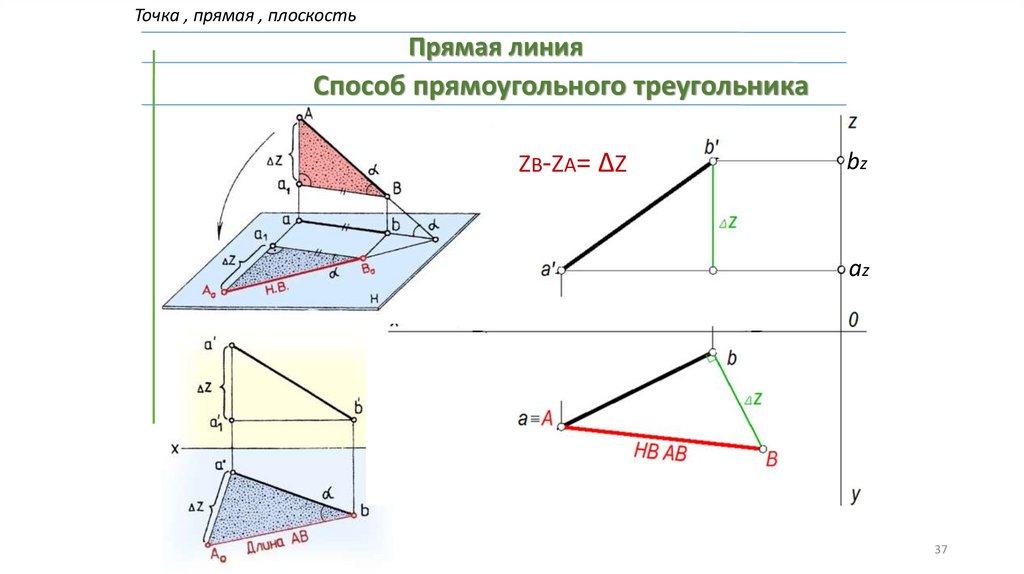
Точка , прямая , плоскость
Прямая линия
Способ прямоугольного треугольника
ZВ-ZА= ΔZ
bz
az
37

38.

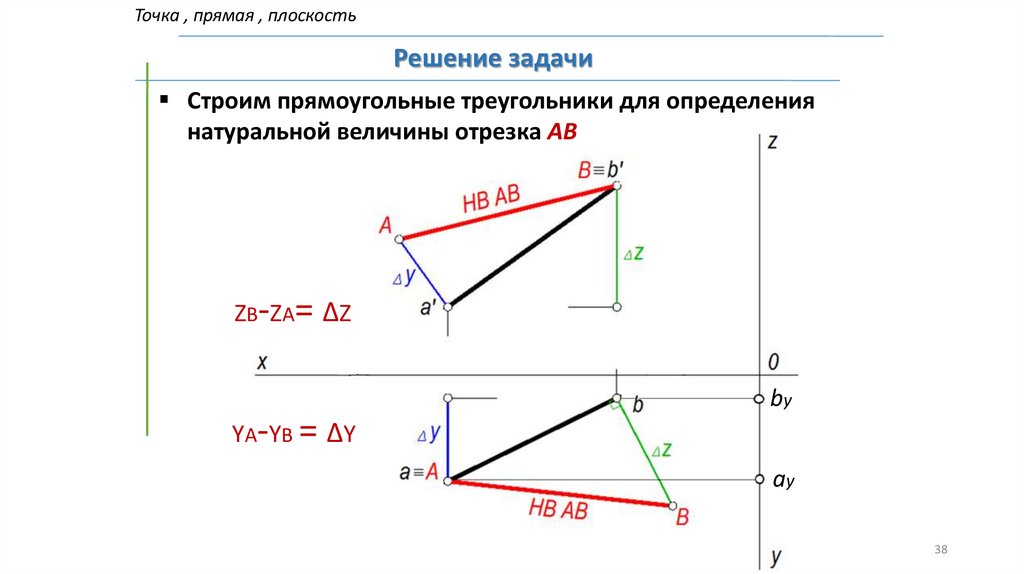
Точка , прямая , плоскость
Решение задачи
Строим прямоугольные треугольники для определения
натуральной величины отрезка АВ
Z В- Z А = Δ Z
by
YА-YВ = ΔY
ay
38

39.

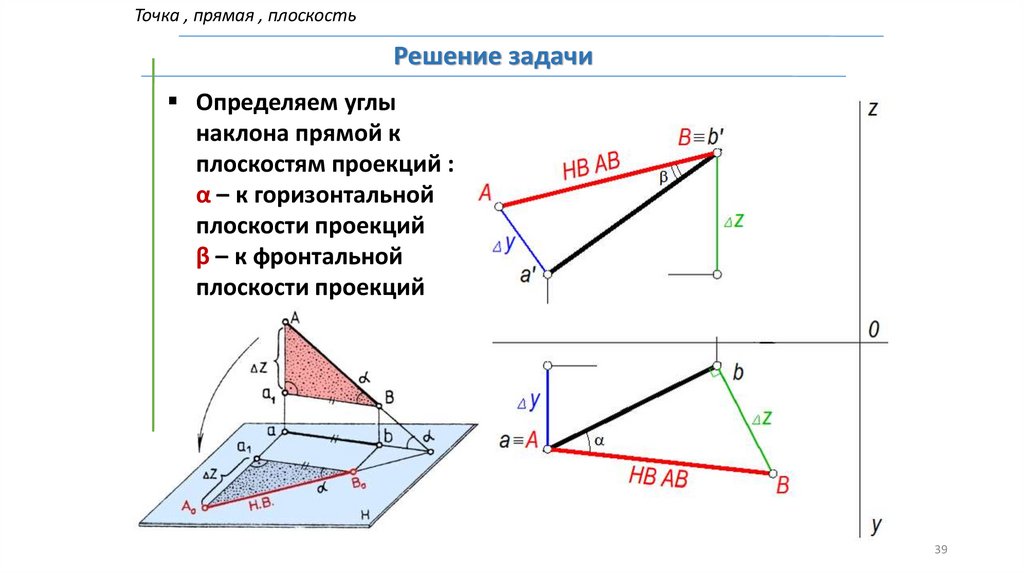
Точка , прямая , плоскость
Решение задачи
Определяем углы
наклона прямой к
плоскостям проекций :
α – к горизонтальной
плоскости проекций
β – к фронтальной
плоскости проекций
39

40.

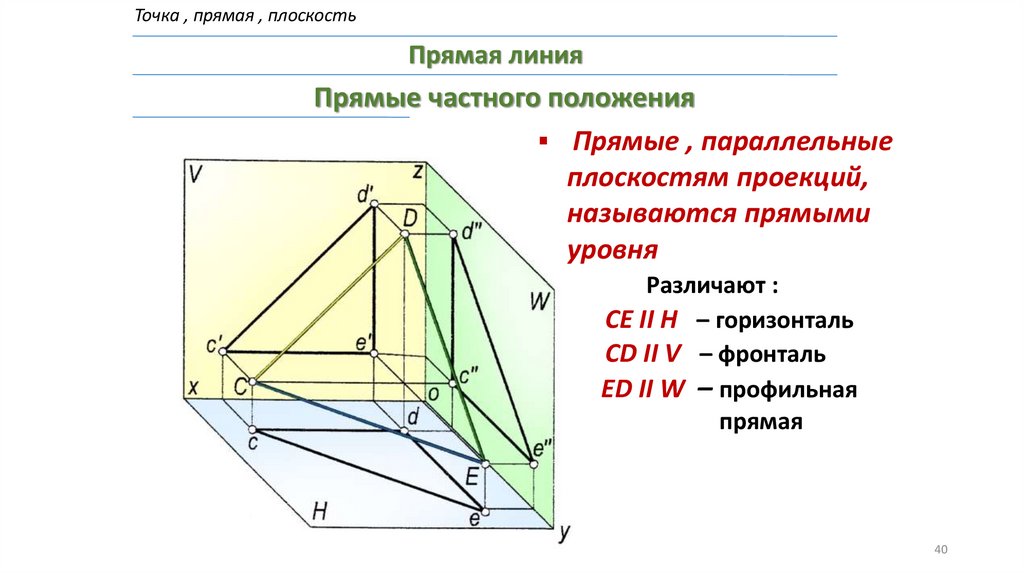
Точка , прямая , плоскость
Прямая линия
Прямые частного положения
Прямые , параллельные
плоскостям проекций,
называются прямыми
уровня
Различают :
CE II H – горизонталь
CD II V – фронталь
ED II W – профильная
прямая
40

41.

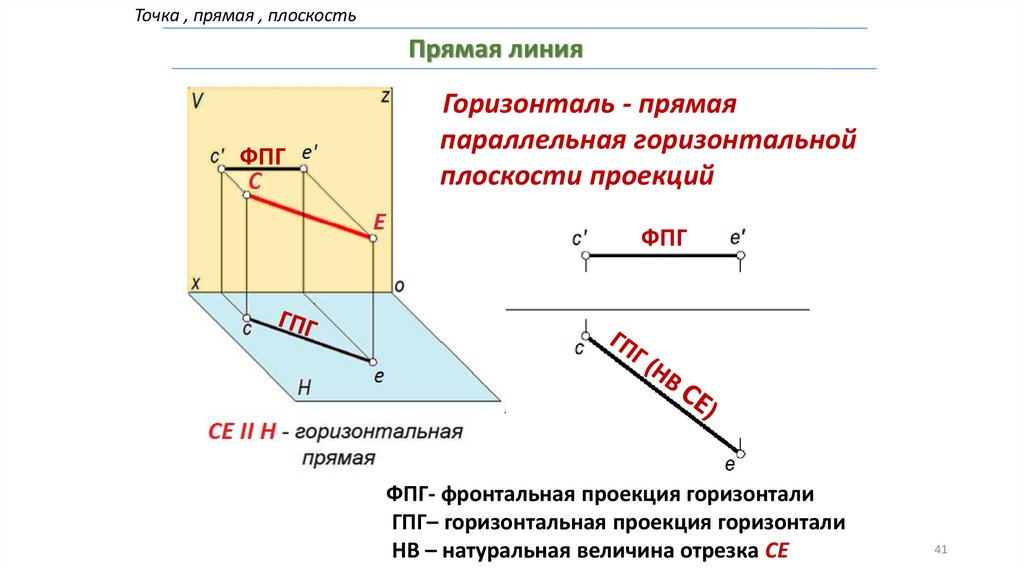
Точка , прямая , плоскость
Прямая линия
ФПГ
Горизонталь - прямая
параллельная горизонтальной
плоскости проекций
ФПГ
ФПГ- фронтальная проекция горизонтали
ГПГ– горизонтальная проекция горизонтали
НВ – натуральная величина отрезка СЕ
41

42.

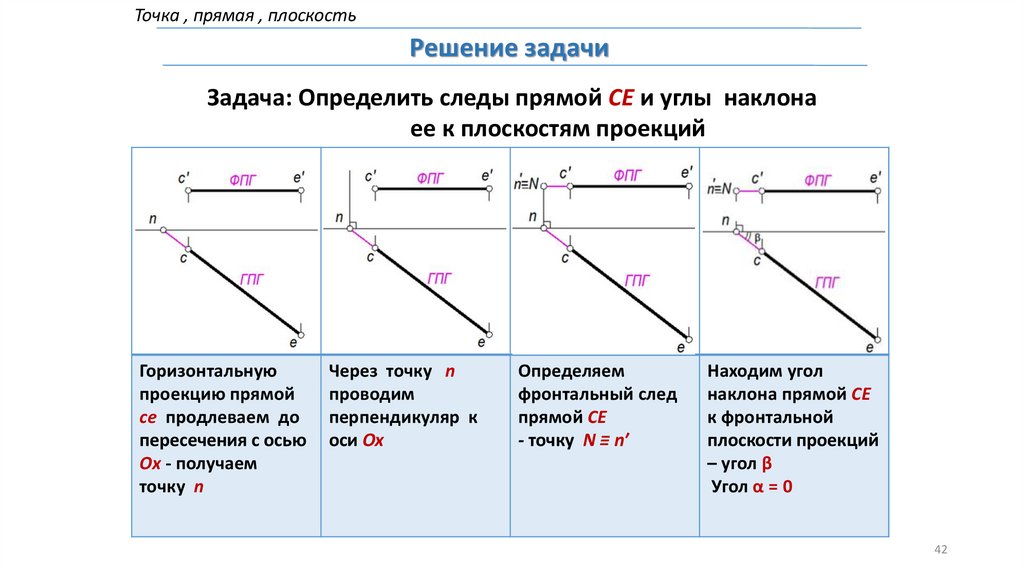
Точка , прямая , плоскость
Решение задачи
Задача: Определить следы прямой СЕ и углы наклона
ее к плоскостям проекций
Горизонтальную
проекцию прямой
ce продлеваем до
пересечения с осью
Ox - получаем
точку n
Через точку n
проводим
перпендикуляр к
оси Ox
Определяем
фронтальный след
прямой СЕ
- точку N ≡ n′
Находим угол
наклона прямой СЕ
к фронтальной
плоскости проекций
– угол β
Угол α = 0
42

43.

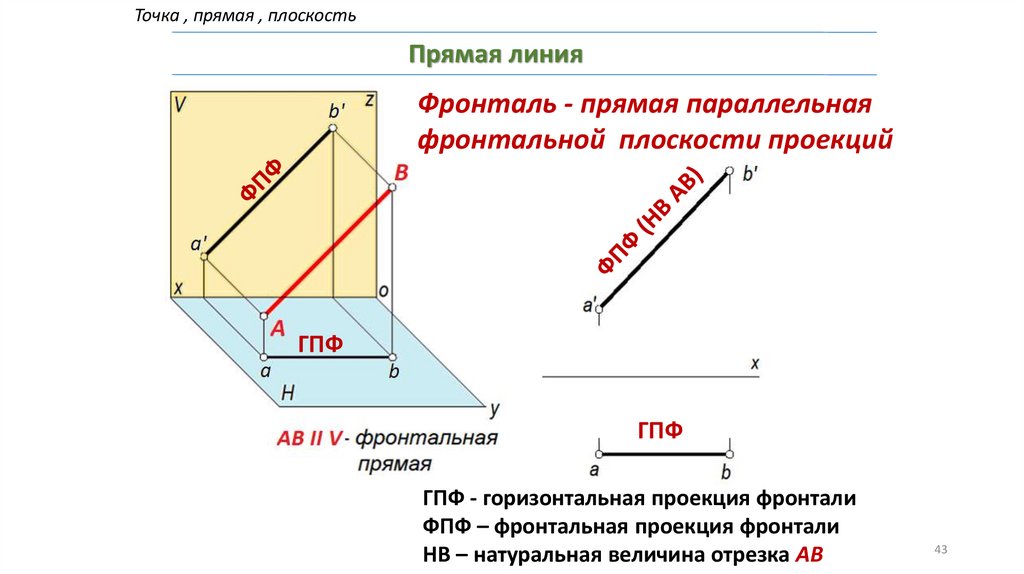
Точка , прямая , плоскость
Прямая линия
Фронталь - прямая параллельная
фронтальной плоскости проекций
ГПФ
ГПФ
ГПФ - горизонтальная проекция фронтали
ФПФ – фронтальная проекция фронтали
НВ – натуральная величина отрезка АВ
43

44.

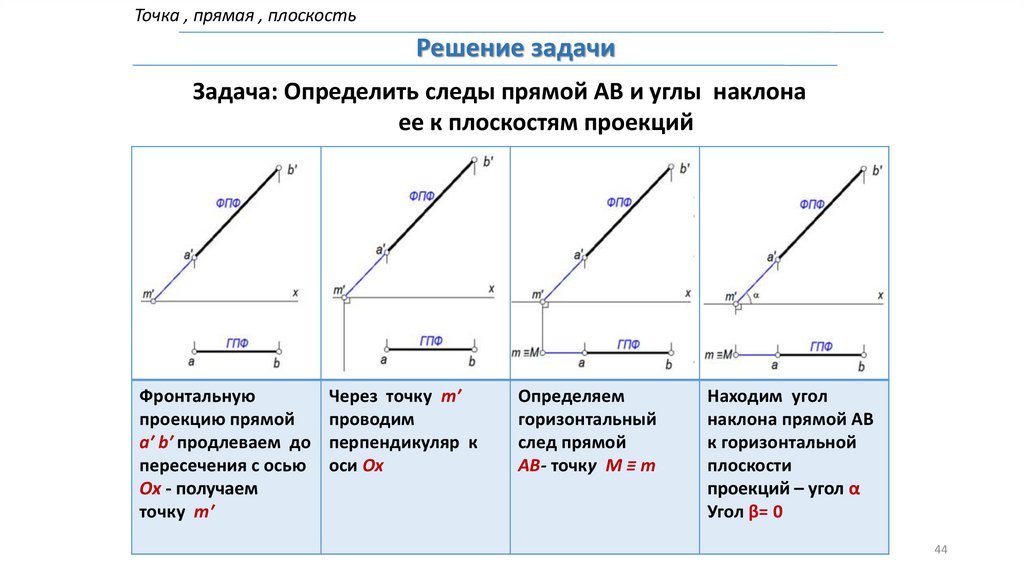
Точка , прямая , плоскость
Решение задачи
Задача: Определить следы прямой АВ и углы наклона
ее к плоскостям проекций
Фронтальную
проекцию прямой
а′ b′ продлеваем до
пересечения с осью
Ox - получаем
точку m′
Через точку m′
проводим
перпендикуляр к
оси Ox
Определяем
горизонтальный
след прямой
АВ- точку M ≡ m
Находим угол
наклона прямой AB
к горизонтальной
плоскости
проекций – угол α
Угол β= 0
44

45.

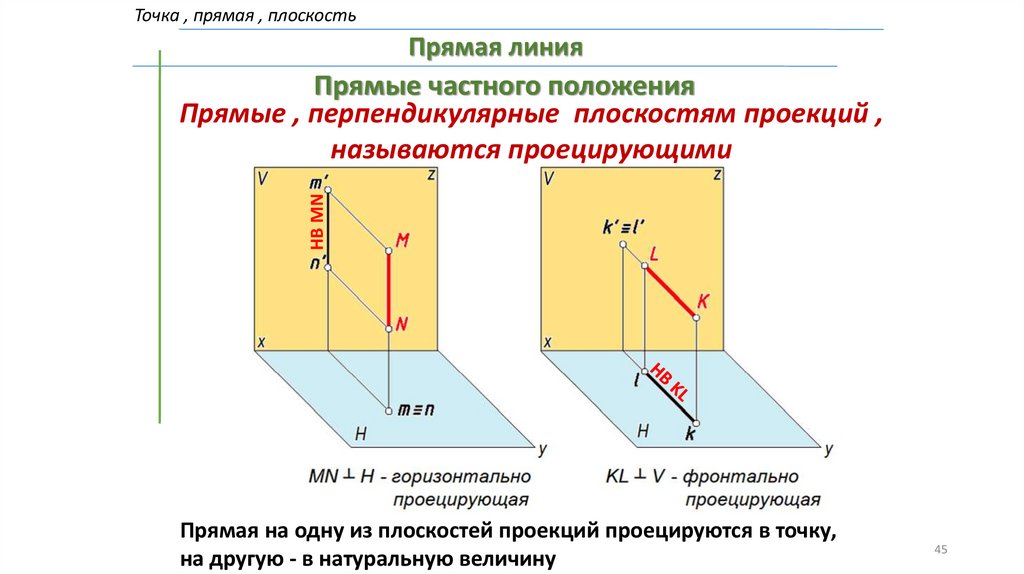
Точка , прямая , плоскость
Прямая линия
НВ МN
Прямые частного положения
Прямые , перпендикулярные плоскостям проекций ,
называются проецирующими
Прямая на одну из плоскостей проекций проецируются в точку,
на другую - в натуральную величину
45

46.

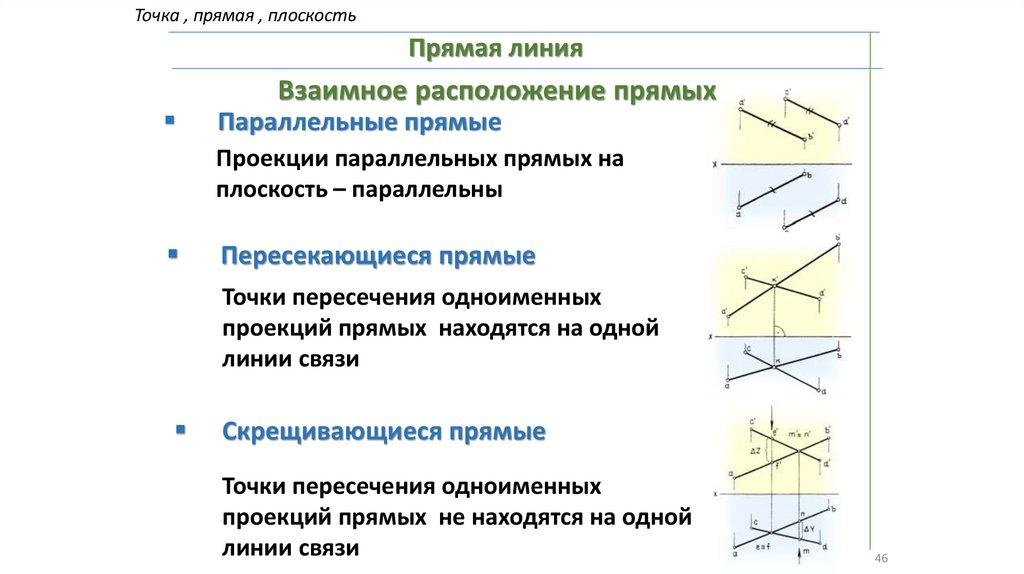
Точка , прямая , плоскость
Прямая линия
Взаимное расположение прямых
Параллельные прямые
Проекции параллельных прямых на
плоскость – параллельны
Пересекающиеся прямые
Точки пересечения одноименных
проекций прямых находятся на одной
линии связи
Скрещивающиеся прямые
Точки пересечения одноименных
проекций прямых не находятся на одной
линии связи
46

47.

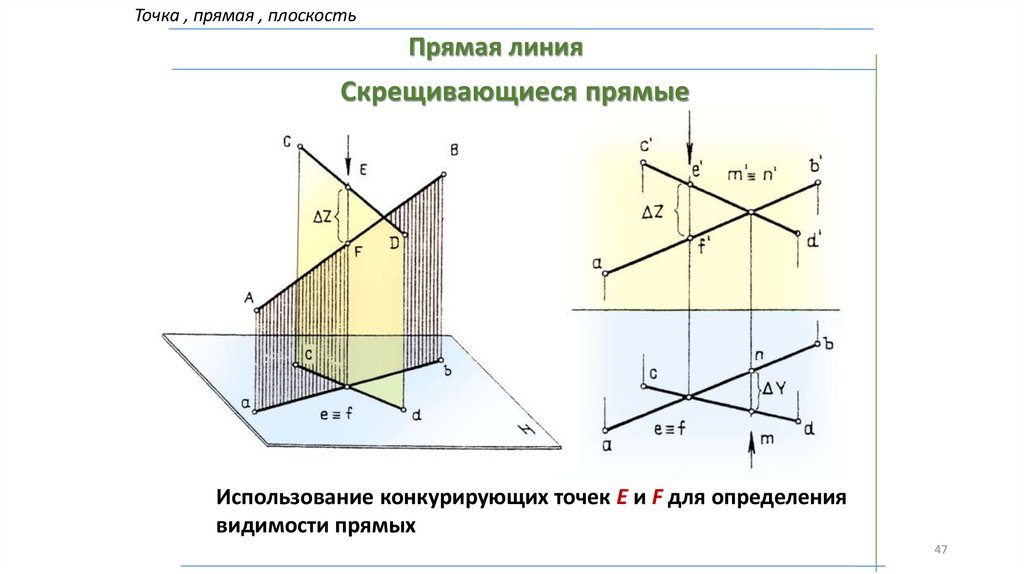
Точка , прямая , плоскость
Прямая линия
Скрещивающиеся прямые
Использование конкурирующих точек E и F для определения
видимости прямых
47

48.

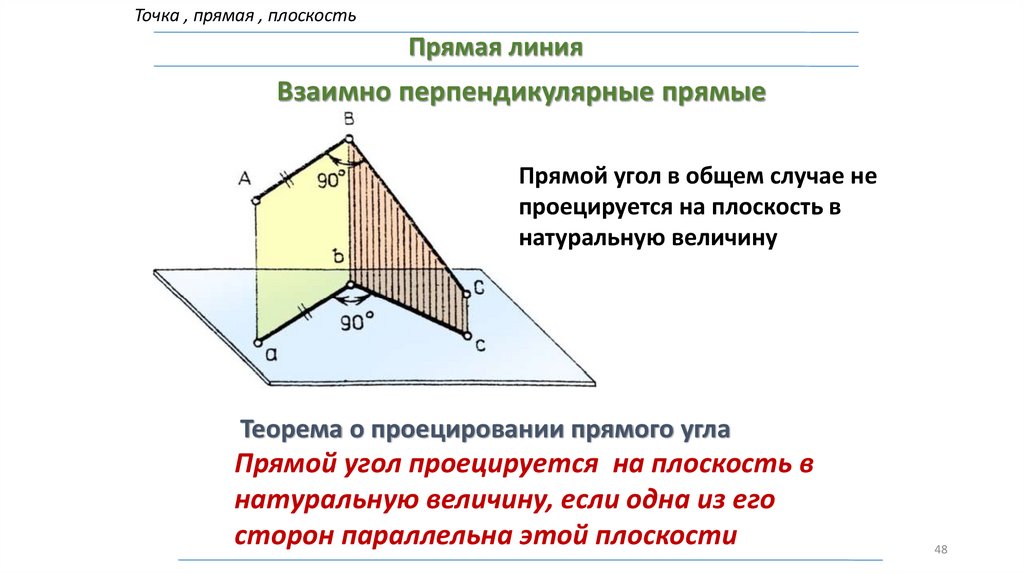
Точка , прямая , плоскость
Прямая линия
Взаимно перпендикулярные прямые
Прямой угол в общем случае не
проецируется на плоскость в
натуральную величину
Теорема о проецировании прямого угла
Прямой угол проецируется на плоскость в
натуральную величину, если одна из его
сторон параллельна этой плоскости
48

49.

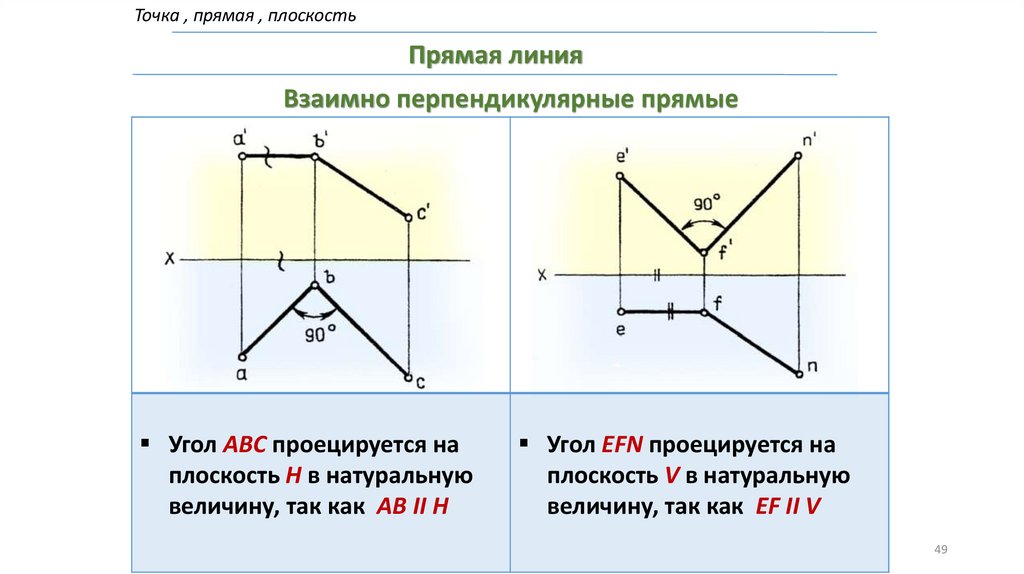
Точка , прямая , плоскость
Прямая линия
Взаимно перпендикулярные прямые
Угол АВС проецируется на
плоскость Н в натуральную
величину, так как АВ II H
Угол EFN проецируется на
плоскость V в натуральную
величину, так как EF II V
49