Начертательная геометрия и инженерная графика

1. Начертательная геометрия и инженерная графика

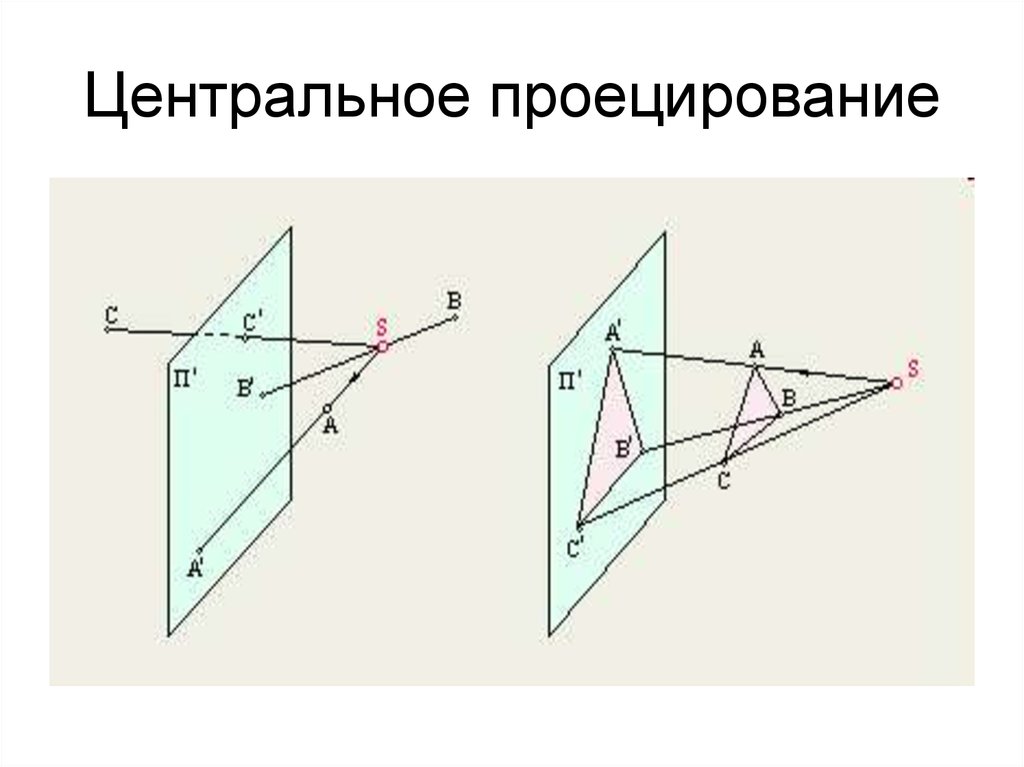
Часть 1

2. Центральное проецирование

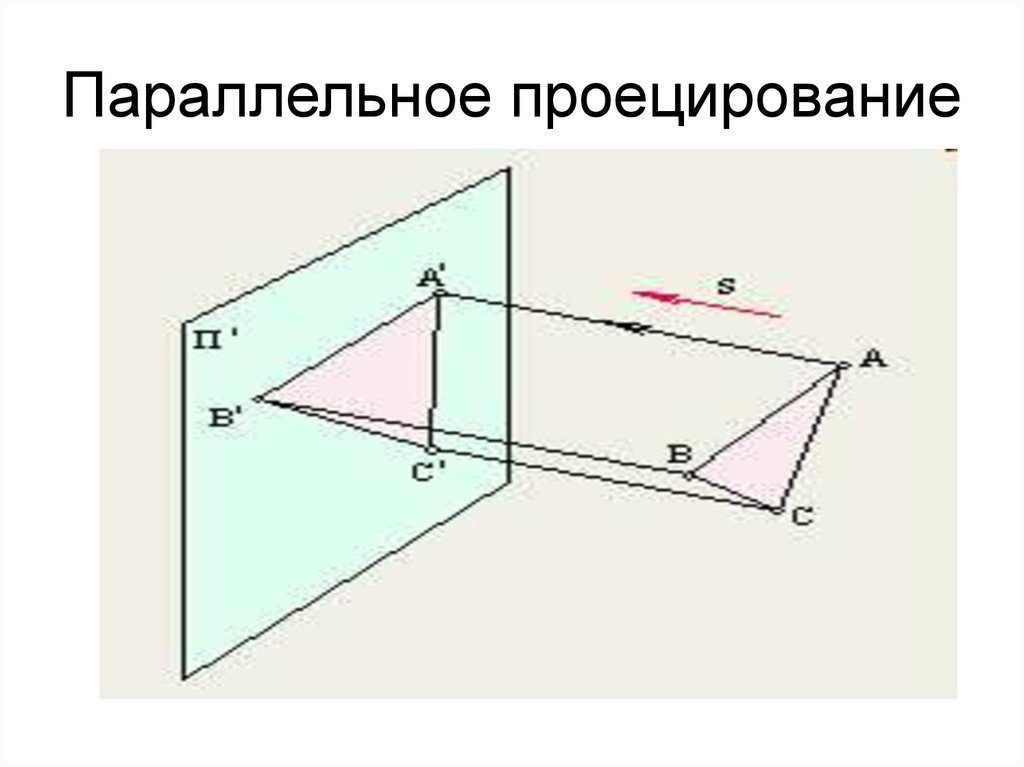
3. Параллельное проецирование

4. Основные свойства параллельного проецирования

• 1. Свойство однозначности. Проекцией точки на плоскость
есть точка.
• 2. Свойство прямолинейности. Проекцией прямой линии на
плоскость есть прямая.
• 3. Свойство принадлежности. Если точка принадлежит
линии, то проекция точки принадлежит проекции этой
линии.
• 4. Свойство сохранения параллельности. Проекциями
параллельных прямых являются параллельные прямые.
• 5. Свойство деления отрезка в отношении. Если отрезок
прямой линии делится точкой в каком-либо отношении, то и
проекция отрезка делится проекцией точки в том же
отношении.
• 6. Свойство параллельного переноса. Проекция фигуры не
меняется при параллельном переносе плоскости проекций.
• Три последние свойства обеспечивают более простое
построение изображения и меньше искажают форму и
размеры оригинала по сравнению с центральной
проекцией.

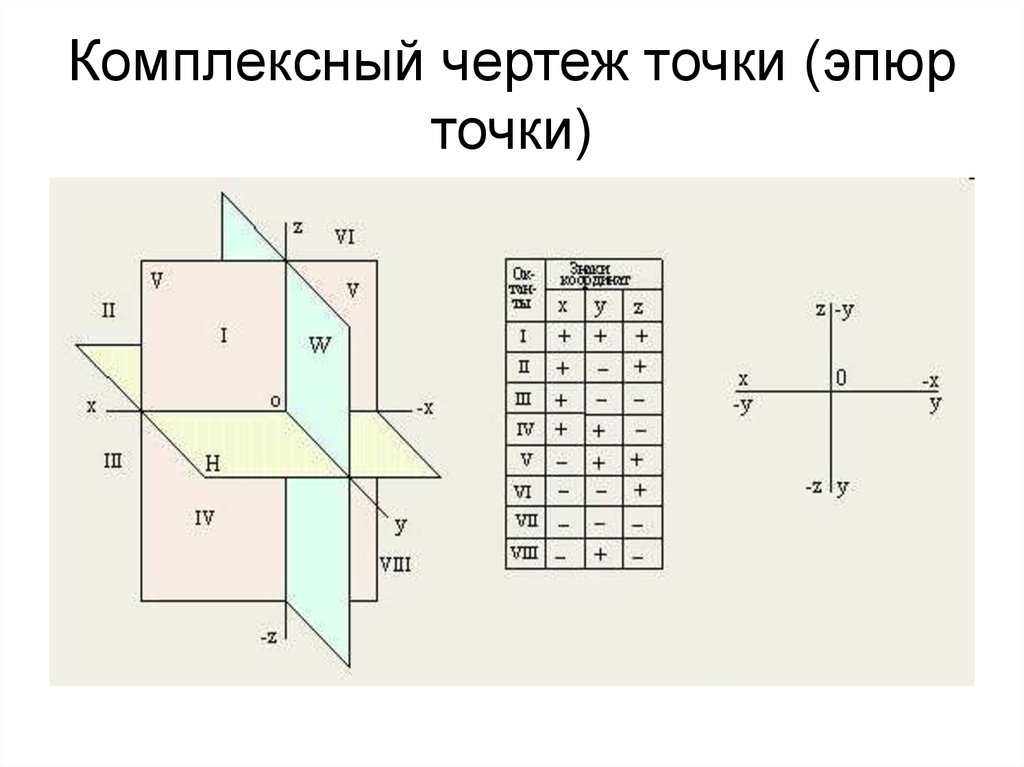
5. Комплексный чертеж точки (эпюр точки)

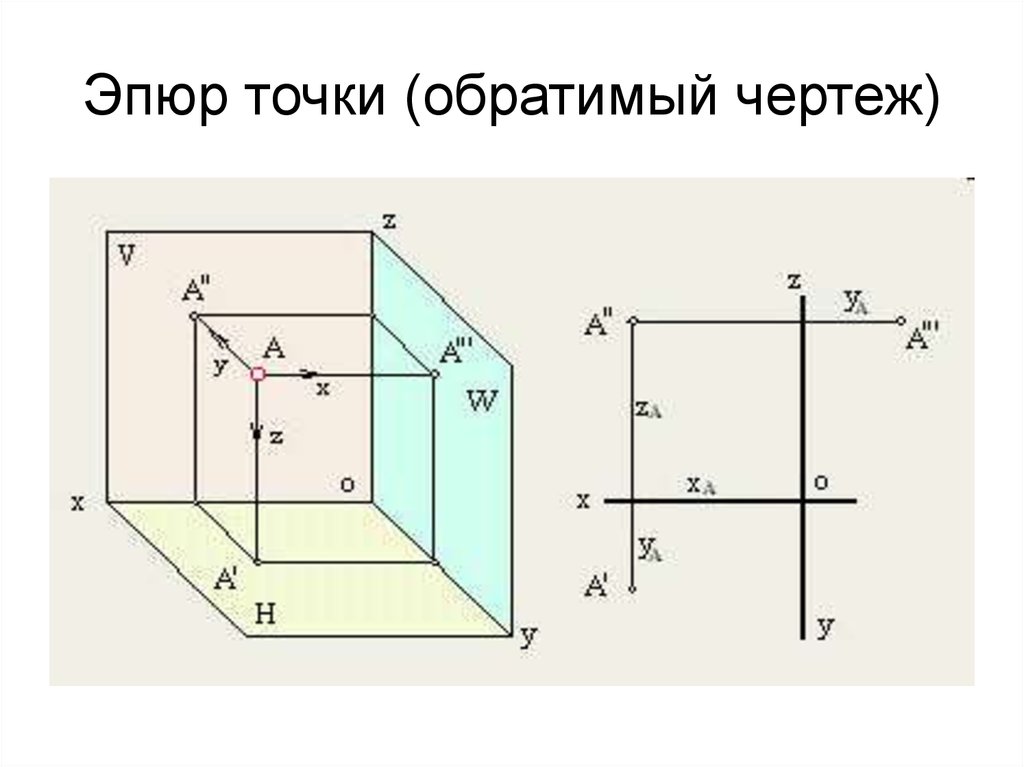
6. Эпюр точки (обратимый чертеж)

7. Пространственная модель координатных плоскостей проекций

• H (П1) - горизонтальная плоскость проекций
V (П2) - фронтальная плоскость проекций
W (П3) - профильная плоскость проекций
Плоскости проекций при пересечении
образуют оси координат:
x - ось абсцисс
y - ось ординат
z - ось аппликат
Оси координат при пересечении образуют
начало координат O (origo - начало).

8.

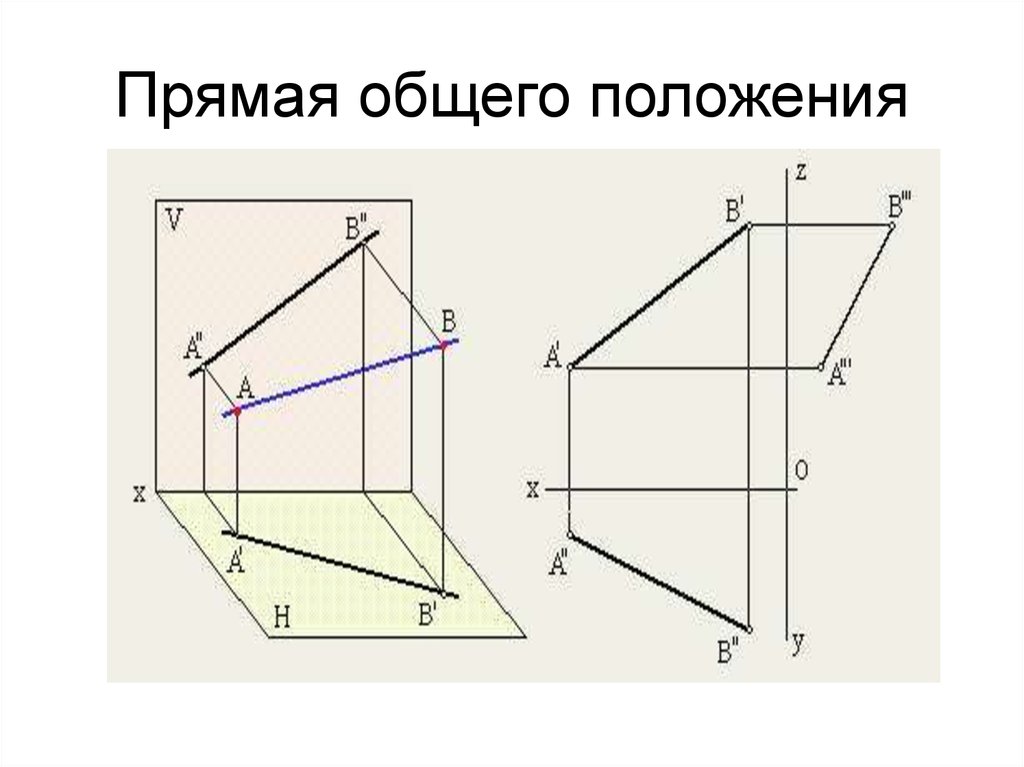
9. Прямая общего положения

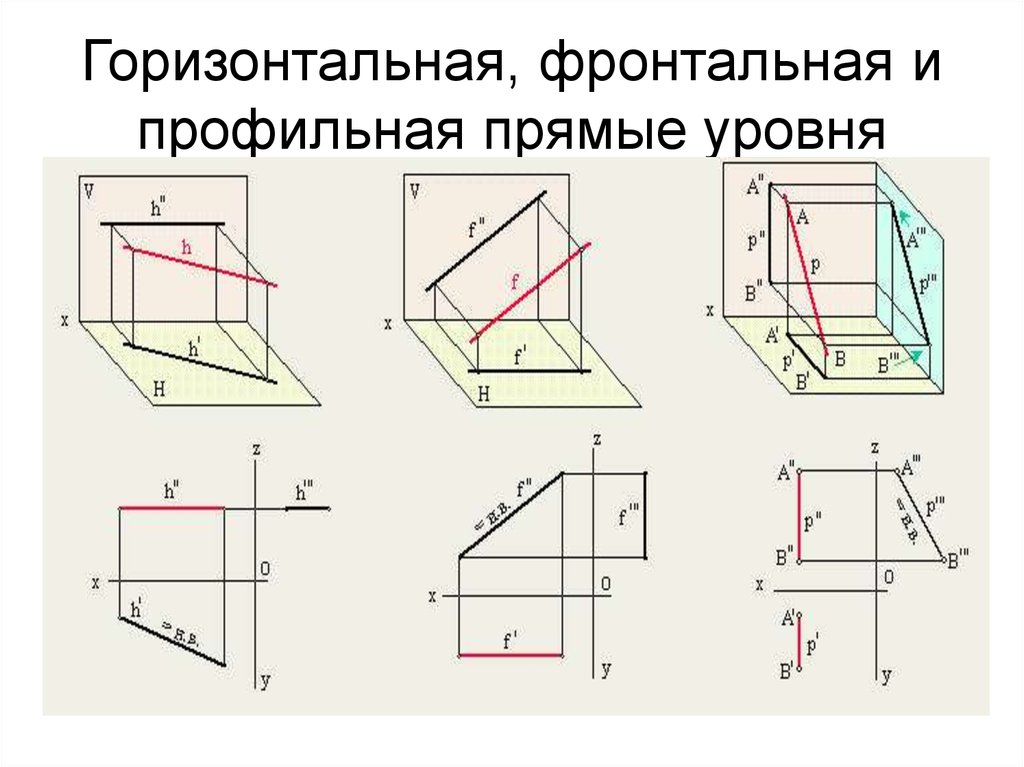
10. Горизонтальная, фронтальная и профильная прямые уровня

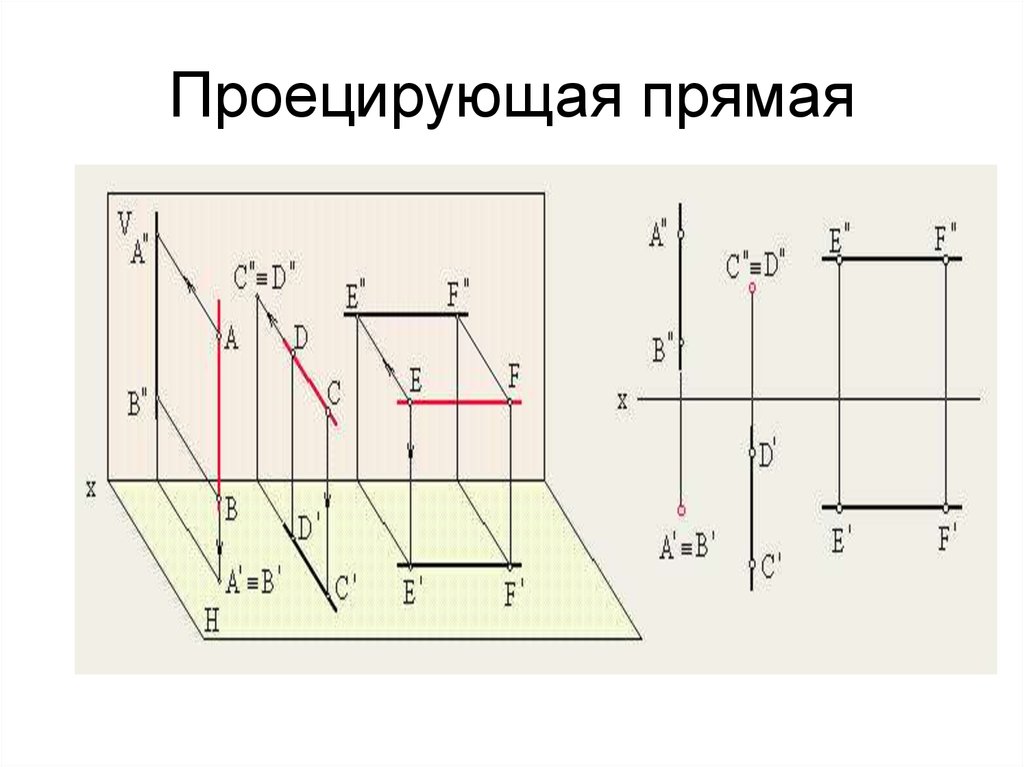
11. Проецирующая прямая

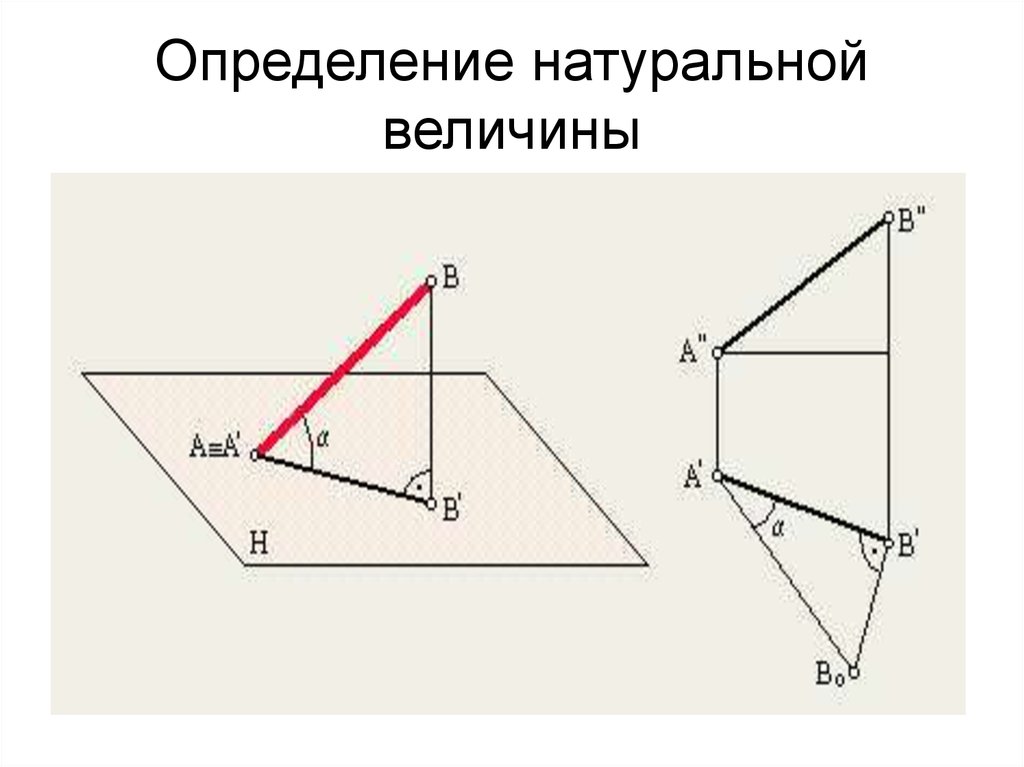
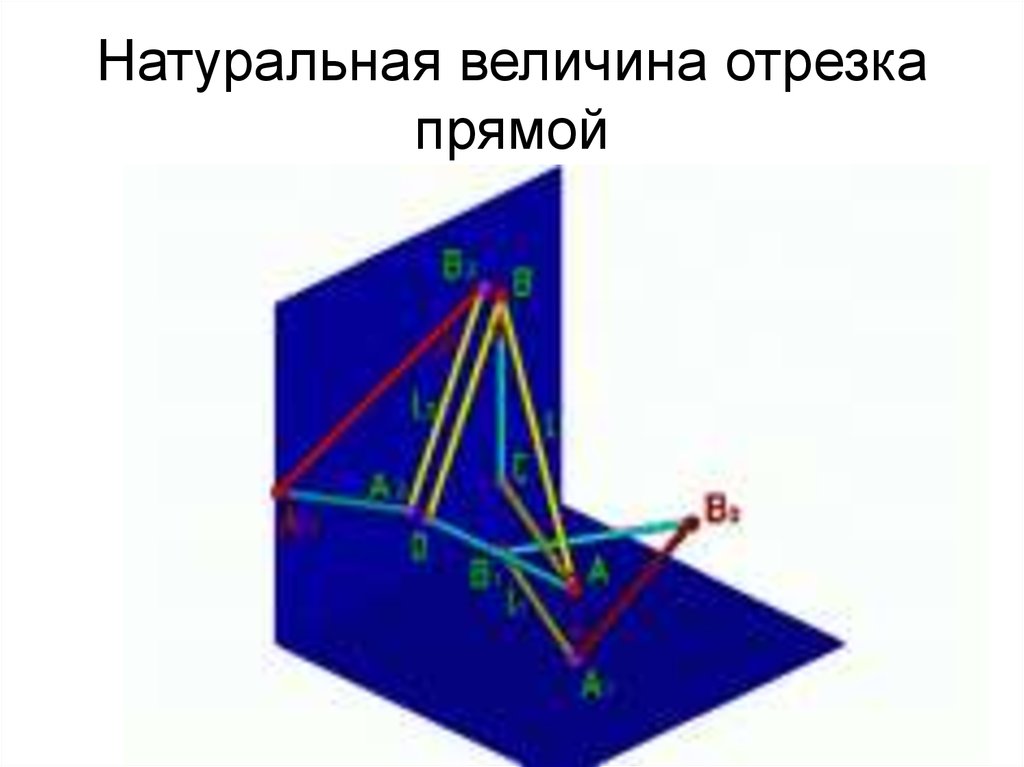
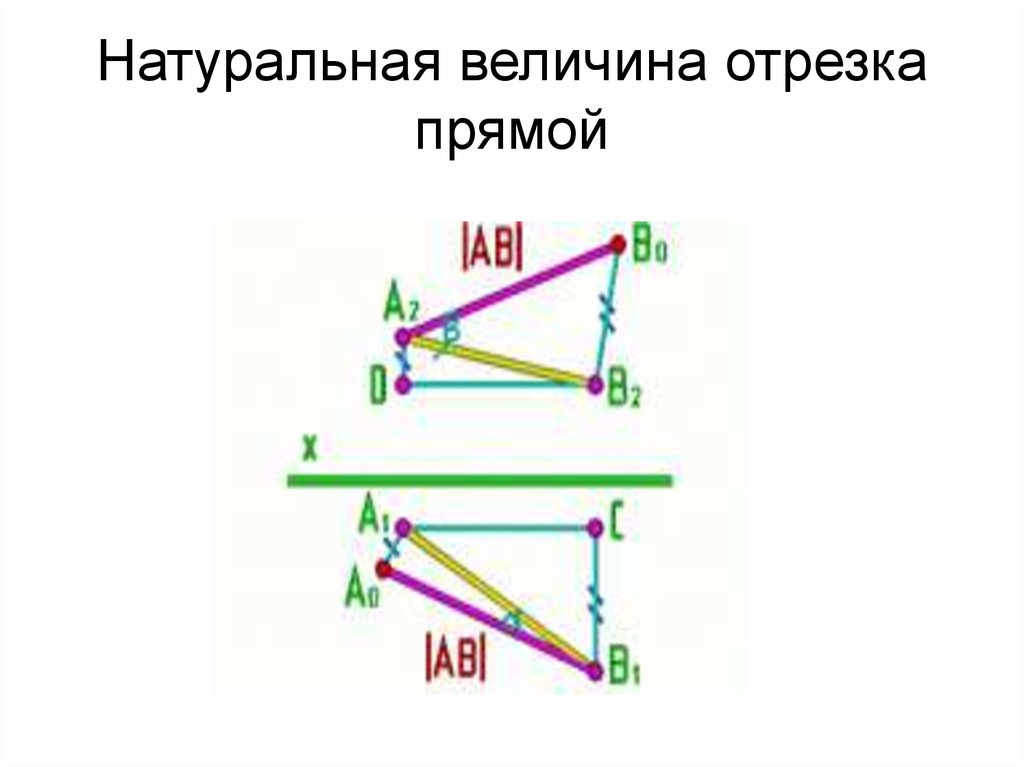
12. Определение натуральной величины

13. Натуральная величина отрезка прямой

14. Натуральная величина отрезка прямой

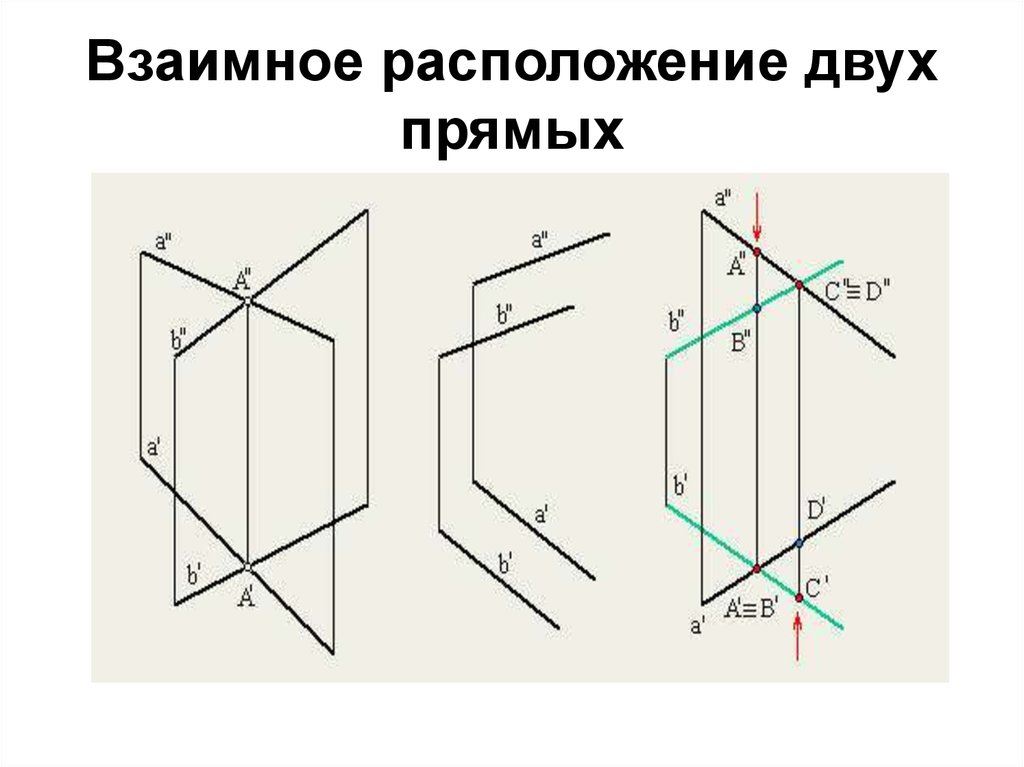
15. Взаимное расположение двух прямых

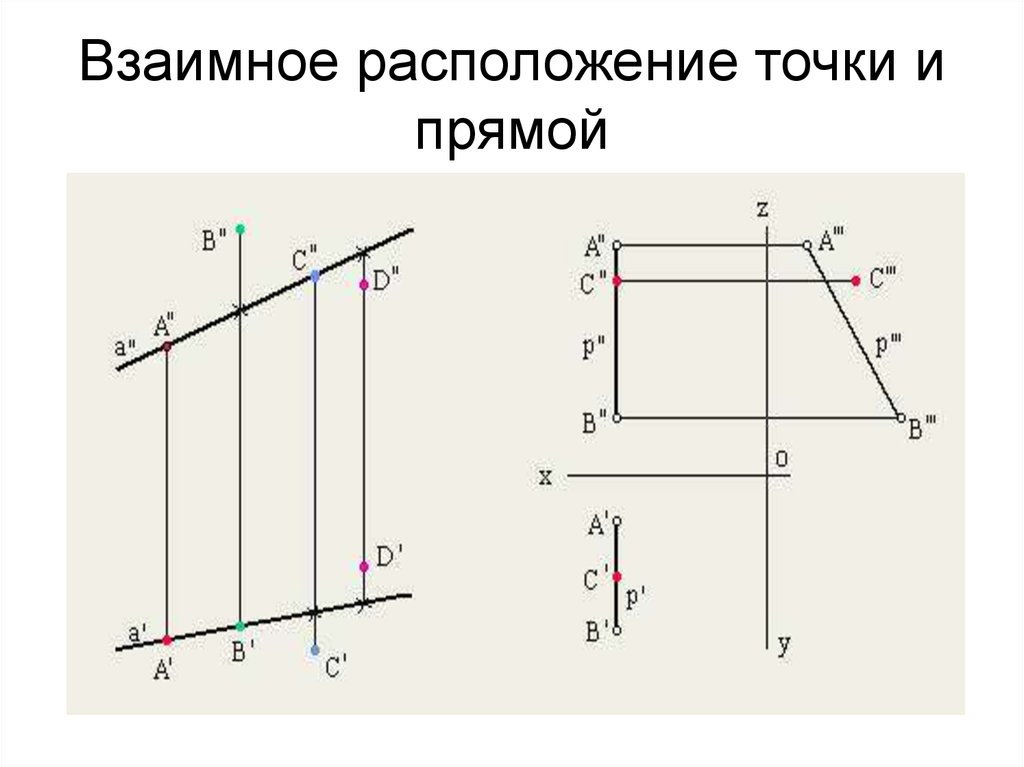
16. Взаимное расположение точки и прямой

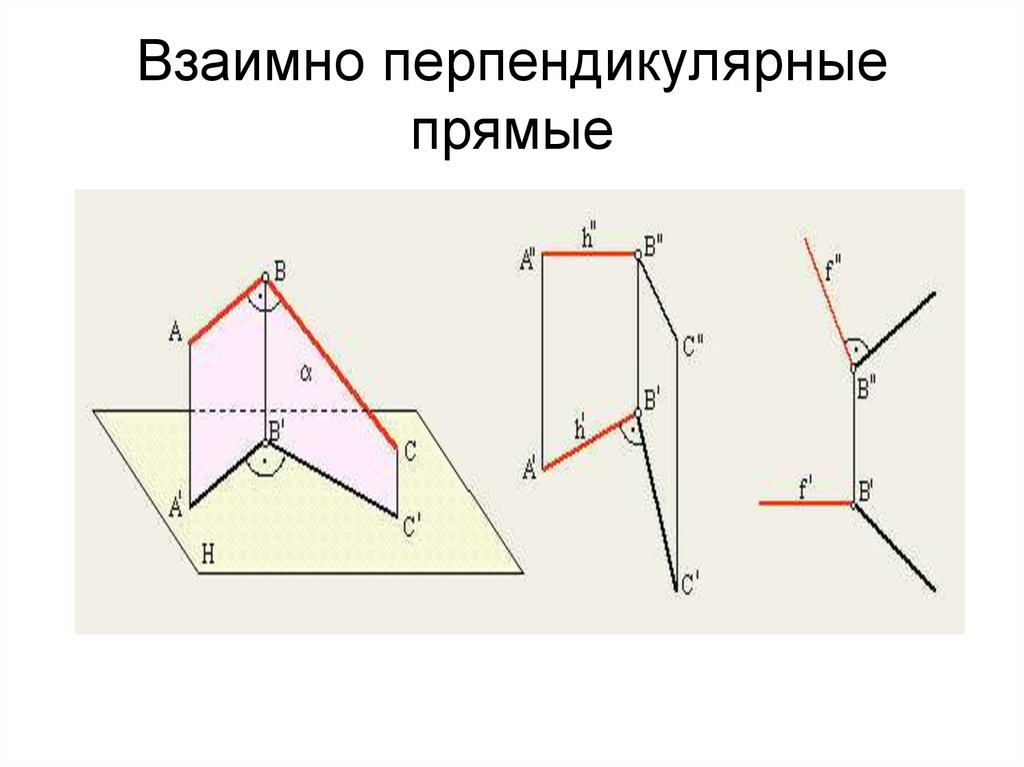
17. Взаимно перпендикулярные прямые

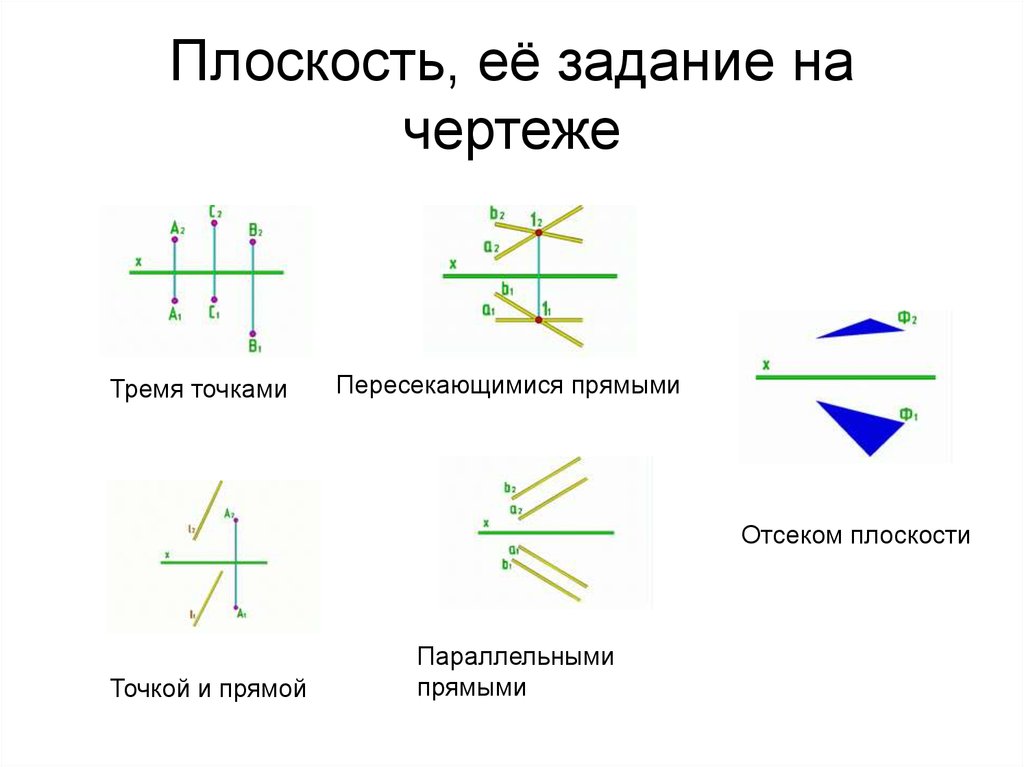
18. Плоскость, её задание на чертеже

Тремя точками
Пересекающимися прямыми
Отсеком плоскости
Точкой и прямой
Параллельными
прямыми

19. Плоскость общего положения Плоскость, у которой углы наклона к плоскостям проекций произвольны (не равны 0 или 90), называют

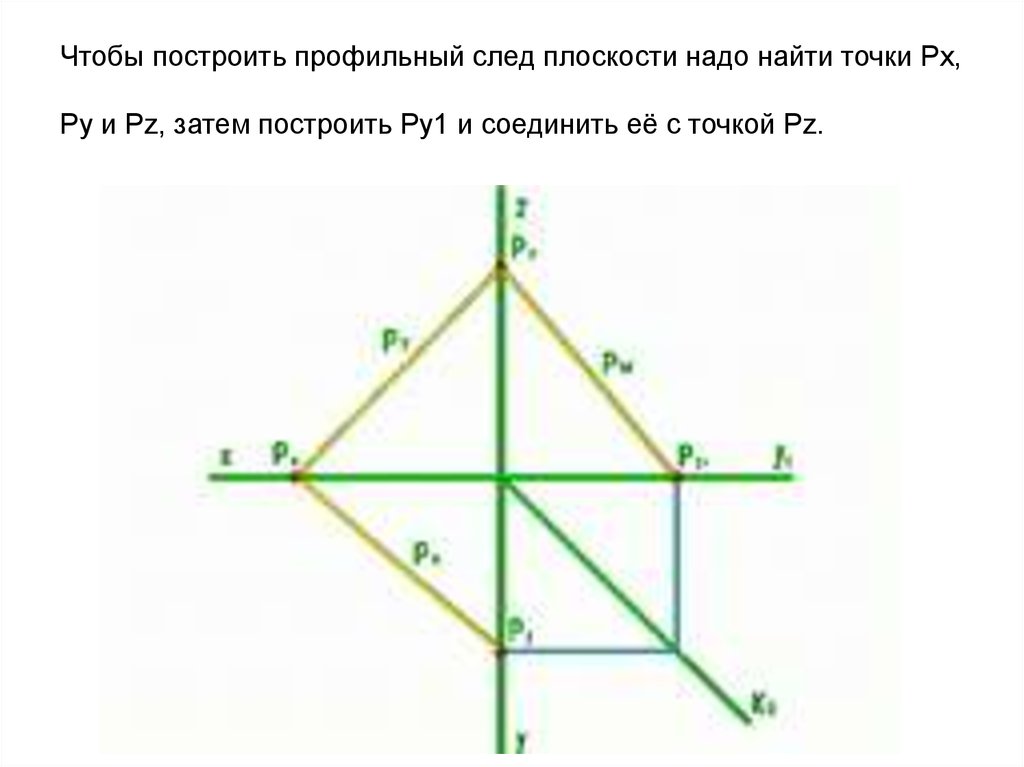
плоскостью общего положения

20. Чтобы построить профильный след плоскости надо найти точки Px, Py и Pz, затем построить Py1 и соединить её с точкой Pz.

21. Частные случаи расположения плоскостей

Плоскости, перпендикулярные к плоскостям проекции называют проецирующими.

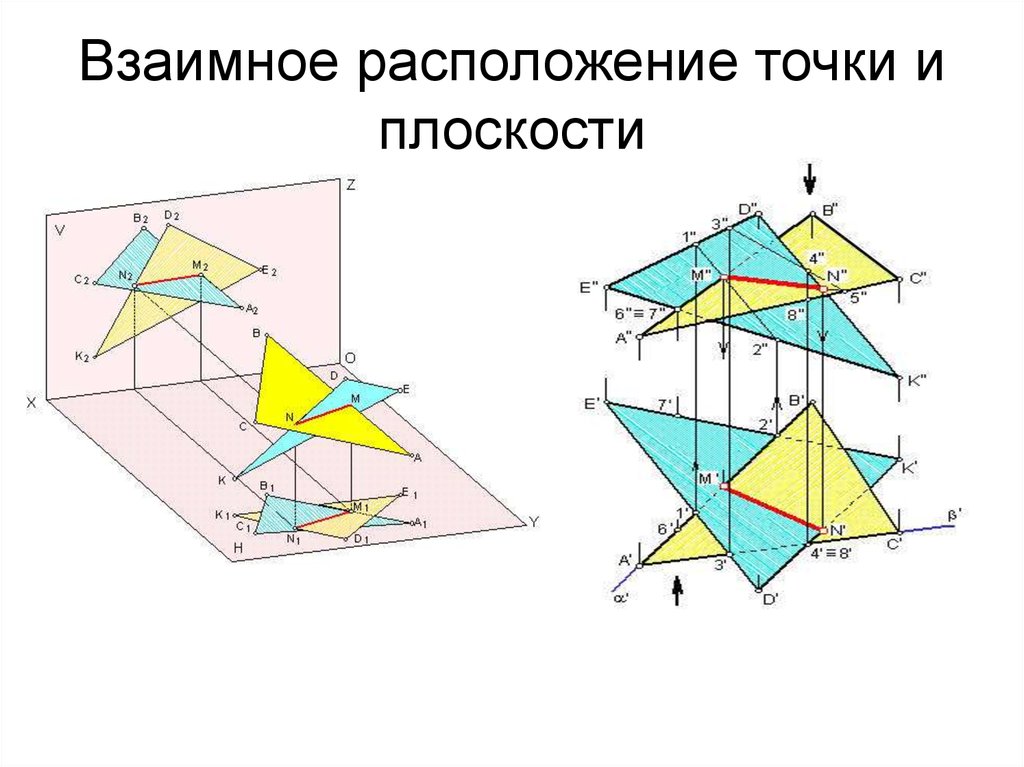
22. Взаимное расположение точки и плоскости

23. Линейчатые поверхности

• Линейчатая поверхность в общем случае
однозначно определяется тремя
направляющими линиями, т.е. при
перемещении по ним образующей.
• Линейчатые поверхности делятся на
развёртывающиеся и неразвёртывающиеся.
• К развёртывающимся относятся:
цилиндрические поверхности, конические
поверхности, поверхности с ребром возврата
(торса), призматические поверхности,
пирамидальные поверхности.

24. Линейчатые поверхности. Цилиндрическая поверхность

Цилиндрическая поверхность
образуется перемещением
прямолинейной образующей l по
криволинейной направляющей m,
причём образующая l остаётся
постоянно параллельной заданной
направляющей S.

25.

26.

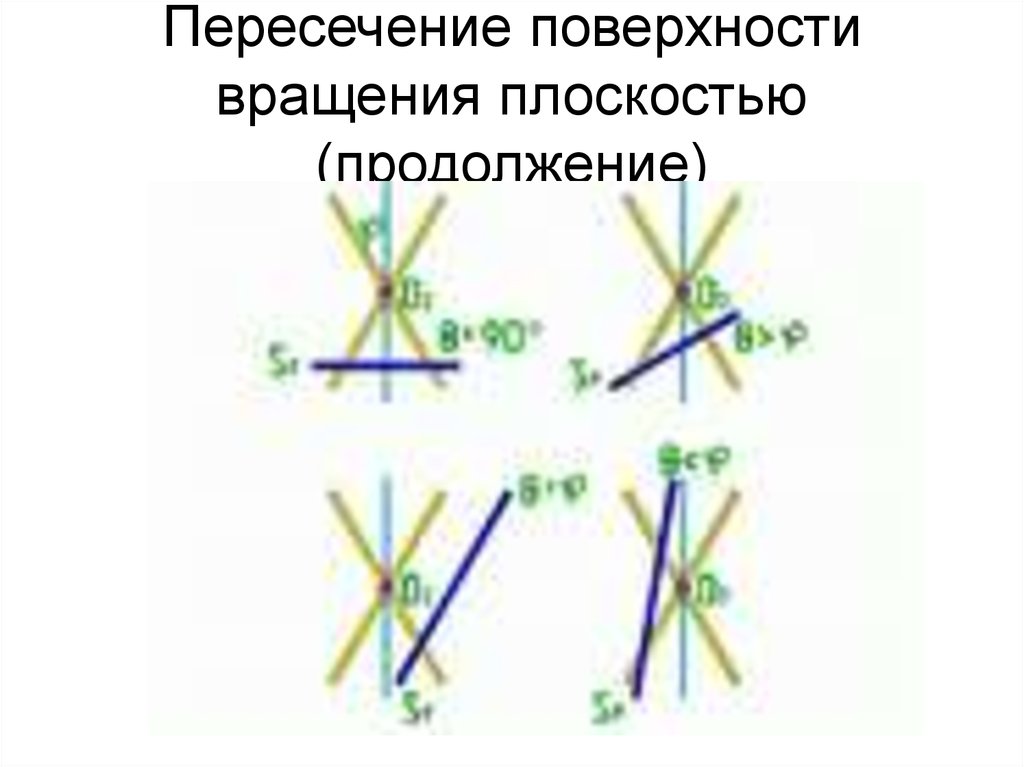
27. Пересечение поверхности вращения плоскостью

• При пересечении поверхности вращения плоскостью
могут получиться следующие кривые:
• а). Цилиндр вращения:
• эллипс - когда секущая плоскость и оси вращения.
• окружность - когда секущая плоскость оси вращения.
• две прямые - когда секущая плоскость оси вращения.
• прямая линия - когда секущая плоскость касательна к
поверхности цилиндра.
• б). Конус вращения:
• Поверхность прямого кругового конуса является
носителем кривых 2-го порядка: окружности, эллипса,
параболы, гиперболы, которые поэтому также
называются коническими сечениями.

28. Пересечение поверхности вращения плоскостью (продолжение)

29.

30.

31.

32.

33. Начертательная геометрия и инженерная графика

Часть 2

34.

35.

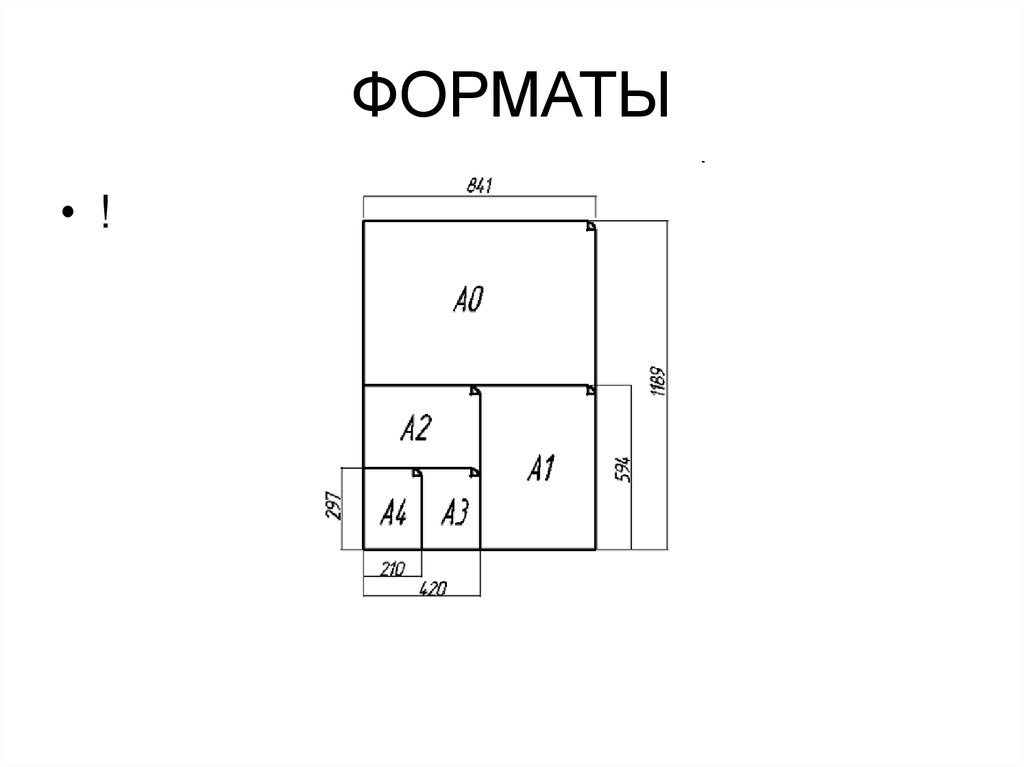
36. ФОРМАТЫ

• !

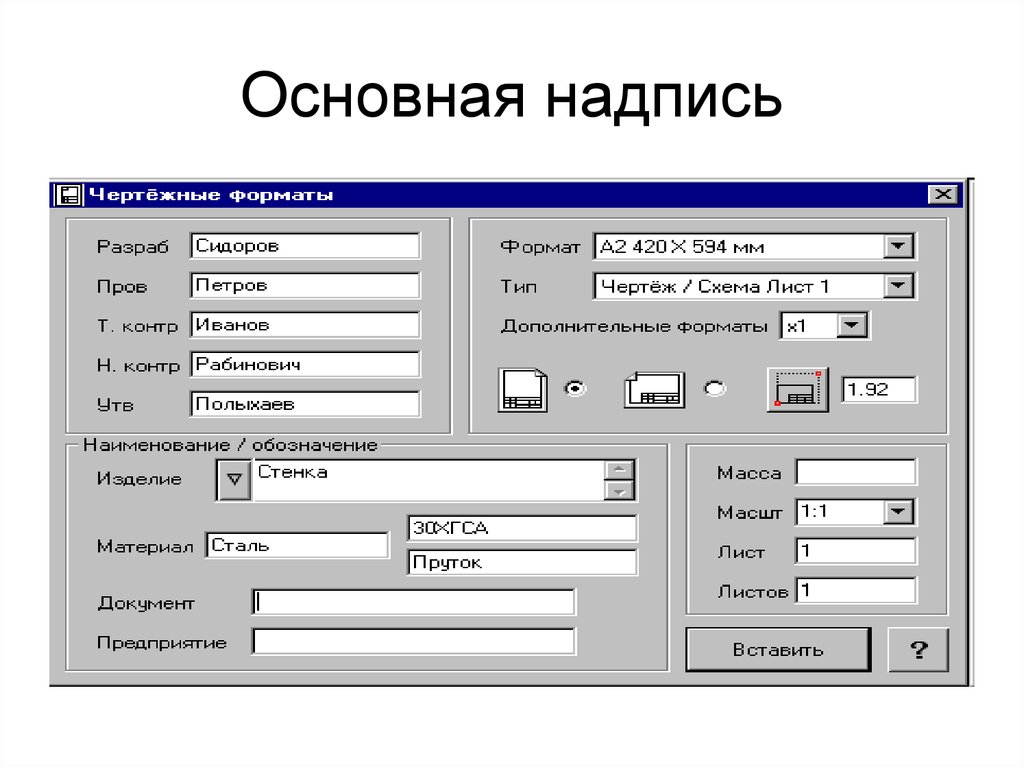
37. Основная надпись

38.

• Таблица 2Масштабы изображений
• выполнение изображениямасштаб следует
выбирать из рядов:в натуральную
величину1:1с
уменьшением1:2 1:2,5 1:4 1:5 1:10 1:15
1:20 1:25 1:40 1:50 1:75 1:100с
увеличением2:1 2,5:1 4:1 5:1 10:1 20:1
40:1 50:1 100:1