ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

1.

Чукин Андрей Владимирович, доцент
(кафедра ТФиПМ) Фт 136-138
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

2.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Т. I.
Механика – М.: Физматлит, 2004.
2. Арнольд В.И. Математические методы классической
механики. – М. Наука,2004.
3. Ольховский И. И. Курс теоретической механики для
физиков – М.: Лань, 2009.
4. Барановский В.Н., Левина Г.А. Теоретическая механика.
Учебное пособие – М.: Лань, 2003.
5. Киттель Ч., Найт У., Рудерман М. Механика.
Берклеевский курс физики. М.: Лань, 2005.
6. Вильке В.Г. Теоретическая механика. – М.: Лань, 2003.
7. Журавлев В.Ф. Основы теоретической механики. – М.:
Физматлит, 2001.

3.

ОСНОВНЫЕ ПОНЯТИЯ
Механика – наука, изучающая движение
объектов в его макропроявлениях.
• Материальная точка (МТ) – физическое тело,
размерами и формой которого можно
пренебречь при описании его движения.
• Система МТ (материальная система) –
совокупность
МТ,
движение
которых
взаимосвязано.

4.

ФИЗИЧЕСКАЯ СИСТЕМА ОТСЧЕТА
Положение МТ в пространстве определяет
радиус-вектор r(t), проведенный из начала
некоторой
системы
координат
(СК),
связанной с наблюдателем.
• В классической механике СК – ДПСК.
• Физическая система отсчета (СО) – система
координат и часы, имеющие в этой системе
«0» скорость.

5.

ПОСТУЛАТЫ НЬЮТОНА
Основа
классической
механики
–
постулаты Ньютона:
• Тело находится в состоянии покоя или
равномерного прямолинейного движения
до тех пор, пока действующие на него силы
не выведут его из этого состояния
(принцип инерции).

6.

ПОСТУЛАТЫ НЬЮТОНА
Изменение количества движения тела равно
силе, действующей на это тело и направлено
в сторону действия этой силы: dp / dt F ;
• ( p mv - импульс).
• Взаимодействующие тела действуют друг на
друга с силами равными по величине и
противоположно направленными F F .
• Действие на тело нескольких сил равно
геометрической сумме этих сил: F F .
ij
ji
i
i

7.

АБСОЛЮТНОЕ ПРОСТРАНСТВО, ВРЕМЯ
Для объяснения постулатов Ньютону пришлось
ввести понятия: абсолютного пространства (АП)
и абсолютного времени (АВ):
• АП – пространство безотносительное к чемулибо внешнему, остающееся всегда постоянным
и неподвижным.
• АВ – время безотносительное к чему-либо
внешнему, протекающее равномерно и иначе
называющееся длительностью.
• Дальнейшее развитие механики опровергло
существование в природе АП.
• Понятие АВ – лежит в основе классической
механики.

8.

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
(ПОГ) В природе существуют СО (назовем их
инерциальными – ИСО), в которых все законы
механики во все моменты времени одинаковы.
• Любая СО, движущаяся относительно ИСО
равномерно и прямолинейно, так же будет
инерциальной.
• В
частности, в ИСО одинаковы законы
«свободного движения» – выполняется принцип
инерции.
• В природе существует не уникальная, а целый
класс ИСО (в каждой из них выполняется
принцип инерции) – не существует АП.

9.

КРИТЕРИИ ИСО
Какая СО будет инерциальной (ИСО) ?
• В ИСО выполняются фундаментальные свойства
пространства и времени:
• Однородность
пространства – физическая
эквивалентность всех точек пространства.
• Однородность
времени
физическая
эквивалентность всех моментов времени.
• Изотропность
пространства – физическая
эквивалентность
всех
направлений
пространства (отсутствие в пространстве
выделенного направления).

10.

ПРИНЦИП ДЕТЕРМИНИРОВАННОСТИ
НЬЮТОНА
Состояние (фаза) механической системы –
информация о координатах и скоростях
(импульсах) всех материальных точек МС в
заданный момент времени.
• ПДН:
Если известно состояние МС в
начальный момент времени, то дальнейшая
динамика определяется характеристической
функцией (ХФ) этой системы.
• Другими словами: координаты и скорости МТ
однозначно связаны с ускорением МТ.

11.

ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ
Характеристическая функция (ХФ) определяет
механическую систему как динамическую (в
классической механике ХФ – сила F.
• Существуют другие подходы к механике
(аналитическая
механика
Лагранжа,
Гамильтона).
• В каждом подходе – у механических систем
своя ХФ: L=T-U (функция Лагранжа); Н=T+U
(функция Гамильтона).

12.

УРАВНЕНИЕ ДВИЖЕНИЯ МТ
Математическое соотношение, связывающее
между собой координаты и скорости МТ с одной
стороны и ускорение с другой, называется
уравнением движения (УД):
d
P m r F r, r,t
dt
С точки зрения математики
УД –
дифференциальное уравнение второго порядка
относительно координат МТ - r(t).
• Зависимость координат МТ от времени r=r(t)–
закон движения – основная задача механики.

13.

СИЛОВОЕ ПОЛЕ
СП: часть пространства в каждой точке которого
на помещенную в него МТ действует сила строго
определенная по величине и направлению.
• Относительно движения МТ, в общем случае,
сила может зависеть от координат, скоростей, и
времени: F=F(r,v,t).
• Если сила не зависит явно от времени – силовое
поле стационарное (F=F(r,v)).
• Если сила не зависит явно от скорости – силовое
поле позиционное (F=F(r,t)) .

14.

СТАЦИОНАРНЫЕ ПОЛЯ
Среди всех F=F(r) особое значение имеют поля,
работа сил которых по перемещению МТ не
зависит от формы траектории, а определяется
только начальным и конечным положениями
точки в пространстве – консервативные
(потенциальные) поля.
• Для
того
чтобы
силовое
поле
было
потенциальным должна существовать функция
U(x,y,z), т.ч. Fx=-∂U/∂x, Fy=-∂U/∂y, Fz=-∂U/∂z
F grad U

15.

ОДНОМЕРНОЕ ДВИЖЕНИЕ
Движение МТ, при котором изменяется
только одна декартова координата,
например х
• Пусть МТ движется вдоль оси Ох под
действием консервативной силы F(x).
Уравнение движения:
dU
m x F ( x)
dx

16.

ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
Умножим обе части уравнения на скорость МТ : x
dx
dx dU
mx
dt
dt dx
Занесем m x под знак дифференциала:
2
d mx
dU
dt 2
dt
Перенесем правую часть выражения влево и
объединим выражение под одну производную:
d mv 2
U
(
x
)
0
dt 2

17.

ПЕРВЫЙ ИНТЕГРАЛ ДВИЖЕНИЯ
d mv 2
U ( x) 0
dt 2
Выражение в скобках – константа.
mv 2
U ( x) Const E
2
Закон сохранения энергии (ЗСЭ)
Комбинация координат и скоростей МТ,
сохраняющаяся в процессе движения –
интеграл движения.
• Первый интеграл движения консервативной
системы
–
полная
энергия:
E=T+U

18.

ЗАКОН ДВИЖЕНИЯ
Выразим скорость МТ из ЗСЭ:
dx
2
v
E U x
dt
m
Выберем знак «+» если движение МТ происходит в сторону
увеличения координаты, знак «-» в противном случае.
Отсюда:
dt
dx
2
E U x
m
Т.о. можно получить зависимость координаты
от времени, т.е. закон движения:
t t0
dx
2
E U x
m

19.

ИНФИНИТНОЕ ДВИЖЕНИЕ Е>U(X)
Допустим, потенциальная энергия системы имеет максимум:
U(x)
E=Const
x
При этом уровень полной энергии «везде» превышает U(x)
mv 2
U ( x) Const E
2
Из ЗСЭ
следует, что в данной системе движение ничем не ограничено
(движение инфинитное) и возможно для любых х:
Область возможного движения (ОВД): x ;

20.

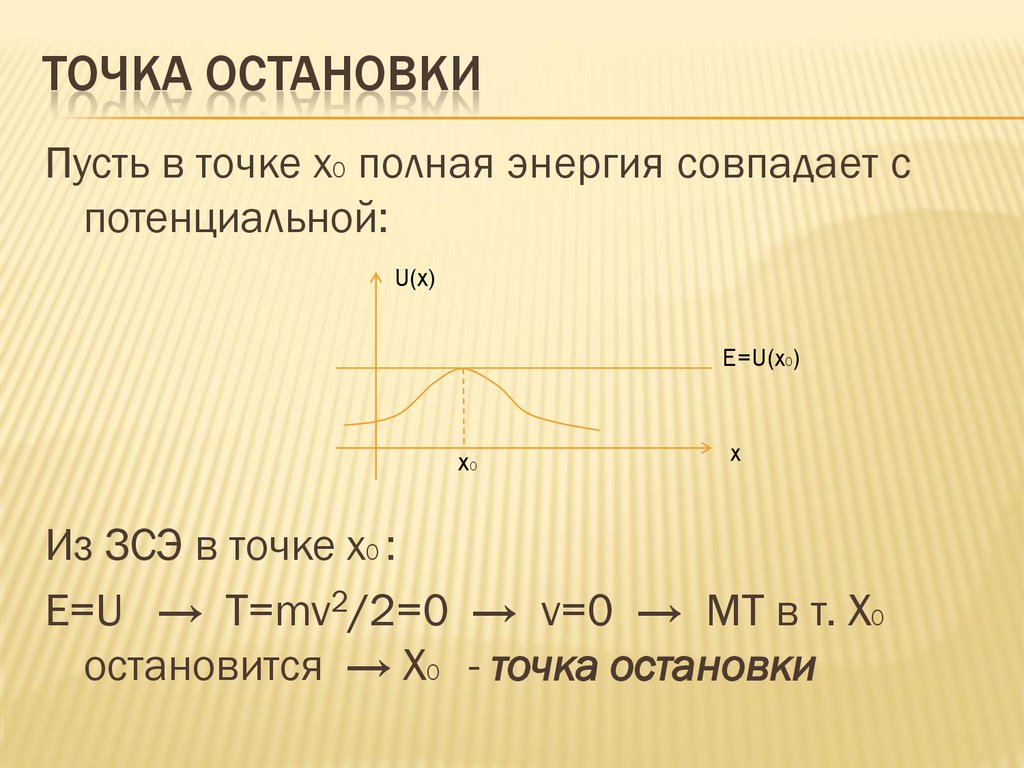
ТОЧКА ОСТАНОВКИ
Пусть в точке x0 полная энергия совпадает с
потенциальной:
U(x)
E=U(x0)
x0
x
Из ЗСЭ в точке x0 :
E=U → T=mv2/2=0 → v=0 → МТ в т. X0
остановится → X0 - точка остановки

21.

ОБЛАСТЬ ЗАПРЕЩЕННОГО ДВИЖЕНИЯ
Пусть уровень полной энергии пересекает график
U(x) в точках х1 и х2:
U(x)
x1
x2
x
Из ЗСЭ в области x1<x<x2 E<U → T=mv2/2<0
чего в классической механике быть не может!
Область x1<x<x2
- область запрещенного
движения (ОЗД).
• x1<x<x2 - точки остановки
x ( ; x1 ];[ x2 ; )
• ОВД:

22.

ИНФИНИТНОЕ ДВИЖЕНИЕ: Н.У. X(0)<X1; V(0)>0
МТ движется от x(0) в сторону увеличения
координаты. Согласно ЗСЭ T+U=E=Const
При движении «в горку» U↑ → T↓ → v(t)↓
U(x)
E
v
V(0)>0
X(0)
x1
x2
x
2
E U x
m
В т. x1 U=E → v(x1)=0 → МТ «остановится»,
«развернется» и «покатится с горки» при этом:
ОВД: x ( ; x1 ]
v
2
E U x
m

23.

ИНФИНИТНОЕ ДВИЖЕНИЕ: Н.У. X(0)>X2; V(0)>0
МТ движется от x(0) в сторону увеличения
координаты. Согласно ЗСЭ T+U=E=Const
При движении «с горки» U↓ → T↑ → v(t)↑
U(x)
E
v
V(0)>0
x1
x2 X(0)
x
2
E U x
m
«Справа» движение системы ничем не ограничено –
МТ →∞
ОВД: x [ x(0); )

24.

ИНФИНИТНОЕ ДВИЖЕНИЕ
Если н.у. x(0)>x2; v(0)<0 или x(0)<x1; v(0)<0
• Ситуация будет аналогична рассмотренным
выше случаям (зеркально).
• ОВД: x [ x2 ; )
• ОВД: x ( ; x(0)]
• Закон движения (инфинитного) определяется
выражением:
t t0
dx
2
E U x
m

25.

ФИНИТНОЕ ДВИЖЕНИЕ
Если потенциальная энергия имеет локальный
минимум, то возникает финитное (ограниченное)
U(x)
движение:
Е
x1 x(0)
x2
x
Пусть н.у.: x1<x(0)<x2; v(0)>0
МТ от x(0) [U↑,T↓] → x2(т.остановки) → «разворот» →
x(0) [U↓,T↑] → x1 (т.остановки) [U↑,T↓] → «разворот»
→ процесс повторяется!!!
ОВД : x1<x<x2

26.

ФАЗОВОЕ ПРОСТРАНСТВО МЕХАНИЧЕСКОЙ
СИСТЕМЫ
Фаза – состояние системы (информация о
координатах и скоростях)
• Фазовое
пространство – пространство
состояний.
• Для
одномерного
движения
фазовое
пространство – фазовая плоскость с
координатами: ( x; x )
• Каждая точка этой плоскости определяет
состояние (фазу) системы в какой-то момент
времени.

27.

ФАЗОВЫЙ ПОРТРЕТ
С течением времени координаты и скорости
движущихся МТ изменяются →
• МТ движется по фазовой плоскости →
Возникает фазовая траектория (фазовый
портрет) механической системы.
• Обычно фазовую плоскость изображают под
графиком потенциальной энергии.

28.

МЕТОД ПОТЕНЦИАЛЬНЫХ КРИВЫХ И
ФАЗОВЫХ ТРАЕКТОРИЙ
U(x)
E2
E1
x
x
x

29.

ПЕРИОД ФИНИТНОГО ДВИЖЕНИЯ
Финитное
движение
периодически
повторяется,
поэтому
для
финитного
движения обычно находят не закон
движения, а период.
• Период движения – это удвоенное время
движения между точками остановки:
x2
T 2
x1
dx
2
E U x
m
x2
2m
x1
dx
E U ( x)