графы

1.

Графы. Применение теории графов
при решении задач

2.

Графы. Применение теории графов при
решении задач
Можно ли нарисовать изображенный на рисунке граф не
отрывая карандаш от бумаги и проводя каждое ребро ровно
один раз?
Решение. Если мы будем рисовать граф так, как сказано в условии, то в
каждую вершину, кроме начальной и конечной, мы войдем столько же раз,
сколько выйдем из нее. То есть все вершины графа, кроме двух должны
быть четными. В нашем же графе имеется три нечетные вершины, поэтому
его нельзя нарисовать указанным в условии способом.

3.

Графы. Применение теории графов при
решении задач
Между девятью планетами солнечной системы установлено
космическое сообщение. Рейсовые ракеты летают по следующим
маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон;
Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн;
Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь
на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты
ракет – линиями.
Теперь сразу видно, что долететь с Земли до Марса нельзя.
Г
Р
А
Ф
Ы

4.

Графы. Применение теории графов при
решении задач
Доска имеет форму двойного креста, который получается, если из
квадрата 4x4 убрать угловые клетки.
Можно ли обойти ее ходом шахматного коня и вернуться на исходную
клетку, побывав на всех клетках ровно по одному разу ?
“
Решение: Занумеруем последовательно клетки доски:
А теперь с помощью рисунка покажем, что
такой обход таблицы, как указано в условии,
возможен:

5.

Графы. Применение теории графов при
решении задач
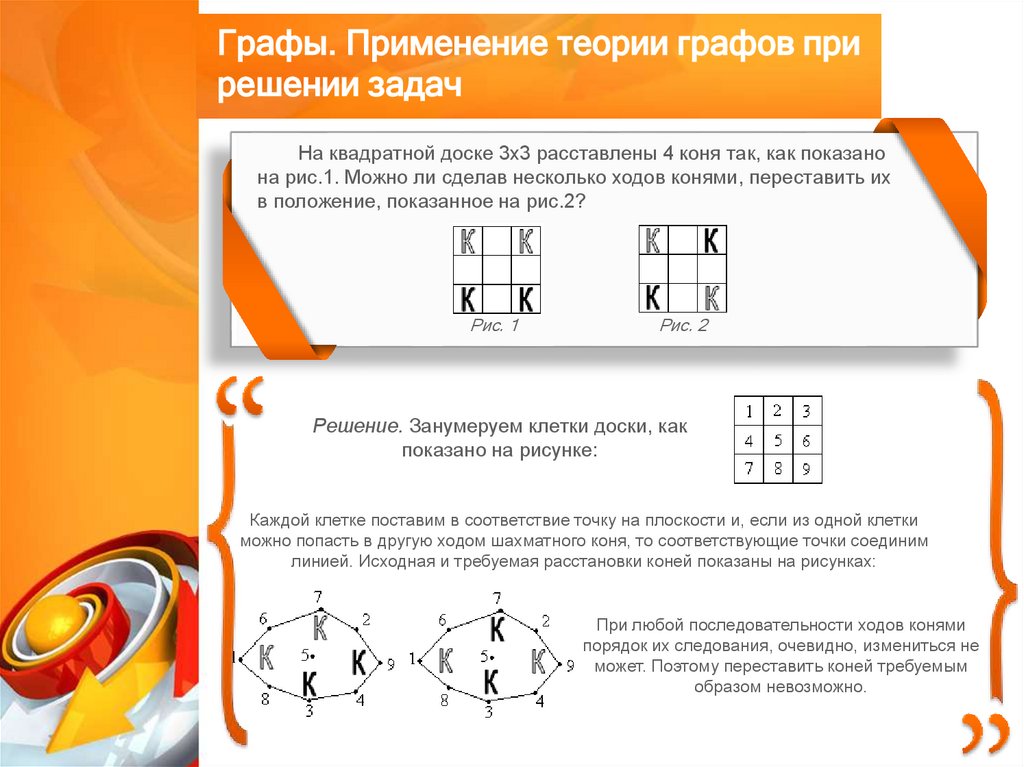
На квадратной доске 3x3 расставлены 4 коня так, как показано
на рис.1. Можно ли сделав несколько ходов конями, переставить их
в положение, показанное на рис.2?
Рис. 1
Рис. 2
Решение. Занумеруем клетки доски, как
показано на рисунке:
Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки
можно попасть в другую ходом шахматного коня, то соответствующие точки соединим
линией. Исходная и требуемая расстановки коней показаны на рисунках:
При любой последовательности ходов конями
порядок их следования, очевидно, измениться не
может. Поэтому переставить коней требуемым
образом невозможно.

6.

Графы. Применение теории графов при
решении задач
Мы рассмотрели непохожие задачи. Однако решения этих задач
объединяет общая идея – графическое представление решения.
При этом и картинки, нарисованные для каждой задачи,
оказались похожими: каждая картинка – это несколько точек,
некоторые из которых соединены линиями.
Г
Р
А
Ф
Ы
Г
Р
А
Ф
Ы
Г
Р
А
Ф
Ы

7.

Графы. Применение теории графов при
решении задач
Граф – это совокупность объектов со связями между ними. Объекты
рассматриваются как вершины, или узлы графа, а связи – как дуги, или
ребра. Ребро графа называется дугой, если одна из его вершин считается
начальной, другая – конечной.
Вершина
графа
Вершина
графа
Б
А
ребро графа
Вершина
графа
В
Дуга графа
Основные элементы графа состоят из вершин графа, ребер графа и др.
графа. Сочетание этих элементов определяет понятия:
неориентированный граф, ориентированный граф и смешанный граф.

8.

Графы. Применение теории графов при
решении задач
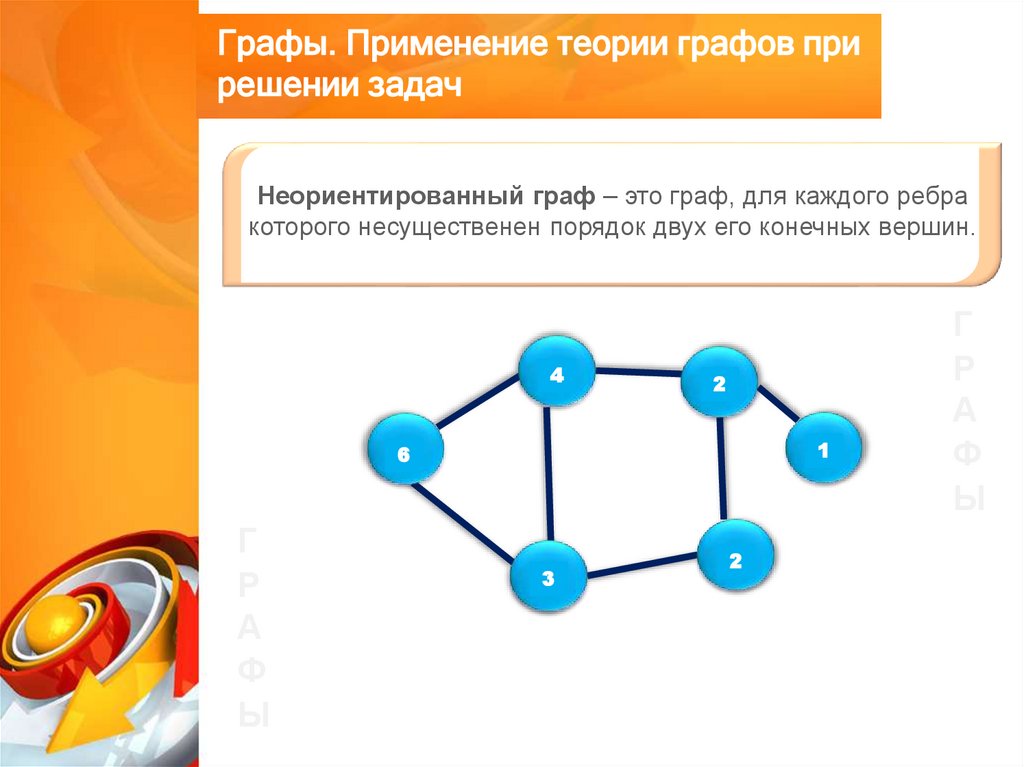
Неориентированный граф – это граф, для каждого ребра
которого несущественен порядок двух его конечных вершин.
4
2
1
6
Г
Р
А
Ф
Ы
3
2
Г
Р
А
Ф
Ы

9.

Графы. Применение теории графов при
решении задач
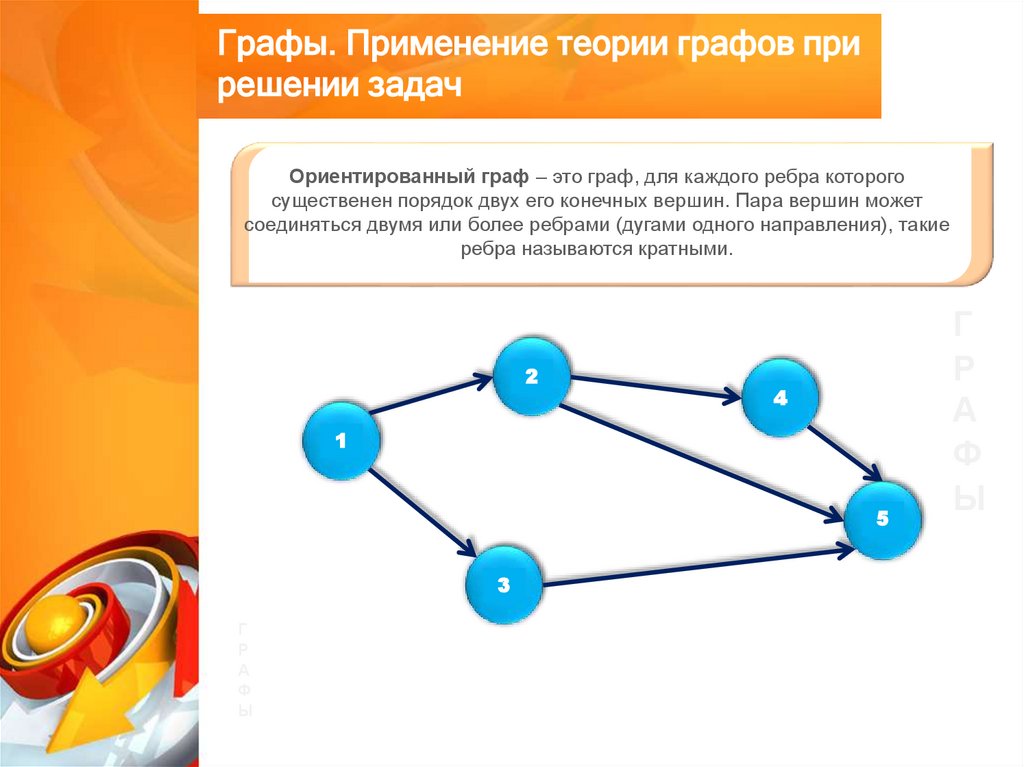
Ориентированный граф – это граф, для каждого ребра которого
существенен порядок двух его конечных вершин. Пара вершин может
соединяться двумя или более ребрами (дугами одного направления), такие
ребра называются кратными.
2
4
1
5
3
Г
Р
А
Ф
Ы
Г
Р
А
Ф
Ы

10.

Графы. Применение теории графов при
решении задач
Смешанный граф – это граф, содержащий как ориентированные, так и
неориентированных ребра. Любой из перечисленных видов графа может
содержать одно или несколько ребер, у которых оба конца сходятся в одной
вершине, такие ребра называются петлями.
2
1
2
1
5
5
3
4
3
4
Путем в графе называют конечную последовательность вершин, в которой
каждая вершина соединена ребром с последующей в последовательности
вершин. Длиной пути во взвешенном графе называют сумму длин звеньев
этого пути. Количество k ребер в пути называется длиной пути. Путь
называют циклом, если в нем первая и последняя вершины совпадают.

11.

Графы. Применение теории графов при
решении задач
На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M.
По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города A в город M?
C
B
A
Г
Р
А
Ф
Ы
K
Г
Р
А
M
Ф
Ы
E
F
G
H
L

12.

Графы. Применение теории графов при
решении задач
Начнем считать количество путей с конца маршрута – с города М.
NX — количество различных путей из города А в город X, N — общее
число путей. В "М" можно приехать из C, F, L или H, поэтому
N = NM = NC + NF + N H + N L (1)
C
F
Г
Р
А
Ф
Ы
M
H
L
Г
Р
А
Ф
Ы

13.

Графы. Применение теории графов при
решении задач
Аналогично:
NC = NB;
NF = NE;
NH = NF + NG;
NL = NK.
Г
Р
А
Ф
Ы
B
C
E
A
F
M
G
K
H
L
Добавим еще вершины:
NB = NA = 1;
NE = NB + NA + NG = 1 + 1 + 2 = 4;
NG = NA + NK = 1 + 1 = 2;
NK = NA = 1.
Г
Р
А
Ф
ЫГ
Р
А
Ф
Ы

14.

Графы. Применение теории графов при
решении задач
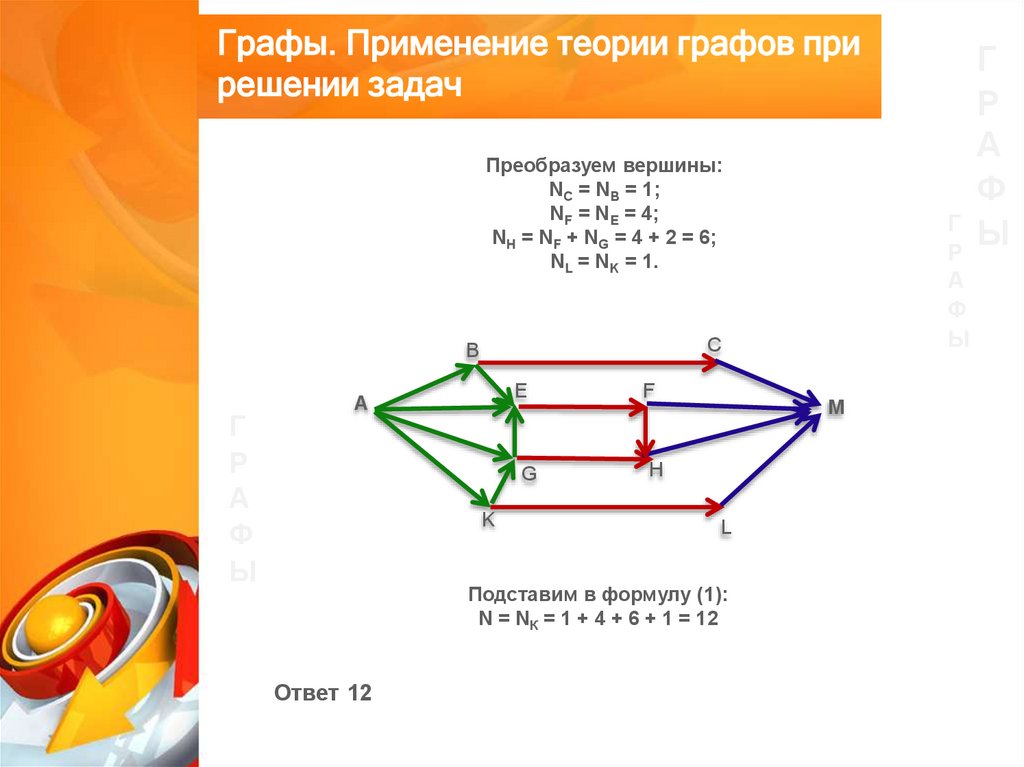
Преобразуем вершины:
NC = NB = 1;
NF = NE = 4;
NH = NF + NG = 4 + 2 = 6;
NL = NK = 1.
Г
Р
А
Ф
Ы
A
K
E
F
G
H
M
L
Подставим в формулу (1):
N = NК = 1 + 4 + 6 + 1 = 12
Ответ 12
А
Ф
Ы
C
B
Г
Р
А
Ф
Г
Ы
Р

15.

Графы. Применение теории графов при
решении задач
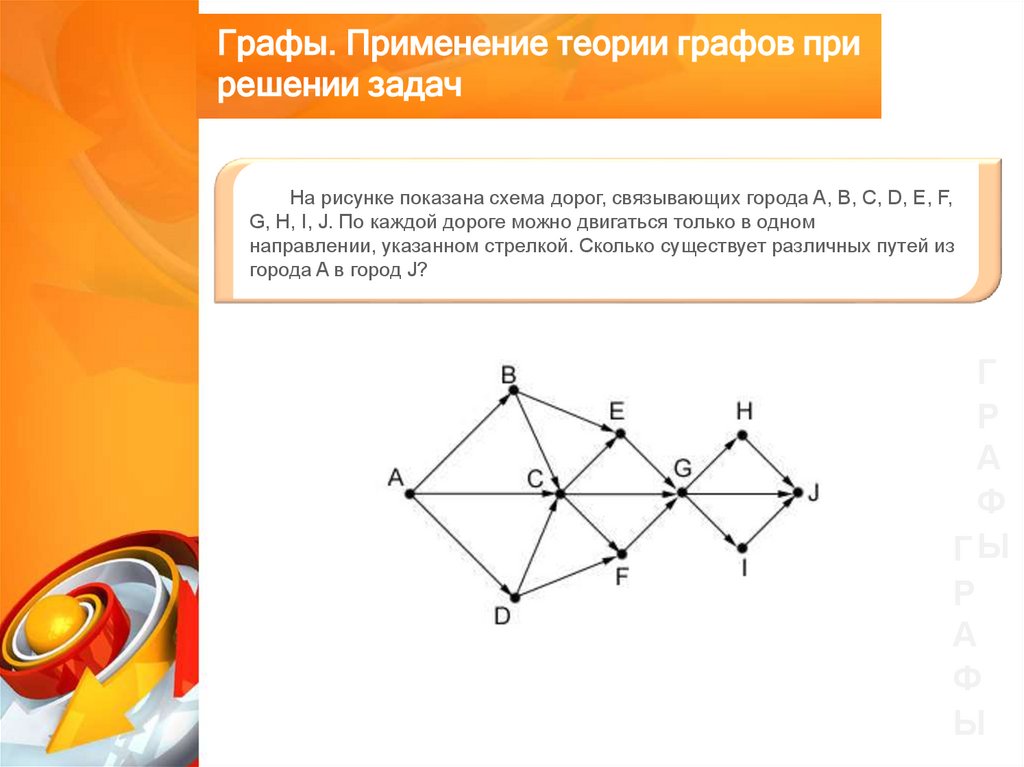
На рисунке показана схема дорог, связывающих города A, B, C, D, E, F,
G, H, I, J. По каждой дороге можно двигаться только в одном
направлении, указанном стрелкой. Сколько существует различных путей из
города A в город J?
Г
Р
А
Ф
ГЫ
Р
А
Ф
Ы

16.

Графы. Применение теории графов при
решении задач
Решение:
Обратите внимание, чтобы попасть в пункт J из пунктов A..F, нужно
обязательно пройти через пункт G, из которого существует три пути в пункт J.
То есть мы можем найти все пути из A в G, и умножить их на 3.
Для решения построим граф:
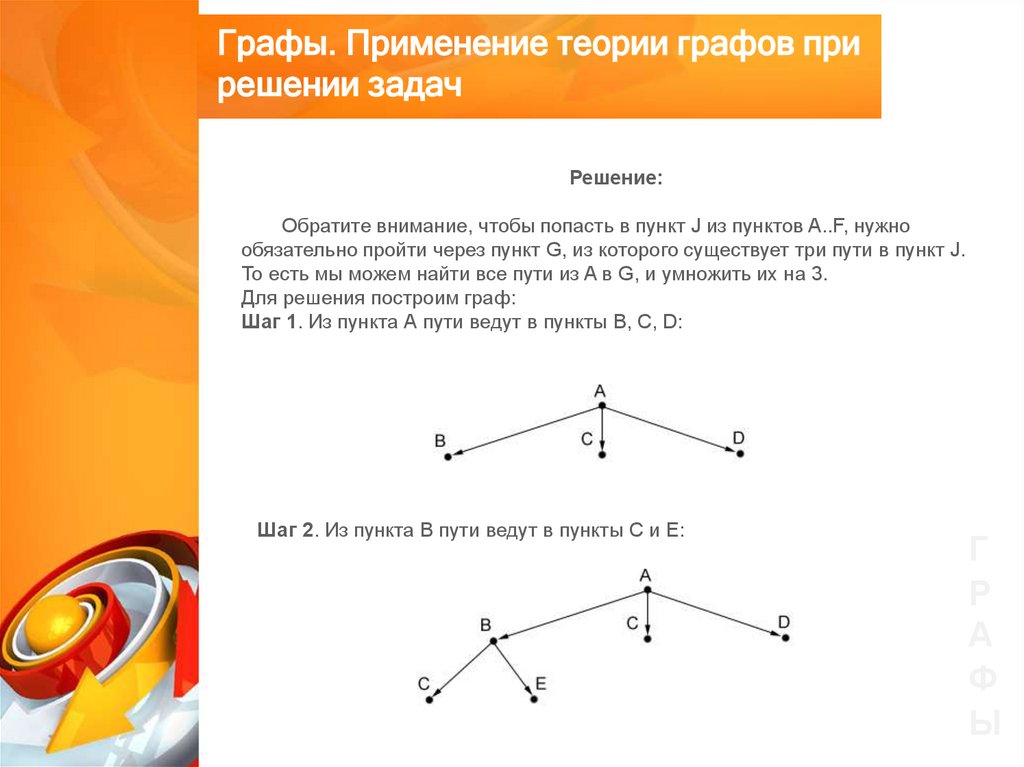
Шаг 1. Из пункта А пути ведут в пункты B, C, D:
Шаг 2. Из пункта B пути ведут в пункты C и E:
Г
Р
А
Ф
Ы

17.

Графы. Применение теории графов при
решении задач
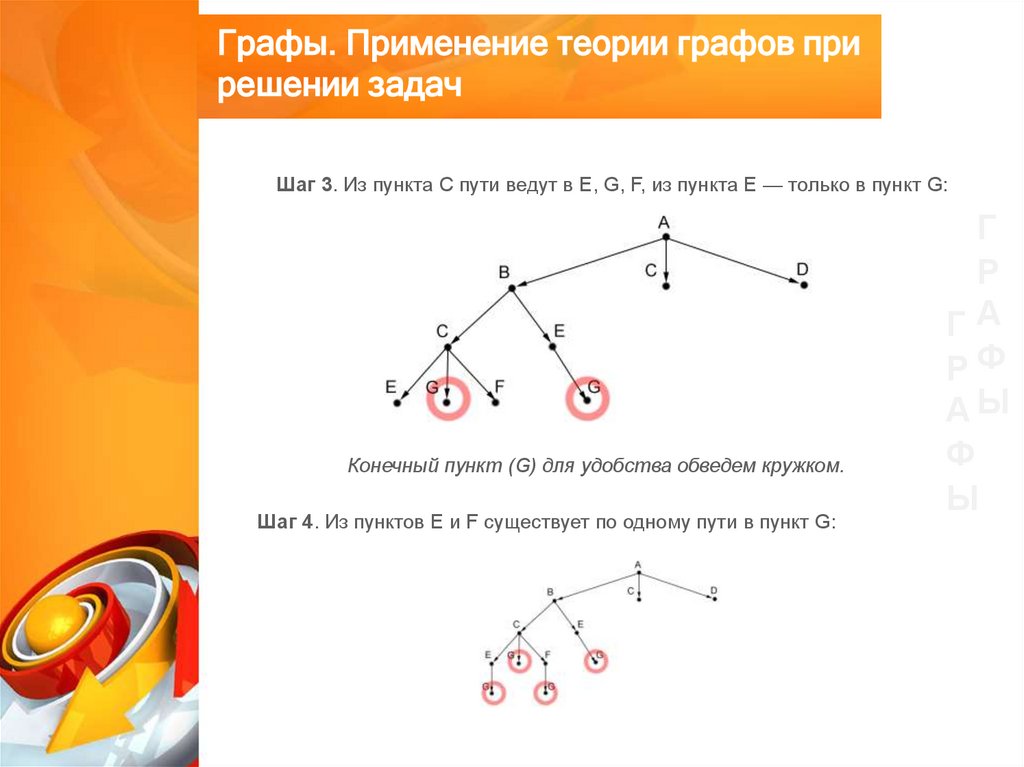
Шаг 3. Из пункта C пути ведут в E, G, F, из пункта E — только в пункт G:
Г
Р
ГА
РФ
АЫ
Конечный пункт (G) для удобства обведем кружком.
Шаг 4. Из пунктов E и F существует по одному пути в пункт G:
Ф
Ы

18.

Графы. Применение теории графов при
решении задач
Шаг 5. Как мы видим по построенному графу, из пункта C существует три
пути в пункт G. Не будем снова расписывать все пути, просто поставим тройку
для пункта C:
Шаг 6. Схема симметрична, логично предположить, что из D в G столько
же путей, сколько из B в G, то есть 4. Отметим это на графе:
Остаётся посчитать:
1+1+1+1+3+4 = 11
Но мы искали пути из A в G, а нам нужно количество путей из A в J. Как мы
решили в начале, для этого нужно умножить количество путей из A в G на 3:
11*3 = 33
Ответ: 33

19.

Г
Р
А
Ф
Ы
Графы. Применение теории графов при
решении задач
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И,
К, Л. По каждой дороге можно двигаться только в одном направлении,
указанном стрелкой. Сколько существует различных путей из города А в
город Л?
Г
Р
А
Ф
Ы
Г
Р
А
Ф
Ы

20.

Графы. Применение теории графов при
решении задач
Пояснение. Начнем считать количество путей с конца маршрута — с
города Л. Пусть NX — количество различных путей из города А в город X, N
— общее число путей.
В город Л можно приехать из И, Е или К, поэтому N = NЛ = NИ + NЕ + N К (*)
Аналогично:
NИ = NД = 7;
NЕ = NВ = 3;
NК = NЕ + NЖ = 3 + 7 = 10.
Г
Р
А
Ф
Ы
Добавим еще вершины:
NД = NБ + NВ + NЕ = 1 + 3 + 3 = 7;
NВ = NБ + NА + NГ = 1 + 1 + 1 = 3;
NЖ = NЕ + NВ + N Г = 3 + 3 + 1 = 7;
NБ = NА = 1;
NГ = NА = 1.
Подставим в формулу (*): N = NЛ = 7 + 3 + 10 = 20.
Ответ: 20.
Г
Р
А
Ф
Ы
Г
Р
А
Ф
Ы

21.

Графы. Применение теории графов при
решении задач
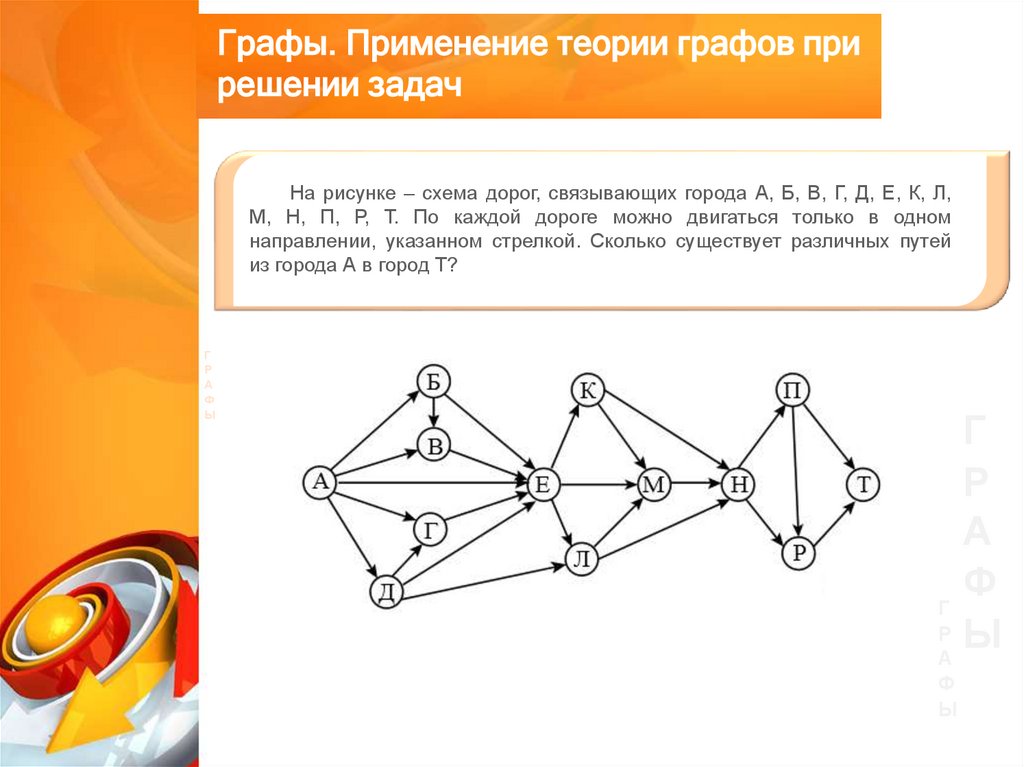
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л,
М, Н, П, Р, Т. По каждой дороге можно двигаться только в одном
направлении, указанном стрелкой. Сколько существует различных путей
из города А в город Т?
Г
Р
А
Ф
Ы
Г
Р
А
Ф
Г
Р Ы
А
Ф
Ы

22.

Графы. Применение теории графов при
решении задач
Пояснение.
Количество путей до города Х = количество путей добраться в любой
из тех городов, из которых есть дорога в Х.
С помощью этого наблюдения посчитаем последовательно
количество путей до каждого из городов:
А=1
Б=А=1
Д=А=1
Г=А+Д=1+1=2
В=А+Б=1+1=2
Е = А + Б + В + Г + Д= 1 + 1 + 2 + 2 + 1 = 7
К=Е=7
Л=Е+Д=7+1=8
М = Е + Л + К = 7 + 8 + 7 = 22
Н = М + К + Л = 22 + 7 + 8 = 37
П = Н = 37
Р = Н + П = 37 + 37 =74
Т = Р + П = 74 + 37 = 111
Ответ: 111.
Г
Р
ГА
РФ
АЫ
Ф
Ы

23.

Графы. Применение теории графов при
решении задач
На рисунке — схема дорог, связывающих
города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой
дороге можно двигаться только в одном
направлении, указанном стрелкой. Сколько
существует различных путей из города А в
город Л?
На рисунке — схема дорог, связывающих города А,
Б, В, Г, Д, Е, Ж, З. По каждой дороге можно
двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из
города А в город З?

24.

Графы. Применение теории графов при
решении задач
На уроке было интересно, у меня
всё получилось.
На уроке было интересно, но
некоторые задания вызвали
затруднения.
Было скучно, мне трудно
выполнять задания.