Похожие презентации:
Теорема о пропорциональных отрезках. Теорема Фалеса (8 класс)
1.
ТеоремаФалеса
И ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ
2.
Ответьте на вопросы:1. Какие отрезки называются равными?
2. Какие прямые называются параллельными?
3. Какие углы называются вертикальными, внутренними накрест
лежащими?
4. Какие углы называются смежными?
5. Сформулируйте теорему о свойстве параллельных прямых,
пересечённых третьей прямой.
3.
Знаете, как без линейки или рулетки разделитькарандаш на равные части?
Ответ на этот вопрос поможет нам дать
теорема, изученная на сегодняшнем уроке.
4.
Перед тем, как познакомиться сэтой теоремой, нам необходимо
перенестись в древнюю Грецию и
познакомиться с создателем
данной теоремы – мудрецом
Фалесом
5.
За много веков в древних цивилизациях было собраномножество геометрических фактов,
использовавшихся без объяснений и доказательств.
Возможно это происходило из-за того, что научными
знаниями обладали лишь особые сословия людей –
жрецы. Любое знание было набором правил или
указаний, с которыми никто не спорил.
Но все изменилось в Древней Греции
6.
Греция тогда не была единым государством — по всемуСредиземному морю возникали маленькие греческие
колонии. Люди в них жили достаточно свободно, над
ними не было единой власти, а жрецы в храмах и власть
выбиралась самим народом.
Свою правоту там необходимо было
доказывать другим людям. Узнав
геометрические факты от египтян, греческие
мудрецы стали их проверять и доказывать —
то есть убеждать других в истине. В этот
момент и появилась настоящая геометрия.
7.
8.
Считают, что 1 греком,который стал заниматься
геометрией, был знаменитый
мудрец Фалес.
Он несколько лет пробыл в
Египте, научился там у жрецов
астрономии, счёту времени и
возведению речных плотин.
Он жил в городе Милет на
берегу Средиземного моря.
Это был портовый город, и
сам Фалес плавал на
кораблях, торговал и много
путешествовал.
9.
Однажды фараон Амасис, желая проверитьмудрость Фалеса, попросил его вычислить
высоту пирамиды Хеопса. Фалес сумел это
сделать, не поднимаясь на саму пирамиду.
Знаете, как он это сделал?
10.
Он догадался, что в солнечный день все предметы одинаково отбрасываютсвои тени. А значит, тень от пирамиды можно вычислить так, как если бы
это была обыкновенная палка.
Это расстояние и равнялось
высоте пирамиды! Такое
рассуждение привело в восторг
фараона, и он признал Фалеса
великим мудрецом.
В этот момент он заметил, куда
упала тень от вершины
пирамиды, и нашёл расстояние
от этого места до центра в её
основании.
Вначале Фалес воткнул в
песок палку и стал ждать,
когда её тень станет равна
длине самой палки.
11.
Возможно, именно Фалес первымдогадался, что луна на небе светится
не сама по себе, а отражает
солнечный свет.
Но достоверно известно лишь то,
что в 585 году до нашей эры он
предсказал полное солнечное
затмение, после которого стал
знаменитым.
12.
13.
А также Фалес создал теорему,помогающую обороняться грекам от
нападений с моря:
14.
Теорема ФалесаЕсли на одной из двух прямых отложить
последовательно несколько равных отрезков и
через их концы провести параллельные прямые,
пересекающие вторую прямую, то они отсекут на
второй прямой равные между собой отрезки.
15.
Вернемся к вопросу о разделении карандаша на равныечасти:
Для этого просто нужно положить его на лист
тетради в линейку так, чтобы концы карандаша
оказались на двух её линиях. На рисунке
показано как этим способом делить карандаш на
5 равных частей.
Как это связано с теоремой Фалеса?
А теперь положите карандаш так, чтобы линии
на бумаге разделили его на 7 равных частей
16.
Часто для деления широкой доски на несколько узких досокодинаковой ширины плотники используют такой прием.
Пусть вам необходимо разрезать данную широкую
доску на три равные узкие доски такой же длины.
Тогда наискосок к доске прикладывают рулетку так,
чтобы расстояние по ней между краями доски было
любым числом сантиметров, которое нацело
делится на 3. Например, на рисунке показано
положение рулетки, когда расстояние АВ равно 27
см. На отрезке АВ карандашом отмечают точки М и
K, которые делят отрезок АВ на три равные части.
Потом берут другое положение рулетки, когда
расстояние СD между краями доски равно,
например, 21 см. На этом отрезке отмечают такие
же точки М1 и K1 . Потом с помощью рулетки
проводят прямые ММ1 и KK1 . По этим прямым и
режут доску на нужные части.
17.
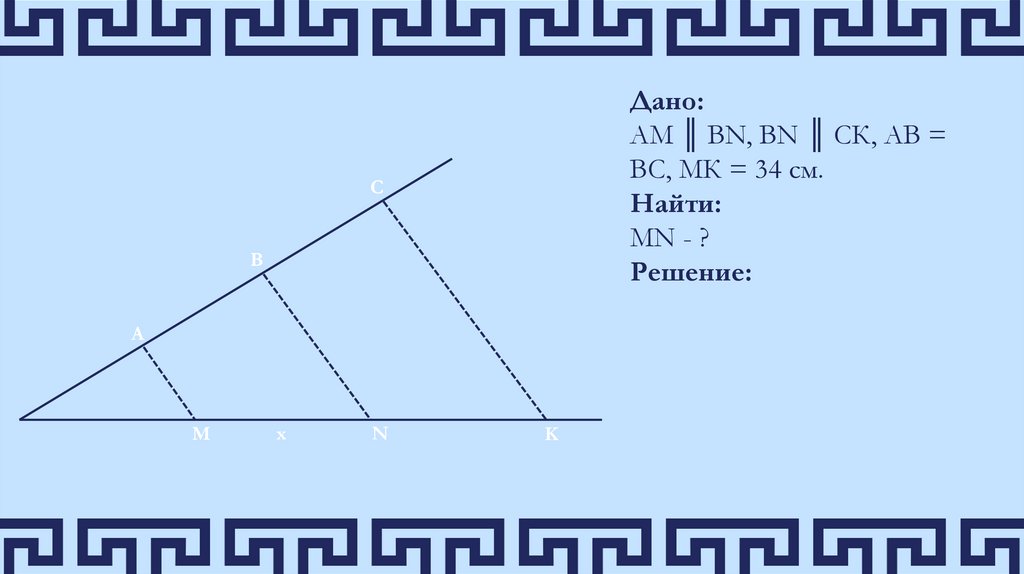
Дано:АМ ║ ВN, ВN ║ СК, АВ =
ВС, МК = 34 см.
Найти:
МN - ?
Решение:
С
В
А
М
x
N
K
18.
ВДано:
МК – средняя линия,
∟АКМ = 112◦
Найти:
∟А - ?
Решение:
М
А
112 ◦
K
С
19.
М 70 ◦Р 70 ◦
Е
110 ◦
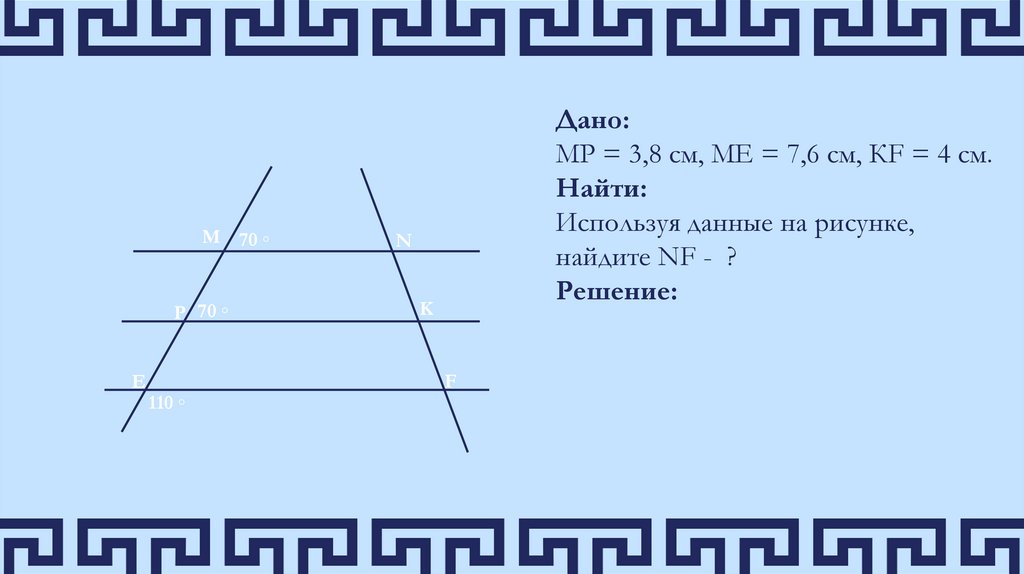
Дано:
МP = 3,8 см, МЕ = 7,6 см, КF = 4 см.
Найти:
Используя данные на рисунке,
найдите NF - ?
Решение:
N
K
F
20.
ABCD – трапеция. BC – 18 см. КТ – средняя линия данной трапеции, пересекающаядиагональ АС в точке О. Найдите длины отрезков, на которые разбивает диагональ
среднюю линию, если один из этих отрезков на 2 см больше другого, а также
меньшее основание трапеции.
А
B
O
K
D
18 см
T
C
Дано:
ABCD – трапеция. KT – средняя линия. DС = 18 см. АС∩КТ в
т.О. KO-OT=2 см.
Найти:
КО - ? ОТ - ? АВ - ?
Решение:
КО || DС, АК = КD, т.к. КТ – средняя линия трапеции,
следовательно АО = ОС (по т. Фалеса). Значит, КО является
средней линией ∆АDС. КО = DС:2, КО = 18:2=9 см. ОТ =
КО-2= 9 - 2 = 7 см. КТ = 16 см.
Если КТ – средняя линия трапеции, то КТ = (АВ + DС):2, АВ
= 2КТ – DС, АВ = 2*16 - 18 = 14 см.
Ответ: КО = 9 см, ОТ = 7 см, АВ = 14 см.
21.
Можно ли разделить данный отрезок на двечасти, длины которых относятся между собой
как два других произвольных отрезка?
Оказывается, сделать так можно, но для этого
применяют уже теорему о пропорциональных отрезках,
которая является обобщением теоремы Фалеса
В теореме Фалеса параллельные прямые на каждой
стороне угла высекали равные между собой отрезки.
Значит, и отношение длин этих отрезков на каждой его
стороне было равно 1. В общем же случае отношение
таких отрезков может быть любым положительным
числом, но будет одинаковым для двух сторон угла.
Именно в этом и заключается ТЕОРЕМА О
ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ
22.
ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ23.
Теорема о пропорциональных отрезкахДано:
∆ АВС. КО || АВ. АО = 2 см, ОС = 5 см, ВС = 21 см
Найти:
КС - ?
Решение:
В
К
АО
ОС
2
5
АВ || КО . = (по т.Фалеса), =
ВК
КС
х
21−х
А
2 см О
5 см
С
2(21-х)=5х
42-2х=5х
7х=42
х=6 см.
ВК = 6 см, КС = 21 – 6 = 15 см.
Ответ: КС = 15 см
24.
Историческая справка• Аргентинская музыкальная группа представила песню,
посвящённую теореме. В видеоклипе для этой песни
приводится доказательство прямой теоремы для
пропорциональных отрезков.
• Теорема Фалеса до сих пор используется в морской
навигации в качестве правила о том, что столкновение судов,
двигающихся с постоянной скоростью, неизбежно, если
сохраняется курс судов друг на друга.
• Вне русскоязычной литературы теоремой Фалеса иногда
называют другую теорему планиметрии, а именно,
утверждение о том, что вписанный угол, опирающийся на
диаметр окружности, является прямым. Открытие этой
теоремы действительно приписывается Фалесу, о чём есть
свидетельство Прокла.






















 Математика
Математика








