Похожие презентации:
Пропорциональные отрезки (метрические соотношения) в прямоугольном треугольнике
1. Пропорциональные отрезки (метрические соотношения) в прямоугольном треугольнике
2.
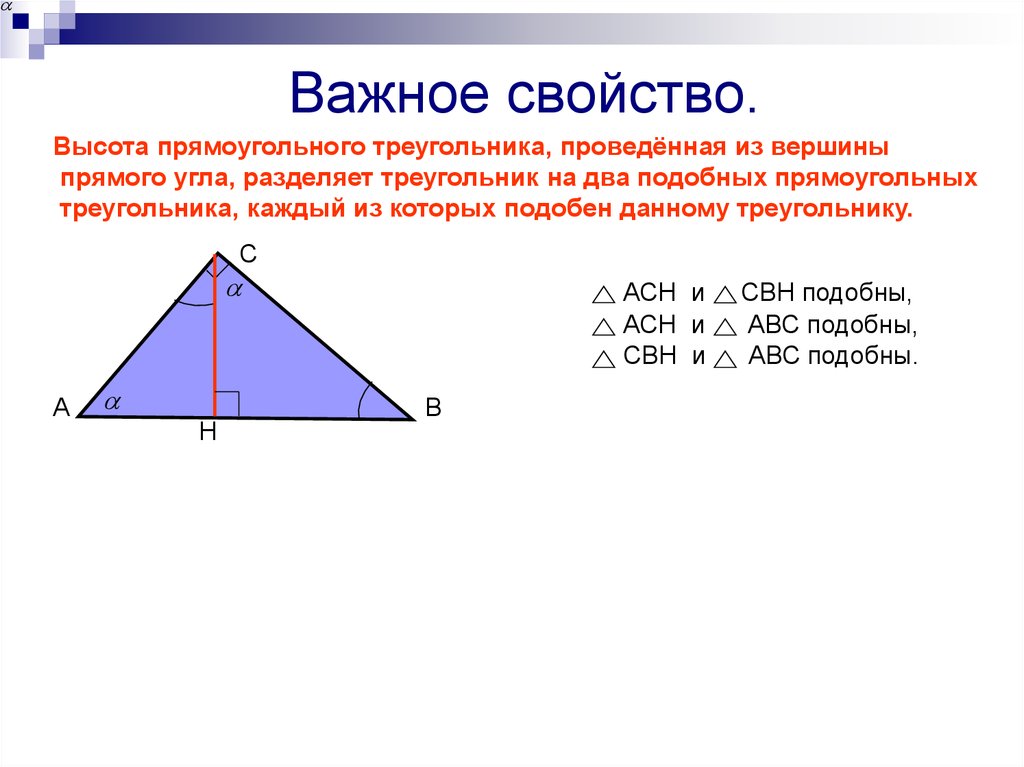
Важное свойство.Высота прямоугольного треугольника, проведённая из вершины
прямого угла, разделяет треугольник на два подобных прямоугольных
треугольника, каждый из которых подобен данному треугольнику.
С
А
Н
АСН и
АСН и
СВН и
В
СВН подобны,
АВС подобны,
АВС подобны.
3.
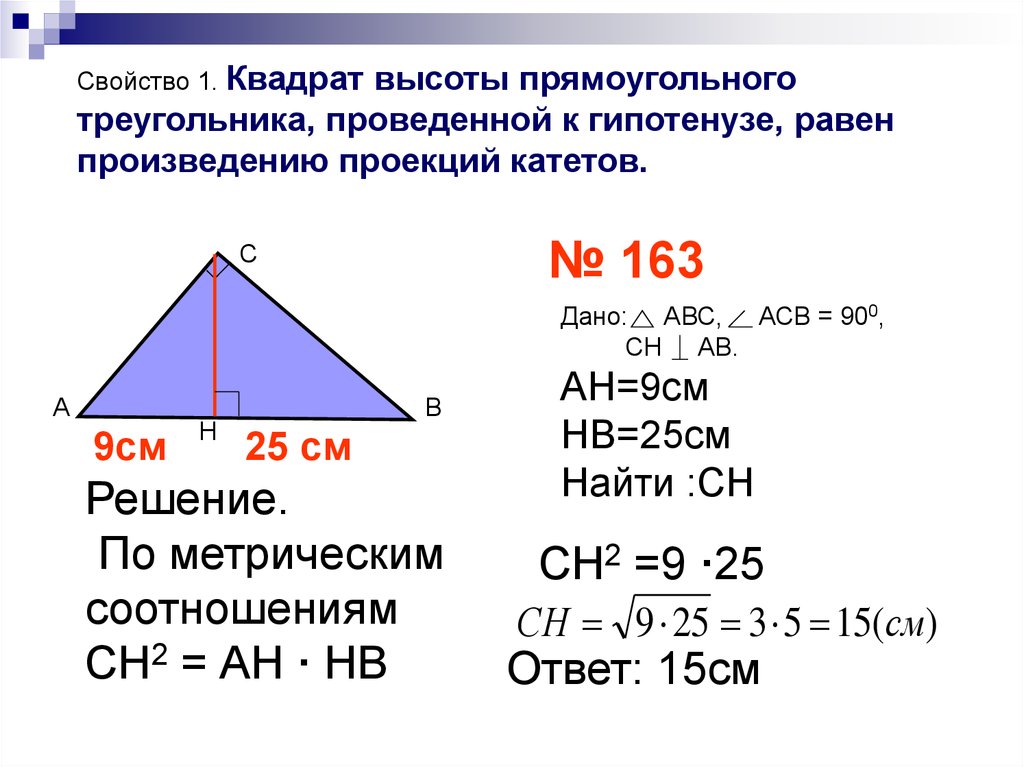
Свойство 1. Квадратвысоты прямоугольного
треугольника, проведенной к гипотенузе, равен
произведению проекций катетов.
№ 163
С
Дано: АВС, АСВ = 900,
СН АВ.
А
9см
Н
В
25 см
Решение.
По метрическим
соотношениям
СН2 = АН · НВ
АН=9см
НВ=25см
Найти :СН
СН2 =9 ·25
СН 9 25 3 5 15(см)
Ответ: 15см
4.
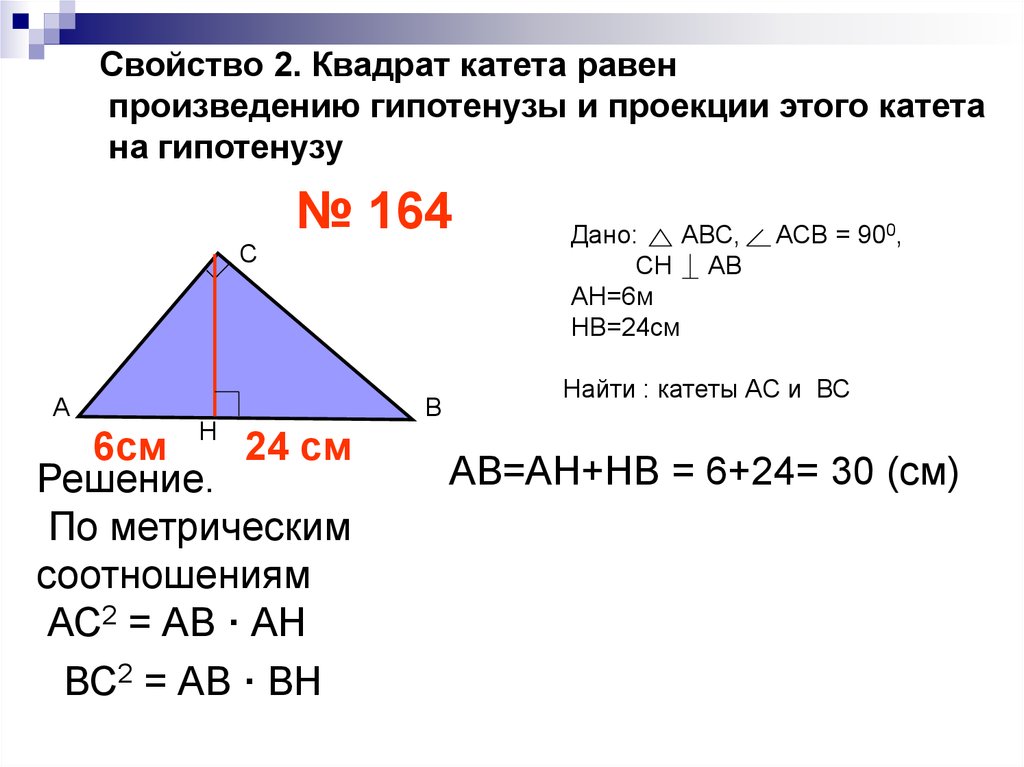
Свойство 2. Квадрат катета равенпроизведению гипотенузы и проекции этого катета
на гипотенузу
С
А
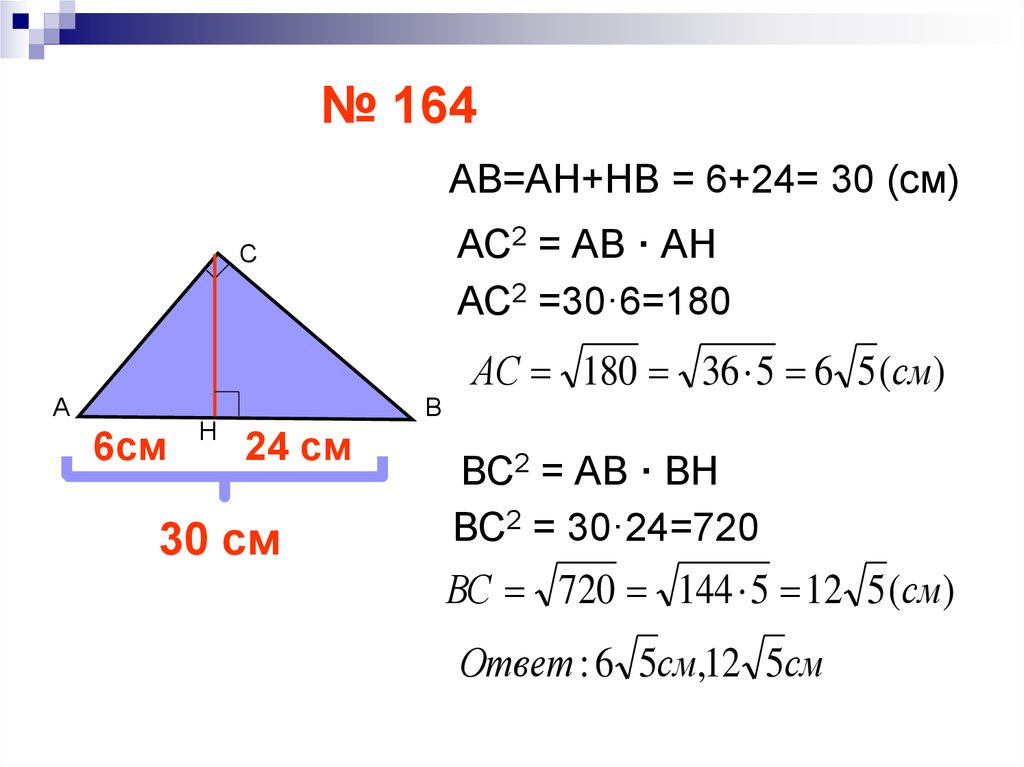
№ 164
6см Н 24 см
Решение.
По метрическим
соотношениям
АС2 = АВ · АН
ВС2 = АВ · ВН
В
Дано:
АВС,
СН АВ
АН=6м
НВ=24см
АСВ = 900,
Найти : катеты АС и ВС
АВ=АН+НВ = 6+24= 30 (см)
5.
№ 164АВ=АН+НВ = 6+24= 30 (см)
АС2 = АВ · АН
АС2 =30·6=180
С
А
6см
Н
В
24 см
30 см
АС 180 36 5 6 5 (см)
ВС2 = АВ · ВН
ВС2 = 30·24=720
ВС 720 144 5 12 5 (см)
Ответ : 6 5см,12 5см
6.
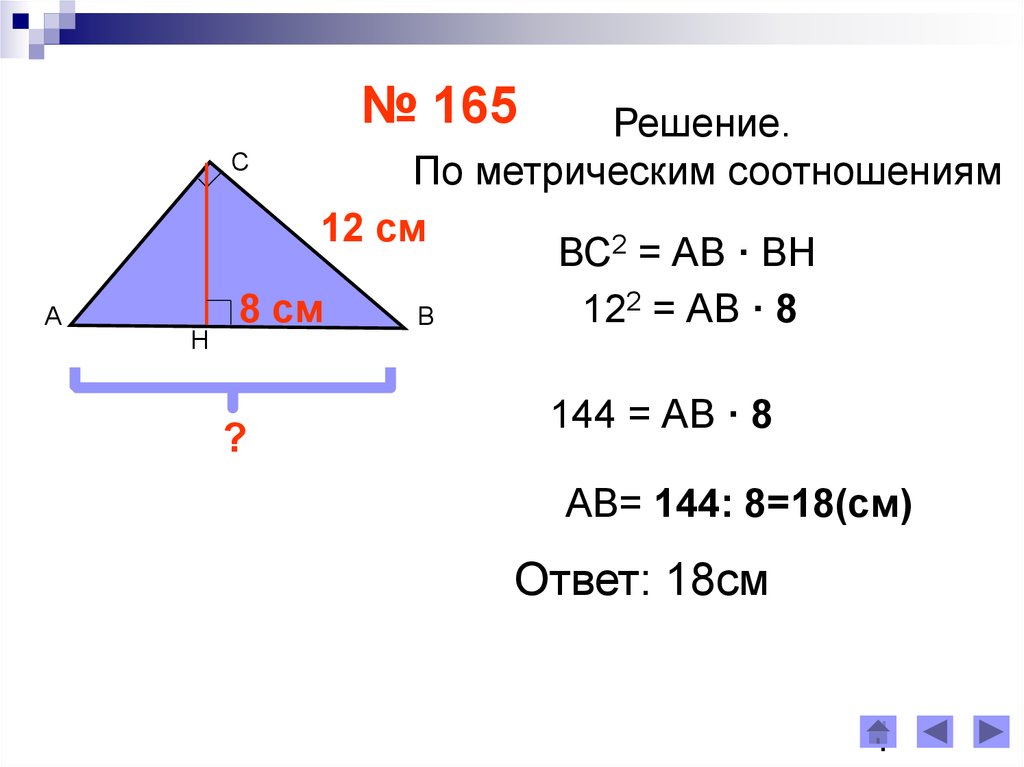
№ 165А
Н
Решение.
С
По метрическим соотношениям
12 см
ВС2 = АВ · ВН
8 см
122 = АВ · 8
В
?
144 = АВ · 8
АВ= 144: 8=18(см)
Ответ: 18см
·
7.
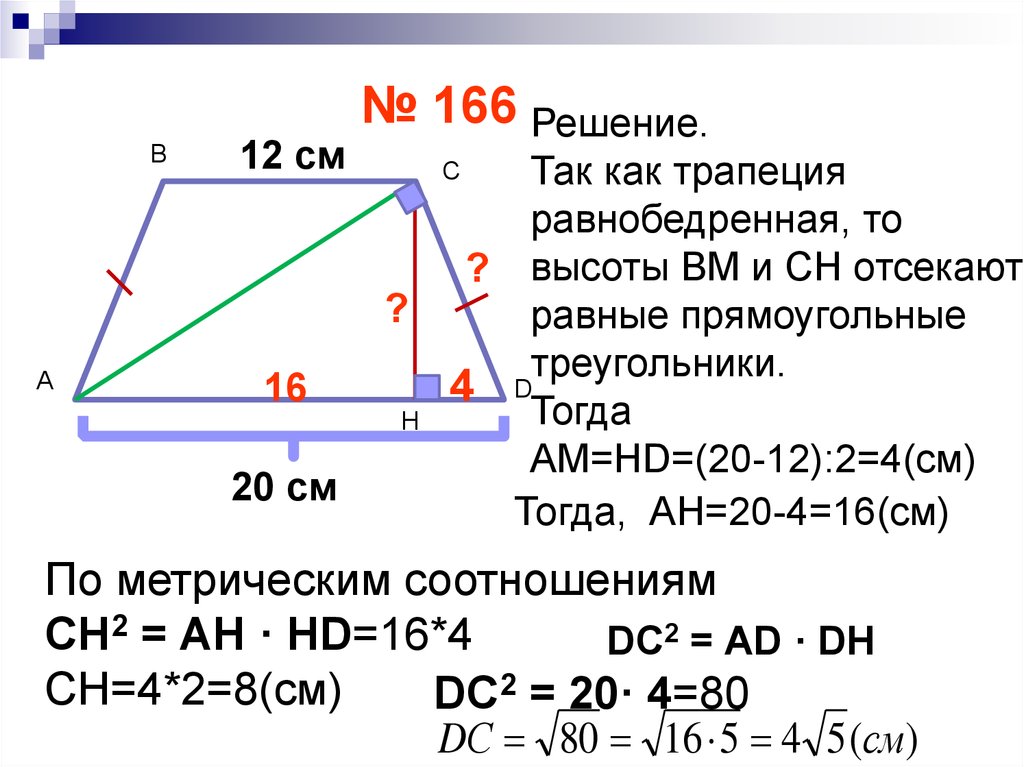
В12 см
№ 166 Решение.
?
А
16
20 см
Так как трапеция
равнобедренная, то
? высоты ВМ и СН отсекают
равные прямоугольные
треугольники.
D
4
Тогда
АМ=НD=(20-12):2=4(см)
Тогда, АН=20-4=16(см)
С
Н
По метрическим соотношениям
СН2 = АН · НD=16*4
DС2 = АD · DН
СН=4*2=8(см)
DC2 = 20· 4=80
DС 80 16 5 4 5 (см)
8.
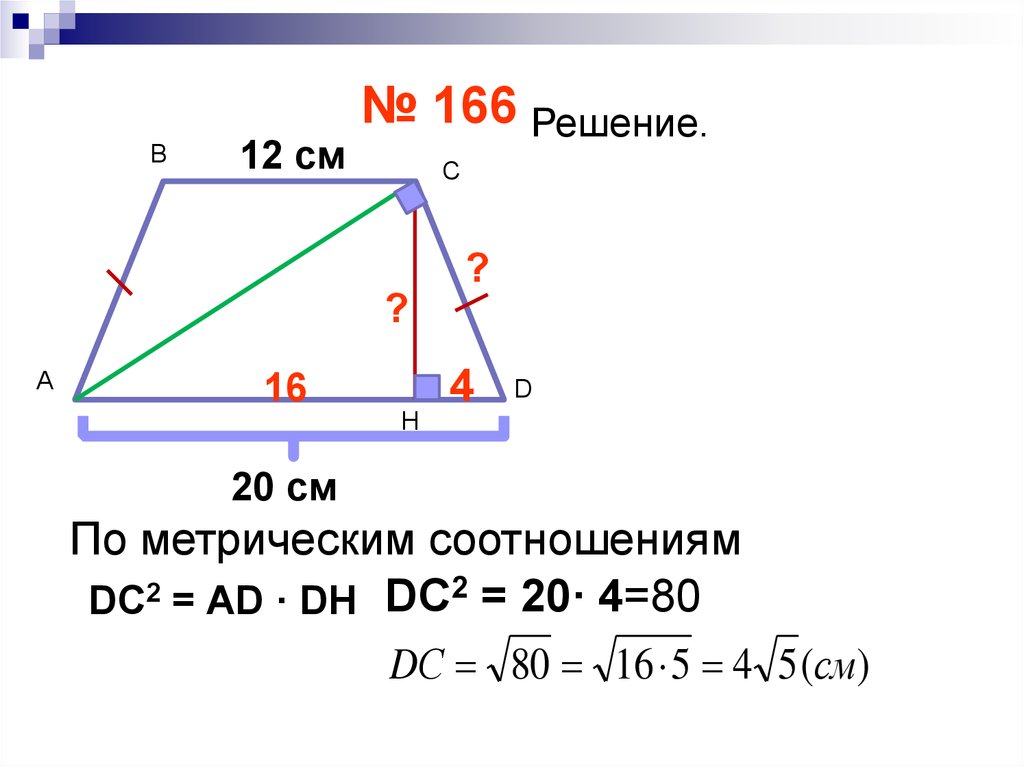
В12 см
№ 166 Решение.
С
?
?
А
16
Н
4
D
20 см
По метрическим соотношениям
DС2 = АD · DН DC2 = 20· 4=80
DС 80 16 5 4 5 (см)
9.
№ 167Диагонали ромба
перпендикулярны
Расстояние от точки до
прямой –перпендикуляр
Рассмотреть метрические
соотношения в
прямоугольном
треугольнике,
найти катеты .
Найти диагонали ромба.
10.
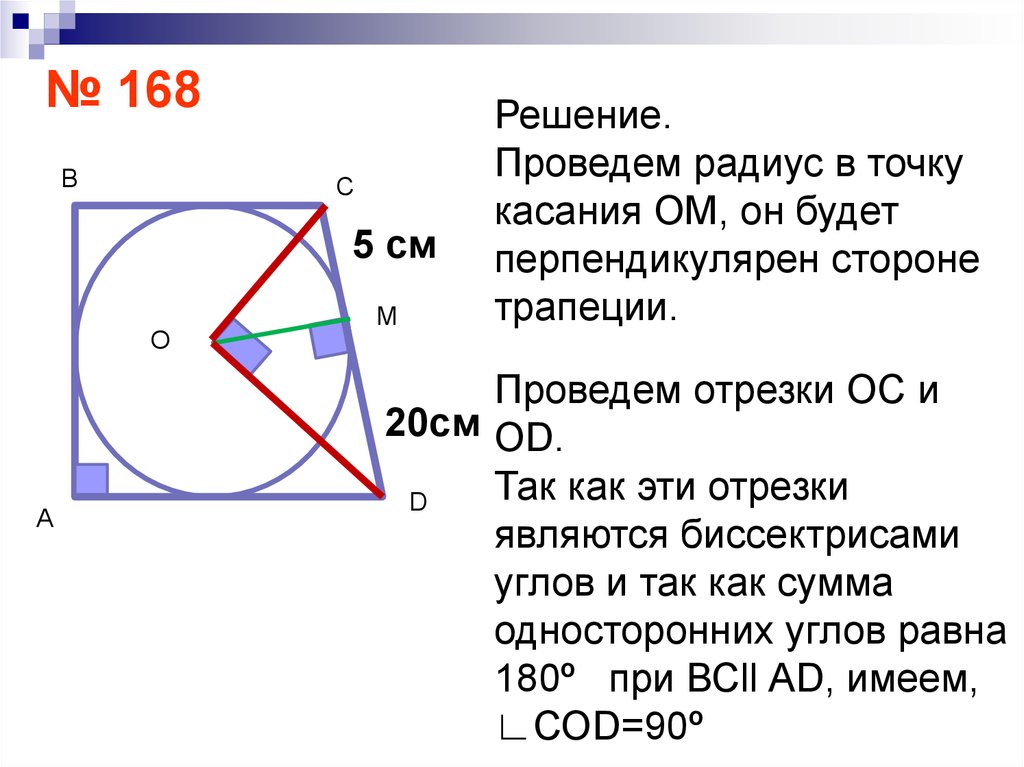
№ 168В
С
5 см
О
А
М
Решение.
Проведем радиус в точку
касания ОМ, он будет
перпендикулярен стороне
трапеции.
Проведем отрезки ОС и
20см ОD.
Так как эти отрезки
D
являются биссектрисами
углов и так как сумма
односторонних углов равна
180º при ВСll АD, имеем,
∟СОD=90º
11.
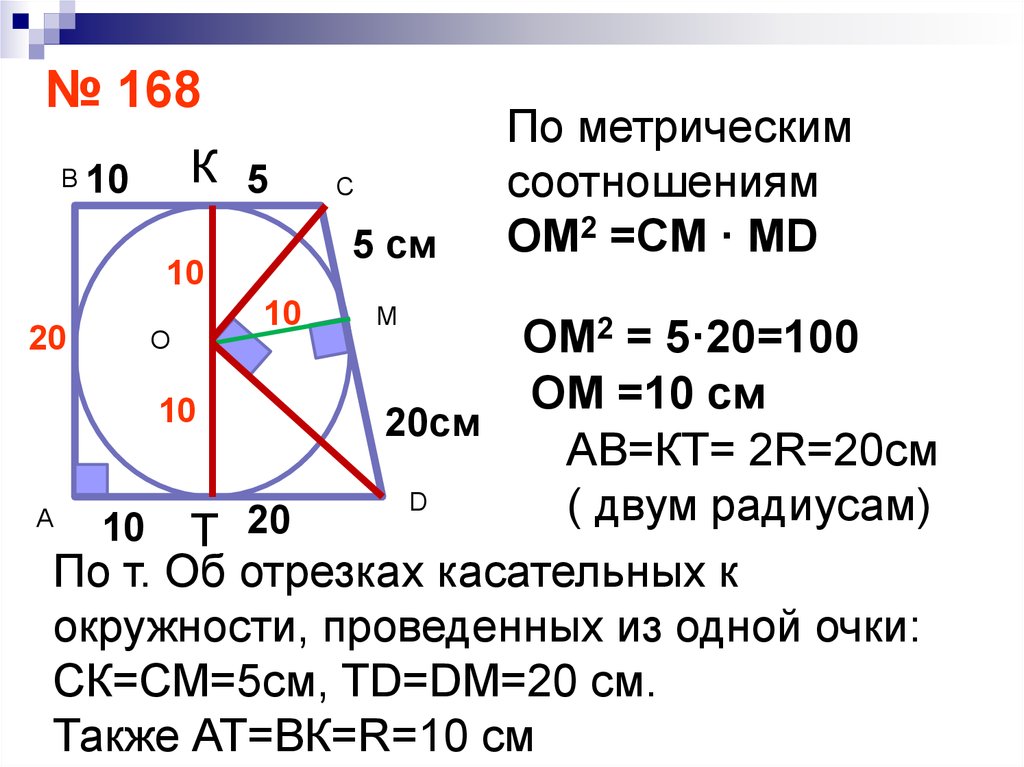
№ 168К 5
В 10
С
5 см
10
10
М
По метрическим
соотношениям
ОМ2 =СМ · МD
ОМ2 = 5·20=100
ОМ =10 см
10
20см
АВ=КТ= 2R=20см
D
(
двум
радиусам)
А
20
10 Т
По т. Об отрезках касательных к
окружности, проведенных из одной очки:
СК=СМ=5см, ТD=DМ=20 см.
Также АТ=ВК=R=10 см
20
О
12.
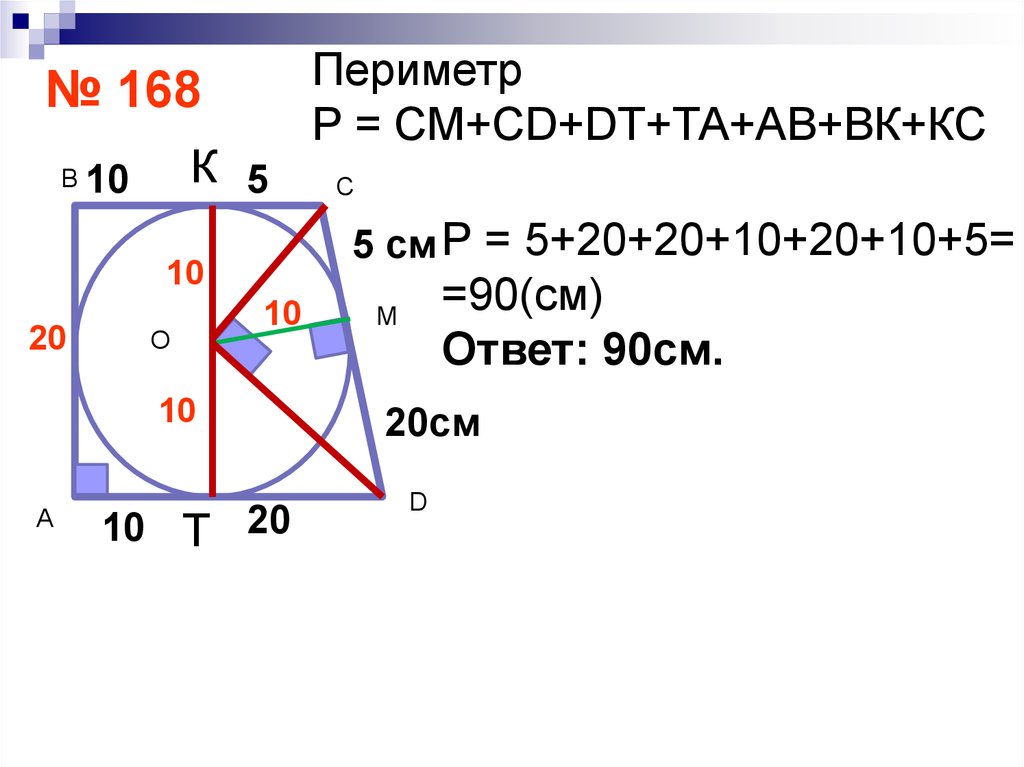
№ 168К 5
В 10
О
10
10
А
С
5 см Р = 5+20+20+10+20+10+5=
10
20
Периметр
Р = СМ+CD+DT+ТА+АВ+ВК+КС
10 Т 20
=90(см)
Ответ: 90см.
М
20см
D
13. Проверочная работа 15 мин
14. «Теорема Пифагора»
c² = a² + b²с
b
а
15. Исторический экскурс Рассказ о Пифагоре(стр 115-прочитайте)
Исторический экскурсРассказ о Пифагоре(стр 115прочитайте)
Пифагор жил в
VI в. до н. э. в
Древней Греции
Основал
философскую
школу –
пифагорейский
союз.
16.
Пифагорейцы занималисьматематикой, философией,
естественными науками.
Ими были сделаны важные
открытия в арифметике и
геометрии. В школе
существовало правило, по
которому авторство всех
работ приписывалось
Пифагору. Так что
достоверно неизвестно,
какие открытия
принадлежат самому
ученому.
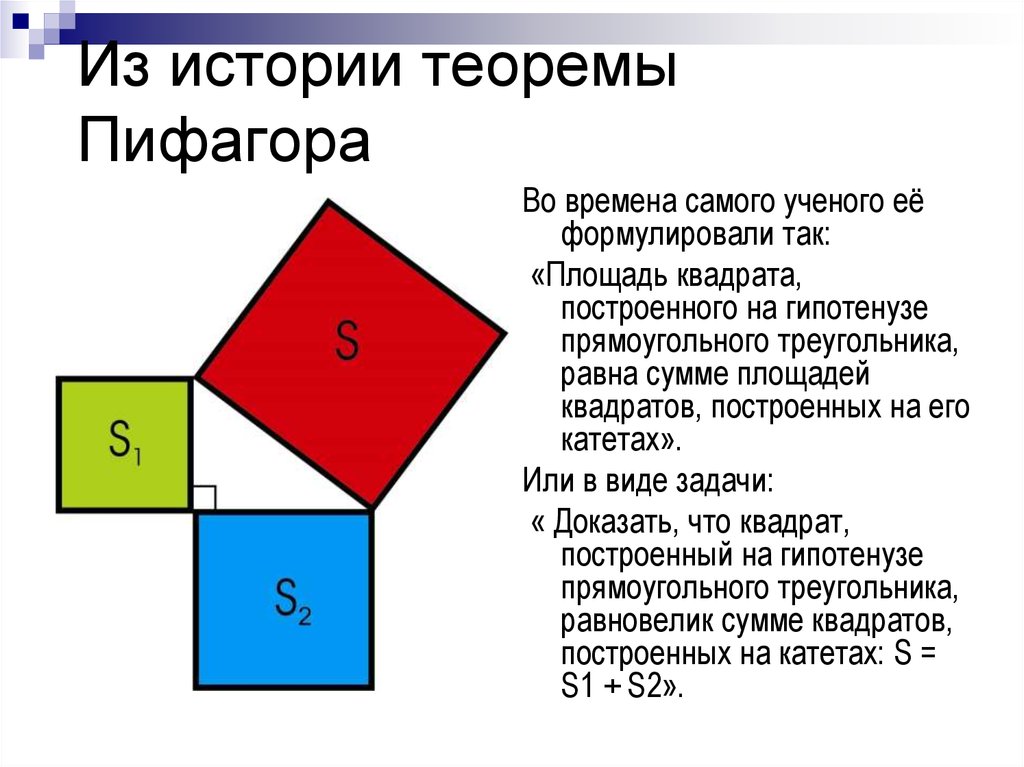
17. Из истории теоремы Пифагора
Во времена самого ученого еёформулировали так:
«Площадь квадрата,
построенного на гипотенузе
прямоугольного треугольника,
равна сумме площадей
квадратов, построенных на его
катетах».
Или в виде задачи:
« Доказать, что квадрат,
построенный на гипотенузе
прямоугольного треугольника,
равновелик сумме квадратов,
построенных на катетах: S =
S1 + S2».
18.
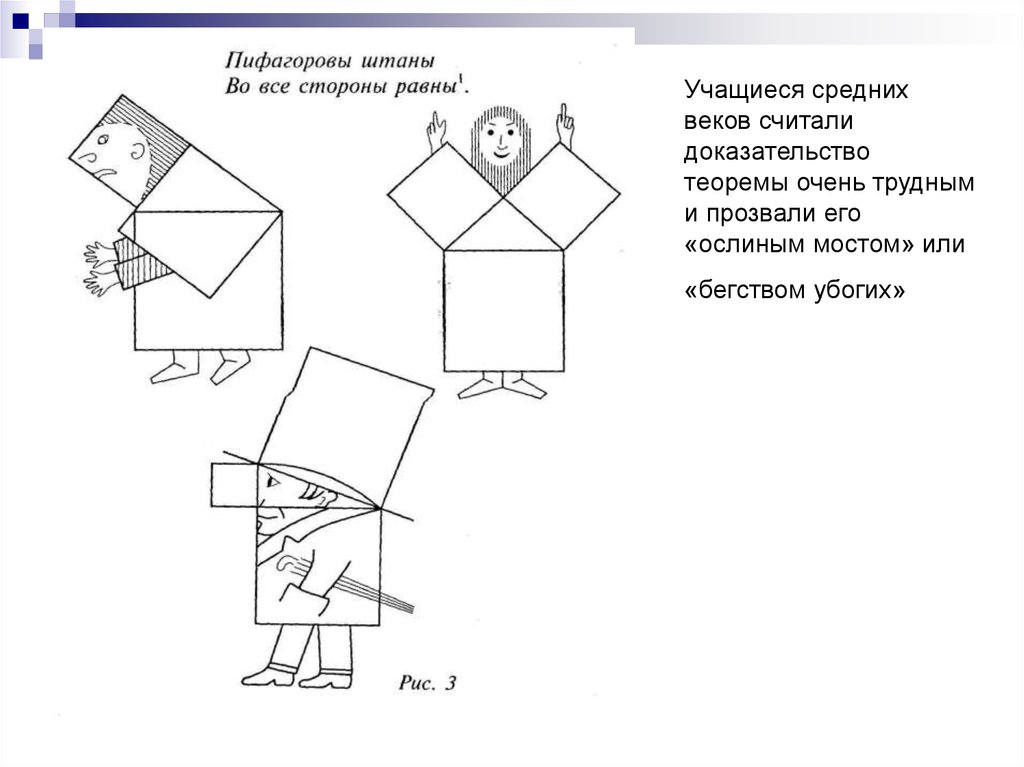
Учащиеся среднихвеков считали
доказательство
теоремы очень трудным
и прозвали его
«ослиным мостом» или
«бегством убогих»
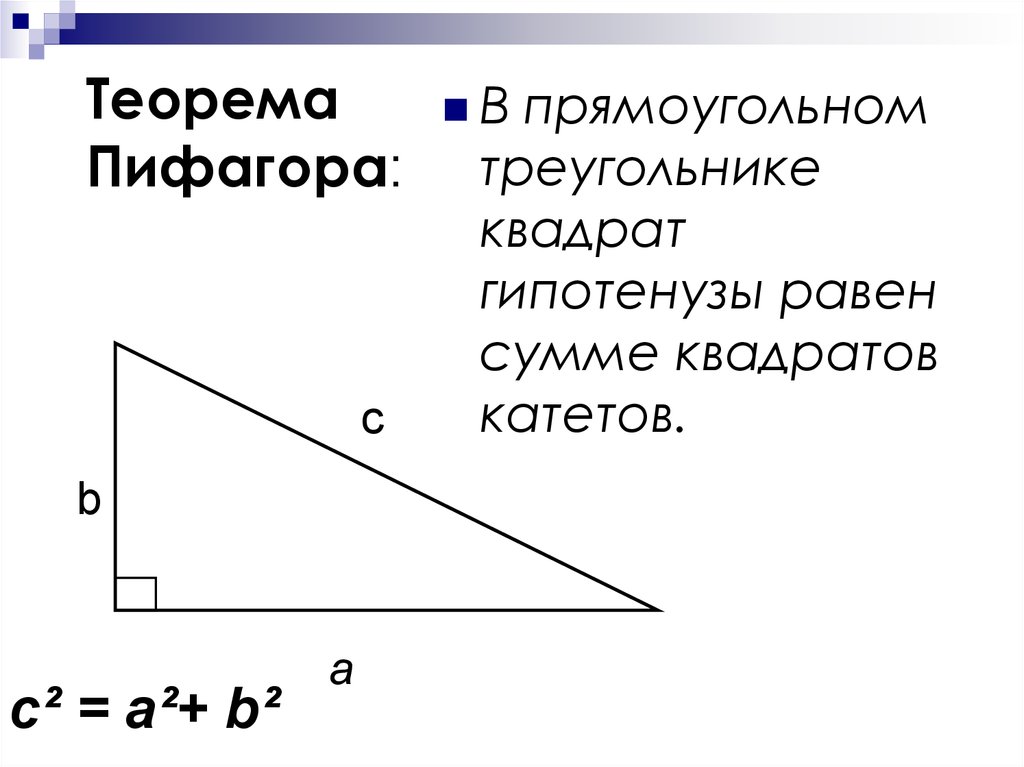
19. Теорема Пифагора:
сb
c² = a²+ b²
а
В
прямоугольном
треугольнике
квадрат
гипотенузы равен
сумме квадратов
катетов.
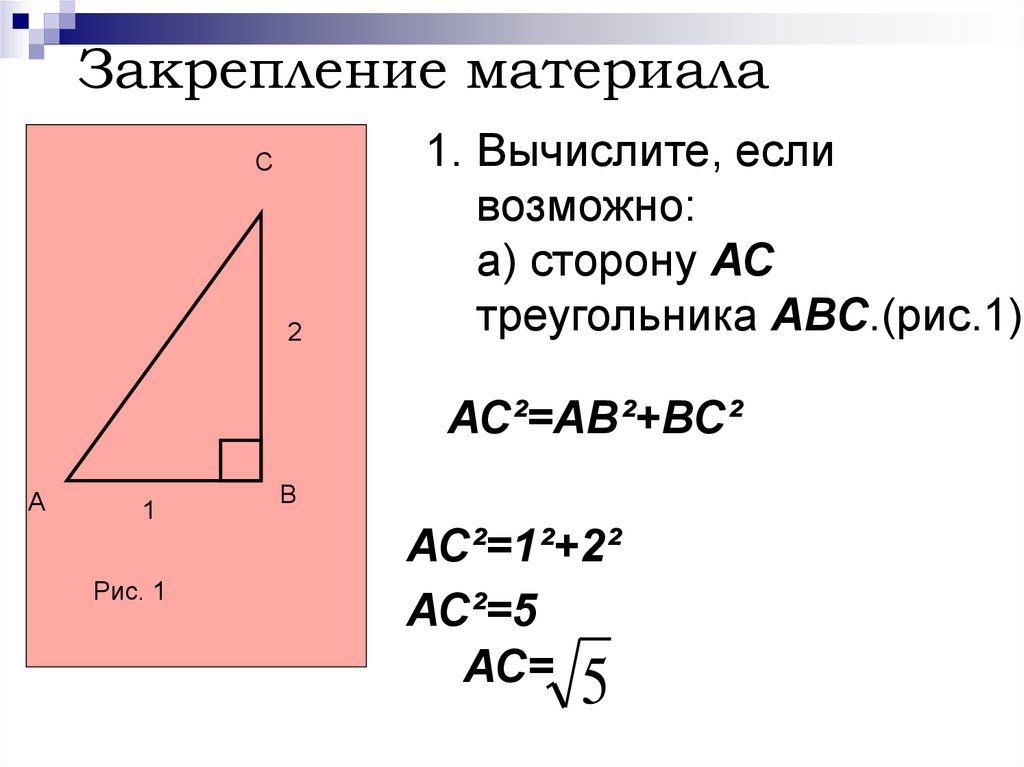
20. Закрепление материала
С2
1. Вычислите, если
возможно:
а) сторону АС
треугольника АВС.(рис.1)
АС²=АВ²+ВС²
А
1
Рис. 1
В
АС²=1²+2²
АС²=5
АС= 5
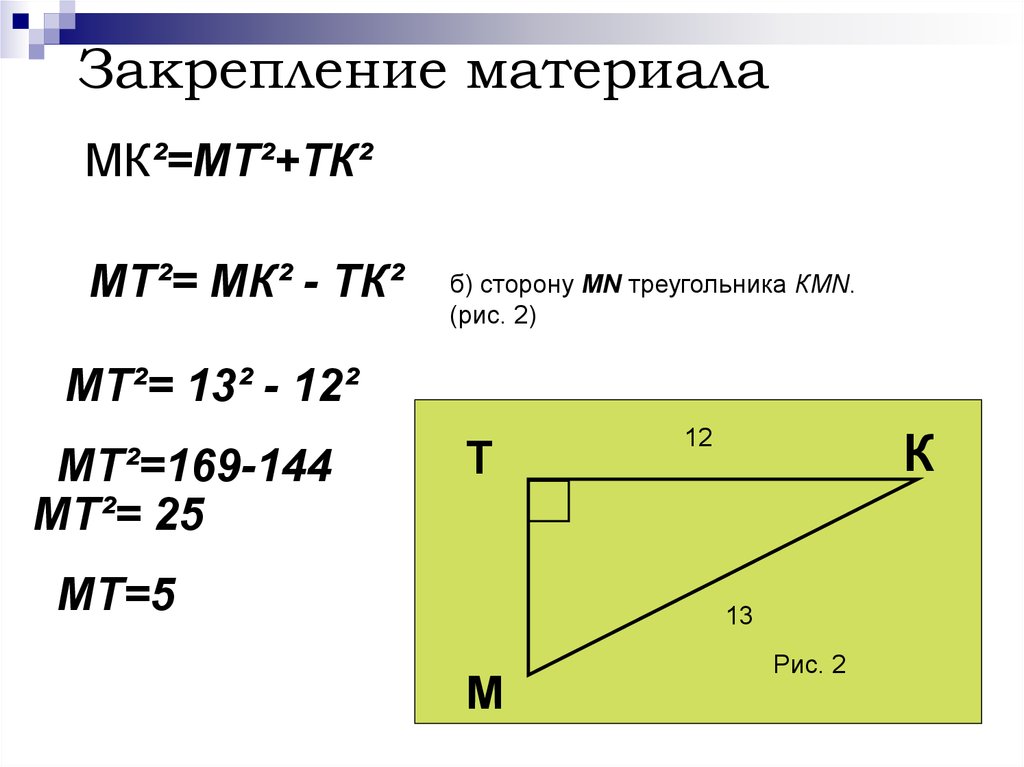
21. Закрепление материала
МК²=МТ²+ТК²МТ²= МК² - ТК²
б) сторону МN треугольника КМN.
(рис. 2)
МТ²= 13² - 12²
МТ²=169-144
МТ²= 25
Т
МТ=5
К
12
13
М
Рис. 2
22. В классе №529(1) №530(2) Дома п.16. учить т. Пифагора с док-вом, знать ответы на вопросы решить № 531
В КЛАССЕ№529(1)
№530(2)
ДОМА П.16.
УЧИТЬ Т. ПИФАГОРА С ДОКВОМ,
ЗНАТЬ ОТВЕТЫ НА
ВОПРОСЫ
РЕШИТЬ № 531





 Математика
Математика








