Похожие презентации:
Система счисления
1.
Система счисления2.
Система счисления – это совокупностьприёмов и правил изображения чисел
цифровыми знаками.
Системы
счисления
делятся
на
непозиционные и позиционные.
3.
Непозиционная система счисления –это система, в которой значение символа не
зависит от его положения в числе. Примером
непозиционной системы счисления может
служить римская система счисления, в
которой цифры обозначаются различными
знаками: Ⅰ – 1, Ⅲ – 3, Ⅵ – 6, L – 50 …
Основным недостатком такой системы
является большое число различных знаков и
сложность выполнения арифметических
операций.
4.
Позиционная система счисления – этосистема, в которой значение символа зависит от
его места (позиции) в ряду цифр, изображающих
число.
Например, в числе 548 первая цифра
означает количество сотен, вторая – десятков,
третья – единиц.
Позиционные
системы
счисления
характеризуются основанием.
Основание (или базис) позиционной системы
счисления – это количество знаков или символов,
используемых для изображения числа в разрядах
данной системы счисления.
5.
В ЭВМвосьмеричная,
счисления.
приняты десятичная,
шестнадцатеричная
двоичная,
системы
Десятичная система счисления –
основание S=10. Набор цифр этой системы 0, 1,
2, …, 9. Любое целое число в десятичной
системе счисления записывается как сумма
величин: 100, 101, 102, …, каждая из которых
может быть взята от 1 до 9 раз.
6.
Двоичная система счисления – основаниеS=2. Для записи числа используются две цифры: 0 и 1.
При этом каждый старший разряд больше соседнего
младшего в два раза. Любое число в двоичной системе
счисления представляется в виде суммы целых
степеней
основания
S=2,
умноженных
на
соответствующие коэффициенты (0 или 1).
Кроме двоичной системы счисления, в ЭВМ
используется восьмеричная и шестнадцатеричная
системы. Основания этих систем соответствуют
целым степеням числа 2 (8=23, 16=24), поэтому для
них исключительно просты правила перевода в
двоичную систему и наоборот.
7.
Восьмеричная система счисления –основание S=8. Используются цифры: 0, 1, 2,
…, 7. Любое число представляется суммой
целых степеней основания S=8, умноженных на
соответствующие коэффициенты ai=0, …, 7.
Шестнадцатеричная система счисления –
основание S=16. Алфавит цифровых знаков
состоит из 16-ти символов: первые десять –
арабские цифры от 0 до 9 и дополнительные –
A(10), B(11), C(12), D(13), E(14), F(15).
8.
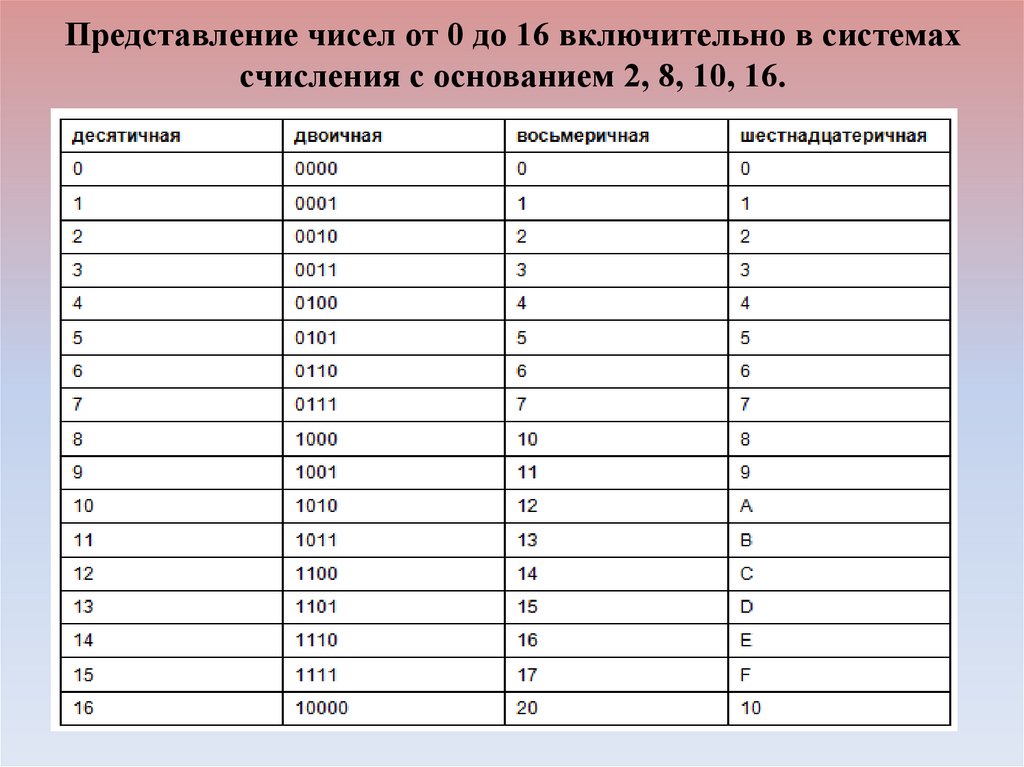
Представление чисел от 0 до 16 включительно в системахсчисления с основанием 2, 8, 10, 16.
9.
В некоторых ЭВМ ввод и вывод информацииосуществляется в смешанных (двоично-кодированных)
системах счисления, имеющих основание S>2, в которых
каждая цифра числа представляется в двоичной системе.
Наибольшее применение в ЭВМ получили восьмеричная,
десятичная и шестнадцатеричная двоично-кодированные
системы счисления.
Двоично-восьмеричная система счисления. В этой
системе каждая восьмеричная цифра представляется
трехзначным двоичным числом – триадой.
Например, = 001 011 111, 100 101 2-8.
1 3 7 4 5
10.
Двоично-десятичная система счисления.В этой системе каждая десятичная цифра
представляет четырёхзначным двоичным числом –
тетрадой. Например:
273,5910= 0010 0111 0011, 0101 1001 2-10.
2
7
3
5
9
Двоично-шестнадцатеричная система
счисления.
В этой системе (как и в двоично-десятичной)
каждая шестнадцатеричная цифра представляется
четырехзначным двоичным числом (тетрадой).
Например,
39C16=0011 1001 1100 2-16
3
9 12=C
11.
При работе со смешанными системами счисления справедливоследующее утверждение: если P=Sk (где P,S – основания систем, k –
положительные целые числа), то запись любого числа в смешанной S-P
системе счисления тождественно совпадает с записью этого же числа в
системе счисления с основанием S с точностью до нулей в начале
записи целой части числа и в конце дробной.
Согласно этому утверждению, если P=8, S=2, k=3, то запись
любого числа в двоично-восьмеричной системе совпадает с записью
этого же числа в двоичной системе.
Например: число 688 в двоично-восьмеричной системе
будет 628=110 010 2-8;
6 2 - это же число в десятичной системе будет ;
если теперь число 5010 представить в двоичной системе, получим
5010=110 0102.
Таким образом, двоичная и двоично-восьмеричная запись одного
итого же числа (628) совпадает.
40510 = 1100101012;
40510 = 19516;
19516 = 1 1001 0101 2-16 .
1 9
5
12.
Перевод чисел из одной системы счисления в другуюЕсли число X из системы счисления с основанием s
необходимо перевести в систему счисления с основанием p,
перевод осуществляется по следующим правилам:
Правило 1.
При равенстве p=sk, где k – целое положительное число
(например, p=8=23, k=3, s=2), в этом случае:
1. при переводе числа из двоичной системы счисления в
восьмеричную, начиная с запятой в левую сторону для целой части
и в правую – для дробной части, число разбивается по триадам и
каждая триада заменяется восьмеричной цифрой;
2. при переводе числа из восьмеричной системы счисления в
двоичную каждая цифра записывается как двоичная по триадам;
3. при переводе числа из двоичной системы счисления в
шестнадцатеричную, число разбивается по тетрадам и каждая
тетрада заменяется шестнадцатеричной цифрой (P=16=24, k=4,
s=2);
4. при сохранении числа из шестнадцатеричной системы
счисления в двоичную каждая цифра записывается как двоичная
по тетрадам.
13.
Например:1) 011 011 011, 101 110 2 = 333,568 ;
3 3 3 5 6
2) 167,568 = 001 110 111, 101 110 2 ;
1 6 7 5 6
3) 0011 1011 0100, 1111 1010 2 = 3B4,FA16 ;
3 B 4
F
A
4) A29,CF16 = 1010 0010 1001, 1100 1111 2.
A
2
9
C
F
14.
Правило2.При не выполнении равенства p=sk (где k – целое
положительное число), в этом случае:
Целая часть числа делится на новое основание p;
полученный от деления первый остаток является
младшей цифрой целой части числа с основанием p;
затем полученное число снова делится на основание p,
в результате определяется второй остаток,
соответствующий следующей после младшей цифре
числа с основанием p; деление продолжается до тех
пор, пока частное не станет меньше делителя;
последнее частное даёт старшую цифру числа с
основанием p. Например:
15.
Перевести число 2610 в двоичную системусчисления:
Таким образом, 2610 = 110102.
16.
Перевести число 19110 в восьмеричнуюсистему счисления:
Таким образом, 19110 = 2778.
17.
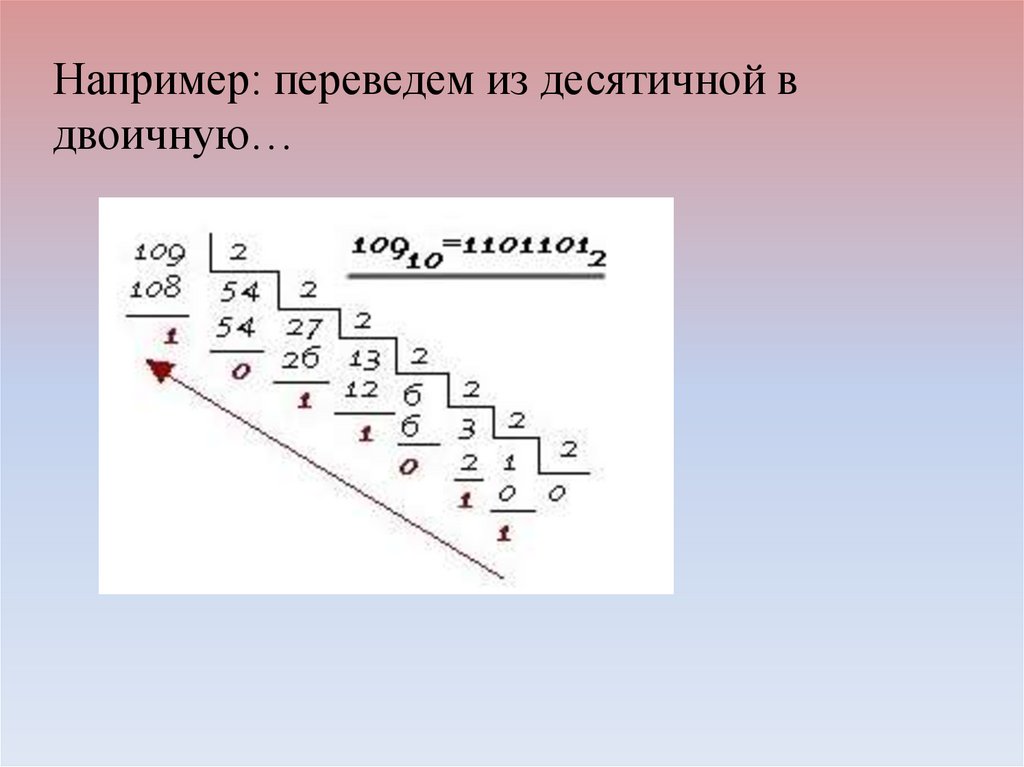
Например: переведем из десятичной вдвоичную…
18.
Пример: Число 327.125, представленное в десятичнойсистеме счисления, перевести в двоичную систему
счисления.
Решение: Так как исходное число содержит ненулевые
целую и дробную части, а для перевода целых и дробных
чисел используются разные алгоритмы, то мы переведем,
сначала целую часть числа, затем дробную и в конце
синтезируем полное число.
1) Переводим целую часть : 327
Разделим 327 на два ( 2 - это основание системы счисления).
Делить будем с остатком, частное запишем в столбец «Част.», а
остаток в столбец «Ост.». Затем полученное частное снова
разделим на два и новое частное и остаток также распределим
по столбцам (см. ниже). Повторять деление будем до тех пор,
пока последнее частное не окажется меньше двух.
19.
Теперь мы можем записать 327 в двоичнойсистеме счисления. Для этого в старший (самый
левый) разряд числа запишем последнее частное,
а в следующие, по порядку, разряды запишем все
полученные выше остатки, беря их снизу вверх.
То есть, в самом младшем разряде оказывается
самый верхний остаток.
И так, целая часть: 32710 = 1010001112
2) Переводим дробную часть : 0.125
Умножим дробную часть числа 0.125 на два. Затем дробную часть полученного
числа снова умножим на два и так далее. Повторять умножение будем до тех пор,
пока последняя дробная часть не обратится в ноль, либо не исчерпается разрядная
сетка машины (в нашем случае 16 двоичных знаков в дробной части).
20.
После последнего умножения получено целоечисло (дробная часть равна нулю). Процесс
умножения прекращаем.
Теперь мы можем записать 0.125 в двоичной
системе счисления. Целая часть у нас равна нулю, а
цифры в дробной части (слева на право) это есть
целые части наших произведений (сверху вниз). То
есть, в самом младшем разряде оказывается целая
часть последнего произведения.
И так, дробная часть: 0.12510 = 0.0012
3) Синтезируем исходное число : 327.125 как
композицию знака, целой и дробной частей.
Ответ: 327.12510 = 101000111.0012
21.
Решение задачПереведите числа из десятичной системы
счисления в двоичную систему счисления.
а) 94810=
б) 76310=
в) 994,12510=
г) 523,2510=
д) 203,8210=


















 Информатика
Информатика








