Системы счисления. Позиционные системы счисления

1.

ТЕМА 1
СИСТЕМЫ СЧИСЛЕНИЯ

2.

Позиционные системы счисления
В
десятичной
системе
счисления
(с/с)
используются десять арабских цифр от 0 до 9.
Располагая цифры в разных позициях, мы получаем
различные
числа.
Такая
с/с
называется
позиционной, в ней величина числа определяется
положением и значением каждой его цифры.
Другим примером позиционной с/с может служить
римская с/с. Наряду с позиционными существуют и
непозиционные системы счисления.

3.

Позиционные системы счисления

4.

Позиционные системы счисления
• Используя те же обозначения, число N можно представить в виде
суммы элементов ряда:

5.

Позиционные системы счисления
Несмотря на то, что десятичная с/с является для
нас наиболее привычной и удобной в
использовании, реализация на её основе
вычислительной техники – не рационально.
Поэтому основной с/с для внутреннего хранения и
обработки данных в компьютере являются
двоичная и производные от неё восьмеричная и
шестнадцатеричная с/с.

6.

Двоичная система счисления
В двоичной системе счисления (2 с/с) используется две цифры 0 и 1,
основание с/с А=2. Например, двоичное число 1011012 соответствует
десятичному числу 4510.
Использование в двоичной с/с минимального количества цифр, для
записи чисел, позволяет наиболее экономично реализовывать
аппаратную часть ЭВМ. Каждая цифра двоичного числа называется
бит. Бит называется также двоичным разрядом. Группа из 8 бит
составляет байт, который может хранить различные типы данных,
такие как буквы алфавита, десятичные цифры или другие знаки.
Таким образом, 1 бит = 2-3 байт.

7.

Двоичная система счисления
• Байт является основной единицей измерения информации.
Кроме этого для измерения объема информации часто
используются следующие производные от байта:
• 1 Кбайт (килобайт) = 1024 байт = 210 байт,
• 1 Мбайт (мегабайт) = 1024 Кбайт = 220 байт,
• 1 Гбайт (гигабайт) = 1024 Мбайт = 230 байт,
• 1 Тбайт (терабайт) = 1024 Гбайт = 240 байт.

8.

Двоичная система счисления
Для перевода чисел из двоичной с/с в десятичную используются
выражения (1, 2).
Пример. Перевести число из двоичной системы счисления в
десятичную. Т.е. 11101,012 (?)10
1413120110,0-11-2 1 24 + 1 23 + 1 22 + 0 21 + 1 20 + 0 2-1 + 1 2-2 = 29,2510
• Существенным недостатком двоичной с/с является громоздкая запись
чисел. Для упрощения записи двоичных чисел могут быть
использованы восьмеричная и шестнадцатеричная с/с.

9.

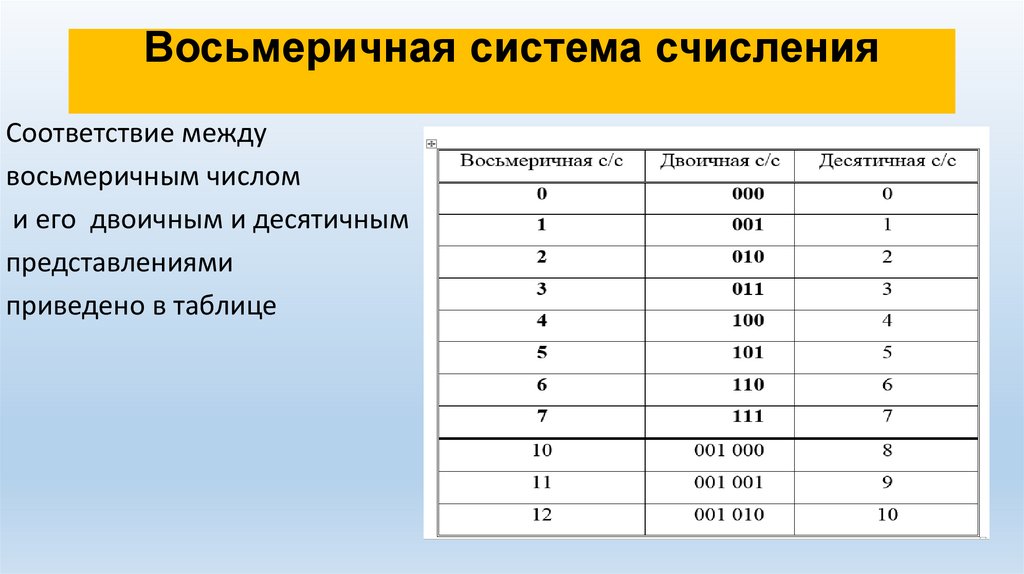
Восьмеричная система счисления
В восьмеричной системе счисления, которая
является производной от двоичной, используется
восемь цифр от 0 до 7, и её основание А=8.
Основание восьмеричной с/с, т. е. число 8, можно
представить в виде 23. Поэтому одной
восьмеричной цифре соответствует три двоичных
разряда – триада.

10.

Восьмеричная система счисления
Соответствие между
восьмеричным числом
и его двоичным и десятичным
представлениями
приведено в таблице

11.

Восьмеричная система счисления
Для перевода двоичного числа в восьмеричное
необходимо разбить двоичное число на триады
следующим образом: целая часть разбивается на триады,
начиная с младших разрядов (с правого края целой части
числа), а дробная часть – с левого края. Разряды, которых
не хватает для формирования триад с левого или правого
краев, заполняются 0. Полученные триады с помощью
таблицы 1.1, заменяются восьмеричными цифрами.
Пример. 1011010110,012 (?)8
1011010110,012 001 011 010 110 , 010 1326,28

12.

Восьмеричная система счисления
Для выполнения обратного перевода (из 8 с/с в 2 с/с)
каждую восьмеричную цифру заменяют соответствующей
двоичной триадой. Незначащие 0 в целой и дробной
частях полученного числа можно отбросить.
Пример. 357,248 (?)2
357,248 011 101 111 , 010 100 11101111,01012

13.

Восьмеричная система счисления
Для перевода числа из восьмеричной с/с в
десятичную также используются выражения (1, 2).
Пример. 357,248 (?)10
последовательность весовых коэффициентов имеет
вид
32 51 70,2-1 4-2 3 82 + 5 81 + 7 80 + 2 8-1 + 4 8-2 =
239,312510

14.

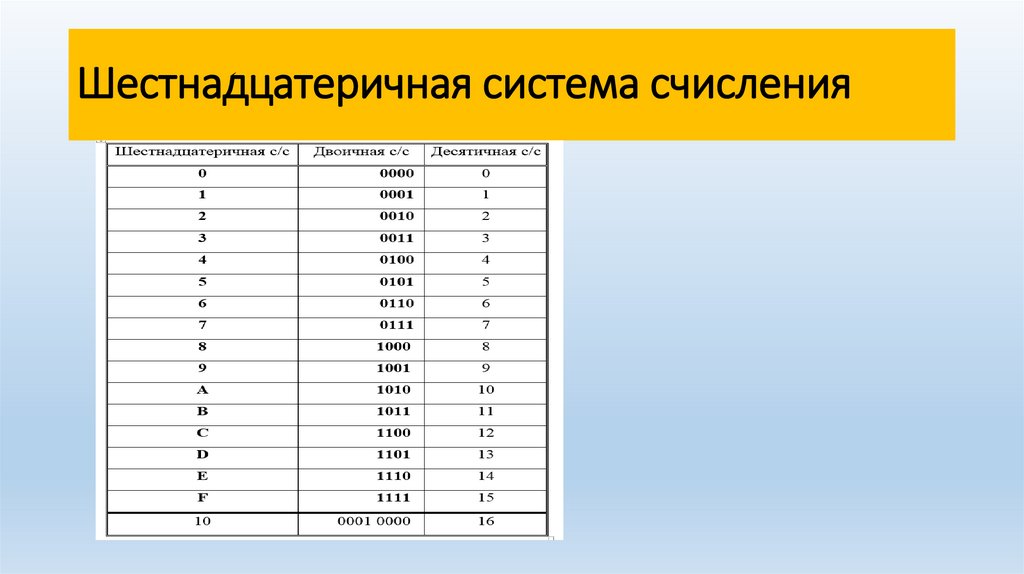
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления используется
десять цифр от 0 до 9 и шесть латинских букв A, B, C, D, E, F.
Основание с/с А=16 можно представить в виде 24. Поэтому
одной шестнадцатеричной цифре соответствует четыре
двоичных разряда – тетрада.

15.

Шестнадцатеричная система счисления

16.

Шестнадцатеричная система счисления
Перевод из двоичной с/с в шестнадцатеричную с/с и обратно
выполняется способом, описанным для восьмеричной с/с. Полученные
при этом тетрады с помощью таблицы 1.2, заменяются
шестнадцатеричными цифрами и наоборот.
Пример: 1011010110,012 (?)16
1011010110,012 0010 1101 0110 , 0100 2D6,216
4А9,В216 (?)2
4А9,В216 0100 1010 1001 , 1011 0010 10010101001,10110012
При переводе из шестнадцатеричной с/с в десятичную также
используются выражения (1, 2).

17.

Шестнадцатеричная система счисления
Пример: 2D6,216 (?)10
последовательность весовых коэффициентов имеет вид
22 D1 60,2-1 2 162 + 13 161 + 6 160 + 2 16-1 = 726,12510
Перевод из шестнадцатеричной с/с в восьмеричную и наоборот
выполняется в два этапа. В начале выполняется перевод в двоичную с/с,
а затем из двоичной в требуемую с/с, описанным выше способом.
Пример: 4А9,В16 (?)8
4А9,В16 0100 1010 1001,10112 010 010 101 001,101 1002 2251,548
357,248 (?)16
357,248 011 101 111,010 1002 0000 1110 1111,0101 00002 EF,516

18.

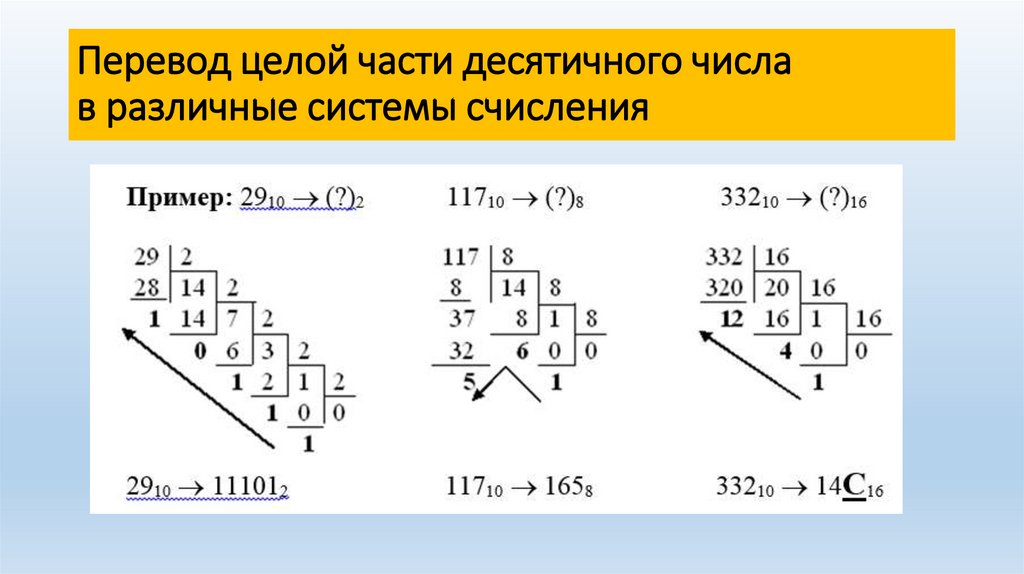
Перевод целой части десятичного числа
в различные системы счисления
Перевод целого числа представленного в
десятичной с/с в двоичную, восьмеричную или
шестнадцатеричную с/с выполняется путём
целочисленного деления исходного числа на
основание новой с/с.

19.

Перевод целой части десятичного числа
в различные системы счисления
При этом необходимо выполнить следующую последовательность
действий:
1. Разделить нацело исходное число на основание новой с/с. Остаток
от деления даёт младшую цифру числа в новой с/с.
2. Если частное от деления не равно 0, то перейти к пункту 3, иначе
перейти к пункту 4.
3. Разделить полученное частное нацело на основание новой с/с.
Остаток от деления даёт следующую цифру числа в новой с/с. Перейти
к пункту 2.
4. Полученные в результате делений остатки, записать в порядке
обратном их вычислению. Это и будет исходное число в новой с/с.

20.

Перевод целой части десятичного числа
в различные системы счисления

21.

Перевод дробной части десятичного числа в
различные системы счисления с заданной точностью
• Перевод дробной части числа представленного в десятичной с/с в
двоичную, восьмеричную или шестнадцатеричную системы
счисления выполняется путём умножения дробной части
исходного числа на основание новой с/с. Так как процесс
последовательного умножения может продолжаться до
бесконечности, то перевод выполняется либо до получения
требуемого количества разрядов в дробной части числа в новой
с/с или до достижения заданной точности.

22.

Перевод дробной части десятичного числа в
различные системы счисления с заданной точностью
ПРИ этом необходимо выполнить следующую последовательность действий:
1. Умножить дробную часть исходного числа на основание новой с/с. Целая
часть полученного произведения даёт первую цифру дробной части числа в
новой с/с.
2. Дробную часть полученного произведения умножить на основание новой с/с.
Целая часть полученного произведения даёт следующую цифру дробной части
числа в новой с/с.
3. Если достигнута заданная точность или получено требуемое количество цифр
в дробной части числа в новой с/с то перейти к п. 4, иначе повторить п. 2.
4. Полученные в результате умножения целые части произведений, записать в
порядке их вычисления. Это и будет дробная часть исходного числа в новой с/с.

23.

Перевод дробной части десятичного числа в
различные системы счисления с заданной точностью

24.

Перевод десятичного числа, содержащего
целую и дробную части
• Перевод десятичного числа, содержащего целую и дробную
части, в двоичную, восьмеричную или шестнадцатеричную
системы счисления, происходит в два этапа. Вначале
переводится целая часть, а затем дробная часть числа.
• Пример. 299,1610 (?)16 = 12B,28F16