Похожие презентации:
Полное исследование функции (тема 6)
1.
МатематикаПреподаватели:
Кормилицына Елена Анатольевна,
Федотова Екатерина Алексеевна
2.
Тема 6.Полное
исследование
функции
3.
План лекции1. Односторонние пределы.
2. Точки разрыва.
3. Асимптоты.
4. Выпуклость функции.
4.
Непрерывность - одно изосновных свойств функций.
Решение о том, непрерывна
данная функция или нет,
позволяет судить о других
важных свойствах
исследуемой функции.
5.
Исследование функции нанепрерывность связанно с так
называемыми односторонними
пределами, т.е пределом слева и
справа.
Односторонние пределы
позволяют сделать вывод о
непрерывности функции.
6.
1. Односторонние пределы7.
8.
9.
ПримерВычислить односторонние
пределы в точке x 3
функции
f ( x) 2
1
x 3
10.
2. Точки разрываx
Опр. Точка
называется
0
точкой разрыва функции
f (x), если в этой точке
нарушается условие
непрерывности. В этом случае
говорят, что функция терпит
разрыв.
11.
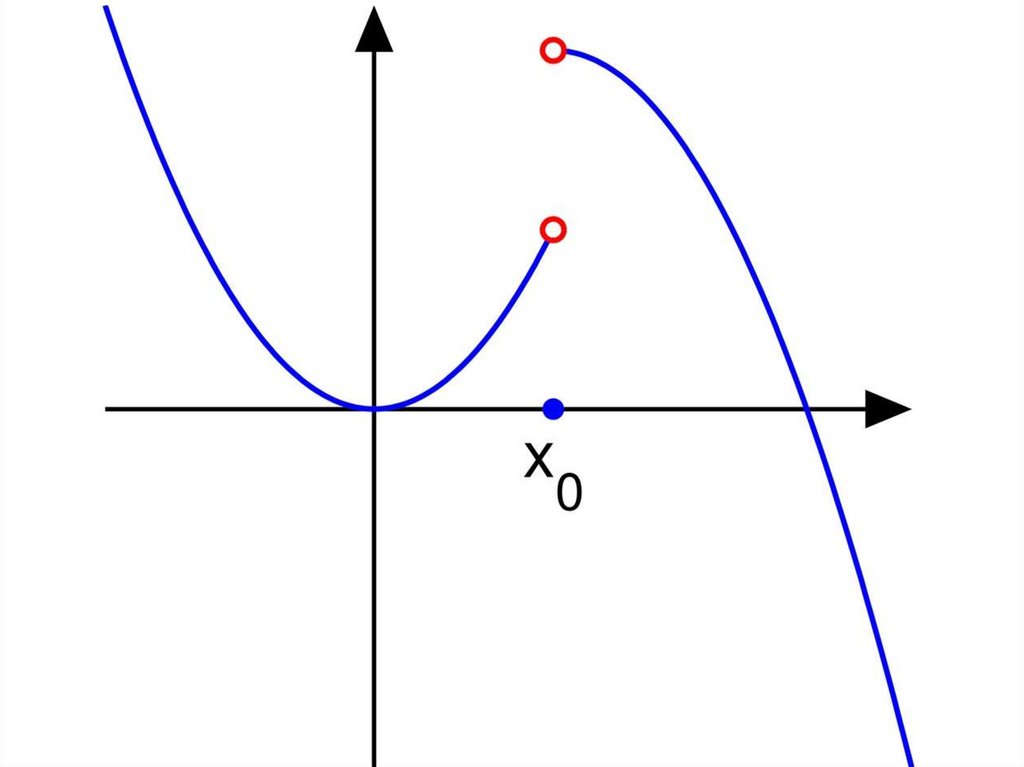
Классификация точек разрыва1. Точка x0 называется
точкой разрыва первого
рода функции f (x ) , если в
этой точке односторонние
пределы конечны и не равны
между собой.
12.
13.
x2. Точка
называется
0
точкой разрыва второго
рода функции f (x ) , если в
этой точке, по крайней мере,
один из односторонних
пределов равен бесконечности
или не существует.
14.
15.
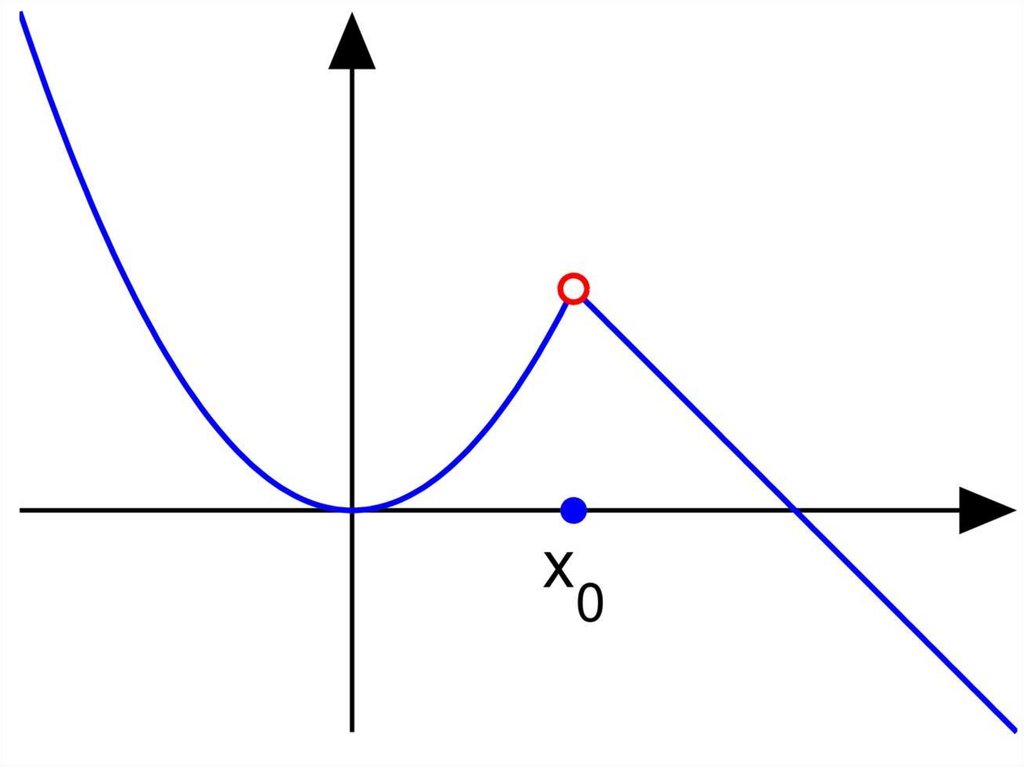
x3. Точка
называется
0
точкой устранимого
разрыва функции f (x ) , если
в этой точке односторонние
пределы конечны и равны
между собой, но не равны
значению функции в этой точке
(функция м.б. не определена).
16.
17.
3. АсимптотыОпр. Асимптотой графика
функции f (x ) называется
прямая линия, обладающая
тем свойством, что расстояние
от переменной точки на
графике до прямой стремится
к нулю
18.
при неограниченномдвижении этой точки по
графику к бесконечности.
Асимптоты могут
быть вертикальными, наклон
ными и горизонтальными.
19.
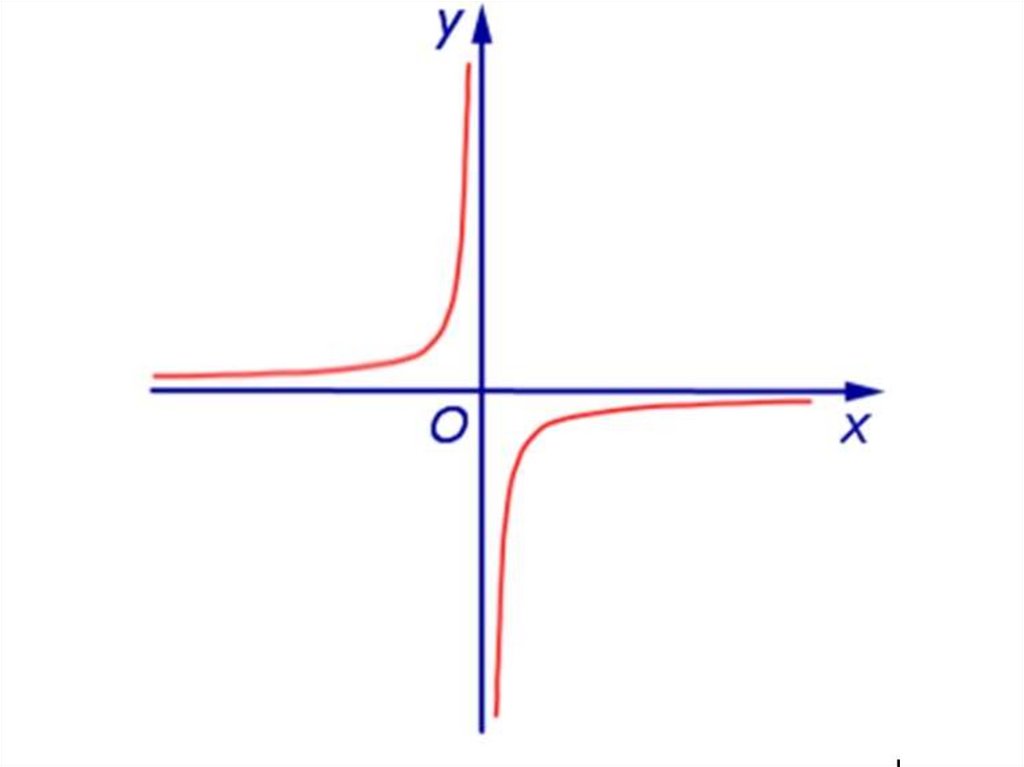
x aОпр. Прямая
называется вертикальной
асимптотой графика функции
f (x ) , если выполнено хотя
бы одно из условий
lim f ( x) ;
x a 0
lim f ( x) .
x a 0
20.
Другими словами, хотя быодин из односторонних
пределов в точке
должен
быть равен бесконечности.
Есть связь вертикальной
асимптоты и точек разрыва
второго рода.
x a
21.
Замечание!Если функция f (x ) в точке
терпит разрыв второго
рода, то прямая
является вертикальной
асимптотой функции f (x ).
a
x a
22.
Опр. Прямая y kx bназывается наклонной
асимптотой графика функции
f (x), если
lim ( f ( x) y ) 0
x
23.
На практике, вычислениенаклонной асимптоты
y=kx+b
сводится к отысканию
коэффициентов k и b , которые
определяются с помощью
следующей теоремы.
24.
Теорема(Необходимое идостаточное условие
существования наклонной
асимптоты).
Для того, что бы прямая
y=kx+b
была наклонной асимптотой
графика функции f (x )
25.
при x , необходимо идостаточно, чтобы
существовали два конечных
f ( x)
предела
lim
x
k;
x
lim ( f ( x) kx) b.
x
26.
Опр. Наклонная асимптотаназывается горизонтальной,
если k=0. Таким образом
уравнение горизонтальной
асимптоты имеет вид
y=b .
27.
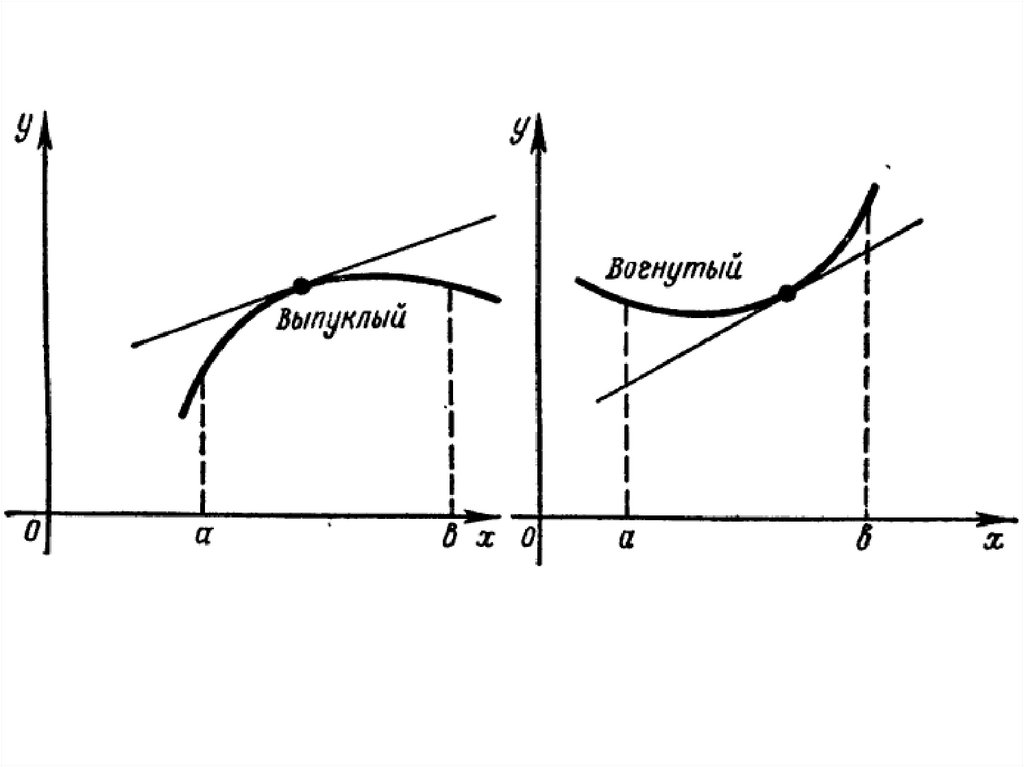
4. Выпуклость функции28.
29.
30.
31.
32.
Алгоритм исследованияфункции
1. Найти область определения
функции и точки пересечения
с осями Ox и Oy;
2. Определить характер
разрыва;
33.
3. Найти асимптоты;4. Исследовать на
монотонность и экстремум;
5. Найти точку перегиба по
Теореме(необходимое условие
существования точки
перегиба);
34.
6. Исследовать на выпуклостьи вогнутость по
Теореме(достаточное условие
выпуклости);
7. Построить эскиз графика
функции.
35.
Примерx ( x 2)
f ( x)
2
( x 1)
2
36.
СПАСИБО ЗАВНИМАНИЕ!
































 Математика
Математика








