Похожие презентации:
Общие сведения о геодезии. Связь геодезии с другими науками
1. Лекция №1 доцент кафедры геологии, геодезии и БЖД Тетерина Ирина Ивановна
1 Общие сведения о геодезии.Связь геодезии с другими науками.
2 Сведения о фигуре Земли: понятие геоида,
референц-эллипсоида.
3 Применяемые в геодезии системы
координат: географическая, полярная,
прямоугольная.
2. Учебники по инженерной геодезии
В. Н. Попов, В. А. Букринский - Геодезия имаркшейдерия
Чекалин С. И. - Основы картографии, топографии и
инженерной геодезии
Г. А. Шеховцов – Инженерная геодезия
Д.Ш. Михелев и др. - Инженерная геодезия
3.
1 Общие сведения о геодезии.Геодезия
как наука занимается изучением формы и размеров
Земли в целом и отдельных её частей.
Геодезия
(в переводе с греч. – «землеразделение») возникла в
глубокой древности и развивалась с ростом
потребностей человека в жилье, делении земельных
массивов, изучении природных богатств и их
освоении.
4. Научно-технические задачи геодезии заключаются в следующем:
‒ определение положения точек в выбраннойсистеме координат;
‒ составление карт и планов местности разного
назначения;
‒ обеспечение топографо-геодезическими данными
нужд обороны страны;
‒ выполнение геодезических измерений для целей
проектирования и строительства, исследования
природных ресурсов.
5.
В геодезии как науке в зависимости отрешаемых задач выделяется ряд дисциплин.
Задачей определения фигуры (формы) и размеров
Земли, а также вопросами создания высокоточных
геодезических опорных сетей занимается высшая
геодезия.
Вопросы, связанные с изображением сравнительно
небольших частей земной поверхности в виде планов и
профилей, решает топография (в строительстве –
инженерная геодезия).
Созданием сплошных изображений значительных
территорий в виде карт занимается картография.
Космогеодезия, маркшейдерия (подземная геодезия)
также являются научными направлениями в геодезии.
6. Задачи геодезии, которые она решает для горной промышленности:
- топографическая съёмка территорий,- перенесение в натуру проектов объектов
горного производства, зданий и сооружений,
- различные измерения на отдельных стадиях
разработки месторождений,
- определение деформаций и сдвигов в процессе
разработки месторождений полезных ископаемых.
7. Решение этих задач осуществляется путём:
– измерения линий и углов на поверхности земли,под землёй (в шахтах и других горных выработках) ‒
для составления планов, профилей;
– обработки результатов измерений;
– графических построений и оформления карт,
планов и профилей.
8.
Горный инженер должен уметь самостоятельновыполнять геодезические измерения на местности с
помощью теодолита, нивелира и других приборов.
Составленные по результатам этих измерений планы,
карты, профили позволяют контролировать ход
горных работ.
Геодезия тесно связана с математикой, астрономией,
географией, геологией, геоморфологией, механикой,
оптикой, электроникой, черчением.
9. 2 Сведения о фигуре Земли: понятие геоида, референц-эллипсоида.
Физическая поверхность Земли состоит изподводной (70,8 %) и надводной (29,2 %) частей.
Надводная часть земной поверхности
характеризуется многообразием форм.
также
10.
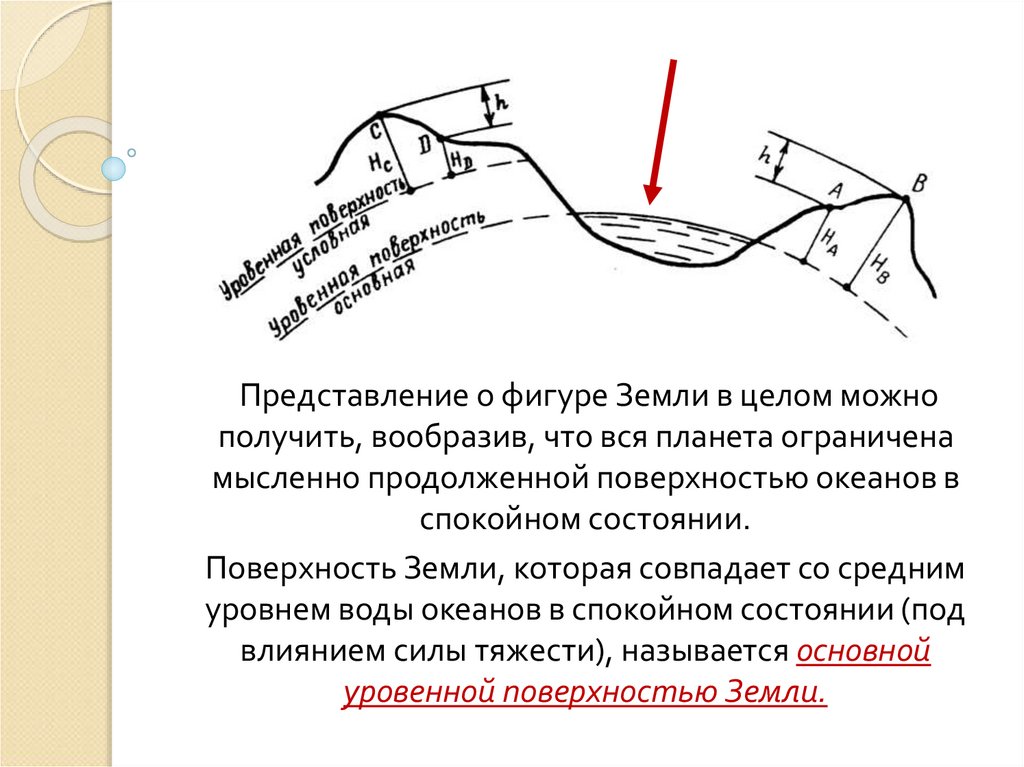
Представление о фигуре Земли в целом можнополучить, вообразив, что вся планета ограничена
мысленно продолженной поверхностью океанов в
спокойном состоянии.
Поверхность Земли, которая совпадает со средним
уровнем воды океанов в спокойном состоянии (под
влиянием силы тяжести), называется основной
уровенной поверхностью Земли.
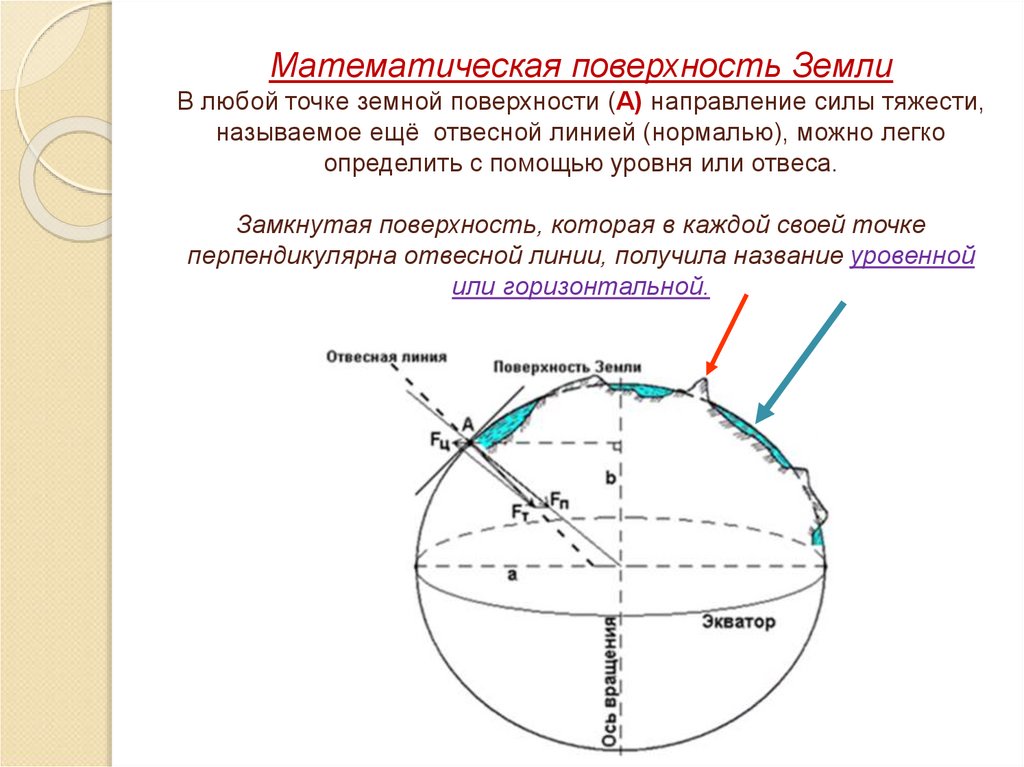
11. Математическая поверхность Земли В любой точке земной поверхности (А) направление силы тяжести, называемое ещё отвесной линией
(нормалью), можно легкоопределить с помощью уровня или отвеса.
Замкнутая поверхность, которая в каждой своей точке
перпендикулярна отвесной линии, получила название уровенной
или горизонтальной.
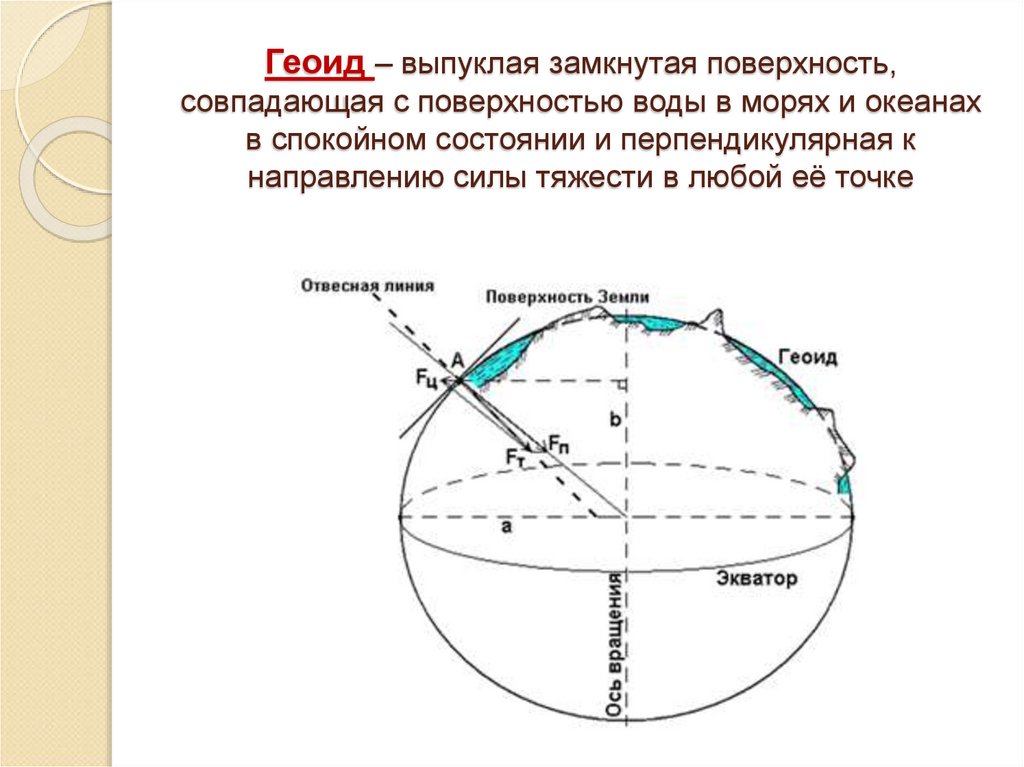
12. Геоид – выпуклая замкнутая поверхность, совпадающая с поверхностью воды в морях и океанах в спокойном состоянии и
перпендикулярная кнаправлению силы тяжести в любой её точке
13. Из-за неравномерного распределения масс внутри Земли геоид не имеет правильной геометрической формы, и в математическом
отношении его поверхность характеризуетсяслишком большой сложностью
14. Поверхность геоида заменяют математической поверхностью эллипсоида вращения – из правильных математических поверхностей он
ближе всего к поверхности геоида.Эта поверхность получается от вращения эллипса АВА1В1 вокруг
малой оси ВВ1.
Изучение формы математической поверхности Земли сводится к
определению размеров полуосей а и b и полярного сжатия
эллипсоида:
15. Для территории нашей страны в качестве математической поверхности Земли утвержден эллипсоид Красовского (референц-эллипсоид).
Для решения большинства задач инженерной геодезии за фигуруЗемли принимают сферу радиусом 6371,11 км.
16. 3 Применяемые в геодезии системы координат: географическая, полярная, прямоугольная.
Задача топографии – построение планов и картЗемной поверхности.
Для этого:
определяют пространственные координаты характерных
точек, необходимых для моделирования местности
относительно поверхности Земли.
Модель местности может быть представлена в виде
геодезических чертежей, планов и карт.
Для построения моделей местности в геодезии применяют
метод проекций.
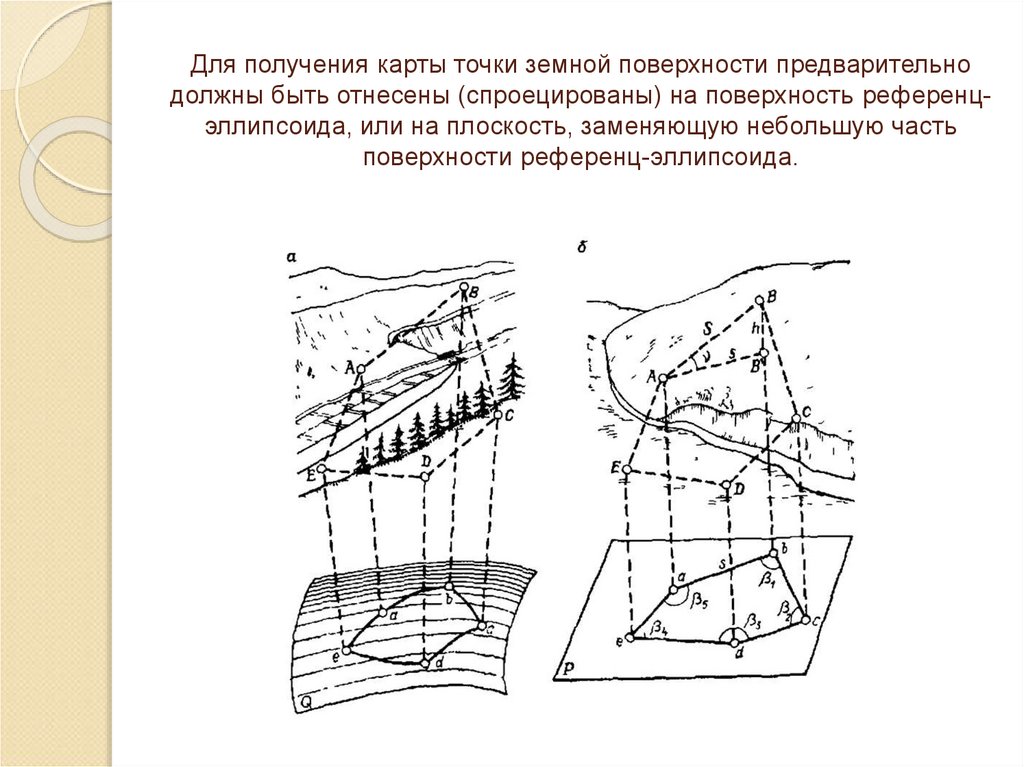
17. Для получения карты точки земной поверхности предварительно должны быть отнесены (спроецированы) на поверхность
референцэллипсоида, или на плоскость, заменяющую небольшую частьповерхности референц-эллипсоида.
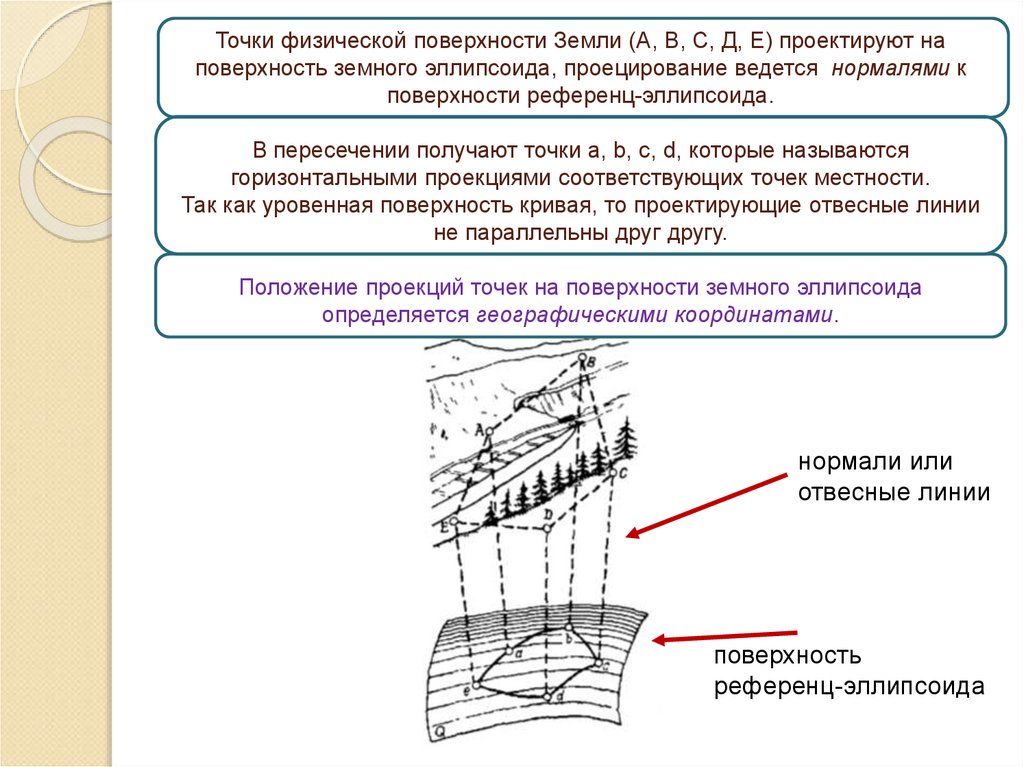
18. Точки физической поверхности Земли (А, В, С, Д, Е) проектируют на поверхность земного эллипсоида, проецирование ведется
нормалями кповерхности референц-эллипсоида.
В пересечении получают точки а, b, с, d, которые называются
горизонтальными проекциями соответствующих точек местности.
Так как уровенная поверхность кривая, то проектирующие отвесные линии
не параллельны друг другу.
Положение проекций точек на поверхности земного эллипсоида
определяется географическими координатами.
нормали
или
отвесные линии
поверхность
референц-эллипсоида
19. На небольшом участке местности кривую уровенную поверхность Q заменяют горизонтальной плоскостью Р. Проектирующие отвесные
линии Аа, Вb, Cc, Дd перпендикулярны кгоризонтальной плоскости Р и параллельны между собой.
Проецирование точек местности на горизонтальную плоскость под прямым
к ней углом называется ортогональным,
а полученные проекции — ортогональными.
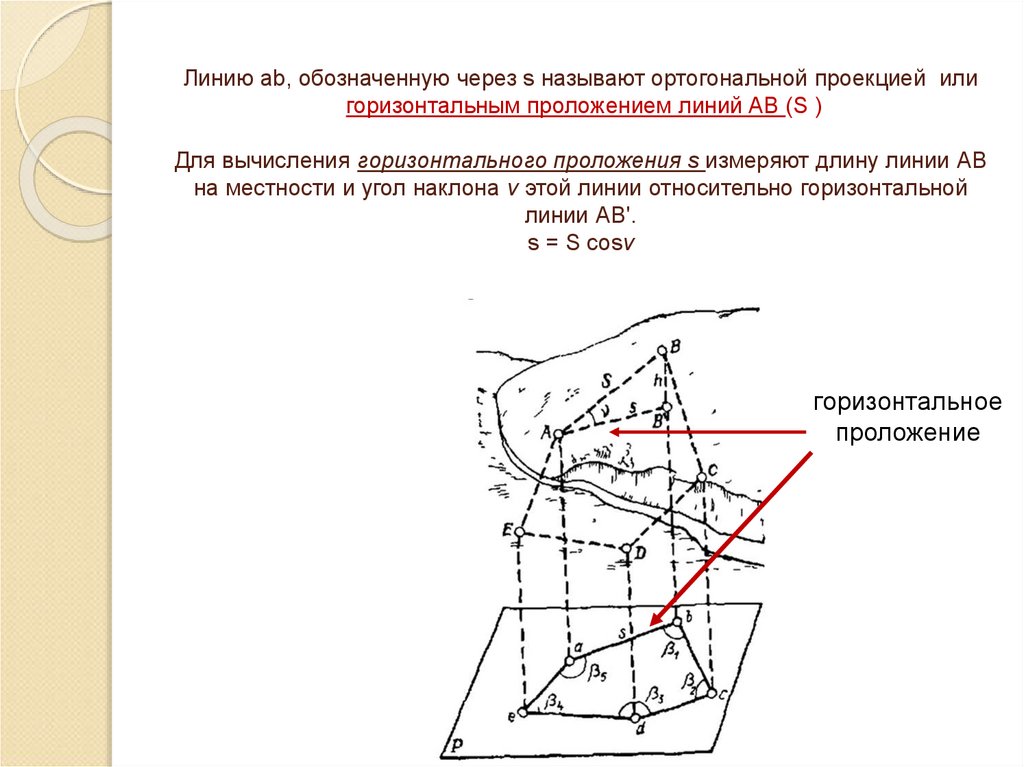
20. Линию ab, обозначенную через s называют ортогональной проекцией или горизонтальным проложением линий AB (S ) Для вычисления
горизонтального проложения s измеряют длину линии АВна местности и угол наклона v этой линии относительно горизонтальной
линии АВ'.
s = S cosv
горизонтальное
проложение
21. Отстояние точек земной поверхности по отвесной линии от поверхности, на которую они проецируются, называется высотой точек.
Высоты считаются абсолютными, если точки проецируются на основнуюуровенную поверхность (геоид), и считаются относительными, если
проецирование ведется на любую другую уровенную поверхность.
Разность h абсолютных или условных высот двух точек называется
превышением.
h = HВ – НА.
22.
Ортометрическая (абсолютная) высота Hо– расстояние,отсчитываемое по направлению отвесной линии от поверхности
геоида до данной точки.
Геодезическая высота Hг – расстояние, отсчитываемое по
направлению нормали от поверхности референц-эллипсоида до
данной точки.
В России абсолютные высоты точек определяются в Балтийской
системе высот (БСВ)относительно нуля Кронштадтского футштока–
горизонтальной черты на медной пластине, прикрепленной к устою
моста через обводной канал в г. Кронштадте.
Местная система высот – Тихоокеанская, её уровенная поверхность
ниже нуля Кронштадтского футштока на 1873 мм.
23. УЧЕТ КРИВИЗНЫ ПОВЕРХНОСТИ ПРИ ОПРЕДЕЛЕНИИ ГОРИЗОНТАЛЬНЫХ И ВЕРТИКАЛЬНЫХ РАССТОЯНИЙ Расчеты показывают, что при замене кривой АВ
= 10кмотрезком касательной d , величина погрешности Δs = 1 см,
что в относительной мере составляет 1:1000 000.
Дугу сферической поверхности Земли длиной до
2s = 20 км можно заменить отрезком касательной, и площадь
участка размером 20 х 20 км может считаться
не частью земного эллипсоида, а плоскостью.
24. При измерении вертикальных расстояний необходимо иметь в виду, что точка В находится на уровенной поверхности и высота равна
нулю.За счет замены криволинейного участка прямой возникает погрешность Δh = BC.
Величину Δh называют поправкой за кривизну Земли.
При передаче высотных отметок на расстояние более 0 ,5 км необходимо учитывать
влияние кривизны Земли.
25. Система координат устанавливает начальные (исходные) точки, поверхности или линии отсчета (начало отсчета координат), а также
единицы их исчисления.В топографии и геодезии наибольшее применение получили
системы географических, прямоугольных и полярных
координат.
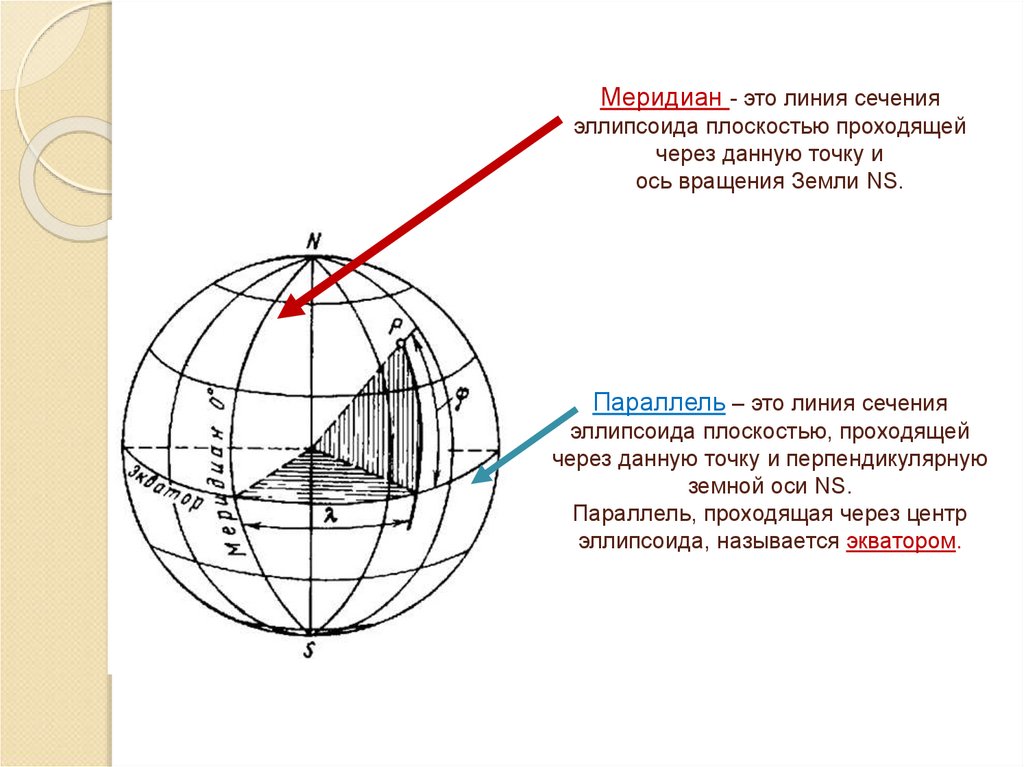
26. Меридиан - это линия сечения эллипсоида плоскостью проходящей через данную точку и ось вращения Земли NS. Параллель – это линия
сеченияэллипсоида плоскостью, проходящей
через данную точку и перпендикулярную
земной оси NS.
Параллель, проходящая через центр
эллипсоида, называется экватором.
27.
Географические координаты могут быть получены наосновании астрономических наблюдений или геодезических
измерений.
В первом случае их называют астрономическими, во
втором - геодезическими.
При астрономических наблюдениях проецирование точек на
поверхность осуществляется отвесными линиями, при
геодезических измерениях - нормалями, поэтому величины
астрономических и геодезических координат несколько
отличаются.
Геодезическими координатами называются угловые
величины (широта и долгота), определяющие положение
точек (объектов) на поверхности земного эллипсоида
(референц-эллипсоида) относительно
плоскости экватора и начального меридиана.
28. Геодезической широтой (В) называется угол, заключенный между плоскостью экватора и нормалью к поверхности земного эллипсоида,
проходящей через данную точку.Геодезической долготой (L) называется двугранный угол, заключенный
между плоскостью начального меридиана и плоскостью геодезического
меридиана, проходящего через данную точку.
29. Астрономические координаты определяют положение точки на поверхности геоида.
Астрономической широтой (φ)называется угол, заключенный
между плоскостью земного
экватора и направлением отвесной
линии в данной точке.
Астрономической долготой (λ)
называется двугранный угол,
заключенный между плоскостью
начального астрономического
меридиана и плоскостью
астрономического меридиана,
проходящего через данную точку.
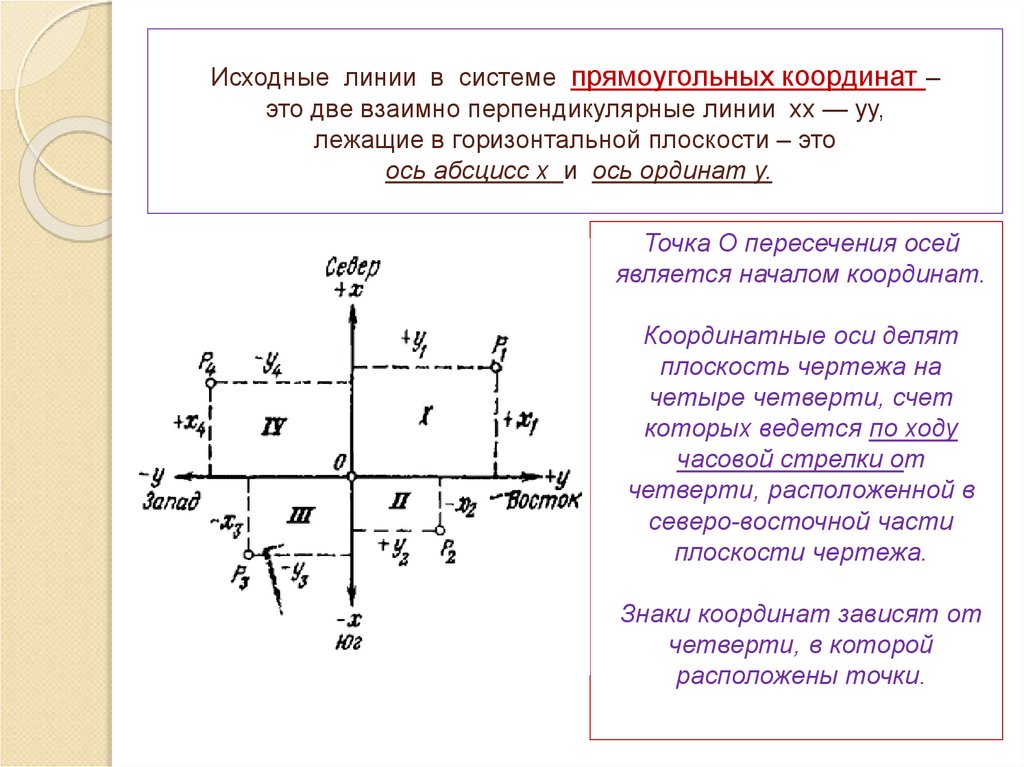
30. Исходные линии в системе прямоугольных координат – это две взаимно перпендикулярные линии хх — уу, лежащие в горизонтальной
плоскости – этоось абсцисс х и ось ординат у.
Точка О пересечения осей
является началом координат.
Координатные оси делят
плоскость чертежа на
четыре четверти, счет
которых ведется по ходу
часовой стрелки от
четверти, расположенной в
северо-восточной части
плоскости чертежа.
Знаки координат зависят от
четверти, в которой
расположены точки.
31. Полярная система координат состоит из полюса О и полярной оси ОР, в качестве которых принимается прямая с известным началом и
Полярная система координатсостоит из полюса О и полярной оси ОР, в качестве которых
принимается прямая с известным началом и направлением.
Для определения
положения точек в данной
системе используют
линейно-угловые
координаты:
- угол β, отсчитываемый по
часовой стрелке от
полярной оси ОР до
направления
на горизонтальную
проекцию точки А',
- полярное расстояние r от
полюса системы О до
проекции А'
32. ЗОНАЛЬНАЯ СИСТЕМА ПРЯМОУГОЛЬНЫХ КООРДИНАТ ГАУССА-КРЮГЕРА
Координаты географической, геодезической иастрономической систем измеряются в градусах,
прямоугольной системы – в метрах,
а полярной системы – в градусах и в метрах.
Для установления связи между ними применяется
четвертая система координат – зональная.
Для уменьшения неизбежных искажений, возникающих
при изображении значительных территорий на плоскости,
прибегают к картографированию территорий по частям.
33. ЗОНАЛЬНАЯ СИСТЕМА ПРЯМОУГОЛЬНЫХ КООРДИНАТ ГАУССА-КРЮГЕРА В зональной системе координат поверхность земного шара (сфероида)
разбивается на зоны (60 зон).Каждая зона ограничена меридианами с разностью долгот 6º и шириной
по экватору 666 км.
Разбивка зон начинается от Гринвичского меридиана с 1-й по 60-ю на
восток.
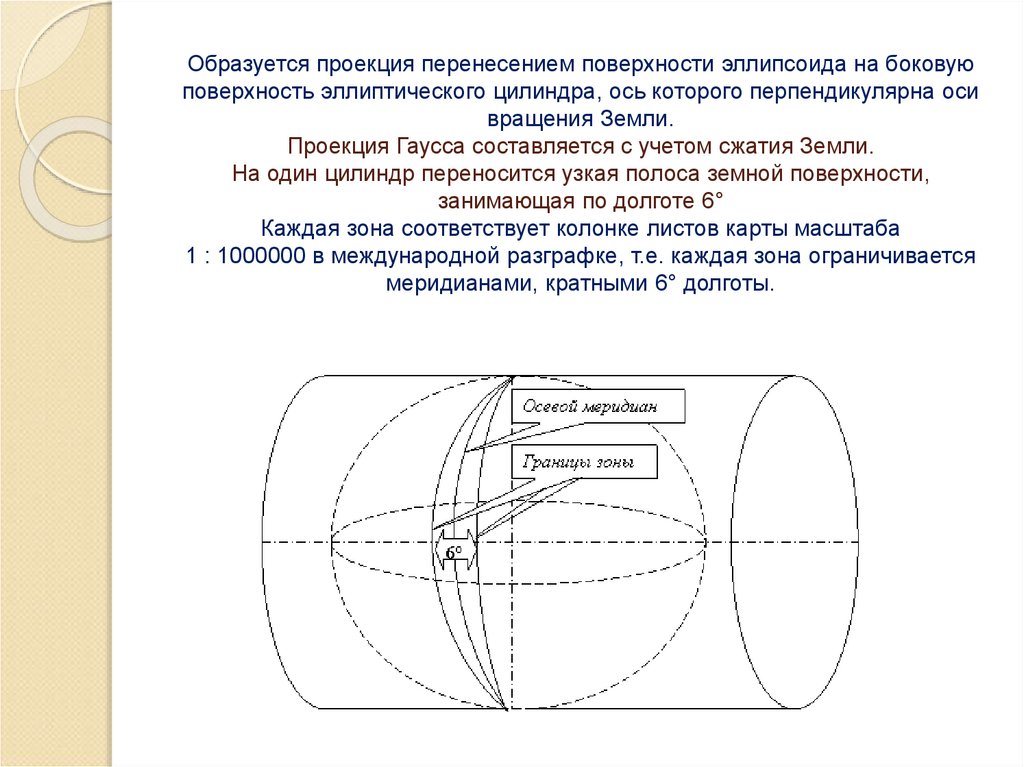
34. Образуется проекция перенесением поверхности эллипсоида на боковую поверхность эллиптического цилиндра, ось которого
перпендикулярна осивращения Земли.
Проекция Гаусса составляется с учетом сжатия Земли.
На один цилиндр переносится узкая полоса земной поверхности,
занимающая по долготе 6°
Каждая зона соответствует колонке листов карты масштаба
1 : 1000000 в международной разграфке, т.е. каждая зона ограничивается
меридианами, кратными 6° долготы.
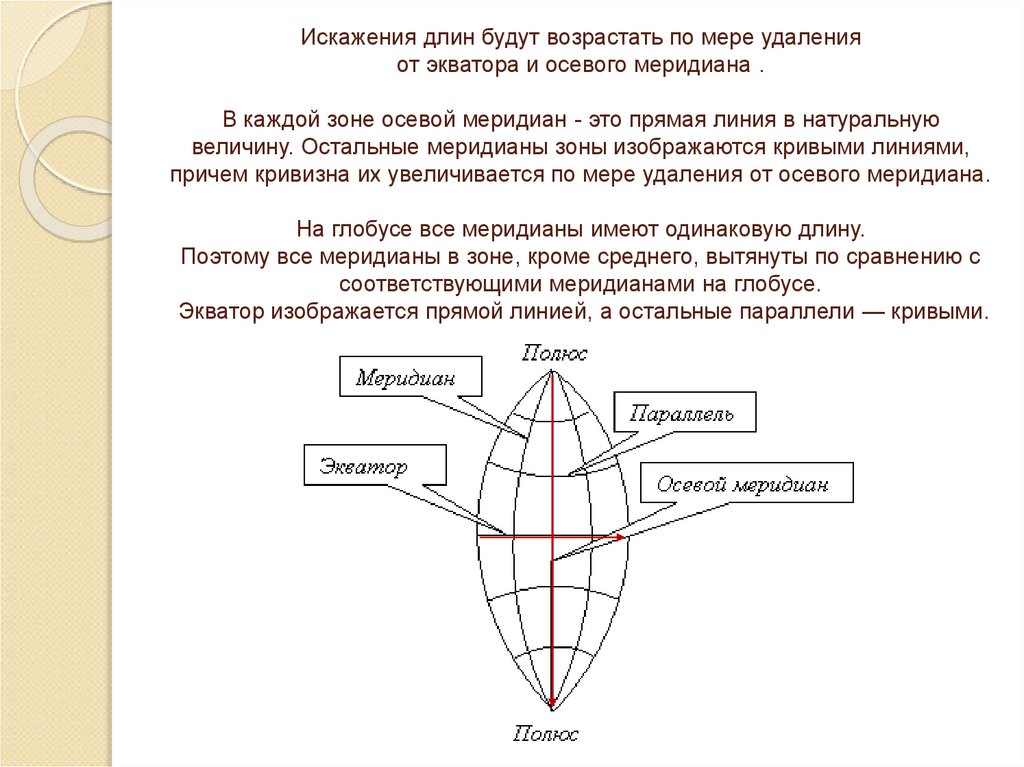
35. Искажения длин будут возрастать по мере удаления от экватора и осевого меридиана . В каждой зоне осевой меридиан - это прямая
линия в натуральнуювеличину. Остальные меридианы зоны изображаются кривыми линиями,
причем кривизна их увеличивается по мере удаления от осевого меридиана.
На глобусе все меридианы имеют одинаковую длину.
Поэтому все меридианы в зоне, кроме среднего, вытянуты по сравнению с
соответствующими меридианами на глобусе.
Экватор изображается прямой линией, а остальные параллели — кривыми.
36.
В каждой развернутой наплоскости зоне осевой
меридиан и экватор взаимно
перпендикулярны, поэтому
их принимают за оси плоской
прямоугольной системы
координат данной зоны.
Знаки координат абсциссы Х
и ордината У будут иметь
такие же знаки как и в
прямоугольной системе:
абсциссы к северу от
экватора положительные, к
югу – отрицательные;
ординаты на восток от
осевого меридиана
положительные, на запад –
отрицательные.
37.
Положение точки А в координатной зоне определяется еерасстоянием хА и yA от осей координат. На территории России все
абсциссы (расстояния от экватора) положительны.
Ординаты в каждой зоне могли бы быть как положительными,
так и отрицательными.
Для удобства работы с картами условились значение ординаты Y
осевого меридиана каждой зоны принимать равным 500 км,
т. е. начало координат как бы вынесли к западу за пределы зоны.
38.
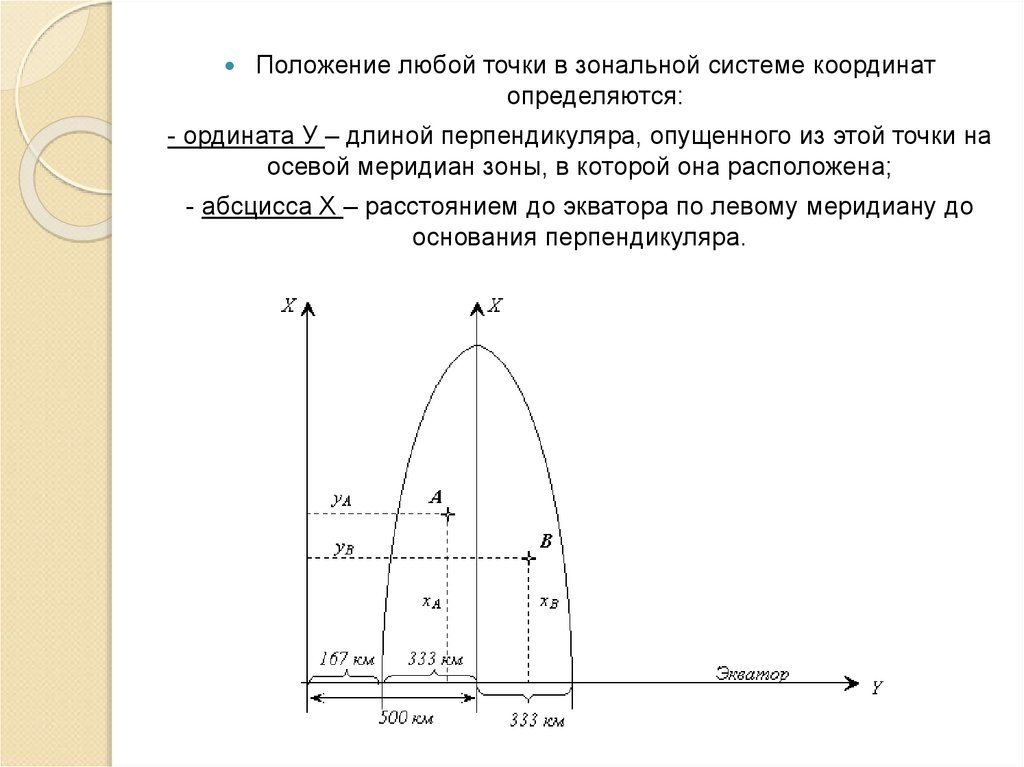
Положение любой точки в зональной системе координатопределяются:
- ордината У – длиной перпендикуляра, опущенного из этой точки на
осевой меридиан зоны, в которой она расположена;
- абсцисса Х – расстоянием до экватора по левому меридиану до
основания перпендикуляра.
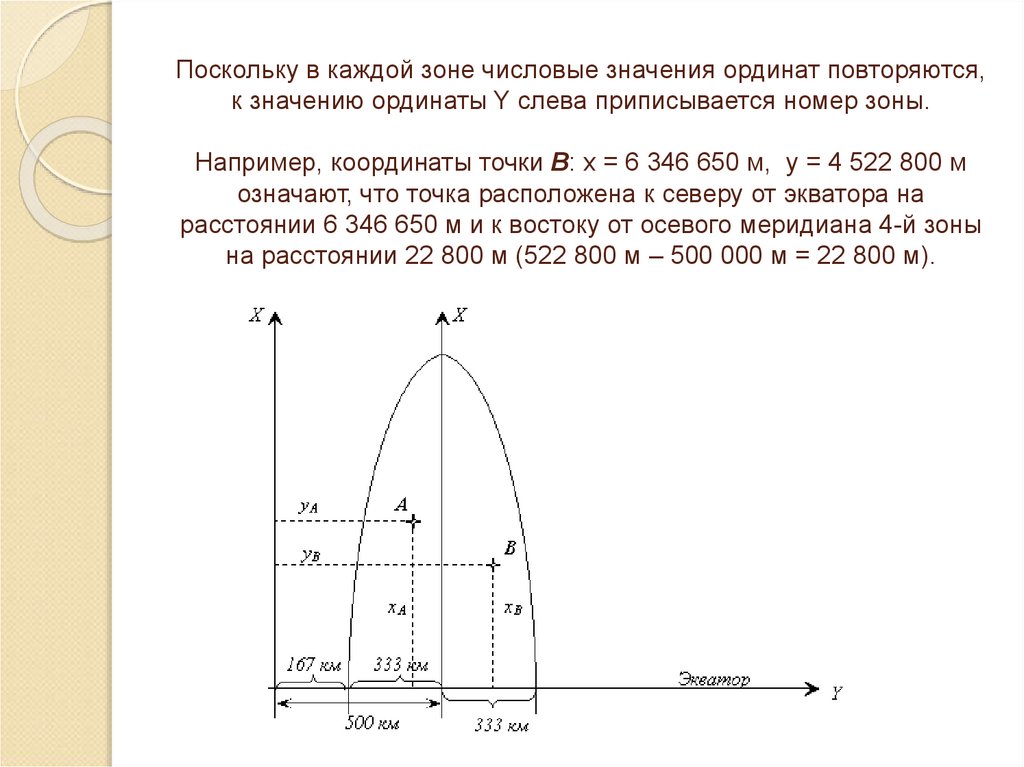
39. Поскольку в каждой зоне числовые значения ординат повторяются, к значению ординаты Y слева приписывается номер зоны. Например,
координаты точки В: х = 6 346 650 м, у = 4 522 800 мозначают, что точка расположена к северу от экватора на
расстоянии 6 346 650 м и к востоку от осевого меридиана 4-й зоны
на расстоянии 22 800 м (522 800 м – 500 000 м = 22 800 м).
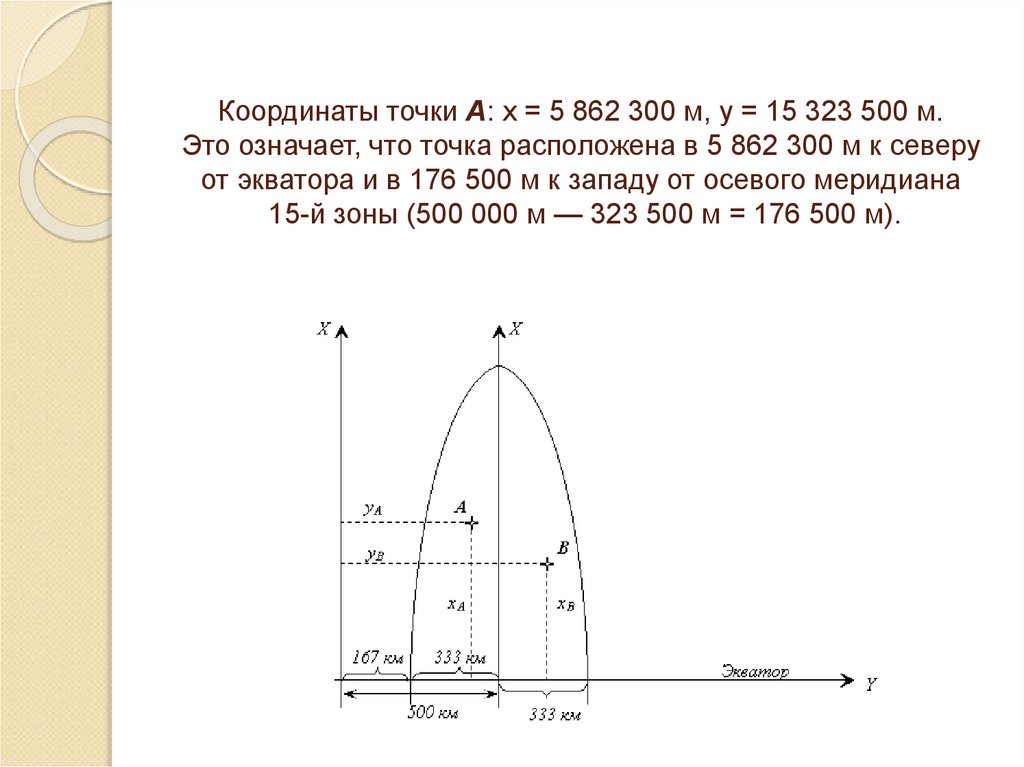
40. Координаты точки А: х = 5 862 300 м, у = 15 323 500 м. Это означает, что точка расположена в 5 862 300 м к северу от экватора и
в 176 500 м к западу от осевого меридиана15-й зоны (500 000 м — 323 500 м = 176 500 м).
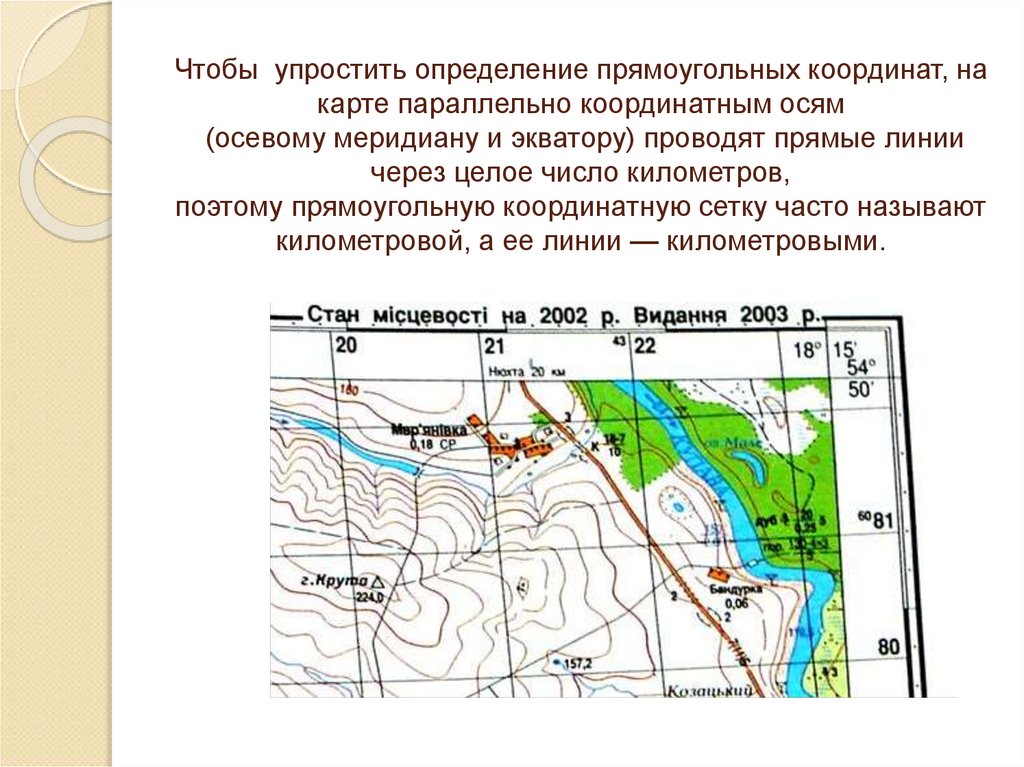
41. Чтобы упростить определение прямоугольных координат, на карте параллельно координатным осям (осевому меридиану и экватору)
проводят прямые линиичерез целое число километров,
поэтому прямоугольную координатную сетку часто называют
километровой, а ее линии — километровыми.
42. С п а с и б о
Спасибоза внимание!



























 География
География








