Похожие презентации:
МД и СУБД. Декомпозиция схем отношений (лекция 8)
1.
МД и СУБДДекомпозиция схем отношений.
Декомпозицией схемы отношения R=(U, F) называется замена ее совокупностью
={R1, R2,..., Rk), где Ri=(Ui), i=l, 2, ..., k, такой, что Ul U2 … Uk=U. При этом не требуется,
чтобы Ui были непересекающимися. Ri будем называть подсхемами отношения R.
Соединение без потерь.
Пусть задана схема отношения R=(U, F) и ее декомпозиция =(R1, R2, …, Rk). Говорят, что эта
декомпозиция обладает свойством соединения без потерь относительно F, если каждое
отношение R для R, удовлетворяющее F, может быть представлено в виде:
R= R1(R) >< R2(R) >< … Rk(R),
то есть R является естественным соединением его проекций на все Ri.
Декомпозиция представляет, вообще говоря, некоторое большее по количеству кортежей
отношение, чем исходное отношение, и если не выполнено условие соединения без
потерь, то мы можем получить кортежи, которых нет в исходном отношении, что
естественно нарушает адекватность базы данных.
Ясно, что свойство соединения без потерь весьма желательно, поскольку в этом случае
может быть восстановлено исходное отношение.
2.
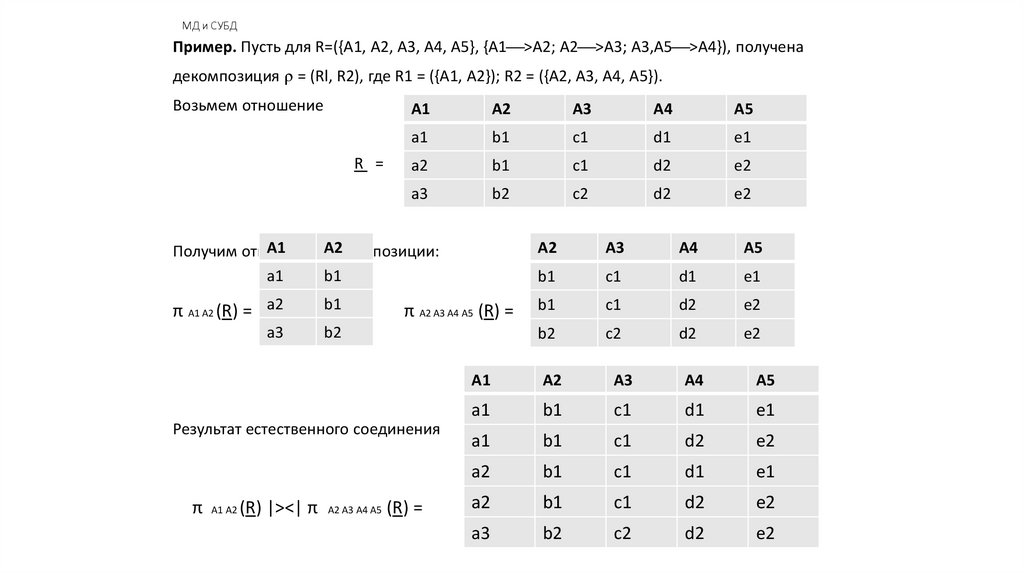
МД и СУБДПример. Пусть для R=({А1, А2, А3, А4, А5}, {A1 >A2; A2 >A3; A3,A5 >A4}), получена
декомпозиция = (Rl, R2), где R1 = ({A1, A2}); R2 = ({A2, A3, A4, A5}).
Возьмем отношение
R =
A1
A2
A3
A4
A5
a1
b1
c1
d1
e1
a2
b1
c1
d2
e2
a3
b2
c2
d2
e2
A1
A2
Получим отношения
декомпозиции:
a1
b1
A2
A3
A4
A5
b1
c1
d1
e1
π A1 A2 (R) = a2
b1
b1
c1
d2
e2
a3
b2
b2
c2
d2
e2
A1
A2
A3
A4
A5
a1
b1
c1
d1
e1
a1
b1
c1
d2
e2
a2
b1
c1
d1
e1
a2
b1
c1
d2
e2
a3
b2
c2
d2
e2
π A2 A3 A4 A5 (R) =
Результат естественного соединения
π A1 A2 (R) |><| π A2 A3 A4 A5 (R) =
3.
МД и СУБДРассмотрим основные свойства отображения проекция-соединение.
Если =(R1, R2, ..., Rk), обозначим через M отображение, которое определяется
соотношением M (R)= R1(R) >< R2(R) >< … Rk(R). Таким образом, условие соединения без
потерь относительно F может быть выражено следующим образом: для всех R,
удовлетворяющих F, R=M (R).
Для любой декомпозиции выполняются следующие условия:
а) R M (R);
б) если S=M (R), то Ri(S)=Ri;
в) M (M (R))=M (R).
Для проверки свойства соединения без потерь можно использовать следующий алгоритм.
Пусть заданы схема отношения R = ({А1, А2, ..., An}, F) и декомпозиция =(R1, R2, ..., Rk),
Ri=(Ui), i=1, 2, ..., k.
Строим таблицу с n столбцами и k строками, столбец j соответствует атрибуту Aj, а строка i
схеме отношения Ri. На пересечении строки i и столбца j поместим символ Aj, если Aj Ui.
B противном случае поместим туда символ *.
Просматриваем каждую из зависимостей Х >Y. Рассматривая зависимость Х—>У,
изменяем строки, которые совпадают по всем столбцам, соответствующим атрибутам из X.
При обнаружении двух таких строк отождествляем их символы в столбцах,
соответствующих атрибутам из Y. Если при этом один из символов в одной из строк равен
Aj, а символ другой строки в этом же столбце равен *, то заменяем * на Aj. Повторяем
просмотр зависимостей до тех пор пока: либо некоторая строка станет равной А1, А2, ..., Аn;
либо больше изменений в таблице провести нельзя. В первом случае декомпозиция
обладает свойством соединения без потерь. Во втором – нет.
4.
МД и СУБДПримеры.
Пусть для схемы R=({А1, А2, А3, А4, А5}, {А1 >А2; А2 >A3; АЗ,А4 >А5; А2 >А4})
получена декомпозиция = (Rl, R2, R3), где R1=({А1, А2}), R2=({А2, АЗ, А4}), R3=({АЗ, А4, А5}).
Требуется проверить, обладает ли она свойством соединения без потерь. Построим
следующие таблицы:
1-я (начальная таблица):
A1
A2
*
*
*
*
A2
A3
A4
*
*
*
A3
A4
A5
2-я таблица:A1
A2
A3
A4
*
*
A2
A3
A4
A5
*
*
A3
A4
A5
A1
A2
A3
A4
A5
3-я таблица:*
A2
A3
A4
A5
*
*
A3
A4
A5
5.
МД и СУБДПримеры.
Пусть для R=({А1, А2, А3, А4, А5}, {A1 >A2; A2 >A3; A3,A5 >A4}), получена декомпозиция =
(Rl, R2), где R1 = ({A1, A2}); R2 = ({A2, A3, A4, A5}).
1-я (начальная таблица):
A1
A2
*
*
*
*
A2
A3
A4
A5
A1
A2
A3
*
*
*
A2
A3
A4
A5
2-я таблица:
Больше никаких изменений в таблице сделать нельзя и строку, содержащую только Аi, мы
не получили, значит, декомпозиция в этом случае не обладает свойством соединения без
потерь.
Справедливо следующее утверждение.
Если =(R1(U1), R2(U2)) – декомпозиция R=(U, F), то обладает свойством соединения без
потерь относительно F тогда и только тогда, когда
((U1 U2) >U1\U2) F+ или ((Ul U2)—>U2\Ul) F+.




 Базы данных
Базы данных








