Статистическая обработка результатов эксперимента

1. Статистическая обработка результатов эксперимента

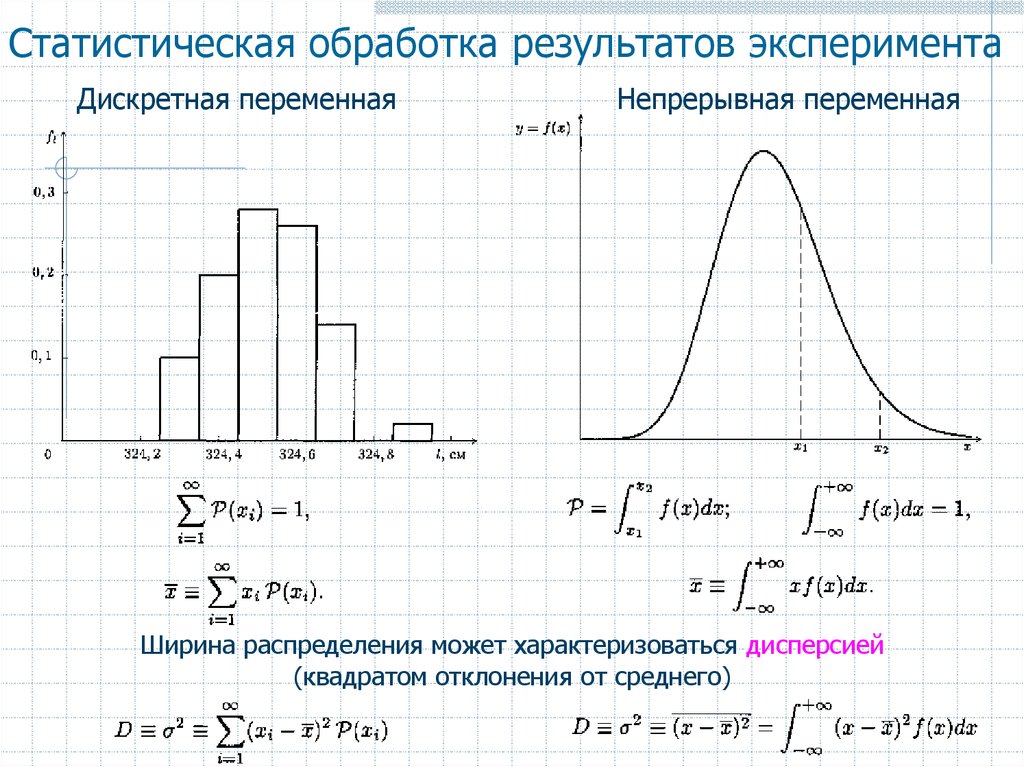
Дискретная переменная
Непрерывная переменная
Ширина распределения может характеризоваться дисперсией
(квадратом отклонения от среднего)

2. Нормальное распределение (распределение Гаусса)

Определение предэкспоненциального множителя

3.

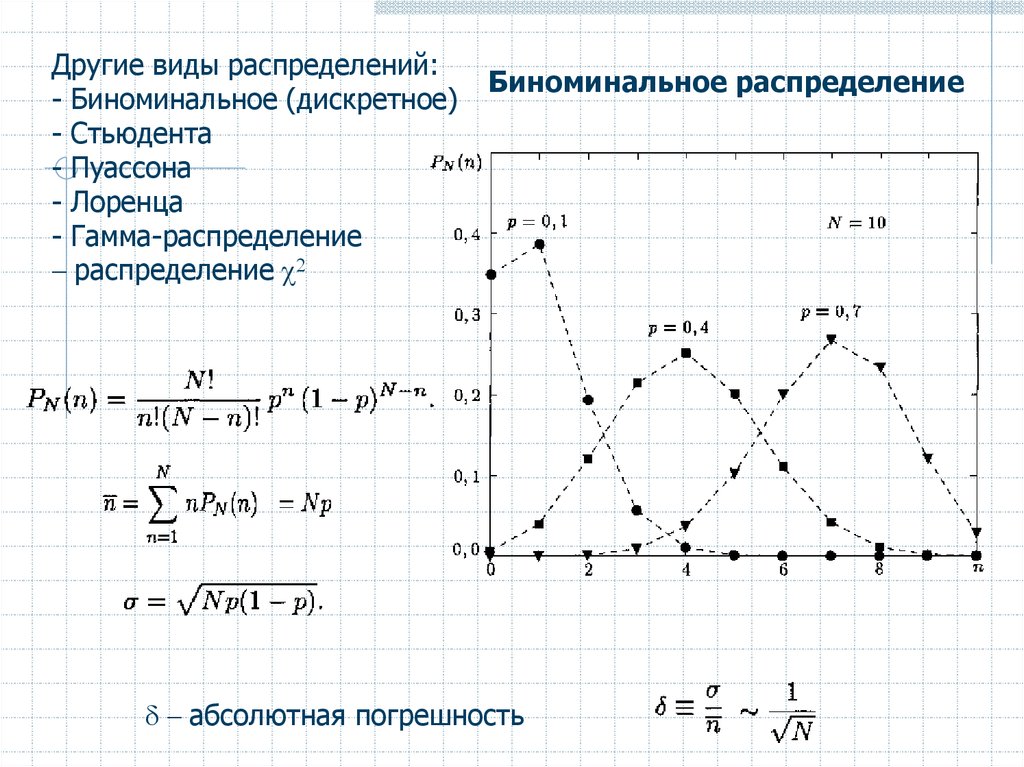
Другие виды распределений:
- Биноминальное (дискретное)
- Стьюдента
- Пуассона
- Лоренца
- Гамма-распределение
- распределение c2
Биноминальное распределение
d - абсолютная погрешность

4.

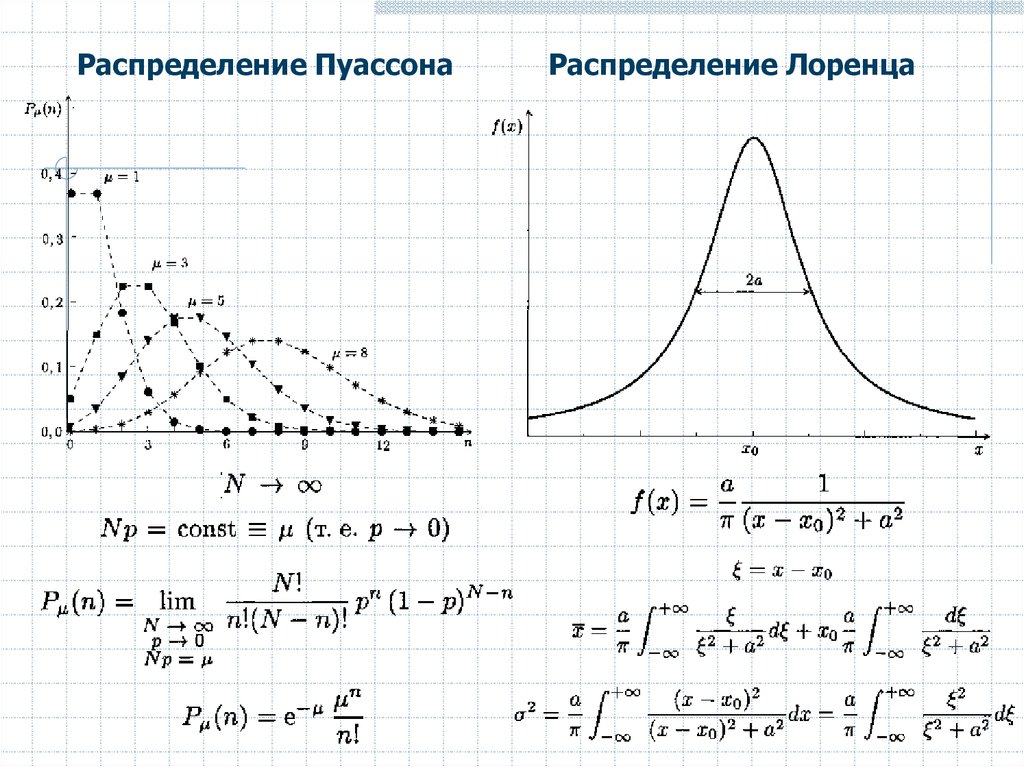
Распределение Пуассона
Распределение Лоренца

5.

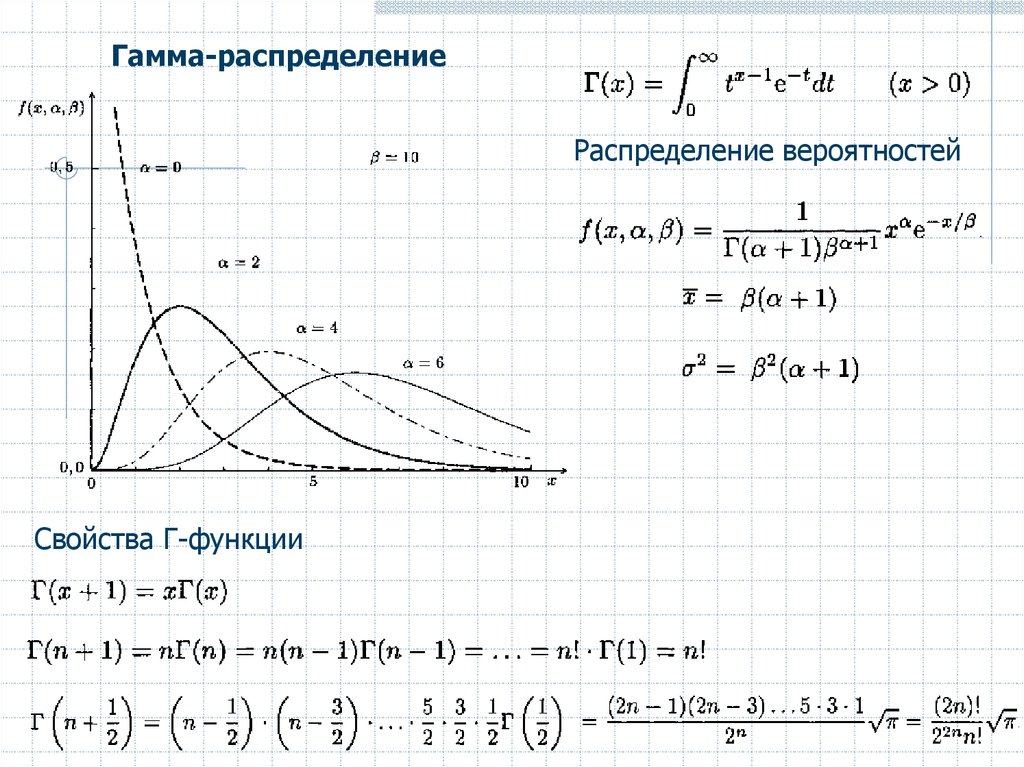
Гамма-распределение
Распределение вероятностей
Свойства Г-функции

6.

Распределение c2
Распределение Стьюдента
При малом n

7.

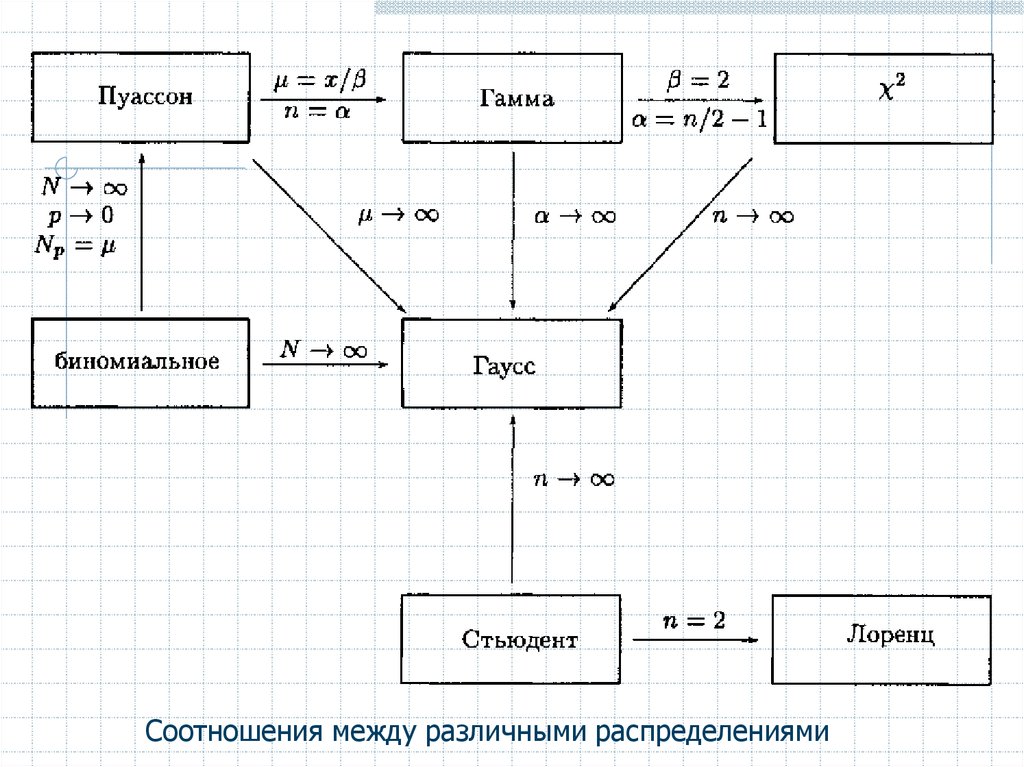
Соотношения между различными распределениями

8.

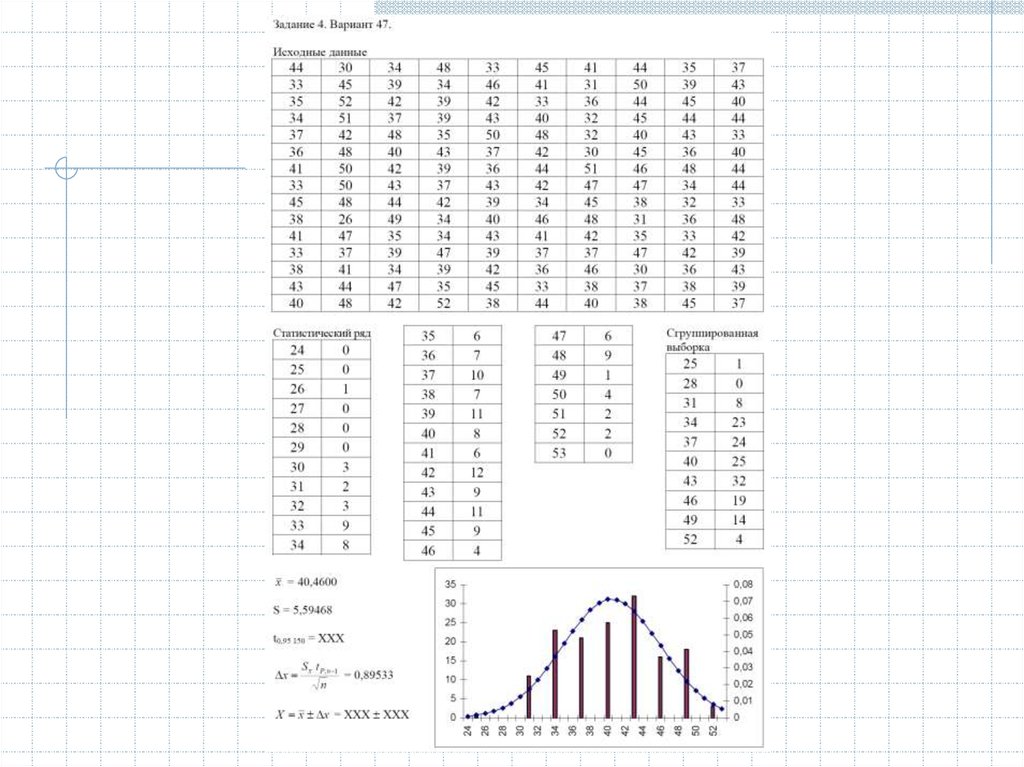
9. Статистическая обработка результатов эксперимента

Если в результате измерения n раз некоторой физической величины x получен
ряд значений x1, x2, ..., xn, то в качестве значения, наиболее близкого к
истинному, принимается среднее арифметическое
1 n
x xi
n i 1
Случайную ошибку измерений оценивают по среднеквадратичному отклонению
от среднего значения измеряемой величины x.
n
Sx
(x - x )
2
i
i 1
n -1
Истинное значение измеренной величины x лежит в интервале от ( x - x ) до
( x x ) , где x называется доверительным интервалом. Вероятность этого
события (доверительная вероятность) составляет P.
Доверительный интервал рассчитывается по формуле
x
S x t P ,n -1
n
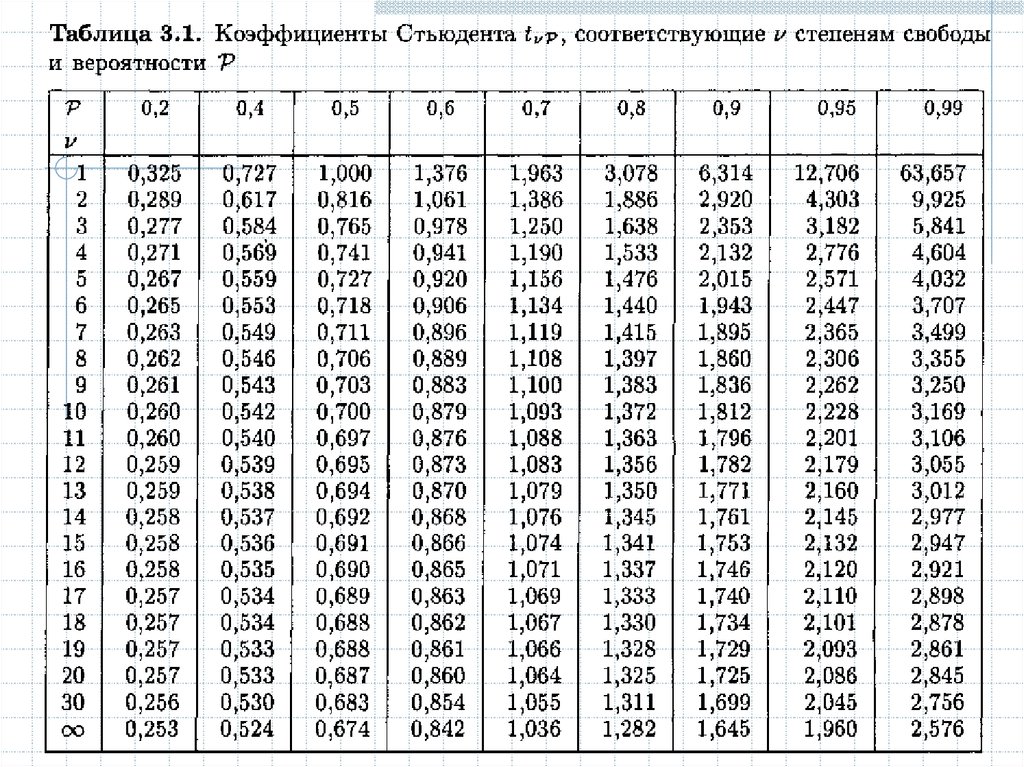
где tP,n-1 - коэффициент Стьюдента, зависящий от доверительной вероятности P
и числа измерений n.
Таким образом, окончательная форма записи результата имеет вид
x x x

10.

11. Правила округления

1. Точность результатов измерений и точность вычислений при
обработке результатов измерений должны быть согласованы с требуемой
точностью получаемой оценки измеряемой величины.
2. Погрешность оценки измеряемой величины следует выражать не
более чем двумя значащими цифрами.
Две значащие цифры в погрешности оценки измеряемой величины
сохраняют:
- при точных измерениях;
- если первая значащая цифра не более трех.
3. Сохраняемую значащую цифру в погрешности оценки измеряемой
величины при округлении увеличивают на единицу, если отбрасываемая
цифра неуказываемого младшего разряда больше либо равна пяти, и не
изменяют, если она меньше пяти.

12. Распространение ошибок

13.

14. Косвенные измерения

Вид функции
Абсолютная погрешность
Относительная погрешность
x a b
x a b
x a b
x
a b
x ab
x a b b a
x
a
b
x ak
x k a
x sin
x cos
x
a b b a
b2
x k a k -1 a
x
a
k a k -1
x cos
x sin
x a b
x
a
b
x a b
x
a
b
x
a
k
x
a
x 1 a
x k a
x
ctg
x
x
tg
x
x tg
x
cos 2
x
2
x cos 2
x ctg
x
sin 2
x
2
x sin 2