Похожие презентации:
Математическая обработка результатов эксперимента
1. Курс «Математическая обработка результатов эксперимента»
2.
В практической работе зависимость между величинами,например x и y, получается в результате опыта, измерений.
На первых порах эта экспериментальная информация в
виде громоздких плохообозримых таблиц. Для лучшего
понимания рассматриваемых явлений необходимо
представить эту информацию в обозримом компактном
виде. В настоящее время ставят эксперименты и по их
результатам строят математические модели реальных
процессов, что позволяет лучше прочувствовать эти
процессы и получить возможность управлять этими
процессами.
Медики, биологи, химики, агрономы, инженеры не могут
обойтись без проведения экспериментов и без их
математической обработки.
Стоимость обработки экспериментов составляет
незначительную часть стоимости самих экспериментов, но
эта обработка может значительно повысить ценность
полученных результатов.
3.
Вопросу математической обработки результатовэкспериментов часто не уделяют должного внимания, и нередки
случаи, когда результаты дорогостоящих экспериментов не
подвергаются даже простейшей обработке; при этом теряется
огромное количество полезной информации. В свою очередь
правильно обработанный с математической точки зрения
эксперимент, поможет улучшить качество самого эксперимента,
помочь его оптимально спланировать.
Методы обработки данных наблюдений базируются на
положениях теории вероятностей и математической статистики.
Напомним без большого обсуждения некоторые положения ТВ и
МС.
Испытание в ТВ – осуществление, какого либо комплекса
условий, который может быть воспроизведен сколь угодно
количество раз.
Результатом испытания являются события,
которые подразделяются на достоверные, невозможные и
случайные.
Случайные события называют несовместимыми, если
появление одного из них исключает появление другого в том же
испытании.
События называют равновозможными, если есть основания
считать, что одно из них не более возможно, чем другое
4.
Относительной частотой (частостью) случайного событияА называется отношение числа М появлений этого
события к общему числу произведенных испытаний N:
P ( A)
M
N
(1)
Формула (1) – формула статистического определения
вероятностей. Частость в больших случаях повторных
испытаний обладает статистической устойчивостью.
Мера объективной возможности появления случайного
события А называется вероятностью и обозначается .
Около числа группируются относительные частоты
события А. Классическое определение вероятности
задается формулой
т
P( A)
,
n
где т – количество шансов, благоприятствующих появлению
события А, n – общее число исходов испытания.
5.
Относительная частота служит приближенной оценкой вероятности Р,
тем более точной, чем больше число испытаний в серии. , , где u –
достоверное событие, v – невозможное событие; .
ФормулаP А1 А2 ... Ат Р А1 Р А2 ... Р Ат
m
m
или P Аi P Аi
i 1
i 1
дает правило сложения вероятностей: вероятность суммы
несовместимых событий равна сумме их вероятностей.
Случайные события образуют полную группу событий, если при
каждом повторении испытания должно произойти хотя бы одно из них.
Пример – бросание кости.
Сумма вероятностей несовместимых событий, образующих
Р А1 Р А2 ... Р Ак 1
полную группу, равна единице:
6.
Когда полная группа состоит из двух несовместимых событий и появлениеодного из них означает невыполнение другого, такие события
Р А Р А А
1и A
называются взаимно противоположными:
Сумма вероятностей двух взаимно противоположных событий равна
единице
Условной вероятностью называют вероятность события В, вычисленную
в предположении, что событие А уже наступило.
Если события независимы, то правило умножения имеет вид
.
P( AВ) Р А Р В
Общее правило сложения вероятностей в случае совместимых или
несовместимых событий имеет вид
P А В Р А Р В Р АВ
,
т.е., вероятность суммы двух событий равна сумме вероятностей этих
событий без вероятности их совместного появления (если события А и
В несовместимы, то и формула сложения вероятностей имеет прежний
вид (*)).
7.
Если событие А может наступить совместно с одним изнесовместимых событий , , …, , образующих полную группу
событий, вероятность появления события А определяется по
формуле полной вероятности
m
P( A) Р В1 РВ1 ( А) Р В2 РВ2 ( А) ... Р Вт РВт ( А) Р Вi РВi ( А)
i 1
Формула Байеса определяет вероятность гипотез того с каким
именно событием совместно произошло рассматриваемое
событие А:
P Bi PBi A
PA Bi m
PA Bi PBi A
i 1
Случайные величины (СВ) – переменные, принимающие в
результате испытания те или иные числовые значения в
зависимости от случайного исхода испытания. Случайная
величина, принимающая отдельные отстоящие друг от друга
значения, которые можно занумеровать называется
дискретной. Напомним, что математическое ожидание
(среднее значение) дискретно заданной СВ определяется по
формуле
n
M ( x) X xi pi
i 1
8.
Характеристики рассеивания СВ вокруг ее среднего значения:Дисперсия
D( x) xi X pi
n
2
i 1
среднее квадратическое отклонение .
x D(x)
Непрерывная СВ – СВ непрерывно заполняющая числовую ось или
некоторый ее отрезок. Она определена сплошной полосой по оси ОХ с
определенной плотностью. Она имеет бесчисленное множество
значений, пересчитать которые невозможно. Именно этому типу СИ мы
будем уделять основное внимание, поскольку будем заниматься
методами статистической обработки результатов экспериментов
(погрешностей измерений), которые по своей природе являются
непрерывно распределенными СВ.
Распределение частостей называется эмпирическим (находится из опыта).
Распределение вероятностей называется теоретическим
распределением.
Параметры или характеристики , D, невозможно определить для
непрерывной СВ по простым формулам применяемым для дискретной
СВ.
Функцией распределения (интегральной) называется вероятность того,
что случайная величина Х в результате испытания примет значение,
меньшее х:
F ( x) P X x)
.
9.
Интегральная функция распределения имеет следующиеосновные свойства:
1. х 0 F ( x) 1
2. F (x) - неубывающая функция, т.е. F ( x ) F ( x ) , если .x x
3. limx F ( x) 0
4. limx F ( x) 1
Примерный график этой функции представлен на рис. 1.
2
1
1.5
1
1
F ( x)
0.5
6
4
2
0
2
4
6
Х
0.5
x
2
1
10.
Плотностью распределения вероятностей(дифференциальной функцией распределения)
непрерывной СВ называется функция :
f ( x) F ( x)
При описании непрерывной СВ часто используют так
называемые квантили.
Квантилем, отвечающим заданному уровню вероятности
«р», называют такое значение x x p , при котором функция
распределения принимает значение, равное р: F x p p
.
Медианой распределения называется квантиль,
отвечающий значению F x p 1 F M e X p 3
2
1
2
4
p
1
4
Квантили, соответствующие
и
, называются
соответственно верхним и нижним квантилями. При и
получаем соответственно и 95% квантили, они называются
соответственно 10% и 5% верхними точками
распределения. А квантили, отвечающие значениям и 10% и 5% нижними точками распределения.
p
11.
Математическое ожидание непрерывной СВ Хопределяется по формуле . Математическое
ожидание функции M ( X ) X x f ( x)dx
Y
(x)
определяется по формуле
. Если , то
- к-ый начальный момент ( начальный момент к-ого
порядка), M (Y ) M ( x) ( x) f ( x)dx
- центральный момент к-ого порядка. Так дисперсия
( находится
x ) f ( x)dx по формуле:
(второй центральный момент)
.
2
D( x) 2 ( x ) 2 f ( x)dx
k
k
12.
• Модой непрерывной СВ называется значение аргумента,при котором плотность распределения f (x) достигает
максимума.
Нормально распределенная СВ имеет плотность
распределения f ( x) 1 1 e x2 a
2
• ,
• где а – математическое ожидание, - среднее
квадратическое отклонение рассматриваемой СВ. График
функции распределения имеет вид
2
2
2
6
f ( x)
a
x
Х
13.
• Предварительная обработка экспериментальных данных– необходима для того, чтобы с наибольшей
эффективностью использовать для построения
эмпирических зависимостей математический
(статистический) аппарат. Содержание предварительной
обработки в основном состоит в отсеивании грубых
погрешностей числового материала( погрешности
измерений, переписывания или ввода в ЭВМ). Сущность
грубых погрешностей можно рассмотреть на следующем
примере: если 10% измерений есть аномальные значения,
отстоящие от среднего значения более чем на 3ℓ, а
остальные 90% наблюдений располагаются в пределах ℓ,
то при оценке дисперсии эти 10% наблюдений, по меньшей
мере удваивают оценку.
Другой момент предварительной обработки –
проверка соответствия распределения результатов
измерения нормальному закону или какому-либо другому
закону. Если возможно, преобразовать по следуемое
распределение к нормальному.
14.
Генеральная совокупность и выборка.Генеральная совокупность – совокупность всех
мыслимых значений наблюдений, которые
возможны в условиях рассматриваемого
эксперимента.
Выборка – из данной генеральной совокупности –
результаты ограниченного ряда наблюдений , , …,
М. (х)
(
Характеристики теоретических распределений
- математическое ожидание, D D( x) 2 - дисперсия,
- среднее квадратическое отклонение и т.д.) можно
рассматривать как характеристики присущие
генеральной совокупности. Характеристики
S
S2
эмпирического
распределения
( X - математическое
ожидание, - дисперсия, - среднее
квадратическое отклонение и т.д.) – характеристики
по выборке (выборочные).
15.
Вычисление выборочных характеристик.Пусть имеем ограниченный ряд наблюдений СВ Х: ,
, …, . Среднее значение вариант наблюдаемой СВ
определяется формулой X 1n x - эмпирическое
или выборочное среднее.
x
d i xi X - отклонение каждого наблюдения
от X
среднего .
1
m S x X - дисперсия или второй центральный
n
момент эмпирического распределения.
2
Несмещенную оценку для ( 2 - дисперсия
теоретического распределения) можно найти по
формуле S n 1 1 x X
.
Выборочные средние квадратические отклонения- S S 2
и
S S2 .
n
i 1
i
i
2
2
n
i 1
2
i
2
n
i 1
2
i
16.
• Выборочные значения коэффициента вариации,
который является мерой относительной изменчивости
S
наблюдаемой СВ, вычисляется
по формуле
.
X
S
Этот коэффициент может
.
100(%) быть вычислен в % :
X
• К оценкам параметров распределения предъявляют
требования состоятельности, несмещенности и
эффективности.
N
• Оценка параметров называется nсостоятельной,
если по
n в случае
мере роста числа наблюдений n (т.е. при
конечной генеральной совокупности объема N и при
S2 2
в случае бесконечной генеральной совокупности) nlim
эта
оценка стремится к оцениваемому параметру. Например,
для дисперсии
.
• Оценка называется несмещенной, если при любом числе
наблюдений n ее математическое ожидание1 nточно2 равно n
xi X S 2 1 xi X
S 2 требованию
значению оцениваемого параметра. Условие
n i 1
несмещенности особенно важно при малом количествеn 1 i 1
наблюдений. Так из двух оценок
дисперсии
и
2
обе оценки состоятельны, но только
из них
MS (n) второе
n
n
является несмещенной, т.к. первая содержит
систематическую отрицательную погрешность
, которая с ростом n убывает.
2
2
2
17.
• Оценка параметра называется эффективной, еслисреди прочих оценок того же параметра она
обладает наименьшей дисперсией. Так если
имеется выборка из нормально распределенной x
генеральной совокупности ,
, …, , то среднее (математическое ожидание) можно
1
оценить
X x двумя способами:
n
• - X x (n) x ; (n)
2
• - 24 ln( n)
.
• Обе эти оценки будут близки, они обе обладают
свойствами состоятельности
и несмещенности,
однако можноn показать,
что дисперсия при первом
способе оценки равна n , а при втором равна
, что существенно больше чем
.
• И здесь первый способ оценки теоретического
среднего является состоятельным, несмещенным и
эффективным, а второй – только состоятельным и
несмещенным.
1
n
i 1
i
min
max
2
2
2
2
18.
Отсев грубых погрешностей.Рассмотрим наиболее простые методы отсева грубых
погрешностей.
Если имеем выборку небольшого объема n 25 , то можно
воспользоваться методом вычисления максимального
относительного
отклонения. Здесь для выделения аномальности
x X
xi
значения
вычисляют
, где - крайний
1 p q, 0,90
S
S
(наибольший или наименьший)Хэлемент
выборки, по которой
1 р
подсчитаны и . Найденное значение
сравнивают
с
табличным значением
статистик , вычисленной при
доверительной вероятности
; 0,95; 0,975; 0,99. На
р 0,05
практике чаще всего используют уровень значимости
и
результат получают с 95% доверительной вероятностью: . Если
последнее неравенство выполняется , то наблюдение не
отсеивают, если не соблюдается, то наблюдение исключают.
После исключения того или иного наблюдения или нескольких
1 р
наблюдений характеристики эмпирического распределения
должны быть пересчитаны по данным уменьшенной выборки.
Данные для
приводятся в таблицах литературы по статистике.
i
19.
• 2. При другом методе отсева грубыхпогрешностей для малой выборки
вычисляют
для , по сравнению с вычислением
. Здесь
в предыдущем методе, введен уточняющий
коэффициент n n 1 . Найденное значение
сравнивается с 1 р .
3. Для больших выборок отсев грубых
погрешностей осуществляется с
использованием таблиц распределения
Стьюдента. Распределение Стьюдента связано
р
с нормальным распределением.
Критическое
значение (где р – процентная точка
нормированного выборочного отклонения)
t p,n 2 значение
выражается через критическое
распределения Стьюдента
по формуле:
t
n 1
.
p ,n p ,n 2
n 2 t 2p ,n 2
xi X
n 1
S
n
20.
• Схема отсева грубых погрешностей (ошибочных)измерения для больших выборок выглядит
следующим образом.
• Из статистических данных выбирают наблюдение,
имеющее наибольшее отклонение. В нашем случае
xi X 189 175,66 13,34
• По предложенной формуле вычисляют
x X
13,34
: 2,40
S
5,55
• По таблице распределения Стьюдента находят
t p ,n 2
процентные точки t-распределения
.В нашем
случае
• По формуле (**) вычисляют соответствующие точки:
• ,.
5. Найденное значение ( у нас ) сравнивается с
и . Если, как в нашем случае, , то в этом случае от
отсева выделяющегося наблюдения
воздерживаются.
i
21.
Таким образом, при рассматриваемомметоде отсева грубых погрешностей,
если
1) 5%,n , то наблюдение
отсеивать нельзя ;
2) 5%,n 0,1%,n , то наблюдение
можно отсеивать, а можно не отсеивать;
3) 0,1%,n , то наблюдение нужно
отсеивать.
22.
• Полигон и гистограмма частот.Разобьем приведенные наблюдения
на классы. Число классов разбиения
можно определить по правилу
• k 1 3,32 lg( n) 1 3,32 lg(56) 1 3,32 1,75 6,81 k 6 7,
.
x
x 189 166 23cm
23 : 6 4cm
• Размах ряда
. Примем
число классов равным 6 со ступенями
max
min
23.
0.1Гистограмма
Гистограмма
0.08
0.06
y
0.04
0.02
161
165
trace 1
Полигон частот
Х
169
173
177
x
181
185
189
193
24.
f (x)Заштрихованная на гистограмме площадь равна S 1 . Построенная линия
(по сути, полигон частот в несколько измененном масштабе) – функция
распределения плотности для рассматриваемой случайной величины.
Площадь, заключенная между линией y f (x) , осью ОХ и
вертикальными прямыми x 165
и x 189 равна единице.
На рис. приводится комулятивная линия - график накопленных частот.
Комулятивная линия оценивает функцию распределения F (x) в точке
х.
Очень многие наблюдения в природе при рассмотренной обработке дают
колоколообразные полигоны распределения. В свою очередь
колоколообразные распределения часто хорошо описываются
нормальным законом распределения.
1
Накопленные
частоты
0.8
0.6
y
0.4
0.2
161
165
trace 1
169
173
177
x
181
185
189
193
Х
25.
• Нормальное распределение случайной величины.Распределение случайной величины
bx
f
(
x
)
ae
называется нормальным, если оно может быть
a, b 0кривой
описано
где
. С увеличением
коэффициента “а” кривая вытягивается в высоту,
при увеличении “b” кривая сплющивается.
В теории вероятностей за основной закон
принят закон Гаусса или нормальный закон
распределения СВ. Согласно этого закона
плотность распределения вероятностей
имеет вид :
x a
1 1
f
(
x
)
e 2
2
(***)
• где
- среднеквадратическое отклонение
теоретического распределения, а – среднее
значение (математическое ожидание)
теоретического распределения.
2
2
2
26.
• Преимущества этого закона распределенияперед другими возможными законами
определяется следующими соображениями:
X X ... X
• согласно предельной теореме Ляпунова,X СВ
представляющая сумму большого числа
независимых СВ, следует закону Гаусса;
• нормальный закон является предельным
законом, к которому приближаются другие
законы распределения при часто
встречающихся типичных условиях;
• распределение ошибок (погрешностей
эксперимента) следует закону Гаусса;
• обработка наблюдений в случае использования
закона Гаусса может быть доведена до конца
посредством простых правил.
1
2
n
27.
• Рассмотрим некоторые свойства нормальногораспределения.
• Из формулы (***) видно, что нормальное распределение
полностью определяется величинами а и .
Математическое ожидание а определяет положение
кривой распределения относительно оси ОХ,
среднеквадратическое отклонение определяет форму
кривой. Чем больше (больше рассеивание СВ), тем
кривая будет более пологой (ее основание более
широкое).
• Кривая нормального распределения симметрична
относительно среднего значения.
x a
• Максимум ординаты кривой при
. Если , то ,
т.е. очень большие и очень малые значения переменной х
маловероятны.
• Примерно всех наблюдаемых значений СВ находятся на
интервале оси ОХ . При большом объеме выборки
примерно 90% значений СВ лежит между и . Границы и
называют вероятными отклонениями, в этом интервале
находится около 50% всех наблюдений.
28.
• Для нормального распределения среднее(математическое ожидание), мода и медиана
совпадают. Мода нормально распределенной
случайной величины – значение аргумента х,
при котором f (x) достигает максимума,
медиана – значение х, при котором вероятность
равна 12 . График функции , определенной
формулой 1, представлен на рис. 2.
• Для статистических методов построения
эмпирических зависимостей очень важно, чтобы
результаты наблюдений подчинялись
нормальному закону распределения, поэтому
проверка нормальности распределения –
основное содержание предварительной
обработки результатов наблюдений.
29.
Проверка гипотезы нормальности распределения.
Существует несколько методик проверки гипотезы нормальности
распределения. Рассмотрим некоторые из них.
1. По среднему абсолютному отклонению. Методика САО 1n x X
приспособлена для не очень больших выборок ( n 120 ). Вычисляется
среднее абсолютное отклонение (САО) по формуле
.
Для выборки, имеющей приближенно нормальный закон САО
0,4
0,7979
распределения, должно быть справедливо соотношение
S
n
.
4,41
0,4
1
248,04
0,7979 0,032
САО x X
4,41
n
56
56
В нашем случае
,5,55
. И таким образом гипотеза в рассматриваемом примере принимается.
R
2.Методика по размаху варьирования R. Применима
для широкого
S
класса выборок 3 n 1000 . Здесь подсчитывают отношение
и R
сопоставляют с критическими верхними и нижними границами этого S
отношения, приведенными в таблицах (Приложение 6). Если
вычисленное отношение находится в указанной вилке, то гипотеза о
нормальном распределении принимается. В противномnслучае
p 0,10
56
нормального распределения нет.
R
23
4,144
R
189
166
23
cм
.
S
5
,55
В нашем случае
,
. При
и
(10% уровень значимости) нижняя граница 4,03, верхняя –
5,23. Следовательно, и т.о. гипотеза нормальности распределения
подтверждается и по этому критерию.
n
i 1
n
i 1
i
i
30.
• 3. По показателям асимметрии и эксцесса. Показательасимметрии можно определить по формуле
m
.
g
m
(1)
m
3
Для симметричных распределений
m 0 и g1 0 . Для
m
нормального распределения
. Для сравнения
эмпирического распределения и нормального
распределения в качестве показателя эксцесса принимают
величину g 2 m42 3
m2
.
45,14
45,14
m
2356 ,27
g
0,271 0
g
3
3 2,57 3 0,43 0
(2)
166,62
m
(30,28)
30,28
В рассматриваемом примере
. Таким образом, некоторая асимметрия имеется.
т.е. имеется и небольшой эксцесс. G2 n 1 (n 1) g 2 6
(n 2)(n 3)
Несмещенные оценки для показателей асимметрии и
эксцесса определяют по формулам:
n(n 1)
G1
g1
56 55
G
0,271 1,028 0,271 0,278588 0,28
n
2
,
54
55
.G2
57 0,43 6 0,0192 18,51 0,355392 0,355
54 53
В нашем случае:
,
3
1
3
2
4
2
2
1
1
3
3
2
4
2
2
2
31.
Для проверки гипотезы нормальностираспределения необходимо вычислить
среднеквадратические отклонения для
показателей асимметрии и эксцесса по
6n(n 1)
24n(n 1)
S
формулам:
S
(n 2)(n 1)(n 3)
(n 3)(n 2)(n 3)(n 5)
,
G 3S
G 5S
.
Если при этом выполняются условия
,
то гипотеза нормальности распределения
может
быть
принята.
6 56 55
24 56 55 55
S
0,319
S
0,628
54 57 59
53 54 59 61
В нашем
примере:
G 0,28 3S 3 0,32 0,96
G 0,355 5S 5 0,63 3,15
;
.
Теперь
,
И таким образом, по данному критерию
2
G1
G2
1
G1
G1
2
G2
G2
1
G1
2
G2
.
32.
• Критерий согласия Пирсона.X S и
• По данным наблюдений определяют
X 175,66
S и5,55
. В нашем случае
.
yi
• Находят ординаты - выравнивающие
n h
y
u теоретической кривой по
частоты
S
формуле
x X
h
x
x
u
где n – количествоS (u ) 21 e
испытаний, h – разность между двумя
соседними вариантами СВ Х (
),
,
i
i
i
i 1
i
i
i
u2
2
33.
Полигон этого распределения приведен на рис. 8. Характерныечерт подробного распределения ( асимметрия) здесь сохранились.
B
18
15
12
y
9
6
3
30
50
70
90
Рис. 7.
110
130
150
170
190
Х
x
В
32
28
24
20
y
16
12
8
4
30
50
70
90
110
x
130
150
170
190
Х
Рис. 8.
1. X
50 29 70 31 90 26 110 21 130 15 150 10 170 5 190 1
92,46
29 31 26 21 15 10 5 1
34.
2931
26
70 92,46 2
90 92,46 2
138
138
138
21
15
10
110 92,46 2
130 92,46 2
150 92,46 2
138
138
138
5
1
170 92,46 2
190 92,46 2
1220 ,02
138
138
D 50 92,46 2
D 1220,02 34,93
S 2 1220 ,02
138
1298,37
137
S 1298,37 36,03
.
2.
nh
yi ui
S ,
,
n=138,
h=20,
u
1
e
2
u2
2
, ui
xi X
S
35.
3.Таблица 8.
xi
ni
xi X
ui
ui
yi
29
-42,46
-1,18
0,1989
15,24
70
31
-22,46
-0,62
0,3292
25,22
90
26
-2,46
-0,07
0,3980
30,49
110
21
17,54
0,49
0,3538
27,10
130
15
37,54
1,04
0,2323
17,79
150
10
57,54
1,60
0,1109
8,49
170
5
77,54
2,15
0,0396
3,03
190
1
97,54
2,71
0,0101
0,8
50
36.
4.2
q
ni yi 2
yi
Таблица 9.
ni
yi
ni yi
ni yi
2
ni yi 2
yi
15,24
13,76
189,3376
12,4237
31
25,22
5,78
33,4084
1,3247
26
30,49
-4,49
20,1601
0,6612
21
27,10
-6,1
37,21
1,3731
15
17,79
-2,79
7,7841
0,4376
10
8,49
1,51
2,2801
0,2686
5
3,03
1,97
3,8809
1,2808
1
0,8
0,2
0,04
0,05
29
2q 17,8197
37.
.k S 3 8 3 5
5.
6. Уровень значимости (У.з.) равен
0.01.
7.
k 5
p 0.0045
2
q 17
p 0.01
k 5
p
0
.
0029
2q 18
Этот критерий тоже отвергает нормальность распределения.
Коэффициент вариации в нашем случае
S
36,03
100%
100% 38.97% 33%
X
92,46
, что является признаком логарифмического нормального распределения.
Проведем преобразованиеx lg x
.
x - 100 x 100 lg x
и для удобства расчетов умножим результаты на 100
. Теперь все данные расписывают до полного состава.
38.
Таблица 10.№ п/п
x
x
№ п/п
x
x
1
40
160,21
86
99
199,56
2
41
161,28
87
100
200,00
3
41
161,28
…
…
…
4
42
162,33
107
119
207,56
5
43
163,35
108
120
207,92
6
44
164,35
…
…
…
7
44
164,35
122
139
214,30
8
45
165,32
123
140
214,61
…
…
…
…
…
…
29
59
177,09
132
158
219,87
30
60
177,82
133
162
220,95
…
…
…
…
…
…
60
79
189,76
137
177
224,80
61
80
190,31
138
186
226,95
…
…
…
39.
изменяютсяв эксперименте от 160 до 227. Разделим этот диапазон на 9 новых классов с
Новые данные
х
интервалом класса равным 8.
Таблица 11.
Границы
Среднее значение
Частота
1
2
3
4
1
160-168
164
10
2
168-176
172
16
3
176-184
180
19
4
184-192
188
21
5
192-200
196
20
6
200-208
204
22
7
208-216
212
17
8
216-224
220
10
9
224-232
228
3
№ класса
138
40.
Теперь критерий согласия для нормальности распределения последнего набора данных СВХ
X
D
по размаха ряда дает:R 232 160 72
.
1
164 10 172 16 180 19 188 21 196 20 204 22
138
212 17 220 10 228 3 193,16
1
(164 193,16) 2 10 (172 193,16) 2 16 (180 193,16) 2 19
138
(188 193,16) 21 (196 193,16) 2 20 (204 193,16) 2 22
(212 193,16) 2 17 (220 193,16) 2 10 (228 193,16) 2 3 283,64
D 16,84
Теперь
S2 D
138
283,64
137
S S 2 16,90
R
72
4,26
S 16,90
. Нижняя граница при n=138 и уровне значимости 0.1 равна 4,65, верхняя граница
– 5,89, и тогда рассматриваемая СВ нормально распределенной считаться не
может.
Рассмотрим критерий Пирсона.
41.
Таблица 12.ui
yi
138 8
ui
16,9
ni
хi Х
10
-29,16
-1,73
0,0893
5,83
172
16
-21,16
-1,25
0,1826
11,93
180
19
-13,16
-0,78
0,2943
19,23
188
21
-5,16
-0,31
0,3802
24,84
196
20
2,84
0,17
0,3932
25,69
204
22
10,84
0,64
0,3251
20,97
212
17
18,84
1,11
0,2155
14,08
220
10
26,84
1,59
0,1127
7,36
228
3
34,84
2,06
0,0478
3,12
хi
ui
164
138
133,05
42.
328
21
y
z
14
7
160
170
180
190
200
210
220
Рис.9.
4.
230
X
x
Таблица 13.
ni yi 2
ni
yi
10
5,83
2,98
16
11,93
1,39
19
19,23
0,003
21
24,84
0,59
20
25,69
1,26
22
20,97
0,05
17
14,08
0,61
10
7,36
0,95
3
3,12
0,005
yi
2q 7,838
43.
5. k 9 3 66. уровень значимости равен 0,01.
7. k 6
2
2
P q 0,2381 0,01
2
q 8
Таким образом, гипотеза о нормальном распределении принимается. Коэффициент вариации
стал
S
16,9
100 %
100 % 8,75%
X
193,16
, что так же говорит о сближении преобразованной СВ с
нормальным распределением.
Таким образом, мы на примере наглядно показали, как можно
преобразовать данные, не подчиняющиеся закону нормального
распределения, чтобы распределение новых, преобразованных данных
стало нормальным.
На примере мы рассмотрели преобразование исходных данных
путем логарифмирования. Из других преобразований можно отметить:
.
x lg x a - такое преобразование часто приводит к нормальному
распределению,
если
исходное
распределение
асимметрично и имеет одну вершину;
44.
n 100х
х
1
х
(обратная величина);
-
1
х
(обратное значение квадратных корней);
-
x x a - степенные преобразования;
тригонометрические преобразования.
Преобразование «обратная величина» - наиболее сильное преобразование. Среднее
значение между логарифмическим преобразованием и «обратной величиной» занимает
a
преобразование «обратное значение квадратных корней». В случае
преобразований а 1,5
берут
x x степенных
-
при умеренном правом смещении значений СВа
и 2 при сильно выраженном правом смещении.
Алгоритм и блок-схема алгоритма предварительной
обработки экспериментальных данных
При больших объемах выборок ( n 100 ) оптимальные
эмпирические зависимости можно построить только с помощью ЭВМ.
Поэтому целесообразно включить в программу машинной обработки и
предварительную обработку экспериментальных данных.
Алгоритм предварительной обработки экспериментальных
данных следующий.
45.
1. Вычисляются выборочные характеристики СВ соответственно по формулам:1 n
2
S m2 xi X
n i 1
1 n
X xi
n i 1
2
S S2
1 n
xi X 2 1 S 2
S
n 1 i 1
n 1
n
1
m1 xi X
n i 1
p; n
1 n
3
m3 xi X :
n i 1
m4
1 n
xi X 4
n i 1
S
100 %
X
и грубых погрешностей:
2. Отсев
d max ; xmax(min); X
вычисляется наибольшее отклонение
,
d
max
вычисляют
S
t 5% ; n 2
в) по соответствующей таблице (табл. П.4) находят процентные точки t-распределения Стьюдента
;
t 0,1% ; n 2 ;
г) вычисляют соответствующие точки
5% ; n
t 5% ; n 2 n 1
(n 2) t 5% ; n 2 2
0,1% ; n
t 5% ; n 2 n 1
(n 2) t 0,1% ; n 2 2
46.
д) сравнивают результаты по п.2б) и п.2г), принимают решение об отсевепервой грубой погрешности (если результат по 2б) значительно больше
результатов по 2г));
е) пересчитывают выборочные характеристикии
Х
S
для нового массива данных (без отсеянного значения
) приxiобъеме массива (n-1).
3. Проверка нормальности распределения (проводят только при 33%
) по одному из критериев, например, критерию Пирсона:
а) разбиваю массив значений СВ на классы количеством k 1 3,32 ; lg n
б) определяют середины классов;
ni
в) подсчитывают частоты для всех классов»«в экспериментальном
материале;
г) вычисляют частоты теоретической кривой
yi»«последовательно по формулам:
u2
2
xi X
n h
ui
e
yi
ui
S
S
2
, где n – общее количество испытаний, h – интервал класса;
ni yi 2
2
q ;
д) вычисляется показатель
y
ui
;1
i
е) вычисляется число степеней свободы
k S 3
, где S – число групп на которые разбита выборка;
ж) выбирается уровень значимости для рассматриваемой задачи У .з. 0,01 0,05
47.
з) по таблице критерия Пирсона ищется по найденным k иq
вероятность
2
P 2 q2
P 2 q2 ; У .з.
и) проверяют выполнение соотношения
4. Преобразование распределений к нормальному.
Для распределений, имеющих крутую левую ветвь полигона и пологую правую
выполняют преобразование столбца исходных данных по
формулам x lg x a 10 b
, или
х
1
х
, или х
1
х
После преобразования проверяют нормальность полученного распределения по одному из
критериев согласия (критерий Пирсона).
-Для распределений, смещенных вправо, столбец СВ исходных данных
преобразуют по формуле
x x( a
;а 1,5 а 2
) и так же используют какой-либо критерий согласия.
Укрупненная блок-схема алгоритма предварительной обработки опытных
данных приведена на рис. 10.
48.
Начало1. Ввод исходных
данных
2. Вычисление выборочных характеристик распределения (п.
1) с выдачей их на печать
10
3. Подготовка к отсеву грубой ошибки наблюдения (п.
2а – 2г)
4. Проверка
нет
5. Формирование
нового столбца
исходных данных (без
отсеянного элемента)
да
нет
да
6. Проверка
условия
9
7. Вычисления необходимые для
критерия Пирсона
(п. 3а – 3з)
10
да
8. Проверка условия
п. 3и
нет
10. Выдача на печать
результатов
Конец
9. Преобразование исходных данных по
п.4 с вычислением и выдачей на печать
нового значения
Рис. 10.
49.
Методы построения парных зависимостей поэкспериментальным данным
Часто требуется установить и оценить зависимость изучаемой СВ Y от одной
или нескольких других величин. Рассмотрим сначала зависимость СВ Y от одной
случайной или неслучайной величины Х
Две случайные величины Y и Х могут быть связаны либо функциональной
зависимостью, либо связаны статистической зависимостью, либо быть
независимыми. Строгая функциональная зависимость реализуется в реальных
процессах исключительно редко , т.к. обе величины или одна из них бывают
подвержены еще и действию случайных факторов, причем среди них могут быть и
общие для обеих величин. В этом случае возникает статистическая зависимость.
Статистической называют зависимость, при которой изменение одной из
величин влечет изменение распределения другой величины. Если при изменении
одной из величин изменяется среднее значение другой величины, то в этом
случае статистическую зависимость называют корреляционной.
Пример. Y – урожай, Х – количество внесенных удобрений. С
одинаковых площадей при равных количествах удобрений снимают различный
урожай, т.е. Y не является функцией Х. Это объясняется влиянием случайных
факторов (влажность, качество земли, температура воздуха и др.). Средний же
урожай по множеству разных участков одинаковой площади является функцией
от количества удобрений, т.е. Y связан с Х корреляционной зависимостью.
50.
Пусть каждому значению Х соответствует несколько значений Y. Например, xпри1 2
величина Y приняла значения:
y1 5 , y 2 6 , y3 10 . Среднее арифметическоеy2
y
y - условное среднее.Черточка на
5 6 10
7
3
2
- обозначение среднего арифметического, индекс 2 указывает на то, что
рассматриваются те значения Y, которые
соответствуют
x1 2
Если каждому значению х соответствует одно значение условной средней, то условная средняя
зависит от х, т.е. является функцией х. В этом случае говорят, что случайная величина Y зависит
от Х корреляционно.
y х от х:
Корреляционной зависимостью Y от Х называют функциональную зависимость условной средней
f (x)
y х f (x) . Это уравнение называют уравнением регрессии Y на Х; функцию
- регрессией Y на Х, а график этой функции – линией регрессии Y на Х.
Две основные
. задачи теории корреляции.
Первая основная задача – установить форму корреляционной связи, т.е. вид
y х f (xЕсли
) и x y ( y)
функции регрессии. Часто функции регрессии называются линейными.
- линейные функции, то корреляцию называют линейной, в противном случае
имеем нелинейную корреляцию. При линейной корреляции – обе линии регрессии
прямые.
Вторая задача теории корреляции – оценить тесноту корреляционной связи. Теснота
корреляционной зависимости Y от Х оценивается по величине рассеяния значений Y вокруг
yх
условного среднего
Большое рассеяние – слабая зависимость Y от Х, либо отсутствие такой зависимости. Малое
рассеяние – достаточно сильная связь Y с Х, возможно даже функциональная связь, которая
оказалась размытой под воздействием второстепенных случайных факторов, в результате при
одном и том же значении х величина Y принимает различные значения.
51.
Методы построения, преобразования и оценки парныхЗависимостей по экспериментальным данным
Метод наименьших квадратов построения уравнения регрессии.
, полученных
при фиксированных значениях независимой
ть имеется n пар наблюдений значений функции
yi
переменной
(фактора):
xi
Таблица 13.
1
2
3
4
5
6
7
8
х
1,5
4,0
5,0
7,0
8,5
10,0
11,0
12,5
y
5,0
4,5
7,0
6,5
9,5
9,0
11,0
9,0
№
Расположение точек на плоскости в прямоугольной системе координат приведено на рис. 11.
Представленная система точек часто получается в эксперименте, когда значение фактора
(аргумента) мы фиксируем сами.
Задача линейного регрессионного анализа состоит в том, чтобы, зная положение точек на
2i
плоскости так провести прямую линию (линию регрессии), чтобы сумма квадратов
отклонений
вдоль оси OY этих точек от проведенной прямой была наименьшей.
y b0 b1 x . В этом случае
Будем считать, что рассматриваемая линия – прямая линия с уравнением
U b0 ;b1 сумма квадратов отклонений
n
n
U b0 ; b1 yi y yi b0 b1 xi 2
i 1
2
i 1
.
52.
U b0 ;b1 - функция двух переменных, которая достигает минимума (экстремума) в точках, вb0 и b1 обращается в ноль (принцип Лежандра).
которых частные производные по переменным
Y
12
7
5
9
3
z ( r)
1
6
8
6
y
4
2
3
X
0
2
4
6
8
10
12
14
x r
2
n
U
U yi b0 b1 xi
0
0 2 yi b0 b1 xi 1 0
b0
bo
bo
i 1
n
2
U
0 U yi b0 b1 xi 0 2 yi b0 b1 xi xi 0
b
i 1
b1
b1
1
n
n
n
n
n
y
b
b
x
0
y
b
n
b
x
0
b
n
b
x
yi
0
1 i
0
1 i
1 i
i
i
0
i 1
i 1
i 1
i 1
i 1
n
n
n
n
n
n
n
2
2
y x b x b x 2 0 x y b
b
x
b
(
x
)
0
x
b
(
x
)
i i 0 i 1 i
xi yi
i i
0 i
1 i
0 i
1 i
i
1
i 1
i 1
i 1
i 1
i 1
i 1
(1)
53.
Решая систему (1) методом Крамера, получаемn
xi
n
i 1
n
n
n
n
xi xi
i 1
2
n xi
2
i 1
n
xi
i 1
yi
2
0
i 1
i 1
n
n
xi
i 1
n
( xi yi ) xi
i 1
2
n
n
n
n
i 1
i 1
i 1
i 1
yi xi 2 xi ( xi yi )
i 1
n
yi
n
1
i 1
n
n
i 1
i 1
xi ( xi yi )
n
b0
n
n
n
n
i 1
i 1
i 1
n xi yi xi ( yi )
n
n
yi ( xi ) 2 xi ( xi yi )
0 i 1
i 1
i 1
i 1
n
n ( xi ) 2 xi
i 1
i 1
n
Следовательно
2
b1 1
n
n
n
i 1
i 1
i 1
2
n ( xi yi ) xi yi
n
n ( xi ) xi
i 1
i 1
n
2
Для построения линии регрессии по приведенным числовым данным
сведем расчетные данные в следующую таблицу.
54.
Таблица 14.xi
yi
xi 2
yi 2
xi yi
xi yi
xi yi 2
1
1,5
5,0
2,25
25,0
7,50
6,5
42,25
2
4,0
4,5
16,0
20,25
18,00
8,5
72,25
3
5,0
7,0
25,0
49,0
35,00
12,0
144,00
4
7,0
6,5
49,0
42,25
45,50
13,5
182,25
5
8,5
9,5
72,25
90,25
80,75
18,0
324,00
6
10,0
9,0
100,0
81,00
90,00
19,0
361,00
7
11,0
11,0
121,0
121,0
121,00
22,0
484,00
8
12,5
9,0
156,25
81,0
112,50
21,5
462,25
59,5
61,5
541,75
509,75
510,25
121,0
2072,0
№
п
/
п
Графы 2, 3, 4, 5 – рабочие, 6,7,8 – проверочные.
55.
Проверка: nxi yi
2
i 1
n
xi yi
2
n
i 1
xi2
2 xi yi
yi2
n
i 1
xi2
n
n
i 1
i 1
2 xi yi yi2
2072,00 541,75 2 510,25 509,75 2072,00
i 1
Таким образом, вычисления выполнены верно и теперь: b0
b1
8 510,25 59,5 61,5
8 541,75 59,5 2
61,5 541,75 59,5 510,25
8 541,75 59,5 2
2959 ,75
3,73
793,75
422,75
0,53
793,75
Теперь уравнение регрессии, т.е. формула, которая отображает с некоторой вероятностью
зависимость y от х, построенная по экспериментальным
имеет
вид
y точкам,
3,73 0,53
x
Некоторые пояснения. Свободный член в уравнении регрессии
b0
b1 tg 0,53 27 o 55
Коэффициентb1 tg - тангенс угла наклона линии регрессии к оси абсцисс:
- отрезок, отсекаемый от оси ординат линией регрессии.
.
На рис. 11 изображено «облако» точек с явно выраженной тенденцией (чем больше «х», тем
больше «y»), хотя имеются некоторые отклонения от этого закона.
Положение линии в системе координат на плоскости полностью определяется числами
b0 и b1
. На рис. 12 даны некоторые характерные положения прямой регрессии в зависимости от
значений коэффициентов регрессии:
56.
YY
b0 0
b1 0
b0 0
b1 0
X
X
а)
б)
Y
Y
b0 0
b1 0
b0 0
b1 0
X
X
в)
г)
Рис. 12
57.
Различают два вида связи: функциональную и стохастическую.Линейная функциональная связь, в данной задаче, если бы
все эти точки располагались на прямой регрессии. При
наличие же погрешностей измерения связь между «х» и «y»
является
стохастической
(вероятностной).
В
случае
стохастической связи функцию «y» называют функцией
отклика, зависимой переменной, предикатом, а независимую
переменную «х» - входной переменной, фактором,
регрессором.
Прямая корреляция.
Статическое оценивание парной корреляции и регрессии.
Если переменные х и y представляют двумерную нормально
распределенную случайную величину, то существует две регрессии (две
прямые регрессии). Одна определяет зависимость y от х, другая - х от y.
Условно модель L1 : y b0 yx b1 yx x называют прямой регрессией, а модель
L2 : x b0 xy b1 xy y - обратной регрессией.
58.
. В общем случае L1x ; y
L2 - разные прямые. Они пересекаются в центре тяжести
и
и образуют «ножницы». Чем уже «ножницы», тем ближе стохастическая связь с функциональной. При
функциональной же связи обе прямые сливаются. Таким образом, уравнение
y b0 b1 x
не является алгебраическим, т.е. из него нельзя получить х как функцию y, т.к. эта модель получена путем
минимизациисуммы квадратов отклонений вдоль оси ОХ. Т.е., при построении прямых прямой и обратной регрессии
минимизируются разные величины.
Y
bи0
b1
Формулы для вычисления коэффициентов
y b0 yx b1 имеют
yx x
в случае прямой регрессии
вид:
n
b0( yx )
Х
b1( yx )
1
n
n
n
i 1
i 1
i 1
2
n ( xi yi ) xi yi
n
n
0 i 1
i 1
i 1
i 1
n
n ( xi ) xi
i 1
i 1
n
2
2
(2)
n
n ( xi ) xi
i 1
i 1
n
2
При обратной регрессии
n
b0( xy )
n
yi ( xi ) 2 xi ( xi yi )
n
вычисляются по следующим формулам:
x b0 xy bкоэффициенты
1 xy y
n
n
xi ( yi ) 2 yi ( xi yi )
0 i 1
i 1
i 1
i 1
n ( yi ) yi
i 1
i 1
n
2
n
2
b1( xy )
1
n
n
n
i 1
i 1
i 1
2
n ( xi yi ) xi yi
n
2
n ( yi ) yi
i 1
i 1
n
(3)
59. Корреляционная таблица.
При большом числе наблюдений одно ито же значение «х» может встретиться
раз, одно и то же значение «y» - n y раз,
одна и та же пара чисел x ; y может
наблюдаться n xy раз. Данные
наблюдений группируются и
записываются в таблицу, которая
называется корреляционной.
60. Построение прямых регрессии по сгруппированным данным.
Для определения параметров уравнения прямой регрессии yна х имеем систему уравнений (1). Здесь предполагалось , что
значение х и соответствующие им значения у наблюдались по
одному разу. Теперь запишем систему (1) так, чтобы она
отражала данные корреляционной таблицы. Воспользуемся
тождествами:
n
n
xi nX
(т.к.
i 1
1 n
X xi pi xi
n i 1
i 1
),
n
yi nY
i 1
n
i 1
xi2
nX
n
n
i 1
i 1
2
xi yi nxy xi yi
(т.к.
n
X
2
i 1
xi2 pi
1 n 2
xi
n i 1
),
(учтено, что пара чисел xi ; yi наблюдаласьn xy раз).
61.
Тогда имеем из системы (1)nY n X 2 nX (n xy xy ) n Y X 2 X (n xy xy )
b0( yx )
2 2
2 2
n X n X
n X2 X2
n (n xy xy ) n 2 X Y (n xy xy ) n X Y
b1( yx )
2
2
2
2
n X n X
n X2 X2
2
2
Поскольку же X X D( x) ( x) , то b1( yx )
2
(n xy xy ) n X Y
n 2 ( x)
( x)
Если умножить теперь обе части последнего равенства на дробь
, то получим
( y)
r
( x) (nxy xy ) n X Y
b1( yx)
rB
( y)
n ( x) ( y)
B
Обозначим в последнем соотношении правую часть через rB -
выборочный
коэффициент корреляции. Теперь
b1( yx)
( x)
rB или b1( yx) rB ( y)
( y)
( x)
Используя понятие коэффициента корреляции, легко запишутся уравнения прямых,
как прямой регрессии
( x)
( y)
так
и
обратной
регрессии
y Y
x
X
r
x X
y x Y rB
y
B
( y)
( x)
62. Свойства коэффициента корреляции
Выборочный коэффициент корреляции ( rB ) имеет важноесамостоятельное значение и обладает следующими самостоятельными
свойствами.
1) Абсолютная величина выборочного коэффициента корреляции не
превосходит единицы, т.е. rB 1 .
2) Если rB 0 и выборочные линии регрессии – прямые, то Х и Y не
связаны линейной корреляционной зависимостью. В этом случае
признаки Х и Y могут быть связаны или нелинейной корреляцией или
даже функциональной зависимостью.
3) Если rB абсолютная величина равна единице, то наблюденные
значения признаков связаны линейной функциональной зависимостью.
4) С возрастанием абсолютной величины rB линейная корреляционная
зависимость становится более тесной и при rB 1 переходит в
функциональную зависимость.
Таким образом, выборочный коэффициент корреляции
характеризует тесноту линейной связи между количественными
признаками в выборке: чем ближе он к единице, тем связь сильнее,
чем ближе rB к нулю, тем связь слабее.
63. Упрощение вычисления выборочного коэффициента корреляции.
Процедура вычисления выборочного коэффициентакорреляции довольно громоздкая, в вычислительном
плане, процедура. Ее можно значительно упростить, если
перейти к условным вариантам:
xi C1
ui
h1
yi C 2
vi
h2
где C1 и C 2 ложные нули. В этом случае
rB
nuvuv nU V
n (u ) (v)
rB вычисляется по формуле
64. Выборочное корреляционное отношение.
Для оценки тесноты линейной корреляционной связи междупризнаками в выборке служит выборочный коэффициент
корреляции rB . Если же корреляционная связь не является
линейной, то для оценки тесноты такой корреляционной связи
вводятся другие характеристики:
yx - выборочное корреляционное отношение Y к X;
xy - выборочное корреляционное отношение Х к Y.
Выборочным корреляционным отношением Y к X называют
отношение межгруппового среднего квадратического
отклонения к общему среднему квадратическому отклонению
признака Y:
2
yx
межгруп. y x
общ.
y
nx y x Y
n
n y y Y
2
n
где n – объем выборки (сумма всех частот), n x - частота
значения х признака Х, n y - частота значения y признака Y, Y общая средняя признака Y, y x - условная средняя признака Y.
Выборочное корреляционное отношение Х к Y
определяется аналогично:
межгруп. x y
xy
общ.
x
65. Основные свойства выборочного корреляционного отношения .
1. 0 1 .2. Если 0 , то признак Y с признаком Х
корреляционной зависимостью не связан.
3. Если 1 , то признак Y связан с Х
функциональной зависимостью.
4. Выборочное корреляционное отношение не
меньше абсолютной величины выборочного
коэффициента корреляции, т.е. rB .
5. Если выборочное корреляционное отношение
равно абсолютной величине выборочного
коэффициента корреляции, то имеет место точная
линейная корреляционная зависимость. Т.е. rB ,
если , то точки M 1 x1 , y1 , M 2 x2 , y2 , …, M n xn , yn лежат
на прямой регрессии, найденной способом
наименьших квадратов.
66.
Из приведенных свойств для видно, что свозрастанием корреляционная связь между
признаками Y и Х становится более тесной и т.о.
служит мерой тесноты корреляционной связи между
признаками Y и Х любой формы ( в том числе и
линейной). В этом состоит преимущество
корреляционного отношения перед
коэффициентом корреляции rB , который оценивает
тесноту лишь линейной зависимости.
Вместе с тем, корреляционное отношение
обладает недостатком: оно не позволяет судить,
насколько близко расположены точки, найденные по
данным наблюдений, к кривой определенного вида,
например к параболе, гиперболе и т.д., что
объясняется тем, что при определении
корреляционного отношения форма связи во
внимание не принималась.
67. Нелинейная парная регрессия.
В случае если связь между Y и Х не являетсялинейной (не описывается прямой линией), это часто
можно увидеть по системе расположения
экспериментальных точек «на глаз», в других
случаях гипотезу линейной связи можно отбросить по
выполнении ряда математически действий, в этом
случае есть смысл получить по экспериментальным
данным нелинейную форму парной зависимости.
Формулу парной квадратичной регрессии будем
искать в виде:
yˆ a bx cx 2
(1)
кубической регрессии:
(2)
yˆ a bx cx 2 dx 3
68.
В случае квадратичной формы регрессии имеемn
n
F (a, b, c) yˆ yi a bxi cxi2 yi
i 1
2
i 1
2
Минимизируем сумму квадратов отклонений, имеем
или
x
i
0
x
0
F n
2
2
a
bx
cx
i
i yi
a
i 1
F n
2 a bxi cxi2 yi
b i 1
F n
2 a bxi cxi2 yi
c i 1
2
0
2
2
2
i
n
n
n
2
an b xi c xi yi
i 1
i 1
i 1
n
n
n
n
2
3
a xi b xi c xi xi yi
i 1
i 1
i 1
(3) i 1
n
n
n
n 2
3
4
a xi b xi c xi xi2 yi
i 1
i 1
i 1
i 1
69.
Система (3) – система нормальных уравнений, из которойопределяются параметры а, b и с квадратичной регрессии (1).
Для определения коэффициентов кубической парной регрессии (2)
система нормальных уравнений имеет вид:
n
n
n
n
2
3
an b xi c xi d xi yi
i 1
i 1
i 1
i 1
n
n
n
n
n
2
3
4
a xi b xi c xi d xi xi yi
i 1
i 1
i 1
i 1
i 1
n
n
n
n
n
a x 2 b x 3 c x 4 d x 5 x 2 y
i i
i i i
i
i
1
i 1
i 1
i 1
i 1
n
a x 3 b n x 4 c n x 5 d n x 6 n x 3 y
i i
i i i
i
i 1
i 1
i 1
i 1
i 1
(4)
Нетрудно составить систему нормальных уравнений для отыскания
параметров зависимостей между Y и Х любого порядка. Впрочем, для
отыскания параметров кубической и более высших порядков
уравнений регрессий недостаточно настольных калькуляторов, и
необходимо использование ЭВМ.
70. Построение нелинейных эмпирических зависимостей с использованием ортогональных полиномов Чебышева.
При аппроксимировании системы точек некоторойлинией, достаточно плотно прилегающей к системе
экспериментальных точек, можно пойти по пути
последовательного увеличения степеней
аппроксимирующих полиномов. Т.е., сначала
искать
2
“y” в виде y a0 a1 x , потом y a0 a1 x a2 x , и далее
y a0 a1 x a2 x 2 a3 x 3 и т.д. При этом до определенного
1 n n – число
момента дисперсия
где
yi f ( xi ) 2
D
l i 1
точек, l – число связей (коэффициентов)n функции
, будет уменьшаться, а затем,
f (x)в основном за счет
увеличения величины
станет возрастать.
n l
Степень аппроксимирующих полиномов следует
увеличивать до тех пор, пока D уменьшается.
Однако, повышая степень аппроксимирующих
полиномов, мы сталкиваемся с двумя
отрицательными моментами.
71.
1)Переходя от полинома низшей степени к
полиному высшей степени, мы теряем всю массу
работы затрачиваемой на отыскания
коэффициентов полинома низшей степени. Т.е.,
скажем, полином второй степени, построенный для
аппроксимации, мы полностью должны забыть и
подбирая коэффициенты для полинома третьей
степени, должны всю работу на отыскания
коэффициентов аппроксимирующего полинома
третьей степени повести с самого начала.
2)
С повышением степени аппроксимирующего
полинома мы переходим к системе линейных
уравнений относительно неизвестных
коэффициентов ( a0 , a1 , …, an ) более высокого
порядка, решение которых при сохранении
точности итоговых результатов требует удержания
все большего количества значащих цифр в
расчетном материале.
72.
Способ Чебышева позволяет значительно упроститьвычислительный процесс аппроксимации. Аппроксимирующий
многочлен строится в виде суммы повышающихся степеней,
причем добавление новых слагаемых не изменяет вычисленных
ранее коэффициентов. Прибавляя таким образом член за
членом к многочлену, можно наблюдать, как убывает остаточная
дисперсия D и такими образом облегчается процесс выбора
степени многочлена.
Требуется построить нелинейный параболический полином
степени т с числом неизвестных коэффициентов l m 1 ,
при этом, как правило, m n . В способе Чебышева
аппроксимирующий многочлен отыскивают в виде комбинации
многочленов, которые подбираются специальным образом.
Искомый многочлен записывается в виде
f ( x) a0 0 ( x) a1 1 ( x) ... am m ( x)
(1)
где
l
l 1
(2)
0 ( x) 1 , 1 ( x) x 1 , …, l ( x) x l x ... ,
где коэффициенты при старшей степени x l в i (x) равны
единице.
73.
Предположим, что многочлены (2) построены, тогда можноотыскивать значения коэффициентов a0 , a1 , …, a m. Для этого
необходимо найти минимум функции
n
n
F (a0 , a1 , ..., am ) yi f ( xi ) yi a0 0 ( xi ) a1 1 ( xi ) ... am m ( xi ) 2
i 1
что приводит к системе:
Или
2
i 1
F n
y
a
(
x
)
a
(
x
)
...
a
(
x
)
(
x
)
0 0 i
1 1 i
m m i
0 i
i
0
a
0 i 1
F n
yi a0 0 ( xi ) a1 1 ( xi ) ... am m ( xi ) 1 ( xi ) 0
a1 i 1
............................................................................................
F n
yi a0 0 ( xi ) a1 1 ( xi ) ... am m ( xi ) m ( xi ) 0
am i 1
n
n 2
n
n
x
a
x
x
a
...
x
x
a
0 i 0 0 i 1 i 1
0 i m i m yi 0 xi
i 1
i 1
i 1
i 1
n
n
n
n
x x a 2 x a ... x x a y x
0 i 1 i 0 1 i 1
1 i m i m i 1 i
i 1
i 1
i 1
i 1
.......... .......... .......... .......... .......... .......... .......... .......... .......... .......... ........
n
n
n
n
0 xi m xi a0 1 xi m xi a1 ... m2 xi a m yi m xi
i 1
i 1
i 1
i 1
(3)
74.
Решая систему (3) можно найти значения коэффициентов a0 , a1 ,…,a m . Многочлены 0 , 1, …, m следует подбирать так, чтобы
система (3) упростилась. Для этого необходимо многочлены (2)
подобрать так, чтобы
n
(4)
l xi k xi 0 , l k ,
i 1 n 2
(5)
x 0 , l 0, m .
i 1
l
i
Многочлены l x и k x , для которых выполняется условие (4)
называют ортогональными многочленами Чебышева.
При выполнений условий (4) – (5) в левой части каждого из
уравнений системы (3) останется только по одному члену и
n
система (3) примет вид
yi 0 xi
n
n 2
0 xi a0 yi 0 xi
i 1
i 1
n
n
2
1 xi a1 yi 1 xi
i 1
i 1
.....................................
n
n 2
m xi am yi m xi
i 1
i 1
a0 i 1
n
02 xi
i 1
n
yi 1 xi
a1 i 1
n
12 xi
i 1
.....................................
n
yi m xi
i 1
a m n
m2 xi
i 1
(6)
75.
Теперь следует убедиться, что условия (4) – (5) выполнимы, инайти соответствующие им выражения для ортогональных
многочленов Чебышева при заданных точках xi . Ранее мы
приняли 0 x 1. Теперь из условия (4), полагая l 0 и k 1 для
многочлена 1 x получаем
0 xi 1 xi 1 1 xi 0 xi 1 0 xi 1 0 xi n 1 0
x
(7)
i x
1
таким образом
n
1
1
xi
n
Для построения многочлена 2 x , положив в соотношении
(4) последовательно l 0 и k 2 получим систему:
1 ( x) x x x
n
0 xi 2 xi 0
i 1
n
x x 0
1 i
2 i
i
1
n
1 2 xi 0
i 1
n
x x 0
1 i
2 i
i
1
(8)
здесь 2 x - многочлен второй степени
с коэффициентом 1 при
2
старшей степени х (т.е. при x ). Будем искать его в виде
2 x x 2 1 x 2 0 x
(*)
76.
Теперь имеем2 xi xi 2 1 xi 2 0 xi xi 1 xi 2 1 xi n 2 0
2
2
x
x
x
x
x
2 1 xi 0
1 i 2 i i 1 i
2 1 i
n
Поскольку по (7) 1 ( xi ) 0 , то последняя система
i 1
перепишется в виде
n
xi 1 xi n 2 0
i 1
n
n
x x 2
1 xi 2 0
i
1
i
2
i 1
i 1
В этих соотношениях
n
n
n
i 1
i 1
i 1
xi 1 xi xi xi 1
n
2
1 xi
i 1
n
n
1 xi
i 1
n
n
n
n
i 1
i 1
i 1
i 1
xi 1 1 xi xi 1 xi 1 1 xi xi 1 xi
2
xi 1 xi
i 1
xi2
n
n
i 1
n
i 1
xi xi 1 1 xi xi2 1 xi 1 xi
i 1
xi2
n
1 xi xi 1
i 1
xi3
n
1
i 1
xi2
n
1 1 xi 1 xi .
i 1
77.
Из последней системы1
n
n
i 1
xi 1 xi
2 xi 1 xi
n
и
2 i 1n
(9)
i 1
n
n
i 1
i 1
xi 1 xi
2
n
1 xi
i 1
2
xi 1 xi
i 1
.
2
1 xi
Таким образом
n
2
n
i 1
xi3
xi2
n
1 xi ,
n
i 1
xi 1 xi
,
(10)
i 1
n
1
i 1
xi2
n
1 1 xi 1 xi
i 1
78.
Таким образом, мы построили многочлены 0 ( x) , 1 ( x) и 2 ( x) .Аналогичным образом строятся последующие многочлены 3 ( x ),
4 ( x) и т.д. Приведем здесь без доказательства рекуррентную
формулу, позволяющую любой последующий многочлен, если
известны два предыдущих:
(11)
( x) x ( x) ( x) ,
r 1
r 1
r
r 1
r 1
где
n
r 1
xi r xi
2
i 1
n
r xi
i 1
2
n
xi r 1 xi r xi
i 1
, r 1
n
r 1 xi
2
.
(12)
i 1
Формулы (*) и (9) являются частным случаем формул (11) – (12).
Используем изложенную методику применительно к
рассмотренному ранее распределению.
79.
n2
1 xi
i 1
n
n
n
n
n
i 1
i 1
i 1
i 1
xi 1 1 xi xi 1 xi 1 1 xi xi 1 xi
2
n
n
i 1
n
i 1
xi 1 xi xi xi 1 1 xi xi2 1 xi 1 xi
i 1
i 1
xi2
n
1 xi xi 1
i 1
xi3
n
1
i 1
xi2
n
1 1 xi 1 xi .
i 1
Из последней системы
n
1 n
2 xi 1 xi
n i 1
xi 1 xi
и
2
2 i 1n
1 xi
2
(9)
i 1
Таким образом
n
n
n
i 1
i 1
i 1
xi 1 xi xi2 1 xi
2
n
1 xi
i 1
n
2
xi 1 xi
i 1
n
i 1
xi3
n
xi 1 xi
i 1
n
1
i 1
xi2
n
1 1 xi 1 xi
i 1
(10)
80.
Приведем ниже без доказательства рекуррентную формулу,позволяющую любой последующий многочлен, если известны два
r 1 ( x) x r 1 r ( x) r 1 r 1 ( x)
предыдущих:
(11)
Где
n
r 1
n
2
xi r xi
xi r 1 xi r xi
i 1
n
r 1 i 1
r xi
2
n
r 1 xi
2
i 1
i 1
(12)
Формулы (*) и (9) являются частным случаем формул (11) – (12).
Используем изложенную методику применительно к рассмотренному ранее
распределению.
x
1.7
3.4
4.0
4.1
5.3
y
25
34
57
82
98
18.5
Построим на первом этапе многочлен первой степени.
1 n
18.5
1 x x 1 x xi x
x 3.70 1 x
n i 1
5
81.
Теперь аппроксимирующий полиномy f1 ( x) a0 0 ( x) a1 1 ( x) a0 1 a1 x 3.70
согласно (6)
n
n
n
yi 0 xi yi 1 yi 1 n
296
i
i 1
i 1
a0 1
y
Y
59.2
i
n
n
n
n i 1
5
2
0 xi
1
i 1
i 1
n
n
n
n
y
x
y
x
y
x
i 1 i
i i 1
i i 1 yi
i 1
i 1
i 1
n i 1
n
a1 n
n
n
2
2
1 xi xi 1 1 xi xi 1 xi 1 1 xi
i 1
i 1
i 1
i 1
i 1
n
yi xi 3.7 yi 1241 .7 3.7 296
i 1
21.23.
n
n
75
.
35
3
.
7
18
.
5
2
xi 1 xi
i 1
i 1
Теперь
Yˆx 59.2 21.23 1 ( x) 59.2 21.23 x 3.7 21.23 x 19.35
82.
окончательноYˆx 21.23 x 19.35
f1 x a0 a1 x 3.7
f1 x 5.2 21.23 x 3.7
f1 x 21.23 x 19.35
Проследим далее, как осуществляется переход от линейного полинома f1 x 21.23 x 19.35
к аппроксимирующему полиному второй степени. Здесь нам необходимо вычислить
только многочлен 2 x и коэффициент a2 :
2 x x 2 1 x 2 0 x x 2 1 x 2 x 2 x 3.7 2
где по формулам (9)
n
1 n
1 n 2
1
2 xi 1 xi xi 1 xi 75.35 3.7 18.5 1.38
n i 1
n i 1
5
i 1
n
xi 1 xi
2
2 i 1n
1 xi
i 1
2
n
i 1
xi3
n
1
i 1
n
xi2
n
1 xi 1 xi
i 1
xi 1 xi
i 1
3.14
83.
Теперь2 x x 2 1 x 2 x 3.14 x 3.7 1.38 x 2 6.84 x 10.24
Аппроксимирующий полином второго порядка теперь
y f 2 ( x) a0 0 ( x) a1 1 ( x) a2 2 ( x)
Где
yi 2 xi yi xi2 6.84 xi 10.24
n
a2 i n1
n
2 xi
i 1
2
i 1n
xi2 6.84 xi 10.24
2
46.34
4.11
11.27
i 1
Следовательно, аппроксимирующий многочлен второго порядка имеет вид
y f 2 x 59,2 21,23 1 ( x) 4,11 2 ( x) 22,74 6,88 x 4,11 x 2
(**)
Ранее найденный аппроксимирующий полином второго порядка для этой же
задачи равнялся f 2 x 22,856 6,958 x 4,12 x 2 (***). Разница
объясняется только точностью счета: при вычислениях (***) оставлялось 4
знака после запятой, а с помощью полиномов Чебышева бралась точность
двух знаков после запятой.
84.
xiyi
f1 xi
f 2 xi
yi f1 xi 2
yi f1 xi 2
1.7
25
16,74
22,92
68,21
4,33
3.4
34
52,83
46
354,57
165,33
4
57
65,57
86
73,45
15,84
4.1
82
67,69
60,98
204,78
337,75
5.3
98
93,17
63,62
23,33
13,88
101,73
724,34
D1
1
724,34 241,45
5 2
D2
1
537,13 286,57
5 3
537 ,13
85.
100Y
80
f1( x)
f2( x)
60
z
40
X
20
2
3
4
x
Рис. 13.
5
6
86. Многофакторные эмпирические зависимости.
Линейный множественныйрегрессионный анализ
При анализе результатов эксперимента часто имеет место ситуация, когда
количественное изменение изучаемого явления (функции отклика) зависит
не от одной, а от нескольких причин (факторов). При проведении
экспериментов исследователь записывает показания приборов о
состоянии функции отклика и всех факторов, от которых она зависит.
Результатами наблюдений являются уже не два столбца (столбец значений
x и столбец значений y), а матрица результатов наблюдений
y1 x11 x12 ... x1 j ... x1 p
y2 x21 x22 ... x2 j ... x2 p
..........................................................
yi xi1 xi 2 ... xij ... xip
...........................................................
y
n xn1 xn 2 ... xnj ... xnp
(1)
где n - количество опытов; p - число факторов; xij– значение j - того
фактора в i-том опыте; y i - значение функции отклика в j -том опыте.
87.
Множественный корреляционный анализ.Расчеты по степени зависимости функции отклика от того или иного
x j с вычисления
фактора по степени корреляции y с начинают
парных коэффициентов корреляции, которые характеризуют
тесноту связи между двумя величинами. В случае множественных
ситуации выполняют два типа парных коэффициентов корреляции:
1)
- коэффициенты, определяющие тесноту связи между
ryx j
функцией
отклика y и одним из факторов ;
2)
- коэффициенты, показывающие тесноту
x j связи между одним
из rфакторов
и другим фактором
x j xm
xj
xm
j, m 1, p
Парные коэффициенты корреляции вычисляются по формулам:
n
ryx j
Qx j y
Qx j Q y
x ji yi
i 1
n
1 n
x
ji yi
n i 1
i 1
2 n
2
n
n
n
1
1
2
2
x
x ji yi yi
ji
i
n i 1 i 1
n i 1
1
n
rx j x m
Qx j x m
Qx j Qx m
n
1 n
x j xm n x j xm
i 1
i 1
i 1
2 n
2
n
n
n
x2 1 x x2 1 x
j
m n m
j
i
n i 1 i 1
1
i 1
88.
Множественный нелинейный регрессивный анализ.Первый этап множественного нелинейного регрессивного анализа состоит
в получении так называемой квадратичной формы:
yˆ b0 b1 x1 b2 x2 ... b p x p b11 x12 b22 x22 ... b pp x 2p b12 x1 x2 b13 x1 x3 ...
,
,
Степень последнего уравнения можно повышать до тех пор, пока
2
уменьшается остаточная дисперсия S ост
. Начиная со второго шага,
каждому повышению степени полинома (от линейного к квадратичному, к
кубическому и т.д.) предшествует замена переменных, линеаризующие
2
переменные x1 x p 1 x22 x p 2 x32 x p 3 и т.д., после чего,
коэффициенты «расширенного» линейного полинома определяют по ранее
рассмотренным формулам.
Для практических целей ограничиваются квадратичной формой.
Другой формой проведения нелинейного регрессивного анализа является
использование так называемых «внутренних линейных» форм уравнений,
которые легко линеаризуются логарифмированием или другим
преобразованием (это формы типа тех, что были в однофакторном
x
анализе с функцией y a b , которая, будучи нелинейной, приводилась к
линейной форме с помощью логарифмирования).
Мерой тесноты связи в нелинейной зависимости служит множественное
корреляционное отношение, которое вычисляют по формуле
y yˆ
n
R 1
i 1
n
2
i
y
i 1
i
Y
2
i
89.
Метод исключения переменных.Уравнения регрессии расширяют сразу до полной квадратичной или
полной кубической формы, чему должна предшествовать
тщательная предварительная обработка результатов наблюдений,
построение линейной модели, вычисление парных и частных
коэффициентов корреляции, предварительное исключение одного из
сильно коррелированных факторов, вычисление остаточной
2 , коэффициента множественной корреляции R и Fдисперсии S ост
критерия Фишера по линейной модели.
Исключения начинают с фактора, имеющего наименьший критерий
Стьюдента. На каждом этапе (после исключения каждого фактора)
для нового уравнения регрессии вычисляют коэффициент
множественной корреляции R, остаточную дисперсию S 2 и F –
ост
критерий Фишера.
Прекращают исключение факторов:
1) когда остаточная дисперсия начнет увеличиваться;
2) назначают уровень значимости p% при вычислении t-критерия
Стьюдента для последнего оставляемого фактора.
90.
Метод включения факторов.В случае метода включения факторов, так же как и в случае метода
исключения , проводят все предварительные вычисления , кроме
расширения модели.
Основным критерием для определения порядка включения факторов
является значение частного коэффициента корреляции. Метод включения
используют в основном при построении линейных моделей или моделей
допускающих линеаризацию. Для квадратичных форм и форм высших
порядков частные коэффициенты корреляции вычислить невозможно и
для этих моделей применяют метод исключения факторов.
При проведении множественности регрессионного анализа методом
включения факторов операции на ЭВМ выполняются в следующем
порядке:
1) строится линейная модель;
2) строится матрица коэффициентов парной корреляции;
3) вычисляются частные коэффициенты корреляции;
4) вычисляются критерии служащие для оценки качества предсказания
2
результатов опыта полной линейной моделью (R, R,2 S ост
);
5) строится линейная модель с одним фактором, у которого частный
коэффициент корреляции наибольший;
2
6) вычисляются R, R 2 S ост
и для полученной в п. 5 модели
91.
Алгоритм метода исключения переменных.1. Предварительная обработка исходных данных.
2. Построение линейной многофакторной модели.
3. Проводится проверка статистической значимости факторов и
модели в целом.
4. Вычисление коэффициентов парной корреляции
5. Вычисление частных коэффициентов корреляции (ч.к.к.) и
проверка их значимости
6. Вычисление множественного коэффициента корреляции и
детерминации и проверка их значимости
7. Построение квадратичной формы
8. Ступенчатый отсев незначимых факторов
9. Выбор момента прекращения отсева.
10. Исследование окончательного уравнения регрессии.
92.
Алгоритм метода включения факторов переменных.1)– 6) из предыдущего метода.
7) Выбор первого фактора для включения в линейную модель:
yˆ b0
p
b j x j
j 1
8) Включение факторов в разных комбинациях с вычислением на
2
2 F̂
каждой ступени характеристик
, ,RR,
нового уравнения.
S ост
9) Исследование окончательного уравнения регресии.
93.
ПримерПрочность металлического сплава Y зависит от двух факторов
x1 - % содержание железа в сплаве и x2- % содержания хрома.
1. План разбивается сеткой. Находится поверхность, находится
точка оптимума на этой поверхности.
2. Движение к оптимуму методом крутого восхождения или крутого
спуска.








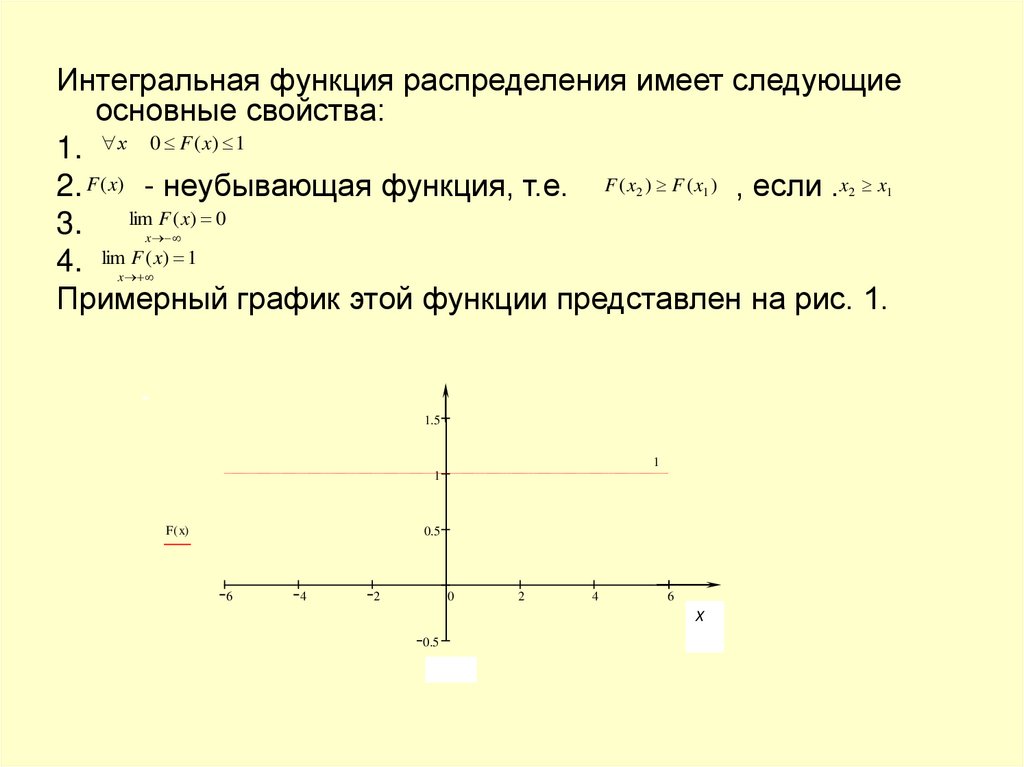













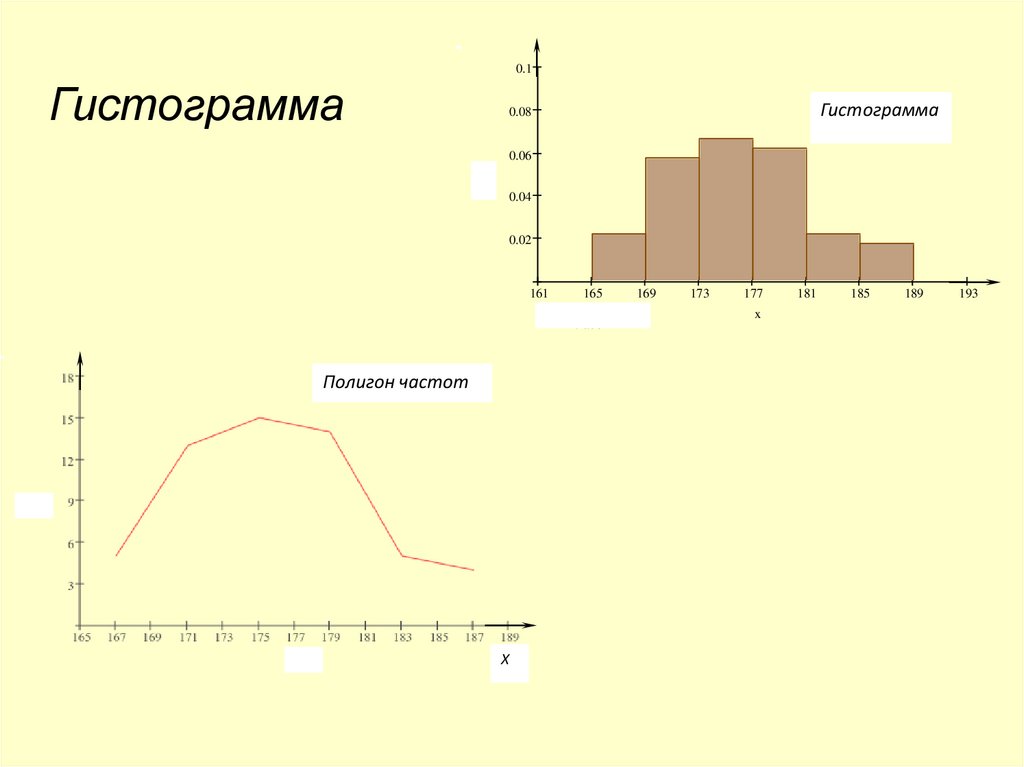
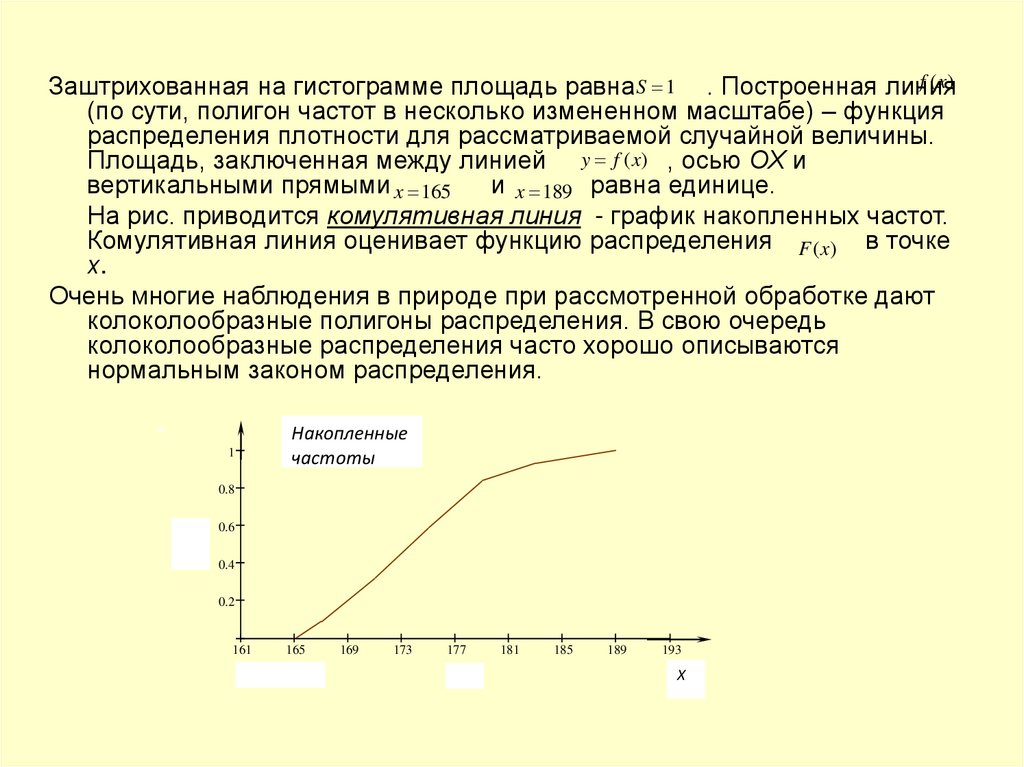








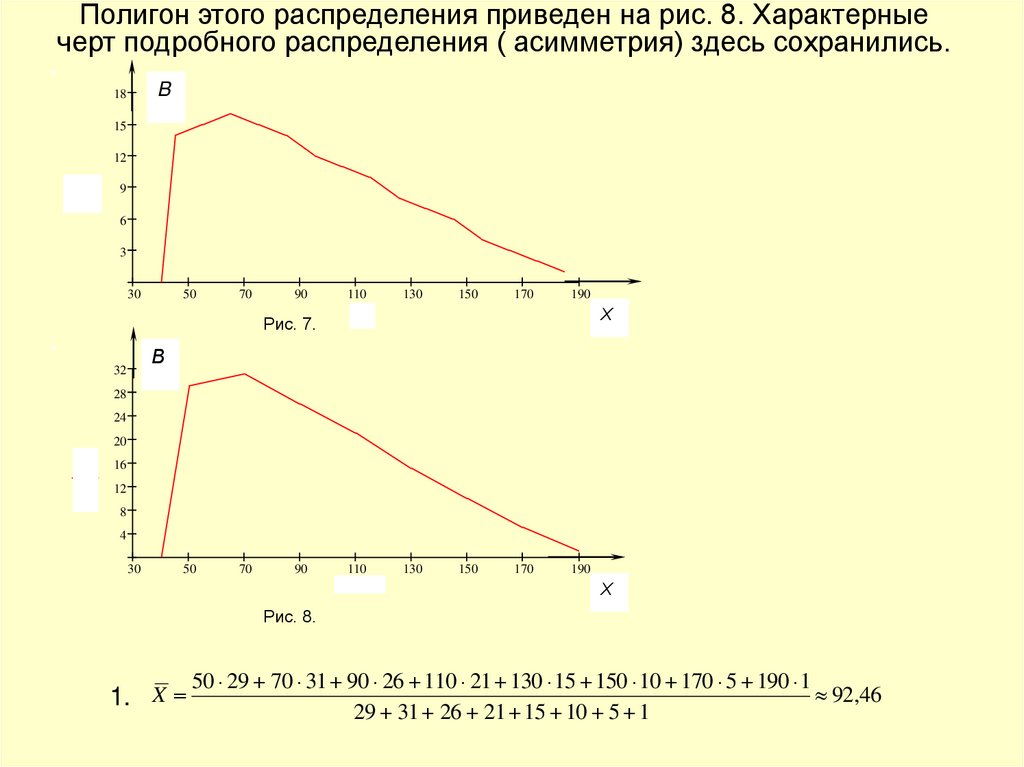

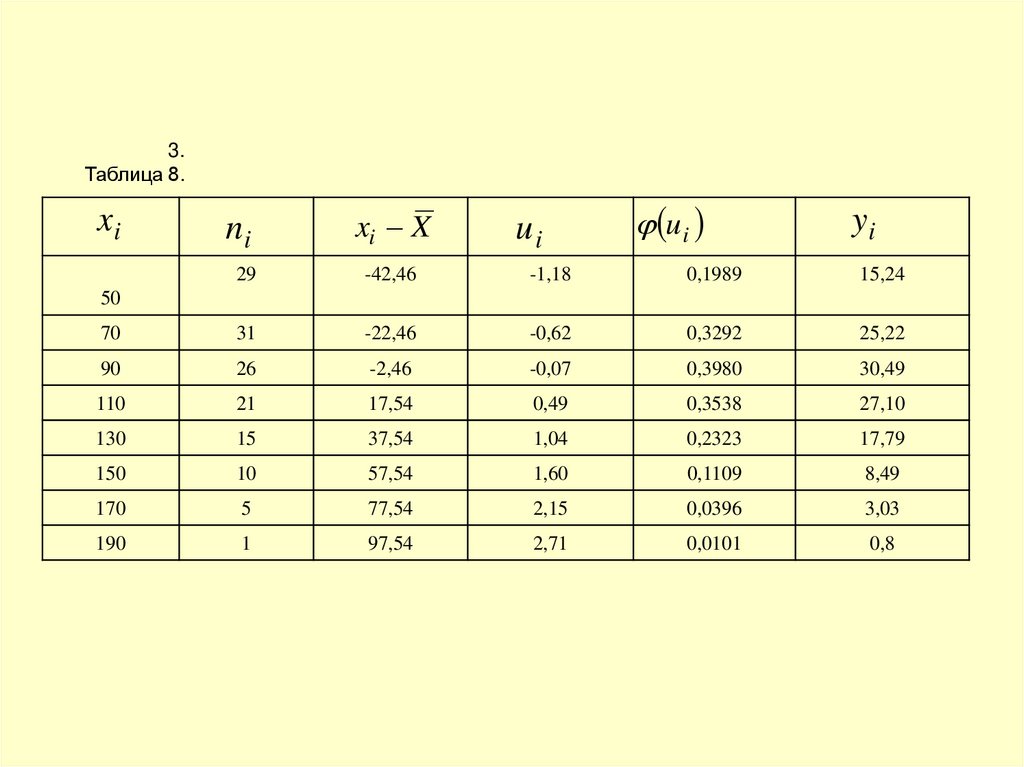
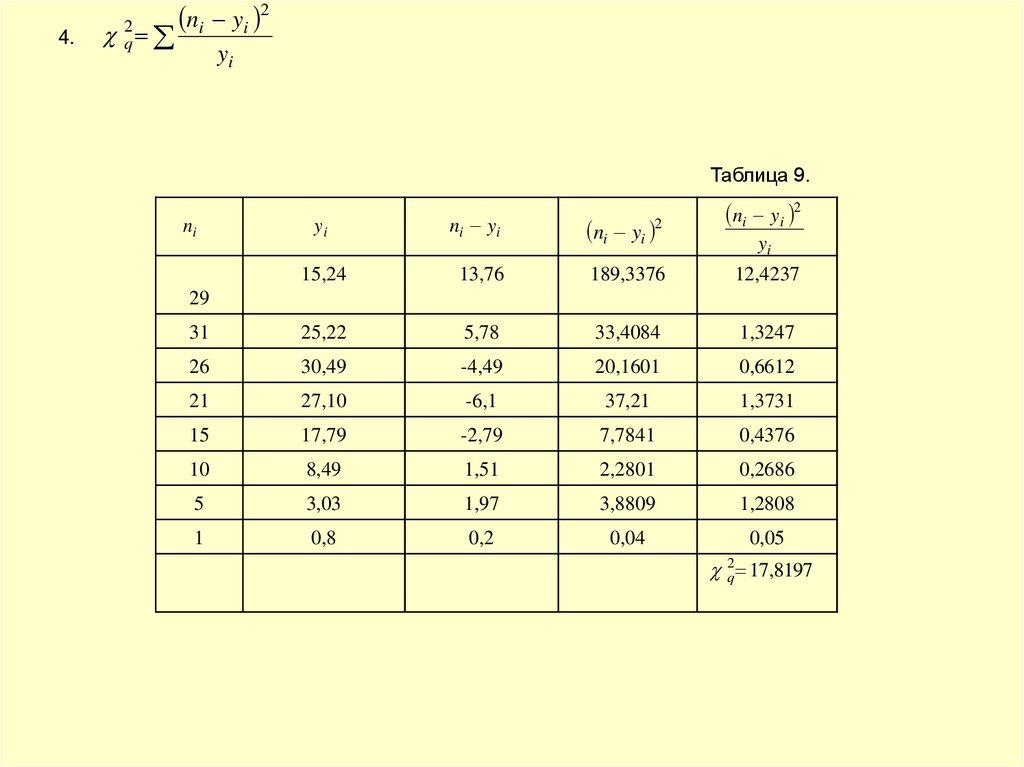

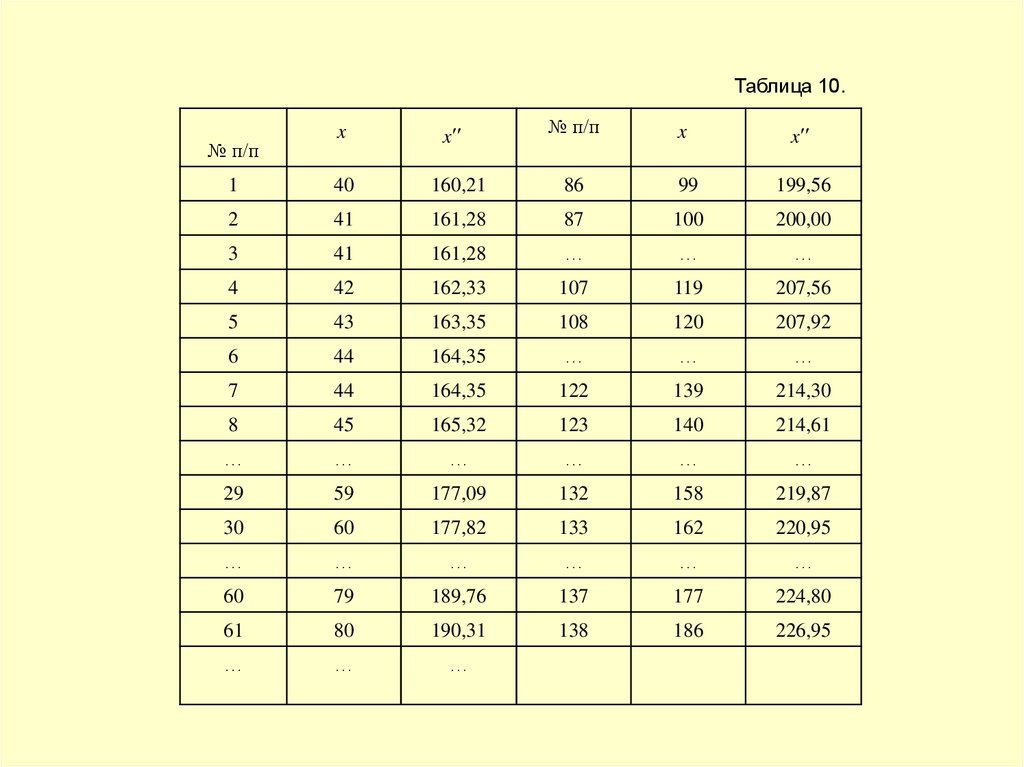
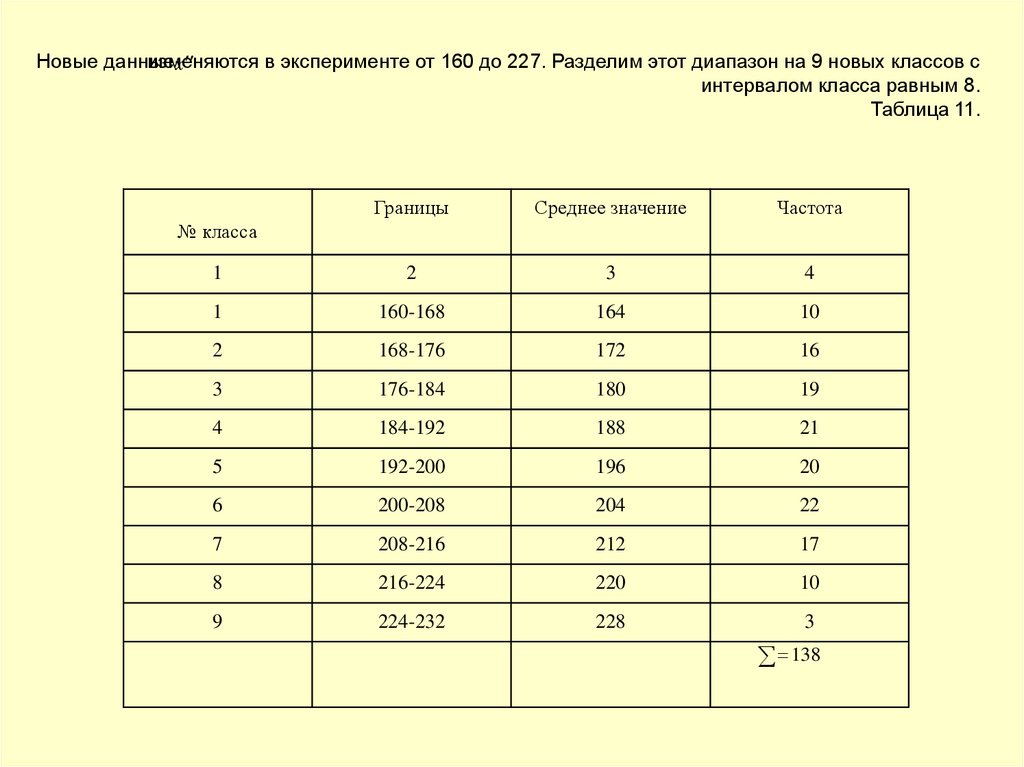

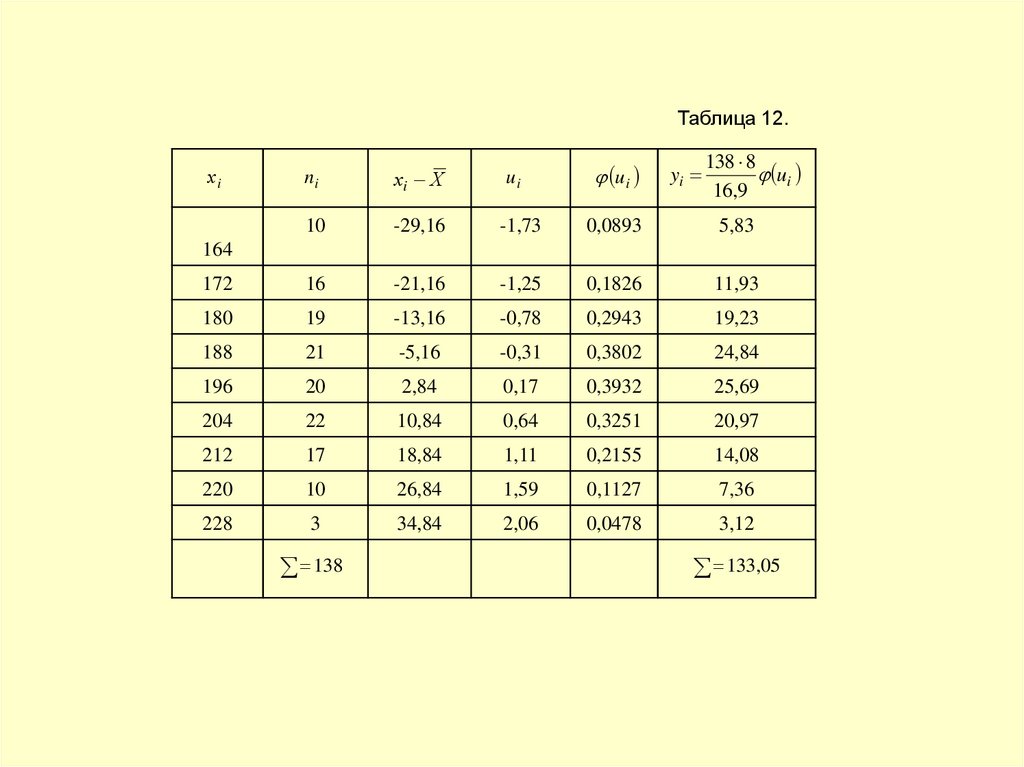
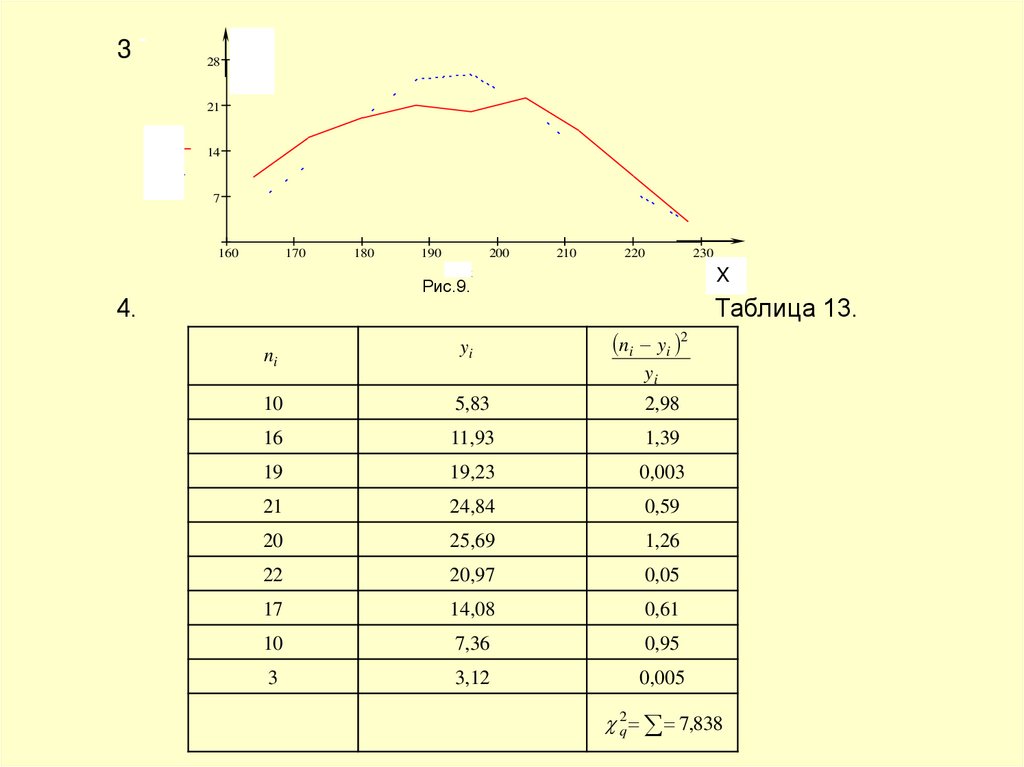





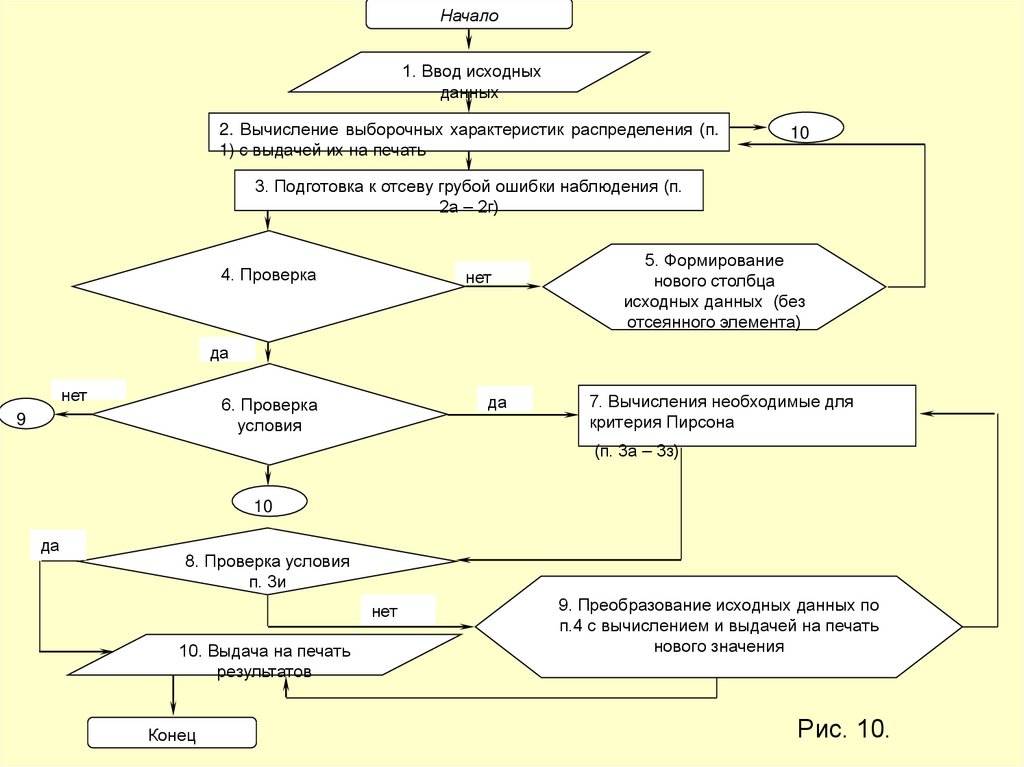





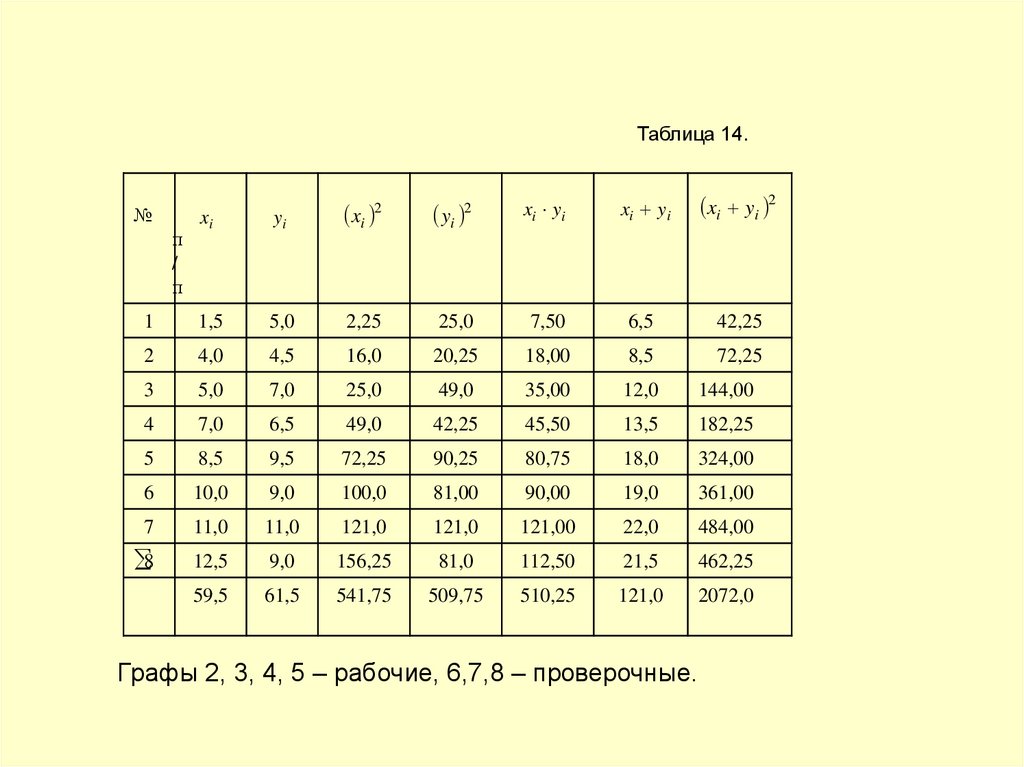

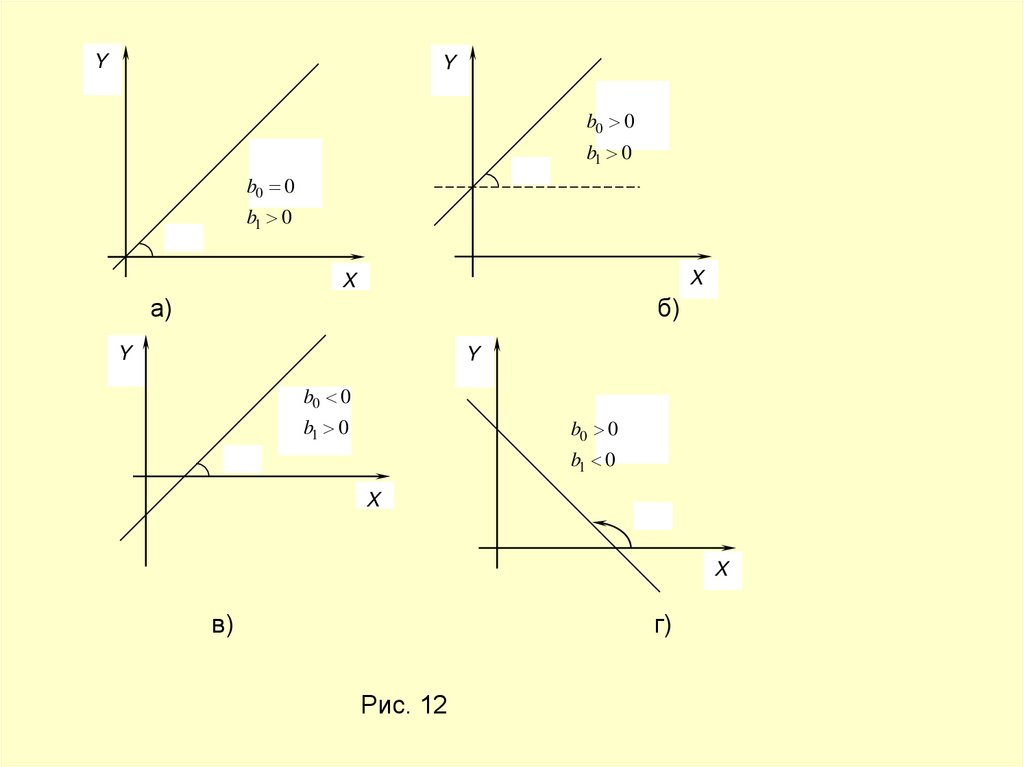



























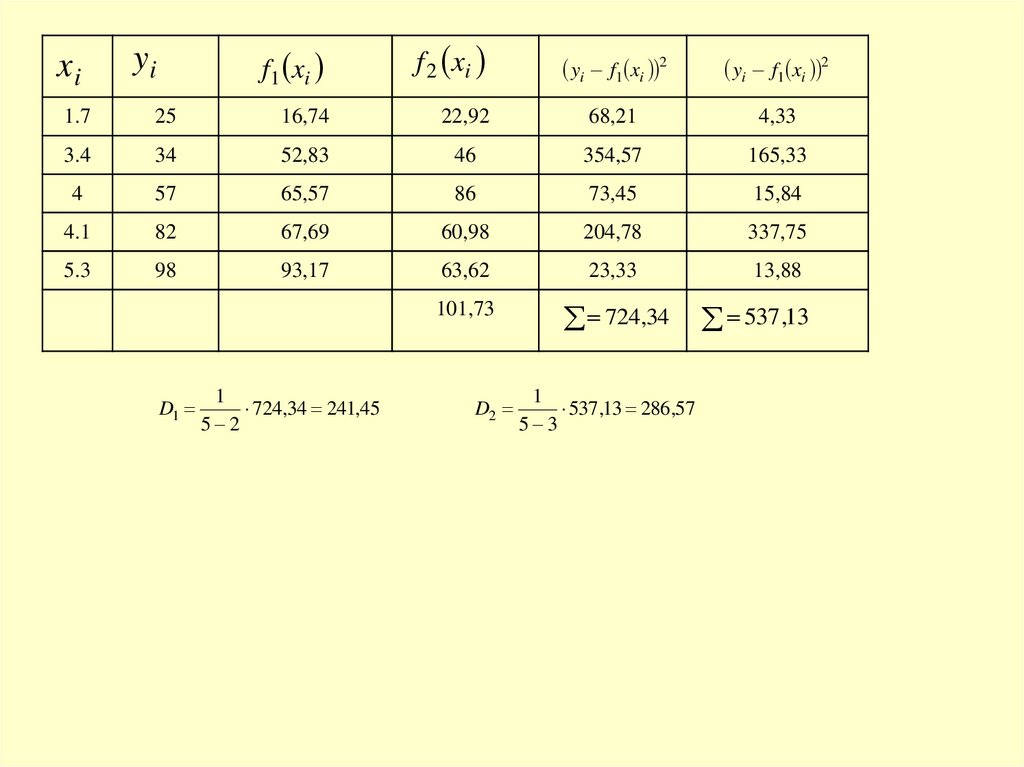
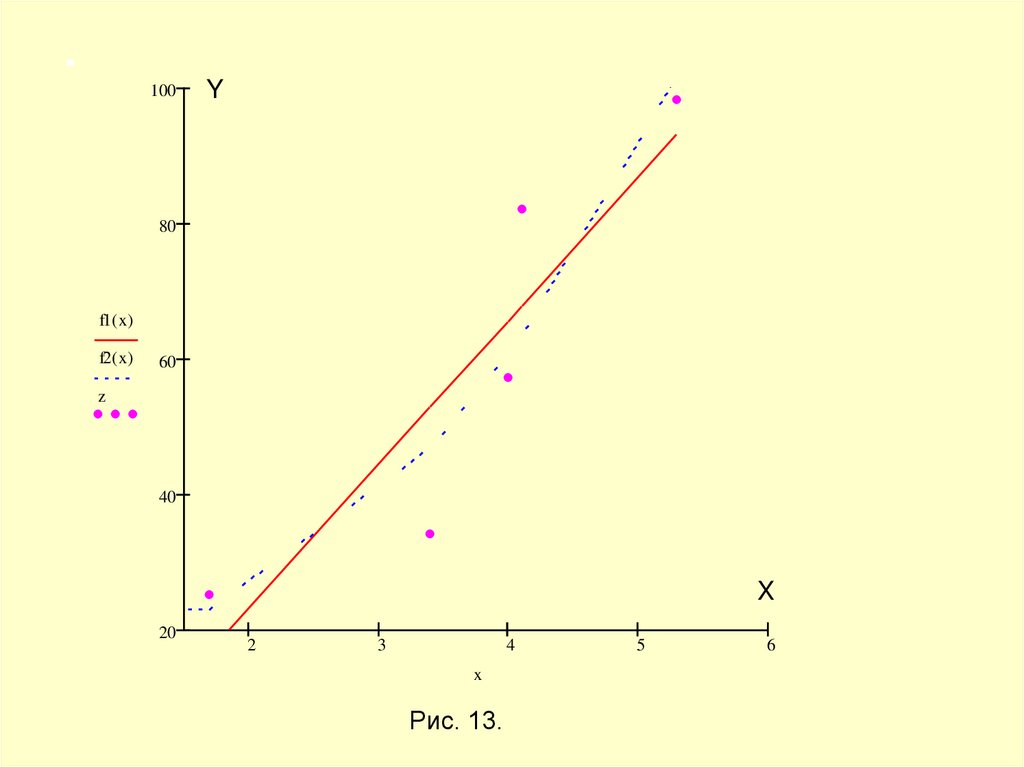








 Математика
Математика








